Explaining the puzzle via chiral-flip in -parity violating MSSM with seesaw mechanism
Abstract
We study the non-leptonic puzzle of decay in the -parity violating minimal supersymmetric standard model (RPV-MSSM) extended with the inverse seesaw mechanism. In this model, the chiral flip of sneutrinos can contribute to the observables and , that is benefit for explaining the relevant puzzle. We also find that this unique effect can engage in the - mixing. We utilize the scenario of complex couplings to fulfill the recent stringent constraint of - mixing, and examine other related bounds of -meson decays, lepton decays, neutrino data, -pole results, CP violations (CPV), etc. Besides, inspired by the new measurement of by Belle II, which shows about higher than the Standard Model (SM) prediction, we also investigate the New Physics (NP) enhancement to this observable.
1 Introduction
In recent years, series of deviations between the experimental measurements and the SM predictions have been witnessed in the context of -meson semileptonic decays, e.g. the lepton flavor universality (LFU) ratios . However, another type of LFU ratios, within the () processes, has recently been reported in agreement with SM predictions [1], and it is already erased from the anomaly list. Since the LFU violation from the NP still needs time to be confirmed, there exist U-spin related observables within rare transitions, i.e. [2], which can also be utilized to search for NP clues. The observables , defined as the ratios of longitudinal branching ratios ( versus ), are recently measured [3, 4, 5, 6, 7, 8, 9]:
| (1.1) |
showing the () pull-values corresponding to the SM predictions within QCD factorisation [2]:
| (1.2) |
This puzzle implies that there may exist new quark-flavor structure in NP. For the model-independent discussion, the Lagrangian of the low energy effective field theory is given by
| (1.3) |
where the CKM factor (). The most relevant operators for the puzzle-explanation are the given QCD penguin operators and magnetic operators [10],
| (1.4) |
where are color indices and a summation over is implied, with the vertex couplings and for . The recent global fit results [11, 2, 12] show that, for the -level, ones need the negative (positive ) with the value of , or positive (negative ) with the value of , while single positive around can only explain the tension of .
Since the recent model-independent researches throw light on the regions of Wilson coefficients, in this work, we will investigate this puzzle in a concrete NP model. Inspired by the recent research on the gluon-penguin contributions, within the -leptoquark model containing the flavor symmetry and inverse seesaw mechanism [13], we utilize the RPV-MSSM extended with the inverse seesaw mechanism (named as RPV-MSSMIS). It is worth mentioning that we had recently proposed this model to study LFU observables, i.e. and , as well as the muon anomalous magnetic moment [14, 15], and this model can provide the particular feature for different quark flavor through the -coupling texture. In this work, we find that the chiral-flip of sneutrino can make unique contributions to the Wilson coefficients , extracted from the gluon-penguin diagrams, through mainly the loop. Also, the strict constraint from the rare decay , can be relaxed by the cancellation of (this relation is induced by the model feature). In this work, we scrutinize all the one-loop gluon()-penguin diagrams of interaction to , as well as the calculations in other related processes, within the RPV-MSSMIS. Among these, we also find significant chiral-flip contribution to the - mixing, and this effect on decays. Recently, Belle II Collaboration has reported the new measurement of the branching ratio, [16], higher than the corresponding SM prediction [17] by around . As is known to all, this decaying into mode is one of the cleanest probe for NP searches due to its highly suppressed theoretical uncertainty. Here we revisit the NP contributions to the transition and discuss the enhancement effects.
This paper is organized as follows. The RPV-MSSMIS model and the theoretical calculations are in Sec. 2. Then, in Sec. 3, we scrutinize the related constraints, which are followed by numerical results and discussions in Sec. 4 and additional discussions on CPV in Sec. 5. Our conclusions are presented in Sec. 6.
2 The tension study in RPV-MSSMIS
In this section, the NP effects, especially the chiral-flip ones, are investigated in the and decays, within the RPV-MSSMIS.
2.1 RPV-MSSMIS framework
First let us briefly review the RPV-MSSMIS [14]. Here are given the superpotential and the soft supersymmetric (SUSY) breaking Lagrangian,
| (2.1) |
where the generation indices while the colour ones are omitted, and squarks (sleptons) are denoted by the symbol “”, and as for the MSSM parts, and , the reader can refer to Refs [18, 19]. All repeated indices are assumed to be summed over throughout this paper unless otherwise stated. The neutral scalar fields of the two Higgs doublet superfields, and , acquire the non-zero vacuum expectation value, i.e. and , respectively, and their mixing is expressed by .
The neutrino sector in the superpotential provides the neutrino mass spectrum at the tree level, and in the basis, the mass matrix is given by
| (2.5) |
where the Dirac mass matrix . Then ones can diagonalize through . As to the sneutrino mass square matrix in the basis, it is expressed as
| (2.9) | ||||
| (2.13) |
where the “”, as well as “”, denotes the even (odd) CP, and the mass square is regarded as the model input, with being the soft mass square of . We set while is non-negligible [20] in Eq. (2.9), which induces the mass splitting between the CP-even and CP-odd sneutrinos for the same flavor. This is different from the degenerate-mass approximation adopted in our recent researches [14, 15]444Although the quasi-degenerate-mass scenario is favored by the direct dark matter (DM) detection [21], we focus on the field of -meson processes, and given RPV is involved, DM is out of the scope of this work.. In the following sections, ones will see that this splitting-mass scenario can provide the chiral-flip contributions in some processes.
Afterwards we introduce the trilinear RPV interaction in this model. The superpotential term induces the relevant Lagrangian in the context of mass eigenstates for the down-type quarks and charged leptons, which is given by
| (2.14) |
where “” indicates the charge conjugated fermions, and the fields , , and (aligned with ) in the flavor basis have been rotated into mass eigenstates by the mixing matrices , , and , respectively. Besides, the index denotes the generation of the physical (s)neutrinos, and the three couplings are deduced as , , and . In the following, we adopt the “single-value-” assumption, i.e. both and are set negligible, and the NP Wilson coefficients are given at the scale TeV.
2.2 puzzle
In RPV-MSSMIS, the most favored operator to explain the puzzle is the magnetic one, , extracted from the gluon-penguins shown in Fig. 1. Given the recent LHC constraints which will be discussed in Sec. 3.1, we set all colored SUSY particles with masses above TeV, so the penguins engaged by squarks and gluinos contribute negligibly.
Next, we will show that, the NP Wilson coefficients and in RPV-MSSMIS can include the chiral-flip contributions, in the mass-splitting scenario mentioned in Sec.2. The coefficient , extracted from the diagrams containing sneutrinos (other suppressed contributions omitted) is given by,
| (2.15) |
and is calculated as because that in the setup of this model, the difference between diagram and one is merely . In Eq. (2.2), ones can find that the chiral-flip is contained in the first two terms containing double- couplings. If we utilize the degenerate-mass scenario, these two terms totally cancel with each other and then only the non-flip terms, are remained, which agrees with the result in Ref. [22], with the formula-sign checked. Instead, if there exists a sufficient split between the masses and for the same , the unique chiral-flip part is dominating, enhanced by logarithm terms. Here we analyse Fig. 1a qualitatively in the flavor basis to illustrate how double- terms are related to the chiral-flip. First the leading order term only contains normal couplings. When we consider the next order with the mixing of chirality for one single virtual quark, the chirality of sneutrino should also be flipped, inducing that double- couplings emerge. This situation is unique since (s)neutrino chiral-flip is forbidden in original RPV-MSSM, with Dirac neutrinos instead of Majorana ones.
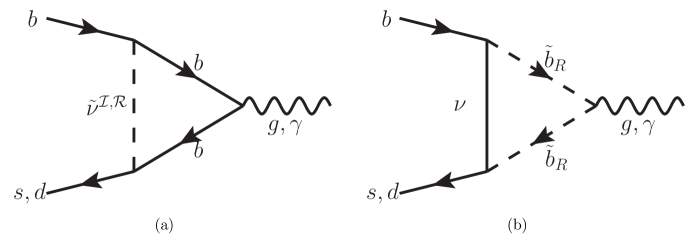
Then it is worth mentioning that we also calculate the Wilson coefficient related to the operator, , which providing the lepton flavor universal contributions to , also dominated by the loop. The result is given that,
| (2.16) |
and ones can find that, the chiral-flip part in Eq. (2.2), expressed by the double- terms, is not enhanced by logarithm terms. In the degenerate-mass scenario, the result returns to the one shown in Ref. [14]. We also examine the -penguin contribution to , and find that it is negligible in the setup of this work.
As mentioned in Sec. 1, there are divergences between the experiment data and SM results, corresponding to the non-leptonic ratios . If we consider NP is only within decays without the decays, the predictions of the ratios, , can be given by [2, 13],
| (2.17) | ||||
| (2.18) |
where the electroweak (EW) broken scale GeV. Then at level, we need to explain the non-leptonic tension. The NP in sector is constrained very strictly which will be shown in Sec. 3.2.
2.3 revisited
In this section, we revisit the processes related to the quark transition , and the corresponding effective Lagrangian is,
| (2.19) |
where the SM contribution is and the loop function with [23]. The NP contribution of vector current is [15]
| (2.20) |
Besides, the NP coefficients and express the chiral-flip contributions of neutrino with sbottoms. However, the global fit shows that, these scalar and tensor contributions are negligible, relative to the vector one [24]. For simplicity, we consider negligible mixing for the sector to omit these two coefficients.
To study the NP effects on as well as , ones can define the ratio, . In RPV-MSSMIS, we get that,
| (2.21) |
The recent Belle-II data [16] of , and the updated SM prediction [17], induce [25]. Recent research [25] shows that, the case of cannot simultaneously fulfill the Belle-II data at level as well as the upper limit [26], i.e. , at confidence level (CL). Besides, with the theoretical result for the single left-handed vector operator, it is also found that this case cannot explain the Belle-II data, without staying below the upper limit of at CL [27, 28]. In this work, we will investigate the degree of approaching to its upper limit , in the parameter space of RPV-MSSMIS.
3 The constraints
Before the numerical analysis of puzzle, the relevant experimental constraints should also be scrutinised.
3.1 Direct searches
Firstly, direct searches for SUSY particles should be considered. Since there are no signs of NP particles until the end of the LHC run II which reaching around fb-1 at the center energy TeV, which providing stringent bounds on SUSY models. The allowed masses of colored sparticles, such as gluinos, the first-two generation squarks, stops and sbottoms have been excluded up to TeV scale [29, 30, 31, 32, 33, 34, 35]. In this work, the masses of all the colored SUSY particles are set above TeV, whereas the masses of sleptons as well as the heavy neutrinos are all around GeV. Some recent experiments have pushed the upper limit of slepton masses over TeV scale [36, 37, 38], however, these searches consider nonzero related to the superpotential . Given that we only consider nonzero in the model, this bound can be relaxed . It is worth mentioning that, ATLAS has recently made searches for the NP signs of this type of model, only containing couplings [39]. Using the first collider limits for this model type, we keep GeV.
3.2 Tree-level processes
Next, we check the tree-level processes exchanging sbottoms, including , , , as well as , , and .
As ones know that the experimental measurement [40] and the SM prediction [41] induce the strong constraint, . Even for with TeV mass, there still exists the bound of . Thus, we assume negligible to avoid this bound from this process, as well as the decay.
In table 1, we collect the experimental results and SM predictions of , decays with the charged current processes, , and , as well as the processes discussed above. Following the same/analogical numerical calculations in the ordinary RPV-MSSM (see Refs. [42, 43]), we update the constraint from , as , and the bound from is negligible due to the small . We also update the calculation of the process , which provides the bound as well as . The functions , , and (see concrete definitions in Ref. [43]), are utilized to express the ratios of the measurement values versus the SM predictions for , , and , respectively, and we also consider these constraints.
As for the decay, similar to the formula in Ref. [44], the bound (here also including -loop corrections) can be shown with
| (3.1) |
where the function and express the non-unitary part of neutrino and -loop corrections to -vertex, respectively, and they are given by [15]
| (3.2) |
where is unitary PMNS-like, and the loop function with , from the dominant -loop diagram. In the inverse seesaw framework, the Hermitian can be figured out, i.e. . We can translate the bound Eq. (3.1) into at the level, with the negligible . In this work, we can set sufficiently small to keep (negative as well as ) negligible to avoid enlarging the Cabbibo anomaly [45, 46].
In RPV-MSSMIS, the neutrino mixing matrix, , is also bounded by the decaying to charged leptons and neutrinos at the tree level. However, at one-loop level, both and couplings are constrained by these decays as well as the charged lepton flavor violating (cLFV) decays. We will address decays totally in the following subsection 3.3, and before that, we can make a summary that couplings and are already set negligible (at scale), considering the constraints investigated above, and that is, NP is mainly not contained in the and sectors.
3.3 Loop-level processes
In this section illustrating loop-level bounds, we firstly investigate the mixing, which is mastered by
| (3.3) |
where the SM contribution is with the defined function , and the non-negligible NP contributions are,
| (3.4) |
where , , , and with , being or , and . The formulas of Passarino-Veltman functions [52], and , are defined as
| (3.5) |
and is given by [53], which is defined as
| (3.6) |
with the limit applied. The chiral-flip contributions are all contained in the coefficient , where the last two terms are extracted from the tree-level diagram. Combined with recent results of bag parameters, , including the new value of [54, 55], we get the ratio,
| (3.7) |
The recent result averaged by HFLAV, [56], along with the SM prediction [57], leads to the strong constraint at level. Given that the mass-splitting of sneutrinos is considered in this work, the tree-level contributions to the ratio need the cancellation to fulfill the bound.
Next we investigate the cLFV processes, i.e. , , () and . It should be stressed that the NP contributions from neutrino part, can be eliminated with the particular structures of (s)neutrino mass matrices. We utilize the structures where only chiral mixing but no flavor mixing exists for the neutrino sector involving right-handed (RH) neutrinos, as well as the whole sneutrino sector (see detailed discussions in Ref. [14] and appendix A). Then, we focus on the contributions. The branching fraction of the decay is given by [58]
| (3.8) |
where the effective couplings and , with the limit of adopted here as well as the other cLFV processes. Because is already set negligible, processes , , , , and , will not make effective bounds. Then the remained ones to be considered are and decays (see the relevant formulas in Ref. [43]), with the experimental upper limits and at CL, respectively [40].
Following the introduction of cLFV, we will mention the decay, which are mastered by the electromagnetic dipole as well as . Although the recent SM prediction ( GeV) [60], agrees very well with the recent measured branching ratio [61], which implies a very strict constraint, both contributions to this branching ratio from and can counteract each other partly, shown as [60], so RPV-MSSMIS can avoid this stringent bound, given the value of is expected around (inducing ) for explaining non-leptonic puzzle.
In the following, we move on to the purely leptonic decays of , bosons. The effective Lagrangian of -boson interaction to generic fermions is given by [62]
| (3.9) |
where and . We first investigate decay, and the relevant couplings, and . In the limit of , the corresponding branching fractions are
| (3.10) |
with -width GeV [40]. For , the branching ratio should be given by . The NP effective couplings, contributed mainly by effects, are expressed as () here and the formulas of functions are given by [42],
| (3.11) |
With the data of the partial width ratios of bosons, i.e. , and [40], we have the bound of with . And the upper limit of branching ratio, at CL [40], makes the bound .
Then we study the invisible -decays, i.e. boson interaction to neutrinos, mainly in this model. The effective number of light neutrinos , defined by [63], will constrain the relevant couplings in Eq. (3.9), via
| (3.12) |
where the coupling and the formulas of is given by [64]
| (3.13) |
Then the measurement result [63] will make constraints.
As for the purely leptonic decays of boson, they can be covered by the stronger ones from and decays. The fraction ratios of these lepton decays, i.e. , and , make the bounds [44] on the model parameters, which can be expressed as
| (3.14) |
Here we only consider the -vertex, which has the interference with the SM contribution, and the LFV-vertex and , which can be embedded in process, are omitted. With the last two formulas of Eq. (3.3) combined with , we should keep and at level.
4 Numerical analyses
In this section, we begin to analyse and numerically within the mass-splitting scenario of RPV-MSSMIS. We consider normal ordering and with the recent data of neutrino oscillation [65]. Then it can be calculated that the three light neutrinos have masses eV with [66]. The sets of model parameters are collected in table 2.
The diagonal inputs of , , , , and here can induce no flavor mixings in sneutrino sector, as well as the neutrino sector which RH neutrinos engage in, and this is benefit for fulfilling the bounds of cLFV decays. Besides, the input values shown in table 2 can induce a diagonal , which induces the mass prediction GeV, fulfilling the recent data [40]. The values of induce physical mass of the lightest sneutrino, as GeV, allowed by the relevant constraints [40] (non- and decoupled-chargino case), while the masses of charged sleptons are not affected by and they are predicted as TeV scale, which in accord with the ATLAS results discussed in section 3.1. The remained parameters, i.e. , , , and , can vary freely in the ranges considered.
| Parameters | Sets |
|---|---|
| TeV | |
| TeV |
With the inputs given above, we can get the numerical results of the Wilson coefficient and observable, which contain chiral-flip effects, as follows,
| (4.1) |
where the mass of sbottom is set as TeV. In Eq. (4), ones can see that cancellations are preferred in both the chiral-flip term and the non-flip one , because of the stringent constraints of - mixing. The chiral-flip term demands for a tuning relation between and , and at least, one of them should be imaginary. In the following, we set that (), and accordingly, the coupling is also set imaginary and approaching to , while couplings and are set real. So we can see that and are the lager ones among these values. Therefore, the Wilson coefficient , which is critical for the puzzle, is dominated by . Then, with the large and , we can get,
| (4.2) |
where is also TeV. As it is shown, even when the sbottom reach TeV scale, can still be close to , provided both and are sufficiently large. However, this case will not make non-negligible effects on the process, because the exchanging squark of its tree diagram is upper type instead, not supported by the single-value- assumption ( engaged). As for one-loop level, the NP contributions are dominated by boxes, given by [14],
| (4.3) |
Given that the cancellation in , this loop contribution is also suppressed. Besides, as mentioned in Sec. 2.2, there also contain chiral-flip effects in the result of , without the logarithmic enhancement. We find that as well as , can be up to in the allowed parameter space. However, the chiral-flip contributions are negligible. We also check the charged processes , and among them, only transition is affected by large . Utilizing Eq. (2.11) in Ref. [15], we find the related NP contribution versus SM one is about scale, which is negligible.
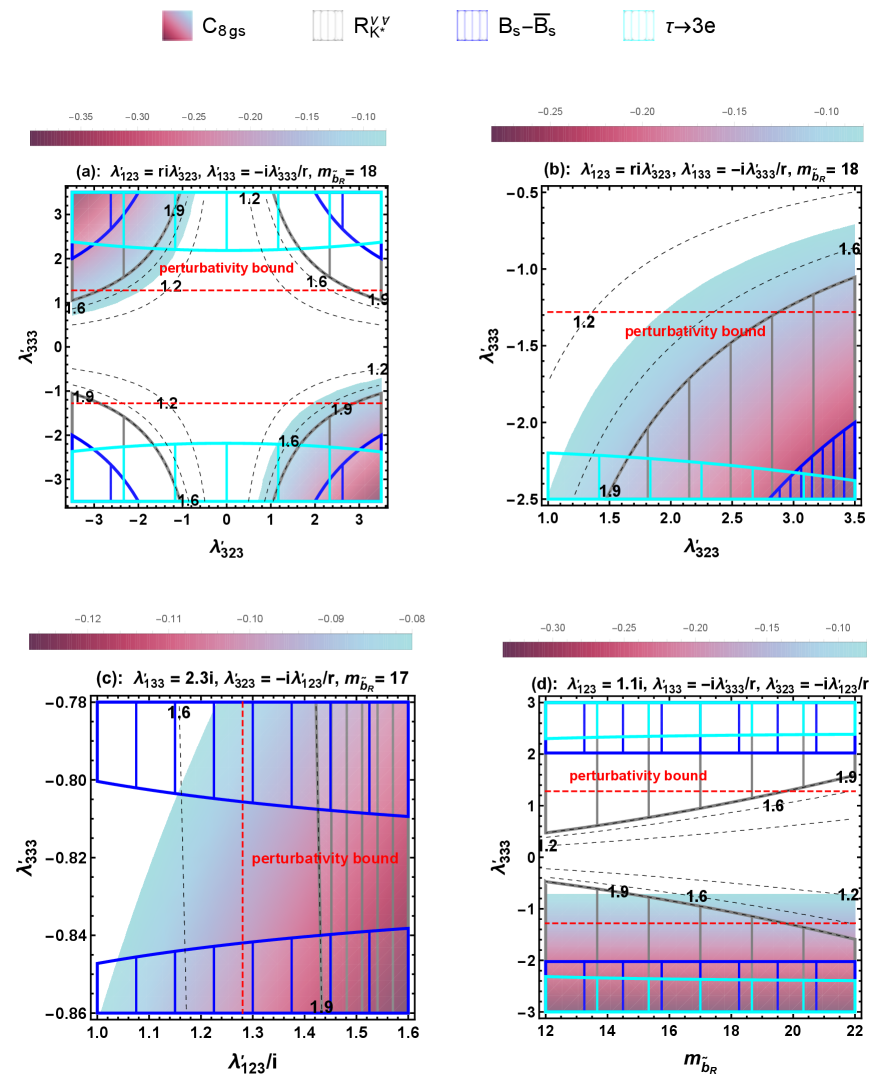
With the rough NP features above, next, we move onto the concrete numerical analysis. As shown in Fig. 2, ones can see that the puzzle can be explained in RPV-MSSMIS, at level. The decay, mixing, and decay, provide the dominant constraints, and the perturbativity limit is also shown. In Fig. 2a, and are set related to and , respectively, and is TeV. The process-bound on are mainly and decays, while nearly overlapped by the exclusion area of perturbativity bound. With the same set, Fig. 2b shows the common region in detail, which shows that should be larger than around and should be lower than around . In Fig. 2c, we set , and then, the ranges for puzzle explanation are and . In Fig. 2d, is set as , ones can see that the ratios increase with sbottom mass increasing for , while decrease with sbottom mass increasing for . The puzzle explanation favors and TeV.
| TeV | |||||||||
| TeV | |||||||||
| TeV |
5 Additional remarks
Before we conclude this work, it is worth making discussions on whether the imaginary couplings may affect CP violations. Firstly we check the NP CPV in the mixing. Given the formulas of Wilson coefficients shown in Eq. (3.3), along with flavor non-mixings in sneutrino content, the extra imaginary part , i.e. NP CPV not from CKM, can be only from the term, , containing factor . However, for light-neutrino content provides suppressing effects due to the unitarity of PMNS. In concrete numerical calculations, we confirm that this imaginary contribution can be omitted.
Next we examine the potential CPV from boson partical decay, which are proportional to ratios of the coupling constants, [68]. Given we set and both purely imaginary, while and both real, these ratios have no imaginary part.
At last, we move onto the electron electric dipole moment (EDM), that is proportional to the factor [69], where the and are the related arguments. In the scenario of this work, we have . With a suppressed non-positive , the EDM constraint can be fulfilled.
6 Conclusions
The recent measurements of show a non-leptonic puzzle, which expresses the deviations between the data and the QCD-factorisation prediction for the U-spin related observable, . Besides, Belle II has recently reported the new measurement of , around above the SM prediction. Both of the tensions imply that, there may exist new quark-flavor structure beyond the SM.
In this work, we study the non-leptonic puzzle and in RPV-MSSMIS. This NP framework connects the trilinear interaction with the (s)neutrino chirality flip to make the unique contribution to , through the gluon-penguin diagrams. The chiral-flip effects are expressed as the double- terms in the Wilson coefficient , which can be enhanced by the logarithm and make the related deviation explained. In the mixing, there also exist chiral-flip contributions, and to fulfill the strict bound of experimental data, the scenario of imaginary , with real , is adopted. The effect on the CPV due to this scenario is investigated as well. As for decays, we find that the large and , can make some enhancements, even when sbottoms are as heavy as TeV. At last, we provide some benchmark points, which also fulfill collider bounds, neutrino data, and series of flavor-physics constraints from ,-semileptonic decays, -pole data, cLFV processes, etc.
Acknowledgements
M.D. thanks Xing-Bo Yuan for valuable discussions. This work is supported in part by the National Natural Science Foundation of China under Grant No. 12275367, the Fundamental Research Funds for the Central Universities, and the Sun Yat-Sen University Science Foundation.
Appendix A The numerical form of the (s)neutrino mixing matrix
With the input set in table 2, the numerical form of the neutrino mixing matrix is listed as
| (A.10) |
which is related to the neutrino mass spectrum around TeV. And the sneutrino mixing matrices are given numerically by
| (A.20) |
related to the spectrum GeV, as well as
| (A.30) |
related to the spectrum GeV.
Then ones can find, all the chargino-sneutrino diagrams and the neutralino-slepton diagrams, among the non- diagrams in the cLFV decays of leptons, make negligible contributions due to the vanishing of flavor mixing in sneutrino sector, as shown in Eq. (A.20) and Eq. (A.30). As to -neutrino diagrams, they are always connected to terms , , and conjugate terms ( and ). Readers can see calculations of these diagrams in Ref. [70]. With the numerical form of Eq. (A.10), the and terms vanish. The term can be decomposed into two parts, and , related to the nearly degenerate heavy neutrinos and light neutrinos respectively [71]. Then ones can also find that the term makes no effective contribution to the cLFV decays. Thus, we conclude that the non- diagrams provide negligible effects on the cLFV decays, as mentioned in section 3.3, in our input sets.
References
- [1] LHCb Collaboration, R. Aaij et al., Test of lepton universality in decays, Phys. Rev. Lett. 131 (2023), no. 5 051803, [arXiv:2212.09152].
- [2] A. Biswas, S. Descotes-Genon, J. Matias, and G. Tetlalmatzi-Xolocotzi, A new puzzle in non-leptonic B decays, JHEP 06 (2023) 108, [arXiv:2301.10542].
- [3] Particle Data Group Collaboration, R. L. Workman et al., Review of Particle Physics, PTEP 2022 (2022) 083C01.
- [4] BaBar Collaboration, B. Aubert et al., Observation of K*0 * 0 and search for K*0 K*0, Phys. Rev. Lett. 100 (2008) 081801, [arXiv:0708.2248].
- [5] LHCb Collaboration, R. Aaij et al., Amplitude analysis of the decays and measurement of the branching fraction of the decay, JHEP 07 (2019) 032, [arXiv:1905.06662].
- [6] BaBar Collaboration, B. Aubert et al., Observation of and , Phys. Rev. Lett. 97 (2006) 171805, [hep-ex/0608036].
- [7] Belle Collaboration, Y. T. Duh et al., Measurements of branching fractions and direct CP asymmetries for , and decays, Phys. Rev. D 87 (2013), no. 3 031103, [arXiv:1210.1348].
- [8] Belle Collaboration, B. Pal et al., Observation of the decay , Phys. Rev. Lett. 116 (2016), no. 16 161801, [arXiv:1512.02145].
- [9] LHCb Collaboration, R. Aaij et al., Measurement of the branching fraction of the decay , Phys. Rev. D 102 (2020), no. 1 012011, [arXiv:2002.08229].
- [10] M. Beneke, G. Buchalla, M. Neubert, and C. T. Sachrajda, QCD factorization in B — pi K, pi pi decays and extraction of Wolfenstein parameters, Nucl. Phys. B 606 (2001) 245–321, [hep-ph/0104110].
- [11] M. Algueró, A. Crivellin, S. Descotes-Genon, J. Matias, and M. Novoa-Brunet, A new -flavour anomaly in : anatomy and interpretation, JHEP 04 (2021) 066, [arXiv:2011.07867].
- [12] A. Biswas, S. Descotes-Genon, J. Matias, and G. Tetlalmatzi-Xolocotzi, Optimised observables and new physics prospects in the penguin-mediated decays , JHEP 08 (2024) 030, [arXiv:2404.01186].
- [13] J. M. Lizana, J. Matias, and B. A. Stefanek, Explaining the non-leptonic puzzle and charged-current B-anomalies via scalar leptoquarks, JHEP 09 (2023) 114, [arXiv:2306.09178].
- [14] M.-D. Zheng and H.-H. Zhang, Studying the anomalies and in -parity violating MSSM framework with the inverse seesaw mechanism, Phys. Rev. D 104 (2021), no. 11 115023, [arXiv:2105.06954].
- [15] M.-D. Zheng, F.-Z. Chen, and H.-H. Zhang, Explaining anomalies of B-physics, muon and W mass in R-parity violating MSSM with seesaw mechanism, Eur. Phys. J. C 82 (2022), no. 10 895, [arXiv:2207.07636].
- [16] Belle-II Collaboration, I. Adachi et al., Evidence for decays, Phys. Rev. D 109 (2024), no. 11 112006, [arXiv:2311.14647].
- [17] D. Bečirević, G. Piazza, and O. Sumensari, Revisiting decays in the Standard Model and beyond, Eur. Phys. J. C 83 (2023), no. 3 252, [arXiv:2301.06990].
- [18] J. Rosiek, Complete Set of Feynman Rules for the Minimal Supersymmetric Extension of the Standard Model, Phys. Rev. D 41 (1990) 3464.
- [19] J. Rosiek, Complete set of Feynman rules for the MSSM: Erratum, hep-ph/9511250.
- [20] V. De Romeri, K. M. Patel, and J. W. Valle, Inverse seesaw mechanism with compact supersymmetry: Enhanced naturalness and light superpartners, Phys. Rev. D 98 (2018), no. 7 075014, [arXiv:1808.01453].
- [21] H. An, P. S. B. Dev, Y. Cai, and R. N. Mohapatra, Sneutrino Dark Matter in Gauged Inverse Seesaw Models for Neutrinos, Phys. Rev. Lett. 108 (2012) 081806, [arXiv:1110.1366].
- [22] T. Besmer and A. Steffen, R-parity violation and the decay b — s gamma, Phys. Rev. D 63 (2001) 055007, [hep-ph/0004067].
- [23] A. J. Buras, J. Girrbach-Noe, C. Niehoff, and D. M. Straub, decays in the Standard Model and beyond, JHEP 02 (2015) 184, [arXiv:1409.4557].
- [24] C. S. Kim, D. Sahoo, and K. N. Vishnudath, Searching for signatures of new physics in to distinguish between Dirac and Majorana neutrinos, Eur. Phys. J. C 84 (2024), no. 9 882, [arXiv:2405.17341].
- [25] X.-G. He, X.-D. Ma, and G. Valencia, Revisiting models that enhance in light of the new Belle II measurement, Phys. Rev. D 109 (2024), no. 7 075019, [arXiv:2309.12741].
- [26] Belle Collaboration, J. Grygier et al., Search for decays with semileptonic tagging at Belle, Phys. Rev. D 96 (2017), no. 9 091101, [arXiv:1702.03224]. [Addendum: Phys.Rev.D 97, 099902 (2018)].
- [27] B.-F. Hou, X.-Q. Li, M. Shen, Y.-D. Yang, and X.-B. Yuan, Deciphering the Belle II data on decay in the (dark) SMEFT with minimal flavour violation, JHEP 06 (2024) 172, [arXiv:2402.19208].
- [28] F.-Z. Chen, Q. Wen, and F. Xu, Correlating and flavor anomalies in SMEFT, Eur. Phys. J. C 84 (2024), no. 10 1012, [arXiv:2401.11552].
- [29] ATLAS Collaboration, M. Aaboud et al., Search for B-L R -parity-violating top squarks in =13 TeV pp collisions with the ATLAS experiment, Phys. Rev. D 97 (2018), no. 3 032003, [arXiv:1710.05544].
- [30] CMS Collaboration, A. M. Sirunyan et al., Search for long-lived particles decaying into displaced jets in proton-proton collisions at 13 TeV, Phys. Rev. D 99 (2019), no. 3 032011, [arXiv:1811.07991].
- [31] ATLAS Collaboration, M. Aaboud et al., Search for heavy charged long-lived particles in the ATLAS detector in 36.1 fb-1 of proton-proton collision data at TeV, Phys. Rev. D 99 (2019), no. 9 092007, [arXiv:1902.01636].
- [32] ATLAS Collaboration, G. Aad et al., Search for long-lived, massive particles in events with a displaced vertex and a muon with large impact parameter in collisions at TeV with the ATLAS detector, Phys. Rev. D 102 (2020), no. 3 032006, [arXiv:2003.11956].
- [33] ATLAS Collaboration, G. Aad et al., Search for R-parity-violating supersymmetry in a final state containing leptons and many jets with the ATLAS experiment using proton–proton collision data, Eur. Phys. J. C 81 (2021), no. 11 1023, [arXiv:2106.09609].
- [34] CMS Collaboration, A. M. Sirunyan et al., Search for top squark production in fully-hadronic final states in proton-proton collisions at 13 TeV, Phys. Rev. D 104 (2021), no. 5 052001, [arXiv:2103.01290].
- [35] CMS Collaboration, A. Tumasyan et al., Combined searches for the production of supersymmetric top quark partners in proton–proton collisions at , Eur. Phys. J. C 81 (2021), no. 11 970, [arXiv:2107.10892].
- [36] ATLAS Collaboration, M. Aaboud et al., Search for supersymmetry in events with four or more leptons in TeV collisions with ATLAS, Phys. Rev. D 98 (2018), no. 3 032009, [arXiv:1804.03602].
- [37] ATLAS Collaboration, M. Aaboud et al., Search for lepton-flavor violation in different-flavor, high-mass final states in collisions at TeV with the ATLAS detector, Phys. Rev. D 98 (2018), no. 9 092008, [arXiv:1807.06573].
- [38] ATLAS Collaboration, G. Aad et al., Search for supersymmetry in events with four or more charged leptons in of TeV collisions with the ATLAS detector, JHEP 07 (2021) 167, [arXiv:2103.11684].
- [39] ATLAS Collaboration, G. Aad et al., Search for heavy Higgs bosons with flavour-violating couplings in multi-lepton plus b-jets final states in pp collisions at 13 TeV with the ATLAS detector, JHEP 12 (2023) 081, [arXiv:2307.14759].
- [40] Particle Data Group Collaboration, S. Navas et al., Review of particle physics, Phys. Rev. D 110 (2024), no. 3 030001.
- [41] J. Aebischer, J. Kumar, P. Stangl, and D. M. Straub, A Global Likelihood for Precision Constraints and Flavour Anomalies, Eur. Phys. J. C 79 (2019), no. 6 509, [arXiv:1810.07698].
- [42] K. Earl and T. Grégoire, Contributions to Anomalies from -Parity Violating Interactions, JHEP 08 (2018) 201, [arXiv:1806.01343].
- [43] Q.-Y. Hu, Y.-D. Yang, and M.-D. Zheng, Revisiting the -physics anomalies in -parity violating MSSM, Eur. Phys. J. C 80 (2020), no. 5 365, [arXiv:2002.09875].
- [44] D. Bryman, V. Cirigliano, A. Crivellin, and G. Inguglia, Testing Lepton Flavor Universality with Pion, Kaon, Tau, and Beta Decays, arXiv:2111.05338.
- [45] A. M. Coutinho, A. Crivellin, and C. A. Manzari, Global Fit to Modified Neutrino Couplings and the Cabibbo-Angle Anomaly, Phys. Rev. Lett. 125 (2020), no. 7 071802, [arXiv:1912.08823].
- [46] M. Blennow, P. Coloma, E. Fernández-Martínez, and M. González-López, Right-handed neutrinos and the CDF II anomaly, Phys. Rev. D 106 (2022), no. 7 073005, [arXiv:2204.04559].
- [47] LHCb Collaboration, R. Aaij et al., Search for the rare decay , Phys. Lett. B 725 (2013) 15–24, [arXiv:1305.5059].
- [48] LHCb Collaboration, R. Aaij et al., Search for Rare Decays of D0 Mesons into Two Muons, Phys. Rev. Lett. 131 (2023), no. 4 041804, [arXiv:2212.11203].
- [49] Belle Collaboration, N. Tsuzuki et al., Search for lepton-flavor-violating decays into a lepton and a vector meson using the full Belle data sample, JHEP 06 (2023) 118, [arXiv:2301.03768].
- [50] S. Nandi, S. K. Patra, and A. Soni, Correlating new physics signals in with , arXiv:1605.07191.
- [51] Q.-Y. Hu, X.-Q. Li, Y. Muramatsu, and Y.-D. Yang, R-parity violating solutions to the anomaly and their GUT-scale unifications, Phys. Rev. D99 (2019), no. 1 015008, [arXiv:1808.01419].
- [52] G. Passarino and M. J. G. Veltman, One Loop Corrections for e+ e- Annihilation Into mu+ mu- in the Weinberg Model, Nucl. Phys. B160 (1979) 151–207.
- [53] A. Denner, Techniques for calculation of electroweak radiative corrections at the one loop level and results for W physics at LEP-200, Fortsch. Phys. 41 (1993) 307–420, [arXiv:0709.1075].
- [54] R. J. Dowdall, C. T. H. Davies, R. R. Horgan, G. P. Lepage, C. J. Monahan, J. Shigemitsu, and M. Wingate, Neutral B-meson mixing from full lattice QCD at the physical point, Phys. Rev. D 100 (2019), no. 9 094508, [arXiv:1907.01025].
- [55] J. T. Tsang and M. Della Morte, B-physics from lattice gauge theory, Eur. Phys. J. ST 233 (2024), no. 2 253–270, [arXiv:2310.02705].
- [56] HFLAV Collaboration, Y. S. Amhis et al., Averages of b-hadron, c-hadron, and -lepton properties as of 2021, Phys. Rev. D 107 (2023), no. 5 052008, [arXiv:2206.07501].
- [57] J. Albrecht, F. Bernlochner, A. Lenz, and A. Rusov, Lifetimes of b-hadrons and mixing of neutral B-mesons: theoretical and experimental status, Eur. Phys. J. ST 233 (2024), no. 2 359–390, [arXiv:2402.04224].
- [58] A. de Gouvea, S. Lola, and K. Tobe, Lepton flavor violation in supersymmetric models with trilinear R-parity violation, Phys. Rev. D63 (2001) 035004, [hep-ph/0008085].
- [59] D. Buttazzo, A. Greljo, G. Isidori, and D. Marzocca, B-physics anomalies: a guide to combined explanations, JHEP 11 (2017) 044, [arXiv:1706.07808].
- [60] M. Misiak, A. Rehman, and M. Steinhauser, Towards at the NNLO in QCD without interpolation in mc, JHEP 06 (2020) 175, [arXiv:2002.01548].
- [61] HFLAV Collaboration, Y. S. Amhis et al., Averages of b-hadron, c-hadron, and -lepton properties as of 2018, Eur. Phys. J. C 81 (2021), no. 3 226, [arXiv:1909.12524].
- [62] P. Arnan, D. Becirevic, F. Mescia, and O. Sumensari, Probing low energy scalar leptoquarks by the leptonic and couplings, JHEP 02 (2019) 109, [arXiv:1901.06315].
- [63] ALEPH, DELPHI, L3, OPAL, SLD, LEP Electroweak Working Group, SLD Electroweak Group, SLD Heavy Flavour Group Collaboration, S. Schael et al., Precision electroweak measurements on the resonance, Phys. Rept. 427 (2006) 257–454, [hep-ex/0509008].
- [64] M.-D. Zheng, F.-Z. Chen, and H.-H. Zhang, The -vertex corrections to W-boson mass in the R-parity violating MSSM, AAPPS Bull. 33 (2023), no. 1 16, [arXiv:2204.06541].
- [65] I. Esteban, M. Gonzalez-Garcia, M. Maltoni, T. Schwetz, and A. Zhou, The fate of hints: updated global analysis of three-flavor neutrino oscillations, JHEP 09 (2020) 178, [arXiv:2007.14792].
- [66] J. S. Alvarado and R. Martinez, PMNS matrix in a non-universal extension to the MSSM with one massless neutrino, arXiv:2007.14519.
- [67] LHCb Collaboration, R. Aaij et al., Amplitude analysis of decays, JHEP 06 (2019) 114, [arXiv:1902.07955].
- [68] R. Barbier et al., R-parity violating supersymmetry, Phys. Rept. 420 (2005) 1–202, [hep-ph/0406039].
- [69] R. Adhikari and G. Omanovic, LSND, solar and atmospheric neutrino oscillation experiments, and R-parity violating supersymmetry, Phys. Rev. D 59 (1999) 073003.
- [70] A. Abada, M. E. Krauss, W. Porod, F. Staub, A. Vicente, and C. Weiland, Lepton flavor violation in low-scale seesaw models: SUSY and non-SUSY contributions, JHEP 11 (2014) 048, [arXiv:1408.0138].
- [71] J. Chang, K. Cheung, H. Ishida, C.-T. Lu, M. Spinrath, and Y.-L. S. Tsai, A supersymmetric electroweak scale seesaw model, JHEP 10 (2017) 039, [arXiv:1707.04374].