Explaining Off-Policy Actor-Critic From A Bias-Variance Perspective

Consider an infinite-horizon Markov Decision Process (MDP) $\langle\mathcal{S},~{}\mathcal{A},~{}T,~{}r,~{}\gamma\rangle,$ where $\mathcal{S},~{}\mathcal{A}$ are finite-dimensional continuous state and action spaces, $r(s,a)$ is a deterministic reward function, $\gamma\in(0,1)$ is the discount factor, and $T(s^{\prime}|s,a)$ is the state transition density; i.e., the density of the next state $s^{\prime}$ given the current state and action $(s,a).$ Given an initial state distribution $\rho_{0},$ the objective of RL is to find a policy $\pi$ that maximizes the $\gamma$-discounted cumulative reward when the actions along the trajectory follow $\pi$:

Let $\rho_{i}(s|\rho_{0},~{}\pi,~{}T)$ be the state distribution under $\pi$ at trajectory step $i$. Define the normalized state occupancy measure by

Ideally, the maximization in (1) is achieved using a parameterized policy $\pi_{\theta}$ and policy gradient updates with (Sutton et al., 1999; Silver et al., 2014):

Here $\rho^{\pi_{\theta}}_{\rho_{0}}(s,a)=\rho^{\pi_{\theta}}_{\rho_{0}}(s)\pi_{\theta}(a|s)$ is given in (2), and $Q^{\pi_{\theta}}$ is the Q function under policy $\pi_{\theta}$:

Off-policy RL estimates $Q^{\pi}$ by approximating the solution of the Bellman fixed-point equation:

It is well-known that $Q^{\pi}$ is the unique fixed point of the Bellman operator $\mathcal{B}^{\pi}$. Hence if $(B^{\pi}\hat{Q})(s,a)\approx\hat{Q}(s,a),$ then $\hat{Q}$ may be a “good” estimate of $Q^{\pi}$. In the next subsection, we will see that an off-policy actor-critic algorithm encourages this to hold for the replay buffer.

We study an off-policy actor-critic algorithm of the form shown in Alg. 1.

In line 2, for episode index $e$, $\pi^{e}$ samples one trajectory of length $L.$ The transitions in this trajectory are then added to the replay buffer. Since the policies for different episodes are distinct, the collection of transitions in the replay buffer are generally inconsistent with the current policy.

Line 3 is a supervised learning that minimizes the Bellman error of $\hat{Q}$, making $(\mathcal{B}^{\pi^{e}}\hat{Q})(s,a)\approx\hat{Q}(s,a)$ for $(s,a)$ in the replay buffer. When this holds, we will prove that the “distance” between $\hat{Q}$ and $Q^{\pi^{e}}$ become smaller over the replay buffer. This is a crucial step for line 4 to be truly useful. In line 4, $Q^{\pi^{e}}$ is replaced by $\hat{Q}$, and the policy is updated accordingly.

In practice, line 3 is replaced by gradient-descent-based mini-batch updates (Fujimoto et al., 2018; Haarnoja et al., 2018). For example, $\phi\leftarrow\phi-\alpha\nabla J(\hat{Q}_{\phi})$ with $\phi$ and $J(\hat{Q}_{\phi})$ being the parameter and the Bellman error of $\hat{Q},$ respectively. In section 5.2, we show that a uniform-weighted mini-batch sampling biases learning towards older samples; this motivates the need for a countermeasure.

Note that Alg. 1 seems to be inconsistent in the horizon because the Q function, Eq. (4), is defined in the infinite horizon but the trajectories are finite-length. In Corollary 1, we will address this inconsistency by approximating the Q function using finite-length trajectories.

Although Alg. 1 doesn’t have a fixed behavior policy, in Lemma 1, we construct a non-stationary policy that generates the averaged occupancy measure at every step. This describes the averaged-over-episode behavior at every trajectory step $i$ of the historical trajectory $\{(s_{i}^{e},a_{i}^{e})\}_{i,e=0,1}^{L-1,N}$. We hence define it to be our behavior policy and use it as a reference when analyzing Alg. 1.

The construction is as follows. Denote the state distribution at trajectory step $i$ in episode $e$ as $\rho_{i}^{e}(s)=\rho_{i}(s|\rho_{0},~{}\pi^{e},T)$. By Eq. (2), $\rho_{\rho_{0}}^{\pi^{e}}$ is the state occupancy measure generated by $(\rho_{0},\pi^{e},T)$. Intuitively, $\rho_{\rho_{0}}^{\pi^{e}}$ describes the discounted state distribution starting at trajectory step 0 in episode $e$.

More generally, define $\rho^{\pi^{e}}_{\rho_{i}^{e}}$ as the state occupancy measure generated by $(\rho_{i}^{e},\pi^{e},T)$. Then, $\rho^{\pi^{e}}_{\rho_{i}^{e}}$ describes the discounted state distribution starting at trajectory step $i$ in episode $e$.

Since Alg. 1 considers trajectories from all episodes, the average-over-episodes distribution $N^{-1}\sum_{e}\rho_{\rho_{i}^{e}}^{\pi^{e}}$ is of interest. It describes the averaged-discounted state distribution at trajectory step $i$ over all episodes.

Observe that the Q function, Eq. (4), is defined on infinite-length trajectories while the errors, Eq. (7), are evaluated on length-$L$ trajectories. Discounting makes it possible to approximate the Q functions using finite-length $L$. To approximate the Q function at trajectory step $i$ up to a constant error, we need samples at least to step $i+\Omega((1-\gamma)^{-1})$. Hence, we first prove the main theorem with $i=0$ and $L=\infty$. Then, we generalize the result to $i\geq 0$ and finite $L$ in Corollary 1.

Theorem 1 expresses the error of $\hat{Q}$ as the sum of Bellman error, bias, and variance terms. To be more specific, the first two terms are understood as the “variance from sampling” because these decrease in the number of episodes $N$. On the other hand, $W_{1}^{0,\infty}$ is the “policy mismatch bias” w.r.t. $\pi^{N}$. Because the behavior policy $\pi_{0}^{D}$ is a mixture of the historical policies $\{\pi^{e}\}_{e=1}^{N},$ Eq. (6), we expect it to increase in $N$ until $\pi^{N}$ begins to converge.

Theorem 1 only indicates the difference between $\hat{Q}$ and $Q^{\pi^{N}}$ at $i=0$ and infinite-length trajectories. We can generalize it to $i\geq 0$ and finite-length trajectories as follows. Recall from Eq. (6) and Lemma 1, the average state distribution at the $i$-th step, $\overline{\rho}_{i},$ and the behavior policy at the $i$-th step, $\pi^{D}_{i},$ generate the average state occupancy measure, i.e., $\rho_{\overline{\rho}_{i}}^{\pi^{D}_{i}}=N^{-1}\sum_{e=1}^{N}\rho_{\rho_{i}^{e}}^{\pi^{e}}~{}a.e.$ Therefore, by restricting attention to the states sampled at time steps $i,i+1,\dots$ the “initial state distribution” and the behavior policy become $\overline{\rho}_{i}$ and $\pi^{D}_{i}$, which generalizes Theorem 1 from $i=0$ to $i\geq 0$. In addition, due to $\gamma$-discounting, we may use length-$L$ trajectories to approximate infinite-length ones, provided that $L\geq i+\Omega((1-\gamma)^{-1})$. These observations lead to the following corollary.

Note that if $i=0$ and $L=\infty,$ Corollary 1 is identical to Theorem 1. Because the Bellman error of $\hat{Q}$ and the bias of the policy are both evaluated using the averaging-discounted operator $\tilde{E}_{i}^{L}$, Corollary 1 implies the difference of $\hat{Q}$ and $Q^{\pi^{N}}$ at trajectory step $i$ mainly depends on states at trajectory steps $\geq i$. Since the Q function is a discounted sum of rewards from the current step to the future, the error at step $i$ should mainly depend on the steps $\geq i$.

In Wang and Ross (2019), the authors use a length-$K$ trajectory ($K$ may differ across episodes) and perform $K$ updates. In the $k$-th ($1\leq k\leq K$) update, a mini-batch is sampled uniformly from the most recent $c_{k}=\max(N_{0}\eta^{k\frac{L_{0}}{K}},c_{\min})$ samples, where $N_{0}$ is the current size of the replay buffer, $L_{0}$ is the maximum horizon of the environment, $\eta$ is the decay parameter, and $c_{\min}$ is the minimum coverage of the sampling. For MuJoCo (Todorov et al., 2012) environments, the paper suggests the values: $(L_{0},~{}\eta,~{}c_{\min})=(1000,~{}0.996,~{}5000)$. One can see that $\eta=1$ does a uniform weighting over the replay buffer, and the emphasis on the recent data becomes larger as $\eta$ becomes smaller. To see how the ERE strategy affects the mini-batch sampling, we prove the following result.

Note that Prop. 1 holds for $\eta\neq 1$ because it is derived from the geometric series formula: $(1-\eta^{n})/(1-\eta)$, which is valid when $\eta\neq 1$. Despite this discontinuity, we may still claim that the ERE strategy performs a uniform weighting when $\eta$ is close to 1. This is because when $\eta\approx 1$, Eq. (8) suggests $w_{t}$ is proportional to $1/(N_{0}\eta^{L_{0}})-1/{N_{0}}$ for all $1\leq t\leq N_{0}$, which is a uniform weighting. The emphasis on the recent experience (indicated by $\mathbbm{1}(t\leq c_{\min})$) is also evident from Eq. (8). Precisely, the second term increases logarithmically $\ln\frac{1}{\eta}$ when $\eta$ becomes smaller, so the smaller $\eta$ indeed gives more weight on the recent experience.

Recall the expected selection numbers are the aggregate weights over time. To understand the merit of balanced selection numbers, we develop an error analysis under non-uniform aggregate weights in the Appendix (Theorem 2 & Corollary 2). Similar to the uniform-weight error in section 4, the non-uniform-weight error is controlled by bias from policy mismatch and variance from sampling. In the following, we discuss these biases and variances in ERE, 1/age weighting, and uniform weighting. We conclude that the ERE and 1/age weighting are better because both of their biases and variances are smaller than that of uniform weighting.

For the bias from policy mismatch, Figure 1 shows the uniform weighting (for each sampling from the replay buffer) makes the aggregate weights (expected selection number) bias toward old samples. Because the old policies tend to be distant from the current policy, the uniform weighting has a larger policy mismatch bias than ERE and 1/age weighting.

As for the variance from sampling, we generalize Corollary 1’s uniform case: $\tilde{O}(1/\sqrt{N})$ to Corollary 2’s weighted case: $\tilde{O}(\sqrt{\sum_{i}w_{i}^{2}}/\sum_{i}w_{i})$ in the Appendix. To see this, let $\{X_{i}\}_{i=1}^{N}$ be a martingale difference sequence with $0\leq X_{i}\leq\Delta$. Consider a weighted sequence $\{w_{i}X_{i}\}_{i=1}^{N}$ with weights $\{w_{i}>0\}$. The Azuma-Hoeffding inequality suggests that with probability $\geq 1-\delta$,

which means that a general non-uniform weight admits a Hoeffding error $\tilde{O}(\sqrt{\sum_{i}w_{i}^{2}}/\sum_{i}w_{i})$ and is reduced to $\tilde{O}(1/\sqrt{N})$ when the weights are equal. Furthermore, one can prove that the Hoeffding error is minimized under uniform weights:

Because the ERE and 1/age weighting have balanced selection numbers (i.e., balanced aggregate weights), their biases and variance are smaller. They should perform better than uniform weighting for off-policy actor-critic RL. We will verify this in the next subsection.

Since we’ve established a theoretical foundation of ERE and 1/age from a bias-variance perspective, we will explore two main propositions from the preceding subsections: (1) Are ERE and 1/age weighting better than uniform weighting? (2) Does the approximated ERE proposed in Eq. (8) track the original ERE well? In addition, since prioritized experience replay (Schaul et al., 2016) (PER) is a popular sampling method, a natural question to ask is (3) Do ERE and 1/age outperform PER?

We evaluate five sampling methods (ERE, ERE_apx, 1/age weighting, uniform, PER) on five MuJoCo continuous-control environments (Todorov et al., 2012): Humanoid, Ant, Walker2d, HalfCheetah, and Hopper. All tasks have a maximum horizon of 1000 and are trained using a Pytorch Soft-Actor-Critic (Haarnoja et al., 2018) implementation on Github (Tandon, 2018). Most hyper-parameters of the SAC algorithm are the same as that in Tandon (2018) except for the batch size, where we find a batch size of 512 tends to give more stable results. Our code is available at https://github.com/sunfex/weighted-sac. The SAC implementation and the MuJoCo environment are licensed under the MIT license and the personal student license, respectively. The experiment is run on a server with an Intel i7-6850K CPU and Nvidia GTX 1080 Ti GPUs.

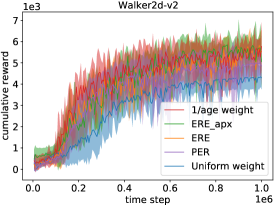
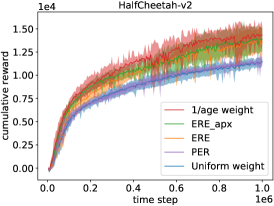
In Figure 2, the ERE and 1/age weighting strategies perform better than the uniform weighting does in all tasks. This verifies our preceding assertion that the ERE and 1/age weighting are superior because their biases and variances of the estimated Q function are smaller. Moreover, ERE and ERE_apx mostly coincide with each other, so Eq. (8) is indeed a good approximation of the ERE strategy. This also explains the implicit connection between ERE and 1/age weighting strategies: ERE is almost equivalent to ERE_apx and 1/age is the main factor in ERE_apx, so ERE and 1/age weighting should produce similar results. Finally, ERE and 1/age generally outperform PER, so the 1/age-based samplings that we study achieve nontrivial performance improvements.