Experimental study of tune-out wavelengths for spin-dependent optical lattice in 87Rb Bose-Einstein condensation
Abstract
We study the periodic potential of one-dimensional optical lattice originated from scalar shift and vector shift by manipulating the lattice polarizations. The ac Stark shift of optical lattice is measured by Kapitza-Dirac scattering of 87Rb Bose-Einstein condensate and the characteristics of spin-dependent optical lattice are presented by scanning the lattice wavelength between the D1 and D2 lines. At the same time, tune-out wavelengths that ac Stark shift cancels can be probed by optical lattice. We give the tune-out wavelengths in more general cases of balancing the contributions of both the scalar and vector shift. Our results provide a clear interpretation for spin-dependent optical lattice and tune-out wavelengths, and help to design it by choosing the appropriate lattice wavelength.
pacs:
34.20.Cf, 67.85.Hj, 03.75.LmI Introduction
Optical lattice for ultracold atoms has become an increasingly important technology in many-body physics Bloch et al. (2008), quantum simulation, quantum computation, quantum information storage and high precision measurements Aidelsburger et al. (2013); Miyake et al. (2013); Chiu et al. (2018); Schnorrberger et al. (2009); Martin et al. (2013). When neutral atoms are trapped in periodic potentials produced by standing wave of light fields, the trapping potentials of various atomic internal states are manipulated by lattice polarizations, which is called the spin-dependent optical lattice Mandel et al. (2003); Duan et al. (2003), which bring more complicated geometry for ultracold atoms such as spin-dependent hexagonal lattice Soltan-Panahi et al. (2011), spin-dependent optical superlattice Yang et al. (2017), and have been used to study many interesting phenomena such as controlled coherent transport Ke et al. (2018); Mandel et al. (2003), spinor BEC Ostrovskaya and Kivshar (2004), spin-orbit coupling and artificial gauge fields Ye et al. (2018); Grusdt et al. (2017), spontaneous emission of matter waves Krinner et al. (2018), twisted-bilayer optical potentials González-Tudela and Cirac (2019).
Tune-out wavelengths that ac Stark shift cancels was initially introduced in species-specific optical manipulation LeBlanc and Thywissen (2007) and can be useful for optical Feshbach resonances Clark et al. (2015) and atomic interferometer Trubko et al. (2015). Since tune-out wavelengths are independent of the light intensity Arora et al. (2011); Jiang et al. (2013); Cheng et al. (2013), it can be precisely measured by various methods Holmgren et al. (2012); Henson et al. (2015); Leonard et al. (2015); Schmidt et al. (2016); Adam and Charles (2016); Trubko et al. (2017); Copenhaver et al. (2019); Décamps et al. (2020). In general, tune-out wavelength is utilized accurately only for the scalar shift by cancelling and neglecting the vector and tensor contribution as much as possible Holmgren et al. (2012); Henson et al. (2015); Leonard et al. (2015); Trubko et al. (2017). In this paper, we investigate the tune-out wavelengths in more general cases of considering the contributions from both the scalar and vector shift. The ac Stark shift of optical lattice is measured by Kapitza-Dirac scattering which diffracts BEC into a number of high momentum states and the characteristics of spin-dependent optical lattice are investigated by scanning the lattice wavelength between the D1 and D2 lines. Kapitza-Dirac scattering becomes a standard tool and shows many applications in calibrating the lattice depth Ovchinnikov et al. (1999); Cahn et al. (1997); Denschlag et al. (2002); Beswick et al. (2019); Chen et al. (2010), detecting the lattice structure Viebahn et al. (2019); Wen et al. (2020), performing high-resolution spectroscopy Stenger et al. (1999) and metrology Gupta et al. (2002); Campbell et al. (2005). The periodic potential originated from scalar shift and vector shift is manipulated by controlling the lattice polarizations, which is used to generate spin-dependent optical lattice. We can design the special spin-dependent optical lattice with the help of tune-out wavelengths.
II theory
II.1 AC Stark shift
As we know, ac Stark effect is the result of an interaction between atoms and a classical light field. Here the total ac Stark shift for alkali-metal atoms in ground state interacting with a far-off-resonance light field can be expressed in terms of its scalar, vector, tensor components Beloy (2009); Lundblad et al. (2010); Le Kien et al. (2013); Becher et al. (2018); Tsyganok et al. (2019)
| (1) | ||||
where are the scalar, vector and tensor polarizabilities respectively. is the total atomic angular momentum, is magnetic quantum number, is the laser field intensity with , and are the frequency and amplitude of optical field, , and are unit vectors along the light wave-vector and magnetic field quantization axis respectively, is the intersection angle between and , is the intersection angle between the linearly polarized component of light field and . This formula comes from the first non-vanishing term (the second order) of a perturbation development. Note that the range of values of light ellipticity is , denotes left and right circular polarization. The left and right elliptical polarization is defined in terms of the light wave-vector. Scalar shift can be interpreted as a spin-independent light shift. Vector shift acts like an effective magnetic field to generate the linear Zeeman splitting (light shift proportional to ), which depends on the ellipticity of the light and the intersection angle between the laser beam wave vector and magnetic field quantization axis . Tensor shift is proportional to . For alkali-metal atoms in ground state, the tensor shift can vanish once light detuning exceed the hyperfine splitting . Because the ground state is , which induces the tensor shift coefficient Becher et al. (2018); Steck (2007); Rosenbusch et al. (2009). In this work, we consider a far detuning of , so that the ac Stark shift only includes two terms of the scalar and vector shift .
For a linear polarized light beam(), vector shift vanishes, but scalar shift keeps. For circular polarization light, the left and right circular polarization can change the sign of vector shift to be positive or negative. Therefore, the different ac Stark shift of two spin states can be cancelled by controlling the ellipticity, or tuning the angle between and (even changing the strength of the external bias magnetic field when considering high order contribution Lundblad et al. (2010); Derevianko (2010); Yang et al. (2016)), which is an important technique for the atomic clock and qubit for quantum computation.
II.2 Scalar and vector shift
For the first excited state of alkali-metal atoms, the fine structure induces the spectral lines of the D1 (the transition) and D2 (the transition) lines. Because the D1 and D2 lines of the first excited state are larger detuned than the the excited-state hyperfine splitting, the coefficients of the scalar and vector shifts in Eq. (1) are expressed as Corwin et al. (1999); Park et al. (2001); Mckay and Demarco (2010); Cao et al. (2012)
| (2) | ||||
where is the decay rate of the excited state for line, , . is the gyromagnetic ratio
| (3) | ||||
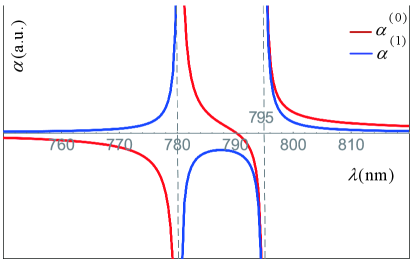
where is the spin angular momentum, is the orbital angular momentum, is the total electronic angular momentum, is the total nuclear angular momentum. For the ground states of 87Rb atoms, , for , for . Here, we study atoms and present the coefficients of the scalar and vector shifts as the function of wavelength in Fig. 1. The resonant wavelengths of the D1 and D2 lines of atom are nm and nm respectively. Obviously has a crossed zero point at nm, and always is negative between the D1 and D2 lines. When the wavelength of light is far red-detuned or blue-detuned by an amount larger than the fine structure splitting of the excited states, the vector shift approaches zero. Here, we study the tune-out wavelengths in more general cases of considering the contributions from both the scalar and vector shift. The tune-out wavelengths of the ground hyperfine states are given in Table 1 with , .
| Polarization | (nm) | ||||
|---|---|---|---|---|---|
| Calc. use Eq. (3) | Calc. in Ref LeBlanc and Thywissen (2007) | Other Calc. | Expt. | ||
| 790.005 | 790.04 | 790.01850(9) Schmidt et al. (2016) | |||
| 790.005 | 790.04 | 790.032439(35) Leonard et al. (2015) | |||
| 790.005 | 790.03 | 790.034(7) Arora et al. (2011) | 790.032388(32) Leonard et al. (2015) | ||
| 790.005 | 790.04 | 790.032602(193) Wang et al. (2016) | |||
| 790.005 | 790.04 | ||||
| 790.005 | 790.04 | 789.85(1) Catani et al. (2009) | |||
| 790.005 | 790.04 | 790.018187(193) Wang et al. (2016) | 790.018(2) Lamporesi et al. (2010), 790.020(25) * | ||
| 790.005 | 790.04 | 790.01858(23) Schmidt et al. (2016) | |||
| none | none | none * | |||
| 792.484 | 792.52 | ||||
| 790.005 | 790.06 | ||||
| 787.541 | 787.59 | ||||
| 785.093 | 785.14 | ||||
| 787.541 | 787.59 | 787.590(31) * | |||
| 790.005 | 790.06 | 790.020(25) * | |||
| 792.484 | 792.53 | ||||
| 785.093 | 785.14 | 785.11516 Wang (2017) | 785.146(12) * | ||
| 787.541 | 787.59 | ||||
| 790.005 | 790.06 | ||||
| 792.484 | 792.52 | ||||
| none | none | none Wang (2017) | |||
| 792.484 | 792.53 | 792.4 Schmidt et al. (2016), 792.462(22) * | |||
| 790.005 | 790.06 | 790.020(25) * | |||
| 787.541 | 787.59 | 787.620 Schmidt et al. (2016) | |||
-
*
Our experimental measurements.
In order to measure the tune-out wavelengths, we employ a one-dimensional (1D) optical lattice along the external bias magnetic field () with different polarization configurations. Here, the two laser beams have the same intensity with . For case 1, two laser beams with the same linear polarization counter-propagate along the z axis. Because of the parallel polarized beams, it can produce the spatial intensity modulation to form a 1D optical lattice,
| (4) |
The optical lattice potential for this case only originates from the scalar shift. Therefor it can be used for measuring the tune-out wavelength for the scalar shift. For case 2, two counter-propagated laser beams have linear orthogonal polarization (linlin polarization configuration). The orthogonally polarized beams can not produce a spatial intensity modulation. In contrast, it can produce the ellipticity modulation of polarization in space. This optical lattice potential is called Sisyphus optical potential, which has been used for Sisyphus cooling Dalibard and Cohen-Tannoudji (1989). The periodic potential is given by
| (5) |
This periodic potential only comes from the vector shift and the scalar term, which gives a uniformed energy shift. For case 3, two laser beams with the same polarized circular polarization counter-propagates along the z axis, which can also produce the spatial intensity modulation to form a 1D optical lattice,
| (6) |
The optical lattice potential for this case includes the scalar and vector shift simultaneously. Therefore, we can study the tune-out wavelengths in presence of contributions of both the scalar and vector shift in this case. And for case 4, like case 2, the scalar shift is a constant only related to the constant intensity of two orthogonal polarized counter-propagating laser beams. But the different with former, is that the vector shift becomes zero since it only produce the rotation of linear polarization in space. Hence it can not produce any spatial modulation to form a 1D lattice.
| (7) |
Here, for a 1D optical lattice along the external bias magnetic field (), it is convenient to define the left and right elliptical polarizations in terms of the magnetic field quantization axis.
III Experiment
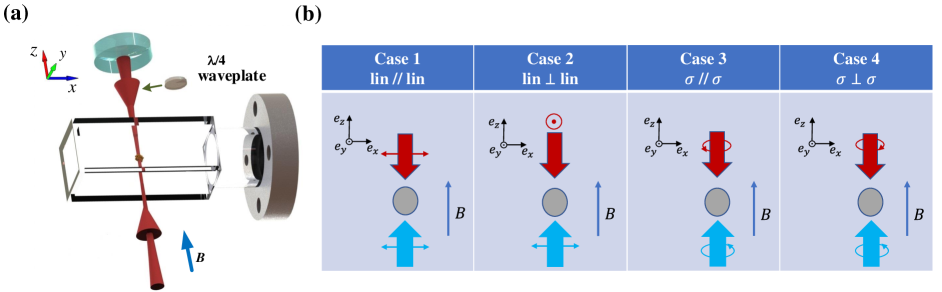
The schematic of experimental setup is shown in Fig. 2(a). Ultracold 87Rb atoms in hyperfine state are loaded in a crossed optical dipole trap Xiong et al. (2010). Forced evaporation in the optical trap is used to create the BEC with up to atoms. In order to obtain the atoms in the different single spin states, BEC is transferred from into via a rapid adiabatic passage induced by a microwave-frequency field with duration of 10 ms at 3.9 G of the bias magnetic field, where the frequency of center is 6.842935 GHz and the width is 0.25 MHz. Then the atoms in can further be transferred into state using a rapid adiabatic passage induced by a radio frequency (rf) field at 28 G of the bias magnetic field. The lattice beam is derived from a single frequency Ti:sapphire laser with broad tuning range of the frequency. An acousto-optical modulator is used to control the intensity of the lattice beam. The lattice beam passes through the polarizing beam splitter to generate the perfect polarization. The polarization extinction ratio of the polarizing beam splitter can reach 500:1. Therefore the linear polarization purity of the lattice beam is about 0.2. Furthermore the circular polarization purity of the lattice beam can reach about 0.5. A lattice beam propagates with z axis and converges on BEC with waist of 100 by a lens (f = 300 mm). Then the beam is reflected by a concave mirror ( curvature radius r=300 mm) and refocused on BEC with the almost same waist size. The advantage of this configuration can reduce phase jitter significantly. Here, we employ Kapitza-Dirac (or Raman-Nath) scattering to measure the ac Stark shift. Kapitza-Dirac scattering is used to diffract the BEC into a number of momentum states by a standing light wave, in which the interaction is sufficiently short and strong Gould et al. (1986). In this process, BEC is kept in a crossed optical dipole trap and the lattice potential imprints a phase modulation on matter wave in position space. Then the phase modulation on matter wave is measured in momentum space via the time-of-flight (TOF) absorption image. It is obvious that higher momentum orders appear in the atomic density distribution of the TOF absorption image, which depends on the potential depth and interaction time. Here, we apply a 1D optical lattice short pulse for 4 with the power of 80 mW on BEC. Then immediately turn off the optical trap, let the atoms ballistically expand in 12 ms and take the absorption images. We obtain the lattice depth from the absorption images by applying the lattice at a fixed laser power for different intervals of time and by observing the interval at which the order atoms in the lattice vanish Ovchinnikov et al. (1999); Cahn et al. (1997); Denschlag et al. (2002); Beswick et al. (2019); Chen et al. (2010). We define the recoil momentum and recoil energy kHz as the nature momentum and energy units, where is the mass of 87Rb atom, is the wavelength of the lattice laser.
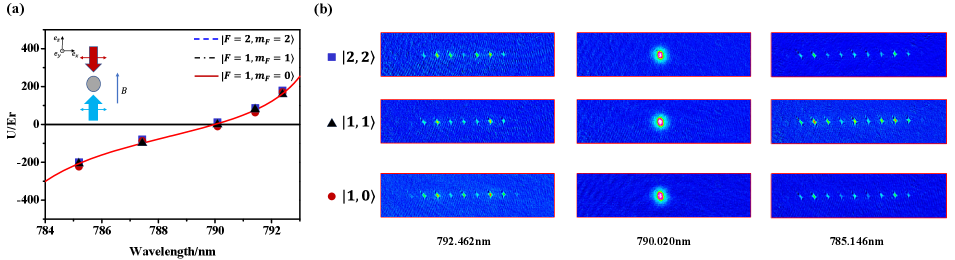
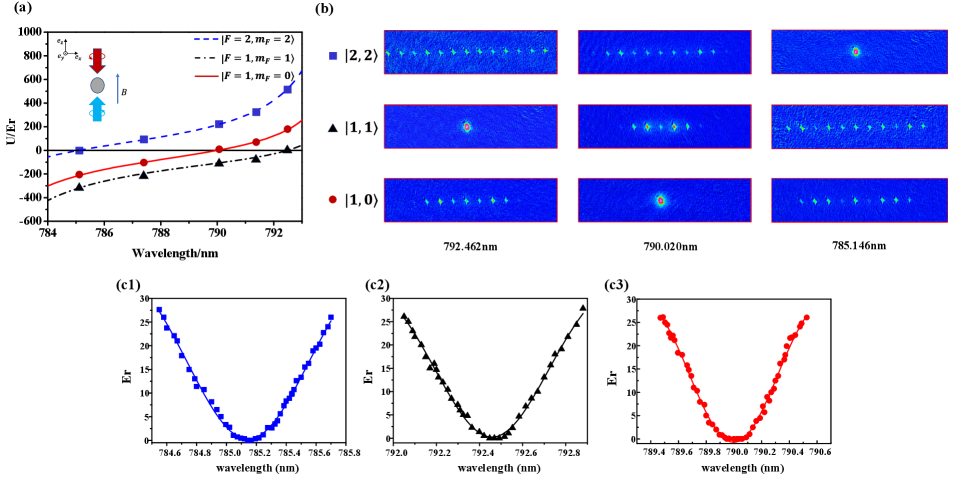

For case 1, a 1D optical lattice with the linear parallel polarization produces the spatial intensity modulation, which only comes from the scalar shift. Thus it is a spin-independent optical lattice and the potential depth as the function of the lattice wavelength are plotted in Fig. 3(a). Here, the positive and negative periodic potentials correspond to blue and red detuned lattice laser. The higher momentum orders are observed in the atomic density distribution of the TOF absorption images as shown in Fig. 3(b), which depends on the potential depth. We measure the tune-out wavelengths by changing the lattice wavelength and find its location at 790.020 nm for all spin states, which is in good agreement with the previous works Leonard et al. (2015); Schmidt et al. (2016).
For case 2, a laser beam with the linear polarization pass through a quarter-wave plate and is reflected by a concave mirror, which produces the linear orthogonal polarization configuration. We plot the potential depth vs different wavelength as shown in Fig. 4(a). This periodic potential is a spin-dependent lattice, which only comes from the contribution of the vector shift. Therefore, there is no lattice potential for the state () for all wavelength as shown in Fig. 4(b). The and states () always experience the lattice potential when adjusting the lattice wavelength.
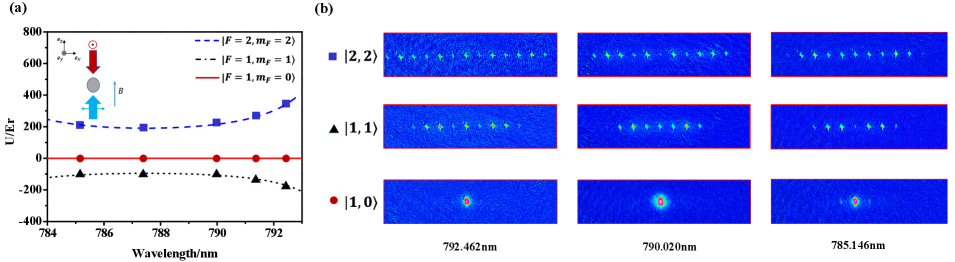
For case 3, a 1D optical lattice with the circular parallel polarization produces the spatial intensity modulation, which includes the contribution of the scalar and vector shift simultaneously. The potential depth of , and are given in Fig. 5(a) and (b). The tune-out wavelengths are generated by balancing the scalar and vector shift, which are 792.462(22)nm, 790.020(25)nm and 785.146(12)nm for , and respectively as shown in Fig. 5(c). Note that the tune-out wavelengths in this case are sensitive to the ellipticity of the lattice polarization, the alignment between the direction of the 1D optical lattice and the external bias magnetic field. This case provides us more controlled ways to generate the different kinds of spin-dependent optical lattice. There is an interesting phenomenon that two neighbouring spin states have the opposite lattice potential (blue and red detuning respectively) by choosing the appropriate wavelength, for example, and states have the opposite lattice potential at the wavelength of 791.24 nm.
For case 4, two counter-propagating laser beams with the orthogonal circular polarization can not generate any spatial modulation on the BEC. The potential depth for , and are given in Fig. 6(a) and (b), showing no effective potential (no density modulation) for these states.
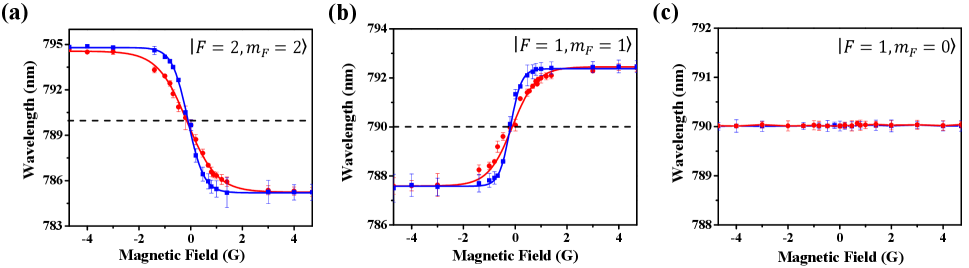
Furthermore, we study the dependence of the tune-out wavelengths on the strength of the external bias magnetic field in more detail. The intersection angle between and is expressed as
| (8) |
where is the external bias magnetic field, is the residual magnetic field (such as the earth magnetic field). We measure the tune-out wavelengths as the function of the strength of the external bias magnetic field as shown in Fig. 7. By changing the bias magnetic field to small value, the direction of the total magnetic field and the intersection angle can be changed. Therefore, the tune-out wavelengths change when the strength of the bias magnetic field is near to the residual magnetic field value. The strength of the external bias magnetic field in one direction is gradually decreased to zero and then increased in the opposite direction. We find that the tune-out wavelengths for jumps into due to inversion the external bias magnetic field direction for the spin and states as shown in Fig. 7(a) and (b). The slope is sensitive to the strength of residual magnetic field in the perpendicular direction of z axis. Here, three pairs of Helmholtz coils are employed to compensate the background magnetic field. When the residual magnetic field in the (x, y, z) directions are suppressed from (0.4 G, 0.46 G, 0.38 G) to (0.25 G, 0.28 G, 0.2 G) which are measured by a triaxial fluxgate magnetometer, the slope is changed from -4.054 nm/G to -6.584 nm/G for and 8.108 nm/G to 13.168 nm/G for as shown in Fig. 7(a) and (b) respectively. Therefore, this method can be utilized to calibrate and measure the residual magnetic field.
IV Conclusion
In conclusion, we present an experiment to measure the ac Stark shift around the tune-out wavelengths of 87Rb BEC in the three different hyperfine ground states , and between D1 and D2 lines. Four different polarization configurations of one-dimensional optical lattice, which are originated from scalar shift, vector shift, both scalar and vector shift respectively by manipulating the lattice polarizations, are investigated. Kapitza-Dirac scattering technique is employed to probe the ac Stark shift of atoms in optical lattice and the characteristics of spin-dependent optical lattice are presented by scanning the lattice wavelength. We present the tune-out wavelengths in more general cases of considering the contributions of both the scalar and vector shift. We further study the dependence of the tune-out wavelengths on the strength of the external bias magnetic field in more detail. Our work provides a clear interpretation for spin-dependent optical lattice and can be used for the realization of two species system, or the same atoms (Rb) with different spin states, in which one of them move freely while the others are trapped to different degrees of optical lattice potential. This system can be a test-bed for observing or simulating phenomena such as entropy cooling Catani et al. (2009); Lamporesi et al. (2010); Mckay and Demarco (2010); Arora et al. (2011); Bause et al. (2020), Kondo effect Zhang et al. (2016); Yao et al. (2019) etc, and even have application in Sr optical lattice clock Heinz et al. (2020).
V Funding Information
This research was supported by the MOST (2016YFA0301602, 2018YFA0307601), NSFC (Grant No. 11804203, 11974224, 11704234), the Fund for Shanxi ”1331 Project” Key Subjects Construction.
References
- Bloch et al. (2008) Immanuel Bloch, Jean Dalibard, and Wilhelm Zwerger, “Many-body physics with ultracold gases,” Rev. Mod. Phys. 80, 885–964 (2008).
- Aidelsburger et al. (2013) M. Aidelsburger, M. Atala, M. Lohse, J. T. Barreiro, B. Paredes, and I. Bloch, “Realization of the Hofstadter hamiltonian with ultracold atoms in optical lattices,” Phys. Rev. Lett. 111, 185301 (2013).
- Miyake et al. (2013) Hirokazu Miyake, Georgios A. Siviloglou, Colin J. Kennedy, William Cody Burton, and Wolfgang Ketterle, “Realizing the Harper hamiltonian with laser-assisted tunneling in optical lattices,” Phys. Rev. Lett. 111, 185302 (2013).
- Chiu et al. (2018) Christie S. Chiu, Geoffrey Ji, Anton Mazurenko, Daniel Greif, and Markus Greiner, “Quantum state engineering of a Hubbard system with ultracold fermions,” Phys. Rev. Lett. 120, 243201 (2018).
- Schnorrberger et al. (2009) U. Schnorrberger, J. D. Thompson, S. Trotzky, R. Pugatch, N. Davidson, S. Kuhr, and I. Bloch, “Electromagnetically induced transparency and light storage in an atomic mott insulator,” Phys. Rev. Lett. 103, 033003 (2009).
- Martin et al. (2013) M. J. Martin, M. Bishof, M. D. Swallows, X. Zhang, C. Benko, J. von Stecher, A. V. Gorshkov, A. M. Rey, and Jun Ye, “A quantum many-body spin system in an optical lattice clock,” Science 341, 632–636 (2013).
- Mandel et al. (2003) Olaf Mandel, Markus Greiner, Artur Widera, Tim Rom, Theodor W Hänsch, and Immanuel Bloch, “Coherent transport of neutral atoms in spin-dependent optical lattice potentials,” Phys. Rev. Lett. 91, 010407 (2003).
- Duan et al. (2003) L. M. Duan, E. Demler, and M. D. Lukin, “Controlling spin exchange interactions of ultracold atoms in optical lattices,” Phys. Rev. Lett. 91, 090402 (2003).
- Soltan-Panahi et al. (2011) P. Soltan-Panahi, J. Struck, P. Hauke, A. Bick, W. Plenkers, G. Meineke, C. Becker, P. Windpassinger, M. Lewenstein, and K. Sengstock, “Multi-component quantum gases in spin-dependent hexagonal lattices,” Nat. Phys. 7, 434–440 (2011).
- Yang et al. (2017) Bing Yang, HanNing Dai, Hui Sun, Andreas Reingruber, ZhenSheng Yuan, and JianWei Pan, “Spin-dependent optical superlattice,” Phys. Rev. A 96, 011602 (2017).
- Ke et al. (2018) Yongguan Ke, Jiahao Huang, Min Zhuang, Bo Lu, and Chaohong Lee, “Compact gravimeter with an ensemble of ultracold atoms in spin-dependent optical lattices,” Phys. Rev. A 98, 053826 (2018).
- Ostrovskaya and Kivshar (2004) Elena A. Ostrovskaya and Yuri S. Kivshar, “Localization of two-component Bose-Einstein condensates in optical lattices,” Phys. Rev. Lett. 92, 180405 (2004).
- Ye et al. (2018) Qinzhou Ye, Xizhou Qin, Yongyao Li, Honghua Zhong, Yuri S Kivshar, and Chaohong Lee, “Band-gap structure and chiral discrete solitons in optical lattices with artificial gauge fields,” Ann. Phys. 388, 173–185 (2018).
- Grusdt et al. (2017) Fabian Grusdt, Tracy Li, Immanuel Bloch, and Eugene Demler, “Tunable spin-orbit coupling for ultracold atoms in two-dimensional optical lattices,” Phys. Rev. A 95, 063617 (2017).
- Krinner et al. (2018) Ludwig Krinner, Michael Stewart, Arturo Pazmino, Joonhyuk Kwon, and Dominik Schneble, “Spontaneous emission of matter waves from a tunable open quantum system,” Nature 559, 589–592 (2018).
- González-Tudela and Cirac (2019) A. González-Tudela and J. I. Cirac, “Cold atoms in twisted-bilayer optical potentials,” Phys. Rev. A 100, 053604 (2019).
- LeBlanc and Thywissen (2007) L. J. LeBlanc and J. H. Thywissen, “Species-specific optical lattices,” Phys. Rev. A 75, 053612 (2007).
- Clark et al. (2015) Logan W. Clark, LiChung Ha, ChenYu Xu, and Cheng Chin, “Quantum dynamics with spatiotemporal control of interactions in a stable Bose-Einstein condensate,” Phys. Rev. Lett. 115, 155301 (2015).
- Trubko et al. (2015) Raisa Trubko, James Greenberg, Michael T. St. Germaine, Maxwell D. Gregoire, William F. Holmgren, Ivan Hromada, and Alexander D. Cronin, “Atom interferometer gyroscope with spin-dependent phase shifts induced by light near a tune-out wavelength,” Phys. Rev. Lett. 114, 140404 (2015).
- Arora et al. (2011) Bindiya Arora, M. S. Safronova, and Charles W. Clark, “Tune-out wavelengths of alkali-metal atoms and their applications,” Phys. Rev. A 84, 043401 (2011).
- Jiang et al. (2013) Jun Jiang, LiYan Tang, and J. Mitroy, “Tune-out wavelengths for Potassium,” Phys. Rev. A 87, 032518 (2013).
- Cheng et al. (2013) Yongjun Cheng, Jun Jiang, and J. Mitroy, “Tune-out wavelengths for the alkaline-earth-metal atoms,” Phys. Rev. A 88, 022511 (2013).
- Holmgren et al. (2012) William F. Holmgren, Raisa Trubko, Ivan Hromada, and Alexander D. Cronin, “Measurement of a wavelength of light for which the energy shift for an atom vanishes,” Phys. Rev. Lett. 109, 243004 (2012).
- Henson et al. (2015) B. M. Henson, R. I. Khakimov, R. G. Dall, K. G. H. Baldwin, LiYan Tang, and A. G. Truscott, “Precision measurement for metastable Helium atoms of the 413 nm tune-out wavelength at which the atomic polarizability vanishes,” Phys. Rev. Lett. 115, 043004 (2015).
- Leonard et al. (2015) R. H. Leonard, A. J. Fallon, C. A. Sackett, and M. S. Safronova, “High-precision measurements of the -line tune-out wavelength,” Phys. Rev. A 92, 052501 (2015).
- Schmidt et al. (2016) Felix Schmidt, Daniel Mayer, Michael Hohmann, Tobias Lausch, Farina Kindermann, and Artur Widera, “Precision measurement of the tune-out wavelength in the hyperfine ground state at 790 nm,” Phys. Rev. A 93, 022507 (2016).
- Adam and Charles (2016) Fallon Adam and Sackett Charles, “Obtaining atomic matrix elements from vector tune-out wavelengths using atom interferometry,” Atoms 4, 12 (2016).
- Trubko et al. (2017) Raisa Trubko, Maxwell D. Gregoire, William F. Holmgren, and Alexander D. Cronin, “Potassium tune-out-wavelength measurement using atom interferometry and a multipass optical cavity,” Phys. Rev. A 95, 052507 (2017).
- Copenhaver et al. (2019) Eric Copenhaver, Kayleigh Cassella, Robert Berghaus, and Holger Müller, “Measurement of a tune-out wavelength by phase-patterned atom interferometry,” Phys. Rev. A 100, 063603 (2019).
- Décamps et al. (2020) B. Décamps, J. Vigué, A. Gauguet, and M. Büchner, “Measurement of the 671 nm tune-out wavelength of by atom interferometry,” Phys. Rev. A 101, 033614 (2020).
- Ovchinnikov et al. (1999) Yu. B. Ovchinnikov, J. H. Müller, M. R. Doery, E. J. D. Vredenbregt, K. Helmerson, S. L. Rolston, and W. D. Phillips, “Diffraction of a released Bose-Einstein condensate by a pulsed standing light wave,” Phys. Rev. Lett. 83, 284–287 (1999).
- Cahn et al. (1997) S. B. Cahn, A. Kumarakrishnan, U. Shim, T. Sleator, P. R. Berman, and B. Dubetsky, “Time-domain de Broglie wave interferometry,” Phys. Rev. Lett. 79, 784–787 (1997).
- Denschlag et al. (2002) J Hecker Denschlag, JE Simsarian, H Häffner, C McKenzie, A Browaeys, Donghyun Cho, Kristian Helmerson, SL Rolston, and William D Phillips, “A Bose-Einstein condensate in an optical lattice,” J. Phys. B: At. Mol. Opt. Phys. 35, 3095 (2002).
- Beswick et al. (2019) Benjamin T. Beswick, Ifan G. Hughes, and Simon A. Gardiner, “Lattice-depth measurement using multipulse atom diffraction in and beyond the weakly diffracting limit,” Phys. Rev. A 99, 013614 (2019).
- Chen et al. (2010) Haixia Chen, Dezhi Xiong, Pengjun Wang, and Jing Zhang, “Pulse loading 87Rb Bose-Einstein condensation in optical lattice: the Kapitza-Dirac scattering and temporal matter-wave-dispersion Talbot effect,” Chin. Opt. Lett. 8, 348–350 (2010).
- Viebahn et al. (2019) Konrad Viebahn, Matteo Sbroscia, Edward Carter, Jr Chiun Yu, and Ulrich Schneider, “Matter-wave diffraction from a quasicrystalline optical lattice,” Phys. Rev. Lett. 122, 110404 (2019).
- Wen et al. (2020) Kai Wen, Zengming Meng, Pengjun Wang, Liangwei Wang, Liangchao Chen, Lianghui Huang, Lihong Zhou, Xiaoling Cui, and Jing Zhang, “Observation of sub-wavelength phase structure of matter wave with two-dimensional optical lattice by Kapitza-Dirac diffraction,” Sci. Rep. 10, 1–8 (2020).
- Stenger et al. (1999) J. Stenger, S. Inouye, A. P. Chikkatur, D. M. Stamper-Kurn, D. E. Pritchard, and W. Ketterle, “Bragg spectroscopy of a Bose-Einstein condensate,” Phys. Rev. Lett. 82, 4569–4573 (1999).
- Gupta et al. (2002) S. Gupta, K. Dieckmann, Z. Hadzibabic, and D. E. Pritchard, “Contrast interferometry using Bose-Einstein condensates to measure and ,” Phys. Rev. Lett. 89, 140401 (2002).
- Campbell et al. (2005) Gretchen K. Campbell, Aaron E. Leanhardt, Jongchul Mun, Micah Boyd, Erik W. Streed, Wolfgang Ketterle, and David E. Pritchard, “Photon recoil momentum in dispersive media,” Phys. Rev. Lett. 94, 170403 (2005).
- Beloy (2009) K. Beloy, Theory of the ac Stark effect on the atomic hyperfine structure and applications to microwave atomic clocks, Ph.D. thesis, University of Nevada, Reno, USA (2009).
- Lundblad et al. (2010) N. Lundblad, M. Schlosser, and J. V. Porto, “Experimental observation of magic-wavelength behavior of atoms in an optical lattice,” Phys. Rev. A 81, 031611 (2010).
- Le Kien et al. (2013) Fam Le Kien, Philipp Schneeweiss, and Arno Rauschenbeutel, “Dynamical polarizability of atoms in arbitrary light fields: general theory and application to Cesium,” Eur. Phys. J. D 67, 92 (2013).
- Becher et al. (2018) J. H. Becher, S. Baier, K. Aikawa, M. Lepers, J. F. Wyart, O. Dulieu, and F. Ferlaino, “Anisotropic polarizability of Erbium atoms,” Phys. Rev. A 97, 012509 (2018).
- Tsyganok et al. (2019) V. V. Tsyganok, D. A. Pershin, E. T. Davletov, V. A. Khlebnikov, and A. V. Akimov, “Scalar, tensor, and vector polarizability of Tm atoms in a 532 nm dipole trap,” Phys. Rev. A 100, 042502 (2019).
- Steck (2007) Daniel A. Steck, “Quantum and atom optics,” (2007).
- Rosenbusch et al. (2009) P. Rosenbusch, S. Ghezali, V. A. Dzuba, V. V. Flambaum, K. Beloy, and A. Derevianko, “ac Stark shift of the Cs microwave atomic clock transitions,” Phys. Rev. A 79, 013404 (2009).
- Derevianko (2010) Andrei Derevianko, “Theory of magic optical traps for Zeeman-insensitive clock transitions in alkali-metal atoms,” Phys. Rev. A 81, 051606 (2010).
- Yang et al. (2016) Jiaheng Yang, Xiaodong He, Ruijun Guo, Peng Xu, Kunpeng Wang, Cheng Sheng, Min Liu, Jin Wang, Andrei Derevianko, and Mingsheng Zhan, “Coherence preservation of a single neutral atom qubit transferred between magic-intensity optical traps,” Phys. Rev. Lett. 117, 123201 (2016).
- Corwin et al. (1999) K. L. Corwin, S. J. M. Kuppens, D. Cho, and C. E. Wieman, “Spin-polarized atoms in a circularly polarized optical dipole trap,” Phys. Rev. Lett. 83, 1311–1314 (1999).
- Park et al. (2001) Chang Yong Park, Heeso Noh, Chung Mok Lee, and D. Cho, “Measurement of the Zeeman-like ac Stark shift,” Phys. Rev. A 63, 032512 (2001).
- Mckay and Demarco (2010) D. Mckay and B. Demarco, “Thermometry with spin-dependent lattices,” New J. Phys. 12, 055013 (2010).
- Cao et al. (2012) MingTao Cao, Liang Han, YueRong Qi, ShouGang Zhang, Gao Hong, and FuLi Li, “Calculation of the spin-dependent optical lattice in Rubidium Bose-Einstein condensation,” Chin. Rev. Lett. 29, 034201 (2012).
- Wang et al. (2016) Xia Wang, Jun Jiang, LuYou Xie, DengHong Zhang, and ChenZhong Dong, “Polarizabilities and tune-out wavelengths of the hyperfine ground states of ,” Phys. Rev. A 94, 052510 (2016).
- Catani et al. (2009) J. Catani, G. Barontini, G. Lamporesi, F. Rabatti, G. Thalhammer, F. Minardi, S. Stringari, and M. Inguscio, “Entropy exchange in a mixture of ultracold atoms,” Phys. Rev. Lett. 103, 140401 (2009).
- Lamporesi et al. (2010) G. Lamporesi, J. Catani, G. Barontini, Y. Nishida, M. Inguscio, and F. Minardi, “Scattering in mixed dimensions with ultracold gases,” Phys. Rev. Lett. 104, 153202 (2010).
- Wang (2017) Xia Wang, Theoretical study of the polarizabilities, tune-out wavelengths, and magic wavelengths of Rb atom, Master’s thesis, University of Northwest Normal, China (2017).
- Dalibard and Cohen-Tannoudji (1989) Jean Dalibard and Claude Cohen-Tannoudji, “Laser cooling below the doppler limit by polarization gradients: simple theoretical models,” J. Opt. Soc. Am. B 6, 2023–2045 (1989).
- Xiong et al. (2010) Dezhi Xiong, Pengjun Wang, Zhengkun Fu, Shijie Chai, and Jing Zhang, “Evaporative cooling of 87Rb atoms into Bose-Einstein condensate in an optical dipole trap,” Chin. Opt. Lett. 8, 627–629 (2010).
- Gould et al. (1986) Phillip L. Gould, George A. Ruff, and David E. Pritchard, “Diffraction of atoms by light: the near-resonant Kapitza-Dirac effect,” Phys. Rev. Lett. 56, 827–830 (1986).
- Bause et al. (2020) Roman Bause, Ming Li, Andreas Schindewolf, XingYan Chen, Marcel Duda, Svetlana Kotochigova, Immanuel Bloch, and XinYu Luo, “Tune-out and magic wavelengths for ground-state molecules,” Phys. Rev. Lett. 125, 023201 (2020).
- Zhang et al. (2016) Ren Zhang, Deping Zhang, Yanting Cheng, Wei Chen, Peng Zhang, and Hui Zhai, “Kondo effect in alkaline-earth-metal atomic gases with confinement-induced resonances,” Phys. Rev. A 93, 043601 (2016).
- Yao et al. (2019) Juan Yao, Hui Zhai, and Ren Zhang, “Efimov-enhanced Kondo effect in alkali-metal and alkaline-earth-metal atomic gas mixtures,” Phys. Rev. A 99, 010701 (2019).
- Heinz et al. (2020) A. Heinz, A. J. Park, N. Šantić, J. Trautmann, S. G. Porsev, M. S. Safronova, I. Bloch, and S. Blatt, “State-dependent optical lattices for the Strontium optical qubit,” Phys. Rev. Lett. 124, 203201 (2020).