Exclusive heavy quark dijet cross section
Abstract
We study the exclusive heavy quark dijet cross section from -annihilation using soft-collinear effective theory. In order to resum the large logarithms of small jet veto parameter and jet radius , we factorize the cross section into the hard, hard-soft, collinear, and collinear-soft parts. Compared with the case of a massless quark, the jet sector with the collinear and collinear-soft parts can be modified to include the heavy quark mass. The factorization of the jet sector can be systematically achieved through matching onto the boosted heavy quark effective theory. Heavy quark mass corrections enhance the cross section sizably and cannot be ignored when the quark mass is comparable with the jet size . We also analyze the exclusive heavy quark pair production in the limit as goes to zero. Using the resummed result, the top isolation effects on the cross section are estimated.
I Introduction
Jets, collimated beams of strongly interacting particles, are an important observable for scrutinizing the Standard Model and for finding new physics signals. Jets are usually characterized by the jet energy () and radius (). If is small, the jets can be handled independently of the hard interactions. Hence QCD factorization to separate short and long distance physics becomes an important tool to study the jet physics, and it enables us to systematically resum large logarithms of small that appears in the scattering cross section with the jet Dasgupta:2014yra ; Kang:2016mcy ; Dai:2016hzf .
If a jet with small radius contains a heavy quark, the heavy quark mass could be comparable with a jet size, which is roughly given by . In this case the finite size of the heavy quark mass can give significant corrections to the predictions of jets in which the heavy quark has been taken as a massless parton. Therefore understanding the heavy quark mass effects is an important ingredient for a precise estimation of the jet, and furthermore for probing electroweak and new physics since the heavy quark is sensitive to Yukawa couple.
In this paper we study the exclusive heavy quark dijet scattering cross section in -annihilation. Basically the dijet cross section does not become additionally singular when we take the massless limit on the heavy quark. Therefore the dijet cross section can be a good testing system for investigating heavy quark mass effects by comparing both the massive and massless cases. The dijet cross section depends on the jet veto parameter and the radius . Since both the parameters are small and produce large logarithms, the perturbative expansion at the fixed order in is not reliable. Hence we consider the resummation of the cross section employing soft-collinear effective theory (SCET) Bauer:2000ew ; Bauer:2000yr ; Bauer:2001yt ; Bauer:2002nz .
The organization of the paper is as follows: In section II we discuss the factorization of the heavy quark dijet cross section. In section III, using the factorization theorem we resum large logarithms and estimated the heavy quark mass impact on the cross section. In section IV, taking the limit of the cross section as , we consider the exclusive heavy quark pair production. Finally we conclude in section V.
II Factorization of the dijet cross section
For construction of dijet events in -annihialation, we apply the Sterman-Weinberg (SW) algorithm Sterman:1977wj . In the SW algorithm, energetic particles that are deposited within a cone with the half angle constitute a jet. At next-to-leading order (NLO) in , if the angle between two energetic particles satisfy
| (1) |
they merge to a jet. So this constraint is the same as the ones for inclusive -type algorithms Catani:1993hr ; Ellis:1993tq ; Dokshitzer:1997in ; Cacciari:2008gp . In addition, to be infrared (IR) safe, soft particles with energies less than are included in the dijet events. Here is the center of mass energy of the incoming electron and positron, and the veto parameter is given to be small, i.e, .
With small and adopted, the dijet cross section with massless partons has been studied in the framework of SCET, and its factorization theorem is formulated as Cheung:2009sg ; Ellis:2010rwa ; Chay:2015ila
| (2) |
where is the Born level cross section, and the jet energy can be given by . is the hard function, is the integrated jet function to describe -collinear interactions inside the jet, and is the soft function for soft gluon radiations that depends on the jet veto. To NLO order in , each factorized function in Eq. (2) is given by
| (3) | |||||
| (4) | |||||
| (5) |
All the large logarithms in and are minimized by the renormalization scale choices of for and for . However, the large logarithms of in the soft function persist even if we set the soft scale as . Therefore the renormalization group (RG) evolution for from the factorization scale to the soft scale does not completely resum all the possible large logarithms, hence we need to additionally factorize to capture scales to minimize all the logarithms. For this, we can subdivide soft interactions into the ‘hard-soft (hsoft)’ and the ‘collinear-soft (csoft)’ interactions. The corresponding modes of gluons scale as
| (6) | |||||
| (7) |
where and . The two lightcone vectors, and , are back-to-back and satisfy . The hsoft mode for Eq. (6) is responsible for wide angle soft radiations, hence cannot resolve the jet boundary with the radius . However, two csoft modes in Eq. (7) radiate over narrow angles around both the jet axes and can recognize the jet boundary.
The refactorization of soft interactions can be performed similarly to the conventional factorization into hard and collinear interactions from full theory. At scale , we first integrate out the hsoft mode matching onto the lower effective theory with the csoft modes, and obtain the hsoft function. Then at the lower scale, , the remaining two csoft modes cannot communicate each other, and thus factorizes.
As a result, the soft function in Eq. (5) can be factorized into the hsoft, - and -csoft functions such as Becher:2015hka ; Chien:2015cka
| (8) |
Here the NLO results for the factorized functions are given by
| (9) | |||||
| (10) |
Therefore the complete factorization theorem for the dijet cross section is given as
| (11) | |||||
The factorization theorem, Eq. (11), can be also applied to the heavy quark dijet cross section that is based on heavy quark pair production. To do so, the jet sector, , needs to be modified to include the heavy quark mass. The produced energetic heavy quarks leading to jets have collinear interactions basically, and the momenta of the heavy quarks in and directions scale as
| (12) |
We will consider the heavy quark mass in the limit, , so the offshellnesses of the heavy quarks scale as .
These collinear interactions of the heavy quark can be described by the massive version of SCET, i.e., Leibovich:2003jd ; Rothstein:2003wh ; Chay:2005ck . However, the jet veto dependences on are not effectively resolved by purely collinear interactions, hence we need the csoft modes to capture the veto dependences. The scaling behavior of the csoft modes have been described in Eq. (7). Hence we notice that these csoft modes can be also subsets of the collinear modes in Eq. (12).
When we separate the csoft interactions from the collinear interactions in the heavy quark sector, we can introduce the boosted heavy quark effective theory (bHQET), i.e, the boosted version of HQET. For example, let us consider an energetic heavy quark moving in direction. With collinear interactions integrated out, at the lower scale , the heavy quark only has csoft interactions. The heavy quark momentum can be written as
| (13) |
where is the heavy quark velocity to be normalized as , and is a residual csoft momentum. Under the csoft interactions, the velocity does not change. Since is -collinear momentum, the velocity scales as , where . Conveniently, if we choose the frame for to be zero, the velocity can be given by
| (14) |
To construct bHQET from , we first integrate out collinear interactions, i.e., collinear gluons, then match the heavy quark collinear field in onto the bHQET field,
| (15) |
Thus, the bHQET field has the same spinor property as and satisfies
| (16) |
This preserves the power counting with respect to large energy that has been applied to . As a result, bHQET at leading power in is
| (17) |
For more details of bHQET Lagrangian, we refer to Ref. DKL .
Therefore the factorization of the heavy quark jet sector can be performed through matching onto bHQET, and the result for the -collinear jet is expressed as
| (18) |
where the subscript ‘’ denotes the heavy quark. The -collinear heavy quark jet sector in the opposite direction can be factorized in the same way.
In Eq. (18), is the integrated heavy quark jet function (iHQJF) Dai:2018ywt , which is the result of integrating out collinear gluon radiations inside the jet. At NLO in , is given by Dai:2018ywt
| (19) | |||||
where and . The functions and have integration forms,
| (20) | |||||
| (21) |
In the limit , these functions are and . In the limit goes to an infinity, corresponding to , they go to .
The heavy quark csoft function in Eq. (18) is analyzed in bHQET and is defined as
| (22) |
where , is the heavy quark with spin , and is the csoft final state, which should be in the phase space that the heavy quark jet and the veto cover. is the csoft Wilson line, where -csoft gluon radiations from other sectors have been eikonalized as
| (23) |
Here ‘P’ denotes the path ordering, and is the csoft gluon propagating in direction. From Eq. (15), the spin sum rule for the bHQET field is given by
| (24) |
So the csoft function at tree level is normalized as .
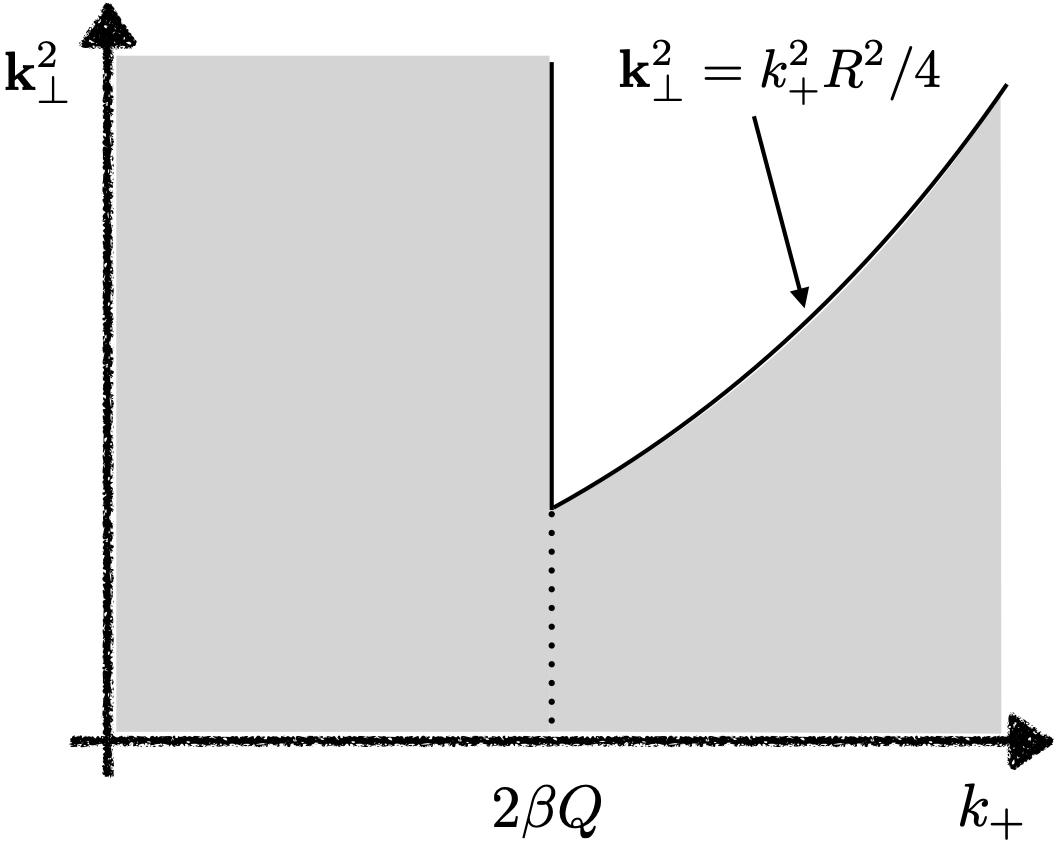
At one loop order, the available phase space for a radiated csoft gluon is illustrated in Fig. 1. The momentum constraint for the gluon to be inside a jet is given by
| (25) |
And, due to the jet veto constraint, the gluon satisfying the condition, , can be counted as part of the dijet events even if it is outside the jet.
In Fig. 1, on the axis we obtain the logarithm of , which becomes singular as . The soft IR divergence arises on the axis. Note that overall one loop result including virtual contributions is given by zero if the real gluon emission covers the full phase space without the dijet event constraint. This indicates that the virtual contributions can be considered as the negative contribution of the real radiations with the full phase space. So, when the virtual contributions are combined, nonvanishing contributions come from the outside of the shaded region in Fig. 1. Hence the net result has only ultraviolet (UV) divergences without the IR divergence or the term with .
As a result, we obtain the csoft function to NLO in as
| (26) | |||||
This is a new result from this paper. for -csoft interactions has the same result. If we take the limit , Eq. (26) becomes the massless result shown in Eq. (10).
Finally, we confirm that the heavy quark dijet cross section can be factorized as
| (27) | |||||
where . We might be able to consider the heavy quark mass correction to the hard function , but it can be safely ignored since it is suppressed by . Compared with the massless case, the hsoft function also remains unchanged since hsoft radiations are insensitive to the quark mass. If we consider the limit in Eq. (27), the result recovers Eq. (11). This is a good consistency check for the heavy quark cross section. Furthermore we can apply Eq. (27) to the limit . In this case the result can be considered as the one with all power corrections in the expansion of .
III Resummation of large logarithms in the heavy quark dijet cross section
In Eq. (27) each factorized function has its own scale to minimize large logarithms. So, through RG evolution of the factorized functions from the factorization scale to their own scales, we can consistently resum the large logarithms. The factorized functions satisfy the following RG equations,
| (28) |
Here , and . To next-to-leading logarithm (NLL) accuracy needed to resum contributions of order unity, the anomalous dimensions are given by
| (29) | |||||
| (30) |
where is for and is for . The scale invariance of the cross section is easily checked through the result,
| (31) |
In Eq. (29) and (30), is the cusp anomalous dimension Korchemsky:1987wg ; Korchemskaya:1992je . We employed the first two terms in the expansion, , where the two coefficients are given as
| (32) |
Solving the RG equations in Eq. (28), we exponentiate large logarithms to NLL accuracy, and the result for the cross section is given by
| (33) |
where the factorization scale dependence in each factorized function in Eq. (27) has been exactly cancelled. Here we set the default scales for the evolutioned functions as , where . The exponentiation factor in Eq. (33) is
| (34) | |||||
Here and are defined as
| (35) |
where , and is QCD beta function to be expanded as .
The exponentiation of Eq. (34) is not sufficient for the full resummation at NLL accuracy since it does not include large nonglobal logarithms Dasgupta:2001sh ; Banfi:2002hw , which start to appear at order . In our case collinear gluon radiations from the heavy quark have a limited phase space bounded by . Then the decoupled csoft gluons from the collinear gluon and the heavy quark can give rise to the nonglobal logarithms at the higher orders than order . Resummation of the nonglobal logarithms involved with a heavy quark is beyond the scope of this paper.111Very recent study of nonglobal logarithm resummation related to top pair production Balsiger:2020ogy would be helpful for the future analysis.

For numerical implementation, we have considered the dijet ratio of -annihilation, i.e., . Here is the inclusive cross section for the heavy quark pair production, and it is given as to NLO in . In Fig. 2 the resummed results for the dijet ratio have been illustrated and compared with the fixed order results at NLO. The resummed result has significant suppression.
In Fig. 2 (a) and (b), the quark mass effects have been estimated by comparing with the results in the massless limit. The inclusion of the heavy quark mass enhances the results sizably. For example, the dijet ratio with at pole increases by due to the quark mass under variation of . If we consider the charm dijet ratio in the same situation, the charm quark mass effect enhances it by .
In Fig. 2 (c) and (d), scale variations of the resummed result have been estimated. When we obtain the errors, we independently vary the scales, , from to . The scale uncertainty from the four scale variations is rather large. In spite of this, we still observe meaningful deviations from the fixed order results. If we obtain the dijet ratio to higher order accuracy in the resummation, the uncertainty should be significantly reduced. This will be the focus of future work.
IV Exclusive heavy quark pair production
If we look into Fig. 2 (a), we see that the heavy quark dijet cross section can be safely extended to the limit . Unlike the massless case, a collinear divergence does not arise in this limit due to the heavy quark mass. So, if we consider the exclusive heavy quark pair production, the IR safe cross section can be obtained from the dijet cross section taking the limit . In this case, the jet veto with in the dijet cross section can be considered as an energy cut of soft hadrons. As a result, the cross section for the heavy quark pair can be regarded as the cross section for “the hemisphere isolation of the heavy quark”.
The factorization theorem for the exclusive heavy quark pair production can be immediately obtained from the result of the dijet cross section in Eq. (27), and it leads to
| (36) |
Here, taking the limit of and as , we obtain the collinear function and the csoft function respectively. The NLO results are given by
| (37) | |||||
| (38) |
Here is the matching coefficient onto bHQET and the result of integrating out virtual collinear interactions of the heavy quark Neubert:2007je ; Fleming:2007xt ; Fickinger:2016rfd .
Using the factorization theorem in Eq. (36), we resum the large logarithms of and to NLL accuracy. The result is free from nonglobal logarithms since . In Fig. 3, we show the rate of the exclusive heavy quark pair production over total cross section for , which is defined as . Like the dijet case, the exclusive cross sections are suppressed due to the resummation of large logarithms.

In Fig. 3 (a), the resummed results for the quark pair production have been illustrated in the range . Compared with the resummed -jet rate with , the suppression of the quark pair production becomes larger as increases. This is not surprising if we consider the dead cone effect Dokshitzer:1991fc ; Dokshitzer:1991fd ; Ellis:1991qj . As the heavy quark mass impact becomes smaller, the probability of collinear gluon radiations from the heavy quark become higher. In case of the exclusive production, in principle no collinear gluon radiation is allowed. Hence the rate for the quark pair production should be suppressed as the energy is large.
The exclusive production for the quark is not realistic and the prediction here can be spoiled by nonperturbative interactions such as hadronization effects. Instead, for example, we may consider the dijet ratio with as shown in Fig. 3 (a) (the dotted lines). In this case the resummed results are more reliable, but still give small fractions, . An interesting point is that the resummed results for both the cases describe very similar situation with a leading process at parton level, i.e., only in the final state. Here the fraction can be also considered as the ratio over LO cross section, , since NLO corrections to the total cross section are quite small. The smallness of implies that we cannot adhere to the view that the parton at leading process can be identified with a sharp jet.
In Fig. 3 (b) and (c), the resummed results for the exclusive top pair production have been illustrated. Here the error bands have been estimated in the same way as the case of the dijet ratio. The top fraction is over in wide range of . This indicates that the top does not radiate many collinear gluons due to the large top quark mass. So, even with the extreme isolation of the top quark, we can expect rather a large cross section.
V Conclusion
We have considered the exclusive heavy quark dijet cross section. The factorization theorem is similar to the cross section for the massless case. But, the jet sector is modified to have the quark mass, and the factorization into the collinear and the csoft part can be systematically performed through matching between and bHQET.
Using the factorization theorem we obtained the resummed result for the heavy quark dijet cross section to NLL accuracy and compared it with the result in the massless limit. As a consequence, the heavy quark dijet ratios become quite suppressed by the resummation of large logarithms, and the heavy quark mass effects sizably enhances the results compared to the massless limit unless is much larger than the quark mass.
Since the heavy quark mass removes the collinear divergence, we can investigate the extreme limit of the dijet cross section as . The resulting cross section has been also analyzed to NLL accuracy. Compared with the LO result, the cross section for the exclusive top pair production is not suppressed much due to the large top quark mass, while the quark production is severely suppressed especially when the energy becomes large. The suppression through resummation of large logarithms implies that the results of some exclusive processes cannot be approximated as the LO results in at the parton level. It would be interesting to apply this idea to exclusive leptonic processes with a tight energy cut of soft photons.
Acknowledgements.
The author is grateful to Adam Leibovich for useful comments. This study was supported by the Research Program funded by Seoul National University of Science and Technology.References
- (1) M. Dasgupta, F. Dreyer, G. P. Salam and G. Soyez, JHEP 1504, 039 (2015) [arXiv:1411.5182 [hep-ph]].
- (2) Z. B. Kang, F. Ringer and I. Vitev, JHEP 1610, 125 (2016) [arXiv:1606.06732 [hep-ph]].
- (3) L. Dai, C. Kim and A. K. Leibovich, Phys. Rev. D 94, no. 11, 114023 (2016) [arXiv:1606.07411 [hep-ph]].
- (4) C. W. Bauer, S. Fleming and M. E. Luke, Phys. Rev. D 63, 014006 (2000) [hep-ph/0005275].
- (5) C. W. Bauer, S. Fleming, D. Pirjol and I. W. Stewart, Phys. Rev. D 63, 114020 (2001) [hep-ph/0011336].
- (6) C. W. Bauer, D. Pirjol and I. W. Stewart, Phys. Rev. D 65, 054022 (2002) [hep-ph/0109045].
- (7) C. W. Bauer, S. Fleming, D. Pirjol, I. Z. Rothstein and I. W. Stewart, Phys. Rev. D 66, 014017 (2002) [hep-ph/0202088].
- (8) G. F. Sterman and S. Weinberg, Phys. Rev. Lett. 39, 1436 (1977)
- (9) S. Catani, Y. L. Dokshitzer, M. H. Seymour and B. R. Webber, Nucl. Phys. B 406, 187 (1993).
- (10) S. D. Ellis and D. E. Soper, Phys. Rev. D 48, 3160 (1993) [hep-ph/9305266].
- (11) Y. L. Dokshitzer, G. D. Leder, S. Moretti and B. R. Webber, JHEP 9708, 001 (1997) [hep-ph/9707323].
- (12) M. Cacciari, G. P. Salam and G. Soyez, JHEP 0804, 063 (2008) [arXiv:0802.1189 [hep-ph]].
- (13) W. M. Y. Cheung, M. Luke and S. Zuberi, Phys. Rev. D 80, 114021 (2009) [arXiv:0910.2479 [hep-ph]].
- (14) S. D. Ellis, C. K. Vermilion, J. R. Walsh, A. Hornig and C. Lee, JHEP 1011, 101 (2010) [arXiv:1001.0014 [hep-ph]].
- (15) J. Chay, C. Kim and I. Kim, Phys. Rev. D 92, no. 3, 034012 (2015) [arXiv:1505.00121 [hep-ph]].
- (16) T. Becher, M. Neubert, L. Rothen and D. Y. Shao, Phys. Rev. Lett. 116 (2016) no.19, 192001 [arXiv:1508.06645 [hep-ph]].
- (17) Y. T. Chien, A. Hornig and C. Lee, Phys. Rev. D 93 (2016) no.1, 014033 [arXiv:1509.04287 [hep-ph]].
- (18) A. K. Leibovich, Z. Ligeti and M. B. Wise, Phys. Lett. B 564, 231 (2003) [hep-ph/0303099].
- (19) I. Z. Rothstein, Phys. Rev. D 70, 054024 (2004) [hep-ph/0301240].
- (20) J. Chay, C. Kim and A. K. Leibovich, Phys. Rev. D 72, 014010 (2005) [hep-ph/0505030].
- (21) L. Dai, C. Kim and A. K. Leibovich, in preparation.
- (22) L. Dai, C. Kim and A. K. Leibovich, JHEP 1809, 109 (2018) [arXiv:1805.06014 [hep-ph]].
- (23) G. Korchemsky and A. Radyushkin, Nucl. Phys. B 283 (1987), 342-364
- (24) I. Korchemskaya and G. Korchemsky, Phys. Lett. B 287 (1992), 169-175
- (25) A. V. Manohar and I. W. Stewart, Phys. Rev. D 76, 074002 (2007) [hep-ph/0605001].
- (26) M. Dasgupta and G. P. Salam, Phys. Lett. B 512, 323 (2001) [hep-ph/0104277].
- (27) A. Banfi, G. Marchesini and G. Smye, JHEP 0208, 006 (2002) [hep-ph/0206076].
- (28) M. Balsiger, T. Becher and A. Ferroglia, [arXiv:2006.00014 [hep-ph]].
- (29) M. Neubert, [arXiv:0706.2136 [hep-ph]].
- (30) S. Fleming, A. H. Hoang, S. Mantry and I. W. Stewart, Phys. Rev. D 77, 114003 (2008) [arXiv:0711.2079 [hep-ph]].
- (31) M. Fickinger, S. Fleming, C. Kim and E. Mereghetti, JHEP 11 (2016), 095 [arXiv:1606.07737 [hep-ph]].
- (32) Y. L. Dokshitzer, V. A. Khoze and S. I. Troian, J. Phys. G 17 (1991), 1481-1492
- (33) Y. L. Dokshitzer, V. A. Khoze and S. I. Troian, J. Phys. G 17 (1991), 1602-1604
- (34) R. K. Ellis, W. J. Stirling and B. R. Webber, Camb. Monogr. Part. Phys. Nucl. Phys. Cosmol. 8, 1-435 (1996)