Excitonic Correlations, Spin-State Ordering, and Magnetic-Field Effects in One-Dimensional Two-Orbital Hubbard Model for Spin-Crossover Region

In this subsection, we present phase diagrams obtained by the numerical analysis with DMRG.

First, we fix the anisotropy factor for the pseudospin interaction at $\eta=1\,(\Leftrightarrow t_{a}=t_{b})$ and make a phase diagram in the plane of the Hund coupling $J$ and the crystal-field splitting $\Delta$, where we set the parameters of the Coulomb interactions to $U/\sqrt{t_{a}^{2}+t_{b}^{2}}=12$, $U^{\prime}=U-2J$, and $J=I$ as a strongly correlated region. The $\Delta$-$J$ phase diagram is shown in Fig. 1(a). In Fig. 1(a), as $\Delta$ increases, the phase shifts as HS $\rightarrow$ EI $\rightarrow$ LS, where HS, EI, and LS stand for a low-spin phase, an excitonic insulating phase, and a high-spin phase, respectively. We obtain the phase boundaries by the rapid changes of the entanglement entropy, which is discussed in SubSect. 3.4.

In Fig. 1(b), we present the populations of the HS state $\braket{P_{H}}$ and LS state $\braket{P_{L}}$ along the dashed line in Fig. 1(a). In the EI phase, the LS state and the HS state coexist, and the population of the LS state increases as $\Delta$ increases.

We can understand the property of the EI phase in the nearest correlation functions. We show the nearest correlation functions, $\braket{\tau_{\Gamma i}^{x}\tau_{\Gamma i+1}^{x}}$, $\braket{\tau_{\Gamma,i}^{y}\tau_{\Gamma,i+1}^{y}}$, $\braket{\tau_{\Gamma,i}^{z}\tau_{\Gamma,i+1}^{z}}$, and $\braket{s_{i}^{z}s_{i+1}^{z}}$ in Fig. 1(c). Note that the product of the nearest pseudospin, $\braket{\tau_{\Gamma i}^{z}}\braket{\tau_{\Gamma i+1}^{z}}$, is not subtracted from $\braket{\tau_{\Gamma i}^{z}\tau_{\Gamma i+1}^{z}}$ although $\braket{\tau_{\Gamma j}^{z}}$ is positive in the HS phase and negative in the LS phase. We compute the correlation function at the center of the system. The values of the pseudospin correlations are independent of the quadrupole basis $\Gamma=X,Y,Z$ because of the rotational symmetry. The large value of $|\braket{\tau_{\Gamma,i}^{x}\tau_{\Gamma,i+1}^{x}}|$ in the EI phase indicates that the EI phase is stabilized by the local kinetic energy of excitons. Compared with $\braket{\tau_{\Gamma,i}^{x}\tau_{\Gamma,i+1}^{x}}$, $\braket{\tau_{\Gamma,i}^{y}\tau_{\Gamma,i+1}^{y}}$ does not show strong antiferrmagnetism. This is because the antiferromagnetic interactions between pseudospins satisfy $J_{x}>J_{y}$. $\braket{\tau_{\Gamma,i}^{z}\tau_{\Gamma,i+1}^{z}}$ also does not show strong antiferromagnetism even near the center of the EI phase as a result of $J_{x}>J_{z}$. Near the HS(LS) phase, large value of $-h_{\tau z}$ $(h_{\tau z})$ makes $\braket{\tau_{\Gamma,i}^{z}\tau_{\Gamma,i+1}^{z}}$ ferromagnetic. In terms of long-range correlation functions, $\braket{\tau_{\Gamma i}^{x}\tau_{\Gamma j}^{x}}$ and $\braket{\tau_{\Gamma i}^{y}\tau_{\Gamma j}^{y}}$ become zero at $|i-j|\rightarrow\infty$. This means that there is no long-range order in the EI phase, that is $\braket{\tau_{\Gamma i}^{x}}=\braket{\tau_{\Gamma i}^{y}}=0$ for $\Gamma=X,Y,Z$ and $i$ at any site. Since there are spin-spin interaction and three types of pseudospin-pseudospin interactions identified by $\Gamma$ in Eq. (27), the long-range order of EI can be suppressed as a result of the competition of the interactions.

The nearest spin correlation $\braket{s_{i}^{z}s_{i+1}^{z}}$ in Fig. 1(c) is antiferromagnetic in the HS and EI phases. In the HS phase, $\braket{P_{H}}\sim 1$. In this region, the effective Hamiltonian reduces to the antiferromagnetic spin-1 Heisenberg model, and the nearest spin correlations becomes negative. In the EI phase, $\braket{P_{H}}$ is finite, and antiferromagnetic spin-spin interaction between the HS states make the nearest spin correlation negative.

Next, we present a phase diagram in the plane of the anisotropy for the pseudospin interaction $\eta$ and the crystal-field splitting $\Delta$ in Fig. 2, where we fix the parameters of Coulomb interactions to $U/\sqrt{t_{a}^{2}+t_{b}^{2}}=12$, $U^{\prime}/\sqrt{t_{a}^{2}+t_{b}^{2}}=8$, and $J/\sqrt{t_{a}^{2}+t_{b}^{2}}=I/\sqrt{t_{a}^{2}+t_{b}^{2}}=2$. In addition to the HS, EI, and LS phases, the SSO phase is found in Fig. 2. In the SSO phase, the spin states show superlattice structures, in which the population of HS states varies from site to site. The spatial structure of SSO changes depending on $\Delta$ and $\eta$. We focus on the spatial structures in the next subsection.

We characterize the SSO phase on the basis of the existence of a superstructure of spin states. The criterion is that a state is in the SSO phase when $\mathrm{max}(\braket{P_{Hi}})-\mathrm{min}(\braket{P_{Hi}})>10^{-2}$ for $i$ in the central 20 sites in a 60-sites system with open boundaries.

The outlines in the phase diagrams in Fig. 1 and Fig. 2 can be understood as the typical configurations of pseudospins which is shown in Table 1, and is consistent with the previous studies with mean-field approximation[10] and dynamical mean-field approximation. [19] However, no spin or pseudospin orderings are observed in the HS and EI phases. This is interpreted as the result of the effect of strong quantum fluctuations in a 1D system, which is considered in the DMRG method. In addition, various types of spin-state structures were obtained by using large 1D clusters.

In this subsection, we present the spatial structures of the spin states in the EI phase and the SSO phase through correlation functions. We set the system size as $L=60$ and use the periodic boundary condition.

We consider a Fourier transformed correlation functions for spin states as

where $X_{i}$ is a one-site operator at a site $i$. Note that the product of one-site expected values are not subtracted in $C_{X}(k)$.

First, we fix the parameters as $U/\sqrt{t_{a}^{2}+t_{b}^{2}}=12,J/\sqrt{t_{a}^{2}+t_{b}^{2}}=I/\sqrt{t_{a}^{2}+t_{b}^{2}}=2,U^{\prime}=U-2J,\eta=0.5$. In this region, the phase transition is HS $\rightarrow$ EI $\rightarrow$ LS as $\Delta/\sqrt{t_{a}^{2}+t_{b}^{2}}$ increases.

In Fig. 3(a), we present the correlation function for the HS state $C_{P_{H}}(k)$ in the EI phase. Since $\braket{P_{Hi}}$ is uniform in the EI phase, $k$-dependence of $C_{P_{H}}(k>0)$ corresponds to the spatial quantum fluctuation in the population of HS states. $C_{P_{H}}(k=0)$ originates in the uniform populations of the HS state. $k$-dependence of $C_{P_{H}}(k>0)$ is small in the HS phase and the LS phase and becomes large in the EI phase. This behavior means that, in the EI phase, there is a strong quantum fluctuation, and the ground state is far from the direct product state such as $(\tau_{\Gamma}:\rightarrow\;\leftarrow\dots\rightarrow\;\leftarrow)$, in which $C_{P_{H}}(k>0)$ is constant. In Fig. 3(a), we also show the wave number at $2\tilde{k}=\mathrm{min}(2\pi\braket{P_{H}},2\pi(1-\braket{P_{H}}))$ by broken lines, where $\braket{P_{H}}$ is the spatial average of the populations of HS states. If excitons are regarded as free fermions, $\tilde{k}$ is interpreted as the Fermi wavenumber. In the EI phase, $C_{P_{H}}(k>0)$ tends to rise as $k$ increases in $k<\tilde{k}$ and becomes constant in $k>\tilde{k}$. This behavior is similar to the behavior of 1D spinless free fermions. As a difference from the case of fermions, $C_{P_{H}}(k\rightarrow 0)$ is non-zero in the EI phase. This originates in the anisotropy of $J_{x}>J_{y}$ in Eq. (27), which means the number of excitons does not conserve.

In Fig. 3(b), we show the Fourier transformed spin correlation $C_{s^{z}}(k)$ with the same parameters as those in Fig. 3(a). $C_{s^{z}}(k)$ has a peak at $k=\pi\braket{P_{H}}$ in the EI and HS phases. This is interpreted as the spin correlation in the EI phase representing a spin density wave whose wavenumber corresponds to the population of the HS state, although there is no spin ordering.

Next, we fix $\eta=0.3$. In this region, the phase transitions are HS $\rightarrow$ EI $\rightarrow$ SSO $\rightarrow$ EI $\rightarrow$ LS as $\Delta/\sqrt{t_{a}^{2}+t_{b}^{2}}$ increases. Figure 4(a) shows $C_{P_{H}}(k)$ in the SSO phase. We also show the peak wavenumbers against the crystal-field splitting in Fig. 4(b). The sharp peaks in Fig. 4(a) represent the structure of the SSO. There is a strong peak for $k=2\pi/3$ in $\Delta/\sqrt{t_{a}^{2}+t_{b}^{2}}=5.75$. This peak represents the LS/HS/HS structure shown in Fig. 4(d).

As shown in Fig. 4(b), the spin-state structure in the SSO phase changes against the crystal-field splitting $\Delta/\sqrt{t_{a}^{2}+t_{b}^{2}}$. The plateau at $k=2\pi/3$ in Fig. 4(b) indicates that the LS/HS/HS structure is stable. According to the Hamiltonian in Eq. (27), the nearest LS-HS pair is stabilized by the $J_{z}$ term, and the nearest HS-HS pair is stabilized by the $J_{s}$ term. The LS/HS/HS structure is realized as a result of the competition between these interactions. In the other region in the SSO phase, two peaks branch from the peak at $k=2\pi/3$. The two peaks have generally incommensurate wavenumbers, and one of them follows the population of the HS state $\braket{P_{H}}$. The discretization of the $k_{\mathrm{peak}}$ in Fig. 4(b) seems to originate from the finite system size $L=60$ and should become continuous in $L\rightarrow\infty$. Some snapshots of the spin-state structures in the SSO phase are shown in Fig. 4(c1)-(c3). Figure 4(c1) shows the LS/HS/HS structure shown in Fig. 4(d). Figure 4(c2) shows the structure at $\Delta/\sqrt{t_{a}^{2}+t_{b}^{2}}=5.77$, which is near the parameter at which LS/HS/HS structure realizes. Here some kinks are inserted into the basic LS/HS/HS structure. Figure 4(c3) shows the structure at $\Delta/\sqrt{t_{a}^{2}+t_{b}^{2}}=5.79$, which is far from the parameter of LS/HS/HS structure. Here a complex spin state is found. In the region where $\braket{P_{H}}<0.5$, the SSO phase is not found. This result indicates that the spin-spin interaction between the HS states contributes to the stabilization of the SSO with the LS/HS/HS structure.

In this subsection, we present the magnetic-field effects in the effective model. Figures 5(a) and 5(b) are phase diagrams in the plane of the crystal-field splitting $\Delta/\sqrt{t_{a}^{2}+t_{b}^{2}}$ and a magnetic field $H/\sqrt{t_{a}^{2}+t_{b}^{2}}$, where we fix the parameters, $U/\sqrt{t_{a}^{2}+t_{b}^{2}}=12$, $J/\sqrt{t_{a}^{2}+t_{b}^{2}}=I/\sqrt{t_{a}^{2}+t_{b}^{2}}=2$, $U^{\prime}=U-2J$ and $\eta=1\,(\Leftrightarrow t_{a}=t_{b})$. In these parameters, the EI phase exists in the intermediate region between the HS and LS phases. In Figs.5(a) and 5(b), in addition to the HS, EI, and LS phases, there appears a type-1 magnetized excitonic insulating phase (MEI-1), a type-2 magnetized excitonic insulating phase (MEI-2), a magnetized high-spin phase (MHS), and a fully polarized phase (Full Polar). We determine the phase boundary on the basis of the discontinuity of the first derivative of the magnetization curve. Basically, we set the system size as $L=60$ and set the truncation number in DMRG as $\chi=64$.

The value of a magnetic field at the phase boundaries for HS-MHS, EI-MEI-2, and LS-MEI-1 corresponds to the spin gaps in HS, EI, and LS phases, respectively. As shown in Figs.5(a) and 5(b), spin gaps are obtained in the HS, EI, and LS phases, and the spin gaps appears to be closed at the EI-LS phase boundary. To determine the spin gaps in the HS and EI phases, system-size extrapolations are performed. The extrapolation is performed with the function

where $\Delta_{s}(\infty)$, $a$, and $b$ are the fitting parameters. $\Delta_{s}(L)$ is a spin gap in the system whose size is $L$. $\Delta_{s}(L)$ is computed by $\Delta_{s}(L)=E^{(m=2)}(L)-E^{(m=0)}(L)$, where $E^{(m)}(L)$ is the energy of the ground state at $\braket{\sum_{i}s^{z}_{i}}=m$. We avoid $E^{(m=1)}(L)-E^{(m=0)}(L)$ because it corresponds to the spin excitation at the edges, and this magnetization is ignored in an infinite system. We use $L=128,192,256$ under the open boundary condition and set the truncation number in DMRG to $\chi=256$. Some examples for the $L$ dependence of the $\Delta_{s}(L)$ are shown in Fig. 6. Figure 6(a) and (b) show that there is a finite spin gap in the HS and EI phases. In the EI phase near the LS phase of $5.90<\Delta/\sqrt{t_{a}^{2}+t_{b}^{2}}<6.15$, the spin gap becomes small and its existence is not obtained with sufficient accuracy. Therefore, we omit the points in this region.

The spin gap in the HS phase is the Haldane-gap because in $\Delta\ll U-U^{\prime}+J$, the low-energy effective Hamiltonian in Eq. (27) reduces to the spin-1 Heisenberg model. In fact, the value of the spin gap in the HS phase in Fig. 5(b) is in good agreement with $\Delta_{\mathrm{Haldane}}J_{s}=0.0293$, where $J_{s}=(t_{a}^{2}+t_{b}^{2})/(U+J)=0.0714$ is the amplitude of spin-spin interaction in Eq. (27), and $\Delta_{\mathrm{Haldane}}=0.4105$ is the value of Haldane gap of the spin-1 Heisenberg model obtained in the previous study.[25]

The spin gap in the EI phase is similar to the one of the spin-1 Heisenberg model as follows. First, the value of spin gap in the EI phase connects to the one in the HS phase. Second, the ground state energies in the EI phase degenerate for $m=0,\pm 1$ under the open boundary condition, and the degeneracy lifts under the periodic boundary condition. This result suggests the existence of free 1/2 spins at edges similar to the case of the AKLT model. We discuss the edge state in detail in Subsect. 3.5 through the observation of entanglement spectra.

The spin gap in the LS phase is due to the energy difference between the LS state and the HS state.

From here, we present the magnetization processes in the phases along the dashed lines (c)-(h) in Fig. 5(a).

The magnetization process in a wide range of the HS phase is HS $\rightarrow$ MHS $\rightarrow$ Full Polar (the dashed line at (c) and (d) in Fig. 5(a)). In the MHS phase, the population of the LS state is almost zero, and $\braket{\tau_{\Gamma,i}^{x}\tau_{\Gamma,i+1}^{x}}$ is almost zero. Therefore, the magnetization process in the MHS phase is the process in which $s=1$ spins are aligned by a magnetic field.

The magnetization process in the EI phase is EI $\rightarrow$ MEI-2 $\rightarrow$ MEI-1 $\rightarrow$ Full Polar (the dashed line at (e) and (f) in Fig. 5(a)), where we call the MEI phase in a low magnetic field MEI-2 and the phase in a high magnetic field MEI-1. As shown in Fig. 5(e), in the MEI-2 phase, the population of the HS state is finite for all bases of $s^{z}=+1,0,-1$, whereas in the MEI-1 phase, the populations of $s^{z}=+1$ is finite, and that of $s^{z}=0,-1$ is almost zero. Therefore, the phase transition of MEI-2 $\rightarrow$ MEI-1 occurs when the $s=1$ spins are fixed to $s^{z}=+1$ by a magnetic field. Because of the antiferromagnetic spin-spin interaction, MEI-2 phase survives even in a finite magnetic field. Regarding the nearest correlation functions shown in Fig. 5(f), while $\braket{\tau_{\Gamma,i}^{x}\tau_{\Gamma,i+1}^{x}}$ for $\Gamma=X,Y,Z$ are all negative in the MEI-2 phase, $\braket{\tau_{Z,i}^{x}\tau_{Z,i+1}^{x}}$ is almost zero in the MEI-1 phase. This means that the MEI-1 phase is stabilized by the kinetic energy of $s^{z}=+1$ excitons. Since $\ket{H_{s^{z}=+1}}=-(P_{X}^{+}\ket{L}+iP_{Y}^{+}\ket{L})/\sqrt{2}$, the $X$ and $Y$ excitons coexist with the $z$-direction magnetization, while the $Z$ excitons compete with the magnetization. As a result, in the MEI-2 phase, the $X$, $Y$, and $Z$ excitons are stabilized, while in the MEI-1 phase, only $s^{z}=+1$ exciton is stabilized.

The magnetization process in the LS phase is LS $\rightarrow$ MEI-1 $\rightarrow$ Full Polar (the dashed line at (g) and (h) in Fig. 5(a)). The MEI-1 phase is the same phase as in the magnetization process in the EI phase. As shown in Figs. 5(g) and 5(h), the properties of the populations and the nearest correlations are consistent with the MEI-1 phase in the magnetization process in the EI phase.

In Fig. 5(a), we presented the magnetic-field effects around the EI phase, where $\eta=1\,(\Leftrightarrow t_{a}=t_{b})$. The magnetic field effects for smaller $\eta$ are left for future work, where the magnetized SSO phase may be found because the LS/HS phase was obtained under a magnetic field with a mean-field analysis.[11]

In this subsection, we present the properties of entanglement entropy in the HS, EI, and LS phases. Generally, entanglement entropy is sensitive to phase transitions, and is useful to determine the phase boundaries [28, 29, 30]

Figure 7 shows the entanglement entropy as a function of crystal-field splitting. The entanglement entropy is defined for the density matrix of a $30$ site subsystem in a $60$ site system. The system has the periodic boundary condition. The truncation number in DMRG is set to $\chi=256$ for Fig. 7. We set $\eta=1.0\,(\Leftrightarrow t_{a}=t_{b})$, $U/\sqrt{t_{a}^{2}+t_{b}^{2}}=12$, $U^{\prime}=U-2J$ and $J=I$, which are the same as the parameters in the dashed line in Fig. 1(a).

The value of entanglement entropy in the HS phase is consistent with the one of the spin-1 Heisenberg model.[31] The entanglement entropy in the HS phase is not far from $2\log 2\sim 1.39$. The value of $2\log 2$ is derived from the valencebond in the AKLT model. The picture of valence bond solid (VBS) in the AKLT model[32] is applied to the picture in the HS phase. In this picture, the value of $2\log 2$ originates in the two valence bonds in the edges of the subsystem, and the additional value comes from the modulation from the AKLT model. In the EI phase, the entropy is larger than the one in the HS and LS phases. The rapid changes in the entanglement entropy are found in the HS-EI and EI-LS boundaries. Based on these changes, we determined the phase boundaries in Fig. 1 and Fig. 2. In the LS phase, the entropy is quite small. This is because the electrons in the LS phase cannot move due to the Pauli exclusion principle.

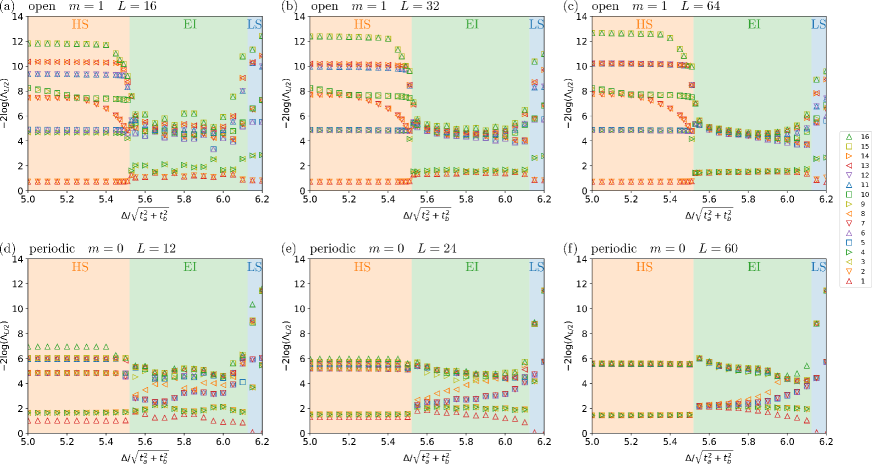
In this section, we discuss the quantum state in the EI phase through the observation of entanglement spectra. As described in SubSect. 3.3, spin gaps are obtained in the HS and EI phases, which suggests the relationship with the Haldane gap.

In the case of the spin-1 Heisenberg model, it is known that the entanglement spectra with the largest singular values are degenerate.[33] This degeneracy comes from the fact that the ground state is understood by the VBS picture in the AKLT model. In the VBS picture, singlet composed by virtual 1/2 spins results in the degeneracy of $\uparrow\downarrow$ and $\downarrow\uparrow$.

In Fig. 8, we show the entanglement spectra for the HS, EI, and LS phases in our model. The parameters are set to $U/\sqrt{t_{a}^{2}+t_{b}^{2}}=12$, $J/\sqrt{t_{a}^{2}+t_{b}^{2}}=2$, $I/\sqrt{t_{a}^{2}+t_{b}^{2}}=2$, $U^{\prime}=U-2J$ and $t_{a}=t_{b}$, which are the parameters at the $H=0$ line in Fig. 5(a). As $\left(\mathrm{boundary}\;\mathrm{condition},m=\braket{\sum_{i}s_{i}^{z}}\right)$, we show the cases of (open, $m=1$) and (periodic, $m=0$). The reasons for adopting these settings are described later in this subsection. For the system sizes, we adopt $L=16,32,64$ for the open boundary condition, and $L=12,24,60$ for the periodic one.

In the HS phase, the entanglement spectra for the maximum singular values degenerate to 2-fold under the open boundary condition as the system size increases as (a)$\rightarrow$(b)$\rightarrow$(c), and degenerate to 4-fold under the periodic boundary condition as (d)$\rightarrow$(e)$\rightarrow$(f). These degeneracies are explained by VBS pictures in Figs. 9(a) and 9(b). When the system is divided, the degeneracy in the entanglement spectra appears due to the singlet composed of 1/2 spins on the cross sections of both sides. Under the open boundary condition, one set of singlets is divided, and under the periodic one, two sets of singlets are divided. Therefore, there appears 2-folded degeneracy under the open boundary condition and 4-folded degeneracy under the periodic boundary condition. The reason why we adopt the condition of $m=1$ under the open boundary condition is to align the almost free 1/2 spins at both edges in the same direction. These results for the entanglement spectra in the HS phase are consistent with previous studies in the spin-1 Heisenberg model.[34, 33]

In the EI phase, as the system size increases, the spectra for the maximum singular values degenerate to 4-fold under the open boundary condition and degenerate to 8-fold under the periodic boundary condition. These degeneracies are explained as follows. First, as in the case of the HS phase, singlets at edges form entanglement of 2-folded degeneracy in the open boundary condition and 4-folded degeneracy in the periodic one. Second, in the EI phase, there are contributions to entanglements due to motions of excitons and fluctuations in the number of excitons. In our model in Eq. (8), we can obtain the following commutation relation $[P_{H}^{(2)},\mathcal{H}^{\mathrm{eff}}]=0$ where $P_{H}^{(2)}$ is a projection operator to the space where the total number of excitons is odd. $P_{H}^{(2)}$ is represented by $P_{H}^{(2)}=\sum_{\Lambda}\left(\prod_{\lambda\in\Lambda}P_{\lambda}^{H}\right)$, where $\Lambda$ denotes any set of site indexes with an odd number of elements. We introduce $N_{H}^{(2)}=0,1$ as a engenvalues of $P_{H}^{(2)}$. The eigenstate of $N_{H}^{(2)}=0$ indicates the superposition of the states where the number of excitons is even, and the other indicates the odd one. We consider the case when whole system is divided into two parts where $N_{H}^{(2)}$ of the whole system is fixed to 0. This condition is used in obtaining Fig. 8. In this case, the possible combinations of $N_{H}^{(2)}$ of subsystems are $(N_{H}^{(2)L},N_{H}^{(2)R})=(0,0)$ or $(1,1)$. If the sizes of the both subsystems and the number of excitons are large enough, the two entanglement spectra originating from $(0,0)$ and $(1,1)$ are degenerate. The degree of degeneracy of this entanglement spectra is not affected by boundary conditions since $N_{H}^{(2)}$ is a property of bulk.

From the above, the combination of singlets in the valence bonds and fluctuations of the excitons explains the 4(8)-folded degeneracy of the entanglement spectra under the open(periodic) boundary condition in Fig. 8. These results suggest that the spin gap obtained in the EI phase is given by the same mechanism as that of Haldane gap.