Examination of the bound-state problem with lattice QCD potentials
Abstract
The developed Faddeev three-body equations are solved to search for bound-state solutions of a phi-meson and two nucleons system. The newly published spin potential based on the -flavor lattice QCD simulations near the physical point, and the realistic Malfliet-Tjon (MT) potential, are employed. Our numerical calculations for system in maximum spin lead to ground state binding energy of about MeV and a matter radius of about fm. Our results indicate the possibility of the formation of new nuclear clusters.
I Introduction
In strangeness nuclear physics, the possibility of the formation of -mesic bound states with nucleons (N) [1, 2, 3, 4] is one the most exciting and important fields due to the quark content of the -meson as being . One of the simplest candidates for -mesic nuclei can be the system [5, 6, 7, 8]. Accordingly, the binding energy of state has been calculated using the folding method [5], solving the Faddeev equations in the coordinate space [6] and in two-variable integro-differential equations on the -dimensional space [7], where mostly attractive phenomenological interaction [9] by central binding energy of MeV and the semi-realistic Malfliet-Tjon (MT) potential[10], are employed. They concluded that the system is bound with a binding energy of about MeV for triplet(singlet) interaction [7].
On the other hand, from the experimental point of view, ALICE collaboration measured the correlation function of proton- in heavy-ion collisions [11], together by indicating a bound state using two-particle correlation functions [12] request the proton bound state hypothesis. To go one step further, the femtoscopic analysis of hadron-deuteron () correlation functions could play a crucial role in understanding the structure and dynamics of the atomic nuclei. Therefore the three-body calculations of the correlation function have special importance [13, 14]. Accordingly, the correlation functions are investigated for some hadron-deuteron systems like [13, 15], [14, 15], [16], [17], and the production of in ultra-relativistic heavy ion collisions are studied in [18, 19]. Hence, it is more desirable to study the properties of system by using the state-of-the-art few-body computational method .
Very recently, the first lattice QCD simulations of the potential in channel (by the notation where and are the total spin, orbital angular momentum and total angular momentum, respectively) are published [20]. The simulation is performed by -flavor with quark masses near the physical point MeV and MeV on a sufficient large lattice size of . Here, we employ this potential to study in the highest spin , this channel is selected because it cannot couple to the lower channels and with the and subsystem in waves. In addition, because of the small phase space, the decay to final states by four or more particles like and are supposed to be suppressed [20].
We should emphasize that since, some coupling constants like are known to be far from being OZI (Okubo-Zweig-Iizuka ) suppressed, the coupling to channels like or could be sizable and, this has been all ignored in the lattice simulations [20]. Such a coupling would change the scenario that will be studied here considerably.
II Three-Body Bound State by Expansion on Hyperspherical Harmonics Method
The expansion on hyperspherical harmonics method is a developed version of the Faddeev equations in coordinate space to study weakly bound three-body systems. The method is well-described in [21, 23, 24], so we present an outline of it very briefly here.
The complete three-body wave function is sum of three components , i.e, . The components are function of the three different sets of Jacobi coordinates (One of the three sets is shown in the Fig. 1), and they satisfy the three Faddeev coupled equations,
| (1) |
where is the kinetic energy, is the total energy, is the two-body interactions between the corresponding pair and the indexes is a cyclic permutation of .
The Jacobi coordinates , as depicted in Fig. 1, are employed to define the framework of three-body systems. The Jacobi-T coordinate set is the most suitable one for the system because the antisymmetrization of the wave function should be preserved under exchange of nucleons linked by the coordinate. The variable represents the relative coordinates between two of the particles and is between their center of mass and the third particle, both with a scaling mass factor. From the Jacobi coordinates, we can define the hyperspherical coordinates , with hyperradius (generalized radial coordinate) and the hyperangle (generalized angle) . The and are the angles defining the direction of and , respectively. For the sake of simplicity, we describe all angular dependencies by .
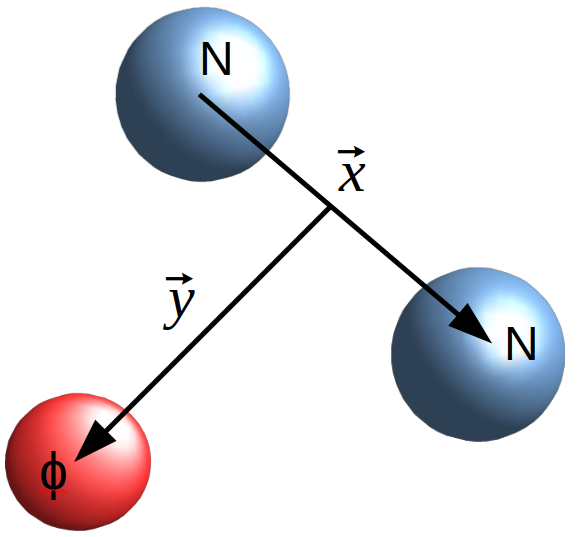
The Hamiltonian of a three-body system in hyperspherical coordinates is defined as follows:
| (2) |
the is potential operator which is the summation of pair interactions and the is the free Hamiltonian operator [25],
| (3) |
where is hyperangular momentum (generalized angular momentum) operator and is a normalization mass for which we choose .
Employing the hyperspherical coordinates, the solutions of the Schrödinger equation with the three-body Hamiltonian of Eq. (2) by total angular momentum can be expanded for each as
| (4) |
where the functions are a complete set of hyperangular functions that can be expanded in hyperspherical harmonics [21, 22, 23], and are the hyperradial wave functions, where the subscript denotes the hyperradial excitation (for the purpose of solving the coupled equations (6) the hyper-radial functions, are expanded in terms of orthonormal discrete basis up to [24]). Moreover, the is a set of quantum numbers coupled to . and are the orbital angular momenta related to the Jacobi coordinates and , respectively. represents the total orbital angular momentum, gives the total spin of pair particles related by , and . The total angular momentum is where indicates the spin of the third particle.
Therefore wave function of the system is defined by
where are the diagonalization coefficients that can be calculated by diagonalizing the three-body Hamiltonian for basis functions. The hyperradial wave functions are solutions to the coupled set of differential equations,
| (6) |
the term is related to the two-body potentials between each pair of particles (), by
| (7) |
III Two-body potentials
In this section, we introduce the two-body interaction of and different analytical form of extracted lattice potential which we used in our calculations for system.
III.1 potentials
For interactions, we use the Yukawa-type Malfliet-Tjon (MT) [10],
| (8) |
the parameters and are given in Table 1. This potential supports a deuteron binding energy of MeV.
III.2 potential
For the potential in the channel, i.e., the concrete parameterizations, are taken straight from Ref. [20] which is published very recently by the HAL QCD collaboration. Where they performed the uncorrelated fit on the lattice QCD extracted potential to calculate physical observables using two different analytic functional forms composed of attractive Gaussian and long-range Yukawa squared attractions [26, 27],
| (9) |
In Ref. [20], it is shown that the long-range part of the potential is clearly dominated by the two-pion exchange (TPE). This behavior suggests the has a TPE tail at long range with a strength coefficient [28]. Also, for comparison, a purely phenomenological Gaussian form is considered,
| (10) |
For the form factor in Eq. (9) two different types commonly used in the potential, is applied a Nijmegen-type form factor [29],
| (11) |
and the Argonne-type form factor [30],
| (12) |
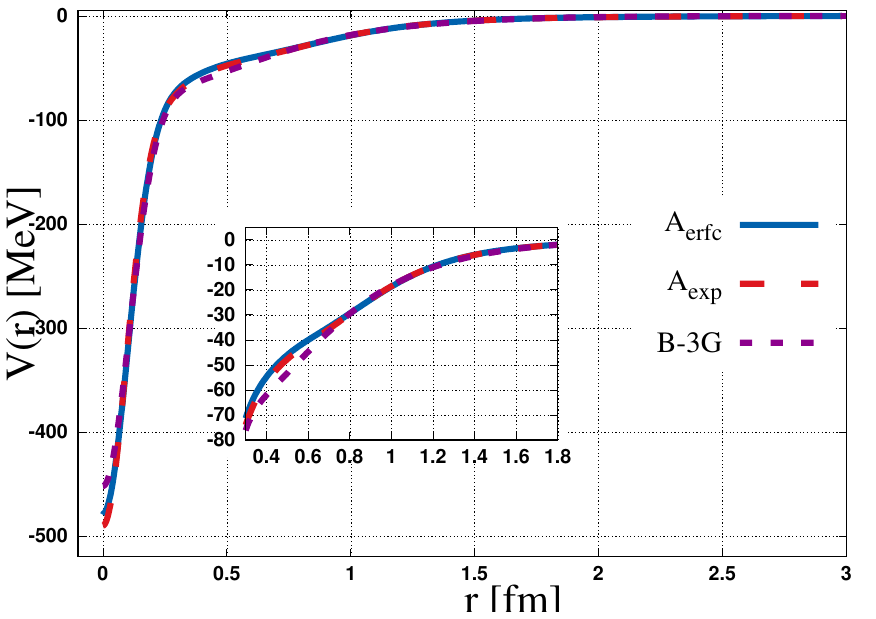
where the lattice pion mass is MeV, and is the complementary error function. Hereafter, we refer to with form factor as model, and model B is applied to in Eq. (10). The parameters of Eq. (9) and Eq. (10) those we employed in our calculations are given in Table 2. The central values of low-energy observables by potential are the scattering length fm, and the effective range fm [20] and no binding energy is observed for this interaction. The number between parentheses is the statistical error.
| ) | ||||||
| ) |
In Fig. 2 we show all three potential models in the channel using the parameters given in Table 2, for better comparison.
IV Numerical Results
Here, we present and discuss our numerical results for the ground state binding energy and nuclear matter radius for three-body state systems. For this purpose, the coupled equations (6) are solved by applying the FaCE computational toolkit [24] employing the two-body interactions described in Sec. III.
In the HH method, the final results depend on a maximum value of hypermomentum due to the expansion of the total three-body wave function in hypermomentum components, which are truncated by , therefore, it is necessary to investigate the convergence of results as a function of and the maximum number of hyperradial excitations (see Eq. (II)). The results converged quite well with the and for state.
The two-body system in channel( Fig. 2) by parametrizations of all three model , , and does not form a bound state as previously predicted in [31, 32] by using the hidden gauge theory with unitary coupled-channel calculations within symmetry, whereas within chiral quark model [33] and unitary coupled-channel approach [34] the existence of a bound state is reported. In older studies, as mentioned in the introduction, in Refs. [5, 6, 7] by using the attractive interaction [9], it is predicted that the binding energy of state could be about MeV for triplet(singlet) interaction.
Nevertheless, in this case, as expected no bound state found for state, i.e. and . While the state in the maximal spin channel is bound for all parametrizations of the potentials, i.e. , , and . The ground state binding energy and nuclear matter radius of state are given in Table 3. To calculate the r.m.s. matter radius of the system, the strong interaction radius of proton, neutron and -meson by the values fm and fm [8, 35], respectively, are have been used as input.
Moreover, the results with the and masses derived from -flavor lattice QCD simulations [20], presented in Table 3. The values of these masses are slightly bigger than the experimental value. As it can be seen from the Table 3, by lattice masses are a bit larger than by the experimental masses. This is because by increasing the masses, repulsive kinetic energy contribution will decrease which in turn leads to an increment in binding energies [36].
| (MeV) | (fm) | (MeV) | (fm) | (MeV) | (fm) | |||
|---|---|---|---|---|---|---|---|---|
| Expt. | ||||||||
| Lattice | ||||||||
V Summary and conclusions
In this work, the binding energy of the three-body system is examined using the first lattice QCD potential in the channel and semi-realistic Malfliet-Tjon interactions. The potential is obtained from QCD on a sufficiently large lattice at almost physical quark masses ( MeV and MeV) and parametrized in three different analytical forms, i.e. , and , where the concrete parameterizations of these models, are taken straight from Ref. [20].
Then, by having a two-body potential between each pair of particles, the coupled Faddeev equations in the coordinate space are solved within the hyperspherical harmonics expansion method.
We have tried to find bound states or resonances that can be observed in future experiments. The numerical results suggest that no bound state or resonances found for and systems. The system in the maximal spin presents a bound state with a binding energy of about MeV and a nuclear matter radius of about fm. The system in the maximal spin channel cannot couple to the lower three-body open channels and because wave subsystems and are kinematically suppressed at low energies. In addition, because of the small phase space, the decay to final states by four or more particles e.g. , and are supposed to be suppressed [20]. Last but not least, in Ref. [20] they have not consider the OZI violating annihilation in their simulations. Nevertheless, considering the coupling to channels like or could change the results obtained here significantly.
In conclusion, adding a -meson to the deuteron could enhance its binding energy. These bound states or resonances could be explored in hadron beam experiments. Recently, for the first time, ALICE collaboration measured the correlation function of proton- in heavy-ion collisions [11], and the existence of bound state has been discussed and explored in [12]. And very recently, the and femtoscopic correlations measured by the ALICE Collaboration in proton-proton (pp) collisions [14, 15], analogously, as the next step, these measurements could be done for system. We desire that our numerical results could help to plan experiments in the future.
References
- Gao et al. [2017] H. Gao, H. Huang, T. Liu, J. Ping, F. Wang, and Z. Zhao, Search for a hidden strange baryon-meson bound state from production in a nuclear medium, Phys. Rev. C 95, 055202 (2017).
- Hirenzaki and Yamagata-Sekihara [2010] S. Hirenzaki and J. Yamagata-Sekihara, Formation of Slow Heavy Mesons in Nuclei, Nucl. Phys. A 835, 406 (2010), proceedings of the 10th International Conference on Hypernuclear and Strange Particle Physics.
- Yamagata-Sekihara et al. [2010] J. Yamagata-Sekihara, D. Cabrera, M. J. Vicente Vacas, and S. Hirenzaki, Formation of Mesic Nuclei, Prog. Theor. Phys. 124, 147 (2010), https://academic.oup.com/ptp/article-pdf/124/1/147/9681103/124-1-147.pdf .
- Cobos-Martínez et al. [2017] J. J. Cobos-Martínez, K. Tsushima, G. Krein, and A. W. Thomas, -meson–nucleus bound states, Phys. Rev. C 96, 035201 (2017).
- Belyaev et al. [2008] V. B. Belyaev, W. Sandhas, and I. I. Shlyk, New nuclear three-body clusters , Few-Body Syst. 44, 347 (2008).
- Belyaev et al. [2009] V. B. Belyaev, W. Sandhas, and I. I. Shlyk, 3- and 4- body meson- nuclear clusters (2009), arXiv:0903.1703v1 [nucl-th] .
- Sofianos et al. [2010] S. A. Sofianos, G. J. Rampho, M. Braun, and R. M. Adam, The and mesic nuclear systems, J. Phys. G Nucl. Part. Phys. 37, 085109 (2010).
- Wang et al. [2023] X.-Y. Wang, C. Dong, and Q. Wang, First characterization of the scattering length distribution of the vector meson interaction with the deuteron, Phys. Rev. C 108, 034614 (2023).
- Gao et al. [2001] H. Gao, T.-S. H. Lee, and V. Marinov, -n bound state, Phys. Rev. C 63, 022201(R) (2001).
- Malfliet and Tjon [1969] R. Malfliet and J. Tjon, Solution of the equations for the triton problem using local two-particle interactions, Nucl. Phys. A 127, 161 (1969).
- Acharya et al. [2021] S. Acharya et al. (ALICE Collaboration), Experimental Evidence for an Attractive Interaction, Phys. Rev. Lett. 127, 172301 (2021).
- Chizzali et al. [2024] E. Chizzali, Y. Kamiya, R. Del Grande, T. Doi, L. Fabbietti, T. Hatsuda, and Y. Lyu, Indication of a bound state from a correlation function analysis, Phys. Lett. B 848, 138358 (2024).
- Viviani et al. [2023] M. Viviani, S. König, A. Kievsky, L. E. Marcucci, B. Singh, and O. V. Doce, Role of three-body dynamics in nucleon-deuteron correlation functions, Phys. Rev. C 108, 064002 (2023).
- Collaboration [2023] A. Collaboration, Exploring the strong interaction of three-body systems at the LHC (2023), arXiv:2308.16120 [nucl-ex] .
- Mrówczyński and Słoń [2020] S. Mrówczyński and P. Słoń, Hadron-deuteron correlations and production of light nuclei in relativistic heavy-ion collisions, Acta Phys. Pol. B 51, 1739 (2020).
- Haidenbauer [2020] J. Haidenbauer, Exploring the -deuteron interaction via correlations in heavy-ion collisions, Phys. Rev. C 102, 034001 (2020).
- Ogata et al. [2021] K. Ogata, T. Fukui, Y. Kamiya, and A. Ohnishi, Effect of deuteron breakup on the deuteron- correlation function, Phys. Rev. C 103, 065205 (2021).
- Zhang et al. [2022] L. Zhang, S. Zhang, and Y.-G. Ma, Production of and in ultra-relativistic heavy-ion collisions, Eur. Phys. J. C 82, 1 (2022).
- Etminan et al. [2023] F. Etminan, Z. Sanchuli, and M. M. Firoozabadi, Geometrical properties of three-body states by realistic and first principles Lattice QCD potentials, Nucl. Phys. A 1033, 122639 (2023).
- Lyu et al. [2022] Y. Lyu, T. Doi, T. Hatsuda, Y. Ikeda, J. Meng, K. Sasaki, and T. Sugiura, Attractive interaction and two-pion tail from lattice QCD near physical point, Phys. Rev. D 106, 074507 (2022).
- Zhukov et al. [1993] M. Zhukov et al., Bound state properties of Borromean halo nuclei: and , Phys. Rep. 231, 151 (1993).
- Casal et al. [2020] J. Casal, J. Singh, L. Fortunato, W. Horiuchi, and A. Vitturi, Electric dipole response of low-lying excitations in the two-neutron halo nucleus , Phys. Rev. C 102, 064627 (2020).
- Raynal and Revai [1970] J. Raynal and J. Revai, Transformation coefficients in the hyperspherical approach to the three-body problem, Il Nuovo Cimento A (1965-1970) 68, 612 (1970).
- Thompson et al. [2004] I. Thompson, F. Nunes, and B. Danilin, : a tool for three body calculations with core excitation, Comput. Phys. Commun 161, 87 (2004).
- Lay et al. [2012] J. A. Lay, A. M. Moro, J. M. Arias, and J. Gómez-Camacho, Particle motion in a deformed potential using a transformed oscillator basis, Phys. Rev. C 85, 054618 (2012).
- Etminan et al. [2014] F. Etminan et al., Spin-2 dibaryon from lattice , Nucl. Phys. A 928, 89 (2014), special Issue Dedicated to the Memory of Gerald E Brown (1926-2013).
- Iritani et al. [2019] T. Iritani et al., dibaryon from lattice near the physical point, Phys. Lett. B 792, 284 (2019).
- Tarrús Castellà and Krein [2018] J. Tarrús Castellà and G. a. Krein, Effective field theory for the nucleon-quarkonium interaction, Phys. Rev. D 98, 014029 (2018).
- Stoks et al. [1994] V. G. J. Stoks, R. A. M. Klomp, C. P. F. Terheggen, and J. J. de Swart, Construction of high-quality nn potential models, Phys. Rev. C 49, 2950 (1994).
- Wiringa et al. [1995] R. B. Wiringa, V. G. J. Stoks, and R. Schiavilla, Accurate nucleon-nucleon potential with charge-independence breaking, Phys. Rev. C 51, 38 (1995).
- Gamermann et al. [2011] D. Gamermann, C. García-Recio, J. Nieves, and L. L. Salcedo, Odd-parity light baryon resonances, Phys. Rev. D 84, 056017 (2011).
- Ramos and Oset [2013] A. Ramos and E. Oset, The role of vector-baryon channels and resonances in the and reactions near the threshold, Phys. Lett. B 727, 287 (2013).
- Huang et al. [2006] F. Huang, Z. Y. Zhang, and Y. W. Yu, states in a chiral quark model, Phys. Rev. C 73, 025207 (2006).
- Bao-Xi Sun and Ying-Ying Fan and Qin-Qin Cao [2023] Bao-Xi Sun and Ying-Ying Fan and Qin-Qin Cao, The bound state in the unitary coupled-channel approximation, Commun. Theor. Phys. 75, 055301 (2023).
- Povh and Hüfner [1990] B. Povh and J. Hüfner, Systematics of strong interaction radii for hadrons, Phys. Lett. B 245, 653 (1990).
- Garcilazo and Valcarce [2019] H. Garcilazo and A. Valcarce, and states, Phys. Rev. C 99, 014001 (2019).