Evidence of pair-density wave in doping Kitaev spin liquid on the honeycomb lattice
Abstract
We study the effects of doping the Kitaev model on the honeycomb lattice where the spins interact via the bond-directional interaction , which is known to have a quantum spin liquid as its exact ground state. The effect of hole doping is studied within the - model on a three-leg cylinder using density-matrix renormalization group. Upon light doping, we find that the ground state of the system has quasi-long-range charge-density-wave correlations but short-range single-particle correlations. The dominant pairing channel is the even-parity superconducting pair-pair correlations with -wave-like symmetry, which oscillate in sign as a function of separation with a period equal to that of the spin-density wave and two times the charge-density wave. Although these correlations fall rapidly (possibly exponentially) at long distances, this is never-the-less the first example where a pair-density wave is the strongest SC order on a bipartite lattice. Our results may be relevant to and - upon doping.
The pair-density wave (PDW) is a superconducting (SC) state in which the order parameter varies periodically in space in such a way that its spatial average vanishes.Berg et al. (2009); Agterberg et al. (2020) The first example of PDW is the Fulde-Ferrell-Larkin-Ovchinnikov (FFLO) stateFulde and Ferrell (1964); Larkin and Ovchinnikov (1965) when a Zeeman magnetic field, , is applied to a s-wave superconductor so that the Fermi surface is spin-split. The SC order has a wave vector which is typically very small. The LO version of this state is accompanied by an induced magnetization density wave and a charge density wave (CDW) with ordering wavevectors . Intense interest in a somewhat different sort of PDW state has emerged due to recent discoveries in underdoped cuprate superconductors, where a direct observation of PDW has been made experimentally via local Cooper pair tunneling and scanning tunneling microscopy in Hamidian et al. (2016); Ruan et al. (2018); Edkins et al. (2019) as well as the dynamical inter-layer decoupling observed in hole doped .Berg et al. (2007); Agterberg and Tsunetsugu (2008) While similar in having oscillatory SC order and associated CDW order, this PDW is conjectured to be stable in zero magnetic field (zero net magnetization), have an ordering vector that is independent of (at least for small or vanishing ), and moreover can either have no associated magnetic order, or possibly have spin density wave order (SDW) with the same ordering vector .
Although much is known about the properties of the PDW stateBerg et al. (2007); Agterberg and Tsunetsugu (2008); Berg et al. (2009); Lee (2014); Jian et al. (2020), there are very few microscopic models which are shown to have PDW ground states. These include the one-dimensional (1D) Kondo-Heisenberg model with 1D electron gas coupled to a spin chainBerg et al. (2010) and the extended two-leg Hubbard-Heisenberg modelJaefari and Fradkin (2012). The evidence of PDW is also observed in the t-J model with four-spin ring exchange on a 4-leg triangular latticeXu et al. (2019) and an extended Hubbard model with a staggered spin-dependent magnetic flux per plaquette on a 3-leg triangular lattice.Venderley and Kim (2019) However, there is no evidence of PDW ordering found in more standard models even with second neighbor interactions.Dodaro et al. (2017); Jiang et al. (2018); Jiang and Devereaux (2019); Jiang et al. (2020)
Theoretically, it has been proposed that superconductivity can also emerge in doping quantum spin liquids (QSLs), which are exotic phases of matter that exhibit a variety of novel features associated with their topological character.Balents (2010); Savary and Balents (2016); Broholm et al. (2020) The QSLs can be viewed as insulating phases with preexisting electron pairs such that upon light doping they might automatically yield high temperature superconductivity.Anderson (1987); Kivelson et al. (1987); Rokhsar and Kivelson (1988); Laughlin (1988); Wen et al. (1989); Lee et al. (2006, 2007); Fradkin et al. (2015) Indeed, recent numerical studies using density-matrix renormalization group (DMRG) have provided strong evidences that lightly doping the QSL and chiral spin liquid on the triangular lattice will naturally give rise to nematic -waveJiang (2019) and -wave superconductivityJiang and Jiang (2020), respectively. Although dominant SC correlations have been observed in both systems, there is still no evidence for PDW ordering.

In this paper, we define a --like extension of the Kitaev model on the honeycomb lattice (Fig.1) so as to address the question of whether SC emerges upon light doping. The Kitaev model, i.e., term in Eq.(1), is exactly solvable and has a gapless spin liquid as its exact ground state.Kitaev (2006) Moreover, it has potential experimental realizations in magnets with strong spin-orbit coupling such as and -.Jackeli and Khaliullin (2009); Jiang et al. (2011); Singh et al. (2012); Hwan Chun et al. (2015); Kim and Kee (2016); Banerjee et al. (2017); Trebst (2017); Takagi et al. (2019); Hickey and Trebst (2019); Jiang et al. (2019); Yokoi et al. (2020); Chern et al. (2020) This provides us a unique theoretical opportunity to test the physics of doping QSLs and may also give us some hints for understanding the mechanism of high temperature superconductiivity in the cuprates. Theoretically, doping Kitaev spin liquid (KSL) has been studied and distinct metallic states were proposed.You et al. (2012); Hyart et al. (2012); Schmidt et al. (2018); Mei (2012) These include the -wave superconductivityYou et al. (2012); Hyart et al. (2012), topological superconductivitySchmidt et al. (2018), and Fermi liquid state.Mei (2012) However, controlled results of the sort that can be obtained using density-matrix renormalization group (DMRG) are still lacking concerning the phase(s) that arise upon doping the KSL.
Principal results: In the present paper, we study the lightly doped Kitaev model in Eq.(1) on the honeycomb lattice using DMRGWhite (1992). Based on DMRG calculations on three-leg cylinders, we find that upon light-doping the KSL state, the system exhibits power-law CDW correlations at long distances corresponding to a local pattern of partially-filled charge stripes. For three-leg cylinders, the wavelength of CDW, i.e., the spacings between two adjacent charge strips in the direction, is , where is the length of unit cell. This corresponds to an ordering wavevector with two thirds of a doped hole per CDW unit cell.
We find that the even-parity SC correlations are the most pronounced SC correlations, far dominant compared with the odd-parity SC or topological superconductivity.You et al. (2012); Hyart et al. (2012); Schmidt et al. (2018) Moreover, the dominant pairing channel oscillates in sign as a function of distance which is consistent with the striped PDW.Agterberg et al. (2020) Its wavelength is the same as that of the spin density wave (SDW) correlations and two times of that of the CDW . Correspondingly, the SC ordering wavevector is half of the ordering wavevector of the CDW. Although quasi-long-range SC correlations are not seen in the range of parameters we have studied, short-range correlations are fairly strong with the corresponding correlation length . This is comparable with the cylindrical width and is notably larger than that of doping the Kagome QSL.Jiang et al. (2017) Similar with doping the QSL on the triangular latticeJiang (2019), we find that the pairing symmetry of SC correlations is also consistent with -wave. To the best of our knowledge, this is the first observation of PDW in doping the KSL.
Model and Method: We employ DMRGWhite (1992) to investigate the ground state properties of the hole-doped Kitaev model on the honeycomb lattice defined by the Hamiltonian
| (1) |
Here () is the electron creation (annihilation) operator with spin- on site , is the -component of the spin operator on site , where labels the three different links of the hexagonal lattice as illustrated in Fig.1. denotes nearest-neighbor (NN) sites and the Hilbert space is constrained by the no-double occupancy condition, , where is the electron number operator. At half-filling, i.e., , Eq.(1) reduces to the Kitaev model, which is known to have a gapless spin liquid ground state that can be gapped out into a non-Abelian topological phase by certain time-reversal symmetry perturbations.Kitaev (2006); Zhu et al. (2018)

The lattice geometry used in our simulations is depicted in Fig.1, where and denote the two basis vectors. We consider honeycomb cylinders with periodic and open boundary conditions in the and directions, respectively. We focus on cylinders of width and length , where and are the number of unit cells ( and are the number of sites) along the and directions, respectively. The total number of sites is . The hole doping concentration is defined as , where is the number of doped holes. We set as an energy unit and consider . In this paper, we focus primarily on three-leg cylinders, i.e., , of length (i.e., ), at doping levels and . We find similar results on four-leg cylinders which are provided in the Supplemental Materials (SM). We keep up to number of states in each DMRG block with a typical truncation error . This leads to excellent convergence for our results when extrapolated to limit.
Pair-density wave: To test the possibility of superconductivity, we have calculated the equal-time SC pair-pair correlations. A diagnostic of the SC order is the SC pair-pair correlation function, defined as
| (2) |
where is the even-parity SC pair-field creation operator, where the bond orientations are labelled as (Fig.1). () is the reference bond with to minimize the boundary effect and is the distance between two bonds in the direction. We have also calculated the odd-parity SC correlations to test the possibility of -wave or topological superconductivity. However, we find that they are much weaker than the even-parity SC correlations (see SM for details), suggesting that -wave or topological superconductivity is unlikely. Therefore, we will focus on the even-parity SC correlation in this paper.
Fig.2 shows the SC pair-pair function for doping and . The SC correlation shows clear spatial oscillation for both doping levels, which can be well fitted by for a large region of as we will discuss below. Here is the envelope function and is a spatial oscillatory function. At long distances, the envelope function is consistent with an exponential decay, i.e., , as shown in Fig.2a-b. The extracted correlation length is , which is comparable with the cylindrical width . Alternatively, the SC correlation at long distances can also be fitted by a power law (see SM for details), i.e., , with an exponent for both doping levels and . We have also measured other types of SC correlations which are provided in the SM. While they are slightly weaker than due to the broken symmetry induced by the cylindrical geometry, they have very similar decaying behavior with . Although the SC correlations can be fitted by either functions, it is clear that the SC susceptibility will not diverge in the thermodynamic limit.
The spatial oscillation of the SC correlation is characterized by the normalized correlation , as shown in Fig.2c. It is clear that varies periodically in real space and can be well fitted by for both cases. This is consistent with the PDW state with vanishing spatial average of . The ordering wavevector of the PDW is as indicated by the peak position of the Fourier transformation of (Fig.2d) and is a fitting phase factor. The corresponding wavelength is , which is for and for . As we will see below that the relation can be clearly seen in our results as expected from that of striped PDW. Here, and are the wavelengths of the CDW and SDW, respectively. According to Ginzburg-Landau theory, the development of charge oscillation corresponds to the cubic term in the free energy, where and are the charge density and PDW order parameters with corresponding momenta and , respectively. This is distinct from the CDW modulated superconductivity with term with coexisting dominant uniform and secondary stripe pairing .
To identify the pairing symmetry, we have calculated the SC correlations using both real-valued and complex-valued DMRG simulations. We first rule out the -wave symmetry as we find that both the wavefunction and SC correlations are real while their imaginary parts are zero. We have further analyzed the relative phase of different SC correlations, e.g., in the insets of Fig.2a-b, where a clear out of phase can be observed as . Therefore, we conclude that the pairing symmetry of the PDW is consistent with -wave.

| 1.0(1) | 1.9(1) | ||||
| 1.2(1) | 1.8(1) |
Charge density wave: In addition to SC correlations, we have also measured the charge density profiles to describe the charge density properties of the system. The rung charge density is shown in Fig.3, where is the rung index of the cylinder and is the local charge density on site . It is clear that the charge density varies periodically in real space along the direction with the wavelength , i.e., and for and , respectively. Therefore, there are two thirds of a doped hole in each CDW unit cell. Moreover, it is clear that the relation holds for both and , which is consistent the striped PDW state. Different with SC correlations, we find power-law decay of the charge density correlation at long distances. The Luttinger exponent of the power-law decay can be extracted by fitting the charge density oscillation (Friedel oscillation) induced by the open boundaries of the cylinderWhite et al. (2002)
| (3) |
Here is the distance in the direction from the open boundary, the average density and is the ordering wavevector. and are the model dependent constants. Examples of the fitting using Eq.(3) on the a sub-lattice are given in Fig.3a for both doping and , where four data points near the boundary are removed to minimize boundary effect for a more reliable fit. The extracted exponent is given in Table 1. It is clear that which demonstrates the dominance of the charge density correlations.
Alternatively, we can estimate from the amplitude of the charge density modulation.Jiang and Devereaux (2019) For a given cylinder of length , the CDW amplitude can be obtained by fitting the central-half region of the charge density profile .Jiang et al. (2018); Jiang and Devereaux (2019); Jiang et al. (2020) For quasi-long-range charge order, the amplitude should follow with similar with that obtained from Friedel oscillation in Eq.(3). This is indeed the case as shown in Fig.3c-d, where the exponent is given in Fig.3b and Table 1.

Spin-spin and single-particle correlations: To describe the magnetic properties of the system, we have further calculated the spin-spin correlation function . Here is the distance between two sites in the direction and . is the reference site with . For the pure Kitaev model without doping, it is known that is nonzero only for NN sites.Kitaev (2006); Baskaran et al. (2007) Upon doping, the flux on each hexagonal plaquette is no longer a conserved quantity, and the spin-spin correlation functions become nonzero even at long distance. For both doping levels and on three-leg cylinders, we find that both and decay exponentially as , where the spin-spin correlation length is given in Table.1. On the contrary, appears to be long-range ordered as shown in Fig.4. This is unexpected but allowed theoretically since there is no continuous spin symmetry in the system. Moreover, we find that all spin-spin correlations show clear spatial oscillation with a wavelength that is the same as that of the SC correlation, i.e., , which is consistent with the striped PDW. However, our results suggest that the long-range correlation is special to three-leg cylinder. On the contrary, decays exponentially on the wider four-leg cylinders (Fig.4b), which is similar with both and . However, the evidences of the striped PDW are robust for both three and four-leg cylinders with similar sign-changing SC correlations (see SM for details).
In addition to superconductivity, we have also measured the single-particle Green function to test the possibility of Fermi liquid state.Mei (2012) It is clear that the single-particle Green function decays exponentially at long distances as (see SM for details). Here is the correlation length which is summarized in Table 1. As a result, our study suggests that the Fermi liquid state is unlikely in the lightly hole-doped KSL.
Central charge: Our results suggest that the ground state of the lightly hole-doped KSL has quasi-long-range CDW correlation with gapless charge mode. To show this, we have calculated the von Neumann entanglement entropy , where is the reduced density matrix of subsystem with length . For 1D critical system described by conformal field theory, it has been establishedCalabrese and Cardy (2004); Fagotti and Calabrese (2011) that for an open finite system of length ,
| (4) | |||||
Here is central charge, denotes the Fermi momentum, and are model dependent parameters. Fig.5a shows an example of for three-leg cylinder at doping level . Here we have calculated by dividing the system into two parts with smooth boundary through both and bonds. The extracted central charge is given in Fig.5 as a function of at doping levels and . It is clear that the central charge quickly converges to with the increase of , although it deviates notably from on short cylinders due to finite-size effect. Therefore, our results show that there is one gapless charge mode which is consistent with the quasi-long-range CDW correlations. We have obtained similar results on four-leg cylinders which are provided in the SM.

Summary and discussion: Admittedly, the DMRG calcualtions are carried out on finite length cylinders. However, based on the results we have obtained we conjecture that the exact ground state for an infinite long three-leg cylinder has the following properties: 1) There is a single gapless charge mode and a gap (which produces exponentially falling correlations) for all spin carrying excitations. 2) Long-range SDW order with the ordered moment oriented in the direction - that is along the circumference of the cylinder - and an ordering vector ; the connected spin correlations fall exponentially with a correlation length . 3) There are power-law CDW correlations with an exponent and an ordering vector . 4) There are strong even-parity d-wave-like PDW correlations with an ordering vector which fall either exponentially with a correlation length or possibly with a high power law . 5) All other forms of SC correlations - those corresponding to odd-parity pairing or spatially uniform even-parity pairing - are much weaker in comparison with the PDW correlations.
There are many aspects of these observations that are surprising, and will need to be understood theoretically. The PDW correlations are sufficiently short-ranged that one would infer (based on any reasonable conjecture concerning their time dependence) that the corresponding PDW susceptibility would be finite. Thus, at present, we can only conclude that the present results are suggestive of a possible PDW ordered state for the 2D (infinite leg) version of this model. However, it is notable that the favored forms of order are remarkably reminiscent of those conjectured to be present in the cuprate high temperature superconductor, LBCO, where direct evidence exists of stripe SDW order with wave vector and CDW order with ordering vector , and indirect evidence has been adduced for PDW order with ordering vector .
In this paper, we primarily focus on the lightly doped Kitaev model, it will be interesting to study the higher doping case as well as the extend Kitaev model with further neighbor hopping which is shown to be essential to enhance the superconductivity on the square lattice.Jiang and Devereaux (2019); Jiang et al. (2020) As other terms such as the Heisenberg interaction and spin-orbit couplings are also present in real materials such as and -,Jackeli and Khaliullin (2009); Jiang et al. (2011); Singh et al. (2012); Hwan Chun et al. (2015); Kim and Kee (2016); Banerjee et al. (2017); Trebst (2017); Takagi et al. (2019); Hickey and Trebst (2019); Jiang et al. (2019); Yokoi et al. (2020) it will be interesting to study these systems as well.
Acknowledgments: We would like to thank Senthil Todadri for insightful discussions, and especially Steve Kivelson for insightful discussion, invaluable suggestions and generous help to understand the results and improve the manuscript. This work was supported by the Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division, under Contract DE-AC02-76SF00515. Parts of the computing for this project was performed on the Sherlock cluster.
References
- Berg et al. (2009) E. Berg, E. Fradkin, S. A. Kivelson, and J. M. Tranquada, New J. Phys. 11, 115004 (2009).
- Agterberg et al. (2020) D. F. Agterberg, J. S. Davis, S. D. Edkins, E. Fradkin, D. J. Van Harlingen, S. A. Kivelson, P. A. Lee, L. Radzihovsky, J. M. Tranquada, and Y. Wang, Annual Review of Condensed Matter Physics 11, 231 (2020).
- Fulde and Ferrell (1964) P. Fulde and R. A. Ferrell, Phys. Rev. 135, A550 (1964).
- Larkin and Ovchinnikov (1965) A. I. Larkin and Y. N. Ovchinnikov, Sov. Phys. JETP 20, 762 (1965).
- Hamidian et al. (2016) M. H. Hamidian, S. D. Edkins, S. H. Joo, A. Kostin, H. Eisaki, S. Uchida, M. J. Lawler, E.-A. Kim, A. P. Mackenzie, K. Fujita, J. Lee, and J. C. S. Davis, Nature 532, 343 (2016).
- Ruan et al. (2018) W. Ruan, X. Li, C. Hu, Z. Hao, H. Li, P. Cai, X. Zhou, D.-H. Lee, and Y. Wang, Nature Physics , 1178 (2018).
- Edkins et al. (2019) S. D. Edkins, A. Kostin, K. Fujita, A. P. Mackenzie, H. Eisaki, S. Uchida, S. Sachdev, M. J. Lawler, E.-A. Kim, J. C. Séamus Davis, and M. H. Hamidian, Science 364, 976 (2019).
- Berg et al. (2007) E. Berg, E. Fradkin, E.-A. Kim, S. A. Kivelson, V. Oganesyan, J. M. Tranquada, and S. C. Zhang, Phys. Rev. Lett. 99, 127003 (2007).
- Agterberg and Tsunetsugu (2008) D. F. Agterberg and H. Tsunetsugu, Nature Physics , 639 (2008).
- Lee (2014) P. A. Lee, Phys. Rev. X 4, 031017 (2014).
- Jian et al. (2020) S.-K. Jian, M. M. Scherer, and H. Yao, Phys. Rev. Research 2, 013034 (2020).
- Berg et al. (2010) E. Berg, E. Fradkin, and S. A. Kivelson, Phys. Rev. Lett. 105, 146403 (2010).
- Jaefari and Fradkin (2012) A. Jaefari and E. Fradkin, Phys. Rev. B 85, 035104 (2012).
- Xu et al. (2019) X. Y. Xu, K. T. Law, and P. A. Lee, Phys. Rev. Lett. 122, 167001 (2019).
- Venderley and Kim (2019) J. Venderley and E.-A. Kim, Science Advances 5, eaat4698 (2019).
- Dodaro et al. (2017) J. F. Dodaro, H.-C. Jiang, and S. A. Kivelson, Phys. Rev. B 95, 155116 (2017).
- Jiang et al. (2018) H.-C. Jiang, Z.-Y. Weng, and S. A. Kivelson, Phys. Rev. B 98, 140505 (2018).
- Jiang and Devereaux (2019) H.-C. Jiang and T. P. Devereaux, Science 365, 1424 (2019).
- Jiang et al. (2020) Y.-F. Jiang, J. Zaanen, T. P. Devereaux, and H.-C. Jiang, Phys. Rev. Research 2, 033073 (2020).
- Balents (2010) L. Balents, Nature 464, 199 (2010).
- Savary and Balents (2016) L. Savary and L. Balents, Reports on Progress in Physics 80, 016502 (2016).
- Broholm et al. (2020) C. Broholm, R. J. Cava, S. A. Kivelson, D. G. Nocera, M. R. Norman, and T. Senthil, Science 367, eaay0668 (2020).
- Anderson (1987) P. W. Anderson, Science 235, 1196 (1987).
- Kivelson et al. (1987) S. A. Kivelson, D. S. Rokhsar, and J. P. Sethna, Phys. Rev. B 35, 8865 (1987).
- Rokhsar and Kivelson (1988) D. S. Rokhsar and S. A. Kivelson, Phys. Rev. Lett. 61, 2376 (1988).
- Laughlin (1988) R. B. Laughlin, Science 242, 525 (1988).
- Wen et al. (1989) X. G. Wen, F. Wilczek, and A. Zee, Phys. Rev. B 39, 11413 (1989).
- Lee et al. (2006) P. A. Lee, N. Nagaosa, and X.-G. Wen, Rev. Mod. Phys. 78, 17 (2006).
- Lee et al. (2007) S.-S. Lee, P. A. Lee, and T. Senthil, Phys. Rev. Lett. 98, 067006 (2007).
- Fradkin et al. (2015) E. Fradkin, S. A. Kivelson, and J. M. Tranquada, Rev. Mod. Phys. 87, 457 (2015).
- Jiang (2019) H.-C. Jiang, (2019), arXiv:1912.06624 [cond-mat.str-el] .
- Jiang and Jiang (2020) Y.-F. Jiang and H.-C. Jiang, (2020), arXiv:2002.04686 [cond-mat.supr-con] .
- Kitaev (2006) A. Kitaev, Annals of Physics 321, 2 (2006).
- Jackeli and Khaliullin (2009) G. Jackeli and G. Khaliullin, Phys. Rev. Lett. 102, 017205 (2009).
- Jiang et al. (2011) H.-C. Jiang, Z.-C. Gu, X.-L. Qi, and S. Trebst, Phys. Rev. B 83, 245104 (2011).
- Singh et al. (2012) Y. Singh, S. Manni, J. Reuther, T. Berlijn, R. Thomale, W. Ku, S. Trebst, and P. Gegenwart, Phys. Rev. Lett. 108, 127203 (2012).
- Hwan Chun et al. (2015) S. Hwan Chun, J.-W. Kim, J. Kim, H. Zheng, C. Stoumpos, C. Malliakas, J. Mitchell, K. Mehlawat, Y. Singh, Y. Choi, T. Gog, A. Al-Zein, M. Sala, M. Krisch, J. Chaloupka, G. Jackeli, G. Khaliullin, and B. J. Kim, Nature Physics 11, 462 (2015).
- Kim and Kee (2016) H.-S. Kim and H.-Y. Kee, Phys. Rev. B 93, 155143 (2016).
- Banerjee et al. (2017) A. Banerjee, J. Yan, J. Knolle, C. A. Bridges, M. B. Stone, M. D. Lumsden, D. G. Mandrus, D. A. Tennant, R. Moessner, and S. E. Nagler, Science 356, 1055 (2017).
- Trebst (2017) S. Trebst, (2017), arXiv:1701.07056 .
- Takagi et al. (2019) H. Takagi, T. Takayama, G. Jackeli, G. Khaliullin, and S. E. Nagler, Nature Reviews Physics 1, 264 (2019).
- Hickey and Trebst (2019) C. Hickey and S. Trebst, Nat Commun 10, 530 (2019).
- Jiang et al. (2019) Y.-F. Jiang, T. P. Devereaux, and H.-C. Jiang, Phys. Rev. B 100, 165123 (2019).
- Yokoi et al. (2020) T. Yokoi, S. Ma, Y. Kasahara, S. Kasahara, T. Shibauchi, N. Kurita, H. Tanaka, J. Nasu, Y. Motome, C. Hickey, S. Trebst, and Y. Matsuda, (2020), arXiv:2001.01899 .
- Chern et al. (2020) L. E. Chern, R. Kaneko, H.-Y. Lee, and Y. B. Kim, Phys. Rev. Research 2, 013014 (2020).
- You et al. (2012) Y.-Z. You, I. Kimchi, and A. Vishwanath, Phys. Rev. B 86, 085145 (2012).
- Hyart et al. (2012) T. Hyart, A. R. Wright, G. Khaliullin, and B. Rosenow, Phys. Rev. B 85, 140510 (2012).
- Schmidt et al. (2018) J. Schmidt, D. D. Scherer, and A. M. Black-Schaffer, Phys. Rev. B 97, 014504 (2018).
- Mei (2012) J.-W. Mei, Phys. Rev. Lett. 108, 227207 (2012).
- White (1992) S. R. White, Phys. Rev. Lett. 69, 2863 (1992).
- Jiang et al. (2017) H.-C. Jiang, T. Devereaux, and S. A. Kivelson, Phys. Rev. Lett. 119, 067002 (2017).
- Zhu et al. (2018) Z. Zhu, I. Kimchi, D. N. Sheng, and L. Fu, Phys. Rev. B 97, 241110 (2018).
- White et al. (2002) S. R. White, I. Affleck, and D. J. Scalapino, Phys. Rev. B 65, 165122 (2002).
- Baskaran et al. (2007) G. Baskaran, S. Mandal, and R. Shankar, Phys. Rev. Lett. 98, 247201 (2007).
- Calabrese and Cardy (2004) P. Calabrese and J. Cardy, J. Stat. Mech. Theory Exp. 2004 (2004).
- Fagotti and Calabrese (2011) M. Fagotti and P. Calabrese, J. Stat. Mech. Theory Exp. 2011 (2011).
Appendix A Supplemental Material
A.1 Results for four-leg cylinders
We provide more results for four-leg cylinder, where we have observed similar features of the striped PDW discussed in the main text. Similar with three-leg cylinders, the density profiles on four-leg cylinders also exhibit similar spatial oscillation (Fig.A1a), with the period corresponding to an ordering vector , where is the length of unit cell.
The SC pair-pair correlation function on four-leg cylinder of length and at doping are shown in Fig.A1b. Similar with three-leg cylinders, the SC pair-pair correlation decays exponentially whose envelope can be well fitted by the function with a correlation length and for and , respectively. The spatial oscillation of is characterized by the normalized pair-pair correlation shown in Fig.A1c. The ordering wavevector of is as indicated by the peak position of the Fourier transformed in Fig.A1d. The relationship between the SC ordering vector and CDW ordering vector also holds true for four-leg cylinders, as expected for the striped PDW state.
On four-leg cylinders, all the spin-spin correlations , where , decay exponentially at long distances, e.g., as shown in Fig.A1e. The envelope of the strongest component (see Fig.4b) can be well fitted by the exponential function with a correlation length from length cylinder. The single-particle Green’s function also decays exponentially at long distances as (Fig.A1f) with the correlation length .

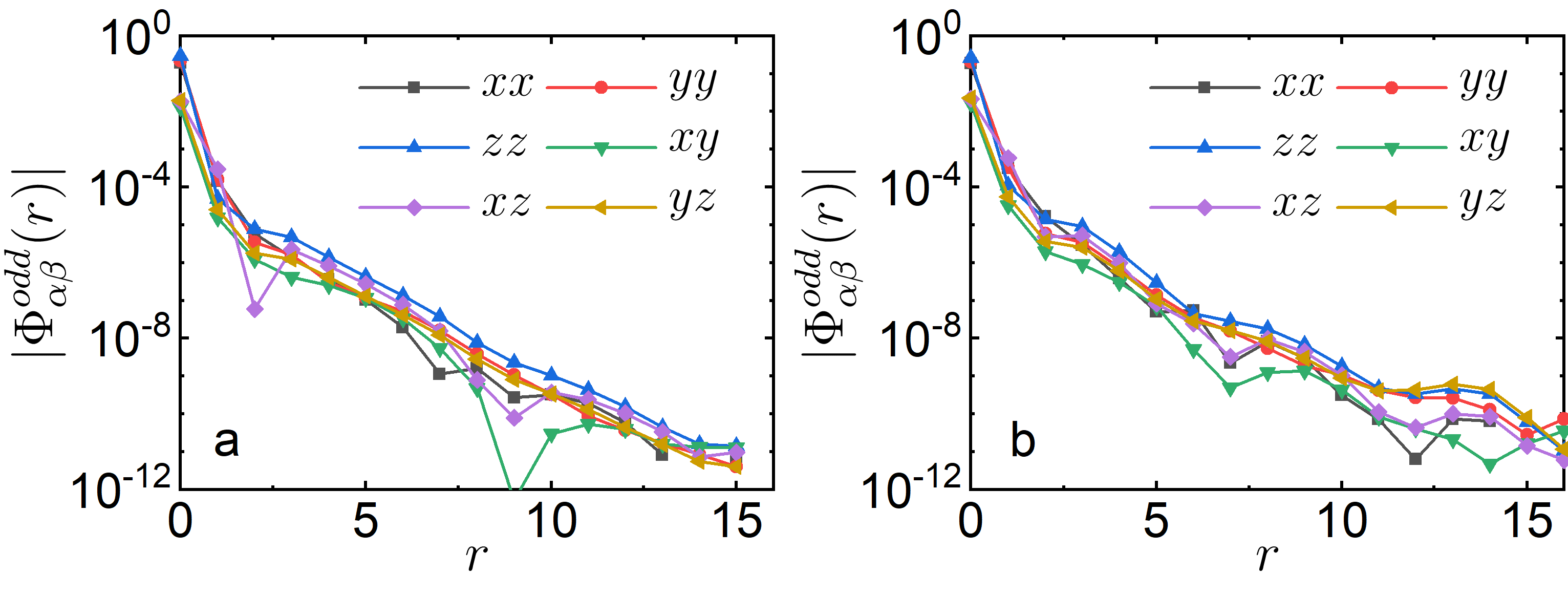
A.2 Odd-parity SC pair-pair correlation function
We measure the odd parity pair-pair correlation function defined as
| (A1) |
where . labels the bond orientations as defined in the main text. Compared with the even-parity SC correlation , shown in Fig.A2 are much weaker which decay faster with shorter correlation length, e.g., at doping and at doping.

A.3 Power-law fitting of SC pair-pair correlation
Here we double-check the alternative power-law fitting for the SC pair-pair correlation. Fig.A3 shows the same SC pair-pair correlations , i.e., Fig.2 in the main text, in double-logarithm scale. At long distances, it is quite clear that deviates from the power-law fitting labelled by the linear dashed lines with the exponent and for and dopings, respectively. This deviation is also reflected in the vanishing normalized correlation at long distance and the rounded peak of located at the momentum shown in Fig.A3c and d.
A.4 All types of even parity pair-pair correlations
In Fig.A4, we list all types of even-parity SC pair-pair correlations on three-leg cylinders of length at doping and . It is clear that they all decay exponentially, similar with discussed in main text, although with slightly different amplitude at long distances. This could be attributed to the fact that the cylinder geometry breaks the rotational symmetry of the honeycomb lattice.

A.5 Single-particle Green function
To check the possibility of other metallic state such as the Fermi liquid state, We have also measured the single-particle Green function , as shown in Fig.A5. It is clear that decays exponentially, which is inconsistent with the Fermi liquid state. For instance, the correlation lengths at doping and are and on three-leg cylinders of length . The correlation length in the long-cylinder limit after finite-size scaling using is slightly longer, which is given in Table I of the main text.
