This paper was converted on www.awesomepapers.org from LaTeX by an anonymous user.
Want to know more? Visit the Converter page.

Evidence of fully-gapped superconductivity in NbReSi:
A combined μ\muSR and NMR study

T. Shang [email protected] Key Laboratory of Polar Materials and Devices (MOE), School of Physics and Electronic Science, East China Normal University, Shanghai 200241, China    D. Tay Laboratorium für Festkörperphysik, ETH Zürich, CH-8093 Zürich, Switzerland    H. Su Center for Correlated Matter and Department of Physics, Zhejiang University, Hangzhou 310058, China Zhejiang Province Key Laboratory of Quantum Technology and Device, Department of Physics, Zhejiang University, Hangzhou 310058, China    H. Q. Yuan Center for Correlated Matter and Department of Physics, Zhejiang University, Hangzhou 310058, China Zhejiang Province Key Laboratory of Quantum Technology and Device, Department of Physics, Zhejiang University, Hangzhou 310058, China Collaborative Innovation Center of Advanced Microstructures, Nanjing University, Nanjing, 210093, China State Key Laboratory of Silicon Materials, Zhejiang University, Hangzhou 310058, China    T. Shiroka Laboratorium für Festkörperphysik, ETH Zürich, CH-8093 Zürich, Switzerland Laboratory for Muon-Spin Spectroscopy, Paul Scherrer Institut, Villigen PSI, Switzerland
Abstract

We report a comprehensive study of the noncentrosymmetric NbReSi superconductor by means of muon-spin rotation and relaxation (μ\muSR) and nuclear magnetic resonance (NMR) techniques. NbReSi is a bulk superconductor with Tc=6.5T_{c}=6.5 K, characterized by a large upper critical field, which exceeds the Pauli limit. Both the superfluid density ρsc(T)\rho_{\mathrm{sc}}(T) (determined via transverse-field μ\muSR) and the spin-lattice relaxation rate T1−1(T)T_{1}^{-1}(T) (determined via NMR) suggest a nodeless superconductivity (SC) in NbReSi. We also find signatures of multigap SC, here evidenced by the field-dependent muon-spin relaxation rate and the electronic specific-heat coefficient. The absence of spontaneous magnetic fields below TcT_{c}, as evinced from zero-field μ\muSR measurements, indicates a preserved time-reversal symmetry in the superconducting state of NbReSi. Finally, we discuss possible reasons for the unusually large upper critical field of NbReSi, most likely arising from its anisotropic crystal structure.

††preprint: Preprint: , 8:33

I Introduction

Superconductors whose crystal structures lack an inversion center, known as noncentrosymmetric superconductors (NCSCs), represent an attractive platform for investigating unconventional- and topological superconductivity (SC) [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]. Besides SC, noncentrosymmetric materials are among the best candidates for studying also topological phenomena. For example, Weyl fermions were discovered as quasiparticles in Ta(As,P) and Nb(As,P) noncentrosymmetric single crystals [12, 13, 14, 15, 16]. In NCSCs, a lack of inversion center sets the scene for a variety of exotic properties, e.g., nodes in the superconducting gap [17, 18, 19, 20], multigap SC [21], upper critical fields beyond the Pauli limit [22, 23, 24], and breaking of time-reversal symmetry (TRS) in the superconducting state [20, 25, 26, 27, 28, 29, 30].

In some NCSCs, the above exotic properties are closely related to admixtures of spin-singlet and spin-triplet superconducting pairing, here tuned by the antisymmetric spin-orbit coupling (ASOC) [1, 2, 3]. In most other cases, however, such connection seems very weak and the superconducting properties resemble those of conventional superconductors, characterized by a fully developed energy gap and a preserved TRS. A notable exception is CaPtAs which, below TcT_{c}, exhibits both TRS breaking and superconducting gap nodes [20, 31]. In general, the causes behind TRS breaking in NCSCs are not yet fully understood and remain an intriguing open question.

After the discovery of TRS breaking in elementary rhenium and in α\alpha-Mn-type ReTT superconductors (TT = transition metal) [28, 29, 30], many other Re-based superconductors have been systematically investigated by means of muon-spin relaxation and rotation (μ\muSR). Later on, μ\muSR studies on Re1−x{}_{1-x}Mox{}_{x} alloys (0≤x≤10\leq x\leq 1) revealed that TRS is broken only in cases of a high rhenium content (x<0.12x<0.12), surprisingly corresponding to simple centrosymmetric structures [32]. For x>0.12x>0.12, instead, all the Re-Mo alloys preserve TRS in their superconducting state, independent of the centro- or noncentrosymmetric crystal structure [32]. Recently, the centrosymmetric Re3{}_{3}B and noncentrosymmetric Re7{}_{7}B3{}_{3} superconductors were systematically studied and shown to exhibit nodeless SC with multiple energy gaps [33]. In both cases, the lack of spontaneous magnetic fields below TcT_{c} indicates that, unlike in ReTT or in elementary rhenium, the TRS is preserved. Such a selective occurrence of TRS breaking in Re-based superconductors, independent of the noncentrosymmetric structure (and thus of ASOC), is puzzling and not yet fully understood, clearly demanding further investigations.

The NbReSi superconductor represents yet another candidate material for studying the TRS breaking effect in the Re-based family of superconductors. NbReSi crystallizes in a hexagonal ZrNiAl-type crystal structure with space group P6¯2mP\overline{6}2m (No. 189) [see inset in Fig. I(b)] [34]. Although its SC was reported in 1980s [35], its physical properties were systematically studied only recently [24]. As shown in Fig. I(a), both magnetic-susceptibility and electrical-resistivity data indicate a Tc=6.5T_{c}=6.5 K in NbReSi. The temperature evolution of the upper critical field Hc2(T)H_{\mathrm{c2}}(T), as established by electrical-resistivity- and heat-capacity measurements, is reported in Fig. I(b), with Hc2(0)H_{\mathrm{c2}}(0) being larger than the weak-coupling Pauli limit value (i.e., 1.86kBTc=12.1k_{\mathrm{B}}T_{c}=12.1 T). This indicates that the effects of paramagnetic limiting may be either reduced or entirely absent in NbReSi and, hence, that it can possibly exihibit unconventional superconductivity.

Although selected properties of NbReSi have been investigated by different techniques [24], at a microscopic level its superconducting properties, in particular, the superconducting order parameter, have not been explored. In this paper, we report on an extensive study of NbReSi carried out mostly by μ\muSR and nuclear magnetic resonance (NMR) methods, both in its superconducting- and normal states. Despite a noncentrosymmetric crystal structure, NbReSi is shown to be a moderately correlated electron material, which adopts a fully gapped superconducting state with preserved TRS.

Refer to caption
Figure 1. : (a) Temperature-dependent magnetic susceptibility χV(T)\chi_{\mathrm{V}}(T) (left-axis) and electrical resistivity ρ(T)\rho(T) (right-axis). While ρ(T)\rho(T) was measured in a zero-field condition, χV(T)\chi_{\mathrm{V}}(T) data were collected in a magnetic field of 1 mT, applied after zero-field cooling (ZFC). The dashed line indicates the Tc=6.5T_{c}=6.5 K. (b) Upper critical field Hc2H_{\mathrm{c2}} vs reduced temperature TcT_{c}/Tc(0)T_{c}(0) for NbReSi. The solid- and dash-dotted lines represent fits to the two-band- and WHH model. The TcT_{c} values determined from μ\muSR- and NMR measurements (this work) are highly consistent with the values determined from electrical-resistivity- and heat-capacity measurements (data taken from Ref. 24). The inset shows the crystal structure of NbReSi, with the lines marking its unit cell.

II Experimental details

Polycrystalline NbReSi samples were prepared by the arc-melting method. The crystal structure and phase purity were checked by powder x-ray diffraction. The bulk SC was characterized by electrical-resistivity-, heat-capacity-, and magnetization measurements [24]. The bulk μ\muSR measurements were carried out at the multipurpose surface-muon spectrometer (Dolly) of the Swiss muon source at Paul Scherrer Institut, Villigen, Switzerland. In this study, we performed three kinds of experiments: transverse-field (TF)-, zero-field (ZF)-, and longitudinal-field (LF) μ\muSR measurements. As to the former, it allowed us determine the temperature evolution of the superfluid density. As to the latter two, we aimed at searching for a possible breaking of time-reversal symmetry in the superconducting state of NbReSi. To exclude the possibility of stray magnetic fields during the ZF-μ\muSR measurements, all the magnets were preliminarily degaussed. All the μ\muSR spectra were collected upon heating and were analyzed by means of the musrfit software package [36].

93{}^{93}Nb NMR measurements, including line shapes and spin-lattice relaxation times, were performed on NbReSi in powder form in a magnetic field of 5 T.

Refer to caption
Figure 2. : (a) TF-μ\muSR spectra of NbReSi collected at TT = 2.1 K (superconducting state) in a field of 30 and 200 mT. (b) TF-μ\muSR spectra of NbReSi collected in the superconducting- (0.3 K) and the normal state (8 K) in an applied magnetic field of 50 mT. The solid lines represent fits to Eq. (1). To clearly show the oscillations at higher fields, the spectra in panel (a) are shown in a time range up to 2 μ\mus.

To cover the 2 to 300 K temperature range we used a continuous-flow CF-1200 cryostat by Oxford Instruments, with temperatures below 4.2 K being achieved under pumped 4{}^{4}He conditions. Preliminary resonance detuning experiments confirmed the TcT_{c} of 6.3 K at 0 T and of 4.4 K at 5 T. The 93{}^{93}Nb NMR signal was detected by means of a standard spin-echo sequence consisting of π/2\pi/2 and π\pi pulses of 3 and 6 μ\mus, with recycling delays ranging from 1 to 60 s in the 2–300 K temperature range. The lineshapes were obtained via fast Fourier transform (FFT) of the echo signal. Spin-lattice relaxation times T1T_{1} were measured via the inversion-recovery method, using a π\pi–π/2\pi/2–π\pi pulse sequence. In all the measurements, phase cycling was used to systematically minimize the presence of artifacts.

III Results and discussion

III.1 μ\muSR study

Refer to caption
Figure 3. : (a) Field-dependent superconducting Gaussian relaxation rate σsc(H)\sigma_{\mathrm{sc}}(H). The dash-dotted and solid lines represent fits to a single-gap and a two-band model. The inset plots the normalized specific-heat coefficient γH/γn\gamma_{\mathrm{H}}/\gamma_{\mathrm{n}} vs the reduced magnetic field H/Hc2(0)H/H_{c2}(0) for NbReSi. At a given applied field, γH\gamma_{\mathrm{H}} is obtained as the linear extrapolation of electronic specific heat Ce/TC_{\mathrm{e}}/T vs T2T^{2} in the superconducting state to zero temperature. Data from different samples (denoted as S1 and S2) are highly consistent. The specific heat data can be found in Ref. 24. The arrow marks a change of slope at μ0H∼1\mu_{0}H\sim 1 T. (b) Temperature dependence of the NbReSi superfluid density. The solid black- and red lines represent fits to a fully-gapped ss-wave model with one- and two gaps, respectively. The dash-dotted and dashed lines (in the inset) are fits to pp- and dd-wave models.

To investigate the superconducting properties of NbReSi at a microscopic level, we carried out systematic temperature-dependent μ\muSR measurements in a transverse field. The optimal field value for such experiments was determined via preliminary field-dependent μ\muSR depolarization-rate measurements at 2.1 K. To track the additional field-distribution broadening due to the flux-line lattice (FLL) in the mixed superconducting state, a magnetic field (up to 380 mT) was applied in the normal state and then the sample was cooled down well below TcT_{c}, where the μ\muSR spectra were collected. Figure II(a) shows two representative TF-μ\muSR spectra collected at 30 and 200 mT, in general, modeled by:

ATF(t)=Ase−σ2t2/2cos(γμBst+ϕ)+Abgcos(γμBbgt+ϕ).A_{\mathrm{TF}}(t)=A_{\mathrm{s}}e^{-\sigma^{2}t^{2}/2}\cos(\gamma_{\mu}B_{s}t+\phi)+A_{\mathrm{bg}}\cos(\gamma_{\mu}B_{\mathrm{bg}}t+\phi). (1)
Refer to caption
Figure 4. : ZF-μ\muSR spectra collected in the superconducting- (0.3 K) and the normal (10 K) states for NbReSi. The LF-μ\muSR in a field of 3 mT was collected at 0.3 K after field cooling.

Here AsA_{\mathrm{s}} (90%) and AbgA_{\mathrm{bg}} (10%) are the sample and the background asymmetries, with the latter not undergoing any depolarization. γμ\gamma_{\mu}/2π\pi = 135.53 MHz/T is the muon gyromagnetic ratio, BsB_{\mathrm{s}} and BbgB_{\mathrm{bg}} are the local fields sensed by implanted muons in the sample and the sample holder, ϕ\phi is a shared initial phase, and σ\sigma is a Gaussian relaxation rate reflecting the field distribution inside the sample. In the superconducting state, the measured σ\sigma includes contributions from both the FLL (σsc\sigma_{\mathrm{sc}}) and a smaller, temperature-independent relaxation, due to nuclear moments (σn\sigma_{\mathrm{n}}) (see also ZF-μ\muSR below). The FLL-related relaxation can be extracted by subtracting the nuclear contribution in quadrature, σsc\sigma_{\mathrm{sc}} = σ2−σ2n\sqrt{\sigma^{2}-\sigma^{2}_{\mathrm{n}}}.

The resulting superconducting Gaussian relaxation rates σsc\sigma_{\mathrm{sc}} vs the applied external magnetic field are summarized in Fig. III.1(a). Above the lower critical field μ0Hc1\mu_{0}H_{c1} (10.1 mT) [24], the relaxation rate decreases continuously. Here, a field of 50 mT was chosen for the temperature-dependent TF-μ\muSR studies. In case of a single-gap superconductor, σsc(H)\sigma_{\mathrm{sc}}(H) generally follows σsc=0.172γμΦ02π(1−h)[1+1.21(1−h)3]λ−2\sigma_{\mathrm{sc}}=0.172\frac{\gamma_{\mu}\Phi_{0}}{2\pi}(1-h)[1+1.21(1-\sqrt{h})^{3}]\lambda^{-2} [37, 38], where h=Happl/Hc2h=H_{\mathrm{appl}}/H_{c2}, with HapplH_{\mathrm{appl}} being the applied magnetic field. As shown by the dash-dotted line in Fig. III.1(a), the single-gap model shows a very poor agreement with the experimental data. In a two-band model, each band is characterized by its own coherence length and a weight ww [or (1−w1-w)], accounting for the relative contribution of each band to the total σsc\sigma_{\mathrm{sc}} and, hence, to the superfluid density [39, 40]. For such a two-band model, the second moment of the field distribution can be calculated within the framework of the modified London model by using the following expression:

⟨B2⟩=σsc2γμ2=B2∑q≠0[we−q2ξ122(1−h1)1+q2λ021−h1+(1−w)−eq2ξ222(1−h2)1+q2λ021−h2]2.\langle B^{2}\rangle=\frac{\sigma_{\mathrm{sc}}^{2}}{\gamma_{\mu}^{2}}=B^{2}\sum\limits_{q\neq 0}\left[w\frac{e^{-\frac{q^{2}\xi_{1}^{2}}{2(1-h_{1})}}}{1+\frac{q^{2}\lambda_{0}^{2}}{1-h_{1}}}+(1-w)\frac{-e^{\frac{q^{2}\xi_{2}^{2}}{2(1-h_{2})}}}{1+\frac{q^{2}\lambda_{0}^{2}}{1-h_{2}}}\right]^{2}. (2)

Here, q=4π/3a(m3/2,n+m/2)q=4\pi/\sqrt{3}a(m\sqrt{3}/2,n+m/2) are the reciprocal lattice vectors for a hexagonal FLL (aa is the inter-vortex distance, mm and nn are integer numbers); B=μ0HB=\mu_{0}H for H≫Hc1H\gg H_{c1}, which is the mean field within the FLL; h1(2)=H/Hc2,1(2)h_{1(2)}=H/H_{c2,1(2)} are the reduced fields within band 1(2) (the same as hh in the above equation) and ξ1(2)\xi_{1(2)} are the coherence lengths for the band 1(2). As shown by the solid line in Fig. III.1(a), with w=0.45w=0.45, the two-band model is in good agreement with the experimental data and provides λ0\lambda_{0} =534(2) nm, ξ1\xi_{1} = 18.0(5) nm, and ξ2\xi_{2} = 5.7(2) nm. The derived λ0\lambda_{0} is comparable with the value estimated from the temperature-dependent TF-μ\muSR measurements in Fig. III.1(b). The upper critical field of 10.1(5) T, calculated from the coherence length of the second band, μ0Hc2=Φ0/(2πξ22)\mu_{0}H_{c2}=\Phi_{0}/(2\pi\xi_{2}^{2}), is highly consistent with the upper critical field determined from bulk measurements [see Fig. I(b)] (The specific-heat data were taken from Ref. 24). The virtual upper critical field μ0Hc2∗=1.02(6)\mu_{0}H_{c2}^{\ast}=1.02(6) T, calculated from the coherence length of the first band ξ1\xi_{1}, is in good agreement with the field value where γH(H)\gamma_{\mathrm{H}}(H) shows a change in slope [as indicated by an arrow in the inset of Fig. III.1(a)]. The virtual Hc2∗H_{c2}^{\ast} corresponds to the critical field which suppresses the small superconducting gap. Clearly, both the field-dependent σsc(H)\sigma_{\mathrm{sc}}(H) and the electronic specific-heat coefficient γH(H)\gamma_{\mathrm{H}}(H) suggest the existence of multiple superconducting gaps in NbReSi.

To further investigate the superconducting pairing in NbReSi, we carried out systematic TF-μ\muSR measurements in an applied field of 50 mT over a wide temperature range. Representative TF-μ\muSR spectra collected in the superconducting (0.3 K)- and normal (8 K) state of NbReSi are shown in Fig. II(b). The broadening of the field distribution due to FLL is clearly visible in the superconducting state. To quantify it, the TF-μ\muSR spectra were analyzed using again the model given by Eq. (1). In NbReSi, the upper critical field Hc2H_{c2} is very large compared to the applied TF field (50 mT). Therefore, the effects of overlapping vortex cores with increasing field can be ignored when extracting the penetration depth from the measured σsc\sigma_{\mathrm{sc}}. The effective magnetic penetration depth λeff\lambda_{\mathrm{eff}} can be calculated from σsc2(T)/γ2μ=0.00371Φ02/λ4eff(T)\sigma_{\mathrm{sc}}^{2}(T)/\gamma^{2}_{\mu}=0.00371\,\Phi_{0}^{2}/\lambda^{4}_{\mathrm{eff}}(T) [37, 38]. Figure III.1(b) summarizes the temperature-dependent inverse square of the magnetic penetration depth, which is proportional to the superfluid density, i.e., λeff−2(T)∝ρsc(T)\lambda_{\mathrm{eff}}^{-2}(T)\propto\rho_{\mathrm{sc}}(T). The latter was then analyzed by means of different models, generally described by:

ρsc(T)=1+2⟨∫∞ΔkEE2−Δk2∂f∂EdE⟩FS.\rho_{\mathrm{sc}}(T)=1+2\,\Bigg{\langle}\int^{\infty}_{\Delta_{\mathrm{k}}}\frac{E}{\sqrt{E^{2}-\Delta_{\mathrm{k}}^{2}}}\frac{\partial f}{\partial E}\mathrm{d}E\Bigg{\rangle}_{\mathrm{FS}}. (3)

Here, f=(1+eE/kBT)−1f=(1+e^{E/k_{\mathrm{B}}T})^{-1} is the Fermi function and ⟨⟩FS\langle\rangle_{\mathrm{FS}} represents an average over the Fermi surface [41]. Δk(T)=Δ(T)δk\Delta_{\mathrm{k}}(T)=\Delta(T)\delta_{\mathrm{k}} is an angle-dependent gap function, where Δ\Delta is the maximum gap value and δk\delta_{\mathrm{k}} is the angular dependence of the gap, equal to 1, cos2ϕ\cos 2\phi, and sinθ\sin\theta for an ss-, dd-, and pp-wave model, respectively, with ϕ\phi and θ\theta being the azimuthal angles. The temperature dependence of the gap is assumed to follow Δ(T)=Δ0tanh{1.82[1.018(Tc/T−1)]0.51}\Delta(T)=\Delta_{0}\mathrm{tanh}\{1.82[1.018(T_{\mathrm{c}}/T-1)]^{0.51}\} [41, 42], where Δ0\Delta_{0} is the gap value at 0 K.

Four different models, including single-gap ss-, pp-, and dd-wave, and two-gap s+ss+s-wave, were used to describe the λeff−2\lambda_{\mathrm{eff}}^{-2}(T)(T) data. For an ss- or pp-wave model, the best fits yield the same zero-temperature magnetic penetration depth λ0=523(2)\lambda_{\mathrm{0}}=523(2) nm, but different gap values, 1.04(3) and 1.33(5) meV, respectively. Note that, ρsc(T)\rho_{\mathrm{sc}}(T) is also consistent with a dirty-limit model [33], which yields a similar superconducting gap [i.e., 0.93(3) meV]. For the dd-wave model, the estimated λ0\lambda_{\mathrm{0}} and gap value are 460(4) nm and 1.28(5) meV.

As can be clearly seen in the inset of Fig. III.1(b), the significant deviation of the pp- or dd-wave model from the experimental data below ∼3\sim 3 K and the temperature-independent behavior of λeff−2(T)\lambda_{\mathrm{eff}}^{-2}(T) for T<1/3Tc∼2T<\nicefrac{{1}}{{3}}T_{c}\sim 2 K strongly suggest a fully-gapped superconductivity in NbReSi. Since Hc2(T)H_{c2}(T), σsc(H)\sigma_{\mathrm{sc}}(H), and γH(H)\gamma_{\mathrm{H}}(H) data [see Fig. I(b) and Fig. III.1(a)] imply the presence of multiple superconducting gaps in NbReSi, λeff−2(T)\lambda_{\mathrm{eff}}^{-2}(T) was also analyzed using a two-gap ss-wave model. In this case, ρsc(T)=wρscΔ0,1(T)+(1−w)ρscΔ0,2(T)\rho_{\mathrm{sc}}(T)=w\rho_{\mathrm{sc}}^{\Delta_{0,1}}(T)+(1-w)\rho_{\mathrm{sc}}^{\Delta_{0,2}}(T), with ρscΔ0,1\rho_{\mathrm{sc}}^{\Delta_{0,1}} and ρscΔ0,2(T)\rho_{\mathrm{sc}}^{\Delta_{0,2}}(T) being the superfluid densities related to the first- (Δ0,1\Delta_{0,1}) and second (Δ0,2\Delta_{0,2}) gap, and ww a relative weight. Here, by fixing the weight ww = 0.45, as determined from σsc(H)\sigma_{\mathrm{sc}}(H), the two-gap s+ss+s-wave model provides almost identical results to the single-gap ss-wave model, reflected in two practically overlapping fitting curves in Fig. III.1(b). The two-gap model yields Δ0,1\Delta_{0,1} = 0.80(5) meV and Δ0,2\Delta_{0,2} = 1.23(5) meV. Since the gap sizes are not significantly different (Δ0,1\Delta_{0,1}/Δ0,2\Delta_{0,2} ∼\sim 0.7), this makes it difficult to discriminate between a single- and a two-gap superconductor based on the temperature-dependent superfluid density alone [40, 43]. Nevertheless, as we show above, the two-gap feature in NbReSi is clearly reflected in its field-dependent superconducting relaxation rate σsc(H)\sigma_{\mathrm{sc}}(H), specific-heat coefficient γH(H)\gamma_{\mathrm{H}}(H), and also in the temperature-dependent upper critical field Hc2(T)H_{c2}(T). The superconducting gap of NbReSi derived from TF-μ\muSR is similar to that of other Re-based superconductors, e.g., ReTT (TT = transition metal) [29, 30, 44, 32, 45] and rhenium-boron compounds [46], the latter exhibiting a multigap SC, too.

To search for a possible breaking of the time-reversal symmetry in the superconducting state of NbReSi, we compared the ZF-μ\muSR results in the normal- and superconducting states. As shown in Fig. III.1, neither coherent oscillations nor fast decays could be identified in the spectra collected above (10 K) and below TcT_{c} (0.3 K), hence implying the lack of any magnetic order or fluctuations. Normally, in the absence of external fields, the onset of SC does not imply any changes in the ZF muon-spin relaxation rate. However, if the TRS is broken, the onset of spontaneous magnetic fields can be detected by ZF-μ\muSR as an increase in the muon-spin relaxation rate. In absence of external fields, the muon-spin relaxation is mainly attributed to the randomly oriented nuclear moments, which can be modeled by means of a phenomenological relaxation function, consisting of a combination of Gaussian- and Lorentzian Kubo-Toyabe relaxations [47, 48], A(t)=As[13+23(1−σZF2t2−ΛZFt)e(−σZF2t22−ΛZFt)]+AbgA(t)=A_{\mathrm{s}}[\frac{1}{3}+\frac{2}{3}(1-\sigma_{\mathrm{ZF}}^{2}t^{2}-\Lambda_{\mathrm{ZF}}t)\mathrm{e}^{(-\frac{\sigma_{\mathrm{ZF}}^{2}t^{2}}{2}-\Lambda_{\mathrm{ZF}}t)}]+A_{\mathrm{bg}}.

Here, AsA_{\mathrm{s}} and AbgA_{\mathrm{bg}} are the same as in the TF-μ\muSR case [see Eq. (1)]. The σZF\sigma_{\mathrm{ZF}} and ΛZF\Lambda_{\mathrm{ZF}} represent the zero-field Gaussian and Lorentzian relaxation rates, respectively. As shown by the solid lines in Fig. III.1, the derived relaxations in the normal- and the superconducting states are almost identical. This lack of evidence for an additional μ\muSR relaxation below TcT_{c} excludes a possible TRS breaking in the superconducting state of NbReSi.

III.2 93{}^{93}Nb NMR study

Refer to caption
Figure 5. : The NMR relaxation rate T1−1T_{1}^{-1} as a function of temperature (here measured at μ0H=5\mu_{0}H=5 T) decays by following an exponential law, T1−1∝exp(−Δ/kBT)T_{1}^{-1}\propto\exp(-\Delta/k_{\mathrm{B}}T), typical of ss-wave superconductivity with a fixed gap Δ\Delta. The vertical line at 1 refers to the TcT_{c} value at 5 T. Inset: Korringa product (T1T)−1(T_{1}T)^{-1} as a function of temperature. Its constant value above TcT_{c} [here, ca. 0.280.28 (sK)−1{}^{-1}] indicates an ideal metallic behavior, followed by a gradual decrease below the superconducting transition. The TcT_{c} value determined from (T1T)−1(T_{1}T)^{-1} is consistent those obtained by other techniques [see Fig. I(b)]

.

NMR is a versatile technique for investigating the electronic properties of materials, in particular, their electron correlations, complementary to μ\muSR with respect to the probe location, coupling to the environment, time window, and field range. Here we employed NMR to investigate the normal- and superconducting-state properties of NbReSi, mostly via 93{}^{93}Nb NMR measurements in a field of 5 T. In selected cases, we conducted also 29{}^{29}Si NMR (I=1/2I=\nicefrac{{1}}{{2}}) measurements. In either case, the NMR reference frequency ν0\nu_{0} was determined from the 27{}^{27}Al resonance signal in an Al(NO3{}_{3})3{}_{3} solution [49]. Successively, the 93{}^{93}Nb (or 29{}^{29}Si) NMR shifts were calculated with respect to each ν0\nu_{0} reference frequency. Considering its good NMR signal and fast relaxation rate, 93{}^{93}Nb was used as the nucleus of choice for investigating the electronic properties of NbReSi. The NMR line shapes shown in Fig. III.2 most likely represent the central transition line and are characterized by a relatively large width (ca. 200 kHz). No satellite transitions were observed within 1 MHz on either side of the central transition line, indicating that quadrupolar coupling is either extremely weak (satellites located within the linewidth of the central line) or extremely large (satellites located at ≥1\geq 1 MHz away from the central transition). Considering the complex and asymmetric coordination of Nb atoms, we expect the latter to be the case [50]111Nb has a 3g3g Wyckoff position, with an m2mm2m local symmetry, implying a single VzzV_{zz} component. Nb is bonded in a 11-coordinate geometry to six Re and five Si atoms. There are two short- (2.87 Å) and four long (2.95 Å) Nb-Re bonds, as well as four short- (2.68 Å) and one long (2.78 Å) Nb-Si bonds. See: https://materialsproject.org/materials/mp-1095061. The central NMR line is sufficient for investigating the superconducting properties of NbReSi.

Two main conclusions can be drawn from our NMR study. Firstly, the temperature dependence of the Korringa product indicates a transition from the metallic to the superconducting phase. Secondly, the exponential dependence of relaxation rate in the superconducting phase confirms the occurrence of a fully-gapped SC phase. Our detailed findings are elaborated on below.

To determine the Tc(H)T_{c}(H) of NbReSi, we use a standard detuning method (see Fig. III.2), which gives Tc(5T)=4.4T_{c}(5\,\mathrm{T})=4.4 K. The superconducting transition is also confirmed by the Korringa product in the 93{}^{93}Nb case (see inset in Fig. III.2) [52]. Above TcT_{c}, we observe an ideal behavior [i.e., (T1T)−1(T_{1}T)^{-1} constant], typical of standard metals. As the temperature drops below TcT_{c} = 4.4 K, we observe a gradual decrease of the (T1T)−1(T_{1}T)^{-1} product, reflecting a slowing down of the relaxation rate due to electron pairing, a key signature of the superconducting state.

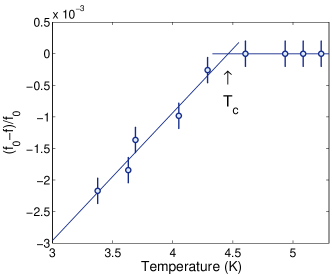
Refer to caption
Figure 6. : 93{}^{93}Nb NMR lineshapes collected at various temperatures, covering both the superconducting- and normal states, in a magnetic field of 5 T. The dashed line indicates the reference frequency. The derived NMR Knight shifts and widths vs temperature are shown in the insets. While Knight shifts show a negligible drop below TcT_{c}, the line widths are independent of temperature.
Refer to caption
Figure 7. : Frequency detuning of the NMR resonant circuit with temperature. At the onset of superconductivity at Tc(5T)=4.4T_{c}(5\,\mathrm{T})=4.4 K the magnetic flux is (partially) expelled, equivalent to a lowering of inductance, and hence to an increase in frequency f=1/(2πLC)f=1/(2\pi\sqrt{LC}).

To determine the nature of the superconducting gap, we turn to the relaxation-rate data. The relaxation of 93{}^{93}Nb nuclei can be modeled by an exponential function T1−1∝exp(−Δ/kBT)T_{1}^{-1}\propto\exp(-\Delta/k_{\mathrm{B}}T) (see Fig. III.2). The fit provides a temperature-independent gap Δ/kB=4.5±0.9\Delta/k_{\mathrm{B}}=4.5\pm 0.9 K (equivalent to Δ/kBTc=1.02\Delta/k_{\mathrm{B}}T_{c}=1.02), lower than that determined by other techniques, most likely reflecting an important quadrupole contribution to relaxation. Independent of the gap value, the exponential decrease of relaxation can be interpreted as a critical slowing down of the electronic spin fluctuations. The fact that the superconducting gap is constant and temperature independent provides strong evidence of conventional ss-wave superconductivity in NbReSi, although NMR is not sensitive enough to distinguish single- from multigap SC. Since unconventional superconductivity would give rise to a power-law-dependent relaxation rate vs. temperature (see, e.g., Ref. 53), the exponential decrease of relaxation is sufficient to prove that the system possesses a fully-opened gap. Nevertheless, for completeness, below we discuss some surprising aspects that, although unexpected, can still be reconciled with the theory of conventional SC.


It is surprising that the NMR relaxation data do not exhibit a Hebel-Slichter (HS) peak just below the superconducting transition, a typical feature of most ss-wave superconductors. Several factors might account for the suppression of the HS peak. Firstly, the impurities may play a role in the reduction of the HS peak, which might also lead to the weak temperature dependence of NMR shifts [54]. Secondly, the HS peak can be smeared out by quadrupole effects, considering that 93{}^{93}Nb has I=9/2I=\nicefrac{{9}}{{2}}. This smearing has been observed in other noncentrosymmetric superconductors with an ss-wave gap (for instance, W3{}_{3}Al2{}_{2}C shows an HS peak in the I=1/2I=\nicefrac{{1}}{{2}} 13{}^{13}C relaxation, but none in that of I=5/2I=\nicefrac{{5}}{{2}} 27{}^{27}Al [55]). To disentangle the contribution of quadrupole effects to the relaxation rate, one has to either measure the same system at lower fields or resort to non-quadrupolar nuclei (here, 29{}^{29}Si). The almost quadratic decrease of the signal-to-noise ratio with field [56] and the appearance of acoustic ringing at low frequencies make this route unpractical. On the other hand, numerical calculations suggest that the density of states at Fermi level is dominated by the Re-5dd and Nb-4dd orbitals, the contribution of Si orbitals being negligible [24]. Hence, we expect a much weaker magnetic hyperfine coupling to 29{}^{29}Si- than to 93{}^{93}Nb nuclei, corresponding to a much slower relaxation in the former case. Indeed, experimentally we find that, in NbReSi, the relaxation rate of 29{}^{29}Si nuclei is prohibitively slow (∼30\sim 30 s at 4 K, becoming exponentially slower below TcT_{c}), thus making the use of 29{}^{29}Si nuclei unfeasible for probing the nuclear relaxation in the superconducting state.

It is also surprising that both the line shift and width (see Fig. III.2) are almost constant with temperature, with the line shapes above and below TcT_{c} being virtually indistinguishable. The insensitivity of the line shift to the superconducting transition, at first seems to suggest a spin-triplet pairing, where electron spins maintain their mutual orientation across TcT_{c}. However, this apparent contradiction is resolved by a comparison with well-known transition-metal superconductors. Indeed, as has been shown for tin, vanadium, niobium, etc., their total shift is given as the sum of spin- and orbital components K=Ks+KorbK=K_{s}+K_{\mathrm{orb}}, with KorbK_{\mathrm{orb}} being the dominant contribution [57]. As the latter is unaffected by the electron-spin pairing in the superconducting state, this accounts for an almost constant NMR shift across TcT_{c}, yet compatible with a standard ss-wave pairing. Indeed, as shown in Fig. III.2, we observe a negligible decrease in frequency, which could indicate that Ks≪KorbK_{s}\ll K_{\mathrm{orb}}. Other mechanisms, such as disorder, could account for the almost constant NMR shift across TcT_{c}. Indeed, in strongly-coupled systems, even tiny amounts of impurities can lead to temperature-independent shifts [54]. Last but not least, sample-heating effects caused by eddy currents might also play a role in reducing the observed line shift [58]. However, such effects are normally relevant only at very low temperatures in good conducting samples (i.e., able to sustain eddy currents), or for fast pulse-repetition rates. Since neither the sample nor the measurement conditions fully satisfy such requirements, it is unlikely that sample heating might explain the weak Knight shifts in NbReSi. In general, although some questions about the role of quadrupole interactions and disorder in suppressing the HS peak remain open, the exponential dependence of the relaxation rate below TcT_{c} unambiguously proves the existence of fully-gapped superconductivity in NbReSi.

III.3 Discussion

According to TF-μ\muSR measurements at various temperatures, the superfluid density ρsc(T)\rho_{\mathrm{sc}}(T) shows an almost temperature-independent behavior below 1/3\nicefrac{{1}}{{3}}TcT_{c} [see Fig. III.1(b)], indicating the absence of low-energy excitations and thus, a nodeless SC in NbReSi. Both the single-gap ss- and two-gap s+ss+s-wave models describe the ρsc(T)\rho_{\mathrm{sc}}(T) data very well. However, the field-dependent superconducting Gaussian relaxation rate σsc(H)\sigma_{\mathrm{sc}}(H) and the electronic specific-heat coefficient γH(H)\gamma_{\mathrm{H}}(H) [see Fig. III.1(a)] provide clear evidence of multigap SC in NbReSi, both datasets showing a distinct field response compared to a single-gap superconductor [59, 60, 33]. As indicated by the arrow in the inset of Fig. III.1(a), γH(H)\gamma_{\mathrm{H}}(H) exhibits a clear change in slope when the applied magnetic field (larger than 1 T) suppresses the small gap, a feature recognized as the fingerprint of multigap superconductors. Conversely, γH(H)\gamma_{\mathrm{H}}(H) would be mostly linear in the single-gap case. Moreover, a single-gap model cannot describe the σsc(H)\sigma_{\mathrm{sc}}(H) data [see main panel of Fig. III.1(a)]. At the same time, the two-band model yields an upper critical field μ0Hc2\mu_{0}H_{c2}(2.1 K) = 10.1 T, consistent with the value determined from other techniques. The derived virtual upper critical field μ0Hc2∗\mu_{0}H_{c2}^{\ast} = 1.02 T is in good agreement with the field value where γH(H)\gamma_{\mathrm{H}}(H) shows a change in slope. Here, Hc2∗H_{c2}^{\ast} corresponds to the critical field which suppresses the small superconducting gap. The multigap SC of NbReSi can be further inferred from the temperature-dependent upper critical field Hc2(T)H_{c2}(T). As shown in Fig. I(b), the two-band model [61] is clearly superior to the Werthamer-Helfand-Hohenberg (WHH) model [62] over the whole temperature range. The analysis of Hc2(T)H_{c2}(T) with the two-band model indicates that the intra-band and inter-band couplings are λ11\lambda_{11} ∼\sim λ22=0.17\lambda_{22}=0.17 and λ12=0.1\lambda_{12}=0.1, respectively. As the inter-band coupling is not much different from intra-band coupling, this makes the SC gaps belonging to different electronic bands less distinguishable [63]. In addition, as has been found in other multigap superconductors [59, 40, 60, 33], a relatively small weight of the second gap, or gap sizes not significantly different, make it difficult to discriminate between a single- and a two-gap superconductor from the temperature-dependent superconducting properties only. However, in the NbReSi case, also the electronic band-structure calculations support a multigap SC, since they indicate that more than four bands cross the Fermi level [24].

The two-band model leads to an upper critical field μ0\mu_{0}Hc2(0)=13.3H_{c2}(0)=13.3 T, which is beyond the weak-coupling Pauli value, i.e., 1.86kBTc=12.11.86k_{\mathrm{B}}T_{c}=12.1 T. In NCSCs, the antisymmetric spin-orbit coupling allows for the occurrence of an admixture of singlet and triplet pairings, which in turn can enhance the upper critical field. Consequently, in this case, a violation of the Pauli limit hints at the presence of unconventional SC. Although in NbReSi the band splitting near the Fermi level is relatively large compared to other NCSCs (i.e., EASOC∼180E_{\mathrm{ASOC}}\sim 180 meV) [1, 2, 24], its superconducting pairing is more consistent with spin-singlet, here reflected in a fully-gapped superconducting state. Indeed, the temperature-dependent zero-field electronic specific heat Ce(T)/TC_{\mathrm{e}}(T)/T, superfluid density ρsc(T)\rho_{\mathrm{sc}}(T), and NMR spin relaxation rate T1−1(T)T_{1}^{-1}(T) all suggest a nodeless SC in NbReSi. Furthermore, the preserved TRS below TcT_{c}, as revealed by ZF-μ\muSR, suggests the absence of spin-triplet pairing in NbReSi. Therefore, the enhanced Hc2H_{c2} of NbReSi is unlikely to be caused by a mixed-type of pairing. Strong electron correlations can also lead to a large Hc2H_{c2}, e.g., the noncentrosymmetric CePt3{}_{3}Si and Ce(Rh,Ir)Si3{}_{3} exhibit Hc2H_{c2} values far beyond the Pauli limit [23, 64, 65]. In NbReSi, however, both the temperature-independent Korringa product (T1T)−1(T_{1}T)^{-1} in the normal state and the small electronic specific-heat coefficient (γn∼8.23\gamma_{\mathrm{n}}\sim 8.23 mJ/mol-K2{}^{2} [24]) suggest weak electron correlations. A large superconducting gap value or a strong electron-phonon coupling may also enhance Hc2H_{c2} [1, 66]. However, the estimated electron-phonon coupling λep\lambda_{\mathrm{ep}} = 0.66 is rather weak in NbReSi [24], while its gap value Δ0=1.95kBTc\Delta_{0}=1.95k_{\mathrm{B}}T_{c}, as determined from TF-μ\muSR [see Fig. III.1(b)], is not much larger than the BCS weak-coupling value (i.e., 1.76kBTc1.76k_{\mathrm{B}}T_{c}).

Having excluded some common causes of a large Hc2H_{c2}, we examine now the role of anisotropy, considering that a highly anisotropic structure can often lead to a sizeable Hc2H_{c2}. For instance, in the quasi-one-dimensional Cr-based A2A_{2}Cr3{}_{3}As3{}_{3} (AA = K, Rb, and Cs) superconductors, despite TcT_{c}s in the 2 to 6 K range, upper critical fields up to 40 T have been reported [67, 68, 69, 70, 71]. Although triplet pairing was proposed in A2A_{2}Cr3{}_{3}As3{}_{3} [72, 73, 74], a violation of the Pauli limit is also possible for singlet SC. In this case, the spins of Cooper pairs are aligned predominantly along the Cr chains, which play the role of the easy magnetization axis, but cause no magnetic order in the normal paramagnetic state. This scenario is consistent with the presence of Pauli-limiting pair breaking and the strong Hc2(T)H_{c2}(T) anisotropy observed in K2{}_{2}Cr3{}_{3}As3{}_{3} [67]. NbReSi adopts a hexagonal crystal structure (P6¯2mP\overline{6}2m, No. 189, with in-plane and out-of-plane lattice parameters a=6.7194a=6.7194 Å and c=3.4850c=3.4850 Å), which is very similar to the crystal structure of A2A_{2}Cr3{}_{3}As3{}_{3} (P6¯m2P\overline{6}m2, No. 187). Both structures lack an inversion center and have a D3hD_{3h} point group. Therefore, the large Hc2H_{c2} of NbReSi is most likely related to its anisotropic crystal structure. Such scenario is indirectly supported by the fact that the sister compound TaReSi, which also adopts a noncentrosymmetric crystal structure (space group Ima2Ima2, No. 46), but is less anisotropic [75], exhibits a relatively small upper critical field, μ0Hc2(0)\mu_{0}H_{c2}(0) = 6.6 T. To clarify the role of anisotropy in enhancing Hc2H_{c2}, measurements on NbReSi single crystals are highly desirable. Besides the above intrinsic effects, also extrinsic effects may enhance the Hc2H_{\mathrm{c2}} of NbReSi. For instance, as previously reported in MgB2{}_{2}, single crystals exhibit a Hc2(0)H_{\mathrm{c2}}(0) up to 18 T [76], while a sizable impurity scattering introduced by disorder significantly enhances this value up to almost 50 T [77]. To exclude (or confirm) this possibility, again, measurements on high-quality single crystals are required. Although to date NbReSi single crystals are not available, future work on crystal growth could make them accessible.

IV Conclusion

To summarize, we studied the superconducting properties of the noncentrosymmetric NbReSi superconductor by means of the μ\muSR and NMR techniques. The superconducting state of NbReSi is characterized by Tc=6.5T_{c}=6.5 K and an upper critical field μ0Hc2(0)=13.3\mu_{0}H_{c2}(0)=13.3 T. The temperature-dependent superfluid density and the NMR spin-lattice relaxation rate reveal a nodeless superconductivity, well described by an isotropic ss-wave model. The NMR Knight shift exhibits only a negligible drop below TcT_{c}, most likely due to a dominant orbital contribution. Field-dependent measurements, including muon-spin relaxation and electronic specific-heat coefficient, imply the presence of multiple superconducting gaps in NbReSi. This is also supported by the temperature dependence of the upper critical field Hc2(T)H_{c2}(T). The lack of spontaneous magnetic fields below TcT_{c} indicates that, unlike in ReTT or elementary rhenium superconductors, time-reversal symmetry is preserved in the superconducting state of NbReSi. In general, the μ\muSR and the NMR relaxation-rate results are highly consistent with a spin-singlet pairing in NbReSi. Finally, the violation of Pauli limit in NbReSi is most likely related to its anisotropic crystal structure rather than to an unconventional type of pairing.

Acknowledgements.
This work was supported from the Natural Science Foundation of Shanghai (Grant Nos. 21ZR1420500 and 21JC1402300) and the Schweizerische Nationalfonds zur Förderung der Wissenschaftlichen Forschung (SNF) (Grant Nos. 200021_188706 and 206021_139082). H.Q.Y. acknowledge support from the National Key R&D Program of China (No. 2017YFA0303100 and No. 2016YFA0300202), the Key R&D Program of Zhejiang Province, China (No. 2021C01002), the National Natural Science Foundation of China (No. 11974306). We acknowledge the allocation of beam time at the Swiss muon source, and thank the scientists of Dolly μ\muSR spectrometer for their support.

References

  • Bauer and Sigrist [2012] E. Bauer and M. Sigrist, eds., Non-Centrosymmetric Superconductors, Vol. 847 (Springer Verlag, Berlin, 2012).
  • Smidman et al. [2017] M. Smidman, M. B. Salamon, H. Q. Yuan, and D. F. Agterberg, Superconductivity and spin–orbit coupling in non-centrosymmetric materials: A review, Rep. Prog. Phys. 80, 036501 (2017).
  • Ghosh et al. [2020] S. K. Ghosh, M. Smidman, T. Shang, J. F. Annett, A. D. Hillier, J. Quintanilla, and H. Yuan, Recent progress on superconductors with time-reversal symmetry breaking, J. Phys.: Condens. Matter 33, 033001 (2020).
  • Kim et al. [2018] H. Kim, K. Wang, Y. Nakajima, R. Hu, S. Ziemak, P. Syers, L. Wang, H. Hodovanets, J. D. Denlinger, P. M. R. Brydon, D. F. Agterberg, M. A. Tanatar, R. Prozorov, and J. Paglione, Beyond triplet: Unconventional superconductivity in a spin-3/23/2 topological semimetal, Sci. Adv. 4, eaao4513 (2018).
  • Sun et al. [2015] Z. X. Sun, M. Enayat, A. Maldonado, C. Lithgow, E. Yelland, D. C. Peets, A. Yaresko, A. P. Schnyder, and P. Wahl, Dirac surface states and nature of superconductivity in noncentrosymmetric BiPd, Nat. Commun. 6, 6633 (2015).
  • Ali et al. [2014] M. N. Ali, Q. D. Gibson, T. Klimczuk, and R. J. Cava, Noncentrosymmetric superconductor with a bulk three-dimensional Dirac cone gapped by strong spin-orbit coupling, Phys. Rev. B 89, 020505(R) (2014).
  • Sato and Fujimoto [2009] M. Sato and S. Fujimoto, Topological phases of noncentrosymmetric superconductors: Edge states, Majorana fermions, and non-Abelian statistics, Phys. Rev. B 79, 094504 (2009).
  • Tanaka et al. [2010] Y. Tanaka, Y. Mizuno, T. Yokoyama, K. Yada, and M. Sato, Anomalous Andreev bound state in noncentrosymmetric superconductors, Phys. Rev. Lett. 105, 097002 (2010).
  • Sato and Ando [2017] M. Sato and Y. Ando, Topological superconductors: A review, Rep. Prog. Phys. 80, 076501 (2017).
  • Qi and Zhang [2011] X.-L. Qi and S.-C. Zhang, Topological insulators and superconductors, Rev. Mod. Phys. 83, 1057 (2011).
  • Kallin and Berlinsky [2016] C. Kallin and J. Berlinsky, Chiral superconductors, Rep. Prog. Phys. 79, 054502 (2016).
  • Xu et al. [2015a] S.-Y. Xu, I. Belopolski, N. Alidoust, M. Neupane, G. Bian, C. Zhang, R. Sankar, G. Chang, Z. Yuan, C.-C. Lee, S.-M. Huang, H. Zheng, J. Ma, D. S. Sanchez, B. Wang, A. Bansil, F. Chou, P. P. Shibayev, H. Lin, S. Jia, and M. Z. Hasan, Discovery of a Weyl fermion semimetal and topological Fermi arcs, Science 349, 613 (2015a).
  • Xu et al. [2015b] S.-Y. Xu, N. Alidoust, I. Belopolski, Z. Yuan, G. Bian, T.-R. Chang, H. Zheng, V. N. Strocov, D. S. Sanchez, G. Chang, et al., Discovery of a Weyl fermion state with Fermi arcs in niobium arsenide, Nat. Phys. 11, 748 (2015b).
  • Lv et al. [2015] B. Q. Lv, H. M. Weng, B. B. Fu, X. P. Wang, H. Miao, J. Ma, P. Richard, X. C. Huang, L. X. Zhao, G. F. Chen, Z. Fang, X. Dai, T. Qian, and H. Ding, Experimental discovery of Weyl semimetal TaAs, Phys. Rev. X 5, 031013 (2015).
  • Xu et al. [2016] N. Xu, H. M. Weng, B. Q. Lv, C. E. Matt, J. Park, F. Bisti, V. N. Strocov, D. Gawryluk, E. Pomjakushina, K. Conder, N. C. Plumb, M. Radovic, G. Autés, O. V. Yazyev, Z. Fang, X. Dai, T. Qian, J. Mesot, H. Ding, and M. Shi, Observation of Weyl nodes and Fermi arcs in tantalum phosphide, Nat. Commun. 7, 11006 (2016).
  • Souma et al. [2016] S. Souma, Z. Wang, H. Kotaka, T. Sato, K. Nakayama, Y. Tanaka, H. Kimizuka, T. Takahashi, K. Yamauchi, T. Oguchi, K. Segawa, and Y. Ando, Direct observation of nonequivalent Fermi-arc states of opposite surfaces in the noncentrosymmetric Weyl semimetal NbP, Phys. Rev. B 93, 161112(R) (2016).
  • Yuan et al. [2006] H. Q. Yuan, D. F. Agterberg, N. Hayashi, P. Badica, D. Vandervelde, K. Togano, M. Sigrist, and M. B. Salamon, ss-wave spin-triplet order in superconductors without inversion symmetry: Li2{}_{2}Pd3{}_{3}B and Li2{}_{2}Pt3{}_{3}B, Phys. Rev. Lett. 97, 017006 (2006).
  • Nishiyama et al. [2007] M. Nishiyama, Y. Inada, and G.-q. Zheng, Spin triplet superconducting state due to broken inversion symmetry in Li2{}_{2}Pt3{}_{3}B, Phys. Rev. Lett. 98, 047002 (2007).
  • Bonalde et al. [2005] I. Bonalde, W. Brämer-Escamilla, and E. Bauer, Evidence for line nodes in the superconducting energy gap of noncentrosymmetric CePt3{}_{3}Si from magnetic penetration depth measurements, Phys. Rev. Lett. 94, 207002 (2005).
  • Shang et al. [2020a] T. Shang, M. Smidman, A. Wang, L.-J. Chang, C. Baines, M. K. Lee, Z. Y. Nie, G. M. Pang, W. Xie, W. B. Jiang, M. Shi, M. Medarde, T. Shiroka, and H. Q. Yuan, Simultaneous nodal superconductivity and time-reversal symmetry breaking in the noncentrosymmetric superconductor CaPtAs, Phys. Rev. Lett. 124, 207001 (2020a).
  • Kuroiwa et al. [2008] S. Kuroiwa, Y. Saura, J. Akimitsu, M. Hiraishi, M. Miyazaki, K. H. Satoh, S. Takeshita, and R. Kadono, Multigap superconductivity in sesquicarbides La2{}_{2}C3{}_{3} and Y2{}_{2}C3{}_{3}, Phys. Rev. Lett. 100, 097002 (2008).
  • Carnicom et al. [2018] E. M. Carnicom, W. Xie, T. Klimczuk, J. J. Lin, K. Górnicka, Z. Sobczak, N. P. Ong, and R. J. Cava, TaRh2{}_{2}B2{}_{2} and NbRh2{}_{2}B2{}_{2}: Superconductors with a chiral noncentrosymmetric crystal structure, Sci. Adv. 4, eaar7969 (2018).
  • Bauer et al. [2004] E. Bauer, G. Hilscher, H. Michor, C. Paul, E. W. Scheidt, A. Gribanov, Y. Seropegin, H. Noël, M. Sigrist, and P. Rogl, Heavy fermion superconductivity and magnetic order in noncentrosymmetric CePt3{}_{3}Si, Phys. Rev. Lett. 92, 027003 (2004).
  • Su et al. [2021] H. Su, T. Shang, F. Du, C. F. Chen, H. Q. Ye, X. Lu, C. Cao, M. Smidman, and H. Q. Yuan, NbReSi: A noncentrosymetric superconductor with large upper critical field, Phys. Rev. Mater. 5, 114802 (2021).
  • Hillier et al. [2009] A. D. Hillier, J. Quintanilla, and R. Cywinski, Evidence for time-reversal symmetry breaking in the noncentrosymmetric superconductor LaNiC2{}_{2}, Phys. Rev. Lett. 102, 117007 (2009).
  • Barker et al. [2015] J. A. T. Barker, D. Singh, A. Thamizhavel, A. D. Hillier, M. R. Lees, G. Balakrishnan, D. M. Paul, and R. P. Singh, Unconventional superconductivity in La7{}_{7}Ir3{}_{3} revealed by muon spin relaxation: Introducing a new family of noncentrosymmetric superconductor that breaks time-reversal symmetry, Phys. Rev. Lett. 115, 267001 (2015).
  • Shang et al. [2020b] T. Shang, S. K. Ghosh, J. Z. Zhao, L.-J. Chang, C. Baines, M. K. Lee, D. J. Gawryluk, M. Shi, M. Medarde, J. Quintanilla, and T. Shiroka, Time-reversal symmetry breaking in the noncentrosymmetric Zr3{}_{3}Ir superconductor, Phys. Rev. B 102, 020503(R) (2020b).
  • Singh et al. [2014] R. P. Singh, A. D. Hillier, B. Mazidian, J. Quintanilla, J. F. Annett, D. M. Paul, G. Balakrishnan, and M. R. Lees, Detection of time-reversal symmetry breaking in the noncentrosymmetric superconductor Re6{}_{6}Zr using muon-spin spectroscopy, Phys. Rev. Lett. 112, 107002 (2014).
  • Shang et al. [2018a] T. Shang, G. M. Pang, C. Baines, W. B. Jiang, W. Xie, A. Wang, M. Medarde, E. Pomjakushina, M. Shi, J. Mesot, H. Q. Yuan, and T. Shiroka, Nodeless superconductivity and time-reversal symmetry breaking in the noncentrosymmetric superconductor Re24{}_{24}Ti5{}_{5}, Phys. Rev. B 97, 020502(R) (2018a).
  • Shang et al. [2018b] T. Shang, M. Smidman, S. K. Ghosh, C. Baines, L. J. Chang, D. J. Gawryluk, J. A. T. Barker, R. P. Singh, D. M. Paul, G. Balakrishnan, E. Pomjakushina, M. Shi, M. Medarde, A. D. Hillier, H. Q. Yuan, J. Quintanilla, J. Mesot, and T. Shiroka, Time-reversal symmetry breaking in Re-based superconductors, Phys. Rev. Lett. 121, 257002 (2018b).
  • Xie et al. [2020] W. Xie, P. R. Zhang, B. Shen, W. B. Jiang, G. M. Pang, T. Shang, C. Gao, M. Smidman, and H. Q. Yuan, CaPtAs: a new noncentrosymmetric superconductor, Sci. China-Phys. Mech. Astron. 63, 237412 (2020).
  • Shang et al. [2020c] T. Shang, C. Baines, L.-J. Chang, D. J. Gawryluk, E. Pomjakushina, M. Shi, M. Medarde, and T. Shiroka, Re1−x{}_{1-x}Mox{}_{x} as an ideal test case of time-reversal symmetry breaking in unconventional superconductors, npj Quantum Mater. 5, 76 (2020c).
  • Shang et al. [2021a] T. Shang, W. Xie, J. Z. Zhao, Y. Chen, D. J. Gawryluk, M. Medarde, M. Shi, H. Q. Yuan, E. Pomjakushina, and T. Shiroka, Multigap superconductivity in centrosymmetric and noncentrosymmetric rhenium-boron superconductors, Phys. Rev. B 103, 184517 (2021a).
  • Yarmolyuk and Gladishevs’kii [1974] Y. P. Yarmolyuk and E. I. Gladishevs’kii, New ternary compounds of equiatomic composition in the systems of two transition metals and silicon or germanium, Dopov. Akad. Nauk Ukr. RSR, Ser. B, 11, 1030 (1974).
  • Rao et al. [1985] G. V. S. Rao, K. Wagner, G. Balakrishnan, J. Janaki, W. Paulus, R. Schöllhorn, V. S. Subramanian, and U. Poppe, Structure and superconductivity studies on ternary equiatomic silicides, MMMM’SiSi, Bull. Mater. Sci. 7, 215 (1985).
  • Suter and Wojek [2012] A. Suter and B. M. Wojek, Musrfit: A free platform-independent framework for μ\muSR data analysis, Phys. Procedia 30, 69 (2012).
  • Barford and Gunn [1988] W. Barford and J. M. F. Gunn, The theory of the measurement of the London penetration depth in uniaxial type-II superconductors by muon spin rotation, Physica C 156, 515 (1988).
  • Brandt [2003] E. H. Brandt, Properties of the ideal Ginzburg-Landau vortex lattice, Phys. Rev. B 68, 054506 (2003).
  • Serventi et al. [2004] S. Serventi, G. Allodi, R. De Renzi, G. Guidi, L. Romanò, P. Manfrinetti, A. Palenzona, C. Niedermayer, A. Amato, and C. Baines, Effect of two gaps on the flux-lattice internal field distribution: Evidence of two length scales in Mg1−x{}_{1-x}Alx{}_{x}B2{}_{2} from μ\muSR, Phys. Rev. Lett. 93, 217003 (2004).
  • Khasanov et al. [2014] R. Khasanov, A. Amato, P. K. Biswas, H. Luetkens, N. D. Zhigadlo, and B. Batlogg, SrPt3{}_{3}P: A two-band single-gap superconductor, Phys. Rev. B 90, 140507(R) (2014).
  • Tinkham [1996] M. Tinkham, Introduction to Superconductivity, 2nd ed. (Dover Publications, Mineola, NY, 1996).
  • Carrington and Manzano [2003] A. Carrington and F. Manzano, Magnetic penetration depth of MgB2{}_{2}, Physica C 385, 205 (2003).
  • Khasanov et al. [2020] R. Khasanov, R. Gupta, D. Das, A. Leithe-Jasper, and E. Svanidze, Single-gap versus two-gap scenario: Specific heat and thermodynamic critical field of the noncentrosymmetric superconductor BeAu, Phys. Rev. B 102, 014514 (2020).
  • Shang et al. [2019a] T. Shang, D. J. Gawryluk, J. A. T. Verezhak, E. Pomjakushina, M. Shi, M. Medarde, J. Mesot, and T. Shiroka, Structure and superconductivity in the binary Re1−x{}_{1-x}Mox{}_{x} alloys, Phys. Rev. Mater. 3, 024801 (2019a).
  • Shang and Shiroka [2021] T. Shang and T. Shiroka, Time-reversal symmetry breaking in Re-based superconductors:: recent developments, Front. Phys. 9, 270 (2021), and references therein.
  • Shang et al. [2021b] T. Shang, W. Xie, J. Z. Zhao, Y. Chen, D. J. Gawryluk, M. Medarde, M. Shi, H. Q. Yuan, E. Pomjakushina, and T. Shiroka, Multigap superconductivity in centrosymmetric and noncentrosymmetric rhenium-boron superconductors, Phys. Rev. B 103, 184517 (2021b).
  • Kubo and Toyabe [1967] R. Kubo and T. Toyabe, A stochastic model for low-field resonance and relaxation, in Magnetic Resonance and Relaxation. Proceedings of the XIVth Colloque Ampère, edited by R. Blinc (North-Holland, Amsterdam, 1967) pp. 810–823.
  • Yaouanc and de Réotier [2011] A. Yaouanc and P. D. de Réotier, Muon Spin Rotation, Relaxation, and Resonance: Applications to Condensed Matter (Oxford University Press, Oxford, 2011).
  • Harris et al. [2002] R. K. Harris, E. D. Becker, S. M. Cabral de Menezes, R. Goodfellow, and P. Granger, NMR nomenclature: Nuclear spin properties and conventions for chemical shifts, Magn. Reson. Chem. 40, 489 (2002).
  • Kentgens [1997] A. P. M. Kentgens, A practical guide to solid-state NMR of half-integer quadrupolar nuclei with some applications to disordered systems, Geoderma 80, 271 (1997).
  • Note [1] Nb has a 3g3g Wyckoff position, with an m2mm2m local symmetry, implying a single VzzV_{zz} component. Nb is bonded in a 11-coordinate geometry to six Re and five Si atoms. There are two short- (2.87 Å) and four long (2.95 Å) Nb-Re bonds, as well as four short- (2.68 Å) and one long (2.78 Å) Nb-Si bonds. See: https://materialsproject.org/materials/mp-1095061.
  • Korringa [1950] J. Korringa, Nuclear magnetic relaxation and resonance line shift in metals, Physica 16, 601 (1950).
  • Bauer et al. [2014] E. Bauer, C. Sekine, U. Sai, P. Rogl, P. K. Biswas, and A. Amato, Absence of time-reversal symmetry breaking in the noncentrosymmetric superconductor Mo3{}_{3}Al2{}_{2}C, Phys. Rev. B 90, 054522 (2014).
  • Hines and Knight [1971] W. A. Hines and W. D. Knight, Spin-orbit coupling and nuclear magnetic resonance in superconducting metals, Phys. Rev. B 4, 893 (1971).
  • Tay et al. [2021] D. Tay, T. Shang, Y. P. Qi, T. P. Ying, H. Hosono, H.-R. Ott, and T. Shiroka, ss-wave superconductivity in the noncentrosymmetric W3{}_{3}Al2{}_{2}C superconductor: An NMR study (2021), submitted to J. Phys.: Condens. Matter.
  • Hoult and Richards [1976] D. Hoult and R. Richards, The signal-to-noise ratio of the nuclear magnetic resonance experiment, J. Magn. Reson. 24, 71 (1976).
  • Clogston et al. [1964] A. M. Clogston, A. C. Gossard, V. Jaccarino, and Y. Yafet, Orbital paramagnetism and the Knight shift in transition metal superconductors, Rev. Mod. Phys. 36, 170 (1964).
  • Pustogow et al. [2019] A. Pustogow, Y. Luo, A. Chronister, Y.-S. Su, D. A. Sokolov, F. Jerzembeck, A. P. Mackenzie, C. W. Hicks, N. Kikugawa, S. Raghu, E. D. Bauer, and S. E. Brown, Constraints on the superconducting order parameter in Sr2{}_{2}RuO4{}_{4} from oxygen-17 nuclear magnetic resonance, Nature 574, 72 (2019).
  • Shang et al. [2019b] T. Shang, A. Amon, D. Kasinathan, W. Xie, M. Bobnar, Y. Chen, A. Wang, M. Shi, M. Medarde, H. Q. Yuan, and T. Shiroka, Enhanced Tc{T}_{c} and multiband superconductivity in the fully-gapped ReBe22{}_{22} superconductor, New J. Phys. 21, 073034 (2019b).
  • Shang et al. [2020d] T. Shang, W. Xie, D. J. Gawryluk, R. Khasanov, J. Z. Zhao, M. Medarde, M. Shi, H. Q. Yuan, E. Pomjakushina, and T. Shiroka, Multigap superconductivity in the Mo5{}_{5}PB2{}_{2} boron–phosphorus compound, New J. Phys. 22, 093016 (2020d).
  • Gurevich [2011] A. Gurevich, Iron-based superconductors at high magnetic fields, Rep. Prog. Phys 74, 124501 (2011), and references therein.
  • Werthamer et al. [1966] N. R. Werthamer, E. Helfand, and P. C. Hohenberg, Temperature and purity dependence of the superconducting critical field, Hc2{{H}}_{c2}. III. Electron spin and spin-orbit effects, Phys. Rev. 147, 295 (1966).
  • Kogan et al. [2009] V. G. Kogan, C. Martin, and R. Prozorov, Superfluid density and specific heat within a self-consistent scheme for a two-band superconductor, Phys. Rev. B 80, 014507 (2009).
  • Kimura et al. [2007] N. Kimura, K. Ito, H. Aoki, S. Uji, and T. Terashima, Extremely high upper critical magnetic field of the noncentrosymmetric heavy fermion superconductor CeRhSi3{}_{3}, Phys. Rev. Lett. 98, 197001 (2007).
  • Sugitani et al. [2006] I. Sugitani, Y. Okuda, H. Shishido, T. Yamada, A. Thamizhavel, E. Yamamoto, T. D. Matsuda, Y. Haga, T. Takeuchi, R. Settai, and Y. Onuki, Pressure-induced heavy-fermion superconductivity in antiferromagnet CeIrSi3{}_{3} without inversion symmetry, J. Phys. Soc. Jpn. 75, 043703 (2006).
  • Okuda et al. [1980] K. Okuda, M. Kitagawa, T. Sakakibara, and M. Date, Upper critical field measurements up to 600 kG in PbMo6{}_{6}S8{}_{8}, J. Phys. Soc. Jpn. 48, 2157 (1980).
  • Balakirev et al. [2015] F. F. Balakirev, T. Kong, M. Jaime, R. D. McDonald, C. H. Mielke, A. Gurevich, P. C. Canfield, and S. L. Bud’ko, Anisotropy reversal of the upper critical field at low temperatures and spin-locked superconductivity in K2{}_{2}Cr3{}_{3}As3{}_{3}, Phys. Rev. B 91, 220505(R) (2015).
  • Bao et al. [2015] J.-K. Bao, J.-Y. Liu, C.-W. Ma, Z.-H. Meng, Z.-T. Tang, Y.-L. Sun, H.-F. Zhai, H. Jiang, H. Bai, C.-M. Feng, Z.-A. Xu, and G.-H. Cao, Superconductivity in quasi-one-dimensional K2{}_{2}Cr3{}_{3}As3{}_{3} with significant electron correlations, Phys. Rev. X 5, 011013 (2015).
  • Zuo et al. [2017] H. Zuo, J.-K. Bao, Y. Liu, J. Wang, Z. Jin, Z. Xia, L. Li, Z. Xu, J. Kang, Z. Zhu, and G.-H. Cao, Temperature and angular dependence of the upper critical field in K2{}_{2}Cr3{}_{3}As3{}_{3}, Phys. Rev. B 95, 014502 (2017).
  • Tang et al. [2017] Z.-T. Tang, Y. Liu, J.-K. Bao, C.-Y. Xi, L. Pi, and G.-H. Cao, Anisotropic upper critical magnetic fields in Rb2{}_{2}Cr3{}_{3}As3{}_{3} superconductor, J. Phys.: Condens. Matter 29, 424002 (2017).
  • Tang et al. [2015] Z.-T. Tang, J.-K. Bao, Z. Wang, H. Bai, H. Jiang, Y. Liu, H.-F. Zhai, C.-M. Feng, Z.-A. Xu, and G.-H. Cao, Superconductivity in quasi-one-dimensional Cs2{}_{2}Cr3{}_{3}As3{}_{3} with large interchain distance, Sci. China Mater. 58, 16 (2015).
  • Zhi et al. [2015] H. Z. Zhi, T. Imai, F. L. Ning, J.-K. Bao, and G.-H. Cao, NMR Investigation of the Quasi-One-Dimensional Superconductor K2{}_{2}Cr3{}_{3}As3{}_{3}, Phys. Rev. Lett. 114, 147004 (2015).
  • Luo et al. [2019] J. Luo, J. Yang, R. Zhou, Q. G. Mu, T. Liu, Z.-a. Ren, C. J. Yi, Y. G. Shi, and G.-q. Zheng, Tuning the Distance to a Possible Ferromagnetic Quantum Critical Point in A2{}_{2}Cr3{}_{3}As3{}_{3}, Phys. Rev. Lett. 123, 047001 (2019).
  • Yang et al. [2021] J. Yang, J. Luo, C. J. Yi, Y. G. Shi, Y. Zhou, and G.-q. Zheng, Spin-Triplet Superconductivity in K2{}_{2}Cr3{}_{3}As3{}_{3}, Sci. Adv. 7, eabl4432 (2021).
  • Sajilesh and Singh [2021] K. P. Sajilesh and R. P. Singh, Superconducting properties of the non-centrosymmetric superconductors TaXSi (X = Re, Ru), Supercond. Sci. Technol. 34, 055003 (2021).
  • Angst et al. [2002] M. Angst, R. Puzniak, A. Wisniewski, J. Jun, S. M. Kazakov, J. Karpinski, J. Roos, and H. Keller, Temperature and field dependence of the anisotropy of MgB2{}_{2}, Phys. Rev. Lett. 88, 167004 (2002).
  • Gurevich et al. [2004] A. Gurevich, S. Patnaik, V. Braccini, K. H. Kim, C. Mielke, X. Song, L. D. Cooley, S. D. Bu, D. M. Kim, J. H. Choi, L. J. Belenky, J. Giencke, M. K. Lee, W. Tian, X. Q. Pan, A. Siri, E. E. Hellstrom, C. B. Eom, and D. C. Larbalestier, Very high upper critical fields in MgB2{}_{2} produced by selective tuning of impurity scattering, Supercond. Sci. Technol. 17, 278 (2004).