[1,2]\fnmYihan \surWang [1,2]\fnmBing \surZhang
[1]\orgdivNevada Center for Astrophysics, \orgnameUniversity of Nevada, \orgaddress\street 4505 S. Maryland Pkwy., \cityLas Vegas, \postcode89154, \stateNV, \countryUSA
2]\orgdivDepartment of Physics and Astronomy, \orgnameUniversity of Nevada, \orgaddress\street505 S. Maryland Pkwy., \cityLas Vegas, \postcode89154, \stateNV, \countryUSA
Evidence of a Past Merger of the Galactic Center Black Hole
Abstract
The origin of supermassive black holes (SMBHs) residing in the centers of most galaxies remains a mystery. The Event Horizon Telescope (EHT) provided direct imaging of the SMBH Sgr A* at the Milky Way’s center, indicating it likely spins rapidly with its spin axis significantly misaligned relative to the Galactic plane’s angular momentum. Through investigating various SMBH growth models, here we show that the inferred spin properties of Sgr A* provide evidence of a past SMBH merger. Inspired by the merger between the Milky Way and Gaia-Enceladus, which has a 4:1 mass ratio as inferred from Gaia data, we have discovered that a 4:1 major merger of SMBH with a binary angular momentum inclination angle of 145-180 degrees with respect to the line of sight (LOS), can successfully replicate the measured spin properties of Sgr A*. This merger event in our galaxy provides potential observational support for the theory of hierarchical BH mergers in the formation and growth of SMBHs. The inferred merger rate, consistent with theoretical predictions, suggests a promising detection rate of SMBH mergers for space-borne gravitational wave detectors expected to operate in 2030s.
The origin of SMBHs residing in the centers of most galaxies remains a profound mystery[1, 2, 3]. Recent advancements, such as the EHT providing direct imaging of the SMBH Sgr A* at the Milky Way’s center, have shed new light on these enigmatic objects. The EHT collaboration took the image of the Sgr A* and provided the first physical interpretation to the data[4, 5]. This interpretation involves comparing resolved EHT data at 230 GHz and unresolved non-EHT observations from radio and X-ray wavelengths. These comparisons are made against predictions from a library of disk models based on time-dependent general relativistic magnetohydrodynamics (GRMHD) simulations, which incorporate radiative transfer based on both thermal and nonthermal electron distribution functions. In this process, 11 constraints were tested for discrete spin magnitudes: -0.94, -0.5, 0, 0.5, and 0.94; and for inclinations between the spin and the LOS of 10∘, 30∘, 50∘ 70∘ and 90∘, based on the assumption that the BH spin is aligned or anti-aligned with respect to the accretion disk. The disk models identified through these tests are the magnetically arrested disk (MAD) models surrounding a spinning Kerr BH. The ‘best-bet’ regions in the parameter space where disk models perform well and explain nearly all the data are: a = 0.5, i = 30∘ or 150∘ and a = 0.94, i = 30∘ or 150∘. The additional constraints from polarized images further narrow down the parameter space to a = 0.94, i = 150∘[6], consistent with interpretations of GRAVITY results[7] (but see Ref. [8]).
If the spin constraints from EHT are accurate, this finding poses challenges to the accretion SMBH growth models, regardless of whether the accretion process is coherent[9] or chaotic[10]. In the coherent accretion model, given the disk galaxy nature of the Milky Way, the prolonged accretion disk around Sgr A* tends to align roughly with the galaxy’s angular momentum[11, 12, 13, 14] in merger-free galaxies. Therefore, if Sgr A*’s spin originates from coherent accretion, its spin axis should not significantly misalign with the galaxy’s angular momentum. Conversely, the chaotic accretion model can naturally explain large spin misalignment, as the accretion disk’s orientation in this model changes with each accretion episode. Hence, if the most recent active phase of Sgr A* has had an accretion disk almost perpendicular to the galactic plane, a misaligned spin with a large angle can be produced. However, this model struggles to account for high spin magnitude, as the random, episodic accretion pattern typically leads to an SMBH with a lower spin. Beyond accretion models, the hierarchical merger model is a promising explanation for SMBH growth[15, 16, 17, 18]. This model posits that galaxies assemble over cosmic time, leading to galaxy mergers, and ultimately, the possible merging of SMBHs at their centers. In hierarchical BH merger scenarios, a significant portion of the SMBH binary’s orbital angular momentum transfers to the final spin of the merged product. As a result, SMBH mergers often yield high-spinning SMBHs. Given the arbitrary orientation of SMBH binaries, a high-spinning SMBH with substantial spin misalignment is possible. To robustly test whether the three models can reproduce the mass and spin of Sgr A* as interpreted from EHT, we performed sophisticated simulations of SMBH growth from three different SMBH seeds[19] (see Methods and Extended Data Figure 1 for details) through accretion models and merger models. We measured the spin and spin orientation with respect to the LOS when the mass of the SMBH matched the current mass of Sgr A*. We then compared the SMBH mass, spin orientation, and magnitude of our simulations with the constrained spin from EHT.
We first tested the two accretion models. Our accretion models are characterized by four parameters: the Eddington accretion ratio, , indicating the efficiency of the accretion process relative to the Eddington accretion rate; the Blandford-Znajek (BZ)[20] jet power efficiency, , which describes the jet outflow’s power in carrying away mass and angular momentum; the active accreting duty cycle fraction, , detailing the SMBH’s activity level; and the coherence factor, , indicating the isotropy of accretion across different episodes (see Methods and Extended Data Figure 2). A zero value of implies that the accretion is completely isotropic between different episodes, while a large value of indicates that the accretion process is coherent, with the accretion disk orientation remaining nearly unchanged between episodes (see Extended Data Figure 2).
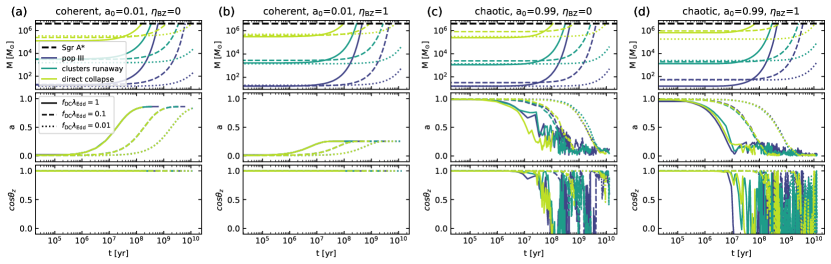
In panel (a) and (b) of Figure 1, we present examples of the time evolution of the SMBH mass (), spin magnitude (), and spin misalignment with respect to the galactic angular momentum () for coherent accretion models with , originating from SMBH seeds from population-III stars, star cluster runaway collisions, and the direct collapse of gas clouds. Here, is the speed of light, the gravitational constant, and denotes the angular momentum of the SMBH. If the accretion process is jet-free, as indicated by the left panel, the SMBH seeds are spun up to approximately 0.9 within the Hubble time, regardless of whether their mass can grow to match that of Sgr A*. On the other hand, if the accretion process is associated with strong jets (which is likely), the spin of the SMBH will saturate at a certain value (see also in Ref. [21]). This value depends on the jet power, where the angular momentum accreted from the accretion disk is balanced by the angular momentum carried away by the jet. Most importantly, in the coherent models, the spin of the SMBH closely aligns with the angular momentum of the galaxy throughout each accretion episode. Conversely, panel (c) and (d) of Figure 1 illustrate examples of the time evolution for isotropic chaotic accretion models. As shown in the mass panels, the mass evolution of these SMBH seeds is very similar to that observed in the coherent accretion models. However, chaotic accretion models can significantly decrease the spin of the SMBH as the seed grows to match Sgr A*, even if the initial spin of the SMBH seeds is high and the accretion process is jet-free. As shown in those panels, While the chaotic accretion models can successfully yield a larger spin misalignment, a feature not attainable by coherent models, it falls short in replicating the high spin magnitude of Sgr A* inferred from EHT observations.
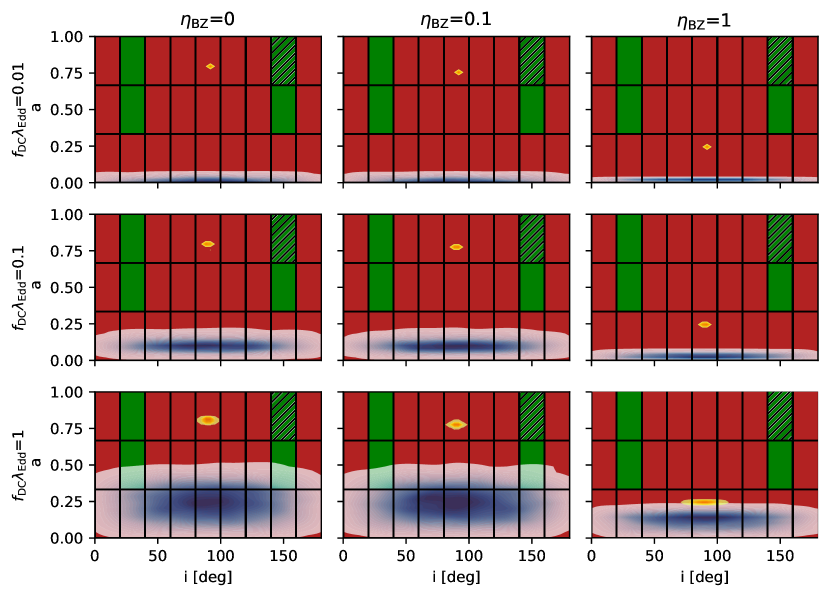
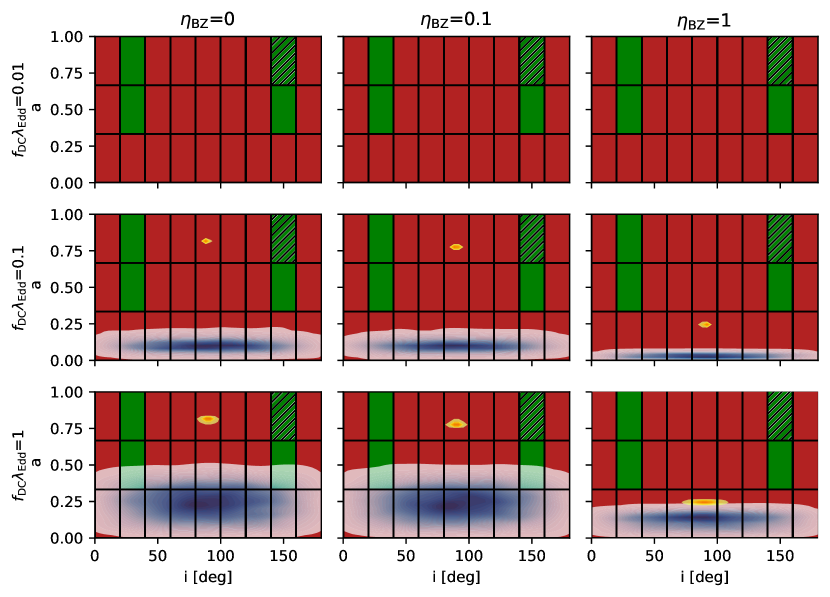
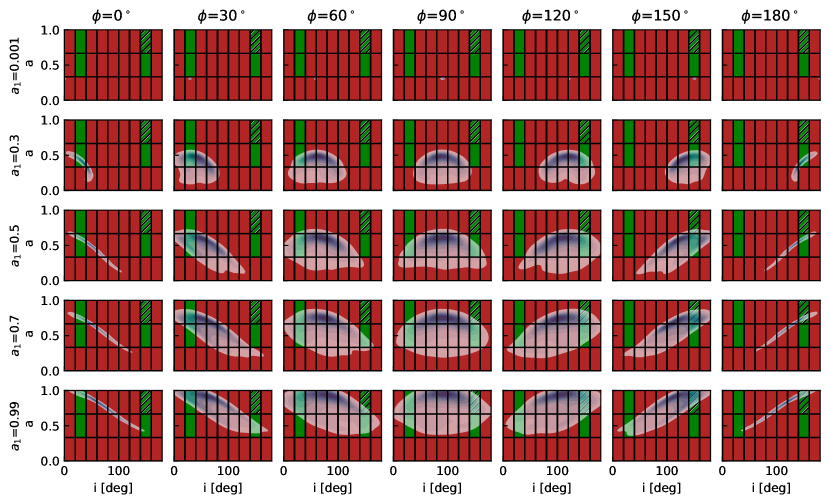
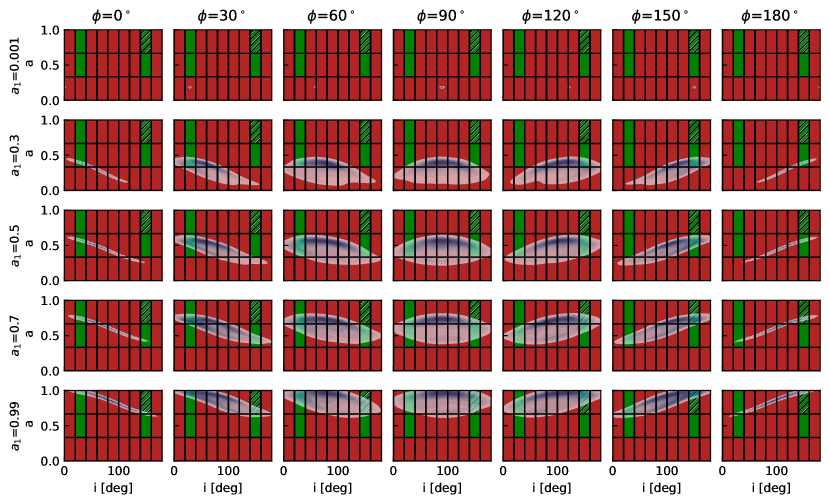
The results from Figure 1 indicate that spin evolution is effectively independent of the SMBH seed models, but is more sensitive to the effective accretion rate and jet power parameter . We conducted a suite of SMBH growth simulations across all three BH seed models, varying the accretion rates and jet powers. Figure 2 displays the spin and spin-LOS angle of SMBH seeds from direct gas cloud collapses (see Extended Figures 3 and 4 for the other two SMBH seeds), as they grow to the mass of Sgr A* under different accretion rates and jet powers. The blue contours illustrate the isotropic chaotic accretion model, the yellow contours represent the coherent accretion model, and the green-red blocks indicate the constraints from EHT observations. Here, the red blocks represent regions disfavored by EHT constraints, while the green blocks denote the preferred parameter space where disk models perform well and explain nearly all the data. The slashed region indicates the best-bet disk models in the parameter space that passed the polarization tests as well. This figure suggests that accretion models alone are insufficient to replicate the best-bet model inferred from EHT observations.
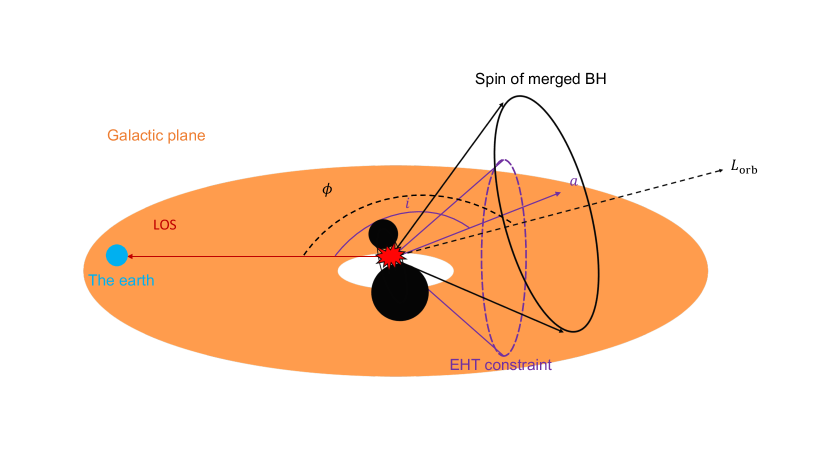
The failure of the accretion models in reproducing the observations drive us to model the merger origin of Sgr A*. The merger model can be parameterized by the pre-merger mass ratio between two SMBHs and their individual spin vectors and . We use the surrogate BH merger model NRSur7dq4EmriRemnant to predict the final spin of the merger product (see Methods). Inspired by the observed evidence of a major 4:1 galaxy merger between the Milky Way and Gaia-Enceladus approximately 10 billion years ago, as indicated by the specific chemical patterns and motion in the nearby halo observed by the Gaia survey[22], we fixed the mass ratio to be 4, considering the empirical near-linear correlation between the masses of the central SMBHs and their host galaxies[23, 24]. We explore the entire parameter space of the pre-merger spin vector and , with arbitrary orientations and magnitude from 0.01 to 0.99. This range is chosen to encompass both the merger-free origin and the hierarchical merger origin of black holes in the merger event. Additionally, we investigate various binary SMBH orientations with respect to the LOS, denoted by , as depicted in Figure 3. Given the smaller mass of the secondary SMBH, we found that its spin does not significantly affect the final spin of the merger product for this 4:1 mass ratio merger (see Extended Data Figure 5). Therefore, the final spin magnitude and its relative angle to the LOS are primarily determined by and .
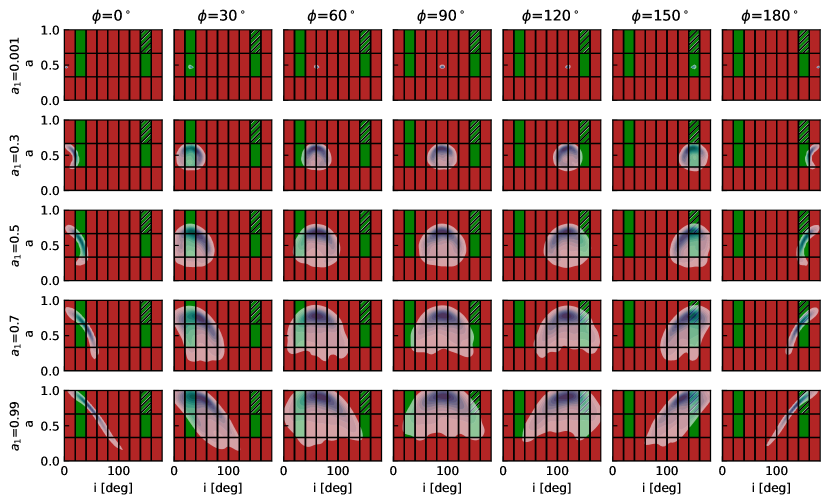
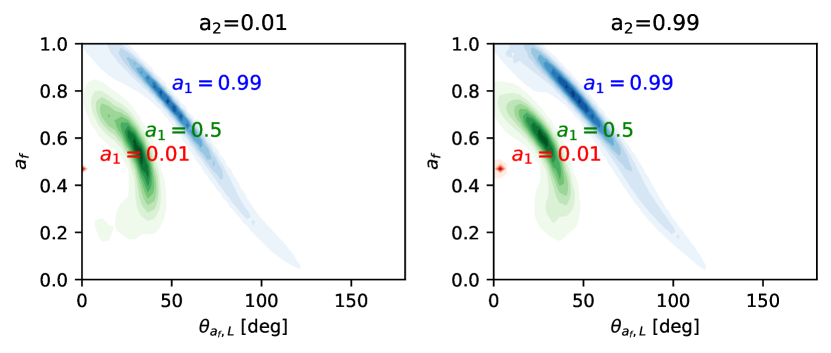
Figure 4 displays the kernel density estimation (KDE) of the spin resulting from simulations of the merger model, for different binary SMBH orientations and primary SMBH spin magnitudes . The orientation of is isotropically distributed. As indicated, reproducing the best-bet model as constrained by the EHT requires a higher pre-merger spin for the primary SMBH, with approximately greater than 0.7 and in the range of . No constraints on can be established, as it does not significantly influence the spin of the merged SMBH. Additional constraints on binary SMBH orientation can be derived from findings in Ref. [22], which reveal that a significant proportion of stellar motions in the nearby halo are in retrograde orbits. This suggests that the last major merger of the Milky Way may have been retrograde. Consequently, the angular momentum needs to be oriented below the Galactic plane. We also explored merger scenarios with various mass ratios and found that a 4:1 ratio is the most promising case for reproducing the current spin of Sgr A*. Although subsequent minor mergers[25] with specific have not been ruled out, minor mergers with mass ratio 1/16 become less likely to reproduce the spin of the Sgr A* (See Extended Data Figure 6 and 7).
While the merger model can explain high-spin SMBHs with significant spin misalignment (see also in Ref. [26]), cosmological simulations predict a relative low galaxy merger rate[17, 27]. Moreover, it is unclear whether galaxy mergers efficiently lead to SMBH mergers. The uncertainty in the timescale needed to bring two SMBHs from a galactic scale (kiloparsecs) to a gravitational wave radiation scale (milliparsecs) — where they could eventually merge within the Hubble time — remains a significant challenge[28, 29, 30, 31]. Although we have observed some merging galaxies or even dual active galactic nuclei (AGNs), direct SMBH mergers have not been observed to date. To validate the merger fact of the Sgr A*, we estimated the cosmological merger rate of galaxies analogous to the Milky Way, integrating data on SMBH binaries from the Millennium-II cosmological simulation[27] and accounting for the time delay to coalescence due to stellar dynamical friction, stellar scattering hardening, and gravitational wave radiation (see Methods).
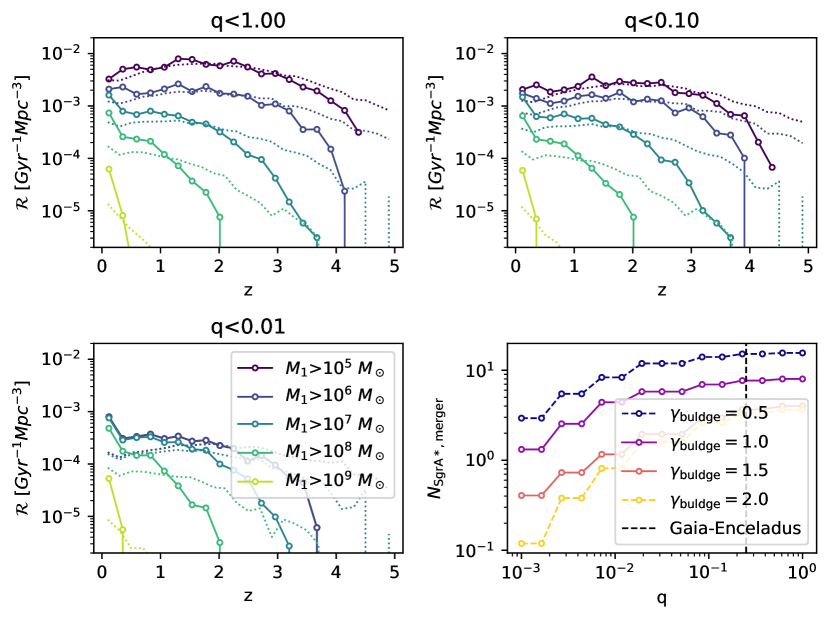
Figure 5 illustrates the formation (dotted lines) and merger (solid lines) rates of SMBH binaries per volume as a function of redshift for various primary SMBH masses and mass ratios. The results indicate that major mergers peak at a redshift between 1-2, and more massive SMBHs tend to merge in the local universe. This is consistent with the hierarchical nature of galaxy formation, where more massive SMBH binaries form later. The estimated major merger rate density of SMBHs similar to Sgr A* in the local universe is approximately Gyr-1 Mpc-3, which is consistent with the results from other works[32, 33, 34]. Based on this rate calculation, we estimate the number of major mergers with mass ratio 0.25 experienced by Sgr A* like SMBH by adopting the galaxy number density in the local universe, which is approximately Mpc-3 [35]. We obtain a total number of mergers of the order of , as shown in the bottom right panel of Figure 5. This finding supports the merger origin of Sgr A*.
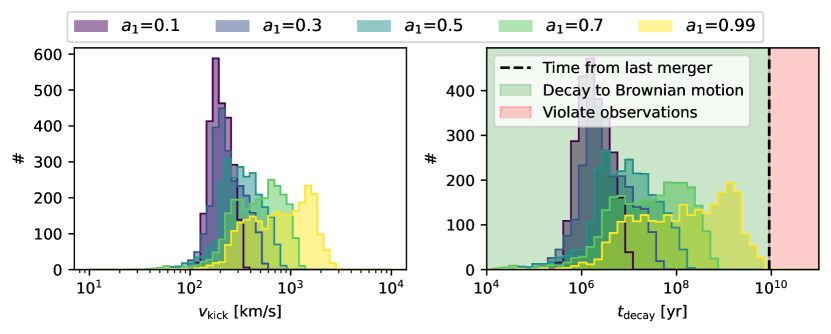
We calculated the time required for Sgr A* to merge with the SMBH in Gaia-Enceladus following the galaxy merger, applying the same methodology used to estimate the SMBH merger rate from galaxy mergers. This duration is estimated to be approximately 1 billion years. Given that the merger between the Milky Way and the Gaia-Enceladus galaxy occurred roughly 10 billion years ago, we conclude that Sgr A* underwent a major merger about 9 billion years ago. This timeline is sufficiently long for the post-merger recoil of Sgr A* to settle back to the galactic center to the observed level of Brownian motion[36, 37, 38], facilitated by dynamical friction[39] (see Methods and Extended Data Figure 8). Additionally, this merger timeframe imposes constraints on the accretion rate following the last merger, as the spin signature imprinted on Sgr A* by the last merger has not been erased by the accretion process. We estimated a constraint of for Sgr A* following the last major merger. The inferred accretion rate onto Sgr A* from EHT ( yr-1)[4, 6] is well below this upper limit. However, we note that the accretion rate onto Sgr A* might have changed significantly in the past after the merger.
The upcoming space-borne GW detectors such as the Laser Interferometer Space Antenna (LISA)[40], Taiji[41] and TianQin[42] are expected to detect inspiraling and merging of SMBH binaries. If the spin constraints on Sgr A* from the EHT are accurate, based on the assumption that Sgr A*’s spin is aligned with the accretion disk, it is likely that Sgr A* experienced one major merger in the past. This suggests an SMBH merger rate of approximately - Gyr-1 Mpc-3 up to a redshift of approximately 4. This gives an optimistic detection rate of space-borne GW detectors. Future direct detections in the 2030s will further confirm that SMBH mergers play a crucial role in the cosmological evolution of SMBHs.
Methods
Traditional theories of SMBH growth involve black hole accretion[43, 29] and galaxy mergers, which lead to the mergers of SMBHs[16, 17]. In this section, we outline the models employed to simulate the growth of BHs to masses equivalent to that of Sgr A*, incorporated with spin evolution during the growth process.
Seed of SMBH
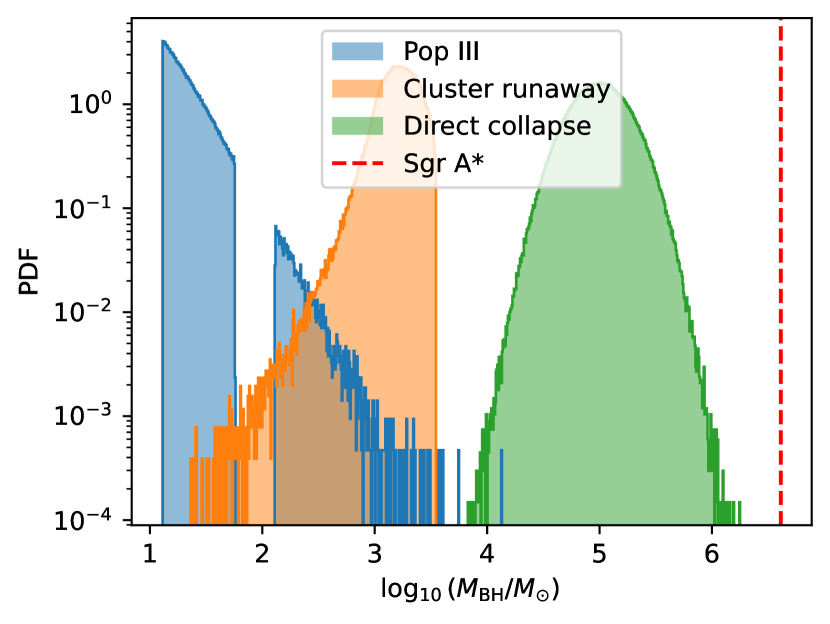
We explore the evolution of SMBH mass and spin starting from three different types of BH seeds: those originating from Population III stars, gravitational runaways in star clusters, and direct collapse. Population III stars, forming within dark matter minihalos of - from primordial gas are thought to be extremely massive, ranging from 10 to 1000 solar masses [44]. Their deaths lead to stellar mass BH seeds with masses ranging from 10-100 [45, 46]. Alternatively, the formation of intermediate-mass black holes (IMBHs), ranging from to , is hypothesized to occur through stellar mergers within the dense cores of stellar clusters in metal-poor protogalaxies[47, 48, 49, 50, 51, 52, 53, 54, 55], with each cluster having a mass of approximately [56, 57]. This process is facilitated by the dense gas environment, which increases the likelihood of stellar collisions. Lastly, some theories posit that the massive BH seeds can be formed from the direct collapse of clouds, resulting in massive BHs with mass ranges from to [58, 59, 60]. Extended Data Figure 1 illustrates the mass distribution of the three types of BH seeds. For BHs from Population III stars, we employ stellar evolution with a Salpeter initial mass function. For gravitational runaways, we reference results from Ref. [57]. In the case of direct collapse, we assume a log-normal distribution centered at with a standard deviation of 0.25.
Accretion models
Black hole accretion dynamics are generally classified into two types: cold flows[61, 62] , characterized by cooler, optically thick material at higher accretion rates, and hot flows[63, 64], which are hotter, optically thin, and occur at lower accretion rates. Hot flows, distinct for their lower radiative efficiency compared to the classical thin disk model, are often associated with the generation of astrophysical jets[65, 66, 67]. Such phenomena are observed in environments like low-luminosity active galactic nuclei and dormant black holes, including Sgr A*, the supermassive black hole at the center of the Milky Way.
Among various jet generation theories, the role of magnetic fields and black hole rotation is considered crucial. The Blandford-Znajek (BZ) model[20], in particular, has gained prominence. This model suggests that the rotational energy of the black hole itself powers the jets. The BZ model’s explanation aligns closely with observations and numerical simulations[68, 69, 70], indicating that relativistic jets primarily originate from the BZ process.
In the BZ model, a large-scale poloidal magnetic field penetrates the ergosphere of a rotating black hole and intersects the event horizon. The rotation of the black hole causes frame-dragging, which in turn generates a toroidal magnetic field and a Poynting flux. The essence of the BZ process is the possibility of an inward electromagnetic energy flux within the ergosphere that appears negative when measured from infinity. This negative flux crosses the event horizon, reducing the black hole’s mass-energy and angular momentum. Consequently, an outgoing jet emerges, Poynting-dominated, carrying away positive energy and angular momentum. The power of the jet in the BZ model can be described as[20],
| (1) |
where and represent the radii of Schwarzschild and Kerr black hole, respectivley, is the normalized black hole spin, and represents the ratio of the actual magnetic flux threading the black hole’s horizon () to the maximum saturated magnetic flux (). A value of signifies that the magnetic flux from the magnetized accretion flow has saturated the black hole, leading to a magnetically arrested disk (MAD)[71, 72]. Conversely, a lower value of suggests that the accretion disk is in a state of Standard And Normal Evolution (SANE)[73]. It is worth noting that Equation 1 applies for low to moderate spins. There are higher-order corrections as spin approaches 1[74, 75, 76]. The angular momentum carried out by the BZ jet then can be estimated by
| (2) |
where denotes the unit vector along the BH spin vector, and
| (3) |
Incorporated with the standard accretion model that excludes jet contributions, the equations governing the mass and angular momentum evolution of an accreting black hole can be expressed as follows[21]:
| (4) | |||
| (5) |
where is the unit vector along the disk angular momentum, and are the specific energy and specific angular momentum at the innermost radius , which are defined as[77]
| (6) | |||||
| (7) |
For each accretion episode, Equations 4 and 5 are numerically solved using given parameterized values for and .
During each accretion episode, we adopt a constant accretion rate , where signifies the accretion efficiency, and represents the Eddington accretion rate. Here, the radiation efficiency is set to be 0.1. Accretion stops when the material within the self-gravitating radius is exhausted. The accretion time for each episode, , can be approximated by , with being the total disk mass inside the self-gravitating radius . The accretion time can be parameterized as[78],
| (8) |
After an accretion episode concludes, the SMBH enters a dormant phase until the onset of the next episode. The interim period, known as the waiting time, is governed by the active galactic nucleus (AGN) duty cycle fraction , which is empirically observed to range from 1% to 10%.
Coherent/Chaotic accretion
The Lense-Thirring precession can result in the counter-alignment of a black hole’s spin vector with the angular momentum vector of its accretion disc[10]. This counter-alignment process is contingent upon the condition that the angle between the vectors exceeds , and that the angular momentum of the disc is less than twice that of the black hole, as .
According to the analysis, if the angular momentum of the disc is less than twice that of the black hole, , then for randomly oriented angular momentum vectors, the proportion of systems that will exhibit counter-alignment is given by the relationship:
| (9) |
In scenarios where the disc’s angular momentum is less than that of the black hole , and accretion occurs through randomly oriented events, the black hole is likely to experience alternating episodes of spinup and spindown, a process referred to as chaotic accretion[10, 78, 79]. Conversely, in situations where , the black hole is expected to consistently gain angular momentum, or spin up, which is indicative of coherent accretion. This behavior would persist even if the black hole and the disc were initially counter-aligned.
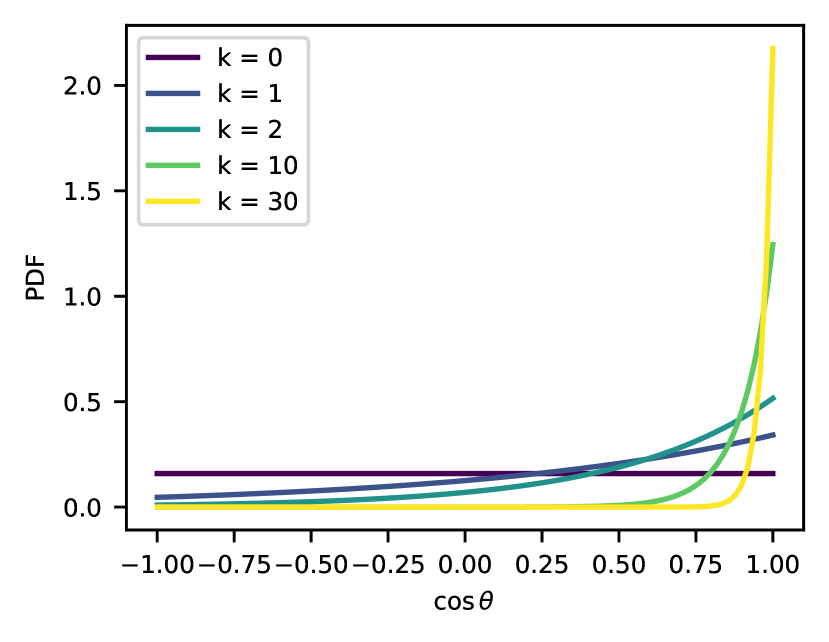
In our accretion models, we characterize the extent of chaotic accretion using the Mises distribution function for the disk angular momentum vector [80]
| (10) |
where is the zero-th order cylindrical Bessel function for the first kind. When , the model yields a perfectly isotropic chaotic accretion. In contrast, a large results in nearly coherent accretion, where is consistently close to zero.
Merger models
In the realm of binary black hole systems, those with black hole spins misaligned from the orbital angular momentum present significant challenges for analytical or semi-analytical modeling. The complex interactions between the spins, the orbital angular momentum, and each other lead to the precession of the system around the total angular momentum vector. To predict the final spin of the merged black hole, several faster approximate models have been developed[81, 82], covering waveforms[83] and remnant properties of merging black holes[84]. Those surrogate models for precessing binary black hole with generic spins and unequal masses are based on large sample of numerical relativity simulations, which are proven to be accurate in predicting the final spin magnitude and orientation with relative error at the order of with 90th percentiles confidence[82]. With those surrogate models, we explore the probability that the SgrA* is the merger product of two SMBHs. We have adopted the latest NRSur7dq4EmriRemnant model[82], which is based on a seven-dimensional parameter space characterizing generically precessing binary black hole systems. This model incorporates the binary black hole mass ratio , along with the two pre-merger spins and .
In addition to the seven parameters described by the NRSur7dq4EmriRemnant model, our SMBH merger model includes an additional parameter, , which represents the inclination angle of the SMBH binary angular momentum with respect to the LOS, as illustrated in Fig. 3. We explore 9 different inclinations ranging from to , with 20∘ equally spaced intervals. The spin magnitudes and orientations of and (with respect to the SMBH binary angular momentum) are randomly distributed, with magnitudes ranging from 0 to 1 to cover all possible pre-merger origins.
Recent studies of stellar surveys show specific chemical patterns and a retrograde motion in the nearby halo, suggesting a major past accretion event in the Galaxy. It has been found that the inner halo mainly consists of debris from a system, named Gaia-Enceladus[22], once larger than the Small Magellanic Cloud. Given the estimated mass ratio of 4:1, the merger between the Milky Way with Gaia-Enceladus around 10 billion years ago likely caused significant dynamical heating of the Galaxy’s early thick disk. Based on this observation, we fix the mass ratio of the merging black holes to be 4:1.
Owing to the 4:1 mass ratio, the final galactic plane is predominantly determined by the galactic plane of the pre-merger massive galaxy, which is our Milky Way. We assume that the final galactic plane aligns with the initial galactic plane of the more massive galaxy. The final spin in our merging model is computed using the surrogate model, which takes the previously described input parameters.
Cosmological merger rate estimation
The cosmic population of SMBHBs is derived from the data of the Millennium-II N-body simulation [27], which has the resolution to distinguish dark matter halos down to . This dark matter framework is augmented with semianalytic models of galaxy evolution to trace the history of galaxies down to , which host central black holes as small as . All post-processing employs the same cosmological parameters as Millennium-II: , , , and . While these cosmological parameters are not the most current, variations of a few percent in , , or do not significantly affect our results.
We identify all mergers between galaxies, each containing an SMBH, totaling events throughout the Millennium-II simulation’s span. This was done by assuming an MBH occupation fraction of unity down to 10 stellar mass halos. This assumption slightly overestimates the SMBH binary merger rate at the lower mass end, as the MBH occupation fraction in these halos can drop to approximately 40%[85] for 10 stellar mass halos. We construct a 3D grid by logarithmically binning and the mass ratio over the intervals and , and linearly binning the redshift from 0 to 5 in line with the redshifts in Millennium-II snapshots. The redshift of each merger is matched with the snapshot where the progenitor galaxy is detected, assuming that the dynamical friction timescale for the SMBHs to form a close binary is shorter than the average 300 Myr between simulation snapshots.
By dividing the number of SMBHBs in each bin by the co-moving volume of the Millennium-II simulation, we approximate the differential SMBHB formation rate as
For those SMBHs that become a bound binary, the SMBHs start a long journey that bring them from separations of tens of kpc down to milli-parsec scales, below which they merge through GWs. The transition into the GW domain depends on energy exchanges with low-angular-momentum stars in the galaxy’s nucleus[86], or on the removal of angular momentum via gravitational torques from a gas disk, which can diminish their separation [87]. It might also involve a mix of these two mechanisms. Recent advancements in direct N-body simulations, Monte Carlo methods, and scattering experiments have provided a more hopeful outlook on what has been deemed the primary bottleneck in binary evolution for nearly four decades: the “final parsec problem”. This issue, described as the depletion of low-angular-momentum stars[86], seems less problematic. Findings suggest that the evolution of SMBHBs through stellar scattering potentially lead to a merger within less than approximately 1 billion years[88, 30, 89], especially when factors such as rotation, the triaxial shape of galaxies, and the granularity of stellar distribution are considered. SMBHB hardening through stellar scattering from pairing to the final coalescence can be described by[30]
with
| (12) |
where the first term represents the rate of binary hardening due to stellar scattering[90, 91], characterized by the dimensionless hardening rate , stellar density and velocity dispersion at the binary influence radius . The influence radius is defined as the radius within which the enclosed stellar mass is twice the mass of the primary SMBH. The second term captures the effects of GW radiation[92, 93], which is characterized by the masses of the primary and secondary SMBHs in the binary ( and , respectively) and the binary’s eccentricity . These terms together describe the evolution of the separation between the SMBHs under the combined influences of dynamical interactions with stars and energy loss due to GW radiation. The SMBHBs spend most of their lifetimes at the transition separation where , which is
| (13) |
The corresponding timescale at this separation is
| (14) |
which can be used to estimate the time from SMBHB formation to final coalescence. The dimentionless hardening rate is estimated to be[30] , and the velocity dispersion can be estimated from the M- relation [24]
| (15) |
where and the stellar density at the influence radius can be obtained from the nuclei stellar cluster model[94]
| (16) |
where denotes the total mass of the stars in the bulge and represents the inner cusp slope. The influence radius can be obtain by equations where[94, 95],
| (17) | |||||
| (18) | |||||
| (21) |
For each pair of SMBHs derived from the Millennium-II simulation, we can estimate the coalescence time starting from binary formation and calculate the redshift at which they ultimately merge using the following equation
| (22) | |||||
where denotes the redshift at which the SMBHB forms, and represents the redshift at which the SMBHB coalesces. If the coalescence delay time, , is sufficiently long, it could result in an unphysical, negative . This indicates that the SMBHB is still in the hardening phase. Such shrinking/stalled SMBHBs are excluded from our dataset. Then the differential SMBHB merger rate can be obtained as
| (23) |
Recoil velocity from SMBH merger
The emission of gravitational waves during the merger of two SMBHs imparts a recoil, or ’kick’, to the resulting SMBH[96, 97]. If Sgr A* underwent a major merger in the past, the recoil velocity from this merger would cause Sgr A* to follow an elliptical orbit. After receiving this kick, the movement of the SMBH undergoes three distinct phases[39]. Initially, the SMBH oscillates back and forth with decreasing amplitude, losing energy through dynamical friction with each pass through the galactic core. This motion can be precisely modeled using dynamical friction. As the magnitude of motion decreases to about the core radius size, the SMBH and the core begin to oscillate around their common center of gravity, with these oscillations diminishing more slowly than the initial dynamical friction phase. In the final phase, the SMBH stabilizes and reaches thermal equilibrium with the surrounding stars. For the Milky Way, the stellar velocity dispersion at the Galactic center is approximately 100 km/s, leading to an equilibrium state of Brownian motion for Sgr A* at about 0.2 km/s[98]. Observations of Sgr A*’s peculiar motion perpendicular to the galactic plane[36, 37, 38] are consistent with this prediction, suggesting that Sgr A* is currently positioned quietly at the center of the Milky Way. However, the peculiar motion in the galactic plane is measured to be above the Brownian motion velocity. Therefore, the existence of a smaller BH or IMBH[99, 100, 101, 102, 103, 104, 105, 106, 107, 108] has not been completely ruled out. The most recent study posits a strong mass constraint on the secondary BH, indicating it to be less than 2000 [109].
We employ the NRSur7dq4Remnant model to calculate the kick velocity of the final SMBH in our merger scenarios, as illustrated in the left panel of Extended Data Figure 8. Given that a 4:1 major merger with a spin parameter greater than or equal to 0.7 can accurately reproduce the spin of Sgr A*, it is likely that Sgr A* would receive a substantial kick velocity, ranging from hundreds to thousands of kilometers per second. By interpolating the results of Ref. [39](model A1 in their figure 15), we calculate the time required for Sgr A* to settle into the Brownian motion phase, with peculiar motion velocity 0.2 km/s. As demonstrated in the right panel of Extended Data Figure 8, for the entire parameter regime we explored, the recoil velocity Sgr A* acquired from the major merger could be sufficiently dissipated by the stars within the Milky Way’s core over the 9 billion years following the merger, consistent with the observations.
Data availability
Data are available at https://figshare.com/articles/dataset/Sgr_A_data/26112379.
Code availability
The code and data process script are available at https://github.com/YihanWangAstro/Sgr-A-PubCode.
Acknowledgements
Y.W. and B.Z. acknowledge the support from NASA 80NSSC23M0104 and the Nevada Center for Astrophysics. Y.W. acknowledges useful discussions with Tamara Bogdanovic regarding the recoil velocity of major mergers, with Douglas N. C. Lin on subsequent accretions following the merger, as well as with Barry McKernan and Daniel Stern concerning coherent accretions.
Author Contributions
B.Z. proposed the idea of this paper; Y.W. developed the theoretical models; Y.W. and B.Z. analyzed the results and discussed the theoretical models. All authors contributed to the analysis or interpretation of the data and to the final version of the manuscript.
Competing Interests
The authors declare no competing interests.
Tables
Figure Legends/Captions
Extended Figure Legends/Captions

References
- \bibcommenthead
- [1] Richstone, D. et al. Supermassive black holes and the evolution of galaxies. Nature 385, A14 (1998).
- [2] Fan, X. et al. A Survey of z5.8 Quasars in the Sloan Digital Sky Survey. I. Discovery of Three New Quasars and the Spatial Density of Luminous Quasars at z~6. AJ 122, 2833–2849 (2001).
- [3] Lawrence, A. et al. The UKIRT Infrared Deep Sky Survey (UKIDSS). MNRAS 379, 1599–1617 (2007).
- [4] Event Horizon Telescope Collaboration et al. First Sagittarius A* Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole in the Center of the Milky Way. ApJ 930, L12 (2022).
- [5] Event Horizon Telescope Collaboration et al. First Sagittarius A* Event Horizon Telescope Results. V. Testing Astrophysical Models of the Galactic Center Black Hole. ApJ 930, L16 (2022).
- [6] Event Horizon Telescope Collaboration et al. First Sagittarius A* Event Horizon Telescope Results. VIII. Physical Interpretation of the Polarized Ring. ApJ 964, L26 (2024).
- [7] GRAVITY Collaboration et al. Dynamically important magnetic fields near the event horizon of Sgr A*. A&A 643, A56 (2020).
- [8] Fragione, G. & Loeb, A. An Upper Limit on the Spin of SgrA* Based on Stellar Orbits in Its Vicinity. ApJ 901, L32 (2020).
- [9] Volonteri, M., Sikora, M. & Lasota, J.-P. Black Hole Spin and Galactic Morphology. ApJ 667, 704–713 (2007).
- [10] King, A. R. & Pringle, J. E. Growing supermassive black holes by chaotic accretion. MNRAS 373, L90–L92 (2006).
- [11] Dubois, Y., Volonteri, M. & Silk, J. Black hole evolution - III. Statistical properties of mass growth and spin evolution using large-scale hydrodynamical cosmological simulations. MNRAS 440, 1590–1606 (2014).
- [12] Beckmann, R. S. et al. Supermassive black holes in merger-free galaxies have higher spins which are preferentially aligned with their host galaxy. arXiv e-prints arXiv:2211.13614 (2022).
- [13] Sala, L., Valentini, M., Biffi, V. & Dolag, K. Supermassive black hole spin evolution in cosmological simulations with OPENGADGET3. A&A 685, A92 (2024).
- [14] Peirani, S. et al. Cosmic evolution of black hole spin and galaxy orientations: Clues from the NewHorizon and Galactica simulations. A&A 686, A233 (2024).
- [15] Menou, K., Haiman, Z. & Narayanan, V. K. The Merger History of Supermassive Black Holes in Galaxies. ApJ 558, 535–542 (2001).
- [16] Volonteri, M., Haardt, F. & Madau, P. The Assembly and Merging History of Supermassive Black Holes in Hierarchical Models of Galaxy Formation. ApJ 582, 559–573 (2003).
- [17] Springel, V. et al. Simulations of the formation, evolution and clustering of galaxies and quasars. Nature 435, 629–636 (2005).
- [18] Tanaka, T. & Haiman, Z. The Assembly of Supermassive Black Holes at High Redshifts. ApJ 696, 1798–1822 (2009).
- [19] Greene, J. E., Strader, J. & Ho, L. C. Intermediate-Mass Black Holes. ARA&A 58, 257–312 (2020).
- [20] Blandford, R. D. & Znajek, R. L. Electromagnetic extraction of energy from Kerr black holes. MNRAS 179, 433–456 (1977).
- [21] Lei, W.-H., Zhang, B., Wu, X.-F. & Liang, E.-W. Hyperaccreting Black Hole as Gamma-Ray Burst Central Engine. II. Temporal Evolution of the Central Engine Parameters during the Prompt and Afterglow Phases. ApJ 849, 47 (2017).
- [22] Helmi, A. et al. The merger that led to the formation of the Milky Way’s inner stellar halo and thick disk. Nature 563, 85–88 (2018).
- [23] Magorrian, J. et al. The Demography of Massive Dark Objects in Galaxy Centers. AJ 115, 2285–2305 (1998).
- [24] Kormendy, J. & Ho, L. C. Coevolution (Or Not) of Supermassive Black Holes and Host Galaxies. ARA&A 51, 511–653 (2013).
- [25] Lang, M. et al. Can a satellite galaxy merger explain the active past of the Galactic Centre? MNRAS 430, 2574–2584 (2013).
- [26] Schmitt, H. R., Pringle, J. E., Clarke, C. J. & Kinney, A. L. The Orientation of Jets Relative to Dust Disks in Radio Galaxies. ApJ 575, 150–155 (2002).
- [27] Boylan-Kolchin, M., Springel, V., White, S. D. M., Jenkins, A. & Lemson, G. Resolving cosmic structure formation with the Millennium-II Simulation. MNRAS 398, 1150–1164 (2009).
- [28] Milosavljević, M. & Merritt, D. Formation of Galactic Nuclei. ApJ 563, 34–62 (2001).
- [29] Yu, Q. & Tremaine, S. Observational constraints on growth of massive black holes. MNRAS 335, 965–976 (2002).
- [30] Sesana, A. & Khan, F. M. Scattering experiments meet N-body - I. A practical recipe for the evolution of massive black hole binaries in stellar environments. MNRAS 454, L66–L70 (2015).
- [31] Ryu, T., Perna, R., Haiman, Z., Ostriker, J. P. & Stone, N. C. Interactions between multiple supermassive black holes in galactic nuclei: a solution to the final parsec problem. MNRAS 473, 3410–3433 (2018).
- [32] Sesana, A., Haardt, F., Madau, P. & Volonteri, M. The Gravitational Wave Signal from Massive Black Hole Binaries and Its Contribution to the LISA Data Stream. ApJ 623, 23–30 (2005).
- [33] Volonteri, M. et al. Black hole mergers from dwarf to massive galaxies with the NewHorizon and Horizon-AGN simulations. MNRAS 498, 2219–2238 (2020).
- [34] Li, K., Bogdanović, T., Ballantyne, D. R. & Bonetti, M. Massive Black Hole Binaries from the TNG50-3 Simulation. I. Coalescence and LISA Detection Rates. ApJ 933, 104 (2022).
- [35] Conselice, C. J., Wilkinson, A., Duncan, K. & Mortlock, A. The Evolution of Galaxy Number Density at z 8 and Its Implications. ApJ 830, 83 (2016).
- [36] Reid, M. J. & Brunthaler, A. The Proper Motion of Sagittarius A*. II. The Mass of Sagittarius A*. ApJ 616, 872–884 (2004).
- [37] Ghez, A. M. et al. Measuring Distance and Properties of the Milky Way’s Central Supermassive Black Hole with Stellar Orbits. ApJ 689, 1044–1062 (2008).
- [38] Reid, M. J. & Brunthaler, A. The Proper Motion of Sagittarius A*. III. The Case for a Supermassive Black Hole. ApJ 892, 39 (2020).
- [39] Gualandris, A. & Merritt, D. Ejection of Supermassive Black Holes from Galaxy Cores. ApJ 678, 780–797 (2008).
- [40] Amaro-Seoane, P. et al. Laser Interferometer Space Antenna. arXiv e-prints arXiv:1702.00786 (2017).
- [41] Ruan, W.-H., Guo, Z.-K., Cai, R.-G. & Zhang, Y.-Z. Taiji Program: Gravitational-Wave Sources. arXiv e-prints arXiv:1807.09495 (2018).
- [42] Luo, J. et al. TianQin: a space-borne gravitational wave detector. Classical and Quantum Gravity 33, 035010 (2016).
- [43] Soltan, A. Masses of quasars. MNRAS 200, 115–122 (1982).
- [44] Hirano, S. et al. One Hundred First Stars: Protostellar Evolution and the Final Masses. ApJ 781, 60 (2014).
- [45] Bond, J. R., Arnett, W. D. & Carr, B. J. The evolution and fate of Very Massive Objects. ApJ 280, 825–847 (1984).
- [46] Madau, P. & Rees, M. J. Massive Black Holes as Population III Remnants. ApJ 551, L27–L30 (2001).
- [47] Bahcall, J. N. & Ostriker, J. P. Massive black holes in globular clusters. Nature 256, 23–24 (1975).
- [48] Begelman, M. C. & Rees, M. J. The fate of dense stellar systems. MNRAS 185, 847–860 (1978).
- [49] Quinlan, G. D. & Shapiro, S. L. The Dynamical Evolution of Dense Star Clusters in Galactic Nuclei. ApJ 356, 483 (1990).
- [50] Lee, M. H. N-Body Evolution of Dense Clusters of Compact Stars. ApJ 418, 147 (1993).
- [51] Ebisuzaki, T. et al. Missing Link Found? The “Runaway” Path to Supermassive Black Holes. ApJ 562, L19–L22 (2001).
- [52] Miller, M. C. & Hamilton, D. P. Production of intermediate-mass black holes in globular clusters. MNRAS 330, 232–240 (2002).
- [53] Portegies Zwart, S. F. & McMillan, S. L. W. The Runaway Growth of Intermediate-Mass Black Holes in Dense Star Clusters. ApJ 576, 899–907 (2002).
- [54] Rose, S. C., Naoz, S., Sari, R. & Linial, I. The Formation of Intermediate-mass Black Holes in Galactic Nuclei. ApJ 929, L22 (2022).
- [55] Atallah, D. et al. Growing black holes through successive mergers in galactic nuclei - I. Methods and first results. MNRAS 523, 4227–4250 (2023).
- [56] Omukai, K., Schneider, R. & Haiman, Z. Can Supermassive Black Holes Form in Metal-enriched High-Redshift Protogalaxies? ApJ 686, 801–814 (2008).
- [57] Devecchi, B. & Volonteri, M. Formation of the First Nuclear Clusters and Massive Black Holes at High Redshift. ApJ 694, 302–313 (2009).
- [58] Loeb, A. & Rasio, F. A. Collapse of Primordial Gas Clouds and the Formation of Quasar Black Holes. ApJ 432, 52 (1994).
- [59] Begelman, M. C., Volonteri, M. & Rees, M. J. Formation of supermassive black holes by direct collapse in pre-galactic haloes. MNRAS 370, 289–298 (2006).
- [60] Lodato, G. & Natarajan, P. Supermassive black hole formation during the assembly of pre-galactic discs. MNRAS 371, 1813–1823 (2006).
- [61] Shakura, N. I. & Sunyaev, R. A. Black holes in binary systems. Observational appearance. A&A 24, 337–355 (1973).
- [62] Lynden-Bell, D. & Pringle, J. E. The evolution of viscous discs and the origin of the nebular variables. MNRAS 168, 603–637 (1974).
- [63] Shapiro, S. L., Lightman, A. P. & Eardley, D. M. A two-temperature accretion disk model for Cygnus X-1: structure and spectrum. ApJ 204, 187–199 (1976).
- [64] Ichimaru, S. Bimodal behavior of accretion disks: theory and application to Cygnus X-1 transitions. ApJ 214, 840–855 (1977).
- [65] Narayan, R. & Yi, I. Advection-dominated Accretion: A Self-similar Solution. ApJ 428, L13 (1994).
- [66] Narayan, R. & Yi, I. Advection-dominated Accretion: Self-Similarity and Bipolar Outflows. ApJ 444, 231 (1995).
- [67] Blandford, R. D. & Begelman, M. C. On the fate of gas accreting at a low rate on to a black hole. MNRAS 303, L1–L5 (1999).
- [68] McKinney, J. C. Total and Jet Blandford-Znajek Power in the Presence of an Accretion Disk. ApJ 630, L5–L8 (2005).
- [69] Ghisellini, G., Tavecchio, F., Maraschi, L., Celotti, A. & Sbarrato, T. The power of relativistic jets is larger than the luminosity of their accretion disks. Nature 515, 376–378 (2014).
- [70] Narayan, R., Chael, A., Chatterjee, K., Ricarte, A. & Curd, B. Jets in magnetically arrested hot accretion flows: geometry, power, and black hole spin-down. MNRAS 511, 3795–3813 (2022).
- [71] Igumenshchev, I. V., Narayan, R. & Abramowicz, M. A. Three-dimensional Magnetohydrodynamic Simulations of Radiatively Inefficient Accretion Flows. ApJ 592, 1042–1059 (2003).
- [72] Narayan, R., Igumenshchev, I. V. & Abramowicz, M. A. Magnetically Arrested Disk: an Energetically Efficient Accretion Flow. PASJ 55, L69–L72 (2003).
- [73] Narayan, R., SÄ dowski, A., Penna, R. F. & Kulkarni, A. K. GRMHD simulations of magnetized advection-dominated accretion on a non-spinning black hole: role of outflows. MNRAS 426, 3241–3259 (2012).
- [74] Tchekhovskoy, A., Narayan, R. & McKinney, J. C. Efficient generation of jets from magnetically arrested accretion on a rapidly spinning black hole. MNRAS 418, L79–L83 (2011).
- [75] Ricarte, A., Narayan, R. & Curd, B. Recipes for Jet Feedback and Spin Evolution of Black Holes with Strongly Magnetized Super-Eddington Accretion Disks. ApJ 954, L22 (2023).
- [76] Lowell, B., Jacquemin-Ide, J., Tchekhovskoy, A. & Duncan, A. Rapid Black Hole Spin-down by Thick Magnetically Arrested Disks. ApJ 960, 82 (2024).
- [77] Page, D. N. & Thorne, K. S. Disk-Accretion onto a Black Hole. Time-Averaged Structure of Accretion Disk. ApJ 191, 499–506 (1974).
- [78] King, A. R., Pringle, J. E. & Hofmann, J. A. The evolution of black hole mass and spin in active galactic nuclei. MNRAS 385, 1621–1627 (2008).
- [79] Chen, Y.-X. & Lin, D. N. C. Chaotic gas accretion by black holes embedded in AGN discs as cause of low-spin signatures in gravitational wave events. MNRAS 522, 319–329 (2023).
- [80] Bustamante, S. & Springel, V. Spin evolution and feedback of supermassive black holes in cosmological simulations. MNRAS 490, 4133–4153 (2019).
- [81] Varma, V. et al. Surrogate models for precessing binary black hole simulations with unequal masses. Physical Review Research 1, 033015 (2019).
- [82] Boschini, M. et al. Extending black-hole remnant surrogate models to extreme mass ratios. Phys. Rev. D 108, 084015 (2023).
- [83] Blackman, J. et al. Numerical relativity waveform surrogate model for generically precessing binary black hole mergers. Phys. Rev. D 96, 024058 (2017).
- [84] Varma, V., Gerosa, D., Stein, L. C., Hébert, F. & Zhang, H. High-Accuracy Mass, Spin, and Recoil Predictions of Generic Black-Hole Merger Remnants. Phys. Rev. Lett. 122, 011101 (2019).
- [85] Tremmel, M. et al. An Enhanced Massive Black Hole Occupation Fraction Predicted in Cluster Dwarf Galaxies. The Open Journal of Astrophysics 7, 26 (2024).
- [86] Begelman, M. C., Blandford, R. D. & Rees, M. J. Massive black hole binaries in active galactic nuclei. Nature 287, 307–309 (1980).
- [87] Goldreich, P. & Tremaine, S. Disk-satellite interactions. ApJ 241, 425–441 (1980).
- [88] Berczik, P., Merritt, D., Spurzem, R. & Bischof, H.-P. Efficient Merger of Binary Supermassive Black Holes in Nonaxisymmetric Galaxies. ApJ 642, L21–L24 (2006).
- [89] Vasiliev, E., Antonini, F. & Merritt, D. The Final-parsec Problem in the Collisionless Limit. ApJ 810, 49 (2015).
- [90] Quinlan, G. D. The dynamical evolution of massive black hole binaries I. Hardening in a fixed stellar background. New A 1, 35–56 (1996).
- [91] Sesana, A., Haardt, F. & Madau, P. Interaction of Massive Black Hole Binaries with Their Stellar Environment. I. Ejection of Hypervelocity Stars. ApJ 651, 392–400 (2006).
- [92] Peters, P. C. & Mathews, J. Gravitational Radiation from Point Masses in a Keplerian Orbit. Physical Review 131, 435–440 (1963).
- [93] Peters, P. C. Gravitational Radiation and the Motion of Two Point Masses. Physical Review 136, 1224–1232 (1964).
- [94] Dehnen, W. A Family of Potential-Density Pairs for Spherical Galaxies and Bulges. MNRAS 265, 250 (1993).
- [95] Dabringhausen, J., Hilker, M. & Kroupa, P. From star clusters to dwarf galaxies: the properties of dynamically hot stellar systems. MNRAS 386, 864–886 (2008).
- [96] Bekenstein, J. D. Gravitational-Radiation Recoil and Runaway Black Holes. ApJ 183, 657–664 (1973).
- [97] Blecha, L. & Loeb, A. Effects of gravitational-wave recoil on the dynamics and growth of supermassive black holes. MNRAS 390, 1311–1325 (2008).
- [98] Merritt, D., Berczik, P. & Laun, F. Brownian Motion of Black Holes in Dense Nuclei. AJ 133, 553–563 (2007).
- [99] Hansen, B. M. S. & Milosavljević, M. The Need for a Second Black Hole at the Galactic Center. ApJ 593, L77–L80 (2003).
- [100] Maillard, J. P., Paumard, T., Stolovy, S. R. & Rigaut, F. The nature of the Galactic Center source IRS 13 revealed by high spatial resolution in the infrared. A&A 423, 155–167 (2004).
- [101] Gürkan, M. A. & Rasio, F. A. The Disruption of Stellar Clusters Containing Massive Black Holes near the Galactic Center. ApJ 628, 236–245 (2005).
- [102] Gualandris, A. & Merritt, D. Perturbations of Intermediate-mass Black Holes on Stellar Orbits in the Galactic Center. ApJ 705, 361–371 (2009).
- [103] Chen, X. & Liu, F. K. Is There an Intermediate Massive Black Hole in the Galactic Center: Imprints on the Stellar Tidal-disruption Rate. ApJ 762, 95 (2013).
- [104] Generozov, A. & Madigan, A.-M. The Hills Mechanism and the Galactic Center S-stars. ApJ 896, 137 (2020).
- [105] Naoz, S. et al. A Hidden Friend for the Galactic Center Black Hole, Sgr A*. ApJ 888, L8 (2020).
- [106] Zheng, X., Lin, D. N. C. & Mao, S. The Influence of the Secular Perturbation of an Intermediate-mass Companion. I. Eccentricity Excitation of Disk Stars at the Galactic Center. ApJ 905, 169 (2020).
- [107] Rose, S. C., Naoz, S., Sari, R. & Linial, I. The Formation of Intermediate-mass Black Holes in Galactic Nuclei. ApJ 929, L22 (2022).
- [108] Will, C. M. et al. Constraining a Companion of the Galactic Center Black Hole Sgr A*. ApJ 959, 58 (2023).
- [109] Gravity Collaboration et al. Where intermediate-mass black holes could hide in the Galactic Centre. A full parameter study with the S2 orbit. A&A 672, A63 (2023).