^†^†thanks: These authors contributed equally^†^†thanks: These authors contributed equally^†^†thanks: Present address: Department of Physics, City University of Hong Kong, Kowloon, Hong Kong

Evidence for nodal superconductivity in infinite-layer nickelates

Shannon P. Harvey Stanford Institute for Materials and Energy Sciences, SLAC National Accelerator Laboratory, Menlo Park, CA USA Department of Applied Physics, Stanford University, Stanford, CA, USA Bai Yang Wang Stanford Institute for Materials and Energy Sciences, SLAC National Accelerator Laboratory, Menlo Park, CA USA Department of Physics, Stanford University, Stanford, CA, USA Jennifer Fowlie Stanford Institute for Materials and Energy Sciences, SLAC National Accelerator Laboratory, Menlo Park, CA USA Department of Applied Physics, Stanford University, Stanford, CA, USA Motoki Osada Stanford Institute for Materials and Energy Sciences, SLAC National Accelerator Laboratory, Menlo Park, CA USA Department of Applied Physics, Stanford University, Stanford, CA, USA Kyuho Lee Stanford Institute for Materials and Energy Sciences, SLAC National Accelerator Laboratory, Menlo Park, CA USA Department of Physics, Stanford University, Stanford, CA, USA Yonghun Lee Stanford Institute for Materials and Energy Sciences, SLAC National Accelerator Laboratory, Menlo Park, CA USA Department of Applied Physics, Stanford University, Stanford, CA, USA Danfeng Li Stanford Institute for Materials and Energy Sciences, SLAC National Accelerator Laboratory, Menlo Park, CA USA Department of Applied Physics, Stanford University, Stanford, CA, USA Harold Y. Hwang Stanford Institute for Materials and Energy Sciences, SLAC National Accelerator Laboratory, Menlo Park, CA USA Department of Applied Physics, Stanford University, Stanford, CA, USA

Abstract

Infinite-layer nickelates present a new family of potential unconventional superconductors. A key open question is the superconducting pairing symmetry. We present low-temperature measurements of the London penetration depth in optimally doped La_0.8Sr_0.2NiO₂, Pr_0.8Sr_0.2NiO₂, and Nd_0.8Sr_0.2NiO₂. For La and Pr-nickelates, the superfluid density shows a quadratic temperature dependence, indicating nodal superconductivity in the presence of disorder. Nd-nickelate exhibits complex low-temperature behavior, which we attribute to magnetic impurities. These results are consistent with $d$ -wave pairing.

An important, enduring problem in condensed matter physics has been the nature and origin of superconductivity in the cuprates [1]. In part due to this motivation, considerable effort has been directed toward searching for similar classes of superconductors [2]. A prominent example is the layered nickelates, due to nickel’s proximity to copper in the periodic table [3, 4, 5, 6] and shared structural and electronic aspects with cuprates. After extensive investigation, superconductivity was discovered in the infinite-layer nickelate (Nd,Sr)NiO₂ [7]. Initial examination of the electronic and magnetic properties has begun to reveal both similarities and differences between nickelates and cuprates [8, 9, 10]. The recent development of rare-earth variants of the infinite-layer nickelates, ( $R$ ,Sr)NiO₂ for $R$ =La or Pr, and subsequently quintuple-layer nickelates [11], has opened the door to exploration of a new family of superconducting compounds [12, 13, 14]. Furthermore, substantial improvements in crystallinity have made it possible to probe their properties at far greater depth than was previously possible [15]. Here, we leverage these developments to investigate whether the superconducting gap has nodes, providing a ‘fingerprint’ of the underlying pairing interaction [16].

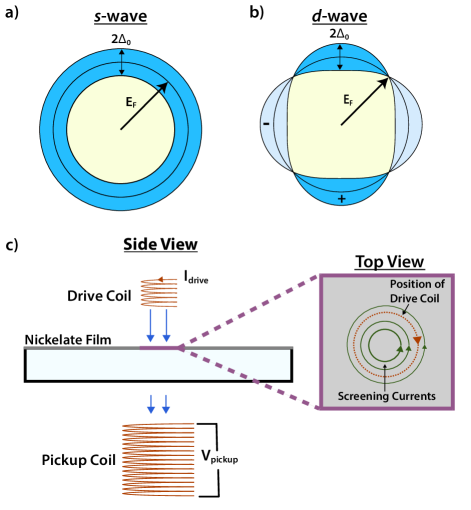
Refer to caption — Figure 1: a) A two-dimensional Fermi surface in momentum space for a conventional superconductor with isotropic $s$ -wave pairing, which has a gap of constant magnitude $\Delta_{0}$ at the Fermi energy $E_{F}$ . b) A two-dimensional Fermi surface for a $d$ -wave superconductor possessing an anisotropic gap with nodes and sign changes in the gap. In particular, a gap with $d_{x^{2}-y^{2}}$ pairing defined by $\Delta_{0}(\theta)=\Delta_{0}\cos(2\theta)$ is shown here. c) Schematic of the measurement apparatus. By sending a current $I_{\mathrm{drive}}$ through the drive coil directly above the nickelate sample, a magnetic field is generated at the sample (upper pair of blue arrows), inducing screening currents locally in the film, as shown in the Top View at right. The voltage across the pickup coil beneath the sample $V_{\mathrm{pickup}}$ measures the sum of the magnetic fields from the drive coil and the nickelate film (lower pair of blue arrows), allowing the film conductance and thereby the superfluid density to be calculated.

The pairing interaction between electrons plays an important role in determining the wave function of the Cooper pairs and the corresponding superconducting gap. Electrons in conventional Bardeen-Cooper-Schrieffer (BCS) superconductors experience phonon-mediated attractive interactions and form an isotropic $s$ -wave superconducting gap, as illustrated by Fig. 1a [17]. By contrast, cuprate superconductors form a $d$ -wave superconducting gap (Fig. 1b) [18, 19], which allows pairing in the presence of predominantly repulsive interactions between electrons. The pairing symmetry in nickelates is under active debate. Upper critical field measurements indicate spin-singlet pairing [20]. A number of theoretical studies have indicated a dominant $d_{x^{2}-y^{2}}$ pairing instability, but other mixed states have been proposed as well, in part due to the presence of electron pockets in the electronic structure in addition to the hole-like Fermi surface common with the cuprates [21, 22, 23, 24, 25, 26]. A scanning tunneling spectroscopy experiment has observed spatially varying gap structures consistent with both $s$ -wave and $d$ -wave pairing [27, 28]. The recent observation of strong antiferromagnetic spin fluctuations [29, 30] could indicate favorable $d_{x^{2}-y^{2}}$ pairing. In this broad context, other experimental probes of the pairing symmetry are of strong interest.

To explore the superconducting gap structure, we perform measurements of the temperature dependence of the London penetration depth, the length scale over which magnetic fields decay in a superconductor, $\lambda(T)=\sqrt{\frac{m^{*}}{4\mu_{0}n_{s}(T)e^{2}}}$ , where $m^{*}$ is the effective mass, $\mu_{0}$ is the vacuum permeability, $e$ is the electron charge, and $n_{s}$ is the superfluid density [31, 32]. The change in superfluid density with temperature can be studied to determine whether the superconducting gap is nodal; at low temperatures $T\lesssim 0.3T_{c}$ , where $T_{c}$ is the superconducting transition temperature, changes in superfluid density are caused by thermal excitation of quasiparticles across the gap, which is a function of the shape and size of the superconducting gap as well as the temperature. An isotropic $s$ -wave superconductor has a nonzero gap at all points, leading to an exponential decrease in superfluid density as temperature increases, so the normalized superfluid density follows the function

\left(\lambda_{0}/\lambda(T)\right)^{2}=1-\sqrt{\frac{c_{1}}{k_{\mathrm{B}}T}}\exp(-\Delta_{0}/k_{\mathrm{B}}T),

(1)

where $\lambda_{0}$ is the minimum value of the penetration depth, $c_{1}$ and $\Delta_{0}$ are fit parameters, and $\Delta_{0}$ represents the minimum gap size (Supplemental Information Sec. II ¹¹1See Supplemental Material for methods, details of fitting, and fits to the Arrhenius and log-log data sets.). By comparison, a gap with nodes, such as those with d-wave pairing, leads to a linear change in superfluid density with temperature, due to the nonzero quasiparticle density of states at the Fermi energy. When such superconductors have disorder, the linear behavior changes to quadratic at low temperatures due to the presence of impurity states at the Fermi energy. This can be parameterized using the equation

(\lambda_{0}/\lambda(T))^{2}=1-2c_{2}\frac{T^{2}}{T+T^{**}},

(2)

where $c_{2}$ and $T^{**}$ are fit parameters and $T^{**}$ represents the crossover temperature between quadratic and linear behavior, with cleaner materials possessing lower values of $T^{**}/T_{c}$ , and the cleanest cuprates reaching values of $T^{**}/T_{c}=0.01$ [34].

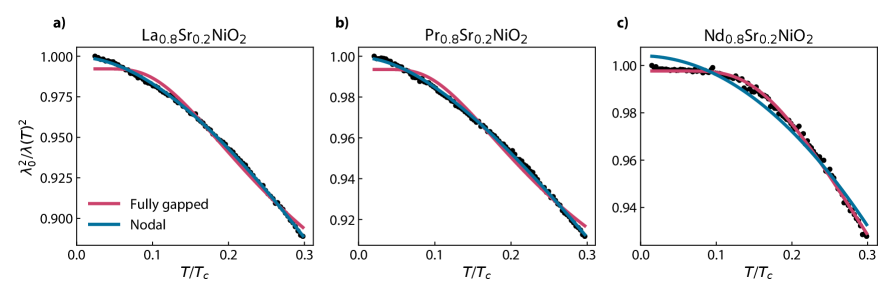
We measure the in-plane London penetration depth $\lambda_{ab}(T)$ (referred to from here on as $\lambda(T)$ ) using a mutual inductance two-coil technique optimal for thin films [35] in a dilution refrigerator (Supplemental Information, Sec. I). A diagram of our apparatus is shown in Fig. 1c; we send a current of 200-300 $\upmu$ A at frequency $f=$ 30-60 kHz through the drive coil directly above the sample to generate a magnetic field at the sample, inducing screening currents in the film. The total magnetic field from the drive coil and screening currents is measured at a pickup coil directly below the sample. The complex conductance $\sigma_{1}(T)-i\sigma_{2}(T)$ can be extracted from the pickup voltage. $\sigma_{2}(T)$ represents the superconducting response, with superfluid density $n_{s}(T)=\frac{m^{*}\pi f}{e^{2}}\sigma_{2}(T)$ . $\sigma_{1}(T)$ represents the dissipative component of the signal; at the superconducting transition, we see a peak that gives a measure of the transition width and therefore the sample homogeneity [36]. $T_{c}$ throughout this manuscript is quantified as the temperature at which $\sigma_{1}(T)$ reaches its maximum. The sample is pressed into a sapphire plate for thermalization and a ruthenium oxide thermometer is attached to the sapphire to measure the sample temperature [37]. Care is taken to determine that the sample remains in the linear response regime.

R	$T_{c}$ (K)	$\lambda_{0}$ ( $\upmu$ m)	$c_{1}$	$\Delta_{0}$	$c_{2}$	$T^{**}$	$c_{2}^{\prime}$
La	7.6	1.35	0.09 (0.04)	0.5 (0.1)	0.5 (0.12)	0.5 (0.18)	-
Pr	10.1	1.3	0.04 (0.02)	0.5 (0.1)	0.3 (0.06)	0.3 (0.12)	-
Nd	11.1	0.75	0.3 (0.1)	0.8 (0.07)	-	-	0.4 (0.025)

Table 1: Properties and fit parameters of the samples discussed.

T_{c}

here is the value at which

\sigma_{1}

is maximum.

\lambda_{0}

is the minimum penetration depth.

c_{1}

and

\Delta_{0}

are fit parameters for Eq. 1, and both are normalized by

k_{\mathrm{B}}T_{c}

in the table.

c_{2}

and

T^{**}

are fit parameters for Eq. 2, both normalized by

T_{c}

in the table. For Nd where

T^{**}\gg T_{c}

, a quadratic fit with coefficient

c_{2}^{\prime}=c_{2}/T^{**}

is appropriate and is presented instead. Errors in fit parameters are displayed in parentheses.

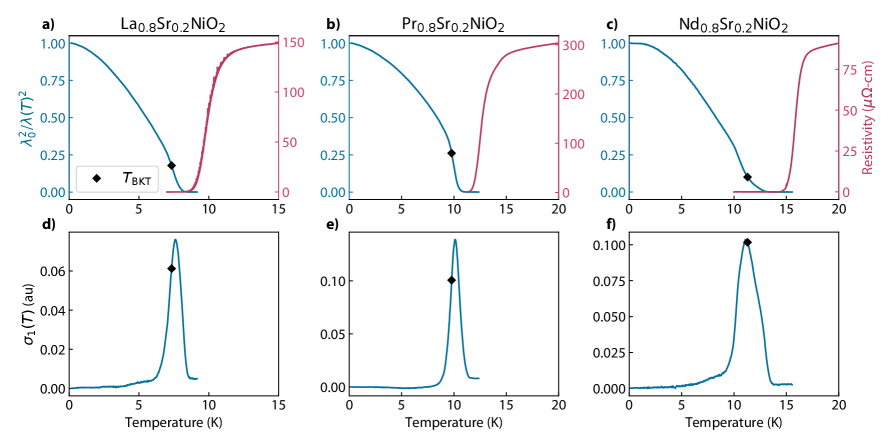
We present measurements of each of the $R$ -site variants $R$ =La, Pr and Nd at optimal doping $R\mathrm{{}_{0.8}Sr_{0.2}NiO_{2}}$ . Samples are approximately 7 nm thick and further capped with SrTiO₃, grown using pulsed laser deposition of the perovskite form of the material on a SrTiO₃ substrate followed by soft chemical reduction to the infinite-layer phase, as described elsewhere [15]. Careful optimization of the film growth has improved film quality considerably, resulting in lower resistivity and superconducting transition width as well as lower defect density in scanning transmission electron microscopy [15, 13]. The resistivity and normalized superfluid density $\lambda_{0}^{2}/\lambda(T)^{2}$ for the three samples is plotted in Fig. 2a-c, showing that the resistance reaches zero at temperatures 1-2 K higher than where the superfluid density appears. The real conductance is plotted in Fig. 2b, showing that the transition width measured through mutual inductance is 1-2 K, and for all samples, the transition is completed at a temperature well over $0.3T_{c}$ , which is necessary for the low temperature behavior to be a reliable guide to the pairing symmetry of the material. A Berezinskii-Kosterlitz-Thouless (BKT) transition, exhibiting an abrupt change in superfluid density close to $T_{c}$ , can be seen for each sample, indicating that they are highly homogeneous [38]. The temperature at which this is predicted to happen, $T_{\mathrm{BKT}}$ , is defined by the point at which $8\pi\mu_{0}/\phi_{0}^{2}k_{\mathrm{B}}T_{\mathrm{BKT}}=d/\lambda(T_{\mathrm{BKT}})^{2}$ , where $d$ is the sample thickness and $\phi_{0}$ is the flux quantum. This point is marked by a diamond in each panel of Figure 2, from which we see that it is located slightly below the temperature for the onset of superfluid density. This is due to disorder in the material and is often observed in superconducting thin films [39]. $\lambda_{0}$ varies from 0.75 $\upmu$ m to 1.35 $\upmu$ m. These values are substantially larger than predicted by density-functional-theory calculations [40], most likely as a result of disorder.

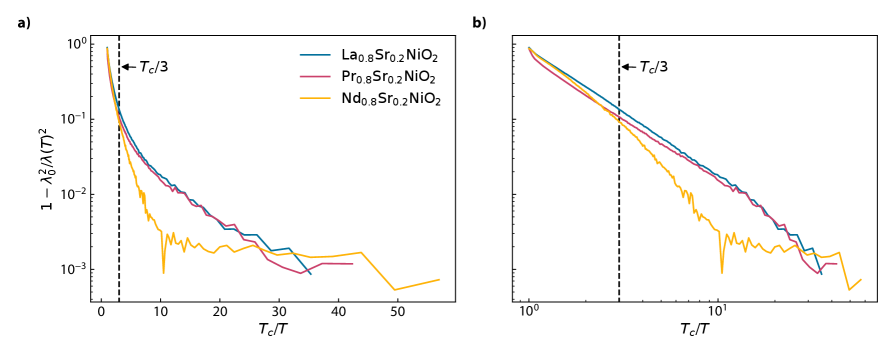
In Fig. 3, the low temperature behavior of the samples and fits to Eqs. 1 and 2 are shown, with the fit parameters displayed in Table 1. For La and Pr, we find that the data is fit closely by Eq. 2 and poorly by Eq. 1, indicating that the gap is nodal and consistent with d-wave pairing. For both samples, $T^{**}$ is of the order of $T_{c}$ , consistent with materials with an intermediate level of disorder. These materials are in the dirty limit of superconductivity, with the electron mean free path shorter than the superconducting coherence length [20], so this is expected. We present an Arrhenius plot and log-log plot of the change in the normalized superfluid density against normalized inverse temperature for all the samples measured in Fig. 4a-b. Surprisingly, the La and Pr samples, exhibit a straight line in Fig. 4b below about 85% $T_{c}$ down to almost the lowest temperatures, indicating power-law scaling, with slope of 1.7 (Supplemental Material, Sec. III). While this is expected at low temperatures given the excellent fit to Eq. (2), it is unexpected that it would continue to such a high temperature. This may have similar origin to the linear scaling of superfluid density with temperature seen in cuprate superconductors [41, 42].

The apparent superfluid density of Nd, shown in Fig. 3c, flattens as the temperature is reduced below 1 K. Because mutual inductance directly measures the magnetic field generated by the sample, it is sensitive to magnetic impurities in the material, which have been seen to impact penetration depth measurements in other superconductors containing rare-earth elements such as Nd [43, 44, 45]. This can impact the measured value of the penetration depth $\lambda_{\mathrm{meas}}(T)=\sqrt{\mu(T)}\lambda(T)$ where $\mu(T)$ is the magnetic permeability of the material. We also note that the Nd sample has the broadest and irregular transition (Fig. 1f). Therefore, while the best fit for Nd is the exponential rather than the quadratic function, this is unlikely to result from the superconducting gap being nodeless, and we ascribe this to the presence of magnetic defects. Another indication that the state is not nodeless comes from the fit parameters of the exponential, which suggest the minimum gap size is equal to $0.8k_{\mathrm{B}}T_{c}$ , well below the BCS weak-coupling limit of 1.76 $T_{c}$ . Finally, examination of the Arrhenius plot for Nd-nickelate sample presented in Fig. 4a shows that it does not follow exponential scaling; while a straight line is expected, we instead see a straight line at higher temperatures, followed by an abrupt flattening, evidence that the flattening at 1 K does not follow an exponential dependence.

In summary, we have performed measurements of the penetration depth in the infinite-layer nickelates down to 150 mK, and found that La_0.8Sr_0.2NiO₂ and Pr_0.8Sr_0.2NiO₂ exhibit quadratic scaling in the low temperature regime, consistent with a superconductor with impurities and a nodal gap, and consistent with dirty $d$ -wave superconductivity. By contrast, Nd_0.8Sr_0.2NiO₂ displays complex behavior inconsistent with simple models for nodal and fully gapped superconductivity, which is most likely to be a function of magnetic impurities. These results situate the infinite-layer nickelates as unconventional superconductors, and likely analogs to high-temperature cuprates in their pairing symmetry.

Note: During the preparation of this manuscript, we became aware of another study of the penetration depth in nickelates [46]. A similar low-temperature magnetic contribution was observed for Nd_0.8Sr_0.2NiO₂. Other aspects of the data, analysis and symmetry conclusion are different from our findings.

Acknowledgements.

We thank Doug Bonn, Varun Harbola, Peter Hirschfeld, Aharon Kapitulnik, Steve Kivelson, Peter Littlewood, Sri Raghu, and David Saykin for useful discussions. This work was supported by the US Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering (contract no. DE-AC02-76SF00515) and the Gordon and Betty Moore Foundation’s Emergent Phenomena in Quantum Systems Initiative (grant no. GBMF9072, synthesis equipment and development of the mutual inductance probe). J.F. was also supported by the Swiss National Science Foundation through Postdoc.Mobility P400P2199297 and Division II 200020 179155.

References

Keimer et al. [2015] B. Keimer, S. A. Kivelson, M. R. Norman, S. Uchida, and J. Zaanen, From quantum matter to high-temperature superconductivity in copper oxides, Nature 518, 179 (2015).
Norman [2016] M. R. Norman, Materials design for new superconductors, Rep. Prog. Phys. 79, 074502 (2016).
Lee and Pickett [2004] K.-W. Lee and W. E. Pickett, Infinite-layer LaNiO₂ : Ni¹⁺ is not Cu²⁺, Phys. Rev. B 70, 165109 (2004).
Anisimov et al. [1999] V. I. Anisimov, D. Bukhvalov, and T. M. Rice, Electronic structure of possible nickelate analogs to the cuprates, Phys. Rev. B 59, 7901 (1999).
Lechermann [2020a] F. Lechermann, Late transition metal oxides with infinite-layer structure: Nickelates versus cuprates, Phys. Rev. B 101, 081110 (2020a).
Botana and Norman [2020] A. S. Botana and M. R. Norman, Similarities and Differences between ${\mathrm{LaNiO}}_{2}$ and ${\mathrm{CaCuO}}_{2}$ and Implications for Superconductivity, Phys. Rev. X 10, 011024 (2020).
Li et al. [2019] D. Li, K. Lee, B. Y. Wang, M. Osada, S. Crossley, H. R. Lee, Y. Cui, Y. Hikita, and H. Y. Hwang, Superconductivity in an infinite-layer nickelate, Nature 572, 624 (2019).
Hepting et al. [2021] M. Hepting, M. P. M. Dean, and W. S. Lee, Soft X-ray Spectroscopy of Low-Valence Nickelates, arXiv:2111.02511 [cond-mat] (2021).
Li et al. [2020] D. Li, B. Y. Wang, K. Lee, S. P. Harvey, M. Osada, B. H. Goodge, L. F. Kourkoutis, and H. Y. Hwang, Superconducting Dome in Nd_1-xSr_xNiO₂, Phys. Rev. Lett. 125, 027001 (2020).
Zeng et al. [2020] S. Zeng, C. S. Tang, X. Yin, C. Li, M. Li, Z. Huang, J. Hu, W. Liu, G. J. Omar, H. Jani, Z. S. Lim, K. Han, D. Wan, P. Yang, S. J. Pennycook, A. T. S. Wee, and A. Ariando, Phase Diagram and Superconducting Dome of Infinite-Layer $\mathrm{Nd_{1-x}Sr_{x}NiO_{2}}$ Thin Films, Phys. Rev. Lett. 125, 147003 (2020).
Pan et al. [2021] G. A. Pan, D. Ferenc Segedin, H. LaBollita, Q. Song, E. M. Nica, B. H. Goodge, A. T. Pierce, S. Doyle, S. Novakov, D. Córdova Carrizales, A. T. N’Diaye, P. Shafer, H. Paik, J. T. Heron, J. A. Mason, A. Yacoby, L. F. Kourkoutis, O. Erten, C. M. Brooks, A. S. Botana, and J. A. Mundy, Superconductivity in a quintuple-layer square-planar nickelate, Nat. Mater. , 1 (2021).
Osada et al. [2020] M. Osada, B. Y. Wang, B. H. Goodge, K. Lee, H. Yoon, K. Sakuma, D. Li, M. Miura, L. F. Kourkoutis, and H. Y. Hwang, A Superconducting Praseodymium Nickelate with Infinite Layer Structure, Nano Lett. 10.1021/acs.nanolett.0c01392 (2020).
Osada et al. [2021] M. Osada, B. Y. Wang, B. H. Goodge, S. P. Harvey, K. Lee, D. Li, L. F. Kourkoutis, and H. Y. Hwang, Nickelate Superconductivity without Rare-Earth Magnetism: (La,Sr)NiO₂, Advanced Materials 33, 2104083 (2021).
Zeng et al. [2021] S. W. Zeng, C. J. Li, L. E. Chow, Y. Cao, Z. T. Zhang, C. S. Tang, X. M. Yin, Z. S. Lim, J. X. Hu, P. Yang, and A. Ariando, Superconductivity in infinite-layer lanthanide nickelates, arXiv:2105.13492 [cond-mat] (2021).
Lee et al. [2020] K. Lee, B. H. Goodge, D. Li, M. Osada, B. Y. Wang, Y. Cui, L. F. Kourkoutis, and H. Y. Hwang, Aspects of the synthesis of thin film superconducting infinite-layer nickelates, APL Materials 8, 041107 (2020).
Hirschfeld and Scalapino [2010] P. J. Hirschfeld and D. J. Scalapino, Led by the nodes, Physics 3 (2010).
Tinkham [1996] M. Tinkham, Introduction to Superconductivity (Courier Corporation, 1996).
Scalapino [1995] D. J. Scalapino, The case for $d_{x^{2}-y^{2}}$ pairing in the cuprate superconductors, Physics Reports 250, 329 (1995).
Tsuei and Kirtley [2000] C. C. Tsuei and J. R. Kirtley, Pairing symmetry in cuprate superconductors, Rev. Mod. Phys. 72, 969 (2000).
Wang et al. [2021] B. Y. Wang, D. Li, B. H. Goodge, K. Lee, M. Osada, S. P. Harvey, L. F. Kourkoutis, M. R. Beasley, and H. Y. Hwang, Isotropic Pauli-limited superconductivity in the infinite-layer nickelate Nd_0.775Sr_0.225NiO₂, Nat. Phys. 17, 473 (2021).
Nomura et al. [2019] Y. Nomura, M. Hirayama, T. Tadano, Y. Yoshimoto, K. Nakamura, and R. Arita, Formation of a two-dimensional single-component correlated electron system and band engineering in the nickelate superconductor ${\mathrm{NdNiO}}_{2}$ , Phys. Rev. B 100, 205138 (2019).
Wu et al. [2020a] X. Wu, D. Di Sante, T. Schwemmer, W. Hanke, H. Y. Hwang, S. Raghu, and R. Thomale, Robust $d_{x^{2}-y^{2}}$ -wave superconductivity of infinite-layer nickelates, Phys. Rev. B 101, 060504 (2020a).
Zhang and Vishwanath [2020] Y.-H. Zhang and A. Vishwanath, Type-II $t\text{$-$}J$ model in superconducting nickelate ${\mathrm{Nd}}_{1-x}{\mathrm{Sr}}_{x}{\mathrm{NiO}}_{2}$ , Phys. Rev. Research 2, 023112 (2020).
Sakakibara et al. [2020] H. Sakakibara, H. Usui, K. Suzuki, T. Kotani, H. Aoki, and K. Kuroki, Model Construction and a Possibility of Cupratelike Pairing in a New $d^{9}$ Nickelate Superconductor (Nd,Sr)NiO₂, Phys. Rev. Lett. 125, 077003 (2020).
Lechermann [2020b] F. Lechermann, Multiorbital Processes Rule the ${\mathrm{Nd}}_{1-x}{\mathrm{Sr}}_{x}{\mathrm{NiO}}_{2}$ Normal State, Phys. Rev. X 10, 041002 (2020b).
Werner and Hoshino [2020] P. Werner and S. Hoshino, Nickelate superconductors: Multiorbital nature and spin freezing, Phys. Rev. B 101, 041104 (2020).
Gu et al. [2020] Q. Gu, Y. Li, S. Wan, H. Li, W. Guo, H. Yang, Q. Li, X. Zhu, X. Pan, Y. Nie, and H.-H. Wen, Single particle tunneling spectrum of superconducting Nd_1-xSr_xNiO₂ thin films, Nature Communications 11, 6027 (2020).
Wu et al. [2020b] X. Wu, K. Jiang, D. Di Sante, W. Hanke, A. P. Schnyder, J. Hu, and R. Thomale, Surface $s$ -wave superconductivity for oxide-terminated infinite-layer nickelates, arXiv:2008.06009 [cond-mat] (2020b).
Lu et al. [2021] H. Lu, M. Rossi, A. Nag, M. Osada, D. F. Li, K. Lee, B. Y. Wang, M. Garcia-Fernandez, S. Agrestini, Z. X. Shen, E. M. Been, B. Moritz, T. P. Devereaux, J. Zaanen, H. Y. Hwang, K.-J. Zhou, and W. S. Lee, Magnetic excitations in infinite-layer nickelates, Science 373, 213 (2021).
Krieger et al. [2021] G. Krieger, L. Martinelli, S. Zeng, L. E. Chow, K. Kummer, R. Arpaia, M. M. Sala, N. B. Brookes, A. Ariando, N. Viart, M. Salluzzo, G. Ghiringhelli, and D. Preziosi, Charge and spin order dichotomy in NdNiO₂ driven by SrTiO₃ capping layer, arXiv:2112.03341 [cond-mat] (2021).
Prozorov and Giannetta [2006] R. Prozorov and R. W. Giannetta, Magnetic penetration depth in unconventional superconductors, Supercond. Sci. Technol. 19, R41 (2006).
Hardy et al. [2002] W. N. Hardy, S. Kamal, and D. A. Bonn, Magnetic Penetration Depths in Cuprates: A short Review of Measurement Techniques and Results, in The Gap Symmetry and Fluctuations in High- $\$$ T $\_$ c $\$$ Superconductors, NATO Science Series: B:, edited by J. Bok, G. Deutscher, D. Pavuna, and S. A. Wolf (Springer US, Boston, MA, 2002) pp. 373–402.
Note [1] See Supplemental Material for methods, details of fitting, and fits to the Arrhenius and log-log data sets.
Hirschfeld and Goldenfeld [1993] P. J. Hirschfeld and N. Goldenfeld, Effect of strong scattering on the low-temperature penetration depth of a $d$ -wave superconductor, Phys. Rev. B 48, 4219 (1993).
Turneaure et al. [1998] S. J. Turneaure, A. A. Pesetski, and T. R. Lemberger, Numerical modeling and experimental considerations for a two-coil apparatus to measure the complex conductivity of superconducting films, Journal of Applied Physics 83, 4334 (1998).
Božović et al. [2016] I. Božović, X. He, J. Wu, and A. T. Bollinger, Dependence of the critical temperature in overdoped copper oxides on superfluid density, Nature 536, 309 (2016).
He et al. [2016] X. He, A. Gozar, R. Sundling, and I. Božović, High-precision measurement of magnetic penetration depth in superconducting films, Review of Scientific Instruments 87, 113903 (2016).
Maccari et al. [2017] I. Maccari, L. Benfatto, and C. Castellani, Broadening of the Berezinskii-Kosterlitz-Thouless transition by correlated disorder, Phys. Rev. B 96, 060508 (2017).
Yong et al. [2013] J. Yong, T. R. Lemberger, L. Benfatto, K. Ilin, and M. Siegel, Robustness of the Berezinskii-Kosterlitz-Thouless transition in ultrathin NbN films near the superconductor-insulator transition, Phys. Rev. B 87, 184505 (2013).
Bernardini et al. [2020] F. Bernardini, V. Olevano, and A. Cano, Magnetic penetration depth and ${T}_{c}$ in superconducting nickelates, Phys. Rev. Research 2, 013219 (2020).
Broun et al. [2007] D. M. Broun, W. A. Huttema, P. J. Turner, S. Özcan, B. Morgan, R. Liang, W. N. Hardy, and D. A. Bonn, Superfluid Density in a Highly Underdoped YBa₂ Cu₃ O_6+y Superconductor, Phys. Rev. Lett. 99, 237003 (2007).
Lee-Hone et al. [2017] N. R. Lee-Hone, J. S. Dodge, and D. M. Broun, Disorder and superfluid density in overdoped cuprate superconductors, Phys. Rev. B 96, 024501 (2017).
Cooper [1996] J. R. Cooper, Power-law dependence of the ab-plane penetration depth in Nd_1.85Ce_0.15 Cu O_4-y, Phys. Rev. B 54, R3753 (1996).
Prozorov et al. [2000] R. Prozorov, R. W. Giannetta, P. Fournier, and R. L. Greene, Evidence for Nodal Quasiparticles in Electron-Doped Cuprates from Penetration Depth Measurements, Phys. Rev. Lett. 85, 3700 (2000).
Martin et al. [2009] C. Martin, M. E. Tillman, H. Kim, M. A. Tanatar, S. K. Kim, A. Kreyssig, R. T. Gordon, M. D. Vannette, S. Nandi, V. G. Kogan, S. L. Bud’ko, P. C. Canfield, A. I. Goldman, and R. Prozorov, Nonexponential London Penetration Depth of FeAs-Based Superconducting $R\mathrm{FeAsO_{0.9}F_{0.1}}$ ( $R$ =La, Nd) Single Crystals, Phys. Rev. Lett. 102, 247002 (2009).
Chow et al. [2022] L. E. Chow, S. K. Sudheesh, P. Nandi, S. W. Zeng, Z. T. Zhang, X. M. Du, Z. S. Lim, E. E. M. Chia, and A. Ariando, Pairing symmetry in infinite-layer nickelate superconductor, arXiv:2201.10038 [cond-mat] (2022).