Event-triggered bipartite consensus for multiagent system with general linear dynamics: an integral-type event triggered control

Nhan-Phu Chung, Thanh-Son Trinh, and Woocheol Choi All authors were supported by the National Research Foundation of Korea (NRF) grants funded by the Korea government No. NRF- 2016R1A5A1008055. N.P. Chung was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government No. NRF-2019R1C1C1007107. W. Choi was supported by the National Research Foundation of Korea(NRF) grant funded by the Korea government No. NRF- 2021R1F1A1059671. N. P. Chung, T. S. Trinh, and W. Choi are with the Department of Mathematics, Sungkyunkwan University, Suwon 16419 (e-mail: [email protected]; [email protected]; [email protected]; [email protected]).

Abstract

In this paper, we propose an integral based event-triggering controller for bipartite consensus of the multi-agent systems whose dynamics are described by general linear system. We prove that the system achieves the bipartite consensus in asymptotic regime and there is a positive minimum inter-event time (MIET) between two consecutive triggering times of each agent. The proof of the asymptotive stability involves a novel argument used to bound the norm of the difference between the true state and its estimated state (for each time) by an integration of its square. Numerical results are provided supporting the effectiveness of the proposed controller.

Index Terms:

bipartite consensus, chattering and genuinely Zeno, integral-based event triggered control, multi-agent systems with linear dynamics.

I Introduction

The coordinated control of multi-agent system (MASs) has recieved a lot of interest in the last decades, thanks to its wide applications in various fields containing engineering and computer science, biology, and social sciences. In particular, distributed controls for the coordinates of multi-agent systems (MASs) over graphs have been studied intensively by variety of researchers [4, 1, 2, 5, 6, 3, 8, 7]. A fundamental problem in the coordinated control of multi-agent system is the consensus problem which requires all agents to asymptotically achieve a common quantity during their cooperative interactions. The main task of the consensus problem in distributed multi-agent systems is to design the control so that all agents will obtain agreement using only interactions of neighbors.

In certain practical problems, some agents collaborate while others are in another competitive group. These systems are represented by signed graphs and the weight of each edge will be positive/negative if the two agents are cooperative/competitive. The agents are said to exhibit a bipartite consensus if they reach agreement in modulus but not in sign [4]. The distributed Laplacian-like control schemes were developed in [4] for the bipartite consensus of single-integrator agents, and extended to directed signed graph [9, 10], general linear systems [12, 13, 11]. Also, the bipartite consensus problems have been studied for general linear system with input-saturation [14] and communication nosies [15].

Due to limitations of sources in the multi-agent systems, we can not assume that agents have continuous access to others’ states. Therefore, agents in the system should have strategy to take various actions in automatically schedules instead of doing so continuously. As an effective solution for the scheduling, event-triggered control designs have been developed for MASs. For event-triggered control systems, controller updates are activated only when a sutiably designed event-triggering condition is satisfied. The event-triggered consensus problem of MASs is first studied by Dimarogonas, Frazzoli and Johansson [16] and has been received tremendous attention after that. Numerous distributed event-triggered consensus protocols were introduced for MASs of first-order [17, 18, 19, 20], of second-order [21], and of linear dynamics [22, 23].

The distributed control with event-triggered communications have been applied to the bipartite consensus problem for the single-integrator agents [24, 8], the double-integrator systems [25], the general linear systems [26, 27], and the heterogeneous systems [28]. In addition, the distributed control with event-triggered communications were studied in the context of the bipartite consensus for the system with input time delay [29] and the prescribed-time bipartite consensus problem [30].

There are two common issues in designing the event-triggered controls for the consensus problems. One is to guarantee that the controlled system actually achieves the consensus in asymptotic regime or in a prescribed time. The other one is to find a lower bound for the difference between two consecutive triggering times. The larger the lower bound is, the better the system is in saving the energy for the communications. These two issues could be in conflict with each other, and so it is important to design a balanced controller satisfying both the two properties. In particular, it is a non-trivial issue to prove that the controlled system has a positive minimum inter-event time (MIET) between two consecutive triggering times while the system achieves the consensus. The works [32, 33, 31] designed event-triggered controllers which guarantee a positive MIET and the consensus is achieved up to a small error.

The idea of integral-based event-triggering condition yielding larger inter-event intervals was proposed by Mousavi, Ghodrat and Marquez [34]. Later, this idea is applied to multi-agent systems in [35] and it has been investigated further in [36, 37, 23, 38, 39]. In particular, Zhang, Lunze and Wang [38] showed that the proposed controller system for the consensus problem has a positive MIET and the consensus is achieved asymptotically without a small error. This kind of idea was not yet applied to bipartite consensus for general linear system. In this article, we propose a novel integral-based event triggering condition for our MASs with linear dynamics for both the bipartite consensus problem which admits the asymptotic bipartite consensus and a positive MIET.

We mention that it is more difficult to prove the consensus for controls based on integral based event-triggering than that based on the point-wise event-triggering, since the Lyapunov stability analysis should be performed after a time integration (see (8)) in order to use the triggering condition. In addition, for applying Barbalat’s lemma [40, Lemma 8.2], one needs to obtain a uniform bound for the difference $\|\hat{z}_{i}(t)-z_{i}(t)\|$ between the true state and the estimated state. We achieve this uniform bound by combining a bound on integration of $\|\hat{z}_{i}(t)-z_{i}(t)\|^{2}$ on an interval and a regularity estimate based obtained in Lemma III.3.

One more subtle issue in the event-triggered controls is the chattering Zeno problem, which means that $t_{k+1}^{i}=t_{k}^{i}$ where $t_{k}^{i}$ is the $k$ -th event-triggering instant of agent $i$ (see (4)). To avoid this issue, we add an exponentially decaying term and show that it does not interrupt the system to achieve the bipartitle asymptotic consensus. Our contributions are summarized as follows.

Statement of contributions:

1.

We design an integral based event-triggered control for the bipartite consensus of general linear multi-agent systems, which is motivated by the control scheme proposed in [38] for consensus of MASs. We add an exponentially decaying term in the triggering function in order to exclude the chattering Zeno behavior. We remark that the previous works [42, 31, 22, 43, 41, 38, 23] implicitly assumed the systems do not have chattering Zeno behavior to establish the Zeno-freeness or the positive MIET of the systems.
2.

We show that the bipartite consensus is achieved with our proposed event-triggered control. One essential step in proving the consensus using integral based event-triggered control is the application of Barbalat’s lemma. This step requires obtaining a uniform bound for the derivative $\dot{V}$ of the a Lyapunov function $V$ used in the proof ([36, 37, 38, 23, 39]). We give a full detail for obtaining the uniform boundedness of the derivative (Lemma III.4).
3.

We extend the work of [8] on Zeno-free analysis on event-triggered bipartite consensus for single-integrator multiagent systems to general linear dynamics. In addition to prove that the Zeno behavior is excluded, we obtain a uniform lower bound for the inter-event intervals for any agent.

Our paper is organized as follows. In section II, we review our notations, basic definitions and properties of graphs, and present our problem formulation of bipartite event-triggered consensus of MASs with general linear dynamics. Our main results will be presented in section III. In section IV, we will illustrate the efficiency and feasibility of our results by a numerical example. And in the last section, our conclusions are given.

II Preliminaries

II-A Notations

Let $\mathbb{R}$ be the set of all real numbers and $\mathbb{N}$ be the set of all nonnegative integer numbers. We denote $|s|$ the absolute value of a number $s\in\mathbb{R}$ . The Euclidean norm of a vector $x\in\mathbb{R}^{n}$ is denoted by $\|x\|$ . We denote $M_{m\times n}(\mathbb{R})$ the set of all matrices of $m$ rows and $n$ columns with real valued entries, and when $m=n$ we write $M_{n}(\mathbb{R})$ instead. The transpose matrix of a matrix $M\in M_{m\times n}(\mathbb{R})$ is denoted by $M^{T}$ . Given $M\in M_{m\times n}(\mathbb{R})$ , we denote by $\|M\|$ its matrix operator norm. For every $N\in\mathbb{N}$ we denote by $1_{N}$ the vector with $N$ columns and all entries are one. The sign function is denoted by ${\rm sgn}(\cdot)$ . If $A\in M_{m\times n}(\mathbb{R})$ and $B\in M_{p\times q}(\mathbb{R})$ then $A\otimes B\in M_{pm\times qn}(\mathbb{R})$ is the Kronecker product.

II-B Graphs

Let $\mathcal{G}=(\mathcal{V},\mathcal{E},\mathcal{W})$ be a signed graph with a set of vertices $\mathcal{V}=\{1,\dots,N\}$ , an edge set $\mathcal{E}\subset\mathcal{V}\times\mathcal{V}$ and an adjacency matrix $\mathcal{W}\in M_{N}(\mathbb{R})$ of the signed weights of $\mathcal{G}$ with $w_{ij}\neq 0$ if $(j,i)\in\mathcal{E}$ and $w_{ij}=0$ otherwise. We always assume that the graph has no self-loops, i.e. $w_{ii}=0$ for every $i\in\mathcal{V}$ . The Laplacian matrix $L$ of $\mathcal{G}$ is defined by $L=C-\mathcal{W}$ , where $C={\rm diag}\bigg{(}\sum_{j=1}^{N}|w_{1j}|,\sum_{j=1}^{N}|w_{2j}|,\cdots,\sum_{j=1}^{N}|w_{Nj}|\bigg{)}$ .

A connected signed graph $\mathcal{G}$ is structurally balanced if there exists a bipartition $\mathcal{V}_{1},\mathcal{V}_{2}$ of nodes such that $w_{ij}\geq 0$ for $i,j\in\mathcal{V}_{k}$ , $k\in\{1,2\}$ , and $w_{ij}\leq 0$ for $i\in\mathcal{V}_{k},j\in\mathcal{V}_{l}$ , $l\neq k$ , $l,k\in\{1,2\}$ .

Definition II.1.

([44, Definition 6]) . For a connected graph $\mathcal{G}=(\mathcal{V},\mathcal{E},\mathcal{W})$ with the Laplacian matrix $L$ , the general algebraic connectivity is defined by

\alpha(L)=\min_{y^{T}\xi=0,y\neq 0}\dfrac{y^{T}Ly}{y^{T}y}.

Furthermore $\alpha(L)=\lambda_{2}(L)$ , where $\lambda_{2}(L)$ is the smallest positive eigenvalue of the Laplacian matrix $L$ .

Lemma II.2.

([4, Lemma 1]) Let $\mathcal{G}=(\mathcal{V},\mathcal{E},\mathcal{W})$ be a connected, structurally balanced signed graph. Then there exists a matrix $D={\rm diag}(\sigma_{1},\sigma_{2},\dots,\sigma_{N})$ such that entries of $D\mathcal{W}D$ are all nonnegative, where $\sigma_{i}\in\{1,-1\}$ for $i\in\mathcal{V}$ .

II-C Problem formulation

Let $A\in M_{n}(\mathbb{R})$ and $B\in M_{n\times m}(\mathbb{R})$ . Consider a group of $N$ agents with linear dynamics under the graph $\mathcal{G}=(\mathcal{V},\mathcal{E},W)$ .

\displaystyle\dot{x}_{i}(t)=Ax_{i}(t)+Bu_{i}(t),\mbox{ }i\in\mathcal{V}=\{1,\dots,N\},

(1)

where $x_{i}(t)\in\mathbb{R}^{n}$ and $u_{i}(t)\in\mathbb{R}^{m}$ are the state and the control input of agent i, respectively. We assume that the signed graph $\mathcal{G}=(\mathcal{V},\mathcal{E},\mathcal{W})$ is structurally balanced and connected.

Every agent $i$ activates a non-decreasing triggering sequence $0=t^{i}_{0}\leq t_{1}^{i}\leq t^{i}_{2}\leq\dots$ . For any state $x_{i}(t)$ of agent $i$ , we define $\hat{x}_{i}(t):=e^{(t-t_{k}^{i})A}x_{i}(t_{k}^{i})$ , where $k:={\rm argmin}\{t-t_{\ell}:t_{\ell}\leq t,\ell\in\mathbb{N}\}$ . We define the error measurements $e_{i}(t):=\hat{x}_{i}(t)-x_{i}(t)$ . We denote $x(t)=[x_{1}^{T}(t),\dots,x_{N}^{T}(t)]^{T}$ , $\hat{x}(t)=[\hat{x}_{1}^{T}(t),\dots,\hat{x}_{N}^{T}(t)]^{T}$ , $e_{x}(t)=[e_{1}^{T}(t),\dots,e_{N}^{T}(t)]^{T}$ .

The event-triggered consensus protocol is given as

\displaystyle u_{i}(t)

\displaystyle=-K\sum_{j=1}^{N}|w_{ij}|(\hat{x}_{i}(t)-{\rm sgn}(w_{ij})\hat{x}_{j}(t)),

(2)

where $K$ is the control matrix which is designed later.

Using Kronecker product, we can write (1) as

\dot{x}(t)=(I_{N}\otimes A-L\otimes BK)x(t)-(L\otimes BK)e_{x}(t).

The system of agents is said to be bipartite consensus if $\lim_{t\to\infty}\|\sigma_{i}x_{i}(t)-\sigma_{j}x_{j}(t)\|=0$ for every $1\leq i,j\leq N$ .

Definition II.3.

We say that an agent $i$ has Zeno behavior if there exists $t_{\infty}\in\mathbb{R}$ such that $\lim_{k\to\infty}t^{i}_{k}=\sum_{k=0}^{\infty}t_{k+1}^{i}-t^{i}_{k}=t_{\infty}$ . There are two different types of Zeno behavior [45] as follows. For an agent $i$ which has Zeno behavior, agent $i$ has

1.

Chattering Zeno if there exists $M\in\mathbb{N}$ such that $t^{i}_{k+1}=t^{i}_{k}$ for every $k\geq M$ .
2.

Genuinely Zeno if $t^{i}_{k+1}-t^{i}_{k}>0$ for every $k\in\mathbb{N}$ .

The system excludes Zeno behavior if all agents do not have Zeno behavior.

We need to find a triggering condition for each agent $i$ such that the system achieves both bipartite consensus and Zeno-freeness.

III Main results

In this section, we will present an event-triggered design such that the system (1) achieves bipartite consensus. Let us introduce some intermediate variables.

We denote $z_{i}(t):=\sigma_{i}x_{i}(t)$ , $\hat{z}_{i}(t)=\sigma_{i}\hat{x}_{i}(t)$ , $e_{z,i}(t)=\hat{z}_{i}(t)-z_{i}(t)$ , $z(t)=[z_{1}^{T}(t),\dots,z_{N}^{T}(t)]^{T}$ , $\hat{z}(t)=[\hat{z}_{1}^{T}(t),\dots,\hat{z}_{N}^{T}(t)]^{T}$ , $e_{z}(t)=[e_{z,1}^{T}(t),\dots,e_{z,N}^{T}(t)]^{T}$ .

We define a new Laplacian matrix $L_{D}:=DLD$ , where $D$ is the matrix given in Lemma II.2. Then from (II-C) we get

\dot{z}(t)=(I_{N}\otimes A-L_{D}\otimes BK)z(t)-(L_{D}\otimes BK)e_{z}(t).

Let $h:[0,\infty)\to(0,\infty)$ be a continuous function satisfying that $\int_{0}^{\infty}h(s)ds=1$ , for example choosing $h(t)=\alpha^{-t}$ for some $\alpha>1$ . We define the triggering functions as

\displaystyle f_{i}^{k}(t):=\int_{t_{k}^{i}}^{t}g_{i}(s)ds,

(3)

where $g_{i}(s)=\|e_{z,i}(s)\|^{2}-\beta_{i}\|\sum_{j=1}^{N}|w_{ij}|(\hat{z}_{i}(s)-\hat{z}_{j}(s))\|^{2}-\beta_{i}h(s)$ and $\beta_{i}$ are constants which will be determined later.

The triggering instants for agent $i$ are defined by

\displaystyle t^{i}_{k+1}:=\inf\{t>t^{i}_{k}:f^{k}_{i}(t)>0\}.

(4)

To our knowledge, the following lemma is the first result in literature of proving the freeness of chattering Zeno for multiagent systems without adding a minimum positive MIET for triggering instants.

Lemma III.1.

For every $i\in\{1,\ldots,N\}$ and $k\in\mathbb{N}$ we have $t^{i}_{k+1}>t^{i}_{k}$ .

Proof.

For $t\geq t^{i}_{k}$ we define $g(t):=\|e_{z,i}(t)\|^{2}-\beta_{i}h(t).$ Then $g(t^{i}_{k})=-\beta_{i}h(t^{i}_{k})<0.$ As the continuity of $g$ we get that there exists $\varepsilon>0$ such that for every $t\in[t^{i}_{k},t^{i}_{k}+\varepsilon]$ one has $g(t)\leq-\frac{1}{2}\beta_{i}h(t^{i}_{k}).$ Hence, for every $t\in[t^{i}_{k},t^{i}_{k}+\varepsilon]$ we get that

	$\displaystyle f^{k}_{i}(t)$	$\displaystyle=\int_{t^{i}_{k}}^{t}g_{i}(s)ds$
		$\displaystyle\leq\int^{t}_{t^{i}_{k}}g(s)ds$
		$\displaystyle\leq-\frac{1}{2}\beta_{i}h(t^{i}_{k})(t-t^{i}_{k}).$

This yields, $f^{k}_{i}(t^{i}_{k}+\varepsilon)\leq-\frac{1}{2}\beta_{i}h(t^{i}_{k})\varepsilon<0.$ By the definition of $t^{i}_{k+1}$ , we obtain that $t^{i}_{k+1}>t^{i}_{k}$ . ∎

Now we provide some standard assumptions on the matrices $A,B$ and the signed graph $\mathcal{G}=(\mathcal{V},\mathcal{E},\mathcal{W})$ .

Assumption III.1.

The pair $(A,B)$ stabilizable, i.e there exists $K_{1}\in M_{n}(\mathbb{R})$ such that all eigenvalues of $A+K_{1}B$ has strictly negative real part. We also assume that the graph $\mathcal{G}$ is structurally balanced and connected.

As $(A,B)$ is stabilizable, applying [46, Theorem 9.5], there exists a positive matrix $P\in M_{n}(\mathbb{R})$ and $\kappa>0$ such that

\displaystyle A^{T}P+PA-\alpha(L)PBB^{T}P<-\kappa I_{n}.

(5)

We choose the control matrix $K:=B^{T}P$ in (2). We define $\bar{z}(t):=\dfrac{1}{N}\sum_{i=1}^{N}z_{i}(t)$ . Then $\dot{\bar{z}}(t)=A\bar{z}(t)$ . To show this, we observe that

\begin{split}\dot{z}_{i}(t)&=\sigma_{i}\dot{x}_{i}(t)\\ &=\sigma_{i}Ax_{i}(t)+\sigma_{i}Bu_{i}(t)\\ &=Az_{i}(t)-\sigma_{i}BK\sum_{j=1}^{N}|w_{ij}|(\hat{x}_{i}(t)-\textrm{sgn}(w_{ij})\hat{x}_{j}(t))\\ &=Az_{i}(t)-BK\sum_{j=1}^{N}|w_{ij}|(\hat{z}_{i}(t)-\hat{z}_{j}(t)).\end{split}

Summing up this for $1\leq i\leq N$ we find $\dot{\bar{z}}(t)=A\bar{z}(t)$ .

Next we note that the difference $e_{i}(t)=\hat{x}_{i}(t)-x_{i}(t)$ satisfies

\dot{e}_{i}(t)=A(\hat{x}_{i}(t)-x_{i}(t))-Bu_{i}(t)=Ae_{i}(t)-Bu_{i}(t).

Since $e_{z,i}(t)=\sigma_{i}e_{i}(t)$ we have

\begin{split}\dot{e}_{z,i}(t)&=\sigma_{i}\dot{e}_{i}(t)\\ &=\sigma_{i}(Ae_{i}(t)-Bu_{i}(t))\\ &=Ae_{z,i}(t)-\sigma_{i}Bu_{i}(t).\end{split}

(6)

We also note that

\begin{split}u_{i}(t)&=-K\sum_{j=1}^{N}|w_{ij}|(\sigma_{i}\hat{z}_{i}(t)-\sigma_{i}\hat{z}_{j}(t))\\ &=-K\sigma_{i}\sum_{j=1}^{N}|w_{ij}|(\hat{z}_{i}(t)-\hat{z}_{j}(t)).\end{split}

Inserting this to (6) we find

\dot{e}_{z,i}(t)=Ae_{z,i}(t)+K\sum_{j=1}^{N}|w_{ij}|(\hat{z}_{i}(t)-\hat{z}_{j}(t)).

(7)

We set $\delta_{i}(t)=z_{i}(t)-\bar{z}(t)$ and $\delta(t)=[\delta_{1}(t)^{T},\cdots,\delta_{N}(t)^{T}]^{T}$ . Also we define the Lyapunov function $V(t):=\delta^{T}(t)(I_{N}\otimes P)\delta(t)$ .

Lemma III.2.

Let $c>0$ such that $\beta:=\kappa-c\|L_{D}\otimes PBB^{T}P\|^{2}>0.$ Put $\beta_{max}:=\max\{\beta_{1},\dots,\beta_{N}\}$ . Assume that $\beta_{max}<\min\bigg{\{}\dfrac{1}{2\|L_{D}\|^{2}},\dfrac{\beta c}{2\|L_{D}\|^{2}(\beta c+1)}\bigg{\}}$ . Then for every $t\geq 0$ we get that

	$\displaystyle V(t)-V(0)$	$\displaystyle\leq-\beta\int_{0}^{t}\\|\delta(s)\\|^{2}ds+\dfrac{1}{c}\int_{0}^{t}\\|e_{z}(s)\\|^{2}ds$
		$\displaystyle=-c_{1}\int_{0}^{t}\\|\delta(s)\\|^{2}ds+c_{2},$

where $c_{1}=\beta-\dfrac{2\beta_{max}\|L_{D}\|^{2}}{c(1-2\beta_{max}\|L_{D}\|^{2})}>0$ and $c_{2}=\dfrac{N\beta_{max}}{c(1-2\beta_{max}\|L_{D}\|^{2})}$ .

Proof.

We have

		$\displaystyle\dot{V}(t)$
	$\displaystyle=$	$\displaystyle\delta^{T}(t)(I_{N}\otimes A^{T}-L_{D}\otimes K^{T}B^{T})(I_{N}\otimes P)\delta(t)$
		$\displaystyle-e^{T}(t)(L_{D}\otimes K^{T}B^{T})(I_{N}\otimes P)\delta(t)$
		$\displaystyle+\delta^{T}(t)(I_{N}\otimes P)[(I_{N}\otimes A-L\otimes BK)\delta(t)-(L_{D}\otimes BK)e_{z}(t)]$
	$\displaystyle=$	$\displaystyle\delta^{T}(t)[I_{N}\otimes(A^{T}P+PA)]\delta(t)-2\delta^{T}(t)(L_{D}\otimes PBB^{T}P)\delta(t)$
		$\displaystyle-2\delta^{T}(t)(L_{D}\otimes PBB^{T}P)e_{z}(t).$

From Definition II.1 we get that

\displaystyle\delta^{T}(t)(L_{D}\otimes PBB^{T}P)\delta(t)\geq\alpha(L_{D})\delta^{T}(t)(I_{N}\otimes PBB^{T}P)\delta(t).

Therefore

	$\displaystyle\dot{V}(t)\leq$	$\displaystyle\delta^{T}(t)[I_{N}\otimes(A^{T}P+PA-\alpha(L)PBB^{T}P)]\delta(t)$
		$\displaystyle-2\delta^{T}(t)(L_{D}\otimes PBB^{T}P)e_{z}(t)$
	$\displaystyle\leq$	$\displaystyle-\delta^{T}(t)(I_{N}\otimes\kappa I_{n})\delta(t)-2\delta^{T}(t)(L_{D}\otimes PBB^{T}P)e_{z}(t)$
	$\displaystyle\leq$	$\displaystyle-\kappa\delta^{T}(t)\delta(t)-2\delta^{T}(t)(L_{D}\otimes PBB^{T}P)e_{z}(t).$

On the other hand,

	$\displaystyle-2\delta^{T}(t)(L_{D}\otimes PBB^{T}P)e_{z}(t)$
	$\displaystyle\leq c\delta^{T}(t)(L_{D}\otimes PBB^{T}P)[\delta^{T}(t)(L_{D}\otimes PBB^{T}P)]^{T}+\dfrac{\\|e_{z}(t)\\|^{2}}{c}$
	$\displaystyle\leq c\\|L_{D}\otimes PBB^{T}P\\|^{2}\delta^{T}(t)\delta(t)+\dfrac{\\|e_{z}(t)\\|^{2}}{c}.$

Hence

\displaystyle\dot{V}(t)\leq-\beta\|\delta(t)\|^{2}+\dfrac{\|e_{z}(t)\|^{2}}{c}.

Therefore

\displaystyle V(t)-V(0)

\displaystyle\leq-\beta\int_{0}^{t}\|\delta(s)\|^{2}ds+\dfrac{1}{c}\int_{0}^{t}\|e_{z}(s)\|^{2}ds.

(8)

From the event triggered conditions (3) and (4), for every $i=1,\dots,N$ , $k\in\mathbb{N}$ and $t\in[t_{k},t_{k+1})$ we get

		$\displaystyle\int_{t^{i}_{k}}^{t}\\|e_{z,i}(s)\\|^{2}ds$
	$\displaystyle\leq$	$\displaystyle\beta_{i}\int_{t^{i}_{k}}^{t}\\|\sum_{j=1}^{N}w_{ij}(\hat{z}_{i}(s)-\hat{z}_{j}(s)\\|^{2}ds+\beta_{i}\int_{t^{i}_{k}}^{t}h(s)ds$
	$\displaystyle=$	$\displaystyle\beta_{i}\int_{t^{i}_{k}}^{t}\\|\sum_{j=1}^{N}w_{ij}(z_{i}(s)-z_{j}(s)+e_{z,i}(s)-e_{z,j}(s)\\|^{2}ds$
		$\displaystyle+\beta_{i}\int_{t^{i}_{k}}^{t}h(s)ds.$

Hence for every $t\geq 0$ we have

		$\displaystyle\int_{0}^{t}\\|e_{z,i}(s)\\|^{2}ds$
	$\displaystyle\leq$	$\displaystyle\beta_{i}\int_{0}^{t}\\|\sum_{j=1}^{N}w_{ij}(z_{i}(s)-z_{j}(s)+e_{z,i}(s)-e_{z,j}(s)\\|^{2}ds$
		$\displaystyle+\beta_{i}\int_{0}^{t}h(s)ds$
	$\displaystyle\leq$	$\displaystyle\beta_{i}\int_{0}^{t}\\|\sum_{j=1}^{N}w_{ij}(z_{i}(s)-z_{j}(s)+e_{z,i}(s)-e_{z,j}(s)\\|^{2}ds+\beta_{i}.$

Let $L_{D,i}$ be the ith row of $L_{D}$ then for every $t\geq 0$ we get

	$\displaystyle\int_{0}^{t}\\|e_{z,i}(s)\\|^{2}ds$	$\displaystyle\leq 2\beta_{i}\int_{0}^{t}(\\|(L_{D,i}\otimes I_{n})z(s)\\|^{2}$
	$\displaystyle+$	$\displaystyle\\|(L_{i}\otimes I_{n})e_{z}(s)\\|^{2})ds+\beta_{i}.$

Therefore we obtain

		$\displaystyle\int_{0}^{t}\\|e_{z}(s)\\|^{2}ds$
	$\displaystyle\leq$	$\displaystyle 2\beta_{max}\int_{0}^{t}(\\|(L_{D}\otimes I_{n})z(s)\\|^{2}+\\|(L_{D}\otimes I_{n})e_{z}(s)\\|^{2})ds$
		$\displaystyle+N\beta_{max}.$

As $(L_{D}\otimes I_{n})\delta(t)=(L_{D}\otimes I_{n})z(t)$ , combining with $\beta_{max}<\dfrac{1}{2\|L_{D}\|^{2}}$ we obtain

	$\displaystyle\int_{0}^{t}\\|e_{z}(s)\\|^{2}ds$	$\displaystyle\leq\dfrac{2\beta_{max}\\|L_{D}\\|^{2}}{1-2\beta_{max}\\|L_{D}\\|^{2}}\int_{0}^{t}\\|\delta(s)\\|^{2}ds$		(9)
	$\displaystyle+$	$\displaystyle\frac{N\beta_{max}}{1-2\beta_{max}\\|L_{D}\\|^{2}}.$		(10)

Combining (8) with (10) we get that

	$\displaystyle V(t)-V(0)\leq$	$\displaystyle-\beta\int_{0}^{t}\\|\delta(s)\\|^{2}ds+\frac{N\beta_{max}}{c(1-2\beta_{max}\\|L_{D}\\|^{2})}$
		$\displaystyle+\dfrac{2\beta_{max}\\|L_{D}\\|^{2}}{c(1-2\beta_{max}\\|L_{D}\\|^{2})}\int_{0}^{t}\\|\delta(s)\\|^{2}ds$
	$\displaystyle=$	$\displaystyle-c_{1}\int_{0}^{t}\\|\delta(s)\\|^{2}ds+c_{2}.$

∎

Lemma III.3.

Suppose that $\dot{y}(t)=Ay(t)$ for $t\geq t_{k}^{i}$ . Then we have

\|y(T)\|_{2}^{2}\leq\|y(t_{k}^{i})\|_{2}^{2}+2\|A\|\int_{t_{k}^{i}}^{T}\|y(t)\|_{2}^{2}dt

for all $T\geq t_{k}^{i}$ , where $\|A\|:=\max_{v\in\mathbb{R}^{n}\setminus\{0\}}\frac{\|Av\|}{\|v\|}$ .

Proof.

We find

\begin{split}\frac{d}{dt}\|y(t)\|^{2}&=2\langle y^{\prime}(t),~{}y(t)\rangle\\ &=2\langle Ay(t),~{}y(t)\rangle\\ &\leq 2\|A\|\|y(t)\|^{2}.\end{split}

Integrating this inequality over $[t_{k}^{i},T]$ we obtain

\int_{t_{k}^{i}}^{T}\frac{d}{dt}\|y(t)\|^{2}dt\leq\int_{t_{k}^{i}}^{T}2\|A\|\|y(t)\|^{2}dt.

This completes the proof. ∎

Lemma III.4.

For every $i$ the function $\|\hat{z}_{i}(t)-z_{i}(t)\|$ is uniformly bounded for $t\geq 0$ .

Proof.

From Lemma III.2 there exists $M>0$ such that $\|z_{i}(t)-\bar{z}(t)\|\leq M$ for every $t>0$ and every $i=1,\dots,N$ . Therefore to prove $\|\hat{z}_{i}(t)-z_{i}(t)\|$ is bounded, it suffices to show that $\|\hat{z}_{i}(t)-\bar{z}(t)\|$ is bounded.

Since $P$ is a positive define matrix, so is $I_{N}\otimes P$ . Hence, $V(t)=\delta^{T}(t)(I_{N}\otimes P)\delta(t)\geq 0$ . Therefore, from Lemma III.2 we get that

\displaystyle\int_{0}^{t}\|\delta(s)\|^{2}ds\leq\frac{V(0)+c_{2}}{c_{1}}.

(11)

Since (11) and (10), for every $i\in\{1,\ldots,N\}$ , we obtain that

\displaystyle\int_{0}^{t}\|e_{z,i}(s)\|^{2}ds\leq\int_{0}^{t}\|e_{z}(s)\|^{2}ds\leq c_{3},

(12)

where $c_{3}:=(2\beta_{\max}\|L_{D}\|^{2}(V(0)+c_{2}))/(c_{1}(1-2\beta_{\max}\|L_{D}\|^{2}))+c_{2}$ .

Furthermore, for every $t\geq 0$ we have that

	$\displaystyle\int_{0}^{t}\\|\hat{z}_{i}(s)-\overline{z}(s)\\|^{2}$
	$\displaystyle\leq 2\int_{0}^{t}\\|\hat{z}_{i}(s)-z_{i}(s)\\|^{2}ds+2\int_{0}^{t}\\|z_{i}(s)-\overline{z}(s)\\|^{2}ds$
	$\displaystyle=2\int_{0}^{t}\\|e_{z,i}(s)\\|^{2}ds+2\int_{0}^{t}\\|\delta_{i}(s)\\|^{2}ds.$

From (11) and (12) for every $t\geq 0$ , we obtain that

\displaystyle\int_{0}^{t}\|\hat{z}_{i}(s)-\overline{z}(s)\|^{2}\leq 2\left(c_{3}+\frac{V(0)+c_{2}}{c_{1}}\right).

(13)

Assume that $\|\hat{z}_{i}(t)-\overline{z}(t)\|$ is not bounded. Then there exists $M_{1}>M^{2}+4\|A\|(c_{3}+(V(0)+c_{2})/c_{1})$ such that $\|\hat{z}_{i}(T)-\overline{z}(T)\|>M_{1}$ for some $T\in[t^{i}_{k},t^{i}_{k+1})$ . Next, we define $y(t):=\hat{z}_{i}(t)-\overline{z}(t)$ . Then $\dot{y}(t)=Ay(t)$ . Therefore, by Lemma III.3 and (13)

	$\displaystyle M_{1}$	$\displaystyle<\\|\hat{z}_{i}(T)-\overline{z}(T)\\|^{2}$
		$\displaystyle\leq\\|\hat{z}_{i}(t^{i}_{k})-\overline{z}(t^{i}_{k})\\|^{2}+2\\|A\\|\int_{t^{i}_{k}}^{T}\\|\hat{z}_{i}(t)-\overline{z}(t)\\|^{2}dt$
		$\displaystyle=\\|z_{i}(t^{i}_{k})-\overline{z}(t^{i}_{k})\\|^{2}+2\\|A\\|\int_{t^{i}_{k}}^{T}\\|\hat{z}_{i}(t)-\overline{z}(t)\\|^{2}dt$
		$\displaystyle\leq M^{2}+4\\|A\\|\left(c_{3}+\frac{V(0)+c_{2}}{c_{1}}\right)$
		$\displaystyle<M_{1}.$

This is a contradiction. Hence, we get that $\|e_{z,i}(t)\|$ is bounded for every $i=1,\ldots,N$ . ∎

Theorem III.5.

Let a multi-agent system as (1) such that the pair $(A,B)$ is stabilizable, and the graph $\mathcal{G}=(\mathcal{V},\mathcal{E},\mathcal{W})$ is connected and structurally balanced. Let $P\in M_{n}(\mathbb{R})$ be a positive matrix being a solution of (5). We consider the event-triggered consensus protocol as (2) with the control matrix $K:=B^{T}P$ . The event triggered times are determined by (3) and (4). Then the system achieves consensus. Furthermore, the multi-agent system has a positive minimum inter-event time, i.e. there exists $\tau>0$ such that $t^{i}_{k+1}-t^{i}_{k}\geq\tau$ for every $i=1,\dots,N$ , $k\in\mathbb{N}$ .

Proof.

As $P$ is a positive matrix so is $I_{N}\otimes P$ . Therefore $V(t)\geq 0$ for every $t$ . Hence from Lemma III.2 we get that $\int_{0}^{t}\|\delta(s)\|^{2}ds\leq\dfrac{V(0)}{c_{1}}$ and therefore $\lim_{t\to\infty}\int_{0}^{t}\|\delta(s)\|^{2}ds$ is finite. Let $\kappa_{1}$ be the smallest eigenvalue of $I_{N}\otimes P$ . Then $V(0)\geq V(t)=\delta^{T}(t)(I_{N}\otimes P)\delta(t)\geq\kappa_{1}\delta^{T}(t)\delta(t)$ . Hence $\delta(t)$ is bounded. On the other hand, as

\displaystyle\dot{\delta(t)}=(I_{N}\otimes A-L_{D}\otimes BK)\delta(t)-(L_{D}\otimes BK)e_{z}(t),

applying Lemma III.4 we get that $\dot{\delta}(t)$ is also bounded. Applying Barbalat’s lemma [40, Lemma 8.2], we get that $\lim_{t\to\infty}\delta(t)=0$ and hence $\lim_{t\to\infty}\|z_{i}(t)-z_{j}(t)\|=0$ for every $i,j$ .

Now we prove that the system has positive minimum inter-event time. We note that

\begin{split}\frac{d}{dt}\|e_{z,i}(t)\|^{2}=&2\langle e_{z,i}(t),~{}\dot{e}_{z,i}(t)\rangle\\ \leq&2\|e_{z,i}(t)\|\|\dot{e}_{z,i}(t)\|\\ \leq&2\|BK\|\|e_{z,i}(t)\|\Big{\|}\sum_{j=1}^{N}w_{ij}(\hat{z}_{i}(t)-\hat{z}_{j}(t))\Big{\|}\\ &+2\|A\|\|e_{z,i}(t)\|^{2}\\ \leq&\Big{\|}\sum_{j=1}^{N}w_{ij}(\hat{z}_{i}(t)-\hat{z}_{j}(t))\Big{\|}^{2}\\ &+(2\|A\|+\|BK\|^{2})\|e_{z,i}(t)\|^{2},\end{split}

where we used (7) in the second inequality. We then have

\begin{split}\|e_{z,i}(t)\|^{2}&\leq\int_{t_{k}^{i}}^{t}e^{(2\|A\|+\|BK\|^{2})(t-s)}\Big{\|}\sum_{j=1}^{N}w_{ij}(\hat{z}_{i}(s)-\hat{z}_{j}(s))\Big{\|}^{2}ds\\ &\leq e^{(2\|A\|+\|BK\|^{2})(t-t_{k}^{i})}\int_{t_{k}^{i}}^{t}\Big{\|}\sum_{j=1}^{N}w_{ij}(\hat{z}_{i}(s)-\hat{z}_{j}(s))\Big{\|}^{2}ds.\end{split}

We rewrite the above inequality by

\|e_{z,i}(s)\|^{2}\leq e^{(2\|A\|+\|BK\|^{2})(s-t_{k}^{i})}\int_{t_{k}^{i}}^{s}\Big{\|}\sum_{j=1}^{N}w_{ij}(\hat{z}_{i}(r)-\hat{z}_{j}(r))\Big{\|}^{2}dr.

Integrating this, we find

\begin{split}&\int_{t_{k}^{i}}^{t}\|e_{z,i}(s)\|^{2}ds\\ &\leq\int_{t_{k}^{i}}^{t}e^{(2\|A\|+\|BK\|^{2})(s-t_{k}^{i})}\int_{t_{k}^{i}}^{s}\Big{\|}\sum_{j=1}^{N}w_{ij}(\hat{z}_{i}(r)-\hat{z}_{j}(r))\Big{\|}^{2}drds\\ &\leq\int_{t_{k}^{i}}^{t}e^{(2\|A\|+\|BK\|^{2})(s-t_{k}^{i})}\int_{t_{k}^{i}}^{t}\Big{\|}\sum_{j=1}^{N}w_{ij}(\hat{z}_{i}(r)-\hat{z}_{j}(r))\Big{\|}^{2}drds\\ &=\Big{(}\int_{t_{k}^{i}}^{t}e^{(2\|A\|+\|BK\|^{2})(s-t_{k}^{i})}ds\Big{)}\int_{t_{k}^{i}}^{t}\Big{\|}\sum_{j=1}^{N}w_{ij}(\hat{z}_{i}(r)-\hat{z}_{j}(r))\Big{\|}^{2}dr.\end{split}

From this and the triggering condition, we see that

\int_{t_{k}^{i}}^{t_{k+1}^{i}}e^{(2\|A\|+\|BK\|^{2})(s-t_{k}^{i})}ds\geq\beta_{i}.

The proof is done. ∎

IV Simulations

In this section, we present a numerical simulation of the bipartite consensus with event-triggered communication given by (4). We consider six agents and take the graph $L$ defined in [8] as

L=\begin{pmatrix}3&-1&2&0&0&0\\ -1&5&4&0&0&0\\ 2&4&8&-2&0&0\\ 0&0&-2&6&-1&-3\\ 0&0&0&-1&1&0\\ 0&0&0&-3&0&3\end{pmatrix}

We take $A$ and $B$ in [14] given as

A=\begin{pmatrix}0&1\\ -1&0\end{pmatrix}\quad B=\begin{pmatrix}0&1\\ 1&1\end{pmatrix}.

The matrix $P$ satisfying (5) is computed as

P=5\times\begin{pmatrix}0.9862&0.0143\\ 0.0143&0.9212\end{pmatrix}.

The initial coordinates of agent $1$ and agent $2$ are selected randomly by a uniform distribution of interval $[0,1]$ while those of other agents are selected randomly by a uniform distribution of interval $[-1,0]$ . We set the constant $\beta_{k}=0.008$ for $1\leq k\leq 6$ .

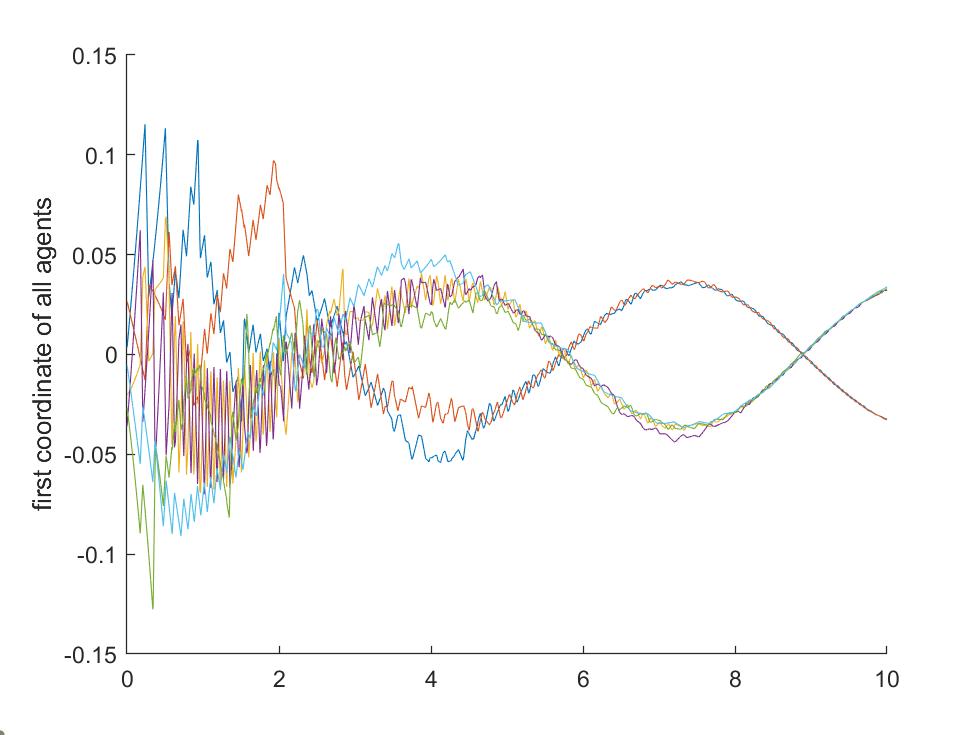
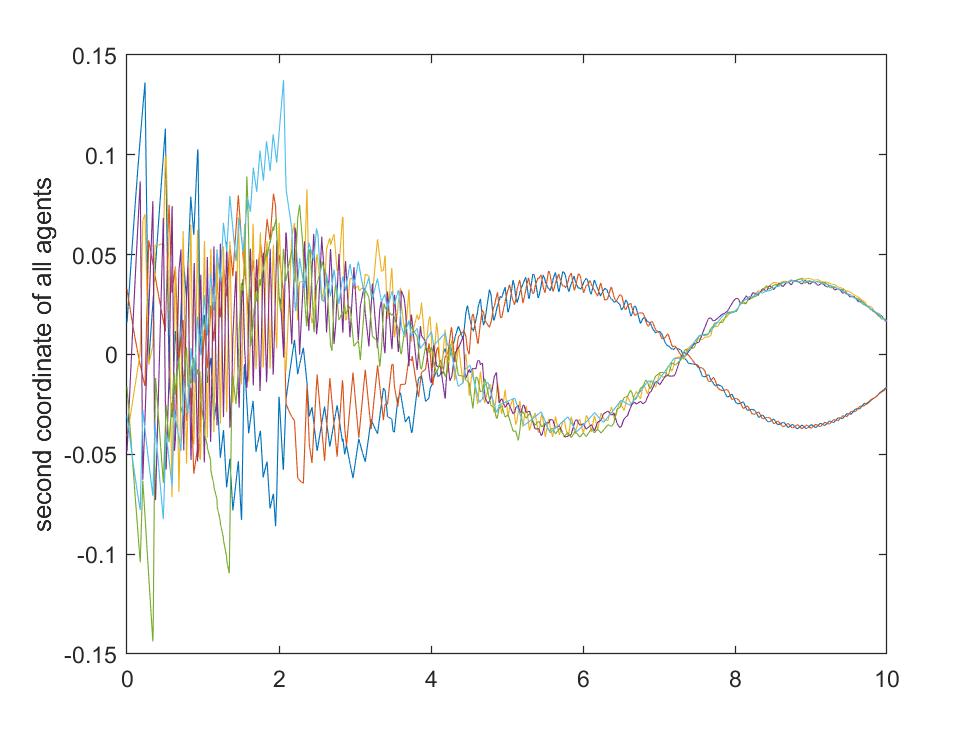
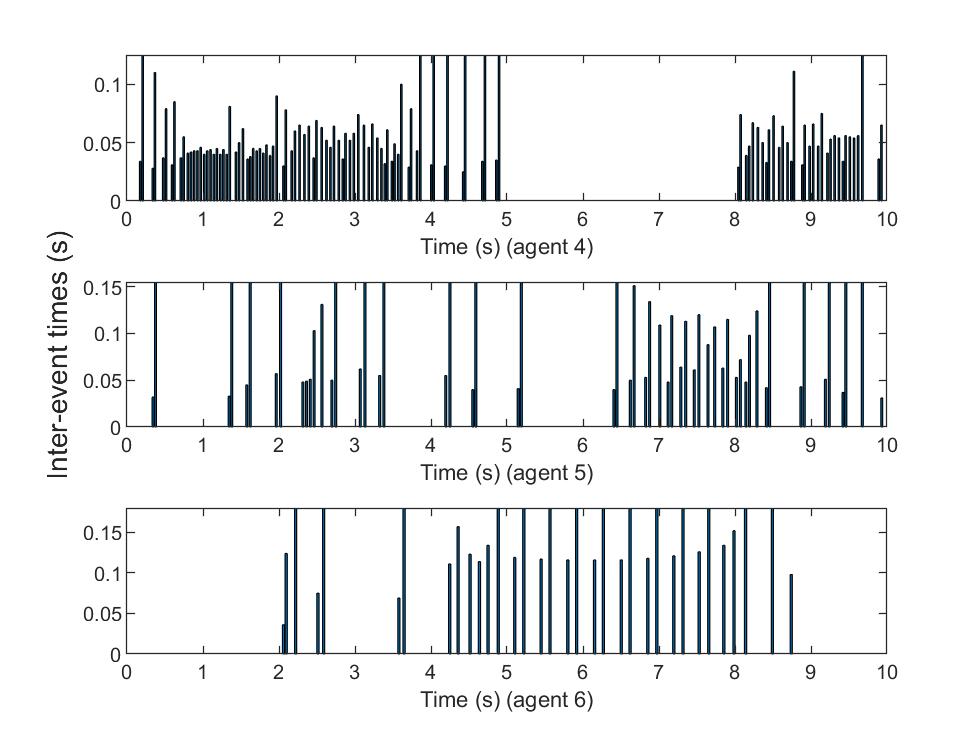
Refer to caption — Figure 1: First coordinates of all agents

In Figures 1 and 2 we see that agent 1 and agent 2 converge to a same trajectory and the other agents converge to another same trajectory. For each $1\leq k$ we let $I_{ev}(k)$ be the minimum interval between two successive event-triggering times of agent $k$ . The values of $I_{ev}(k)$ are given in Table I.

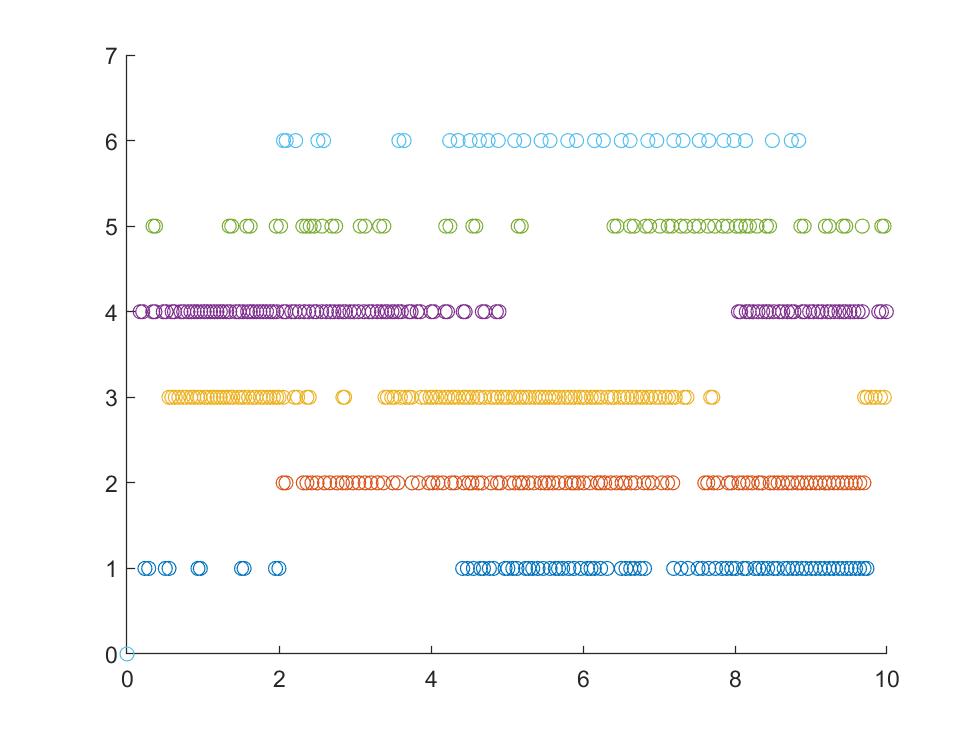
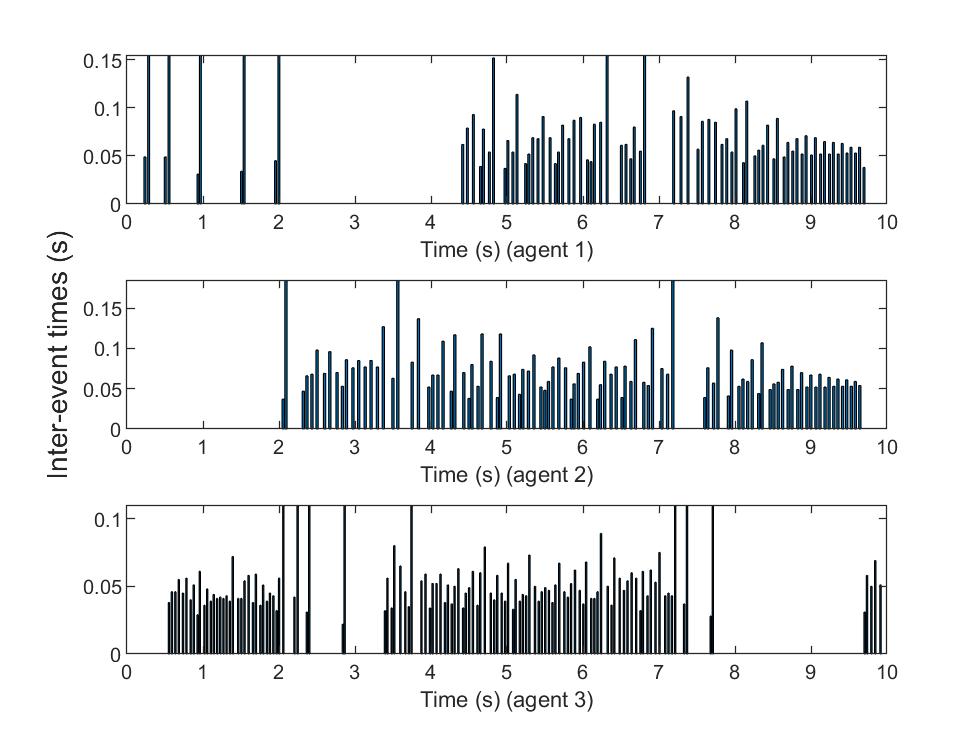
Figure 3 indicates the event-triggering times of each agent. The interval lengths between two successive event-triggering times of each agent are given in Figures 4 and 5. The ranges of $y$ -axis in the diagrams are fixed by $[0,5*I_{ev}(k)]$ for each agent $1\leq k\leq 6$ .

TABLE I: Minimun interval between triggering times

k	1	2	3	4	5	6
$I_{ev}(k)\,(s)$	0.031	0.037	0.022	0.025	0.031	0.036

V Conclusion

In this work, we designed an integral based event-triggered controller for bipartite consensus of the general linear system. We rigorously proved that the bipartite consensus is achieved and there is a positive MIET for the controlled system. The numerical simulation was provided supporting the theoretical results.

References

[1] Y. Cao, W. Yu, W. Ren and G. Chen, ”An Overview of Recent Progress in the Study of Distributed Multi-Agent Coordination,” in IEEE Transactions on Industrial Informatics, vol. 9, no. 1, pp. 427-438, Feb. 2013.
[2] S. Knorn, Z. Chen and R. H. Middleton, ”Overview: Collective Control of Multiagent Systems,” in IEEE Transactions on Control of Network Systems, vol. 3, no. 4, pp. 334-347, Dec. 2016.
[3] J. Qin, Q. Ma, Y. Shi and L. Wang, ”Recent Advances in Consensus of Multi-Agent Systems: A Brief Survey,” in IEEE Transactions on Industrial Electronics, vol. 64, no. 6, pp. 4972-4983, June 2017.
[4] Altafini, Claudio, “Consensus problems on networks with antagonistic interactions,” IEEE Transactions on Automatic Control, Vol 58, No 4, 2013.
[5] R. Olfati-Saber and R. M. Murray, ”Consensus problems in networks of agents with switching topology and time-delays,” in IEEE Transactions on Automatic Control, vol. 49, no. 9, pp. 1520-1533, Sept. 2004.
[6] J. Qin, H. Gao and C. Yu, ”On Discrete-Time Convergence for General Linear Multi-Agent Systems Under Dynamic Topology,” in IEEE Transactions on Automatic Control, vol. 59, no. 4, pp. 1054-1059, April 2014.
[7] H. Zhang, G. Feng, H. Yan and Q. Chen, ”Observer-Based Output Feedback Event-Triggered Control for Consensus of Multi-Agent Systems,” in IEEE Transactions on Industrial Electronics, vol. 61, no. 9, pp. 4885-4894, Sept. 2014.
[8] H. Yu, X. Chen, T. Chen and F. Hao, “Event-triggered bipartite consensus for multiagent systems: A Zeno-free analysis”, IEEE Transactions on Automatic Control, Vol 65, No 11, 2020.
[9] J. Hu and W. X. Zheng, ”Bipartite consensus for multi-agent systems on directed signed networks,” 52nd IEEE Conference on Decision and Control, 2013, pp. 3451-3456.
[10] D. Meng, M. Du and Y. Jia, ”Interval Bipartite Consensus of Networked Agents Associated With Signed Digraphs”, in IEEE Transactions on Automatic Control, vol. 61, no. 12, pp. 3755-3770, Dec. 2016.
[11] M. E. Valcher and P. Misra, ”On the consensus and bipartite consensus in high-order multi-agent dynamical systems with antagonistic interactions”, Systems $\&$ Control Letters Volume 66, April 2014, Pages 94-103.
[12] H. Zhang and J. Chen, “Bipartite consensus of general linear multi-agent systems,” in Proc. Amer. Control Conf., Portland, OR, USA, Jun. 2014, pp. 808–-812.
[13] H. Zhang, “Output feedback bipartite consensus and consensus of linear multi-agent systems,” in Proc. 54th IEEE Conf. Decis. Control, Osaka, Japan, Dec. 2015, pp. 1731–-1735.
[14] J. Qin, W. Fu, W. X. Zheng and H. Gao, ”On the Bipartite Consensus for Generic Linear Multiagent Systems With Input Saturation,” in IEEE Transactions on Cybernetics, vol. 47, no. 8, pp. 1948-1958, Aug. 2017.
[15] J. Hu, Y. Wu, T. Li, and B. Ghosh, “Consensus control of general linear multi-agent systems with antagonistic interactions and communication noises,” IEEE Transactions on Automatic Control, vol. 64, no. 5, pp. 2122-2127, May 2019.
[16] D. V. Dimarogonas, E. Frazzoli and K. H. Johansson, ”Distributed Event-Triggered Control for Multi-Agent Systems,” in IEEE Transactions on Automatic Control, vol. 57, no. 5, pp. 1291-1297, May 2012.
[17] G. S. Seyboth, D. V. Dimarogonas, K. H. Johansson, ”Event-based broadcasting for multi-agent average consensus,” in Automatica Volume 49, Issue 1, January 2013, Pages 245-252.
[18] Z. Sun, N. Huang, B. D. O. Anderson and Z. Duan, ”Event-Based Multiagent Consensus Control: Zeno-Free Triggering via $\mathcal{L}^{p}$ Signals,” in IEEE Transactions on Cybernetics, vol. 50, no. 1, pp. 284-296, Jan. 2020.
[19] Y. Wu, X. Meng, L. Xie, R. Lu, H. Su, Z-G. Wu, ”An input-based triggering approach to leader-following problems”, Automatica Volume 75, January 2017, Pages 221-228.
[20] X. Yi, T. Yang, J. Wu and K. H. Johansson, ”Distributed event-triggered control for global consensus of multi-agent systems with input saturation”, Automatica Volume 100, February 2019, Pages 1-9.
[21] H. Li, X. Liao, T. Huang and W. Zhu, ”Event-Triggering Sampling Based Leader-Following Consensus in Second-Order Multi-Agent Systems,” in IEEE Transactions on Automatic Control, vol. 60, no. 7, pp. 1998-2003, July 2015.
[22] W. Hu, L. Liu and G. Feng, ”Consensus of Linear Multi-Agent Systems by Distributed Event-Triggered Strategy,” in IEEE Transactions on Cybernetics, vol. 46, no. 1, pp. 148-157, Jan. 2016.
[23] W. Zhu, Z. Jiang, G. Feng, “Event-based consensus of multi-agent systems with general linear models,” Automatica Volume 50, Issue 2, February 2014, Pages 552-558.
[24] J. Li, X. Chen, F. Hao, and J. Xie, “Event-triggered bipartite consensus for multi-agent systems with antagonistic interactions,” International Journal of Control, Automation and Systems, vol. 17, no. 8, pp. 2046-2058, July 2019.
[25] J. Ren, Q. Song, and G. Lu, “Event-triggered bipartite leader-following consensus of second-order nonlinear multi-agent systems under signed digraph,” Journal of the Franklin Institute, vol. 356, no. 12, pp. 6591-6609, August 2019.
[26] Y. Cai, H. Zhang, J. Duan, and J. Zhang, “Distributed bipartite consensus of linear multiagent systems based on event-triggered output feedback control scheme,” IEEE Trans. Syst., Man, Cybern., Syst., early access, Jan. 27, 2020, doi: 10.1109/TSMC.2020.2964394.
[27] J. Zang, X. Chen, F. Hao, “Observer based Event-triggered Bipartite Consensus of Linear Multi-agent systems,” International Journal of Control, Automation and Systems volume 19, pages 1291–1301 (2021).
[28] X. Wang, K. Liu, Z. Ji, and S. Han, “Bipartite consensus of heterogeneous multiagent systems based on distributed event-triggered control,” Complexity, vol. 2020, pp. 1–14, Mar. 2020.
[29] Y. Cai, H. Zhang, J. Zhang, and Q. He, “Distributed bipartite leader-following consensus of linear multiagent systems with input time delay based on eventtriggered transmission mechanism,” ISA Transactions, November 2019.
[30] X. Chen, H. Yu, and F. Hao, “Prescribed-time event-triggered bipartite consensus of multiagent systems,” IEEE Trans. Cybern., early access, Jul. 17, 2020, doi: 10.1109/TCYB.2020.3004572.
[31] E. Garcia, Y. Cao, D. W. Casbeer, “Decentralized event-triggered consensus with general linear dynamics,” Automatica Volume 50, Issue 10, October 2014, Pages 2633-2640.
[32] Y. Cheng, V. Ugrinovskii, “Event-triggered leader-following tracking control for multivariable multi-agent systems,” Automatica, 70, 204-210 (2016).
[33] O. Demir, J. Lunze, “Synchronization of multi-agent systems with event-based communication,” at-Automatisierungstechnik, 62(8), 535-546 (2014).
[34] S. H. Mousavi, M. Ghodrat, and H. J. Marquez, “Integral-based event-triggered control scheme for a general class of non-linear systems,” Control Theory $\&$ Applications, 13(9), 1982-1988, 2015.
[35] M. Ghodrat and H. J. Marquez, “An integral based event triggered control scheme of distributed network systems,” 2015 European Control Conference (ECC), 2015, pp. 1724-1729.
[36] Y. Ma, J. Zhao, “Distributed integral-based event-triggered scheme for cooperative output regulation of switched multi-agent systems,” Information Sciences 457-458 (2018), 208-221.
[37] X. Wu, X. Mu, “Observer-based leaderless and leader-following consensus for multiagent systems: A modified integral-type event-triggered design,” Volume 30, Issue 9, June 2020, Pages 3753-3772.
[38] Z. Zhang, J. Lunze and L. Wang, “Integral-based event-triggered control for multi-agent systems with general linear dynamics,” International Journal of Control, 93:5, 1005-1014, 2020.
[39] Z. Zhang and L. Wang, “Distributed integral-type event-triggered synchronization of multiagent systems,” Volume 28, Issue 14,September 2018, Pages 4175-4187.
[40] Khalil, Nonlinear systems (3rd edition). Upper Saddle River, New Jersey, Prentice Hall, 2002.
[41] D. Yang, W. Ren, X. Liu, W. Chen, “Decentralized event-triggered consensus for linear multi-agent systems under general directed graphs,” Automatica Volume 69, July 2016, Pages 242-249.
[42] B. Cheng and Z. Li, “Fully Distributed Event-Triggered Protocols for Linear Multiagent Networks,” in IEEE Transactions on Automatic Control, vol. 64, no. 4, pp. 1655-1662, April 2019.
[43] Z. Li, G. Wen, Z. Duan and W. Ren, ”Designing Fully Distributed Consensus Protocols for Linear Multi-Agent Systems With Directed Graphs,” in IEEE Transactions on Automatic Control, vol. 60, no. 4, pp. 1152-1157, April 2015.
[44] W. Yu, G. Chen, M. Cao and J. Kurths, ”Second-Order Consensus for Multiagent Systems With Directed Topologies and Nonlinear Dynamics,” in IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), vol. 40, no. 3, pp. 881-891, June 2010.
[45] A. D. Ames and S. Sastry, “Characterization of Zeno behavior in hybrid systems using homological methods,” Proceedings of the 2005, American Control Conference, 2005., 2005, pp. 1160-1165 vol. 2.
[46] J. Zabczyk, Mathematical control theory—an introduction, 2nd edition. Birkhäuser/Springer, Cham 2020.

	$\displaystyle\int_{0}^{t}\\|e_{z,i}(s)\\|^{2}ds$	$\displaystyle\leq 2\beta_{i}\int_{0}^{t}(\\|(L_{D,i}\otimes I_{n})z(s)\\|^{2}$
	$\displaystyle+$	$\displaystyle\\|(L_{i}\otimes I_{n})e_{z}(s)\\|^{2})ds+\beta_{i}.$

	$\displaystyle V(t)-V(0)\leq$	$\displaystyle-\beta\int_{0}^{t}\\|\delta(s)\\|^{2}ds+\frac{N\beta_{max}}{c(1-2\beta_{max}\\|L_{D}\\|^{2})}$
		$\displaystyle+\dfrac{2\beta_{max}\\|L_{D}\\|^{2}}{c(1-2\beta_{max}\\|L_{D}\\|^{2})}\int_{0}^{t}\\|\delta(s)\\|^{2}ds$
	$\displaystyle=$	$\displaystyle-c_{1}\int_{0}^{t}\\|\delta(s)\\|^{2}ds+c_{2}.$

	$\displaystyle M_{1}$	$\displaystyle<\\|\hat{z}_{i}(T)-\overline{z}(T)\\|^{2}$
		$\displaystyle\leq\\|\hat{z}_{i}(t^{i}_{k})-\overline{z}(t^{i}_{k})\\|^{2}+2\\|A\\|\int_{t^{i}_{k}}^{T}\\|\hat{z}_{i}(t)-\overline{z}(t)\\|^{2}dt$
		$\displaystyle=\\|z_{i}(t^{i}_{k})-\overline{z}(t^{i}_{k})\\|^{2}+2\\|A\\|\int_{t^{i}_{k}}^{T}\\|\hat{z}_{i}(t)-\overline{z}(t)\\|^{2}dt$
		$\displaystyle\leq M^{2}+4\\|A\\|\left(c_{3}+\frac{V(0)+c_{2}}{c_{1}}\right)$
		$\displaystyle<M_{1}.$