\useunder

\ul

Evaluating Generalizability of Fine-Tuned Models for Fake News Detection

Abhijit Suprem [email protected] Georgia Institute of TechnologyAtlantaGAUSA and Calton Pu [email protected] Georgia Institute of TechnologyAtlantaGAUSA

Abstract.

The Covid-19 pandemic has caused a dramatic and parallel rise in dangerous misinformation, denoted an ‘infodemic’ by the CDC and WHO. Misinformation tied to the Covid-19 infodemic changes continuously; this can lead to performance degradation of fine-tuned models due to concept drift. Degredation can be mitigated if models generalize well-enough to capture some cyclical aspects of drifted data. In this paper, we explore generalizability of pre-trained and fine-tuned fake news detectors across 9 fake news datasets. We show that existing models often overfit on their training dataset and have poor performance on unseen data. However, on some subsets of unseen data that overlap with training data, models have higher accuracy. Based on this observation, we also present KMeans-Proxy, a fast and effective method based on K-Means clustering for quickly identifying these overlapping subsets of unseen data. KMeans-Proxy improves generalizability on unseen fake news datasets by 0.1-0.2 f1-points across datasets. We present both our generalizability experiments as well as KMeans-Proxy to further research in tackling the fake news problem.

1. Introduction

The rapid spread of the Covid-19 virus has led to a parallel surge in misinformation and disinformation (Enders et al., 2020a) This surge of false information, coined an ‘infodemic’ by the CDC (Enders et al., 2020b) can be life-threatening, destabilizing, and potentially dangerous (Quinn et al., 2021). The infodemic is multimodal, meaning associated fake news can take forms of social media posts, tweets, articles, blogs, commentary, misrepresented titles and headlines, videos, and audio content.

\IfEndWith

Current Research..Current Research.Current Research.. There is significant progress on developing domain-specific automated misinformation detection and classification tools (Cui and Lee, 2020; Weinzierl et al., 2021; Hossain et al., 2020; Serrano et al., 2020; Kou et al., 2021; Wahle et al., 2022). Such tools analyze labeled datasets in aforementioned modalities to classify fake news. Recent approaches focus on transformer-based classifiers and language modelers (Wahle et al., 2022; Serrano et al., 2020).

Such fake news detectors are specific to the datasets they are trained with (Hossain et al., 2020; Wahle et al., 2022). More recently, there is a focus on addressing generalizability concerns in these models (Wahle et al., 2022; Bang et al., 2021; Kaliyar et al., 2021; Walambe et al., 2022; Das et al., 2021; Chen et al., 2021). For example, (Wahle et al., 2022) explores the impact of generalization of 15 transformer models on 5 fake news datasets. The results show there is a generalizability gap in fake news detection: a fine-tuned model trained on one fake news dataset performs poorly on other unseen, but related, fake news datasets.

\IfEndWith

Generalization Study..Generalization Study.Generalization Study.. In this paper, we study the generalizability and fine-tuning tradeoff and present our findings for furthering the research interest. We study several fake news detection architectures across 9 fake news text datasets of different modalities. We find that fine-tuned models often have reduced accuracy on any unseen dataset. However, when paired with a reject option to abstain from low-confidence predictions, fine-tuned models perform significantly better. These abstention results can then be labeled with active learning, crowdsourcing, weak label integration, or a variety of other methods present in literature.

\IfEndWith

KMeans-Proxy.KMeans-ProxyKMeans-Proxy. Through observations on our generalizability results, we present a simple ‘reject option’ (Hendrickx et al., 2021; Brinkrolf and Hammer, 2018; Geifman and El-Yaniv, 2019) for fake news detectors, called KMeans-Proxy. KMeans-Proxy is based on KMeans clustering, and is inspired by research into proxy losses (Movshovitz-Attias et al., 2017; Wern Teh et al., 2020) and foundation models (Bommasani et al., 2021; Chen et al., 2022; Orr et al., 2021). It is written as a PyTorch layer and requires only a few lines of code to implement for most feature extractors. We show in our results that KMeans-Proxy improves generalization on fake news datasets by 0.1 to 0.2 f1 points across several experiments.

\IfEndWith

Contributions.ContributionsContributions. In summary, our contributions are:

1.

Extensive set of experiments across 9 fake news datasets on the generalizability/fine-tuning trade off.
2.

KMeans-Proxy, a simple reject-option for feature extractors. KMeans-Proxy uses cluster proxies from ProxyNCA to estimate embedding cluster centers of the training data. During prediction, KMeans-Proxy provides a reject option based on label difference between sample prediction and nearest training data cluster center.

Our code for running experiments and for KMeans-Proxy are provided¹¹1https://github.com/asuprem/GLAMOR/blob/colabel-multicb/src/ednaml/utils/blocks/KMeansProxy.py.

2. Related Work

2.1. Generalizability and Fine-Tuning

Since 2002, there are increasing numbers of Covid-19 fake news datasets and associated models for these datasets (Cui and Lee, 2020; Kou et al., 2021). Recently, there is increasing interest in gauging the effectiveness of each of these fine-tuned models on related, but unseen datasets (Wahle et al., 2022). The authors of (Wahle et al., 2022) conduct a generalization study over 15 model architectures over 5 datasets, and find that fine-tuning offers little advantage in classification accuracy. There is also an abundance of research in unsupervised domain adaptation to recover accuracy under changing domains or concept drift (Suprem et al., 2020; Gama et al., 2014; Kouw and Loog, 2018; Žliobaitė, 2010).

2.2. Concept Drift

Concept drift occurs when testing or prediction data exhibits distribution shift (Gama et al., 2014), either in the data domain, or in the label domain (Žliobaitė, 2010). Data domain shift can include introduction of new vocabularies, disappearance of existing words, and word polysemy (Suprem et al., 2019). Label domain shift occurs when the label space itself changes for the same type of data (Kouw and Loog, 2018; Pu et al., 2020). For example, when new types of misinformation are detected, then the boundary between misinformation and true information must be adjusted (Pu et al., 2020). We show label shift in Figure 1, where subsets of true and fake news occupy the same embedding space across datasets due to fine-grained differences.

2.3. Reject Options

One drawback of classification models is that they provide a prediction for every data point (Hendrickx et al., 2021), regardless of confidence. Reject options perform external or internal diagnosing. This can help detect either low confidence due to low coverage or divergence from training data distributions due to concept drift. Several approaches are covered in a recent survey (Hendrickx et al., 2021). We present a reject option that uses recent findings in (Chen et al., 2022) and (Urner and Ben-David, 2013) on the topology of the embedding space: (i) find that local smoothness of the label space is indicative of local accuracy and coverage (Urner and Ben-David, 2013), and (ii) local label shift, where nearby samples have different labels, is a good predictor of local smoothness (Chen et al., 2022). Our reject option, described in Section 3.3 is a clustering approach that calculates cluster centers in the feature extractor embedding space for the training data. Then, during prediction, a model can provide a prediction as well the label for the nearest training data cluster center. Flipped, or different, labels can indicate reduced local smoothness, confidence, and coverage, leading to a reject decision.

2.4. Motivation

It is well known that fine-tuned models suffer performance degradation over time due to data domain shift (Pu et al., 2020; Yang et al., 2015; Lazer et al., 2014). Usually, this performance degradation is detected, and a new model is trained on new labeled data. Recently, the velocity and size of new data makes obtaining labeled data quickly and at scale, very expensive (Li et al., 2021). Updating models during data domain shift requires relying on weak labels, authoritative sources, and hierarchical models (Li et al., 2021; Ratner et al., 2017; Rühling Cachay et al., 2021). In such cases, a team of prediction models is pruned and updated with new training data (Pu et al., 2020). However, we still need predictions in the period when data domain shift is occurring, and new models have not been trained. Our work, as well as recent research in generalizability (Wahle et al., 2022), weak labeling (Ratner et al., 2017), foundation models (Chen et al., 2022), and rapid fake news detection (Li et al., 2021) falls in this period. Our generalizability experiments in Section 3 show that fine-tuned models, while having lower performance on unseen data, do have better accuracy on some subsets. Our KMeans-Proxy solution finds these subsets where fine-tuned models have higher accuracy.

3. Generalization Experiments

We transformer-based text feature extractors for fake news classification generalizability with several experiments. We cover the datasets, architectures, and experiments below.

\IfEndWith

Datasets..Datasets.Datasets.. We used 9 fake news datasets, consisting of blog articles, news headlines, news content, tweets, social media posts, and article headlines. We have described our dataset below in Table 1.

Table 1. Datasets used for our experiments. If splits were not available, we used a random class-balanced split. For Tweet datasets, sample counts are after rehydration, which removed some samples due to missing tweets.

Dataset	Training	Testing	Type
k_title (Patel, 2021)	31k	9K	Article Titles
coaid (Cui and Lee, 2020)	5K	1K	News summary
c19_text (Agarwal, 2020)	2.5K	0.5K	Articles
cq (Mutlu et al., 2020)	12.5K	2K	Tweets
miscov (Memon and Carley, 2020)	4K	0.6K	Headlines
k_text (Patel, 2021)	31k	9K	Articles
rumor (Cheng et al., 2021)	4.5K	1K	Social Posts
cov_fn (Das et al., 2021)	4K	2K	Tweets
c19_title (Agarwal, 2020)	2.5K	0.5K	Article Titles

Where possible, we have used the provided training and validation sets; otherwise, we performed a random, class-balanced 70-30 split for training and testing. For (Mutlu et al., 2020) and (Das et al., 2021) datasets, we performed tweet rehydration, which removed some samples due to missing tweets. We show example of label shift due to label overlap in Figure 1. Here, samples from each dataset are passed through a pre-trained BERT classifier. The BERT embeddings are then reduced to 50 components with PCA then to 2 components with tSNE. There are several regions with label overlaps, where samples with positive and negative labels occupy similar spaces.

Figure 1. Overlap of label embeddings: We show label embeddings for all 9 datasets here. There are several regions where true news (blue) overlap with fake news (red) across different datasets. This can make models for one dataset perform worse on unseen, but related text-based fake news datasets.

\IfEndWith

Architectures..Architectures.Architectures.. We use BERT and AlBERT architectures for our experiments (Devlin et al., 2018; Lan et al., 2019). Each transformer architecture converts input tokens to a classification feature vector. We used pretrained architectures as starting points; our selections include the BERT (Devlin et al., 2018), AlBERT (Lan et al., 2019), and COVID-Twitter-BERT (Müller et al., 2020).

\IfEndWith

Experiments.ExperimentsExperiments. We performed 3 experiments to evaluate generalizability of covid fake news detectors. In each case, our starting point is a pre-trained foundation model, described in previous section. We then conduct the following experiments:

1.

Static-Backbone. We freeze the pre-trained feature extractor backbone, and train only the classifier head. This is analogous to using a static foundation model.
2.

Static-Embedding. We fine-tune the transformer part of the pre-trained feature extractor along with the classifier head together with a single optimizer, and freeze the embedding module
3.

Fine-Tuned Backbone. We fine-tune the entire feature extractor backbone along with the classifier head.

\IfEndWith

Evaluation..Evaluation.Evaluation.. We average results across multiple runs of each transformer architecture. To show results in limited space, we have provided complete evaluation results for backbones using Covid-Twitter-BERT. To test generalizability, we train each model on a single dataset, and evaluate on the test-sets of the remaining, unseen datasets as well as its own testing dataset. Our results are presented as a confusion matrix. All approaches are trained for 5 epochs with an AdamW optimizer, with a learning rate of 1e-4, with a batch size of 64.

3.1. Generalizability Results

We show generalizability results using the COVID-Twitter backbone in for static-backbone training in Figure 2, static-embedding training in Figure 3, and fine-tuned backbone training in Figure 4.

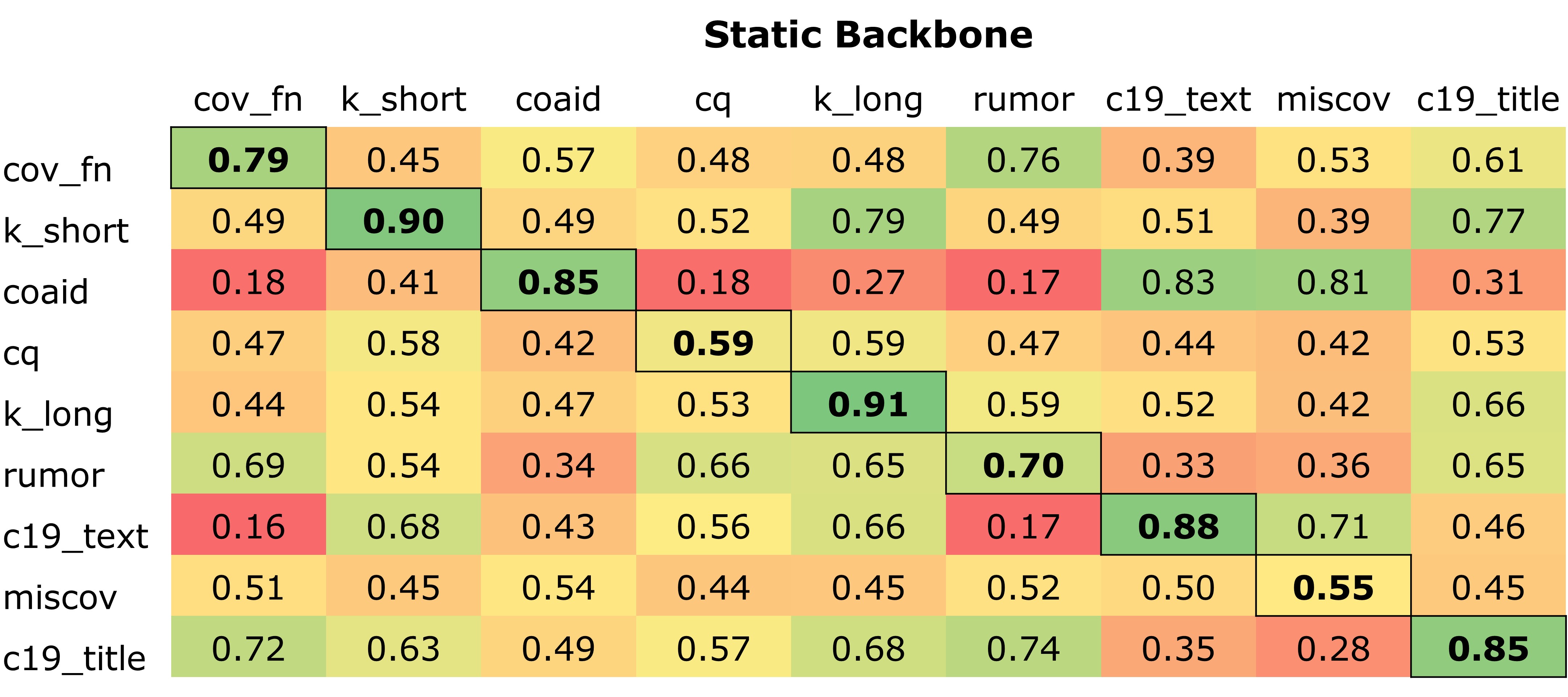
Refer to caption — Figure 2. Confusion Matrix for Static Backbone

\IfEndWith

Static backbone vs Fine-Tuning..Static backbone vs Fine-Tuning.Static backbone vs Fine-Tuning.. The confusion matrices show that upon fine-tuning, each model increases accuracy on its corresponding test dataset. For example, accuracy on ‘k_short’ increases from 0.90 to 0.97 between the static backbone and the fine-tuned backbone. However, this fine-tuning comes at the cost of generalization in some cases: across several datasets, model accuracy on unseen data suffers in the fine-tuned backbone experiments. For example, a model trained on ‘cov_fn’ achieves f1 of 0.72 when tested on ‘c19_title’ in the static-backbone experiment in Figure 2. On the fine-tuned experiment, the same trained model achieves f1 of 0.57, approximately a 20% drop. SImilarly, a model trained on ‘miscov’ and tested on ‘c19_text’ achieves f1 of 0.71 with static backbone, versus f1 of 0.43 with fine-tuned backbone. This indicates once a model is fine-tuned on a specific covid dataset, it loses some generalization information compared to the static-backbone version. However, this is not consistent. In some cases, generalization accuracy increases: ‘rumor’ performs better on ‘cov_fn’ after fine-tuning, with f1 of 0.52 on the static backbone, versus an f1 of 0.75 after fine-tuning. Furthermore, ‘rumor’ achieves f1 of 0.67 when tested on ‘c19_title‘ on the static backbone, and f1 of 0.81 on the fine-tuned backbone (conversely, it performs worse on ‘coaid‘, with f1 dropping from 0.83 to 0.40).

(a) Static-Backbone

(b) Static-Embedding

(d) F1-Score Variance

Figure 5. Overlap vs Accuracy for each of our experiment approaches. In Figure 5(c), we have also provided the trendlines from the other experiments for comparison.

\IfEndWith

Static Embedding..Static Embedding.Static Embedding.. A middle ground between complete fine-tuning and a fully static foundation feature extractor is to freeze the embedding layer and fine-tune the transformer layer of the backbone. Recent work finds freezing the embedding layer during training can reduce computation costs while achieving 90% of the accuracy of a fully fine-tuned model (Lee et al., 2019; Hulburd, 2020; Moon et al., 2019; Jiao et al., 2021; Merchant et al., 2020). We find similar results, where freezing the embedding layer achieves accuracy similar to the corresponding fine-tuned model on the testing dataset, shown in Figure 3 However, on unseen data, accuracy drop has higher variance. It is not immediately clear what impact embedding freezing has on unseen data accuracy. For this, we must explore the actual overlap between datasets.

3.2. Data Overlap and Accuracy

We have seen that there is label overlap between datasets in Figure 1. We have also seen accuracy variances on unseen data: rather than a linear drop across unseen data, some models perform better and some perform worse after fine-tuning. These can be explained by directly measuring dataset overlap.

\IfEndWith

O-Metric..O-Metric.O-Metric.. To compute overlap, we use the O-metric to calculate point-proximity overlap from (Cardillo and L. Warren, 2016). The O-metric computes overlap between 2 sets of points in n-dimensional space using a distance-metric. We find overlap as follows: given two datasets A and B, we compute the fraction of points in each dataset where the nearest neighbor is not from the same dataset. So, for each point $x\in A$ , first we obtain:

O_{A}(x)=w_{A}(x)/b_{A}(x)

where $w_{A}()$ is the distance to the nearest point to $x$ in A, and $b_{A}()$ is the distance to the nearest point to $x$ in B. Then we can compute the ratio $p_{A}=|O_{A}>1|/|A|$ to find overlap of B in A. $p_{A}$ is bounded in $[0,1]$ ; as $p_{A}$ approaches 1, this indicates most points in $A$ are closer to a point in $B$ than in $A$ . The O-metric is bidirectional in computing overlap and includes both $p_{A}$ and $p_{B}$ :

$O=\frac{p_{A}+p_{B}}{2}$

Since we are interested in evaluating generalization, where we want to see only the overlap of unseen data on training data, we use a directional O-metric. That is, we let $O=p_{A}$ for the final overlap value in a context where A is the training dataset and B is the unseen dataset. We compute the overlap value between each dataset pair using cosine similarity on the embeddings of each data point. So, for each model, we compute embeddings of every sample across all 9 datasets, then compute the directional O-metric overlap of each dataset on the model’s training dataset [ALGO???].

\IfEndWith

Accuracy and Overlap.Accuracy and OverlapAccuracy and Overlap. We show in Figure 5 the comparison of overlap to accuracy across all 9 datasets on static-backbone, static-embedding, and fine-tuned backbone experiments. First, we see that as overlap increases, accuracy also increases for the fine-tuned backbone in Figure 5(c). Second, and perhaps more striking, there is higher variance in accuracy on the static-embedding versus fine-tuned backbone models. This fits the observations from (Merchant et al., 2020) that the embedding layers capture more domain-specific information than the deeper layers. In this cases, because the embedding layers were frozen, they never learned the domain-specific fake news information. Consequently, the static-embedding models’ accuracy on unseen data sees significant variance, compared to the fine-tuned backbone and static-backbone models, shown in Figure 5(d).

\IfEndWith

Generalization and Overlap..Generalization and Overlap.Generalization and Overlap.. Clearly, higher overlap between evaluation data and training data is indicative of accuracy. During testing, however, it may be difficult to calculate this overlap on data for each sample. Further, evaluation data changes continuously, so the overlap may itself change due to concept drift. Recent research has shown the importance of exploring a model’s feature space to identify embedding clusters (Chen et al., 2022; Urner and Ben-David, 2013). These embedding clusters signify regions of the data space a model has captured. Metrics such as probabilistic Lipschitzness show that accuracy on embedding clusters can be bounded using the smoothness, or gradient, in the embedding space (Urner and Ben-David, 2013). Further, LIGER (Chen et al., 2022) shows that nondeterministic label regions, i.e. where labels overlap, indicate non-smoothness. We extend these findings to present KMeans-Proxy - a plug-and-play pytorch layer.

3.3. KMeans-Proxy

Intuitively, if we can store the coverage of a model’s embedding space, then for any sample point, we can check if it falls inside the coverage. Further, we can also check if a model’s prediction on the sample matches the prediction for the coverage. We can pair this with a coverage radius, e.g. by computing $r$ that constitutes coverage of all points in a cluster that are 1 standard deviation away from the cluster center with respect to a distance metric, such as the l2 norm. Then, if the predictions do not match or a point falls outside the single standard deviation coverage radius, this is a strong abstention/reject signal.

\IfEndWith

Implementation..Implementation.Implementation.. We can capture the coverage of the embedding space by using embedding proxies. Proxies are common in cluster and proxy NCA losses (Movshovitz-Attias et al., 2017; Wern Teh et al., 2020). We adapt them as the KMeans cluster centroids by acting as proxies for the cluster centers. This allows our approach to extend to online or continuous learning domains as well. The findings in (Chen et al., 2022) suggest increased partitioning of the embedding space can yield better local region coverage. So, KMeans-Proxy is initialized with 2 parameters: the number of classes $c$ , and a proxy factor $k$ . Then, we then obtain $k\cdot c$ centers, with $k$ proxies for each class, so that each cluster is a smaller, more representative local region.

⬇

1self.proxy = KMeansProxy(proxy_factor = 4, classes = 3, dimensions = 768)

During model training, KMeans-Proxy performs minibatch online KMeans clustering to obtain the embedding space proxies for cluster centers. Online clustering converges asymptotically, per (So et al., 2022).

⬇

1def forward(x): # Proxy forward function

2 if self.training:

3 self.update_proxies(x)

4 return x, None, None

5 return x, self.nearest_proxy(x), self.nearest_proxy_label(x)

During prediction, a model using KMeans-Proxy can predection, as well as nearest proxy label and nearest proxy. A meta abstention policy can review for label flipping, or coverage radius.

⬇

1def forward(x): # Model forward function

2 x = self.feature_extractor(x)

3 x, proxy, proxy_label = self.proxy(x)

4 label = self.classifier(x)

5 return label, proxy, proxy_label

Table 2. Generalization improvement with KMP for model trained on ‘coaid’.

Trained on ‘coaid’
Testing Dataset	Approach
Testing Dataset	SB	SE	FT	FT+KMP
cov_fn	0.57	0.44	0.51	\ul0.53
k_short	0.49	\ul0.57	0.56	0.57
coaid	0.85	0.95	\ul0.97	0.98
cq	0.42	0.59	0.55	\ul0.57
k_long	0.47	0.51	0.58	\ul0.55
rumor	0.34	0.31	\ul0.55	0.68
c19_text	0.43	0.64	\ul0.79	0.94
miscov	\ul0.54	0.45	0.47	0.57
c19_title	0.49	0.75	\ul0.77	0.90

Table 3. Generalization improvement with KMP for model trained on ‘rumor’

Trained on ‘rumor’
Testing Dataset	Approach
Testing Dataset	SB	SE	FT	FT+KMP
cov_fn	\ul0.76	0.48	0.75	0.77
k_short	0.49	\ul0.52	0.52	0.54
coaid	0.17	0.17	\ul0.40	0.76
cq	0.47	0.59	0.42	\ul0.58
k_long	0.59	0.52	0.43	\ul0.53
rumor	0.70	0.66	\ul0.83	0.86
c19_text	0.17	0.57	\ul0.58	0.73
miscov	0.52	0.45	\ul0.54	0.54
c19_title	0.74	0.57	0.81	\ul0.76

3.4. KMeans-Proxy Results

We now show results from using KMeans-Proxy as a reject option in Table 2 and Table 3. With rejection, we can increase generalization accuracy on unseen data. This is a faster approach than domain adaptation, since proxies are updated during training. Further, it is a plug-and-play solution, allowing for faster iteration on overall model design.

With KMeans-Proxy, we are able to improve generalization performance across the board. Here, we compare models trained on ‘coaid’ and ‘rumor’ in Table 2 and Table 3, respectively. Models are compared across static backbone (SB), static embedding (SE), fine-tuned (FT), and fine-tuned with KMeans-Proxy (FT+KMP).

For models trained on ‘coaid’ (in Table 2) and tested on all datasets, incorporating KMeans-Proxy improves generalization performance. In each case, FT+KMP is either the best or the runner-up model by at most 0.05 f1 f1 points. We see similar result for models trained on ‘rumor’ in Table 3, where KMeans-Proxy is either the best model or runner up for every testing dataset.

\IfEndWith

Choice of Proxy Factor.Choice of Proxy FactorChoice of Proxy Factor. Increasing the proxy factor leads to better generalization performance. Table 4 shows performance of a model trained on ‘c19_text‘ that has poor generalization without KMeans-Proxy (see Figure 4). As we increase the proxy factor, we gain better generalization across testing datasets. We test with different proxy factors and compare generalization performance of each model. We find that increasing the proxy factor leads to small, but measurable increase in accuracy.

Table 4. Impact of changing proxy factor: increasing the proxy factor increases accuracy, since more proxies allow tighter bounds on local coverage estimates.

Testing Dataset	Trained on c19_text
Testing Dataset	FT	k=1	k=2	k=3	k=5	k=10
cov_fn	0.44	0.50	0.54	0.58	0.58	0.58
k_short	0.59	0.70	0.73	0.73	0.73	0.75
coaid	0.76	0.88	0.84	0.89	0.89	0.90
cq	0.51	0.56	0.58	0.58	0.60	0.63
k_long	0.60	0.70	0.72	0.73	0.73	0.73
rumor	0.47	0.45	0.51	0.58	0.58	0.67
c19_text	0.97	0.98	0.99	0.99	0.99	0.99
miscov	0.48	0.45	0.44	0.53	0.58	0.58
c19_title	0.58	0.61	0.64	0.69	0.68	0.73

3.5. Discussion

There are several observations we can make from our generalization studies and KMeans-Proxy experiments. \IfEndWithGeneralization.GeneralizationGeneralization. For fake news detection, fine-tuned models must be used carefully to take advntage of learned parameters. As we showed in the confusion matrices, fine-tuning improves performance only on subsets of unseen data. These subsets are regions of the data space where the unseen data overlaps with training data. On completely new regions of the data space, fine-tuned models make mistakes. These mistakes are because of label overlap.

We must make a distinction between label and data overlap. Data overlap means a model has coverage on the unseen data, and can make predictions with higher confidence. Label coverage, as we showed in Fig, indicates where different labels occur close to each other in the embedding space. Both can coincide: unseen data points can have both data and label overlap. For these points, fine-tuned models that have better captured a local region with training data are better poised to provide high-confidence labels.

\IfEndWith

KMeans-Proxy.KMeans-ProxyKMeans-Proxy. KMeans-Proxy allows us to identify these regions. With KMeans-Proxy, we partition the data space into clusters representing model coverage and labels. Our inclusion of the proxy factor $k$ , where we create $k$ clusters for each class label, allows fine-grained partitioning of the embedding space. This means we can better capture local characteristics of the embedding space (Chen et al., 2022). In our experiments, we focus on 2 such characteristics: (i) whether the label for an unseen point matches the label for nearest proxy, and (ii) whether this unseen point is within one standard-deviation radius of the proxy. In our experiments, we show that using these provides improvements in generalizing to unseen data points.

Clearly, there is significant progress to be made in capturing local characteristics. For example, when using an ensemble of fine-tuned models, local smoothness (Urner and Ben-David, 2013; Chen et al., 2022) can be computed for each non-abstaining model to rank them on coverage. There may also be advantages in using dynamic proxy allocation. If prior class balance is known, then we could use a class-specific proxy factor.

4. Conclusion

In this paper, we have presented generalizability experiments and KMeans-Proxy. We perform generalization studies across 9 fake news datasets using several transformer-based fake news detector models. Our generalizability experiments show that fine-tuned models generalize well to unseen data when there is overlap between unseen and training data. On unseen data that does not overlap, fine-tuned models make mistakes due to poor coverage, label flipping, and concept drift.

Using our observations and recent research into local embedding regions, we develop and present KMeans-Proxy, a simple online KMeans clusterer paired with a proxy factor. With KMeans-Proxy, we partition the embedding space into local regions and use local characteristics to create a reject option for models. We show that KMeans-Proxy improves generalization accuracy for fine-tuned models across all 9 fake news datasets. We welcome future research in this area to better explore the generalizability and fine-tuning tradeoff.

References

(1)
Agarwal (2020) Isha Agarwal. 2020. Covid 19 Fake News Dataset. (6 2020). https://doi.org/10.6084/m9.figshare.12489293.v1
Bang et al. (2021) Yejin Bang, Etsuko Ishii, Samuel Cahyawijaya, Ziwei Ji, and Pascale Fung. 2021. Model generalization on covid-19 fake news detection. In International Workshop on Combating Hostile Posts in Regional Languages during Emergency Situation. Springer, 128–140.
Bommasani et al. (2021) Rishi Bommasani, Drew A Hudson, Ehsan Adeli, Russ Altman, Simran Arora, Sydney von Arx, Michael S Bernstein, Jeannette Bohg, Antoine Bosselut, Emma Brunskill, et al. 2021. On the opportunities and risks of foundation models. arXiv preprint arXiv:2108.07258 (2021).
Brinkrolf and Hammer (2018) Johannes Brinkrolf and Barbara Hammer. 2018. Interpretable machine learning with reject option. at-Automatisierungstechnik 66, 4 (2018), 283–290.
Cardillo and L. Warren (2016) Marcel Cardillo and Dan L. Warren. 2016. Analysing patterns of spatial and niche overlap among species at multiple resolutions. Global Ecology and Biogeography 25, 8 (2016), 951–963. https://doi.org/10.1111/geb.12455
Chen et al. (2021) Ben Chen, Bin Chen, Dehong Gao, Qijin Chen, Chengfu Huo, Xiaonan Meng, Weijun Ren, and Yang Zhou. 2021. Transformer-based language model fine-tuning methods for COVID-19 fake news detection. In International Workshop on Combating Hostile Posts in Regional Languages during Emergency Situation. Springer, 83–92.
Chen et al. (2022) Mayee F Chen, Daniel Y Fu, Dyah Adila, Michael Zhang, Frederic Sala, Kayvon Fatahalian, and Christopher Ré. 2022. Shoring Up the Foundations: Fusing Model Embeddings and Weak Supervision. arXiv preprint arXiv:2203.13270 (2022).
Cheng et al. (2021) Mingxi Cheng, Songli Wang, Xiaofeng Yan, Tianqi Yang, Wenshuo Wang, Zehao Huang, Xiongye Xiao, Shahin Nazarian, and Paul Bogdan. 2021. A COVID-19 Rumor Dataset. Frontiers in Psychology 12 (2021), 1566.
Cui and Lee (2020) Limeng Cui and Dongwon Lee. 2020. Coaid: Covid-19 healthcare misinformation dataset. arXiv preprint arXiv:2006.00885 (2020).
Das et al. (2021) Sourya Dipta Das, Ayan Basak, and Saikat Dutta. 2021. A heuristic-driven uncertainty based ensemble framework for fake news detection in tweets and news articles. Neurocomputing (2021).
Devlin et al. (2018) Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. 2018. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. arXiv preprint arXiv:1810.04805 (2018).
Enders et al. (2020a) Adam M Enders, Joseph E Uscinski, Casey Klofstad, and Justin Stoler. 2020a. The different forms of COVID-19 misinformation and their consequences. The Harvard Kennedy School Misinformation Review (2020).
Enders et al. (2020b) Adam M Enders, Joseph E Uscinski, Casey Klofstad, and Justin Stoler. 2020b. The different forms of COVID-19 misinformation and their consequences. The Harvard Kennedy School Misinformation Review (2020).
Gama et al. (2014) João Gama, Indrė Žliobaitė, Albert Bifet, Mykola Pechenizkiy, and Abdelhamid Bouchachia. 2014. A survey on concept drift adaptation. ACM computing surveys (CSUR) 46, 4 (2014), 1–37.
Geifman and El-Yaniv (2019) Yonatan Geifman and Ran El-Yaniv. 2019. Selectivenet: A deep neural network with an integrated reject option. In International Conference on Machine Learning. PMLR, 2151–2159.
Hendrickx et al. (2021) Kilian Hendrickx, Lorenzo Perini, Dries Van der Plas, Wannes Meert, and Jesse Davis. 2021. Machine Learning with a Reject Option: A survey. arXiv preprint arXiv:2107.11277 (2021).
Hossain et al. (2020) Tamanna Hossain, Robert L Logan IV, Arjuna Ugarte, Yoshitomo Matsubara, Sean Young, and Sameer Singh. 2020. COVIDLies: Detecting COVID-19 misinformation on social media. (2020).
Hulburd (2020) Eric Hulburd. 2020. Exploring BERT Parameter Efficiency on the Stanford Question Answering Dataset v2.0. (2020). https://doi.org/10.48550/ARXIV.2002.10670
Jiao et al. (2021) Xiaoqi Jiao, Yichun Yin, Lifeng Shang, Xin Jiang, Xiao Chen, Linlin Li, Fang Wang, and Qun Liu. 2021. LightMBERT: A Simple Yet Effective Method for Multilingual BERT Distillation. https://doi.org/10.48550/ARXIV.2103.06418
Kaliyar et al. (2021) Rohit Kumar Kaliyar, Anurag Goswami, and Pratik Narang. 2021. MCNNet: generalizing Fake News Detection with a Multichannel Convolutional Neural Network using a Novel COVID-19 Dataset. In 8th ACM IKDD CODS and 26th COMAD. 437–437.
Kou et al. (2021) Ziyi Kou, Lanyu Shang, Yang Zhang, Christina Youn, and Dong Wang. 2021. Fakesens: A social sensing approach to covid-19 misinformation detection on social media. In 2021 17th International Conference on Distributed Computing in Sensor Systems (DCOSS). IEEE, 140–147.
Kouw and Loog (2018) Wouter M Kouw and Marco Loog. 2018. An introduction to domain adaptation and transfer learning. arXiv preprint arXiv:1812.11806 (2018).
Lan et al. (2019) Zhenzhong Lan, Mingda Chen, Sebastian Goodman, Kevin Gimpel, Piyush Sharma, and Radu Soricut. 2019. Albert: A lite bert for self-supervised learning of language representations. arXiv preprint arXiv:1909.11942 (2019).
Lazer et al. (2014) David Lazer, Ryan Kennedy, Gary King, and Alessandro Vespignani. 2014. Google Flu Trends still appears sick: An evaluation of the 2013-2014 flu season. Available at SSRN 2408560 (2014).
Lee et al. (2019) Jaejun Lee, Raphael Tang, and Jimmy Lin. 2019. What Would Elsa Do? Freezing Layers During Transformer Fine-Tuning. (2019). https://doi.org/10.48550/ARXIV.1911.03090
Li et al. (2021) Yichuan Li, Kyumin Lee, Nima Kordzadeh, Brenton Faber, Cameron Fiddes, Elaine Chen, and Kai Shu. 2021. Multi-Source Domain Adaptation with Weak Supervision for Early Fake News Detection. In 2021 IEEE International Conference on Big Data (Big Data). IEEE, 668–676.
Memon and Carley (2020) Shahan Ali Memon and Kathleen M Carley. 2020. Characterizing covid-19 misinformation communities using a novel twitter dataset. arXiv preprint arXiv:2008.00791 (2020).
Merchant et al. (2020) Amil Merchant, Elahe Rahimtoroghi, Ellie Pavlick, and Ian Tenney. 2020. What Happens To BERT Embeddings During Fine-tuning? https://doi.org/10.48550/ARXIV.2004.14448
Moon et al. (2019) Taesun Moon, Parul Awasthy, Jian Ni, and Radu Florian. 2019. Towards Lingua Franca Named Entity Recognition with BERT. (2019). https://doi.org/10.48550/ARXIV.1912.01389
Movshovitz-Attias et al. (2017) Yair Movshovitz-Attias, Alexander Toshev, Thomas K Leung, Sergey Ioffe, and Saurabh Singh. 2017. No fuss distance metric learning using proxies. In Proceedings of the IEEE International Conference on Computer Vision. 360–368.
Müller et al. (2020) Martin Müller, Marcel Salathé, and Per E Kummervold. 2020. Covid-twitter-bert: A natural language processing model to analyse covid-19 content on twitter. arXiv preprint arXiv:2005.07503 (2020).
Mutlu et al. (2020) Ece C Mutlu, Toktam Oghaz, Jasser Jasser, Ege Tutunculer, Amirarsalan Rajabi, Aida Tayebi, Ozlem Ozmen, and Ivan Garibay. 2020. A Stance Data Set on Polarized Conversations on Twitter about the Efficacy of Hydroxychloroquine as a Treatment for COVID-19. Data in Brief (2020), 106401.
Orr et al. (2021) Laurel Orr, Karan Goel, and Christopher Ré. 2021. Data management opportunities for foundation models. In 12th Annual Conference on Innovative Data Systems Research.
Patel (2021) Sameer Patel. 2021. Covid-19 Fake News Dataset (Kaggle). (2021). https://www.kaggle.com/code/therealsampat/fake-news-detection/
Pu et al. (2020) Calton Pu, Abhijit Suprem, Rodrigo Alves Lima, Aibek Musaev, De Wang, Danesh Irani, Steve Webb, and Joao Eduardo Ferreira. 2020. Beyond artificial reality: Finding and monitoring live events from social sensors. ACM Transactions on Internet Technology (TOIT) 20, 1 (2020), 1–21.
Quinn et al. (2021) Emma K Quinn, Sajjad S Fazel, and Cheryl E Peters. 2021. The Instagram infodemic: cobranding of conspiracy theories, coronavirus disease 2019 and authority-questioning beliefs. Cyberpsychology, Behavior, and Social Networking 24, 8 (2021), 573–577.
Ratner et al. (2017) Alexander Ratner, Stephen H Bach, Henry Ehrenberg, Jason Fries, Sen Wu, and Christopher Ré. 2017. Snorkel: Rapid training data creation with weak supervision. In Proceedings of the VLDB Endowment. International Conference on Very Large Data Bases, Vol. 11. NIH Public Access, 269.
Rühling Cachay et al. (2021) Salva Rühling Cachay, Benedikt Boecking, and Artur Dubrawski. 2021. End-to-End Weak Supervision. Advances in Neural Information Processing Systems 34 (2021).
Serrano et al. (2020) Juan Carlos Medina Serrano, Orestis Papakyriakopoulos, and Simon Hegelich. 2020. NLP-based feature extraction for the detection of COVID-19 misinformation videos on YouTube. In Proceedings of the 1st Workshop on NLP for COVID-19 at ACL 2020.
So et al. (2022) Geelon So, Gaurav Mahajan, and Sanjoy Dasgupta. 2022. Convergence of online k-means. In International Conference on Artificial Intelligence and Statistics. PMLR, 8534–8569.
Suprem et al. (2020) Abhijit Suprem, Joy Arulraj, Calton Pu, and Joao Ferreira. 2020. Odin: automated drift detection and recovery in video analytics. arXiv preprint arXiv:2009.05440 (2020).
Suprem et al. (2019) Abhijit Suprem, Aibek Musaev, and Calton Pu. 2019. Concept drift adaptive physical event detection for social media streams. In World Congress on Services. Springer, 92–105.
Urner and Ben-David (2013) Ruth Urner and Shai Ben-David. 2013. Probabilistic lipschitzness a niceness assumption for deterministic labels. In Learning Faster from Easy Data-Workshop NIPS, Vol. 2. 1.
Wahle et al. (2022) Jan Philip Wahle, Nischal Ashok, Terry Ruas, Norman Meuschke, Tirthankar Ghosal, and Bela Gipp. 2022. Testing the generalization of neural language models for COVID-19 misinformation detection. In International Conference on Information. Springer, 381–392.
Walambe et al. (2022) Rahee Walambe, Ananya Srivastava, Bhargav Yagnik, Mohammed Hasan, Zainuddin Saiyed, Gargi Joshi, and Ketan Kotecha. 2022. Explainable Misinformation Detection Across Multiple Social Media Platforms. arXiv preprint arXiv:2203.11724 (2022).
Weinzierl et al. (2021) Maxwell Weinzierl, Suellen Hopfer, and Sanda M Harabagiu. 2021. Misinformation adoption or rejection in the era of covid-19. In Proceedings of the International AAAI Conference on Web and Social Media (ICWSM), AAAI Press.
Wern Teh et al. (2020) Eu Wern Teh, Terrance DeVries, and Graham W Taylor. 2020. ProxyNCA++: Revisiting and Revitalizing Proxy Neighborhood Component Analysis. arXiv e-prints (2020), arXiv–2004.
Yang et al. (2015) Shihao Yang, Mauricio Santillana, and Samuel C Kou. 2015. Accurate estimation of influenza epidemics using Google search data via ARGO. Proceedings of the National Academy of Sciences 112, 47 (2015), 14473–14478.
Žliobaitė (2010) Indrė Žliobaitė. 2010. Learning under concept drift: an overview. arXiv preprint arXiv:1010.4784 (2010).