EV-Planner: Energy-Efficient Robot Navigation via Event-Based Physics-Guided Neuromorphic Planner
Abstract
Vision-based object tracking is an essential precursor to performing autonomous aerial navigation in order to avoid obstacles. Biologically inspired neuromorphic event cameras are emerging as a powerful alternative to frame-based cameras, due to their ability to asynchronously detect varying intensities (even in poor lighting conditions), high dynamic range, and robustness to motion blur. Spiking neural networks (SNNs) have gained traction for processing events asynchronously in an energy-efficient manner. On the other hand, physics-based artificial intelligence (AI) has gained prominence recently, as they enable embedding system knowledge via physical modeling inside traditional analog neural networks (ANNs). In this letter, we present an event-based physics-guided neuromorphic planner (EV-Planner) to perform obstacle avoidance using neuromorphic event cameras and physics-based AI. We consider the task of autonomous drone navigation where the mission is to detect moving gates and fly through them while avoiding a collision. We use event cameras to perform object detection using a shallow spiking neural network in an unsupervised fashion. Utilizing the physical equations of the brushless DC motors present in the drone rotors, we train a lightweight energy-aware physics-guided neural network (PgNN) with depth inputs. This predicts the optimal flight time responsible for generating near-minimum energy paths. We spawn the drone in the Gazebo simulator and implement a sensor-fused vision-to-planning neuro-symbolic framework using Robot Operating System (ROS). Simulation results for safe collision-free flight trajectories are presented with performance analysis, ablation study and potential future research directions.
Index Terms:
Event cameras, Neuromorphic vision, Physics-based AI, Spiking Neural Networks, Vision-based navigationI Introduction
For performing vision-based robot navigation [1], object tracking is a fundamental task. As navigation environments become increasingly challenging [2] (due to increased demands on robot speed or to fly under reduced lighting conditions), the need for newer vision sensors arises. Biologically inspired event cameras or Dynamic Vision Sensors (DVS) [3, 4, 5, 6], which are capable of triggering events in response to changes in the logarithm of pixel intensities past a certain threshold, have emerged as a promising candidate. Event cameras are relatively immune to problems such as motion blur, can withstand higher temporal resolution ( vs ), operating frequencies with wider dynamic illumination ranges ( vs ), and consume lower power ( vs ), compared to traditional frame-based cameras [7]. Consequently, there has been considerable interest in the autonomous systems community, in using event cameras as vision sensors, for navigation purposes. Inspired by the neuronal dynamics observed in biological brains, spiking neurons, specifically Leaky Integrate and Fire (LIF) neurons [8] have been designed for leveraging temporal information processing – quite similar to the signals produced by event cameras. Furthermore, the asynchronous event-driven nature of spiking neuron firing makes it a natural candidate for handling asynchronous events [9]. A recent work [10] utilized a shallow spiking architecture for spatio-temporal event processing to perform low latency object detection for autonomous navigation systems.
On the other hand, physics-based machine learning/artificial intelligence [11, 12, 13, 14] is gaining momentum, as they enable encoding prior knowledge of physical systems while learning from data. In robotic systems, symbolic dynamics have been used traditionally to describe physical properties (of both systems and environments) [15]. Works on predictive control [16, 17, 18, 19] have incorporated such physics-encoded prior inside neural network pipelines, and have shown to present advantages in terms of training efficiency (data and hence compute) as well as inference (latency and therefore energy). Moreover, adding physical knowledge as priors reduces laborious dataset preparation efforts [20] and makes neural networks more robust and interpretable – a quality immensely desired by the AI community in mission-critical scenarios.
Considering today’s actuators with a supply, the average instantaneous power for a simulated Parrot Bebop2 is (see Section III-B), while the maximum hovering time without any maneuver is minutes for a battery [21]. For agile navigation tasks, the power increases, further reducing the flight time. To that effect, we present EV-Planner – an event-based physics-guided neuromorphic planner to perform autonomous navigation energy-efficiently using neuromorphic event cameras and physics-based AI. Exploiting the energy-efficient nature of spike-based computation while efficiently capturing the temporal event information, and harnessing the benefits of physics-based simulations in training neural networks, the main goal of this work is to perform energy-efficient generalizable planning using a sensor fusion of event and depth cameras for small drones. We consider the task of autonomous quadrotor navigation where the mission is to detect moving gates and fly through them without collisions.
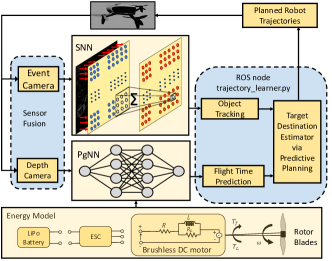
Figure 1 illustrates the logical overview of the EV-Planner framework. We consider two sensors – an event camera and a depth camera. The Spiking Neural Network (SNN) block detects objects using event camera inputs. The Physics-guided Neural Network (PgNN) block learns to predict near-optimal trajectory times to the target destination from the depth input. The main contributions of this work are:
-
•
We use event cameras to perform object detection in a 3D environment using a shallow low-latency spiking neural architecture in an unsupervised fashion (Section III-A).
-
•
Utilizing the physical equations of the brushless DC motors present in the drone rotors, we train a PgNN with depth camera inputs. The pre-trained network predicts near-optimal flight times responsible for generating near-minimum energy paths during inference (Section III-B).
- •
- •
To the best of our knowledge, this is the first work that uses event-based spike-driven neuromorphic vision coupled with physics-based AI for vision-based autonomous navigation. This results in a hybrid neuro-symbolic network architecture for energy-efficient generalizable robot planning.
II Background and Related Work
We consider vision-based autonomous navigation systems which use event-based perception for obstacle avoidance and physics-guided robot learning for planning and control. Relevant research pursuits to achieve this are briefly discussed.
II-A Event-based Robot Perception
Event cameras such as Dynamic Vision Sensors (DVS) capture asynchronous changes in the logarithm of light intensities. Events are encoded as arrayed tuples of event instances, given as across time-steps. Each discrete event is represented as , where is the location of the camera pixel, represents the polarity (or sign-change of logarithm of intensity), and corresponds to -th time-step.
Early efforts on event-based object detection applied simple kernels on event outputs to capture salient patterns [23, 24, 25].
Although these works paved the way for future endeavors, they failed to capture events generated by the background. To overcome this, [26] proposed a motion compensation scheme using ego-motion filtering to eliminate background events.
For object-tracking, [27] utilized both frames as well as event cameras. These hybrid techniques were computationally expensive as they relied on frame inputs to detect objects. Works in [28, 29] estimate time-to-collision using events.
Related to our work, event cameras have been mounted on drones for dynamic obstacle dodging [30]. However, optical flow and segmentation using learning-based techniques require bulky neural networks with lots of parameters. In this work, we focus on object detection for tracking using spiking neurons [10] – achievable with low-latency neural networks.
| Sensor Modality | Available Literature |
|---|---|
| Events | [10, 24, 25, 26, 31, 32] |
| Depth | [33, 34, 35, 36] |
| Events + Depth | EV-Planner |
Why Sensor Fusion of Events and Depth? In order to track an object in a 3D environment, the notion of depth is of utmost importance. As shown in Table I, there are works that either 1) estimate depth using non-depth sensors[10, 24, 25, 26, 31, 32] or 2) use depth sensors[33, 34, 35, 36]. The absence of an event sensor makes sensing and perception energy-expensive. On the other hand, the absence of a depth sensor will require estimating depth adding to the processing delay of the perception algorithm. Hence, in order to limit the overheads of perception delays (which is responsible for real-time object tracking), it is imperative that there are dedicated sensors for both events and depth. While adding sensors increases the robot payload, future designs will consider embedding multiple sensors into a single device. The reduced perception time will make the design more energy-efficient, rendering sensor fusion a promising design paradigm.
II-B Physics-Based Robot Learning for Planning/Control
Physics-based AI shows promise as these approaches embed system knowledge via physical modeling inside neural networks, making them robust and interpretable. Traditionally, in robotic systems, symbolic methods have been used for describing physical properties as they are fast and accurate [15, 37]. For controlling dynamical systems, the work in [13] added the provision of control variables to physics-informed neural networks. The work in [18] has showcased the advantages of using physical priors in control tasks. The research presented in [16] used [13] for controlling multi-link manipulators, while the work in [17] extended the previous framework for trajectory tracking of drones subjected to uncertain disturbances. The authors in [19] used neural ordinary differential equations (ODEs) for drones. While all these works use physics to solve differential equations, the same principle can be applied to add non-ODE (or non-PDEs) as soft constraints to neural network training, which is explored in this work. Incorporating physics into neural networks as a hard constraint still remains unexplored and is beyond the scope of this work.
III EV-Planner
We present EV-Planner – an event-based physics-guided neuromorphic planner to perform obstacle avoidance using neuromorphic event cameras and physics-based AI. For object tracking, we use event-based low-latency SNNs and train a lightweight energy-aware neural network with depth inputs. This makes our design loosely coupled with no interaction between the SNN and PgNN block (see Figure 1). Information about the current object position (via SNN block) and estimated trajectory time (via PgNN block) is consumed by a symbolic program (a ROS node2) for predictive planning.
III-A Event-based Object Tracking via Spiking Neural Network
Due to a lack of photo-metric features such as light intensity and texture in event streams, traditional computer vision algorithms fail to work on events. Hence, we use a modified version of [10] which utilizes the inherent temporal information in the events with the help of a shallow architecture of spiking LIF neurons. The SNN can separate events based on the object’s speed (present in the robot’s field of view).
III-A1 Filtering out objects based on Speed
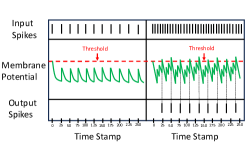
The network architecture used for filtering objects based on their motion consists of a single spike-based neural layer, whose parameters are fine-tuned to directly represent the speed of the moving object. The LIF neuron model [8] has a membrane potential () and a leak factor (). At first, the initial membrane potential () and the threshold value () get initialized. Next, according to equation [1] for each time step () the weighted sum of the inputs () gets stored in . Finally, if at any instance of time, the stored exceeds then the neuron produces an output spike and resets .
| (1) |
In our approach hyper-parameters like and are fine-tuned to select nearby input spikes during any given instance of time. Figure 2 demonstrates the difference in the output spikes generated from the neuron according to the frequency of the input events. As shown, the frequency of the generated events is directly proportional to the speed of the moving object. Exploiting this property of spiking neurons and event data, we consequently design an SNN capable of filtering out a particular object of interest, based on speed.
III-A2 Finding Center of the Bounding box
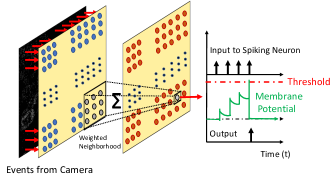
To detect an object, the initial step involves connecting the output pixels from the event camera to the spiking neurons. Then, we apply a weighted sum () from a neighborhood of pixels and pass that as input to the spiking neuron. Here, the neurons connected to the specific neighborhood will register more than one input pixel every consecutive time step. This enables the SNN with the ability to identify pixels as fast-moving. In the next step, we locate the minimum () and maximum () pixel values in two dimensions and subsequently draw the bounding box. Finally, we obtain the center coordinates of the moving object using Eqn. (2).
| (2a) | |||
| (2b) | |||
Figure 3 depicts our network architecture. We selected a reasonable weighted neighborhood size () (see Section IV) as input to every spiking neuron. The weights for the neighborhood were normalized to obtain a summation value close to one. Note that the SNN mentioned above detects the moving object. But we still need to isolate the input events which represent the object of interest. Therefore, after detection, we recover the input events around the neighborhood of the spiking neuron output. Hence, the SNN works asynchronously to find the output spikes and recover the inputs from the previous time step (one-time step delay). Generally, after separating the objects based on the movement speed, their corresponding events are spatially grouped together using some clustering technique for predicting the object class. However, in this work, we only consider a single moving object. Hence, our current SNN-based design does not require any spatial clustering technique, which reduces the latency and energy overheads of our object detection and tracking. Please note that the SNN is scene-independent and can be deployed in various scenarios with minimal fine-tuning. Figure 4 illustrates the output of the event-based object (gate) tracking using SNN, situated at different depths (see Section V-A for more details).

III-B Physics-Based Robot Modelling
III-B1 Energy model
We model the actuation energy of the drone in flight by considering an electrical model of the LiPo battery-powered brushless DC (BLDC) motors of the rotor propellers [38]. Figure 5 represents the equivalent circuit of each BLDC motor by considering the resistive and inductive windings. The energy for a particular flight path requires overcoming the motor and load frictions (given by the coefficients and ). The instantaneous motor current is:
| (3) |
is the torque constant. and are the motor and load friction torques respectively. represents the viscous damping coefficient. For the BLDC motors of drone propellers, we can safely neglect and .
| (4) |
is the number of propeller blades, is the mass of the blade and is the propeller radius. is the clearance between the blade and motor.
| Parameters | Values |
|---|---|
| Motor Resistance () | ohm |
| Supply Voltage () | V |
| Maximum Motor Speed | rpm |
| Motor Friction Torque () | Nm |
| Aerodynamic Drag Coefficient () | |
| Viscous Damping Coefficient () | Nm |
| Motor Voltage Constant () | V/rpm |
| Motor Moment of Inertia () | kgm2 |
| Number of blades () | |
| Mass of blade () | kg |
| Radius of blade () | m |
| Blade clearance () | m |
The motor voltage is as follows:
| (5) |
and denote the resistive and inductive impedances of the phase windings respectively. represents the motor voltage constant. We also neglect the electronic speed controller (ESC) voltage drops and any non-idealities present in the LiPo battery. For small drones (which we assume in this work), the propellers have direct connections with the shafts. At steady-state operation, the motor voltage becomes:
| (6) |
For flight from time to , then the total actuation energy of the flight path for all practical purposes can be written as:
| (7) |
Using equations (3) and (6), the energy expression becomes:
| (8) | |||
where,
| (9a) | |||
| (9b) | |||
| (9c) | |||

This only considers linear motion along one direction.
Using the expression given in equation (8), and plugging in the constant values given in equations (9), we are thus able to calculate the energy for a particular trajectory up to time . Given a certain distance away from a target destination (depth), an energy-efficient planner should be able to approximately estimate the flight time that would minimize the energy. We utilize the knowledge obtained through the aforementioned equations by simulating several trajectories to reach targets situated at different depths.
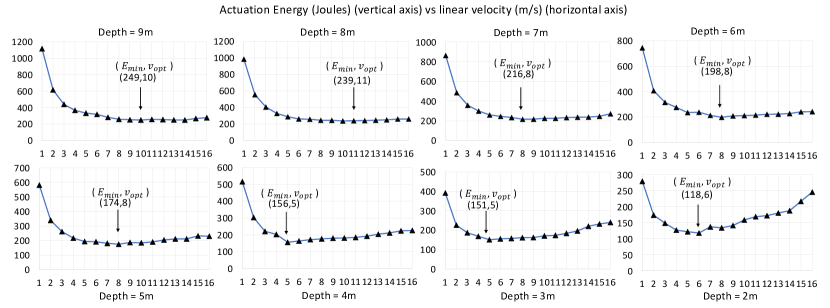
III-B2 Energy characterization as a function of velocity
We implemented the energy model using the values in Table II. We present key insights into our physics-guided simulation. Figure 7 presents the actuation energy for traversing different depths. Using our physics-guided simulation, we report an average instantaneous power of for a battery. For each depth, we swipe the linear velocity as the control variable from m/s to m/s (the top speed of the drone in this study) in steps of m/s. We observe that the energy is the highest when the robot speed is the minimum. The time taken by the drone to reach the destination varies inversely with speed. As a consequence, if we use Eqn. (8) to estimate the energy, then the effect of time dominates at a lower speed for which the energy adds up. With increasing speed, the energy burned drops dramatically in the beginning due to a reduction in flight time. Beyond a certain speed, the energy again increases. This is because, for higher speeds, the motor currents drawn from the battery increases, resulting in an increase in instantaneous power and consequently energy. We observe there is a sweet spot for a near-optimal velocity which yields the least energy for a particular trajectory. This establishes the need for an interpolation a near-optimal velocity, given the target depth.
III-B3 Physics-Guided Neural Network
We collect several trajectories as part of our training dataset by flying the drone across different depths and by varying the linear velocity as shown in Figure 7. A vanilla ANN can be trained with several such depth-velocity pairs. However, the ANN will have no knowledge about the underlying source data distribution.
| (10a) | |||
| (10b) | |||
As shown in Equation (10a), we fit 5th-order polynomial curves to the energy-velocity profile obtained from the simulations, for each depth. To approximately evaluate the optimal velocity for near-minimum energy, we equate the derivative of the fitted polynomial to zero as shown in Eqn. (10b). As shown in Table III, for each training data point, the expression from Eqn. (10b) using the corresponding polynomial coefficients is added as an additional regularization term in the loss function. While a mid-range value of will cover most cases, addition of physical equations makes the model more interpretable. We use the standard mean-square error loss along with the additional physical constraints:
| (11) |
is the number of training samples. is the desired velocity obtained from the groundtruth, while is the velocity the network learns. is the regularization coefficient.
| Depth | Velocity | Constraint |
| = 0 | ||
| ….. | …. | …. |
| = 0 |
| (12) |
Note, the output of the PgNN is a velocity. Using Eqn. (12), we calculate an approximate trajectory time using which we estimate the position of the moving gate, in the future. Also, the training set is small because we are constraining the training via physical equations. This enhances sample-efficiency which accelerates training. While the training set consists of a similar range of depths as seen during inference, the inference can have a depth value not available in training data, making the proposed method superior than a regression-less lookup-based approach.
III-C Planning Robot Trajectories
III-C1 Motion Estimation of Moving Gate
As shown in Figure 7, we assume the moving gate has a linear velocity along the Y axis as . We use our SNN-based object tracking to estimate . Consider the position of the gate along the Y axis to be at any given instant, obtained from the object tracker. For a sensing interval of , let the position of the same point in the gate after be . Then, to estimate the instantaneous velocity of the gate, we use the expression given:
| (13) |
III-C2 Symbolic Planning
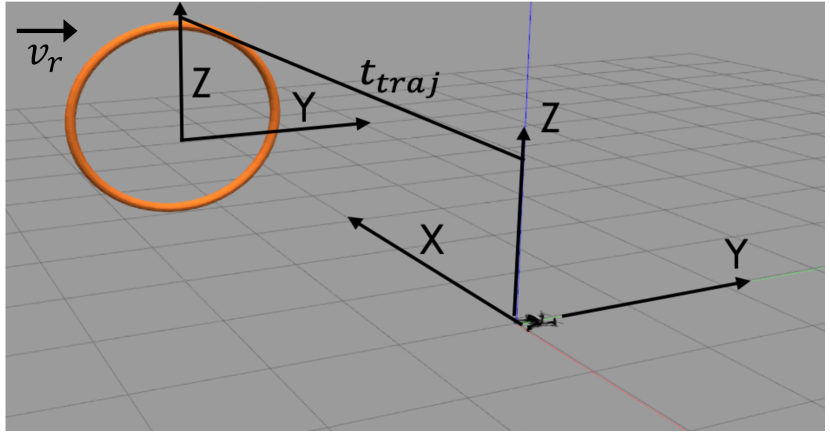
We assume the gate is constrained within distances and , beyond which the gate reverses the direction of motion. This is the only prior knowledge that we use during inference. Algorithm 1 presents the pseudo-code of our symbolic predictive planner. The planner accepts the variables (trajectory time) and as the input arguments along with and . , are the outputs from the SNN and is the output from the PgNN. The information from the two networks are now combined as discussed next. The algorithm outputs – the desired destination of the robot after , which will enable collision-free gate crossing. The distance traversed by the gate is computed during the trajectory time (Line 3). Also, the distance (which is the distance of the gate from the nearest end ( or ) ) is computed by considering the different sub-cases. If the gate moves right (line 5), then we consider the cases where the gate is in the positive Y axis (Line 6), or negative Y axis (Line 9). Accordingly, the value of is evaluated (Line 7 or Line 10). If , then the gate will change the direction of motion (from right to left), and is computed (Line 15). If , then the gate keeps moving right, and is computed accordingly (Line 18). Similarly, if the gate is detected to be moving left (Line 21), is evaluated symbolically by stepping through the hard-coded rules (Lines 22 - 36). Once is obtained, we use the minimum jerk trajectory [39] which is optimized to make sure the amount of current drawn from the battery is the lowest possible which results in almost zero rate of change of acceleration. Consequently, the planned trajectory burns near-minimum motor currents for the concerned navigation task. Note, that during PgNN training, the predicted velocity is along the depth axis (path AB = depth in Figure 8). However, during inference, there will be a component of the drone velocity along the Y axis ( in Figure 8) in the same direction as , as the target destination is C which depends on the speed of the moving ring ( which cannot be known in advance). The predicted drone velocity is only a proxy to calculate (see Eqn. 12). However, a lower value of will reduce the difference between paths AB and AC, making the actuation-energy near-minimum. Also, note, the flight path has a parabolic nature, but for the sake of explanation we simplified them as straight lines in Figure 8. While it is beyond the scope of this work to mathematically derive lower bounds, our method is reasonably energy-efficient (see Sections V-C, V-D and V-E).
| SNN Parameters | Physics-guided ANN Parameters | ||
|---|---|---|---|
| Kernel (W) Size | Number of Layers | ||
| W[0,0,1,1] | Neurons per layer | [] | |
| Leak Factor () | Coefficient () | ||
| Threshold () | Epochs | ||
IV Methodology
We implemented the SNN for event-based tracking using SNNTorch [40], whereas the physics-guided ANN was implemented using Tensorflow [41]. For the PgNN, we also used batch normalization after each layer. The moving gate was created using blender [42]. To integrate the proposed planner with a controller, we used the RotorS simulator [22] and spawned the drone using the Gazebo physics engine [43]. Table IV mentions the parameters used for the networks.
V Experimental Results
As a comparative scheme, we implemented an equivalent fusion-less physics-guided planner. It uses a depth camera to track the gate as well. We call this the Depth-Planner.
V-A Object Tracking
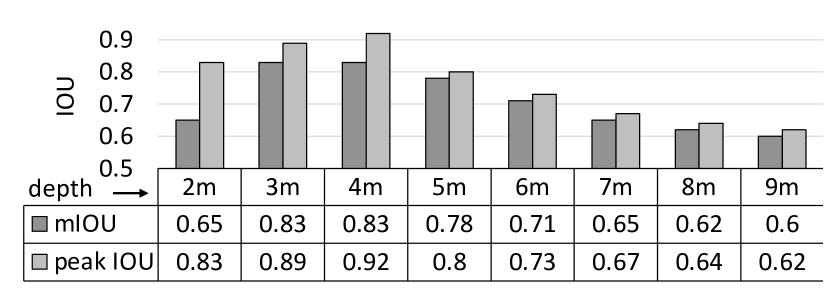
Figure 10 illustrates the mean and peak intersection-over-union (IOU) values for the object tracking using event-based SNN for different depths. The corresponding visual representations are shown in Figure 4. For depth m, the IOU is lesser than depths m or m (where we observe best tracking). At a depth less than m, the moving gate (which has a diameter of m) comes too near to fit within the viewing window (see Figure 4). For depth greater than m, the performance degrades. The success rate of the overall design reduces with increased perception overhead. Hence, we only report performance statistics up to a depth of m subsequently.
V-B Success Rate
Figure 10 illustrates in a time-series snapshot the Parrot Bebop2 drone flying through the moving gate using EV-Planner. Table V enumerates the success rate of collision-free gate crossing for different starting points of both the drone and the gate. Hence, the results showcase the generalization capability of our design for points not present in the training data. The success rates are lower when the drone starts from as the gates are detected (entirely) for lesser duration (especially at depths m). For certain cases, the sensor-fused EV-Planner performs better than fusion-less Depth-Planner. Tracking an object using depth involves a series of intermediate image processing steps that incur significant latency. By the time the target is evaluated, the gate shifts by a little, which Depth-Planner struggles to take into account (for greater depths mostly). As the depth becomes greater, this effect is observed more for both methods (IOU reduces in Figure 10). EV-Planner still performs better, as event-based tracking is faster than depth-based tracking.

| Depth | 2m | 3m | 4m | 5m | 6m | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Starting Points | Drone (x,y) | (0,0) | (0,1) | (0,2) | (1,0) | (1,1) | (1,2) | (2,0) | (2,1) | (2,2) | (3,0) | (3,1) | (3,2) | (4,0) | (4,1) | (4,2) | |
| Ring (-2,y) | 2 | 1 | 1 | 2 | 1 | 1 | 2 | 1 | 1 | 0 | 0/1 | 0 | 2 | 1/2 | 2 | ||
| Success Rate |
|
0.8 | 0.7 | 0.7 | 1 | 0.9 | 0.8 | 1 | 0.9 | 0.8 | 0.9 | 0.8 | 0.7 | 0.7 | 0.6 | 0.5 | |
|
1 | 0.8 | 0.8 | 1 | 0.9 | 0.9 | 1 | 1 | 0.9 | 0.9 | 0.9 | 0.8 | 0.7 | 0.7 | 0.6 | ||
Lower is better.

the contribution of each design component. Lower is better.
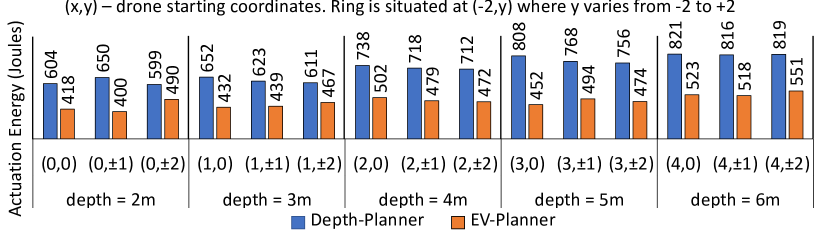
V-C Actuation Energy: Event vs Depth
Figure 12 presents the average actuation energy for EV-Planner compared to Depth-Planner for different starting locations of the drone. Although we do not compare computation energy for perception, the increased latency for depth-based tracking increases the actuation energy. This is because, the drone hovers longer for the depth-based tracking, which in turn burns more rotor currents. On average, Depth-Planner takes seconds longer for the symbolic planner. For an average instantaneous power of , this translates to an additional of energy, as depth-based perception overhead. On the other hand, EV-Planner relies on events for faster object tracking using low-latency SNNs. For flights (each averaged over 10 runs), EV-Planner achieves lower actuation energy compared to Depth-Planner.
V-D Ablation Study
Figure 12 presents an ablation study to quantify the contribution of each design component (i.e the SNN based perception and PgNN based flight-time estimator). Note that when SNN is not used, the depth-sensor based tracking is employed (Depth-Planner). In absence of the PgNN, a vanilla ANN without any underlying physical prior is used for time-estimation. A systematic comparison among the four possible cases reveal that SNN + PgNN based EV-Planner results in lower actuation energy compared to the baseline which uses depth-based perception and physics-less planning, highlighting the energy-efficiency of our proposed design.
V-E Comparison with SOTA Event-based Perception
Table VI presents a summary by comparing two state-of-the-art (SOTA) perception works which use events for object-detection – a) Recurrent Vision Transformers (RVT) [31] and b) Asynchronous Event-based Graph Neural Networks (AEGNN) [32]. EV-Planner which uses a lightweight variant of [10] is scene-independent without requiring any training and is also orders of magnitude more parameter-efficient. RVT and AEGNN both detect objects elegantly, but require curated datasets with lots of instances and labelling. AEGNN uses different configurations for different datasets. To use any supervised-learning (SL) technique in place of our shallow SNN, one has to prepare a dataset with several instances of the ring along with proper labels resulting in training overhead. Also, since the model complexity is greater than the shallow SNN, we did not use SL-based methods as perception block.
VI Limitations, Discussions and Future Work
The results clearly highlight the benefits associated with sensor-fused (events and depth) perception for navigation via SNNs and PgNNs. For future evaluations in real-world, noise could be an issue for which the perception pipeline needs modification. While event cameras are more robust to low-light and motion blur[7], it is possible to encounter spurious events in the environment. One way to filter those spurious events would be to introduce clustering [10]. However, that will add to the latency overhead which may be unavoidable in real-world experiments but not encountered in a simulator. Also, note that, though the PgNN predicted velocities would result in actuation energies (as low as ), the planner burns more power during the perception window for gate tracking and due to the Y component of the velocity as shown in Figure 8. Hence, the energies reported for the actual navigation are higher. There have been works that evaluate compute energy for object detection by considering special-purpose hardware [44, 45]. Compute or non-actuation energy refers to the perception energy which is typically executed on low-power processors with current ratings of nano-Amperes. The actuators are the rotor blades which draws currents of several Amperes ( more w.r.t compute current) from a 15 V battery, making the actuation energy orders of magnitude higher. Hence, we limit our energy calculations in this work only to actuation energy. Research on reducing compute energy will consider designing embedded sensor-fused controllers with scaled in-robot compute hardware with programming support in future. This will reduce the payload mass, and hence the actuation energy. Future work will also consider deploying the proposed method in a real robot with the aforementioned considerations.
VII Summary
We presented EV-Planner – an event-based physics-guided neuromorphic planner to perform obstacle avoidance using neuromorphic event cameras and physics-based AI. For object tracking, we used event-based low-latency SNNs. Utilizing the physical equations of the drone rotors, an energy-aware PgNN was trained with depth inputs to predict flight times. The outputs from the neural networks were consumed by a symbolic planner to publish the robot trajectories. The task of autonomous quadrotor navigation was considered with the aim to detect moving gates and fly through them while avoiding a collision. Extensive simulation results show that sensor-fusion based EV-Planner performs generalizable collision-free dynamic gate crossing with decent success rates, with lower actuation energy compared to ablated variants.
References
- [1] G. Desouza and A. Kak, “Vision for mobile robot navigation: a survey,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 24, no. 2, pp. 237–267, 2002.
- [2] S. Li, M. M. Ozo, C. De Wagter, and G. C. de Croon, “Autonomous drone race: A computationally efficient vision-based navigation and control strategy,” Robotics and Autonomous Systems, vol. 133, p. 103621, 2020.
- [3] A. Amir, B. Taba, D. Berg et al., “A low power, fully event-based gesture recognition system,” in 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2017, pp. 7388–7397.
- [4] P. Lichtsteiner, C. Posch, and T. Delbruck, “A 128 128 120 db 15 s latency asynchronous temporal contrast vision sensor,” IEEE Journal of Solid-State Circuits, vol. 43, no. 2, pp. 566–576, 2008.
- [5] C. Posch, D. Matolin, and R. Wohlgenannt, “A qvga 143 db dynamic range frame-free pwm image sensor with lossless pixel-level video compression and time-domain cds,” IEEE Journal of Solid-State Circuits, vol. 46, no. 1, pp. 259–275, 2011.
- [6] C. Brandli, R. Berner, M. Yang, S.-C. Liu, and T. Delbruck, “A 240 × 180 130 db 3 µs latency global shutter spatiotemporal vision sensor,” IEEE Journal of Solid-State Circuits, vol. 49, no. 10, pp. 2333–2341, 2014.
- [7] G. Gallego, T. Delbrück, G. Orchard, C. Bartolozzi, B. Taba, A. Censi, S. Leutenegger, A. J. Davison, J. Conradt, K. Daniilidis, and D. Scaramuzza, “Event-based vision: A survey,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 44, no. 1, pp. 154–180, 2022.
- [8] A. Delorme, J. Gautrais, R. van Rullen, and S. Thorpe, “Spikenet: A simulator for modeling large networks of integrate and fire neurons,” Neurocomputing, vol. 26-27, pp. 989–996, 1999.
- [9] C. Lee, A. K. Kosta, A. Z. Zhu, K. Chaney, K. Daniilidis, and K. Roy, “Spike-flownet: event-based optical flow estimation with energy-efficient hybrid neural networks,” in Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, 2020, pp. 366–382.
- [10] M. Nagaraj, C. M. Liyanagedera, and K. Roy, “Dotie - detecting objects through temporal isolation of events using a spiking architecture,” in 2023 International Conference on Robotics and Automation (ICRA). IEEE, 2023, pp. 4858–4864.
- [11] M. Raissi, P. Perdikaris, and G. E. Karniadakis, “Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations,” Journal of Computational physics, vol. 378, pp. 686–707, 2019.
- [12] G. E. Karniadakis, I. G. Kevrekidis, L. Lu, P. Perdikaris, S. Wang, and L. Yang, “Physics-informed machine learning,” Nature Reviews Physics, vol. 3, no. 6, pp. 422–440, 2021.
- [13] E. A. Antonelo, E. Camponogara, L. O. Seman, E. R. de Souza, J. P. Jordanou, and J. F. Hubner, “Physics-informed neural nets for control of dynamical systems,” SSRN Electronic Journal, 2021.
- [14] S. Sanyal and K. Roy, “Neuro-ising: Accelerating large-scale traveling salesman problems via graph neural network guided localized ising solvers,” IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, vol. 41, no. 12, pp. 5408–5420, 2022.
- [15] C. Belta, A. Bicchi, M. Egerstedt, E. Frazzoli, E. Klavins, and G. J. Pappas, “Symbolic planning and control of robot motion [grand challenges of robotics],” IEEE Robotics & Automation Magazine, vol. 14, no. 1, pp. 61–70, 2007.
- [16] J. Nicodemus, J. Kneifl, J. Fehr, and B. Unger, “Physics-informed neural networks-based model predictive control for multi-link manipulators,” IFAC-PapersOnLine, vol. 55, no. 20, pp. 331–336, 2022, 10th Vienna International Conference on Mathematical Modelling MATHMOD 2022.
- [17] S. Sanyal and K. Roy, “Ramp-net: A robust adaptive mpc for quadrotors via physics-informed neural network,” in 2023 International Conference on Robotics and Automation (ICRA). IEEE, 2023, pp. 1019–1025.
- [18] A. Salehi and S. Doncieux, “Data-efficient, explainable and safe payload manipulation: An illustration of the advantages of physical priors in model-predictive control,” arXiv preprint arXiv:2303.01563, 2023.
- [19] K. Y. Chee, T. Z. Jiahao, and M. A. Hsieh, “Knode-mpc: A knowledge-based data-driven predictive control framework for aerial robots,” IEEE Robotics and Automation Letters, vol. 7, no. 2, pp. 2819–2826, 2022.
- [20] S. N. Wadekar, B. J. Schwartz, S. S. Kannan, M. Mar, R. K. Manna, V. Chellapandi, D. J. Gonzalez, and A. E. Gamal, “Towards end-to-end deep learning for autonomous racing: On data collection and a unified architecture for steering and throttle prediction,” arXiv preprint arXiv:2105.01799, 2021.
- [21] [Online]. Available: https://www.parrot.com/assets/s3fs-public/media-public/EN_Pressrelease2015/parrotbebop2theall-in-onedrone.pdf
- [22] F. Furrer, M. Burri, M. Achtelik, and R. Siegwart, Robot Operating System (ROS): The Complete Reference (Volume 1). Cham: Springer International Publishing, 2016, ch. RotorS—A Modular Gazebo MAV Simulator Framework, pp. 595–625.
- [23] T. Delbruck and P. Lichtsteiner, “Fast sensory motor control based on event-based hybrid neuromorphic-procedural system,” in 2007 IEEE International Symposium on Circuits and Systems, 2007, pp. 845–848.
- [24] X. Lagorce, C. Meyer, S.-H. Ieng, D. Filliat, and R. Benosman, “Asynchronous event-based multikernel algorithm for high-speed visual features tracking,” IEEE Transactions on Neural Networks and Learning Systems, vol. 26, no. 8, pp. 1710–1720, 2015.
- [25] X. Clady, S.-H. Ieng, and R. Benosman, “Asynchronous event-based corner detection and matching,” Neural Networks, vol. 66, pp. 91–106, 2015.
- [26] A. Mitrokhin, C. Fermüller, C. Parameshwara, and Y. Aloimonos, “Event-based moving object detection and tracking,” in 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2018, pp. 1–9.
- [27] D. Gehrig, H. Rebecq, G. Gallego, and D. Scaramuzza, “Asynchronous, photometric feature tracking using events and frames,” in Proceedings of the European Conference on Computer Vision (ECCV), 2018, pp. 750–765.
- [28] C. Walters and S. Hadfield, “Evreflex: Dense time-to-impact prediction for event-based obstacle avoidance,” in 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2021, pp. 1304–1309.
- [29] Z. Wang, F. C. Ojeda, A. Bisulco, D. Lee, C. J. Taylor, K. Daniilidis, M. A. Hsieh, D. D. Lee, and V. Isler, “Ev-catcher: High-speed object catching using low-latency event-based neural networks,” IEEE Robotics and Automation Letters, vol. 7, no. 4, pp. 8737–8744, 2022.
- [30] D. Falanga, K. Kleber, and D. Scaramuzza, “Dynamic obstacle avoidance for quadrotors with event cameras,” Science Robotics, vol. 5, no. 40, p. 9712, 2020.
- [31] M. Gehrig and D. Scaramuzza, “Recurrent vision transformers for object detection with event cameras,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2023, pp. 13 884–13 893.
- [32] S. Schaefer, D. Gehrig, and D. Scaramuzza, “Aegnn: Asynchronous event-based graph neural networks,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2022, pp. 12 371–12 381.
- [33] L. Zhang, J. Sturm, D. Cremers, and D. Lee, “Real-time human motion tracking using multiple depth cameras,” in 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2012, pp. 2389–2395.
- [34] M. Wüthrich, P. Pastor, M. Kalakrishnan, J. Bohg, and S. Schaal, “Probabilistic object tracking using a range camera,” in 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2013, pp. 3195–3202.
- [35] C. Reading, A. Harakeh, J. Chae, and S. L. Waslander, “Categorical depth distribution network for monocular 3d object detection,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2021, pp. 8555–8564.
- [36] Z. Ren, J. Meng, and J. Yuan, “Depth camera based hand gesture recognition and its applications in human-computer-interaction,” in 2011 8th International Conference on Information, Communications & Signal Processing, 2011, pp. 1–5.
- [37] R. K. Manna, D. J. Gonzalez, V. Chellapandi, M. Mar, S. S. Kannan, S. Wadekar, E. J. Dietz, C. M. Korpela, and A. El Gamal, “Control challenges for high-speed autonomous racing: Analysis and simulated experiments,” SAE International Journal of Connected and Automated Vehicles, vol. 5, no. 1, pp. 101–114, jan 2022.
- [38] F. Morbidi, R. Cano, and D. Lara, “Minimum-energy path generation for a quadrotor uav,” in 2016 IEEE International Conference on Robotics and Automation (ICRA), 2016, pp. 1492–1498.
- [39] D. Mellinger and V. Kumar, “Minimum snap trajectory generation and control for quadrotors,” in 2011 IEEE international conference on robotics and automation. IEEE, 2011, pp. 2520–2525.
- [40] J. K. Eshraghian, M. Ward, E. Neftci, X. Wang, G. Lenz, G. Dwivedi, M. Bennamoun, D. S. Jeong, and W. D. Lu, “Training spiking neural networks using lessons from deep learning,” arXiv preprint arXiv:2109.12894, 2021.
- [41] M. Abadi, A. Agarwal et al., “TensorFlow: Large-scale machine learning on heterogeneous systems,” 2015, software available from tensorflow.org. [Online]. Available: https://www.tensorflow.org/
- [42] B. O. Community, Blender - a 3D modelling and rendering package, Blender Foundation, Stichting Blender Foundation, Amsterdam, 2018. [Online]. Available: http://www.blender.org
- [43] N. Koenig and A. Howard, “Design and use paradigms for gazebo, an open-source multi-robot simulator,” in 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), vol. 3, 2004, pp. 2149–2154 vol.3.
- [44] S. Sanyal, A. Ankit, C. M. Vineyard, and K. Roy, “Energy-efficient target recognition using reram crossbars for enabling on-device intelligence,” in 2020 IEEE Workshop on Signal Processing Systems (SiPS), 2020, pp. 1–6.
- [45] A. Roy, M. Nagaraj, C. M. Liyanagedera, and K. Roy, “Live demonstration: Real-time event-based speed detection using spiking neural networks,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, June 2023, pp. 4080–4081.