Euclidean rings of $S$-integers in complex quadratic fields

In a first course on elementary number theory, one establishes the Fundamental Theorem of Arithmetic, which says that every positive integer factors uniquely as product of primes. In the standard proof, one needs to know that for any prime $p$, if $p$ divides $ab$, then $p$ divides $a$ or $p$ divides $b$. This seemingly obvious fact about primes is usually derived from the Euclidean algorithm. The following crucial property of $\mathbb{Z}$ allows one to show that the Euclidean algorithm terminates in a finite number of steps: For all $a,b\in\mathbb{Z}$, $b\neq 0$, there exists $q,r\in\mathbb{Z}$ such that $a=qb+r$ and $|r|<|b|$. Equivalently, this “Euclidean property” reads: For all $x\in\mathbb{Q}$ there exists $c\in\mathbb{Z}$ such that $|x-c|<1$.

Algebraic number fields are one of the main objects of study in algebraic number theory. The simplest number fields other than the rational numbers $\mathbb{Q}$ are the complex quadratic fields which take the form

$$K=\mathbb{Q}(\sqrt{-d})=\{x+y\sqrt{-d}\mid x,y\in\mathbb{Q}\}\,,$$

where $d>0$ is squarefree. We view $K$ as a subset of the complex numbers $\mathbb{C}$. Let $N:K\to\mathbb{Q}$ denote the norm function (which multiplies an element by its conjugate)

$$N(x+y\sqrt{-d})=(x+y\sqrt{-d})(x-y\sqrt{-d})=x^{2}+dy^{2}.$$

One has $N(\xi\eta)=N(\xi)N(\eta)$ for all $\xi,\eta\in K$, as is verified by direct computation. Let $\mathcal{O}$ denote the ring of integers in $K$, which consists of those elements that satisfy a monic polynomial with integer coefficients. One can show $\mathcal{O}=\mathbb{Z}[w]=\{a+bw\mid a,b\in\mathbb{Z}\}$ with

$$w=\begin{cases}\sqrt{-d}&-d\equiv 2,3\pmod{4}\\[4.30554pt] \frac{1+\sqrt{-d}}{2}&-d\equiv 1\pmod{4}\,.\end{cases}$$

The ring $\mathcal{O}$ in $K$ is the analogue of $\mathbb{Z}$ in $\mathbb{Q}$, but properties enjoyed by $\mathbb{Z}$ (such as unique factorization) do not always hold in $\mathcal{O}$.

We now give the classical generalization of the Euclidean algorithm. We call $K$ norm-Euclidean if for every $\xi\in K$ there exists $\gamma\in\mathcal{O}$ such that $N(\xi-\gamma)<1$; this is equivalent to the condition that $\mathcal{O}$ is a Euclidean ring with respect to the function $N$. It is known that $K$ is norm-Euclidean exactly when $d=-1,-2,-3,-7,-11$. This goes back to Dedekind’s supplement to Dirichlet’s book [4].

Let $S\subseteq\mathbb{Z}^{+}$ be a finite (possibly empty) set of primes, and let $T\subseteq\mathbb{Z}^{+}$ be the set of all finite products of elements in $S$ (where $1\in T$ by convention). In this paper, we are interested in the so-called ring of $S$-integers

$$\mathcal{O}_{S}=\left\{\frac{a+bw}{c}:a,b,\in\mathbb{Z},c\in T\right\}\subseteq K\,.$$

This is an example of the ring-of-fractions construction one might encounter in a first course on ring theory.

We define the $S$-norm of an element $\xi\in K$, denoted by $N_{S}(\xi)$, by deleting the primes in $S$ from the prime factorization of the numerator and denominator of the rational number $N(\xi)$. For example, when $K=\mathbb{Q}(\sqrt{-5})$, $S=\{2\}$, $\xi=(3+3\sqrt{-5})/7$ one has $N(\xi)=54/49$ and hence $N_{S}(\xi)=27/49$. It follows from the multiplicative property of $N$ that the function $N_{S}$ is also multiplicative.

We call $K$ $S$-norm-Euclidean if for every $\xi\in K$ there exists $\gamma\in\mathcal{O}_{S}$ such that $N_{S}(\xi-\gamma)<1$; this is equivalent to the statement that $\mathcal{O}_{S}$ is a Euclidean ring with respect to the function $N_{S}$. One would like to know: When is $K$ $S$-norm-Euclidean? Even in our setting, where $K$ is a complex quadratic field, this question is, in general, unsolved. To give a simple example, if $K=\mathbb{Q}(\sqrt{-5})$ and $S=\{2\}$, then $\mathcal{O}_{S}=\mathbb{Z}\left[\sqrt{-5},\frac{1}{2}\right]$; in this case $K$ is $S$-norm-Euclidean, although $K$ is not norm-Euclidean.

In this paper we give an elementary approach that allows us to prove a few results about $S$-norm-Euclidean fields in the complex quadratic setting. Our first result furnishes a number of examples.

Note the previous theorem is not claiming these lists are complete or even finite, although both are true when $S=\emptyset$. As discussed, when $S=\emptyset$, this result is classical. When $S=\{2\}$ these examples appear in [8, 14]. However, we have not seen any examples with $S=\{2,3\}$ explicitly given in the literature.

A natural question arises: Does there always exists a set $S$ so that $K$ is $S$-norm-Euclidean? The answer to this question is yes, and we give a quantified version of this claim. Before stating this result, we require an additional piece of terminology and notation. We write $D$ to denote the absolute value of the discriminant of $K$. By definition, the discriminant is $\det([1,w;1,\overline{w}])^{2}$ where $\overline{w}$ denotes the complex conjugate of $w$; therefore the discriminant equals $-D$ where

$$D=\begin{cases}4d&-d\equiv 2,3\pmod{4}\\ d&-d\equiv 1\pmod{4}.\end{cases}$$

Given $x\in\mathbb{R}$ we write $\lceil x\rceil$ to denote the ceiling of $x$; i.e., $\lceil x\rceil$ is the smallest integer greater than $x$.

In a first course in algebraic number theory, one shows that the class group is generated by the set of all prime ideals whose norm is less than the Minkowski bound; it turns out that Theorem 2 implies this result in our setting. However our proof of Theorem 2 does not use the Minkowski bound, the class group, or even the notion of an ideal! For those familiar with the rudiments of algebraic number theory, further discussion is given in an appendix (see §6). We should note that Theorem 2 appears in [11] but that our proof is different.

To give another example, consider $K=\mathbb{Q}(\sqrt{-163})$ and $S=\{2,3,5,7\}$, where

$$\mathcal{O}_{S}=\mathbb{Z}\left[\frac{1+\sqrt{-163}}{2},\frac{1}{120}\right]=\mathbb{Z}\left[\sqrt{-163},\frac{1}{120}\right]\,.$$

Theorem 2 implies that $K$ is $S$-norm-Euclidean; however, $K$ is not norm-Euclidean (even though $\mathcal{O}=\mathbb{Z}\left[(1+\sqrt{-163})/2\right]$ is a PID and hence a UFD).

On the other hand, one might consider a fixed set $S$ and ask which complex quadratic fields $K$ are $S$-norm-Euclidean. When $S$ contains several elements, this seems to be a difficult problem, so we restrict ourselves to the case where $S$ contains a single prime $p\in\mathbb{Z}$. Even in this simplest case, we will further restrict which $(d,p)$ pairs we consider in order to obtain a complete classification. In what follows $(n/p)$ denotes the usual Legendre symbol; namely $(n/p)=1$ if $x^{2}\equiv n\pmod{p}$ has a solution with $x\not\equiv 0\pmod{p}$, $(n/p)=0$ if $p$ divides $n$, and $(n/p)=-1$ otherwise.

We note that the previous theorem follows from Theorem 0.19 of [14]; however, our approach requires very little background knowledge and our proof is relatively short. In comparing Theorem 1 with Theorem 3, the reader may have noticed the addition of $d=10$ to the list when $S=\{2\}$. It turns out the technique used to prove Theorem 1 does not quite apply in the case of $(d,p)=(10,2)$, but we find a way to treat this case and four other “exceptional cases” in Section 5.

We view the following question as a natural one. In light of Theorem 3 one can restrict attention to those $(d,p)$ pairs such that $(-d/p)=1$.

Associated to any number field $K$ is a finite abelian group, called the class group of $K$. Roughly speaking, this group governs the complexity of factorizations of elements of $\mathcal{O}$ into irreducible elements, and this group is trivial if and only if unique factorization holds. It turns out that if $K$ is $S$-norm-Euclidean with $S=\{p\}$, then the class group of $K$ is cyclic. According to the Cohen–Lenstra heuristics (see [3]), the latter event should happen quite often (roughly 97.75% of the time) for fields of prime discriminant, but we currently cannot even prove that it happens infinitely often. (See §6 for additional discussion.) If one were to resolve the problem above in the affirmative, then one would prove that class group of $K$ is cyclic infinitely often, resolving a major open problem. (Of course, this likely means that producing such a proof may be difficult.) On the other hand, if the resolution of this problem is in the negative, then proving such a result would be interesting in its own right. We note that Stark has already suggested looking at Euclidean rings of $S$-integers in connection with class number problems (see [13]).

Finally, since we are posing problems anyway, here is another:

In this section, we develop the main idea of this paper, which provides sufficient conditions for $K$ to be $S$-norm-Euclidean. We will see that Theorems 1 and 2 will then immediately follow. We will give a small amount of additional background material along the way as necessary. Let $K$ denote a complex quadratic field and adopt all the notation given in §1. In particular, we write $K=\mathbb{Q}(\sqrt{-d})$ with $d>0$ squarefree and discriminant $-D$.

The norm function $N:K\to\mathbb{Q}$ also maps $\mathcal{O}\to\mathbb{Z}$. In the case $-d\equiv 2,3\pmod{4}$ this is evident from our definition; in the case where $-d\equiv 1\pmod{4}$, observe that

$$N(a+bw)=\left(a+\frac{b}{2}\right)^{2}+d\left(\frac{b}{2}\right)^{2}=a^{2}+ab+\left(\frac{d+1}{4}\right)b^{2}\,,$$

where $(d+1)/4\in\mathbb{Z}$. It follows from this that $N_{S}(\alpha)\leq N(\alpha)$ for all $\alpha\in\mathcal{O}$. The following lemma gives an inequality that involves elements of $K$ that are not integral.

We define the fundamental domain for $K$ as

$$\mathcal{F}=\{x+yw\mid 0\leq x,y\leq 1\}\subseteq\mathbb{C}\,.$$

This will assist us in visualizing the norm-Euclidean property graphically. When $-d\equiv 2,3\pmod{4}$, $\mathcal{F}$ takes the shape of a rectangle, and when $-d\equiv 1\pmod{4}$, $\mathcal{F}$ takes the shape of a parallelogram. Notice that any $z\in\mathbb{C}$ can be written as $z=z^{\prime}+\alpha$ where $z^{\prime}\in\mathcal{F}$ and $\alpha\in\mathcal{O}$. Indeed, translations of $\mathcal{F}$ give a tessellation of $\mathbb{C}$. Hence, when studying the norm-Euclidean property, we can focus our attention on the points in $\mathcal{F}$. Indeed, observe that $K$ is norm-Euclidean if and only if for all $\xi\in K\cap\mathcal{F}$ there exists $\gamma\in\mathcal{O}$ such that $|\xi-\gamma|<1$. In particular, $N(\xi-\gamma)=|\xi-\gamma|^{2}$ where $|\cdot|$ denotes the complex modulus.

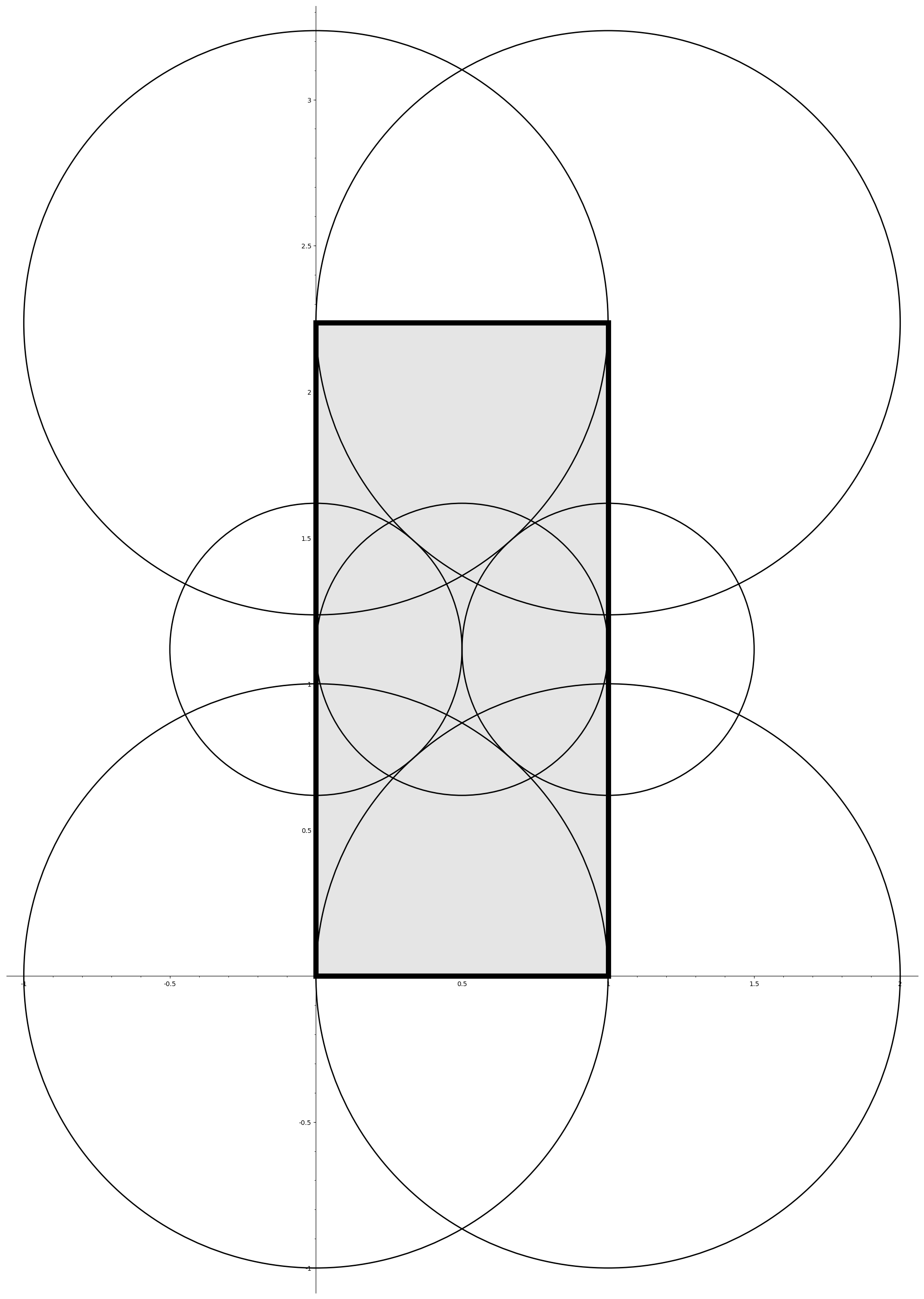
We now generalize the idea presented in the previous example. Consider the collection of all $S$-integers in the fundamental domain (i.e., elements of $\mathcal{O}_{S}\cap\mathcal{F}$). This collection is precisely the set of all $\alpha_{i,j}^{k}=(i+j\omega)/k$ for $k\in T$ and $0\leq i,j\leq k$. In light of Lemmas 1 and 2, we know that the condition $\mathcal{F}\subseteq\bigcup_{i,j,k}B_{1/k}(\alpha_{i,j}^{k})$ is sufficient for $K$ to be $S$-Euclidean. Moreover, we will only need to consider the $B_{1/k}(\alpha_{i,j}^{k})$ where $\gcd(j,k)=1$. To to each “row of circles” $\bigcup_{i=0}^{k}B_{1/k}(\alpha_{i,j}^{k})$, we can associate a horizontal strip

$$R_{j}^{k}=\left\{x+iy\in\mathcal{F}:\left|y-\frac{j\operatorname{Im}(w)}{k}\right|<\frac{\sqrt{3}}{2k}\right\}\,.$$

Note that the $R_{j}^{k}$ are maximal with the property that $R_{j}^{k}\subseteq\mathcal{F}\cap\bigcup_{i}B_{1/k}(\alpha_{i,j}^{k})$. The $R_{j}^{k}$ give rise to intervals via the projection map $\pi(x+iy)=y/\operatorname{Im}w$. We define

$$I_{j}^{k}=\left(\frac{j}{k}-\frac{\sqrt{3}}{2k\operatorname{Im}\omega},\;\frac{j}{k}+\frac{\sqrt{3}}{2k\operatorname{Im}\omega}\right)=\left(\frac{j-\sqrt{3/D}}{k},\;\frac{j+\sqrt{3/D}}{k}\right)\,.$$

Notice that $\operatorname{Im}(w)=\sqrt{D}/2$, which allowed us to rewrite the intervals in terms of $D$ rather than $\operatorname{Im}w$. The following lemma gives sufficient conditions for $K$ to be $S$-norm-Euclidean.

We rephrase Lemma 3 in a slightly different form, that will be convenient in the sequel. In what follows, we write $\{x\}=x-\lfloor x\rfloor$ to denote the fractional part of a real number $x$.

As illustrated in the previous example, our results thus far lead to the following simple procedure:

1. 1.

   Let $q$ be the smallest prime not in $S$ and set $X=3q^{2}$.

2. 2.

   Enumerate the intervals $I_{j}^{k}$ for $0\leq j\leq k\leq X$ with $\gcd(j,k)=1$.

3. 3.

   If $[0,1]\subseteq\bigcup_{j,k}I_{j}^{k}$, then $K$ is $S$-norm-Euclidean.

Notice that this procedure will never prove that $K$ is not $S$-norm-Euclidean. However, as was stated in Theorem 1 it allows us to show a number of complex quadratic fields $K$ are, in fact, $S$-norm-Euclidean.

Since Theorem 3 gives a classification of sorts, the proof will require some effort. The first part concerns the case where $S=\{p\}$ with $p$ odd, and the second part concerns the case where $S=\{2\}$. In each part we must treat the cases of $-d\equiv 2,3\pmod{4}$ and $-d\equiv 1\pmod{4}$ separately. As first pass, the reader may wish to skip one or more of these subproofs.

It may be useful to remark that we have now completely dealt with the “only if” portion of Theorem 3. The “if” portion of the theorem follows from Theorem 1 except for the five $(d,p)$ pairs which we will now consider.

Here we deal with the cases where $(d,p)$ is one of the following pairs:

$$(10,2),(15,3),(15,5),(35,5),(35,7)\,.$$

It turns out that our criterion from §2 just barely fails for the cases $d=10$ and $d=15$. In particular, the countable union of intervals $\bigcup_{j,k}I_{j}^{k}$ fail to cover $[0,1]$ by just finitely many points. The case of $d=35$ is a little more difficult to deal with.