Estimation of Scalar Field Distribution in the Fourier Domain

Motivated by the above discussion, we propose to approximate (2) by

where $\tilde{\mathcal{U}}\subseteq\mathcal{U}$ is the subset of low order modes that we wish to retain.²²2In general, we could in (3) use coefficients $\tilde{C}(u,v)$ which are not necessarily equal to $C(u,v)$. One reason for taking the coefficients to be equal to $C(u,v)$ is given in Lemma 1.

For example, we could retain the first $\tilde{N}_{x}\times\tilde{N}_{y}$ modes, with $\tilde{N}_{x}\leq N_{x},\tilde{N}_{y}\leq N_{y}$, so that

The total number of modes retained $\tilde{N}$ is thus equal to $\tilde{N}=\tilde{N}_{x}\tilde{N}_{y}$.

Another possibility is the following:

which tries to retain the $\tilde{N}$ “largest” (in magnitude) modes.³³3This is of course an approximation, as exactly determining the $\tilde{N}$ largest modes depends on and requires knowledge of the very field that we are trying to estimate. The motivation for (5) comes from a result that the DCT coefficients $C(u,v)$ decay as $O\big{(}\frac{1}{(u+1)^{2}+(v+1)^{2}}\big{)}$ for $u,v\rightarrow\infty$ [26]. Thus the larger components will usually have smaller values of $(u+1)^{2}+(v+1)^{2}$, leading to the choice (5). In numerical simulations, we have found (5) to give better approximations than (4) (for the same number of retained modes $\tilde{N}$) in many, though not all, cases.

In this paper we consider the following noisy quantized measurement model for a vehicle at position index $(I_{x},I_{y})$:

where $n(\bm{\cdot},\bm{\cdot})$ is random noise and $q(\bm{\cdot})$ is a quantizer of $L$ levels, say $\{0,1,\dots,L-1\}$. The quantizer can be expressed in the form

where the quantizer thresholds $\{\tau_{0},\dots,\tau_{L-2}\}$ satisfy $\tau_{0}\leq\tau_{1}\leq\dots\leq\tau_{L-2}$. The use of a quantized measurement model is motivated by the fact that many chemical sensors can only provide output from a small number of discrete bars [27, 28].

The problem we wish to consider in this paper is to estimate the coefficients⁴⁴4When we refer to estimation of components/modes in this paper, we specifically mean estimation of the coefficients $C(u,v)$.

of the field $\phi_{d}(I_{x},I_{y})$, from quantized measurements $\{z(I_{x},I_{y})\}$ collected by an unmanned autonomous vehicle under the measurement model (6). The estimation should be done in an online manner such that the estimates are continually updated as new measurements are collected.

Define the mean squared error (MSE):

where $\phi_{d}(I_{x},I_{y})$ is the (discretized) true field given by (2) and

is the approximation of the true field using a subset of modes $\tilde{U}$ and coefficients $\tilde{C}(u,v)$. The expression for $\tilde{\phi}_{d}(I_{x},I_{y})$ is the same as (3) except that the coefficients $\tilde{C}(u,v)$ may be different from $C(u,v)$. However, it turns out that setting $\tilde{C}(u,v)$ to be equal to $C(u,v)$ will minimize the MSE.

The following RBF field model is used in [20, 21, 22, 23]:

where $\mathbf{x}\triangleq(x,y)$ and $K_{j}(\mathbf{x}),j=1,\dots,J$ are radial basis functions. In particular, we consider the choice

which results in a Gaussian mixture model [17]. For a given number of basis functions $J$, we assume that the $\mathbf{c}_{j}$’s and $\sigma_{j}$’s are chosen,⁵⁵5The case where the $\mathbf{c}_{j}$’s and $\sigma_{j}$’s are also estimated has been considered, but was found to suffer from identifiability issues and sometimes give very unreliable results [21]. while the $\beta_{j}$’s are free parameters. Algorithms for estimating the $\beta_{j}$’s are studied in, e.g., [20, 21, 22, 23]. Here we consider instead the problem of finding the optimal $\beta_{j}$’s in order to minimize the mean squared error, to see how good the RBF model can be when approximating a field for a given set of basis functions. Define

where $\phi(\mathbf{x})$ is the true field value at position $\mathbf{x}$, $\mathcal{S}_{d}$ is a discretized set of points in the search region $\mathcal{S}$, and $|\mathcal{S}_{d}|$ is the cardinality of $\mathcal{S}_{d}$.

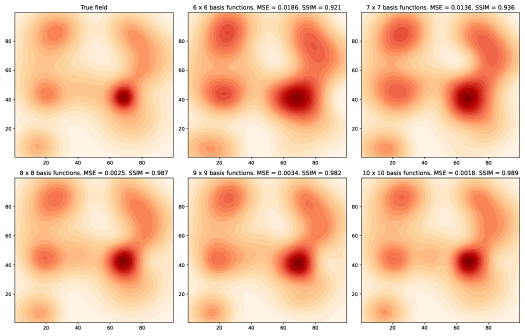
In Figs.1-4 we show two example fields, and the field approximations that are obtained when various different numbers of modes (for Fourier component model) or radial basis functions (for RBF model) are used. The discretization in the true fields is set as $N_{x}=N_{y}=100$ (so that there are $100^{2}=10000$ modes in total). For the RBF model we set $\mathcal{S}_{d}=\mathcal{X}_{d}\times\mathcal{Y}_{d}$, so that the discretized set of points are the same in the MSE calculations. For the Fourier component model, we use the optimal choice of $\tilde{C}^{*}(u,v)$ given in Lemma 1 (which corresponds to the model (3)), and we choose $\tilde{\mathcal{U}}$ as in (5) to retain the $\tilde{N}$ “largest” modes. For the RBF model, we use $J=J_{x}\times J_{y}$ radial basis functions with $\mathbf{c}_{j}$’s in (12) placed uniformly on a grid at locations $\mathcal{X}_{RBF}\times\mathcal{Y}_{RBF}$, where

and

The $\sigma_{j}$’s in (12) are chosen to be equal to $\sigma_{j}=\max(\delta_{x},\delta_{y}),\forall j$. The $\beta_{j}$’s used in (11) are the optimal values computed according to Lemma 2.

In the figures we show two performance measures, 1) the MSE, and 2) the structural similarity (SSIM) index, which originated in [31] and has been widely adopted in the image processing community. The structural similarity index is a measure of the similarity between two images. In our case, we can regard $\Phi=\{\phi_{d}(I_{x},I_{y}):I_{x}=0,\dots,N_{x}-1,I_{y}=0,\dots,N_{y}-1\}$ and $\tilde{\Phi}=\{\tilde{\phi}_{d}(I_{x},I_{y}):I_{x}=0,\dots,N_{x}-1,I_{y}=0,\dots,N_{y}-1\}$ as the image representations of the true and approximated fields respectively, and compute the SSIM between these two images. The SSIM gives a scalar value between 0 and 1, with $\textnormal{SSIM}=1$ if the two images to be compared are identical. We refer to [31, 32] for the specific equations used to compute the SSIM.

We see from Figs.1-4 that as more modes (for Fourier component model) or basis functions (for RBF model) are used, the approximations to the true field improves. When using a smaller number of modes / basis functions the RBF model seems to give better approximations than the Fourier component model, while for larger numbers of modes / basis functions the two approaches perform similarly. We also observe that for these two examples, using a relatively small number of modes (when compared to the total number of modes of 10000) or basis functions will still result in a qualitatively reasonable approximation to the true field.

While the Fourier component model does not seem to offer a significant advantage in terms of approximation quality, there are other reasons where one may consider its use. One advantage of the Fourier model is that it provides a natural way to control the number of model parameters (the coefficients $C(u,v)$) that need to be estimated, in that we simply choose however many modes we wish to retain, whereas with the RBF model one would need to also choose the locations $\mathbf{c}_{j}$ to place the basis functions and what the values of $\sigma_{j}$ should be. Additionally, if we want to refine our field model with finer structure by including more model parameters, in the Fourier component model we can reuse any previous estimates (and further improve them) of the lower order modes (see Section V-C), since these remain the same in a model with more modes, whereas in the RBF model one would likely need to recalculate the estimates of all the parameter values when more basis functions are utilized.

In this subsection we describe an approach to estimating the parameters $C(u,v),\,u=0,\dots,\tilde{N}-1$, which assumes the quantized measurement model (6)-(7), with the parameters estimated recursively. The algorithm uses an online optimization approach similar to [22], however in this paper we will generalize [22] from binary measurements to multi-level quantized measurements, and also extend the approach to handle time-varying fields.

For the measurement model (6)-(7), $n(\bm{\cdot},\bm{\cdot})$ is taken as zero mean noise (not necessarily Gaussian). Recalling the observation in Remark 3, we consider the following scaling of the DCT coefficients:

and define

as the vector of parameters that are to be estimated.

We first introduce some notation. Let $z_{k}$ denote the measurement, and $(I_{x,k},I_{y,k})$ the position index, at time/iteration $k$. For notational compactness we also denote

and

where

Denote

as the set of measurements collected up to time $k$, with corresponding position indices

The idea is to recursively estimate $\bm{\beta}$ by trying to minimize a cost function

using online optimization techniques [33]. For binary measurements (8), the following per stage cost function from [22] can be used:

where $\eta>0$ is a parameter in the logistic function $\ell(x)\triangleq 1/(1+\exp(\eta x))$, where larger values of $\eta$ will more closely approximate the function $\mathds{1env}(x>0)$. The cost function (22) is similar to cost functions used in binary logistic regression problems [29, p.516]. In the current work, we wish to define a cost suitable for multi-level quantized measurements. Note that there are cost functions used in multinomial logistic regression problems [30], however they are unsuitable for our problem as they usually involve multiple sets of parameters for each possible output $z$, whereas here we just have a single set of parameters $\bm{\beta}$.

To motivate our cost function, let us look more closely at the binary measurements cost function (22). In the case where the measurement $z_{t}$ at time $t$ and position index $\bm{I}_{\textbf{x},t}$ is equal to 0, the cost $g_{t}(\bm{\beta};\bm{I}_{\textbf{x},t},z_{t})$ will be small if $\bm{\beta}^{T}\mathbf{K}(\bm{I}_{\textbf{x},t})$ is less than the quantizer threshold $\tau$, and large otherwise. Similarly, when $z_{t}=1$, $g_{t}(\bm{\beta};\bm{I}_{\textbf{x},t},z_{t})$ will be small if $\bm{\beta}^{T}\mathbf{K}(\bm{I}_{\textbf{x},t})$ is greater than $\tau$, and large otherwise. For the case of multi-level quantized measurements with $L$ levels given by (7), we would like to have a cost function such that 1) when $z_{t}=0$, $g_{t}(\bm{\beta};\bm{I}_{\textbf{x},t},z_{t})$ is small for $\bm{\beta}^{T}\mathbf{K}(\bm{I}_{\textbf{x},t})<\tau_{0}$, and large otherwise, 2) when $z_{t}=l,\,l\in\{1,\dots,L-2\}$, $g_{t}(\bm{\beta};\bm{I}_{\textbf{x},t},z_{t})$ is small for $\tau_{l-1}\leq\bm{\beta}^{T}\mathbf{K}(\bm{I}_{\textbf{x},t})<\tau_{l}$, and large otherwise, and 3) when $z_{t}=L-1$, $g_{t}(\bm{\beta};\bm{I}_{\textbf{x},t},z_{t})$ is small for $\bm{\beta}^{T}\mathbf{K}(\bm{I}_{\textbf{x},t})>\tau_{L-2}$, and large otherwise. In this paper we will choose the following per stage cost function, which can be easily checked to satisfy these three requirements:

We remark that (23) reduces to (22) when the measurements are binary.

Now that the per stage cost (23) has been defined, we will present the online estimation algorithm. First, the gradient of $g_{t}(\bm{\cdot};\bm{\cdot},\bm{\cdot})$ can be derived as

while the Hessian of $g_{t}(\bm{\cdot};\bm{\cdot},\bm{\cdot})$ can be derived as

An approximate online Newton method [22] for estimating the parameters $\bm{\beta}$ is now given by:

where

The terms $G_{k}$ and $H_{k}$ represent approximate gradients and Hessians respectively for the cost function (21). The initialization $H_{0}(\hat{\bm{\beta}}_{0})=\varsigma I$ is a Levenberg-Marquardt type modification [34] to ensure that the matrices $\{H_{k}\}$ are always non-singular.⁶⁶6In [22] this is equivalently expressed as a full rank initialization on $\left(H_{0}(\hat{\bm{\beta}}_{0})\right)^{-1}$.

In the case where the field (and hence the parameters $\bm{\beta})$ is time-varying, the algorithm (35)-(36) may not be able to respond quickly to changes in $\bm{\beta}$, due to all past Hessians (including Hessians from old fields) being used in the computation of $H_{k}(\hat{\bm{\beta}}_{k};\bm{I}_{\textbf{x},1:k},z_{1:k})$ in (36). To overcome this problem, we will introduce a forgetting factor [35] into the algorithm, where the forgetting factor $\delta$ satisfies $0<\delta\leq 1$, and typically chosen to be close to one. The final estimation procedure is summarized as Algorithm 1. Compared to (36), we note that the Levenberg-Marquardt modification in Algorithm 1 is done at every time step by adding $\varsigma I$ to $\tilde{H}_{k}$, as we found that only doing it once at the beginning can lead to algorithm instability due to exponential decay of initial conditions when using a forgetting factor. We also remark that Algorithm 1 reduces to (35)-(36) when the forgetting factor $\delta=1$.