\includeversion

arxiv \excludeversionsubmission

{arxiv}

{submission}

Espresso: Robust Concept Filtering in Text-to-Image Models

Anudeep Das University of Waterloo [email protected] , Vasisht Duddu University of Waterloo [email protected] , Rui Zhang Zhejiang University [email protected] , N. Asokan University of Waterloo [email protected] and .. .

Abstract.

Diffusion based text-to-image models are trained on large datasets scraped from the Internet, potentially containing unacceptable concepts (e.g., copyright-infringing or unsafe). We need concept removal techniques (CRTs) which are i) effectivein preventing the generation of images with unacceptable concepts ii) utility-preservingon acceptable concepts, and iii) robustagainst evasion with adversarial prompts. No prior CRT satisfies all these requirements simultaneously. We introduce Espresso, the first robust concept filter based on Contrastive Language-Image Pre-Training (CLIP). We identify unacceptable concepts by using the distance between the embedding of a generated image to the text embeddings of both unacceptable and acceptable concepts. This lets us fine-tune for robustness by separating the text embeddings of unacceptable and acceptable concepts while preserving utility. We present a pipeline to evaluate various CRTs to show that Espresso is more effective and robust than prior CRTs, while retaining utility.

^†^†copyright: none

1. Introduction

Diffusion-based text-to-image (T2I) models have demonstrated a remarkable ability to generate high quality images from textual prompts (stable-diffusion; Rombach_2022_CVPR; ramesh2021dalle). They are trained on large datasets of unfiltered content from the Internet (radford2021learning; schuhmann2022laion). Due to their large capacity, T2I models memorize specific concepts, as seen in the generated images (Korn_2023; somepalli2022diffusion; carlini2023extracting). Some of these concepts, may be unacceptable for various reasons, such as copyright infringement (e.g., a movie character or celebrity), or inappropriateness (e.g., “nudity” or “violence”) (gandikota2023erasing; schramowski2022safe; heng2023selective). We need concept removal techniques (CRTs) to minimize unacceptable concepts in generated images.

Ideally, CRTs should be effective in reducing generation of unacceptable concepts while preserving utility on all others, and robust to evasion with adversarial prompts. No existing CRT simultaneously satisfies these requirements (§ 6): i) fine-tuning CRTswhich modify T2I models, trade-off effectiveness for utility (gandikota2023erasing; kumari2023ablating; heng2023selective; schramowski2022safe), and lack robustness (Tsai2023RingABellHR; wen2023hard; pham2023circumventing; yang2023sneakyprompt) ii) filtering CRTs, which detect unacceptable concepts, lack robustness ((rando2022redteaming) and § 6.3). Our goal is to design a CRT that can simultaneously meet all the requirements.

We opt to use a filter as it will not alter the T2I model, thus minimizing impact on utility. We construct our filter using a Contrastive Language-Image Pre-Training (CLIP) model (radford2021learning), an essential component of T2I models. CLIP is pre-trained on a vast dataset encompassing a broad spectrum of concepts (radford2021learning), making it a versatile choice for a filter, unlike specialized classifiers (e.g., (unsafeDiff)). However, a naive CLIP-based filter is susceptible to evasion (rando2022redteaming). {arxiv} Subsequently, prior works have identified the design of a robust filtering-based CRT as an open problem (rando2022redteaming; li2024safegen).

We present a robust content filter, Espresso, by configuring CLIP to identify unacceptable concepts in generated images using the distance of their embeddings to the text embeddings of both unacceptable and acceptable concepts. This allows fine-tuning to improve robustness by increasing the separation between the text embeddings of unacceptable and acceptable concepts, while preserving utility by maintaining the closeness between embeddings of prompts and their images. Our contributions are presenting

(1)

Espresso ¹¹1We will open-source the code upon publication., the first robust content filter (§ 4), which identifies unacceptable concepts in generated images by measuring the distance of their embeddings to the text embeddings of both unacceptable and acceptable concepts
(2)

a complete pipeline for comparative evaluation of CRTs and attacks, (§ 5), and
(3)

a comprehensive evaluation of Espresso against seven fine-tuning CRTs, and one filtering CRT, showing that it is more effective and robust while retaining utility (§ 6).

In § 7 and Appendix A, we present the first approach for certifiable robustness of CRTs, exploring theoretical robustness bounds of Espresso against a hypothetically strong adversary. We analyze these bounds to show that Espresso is more robust in practice.

2. Background

We describe T2I models (§ 2.1), different CRTs (§ 2.2), and attacks against them (§ 2.3).

2.1. Diffusion based T2I Models

A diffusion based T2I model is a function $\emph{f}:\texttt{p}\rightarrow\texttt{$x$}$ which generates an image $x$ for a given a textual prompt p. It comprises two key components: an encoder ( $\phi$ ) which is used to incorporate the textual prompt in the image generation process, and a diffusion model ( $\epsilon_{\theta}$ ) which is responsible for the generation of the image.

A popular encoder is CLIP, trained on a large dataset of image-text pairs, to map the embeddings of images and their corresponding text closer together in a joint text-image embedding space (radford2021learning). Given $N$ images $\{\texttt{$x$}_{j}\}_{j=1}^{N}$ and their corresponding text prompts $\{\texttt{p}_{j}\}_{j=1}^{N}$ , the training data is $\mathcal{D}=\{(\texttt{$x$}_{j},\texttt{p}_{j})\}_{j=1}^{N}$ .

CLIP is trained to maximize the cosine similarity between the embeddings of a prompt $\texttt{p}_{j}$ and its corresponding image $\texttt{$x$}_{j}$ while minimizing the similarity between $\texttt{p}_{j}$ and any other $\texttt{$x$}_{k}$ for a $k\neq j$ . We denote the cosine similarity as cos( $\phi_{p}(\texttt{p}_{j}),\phi_{x}(\texttt{$x$}_{j}))$ , where $\phi_{x}(\texttt{$x$}_{j})$ is the CLIP image embedding of the image $\texttt{$x$}_{j}$ , and $\phi_{p}(\texttt{p}_{j})$ is the CLIP text embedding of the prompt $\texttt{p}_{j}$ . To achieve this, CLIP is trained using a contrastive loss function (yang2023robust; oord2019representation):

\mathcal{L}_{\text{Con}}(\mathcal{D})=-\frac{1}{N}\sum_{j=1}^{N}\log\frac{\exp(\text{cos}(\phi_{x}(x_{j}),\phi_{p}(\texttt{p}_{j}))/\tau)}{\sum_{k=1}^{N}\exp(\text{cos}(\phi_{x}(x_{j}),\phi_{p}(\texttt{p}_{k}))/\tau)}

where $\tau$ is the temperature parameter to scale predictions (radford2021learning; ModalityGap).

Given access to a pre-trained encoder $\phi$ , the actual images in T2I models are generated by a diffusion model, $\epsilon_{\theta}$ , parameterized by $\theta$ . During training of $\epsilon_{\theta}$ , Gaussian noise is added to an initial image $x_{0}$ for $T$ time steps to produce $x_{T}$ , in a process known as the forward diffusion process. The noise is then iteratively removed to approximate the initial image $\tilde{x_{0}}$ in the reverse diffusion process. During inference, the reverse diffusion process generates an image from noise. Further, $\epsilon_{\theta}$ can be conditioned with a textual prompt p to guide the generation of $\tilde{x_{0}}$ to match the description in p. After generating $\phi_{p}(\texttt{p})$ , $\epsilon_{\theta}$ is trained by minimizing the following loss function: $\mathcal{L}=\mathbb{E}_{\epsilon,\phi_{p}(\texttt{p}),t}[||\epsilon-\epsilon_{\theta}(\texttt{$x$}_{t},\phi_{p}(\texttt{p}),t)||_{2}^{2}]$ for each time step $t$ , and random Gaussian noise $\epsilon\sim\mathcal{N}(0,1)$ .

Several prominent T2I models (e.g., Stable Diffusion v1.4 (SDv1.4)) improve the efficiency of the diffusion process by computing in the embedding space of a variational autoencoder (VAE), rather than on images (stable-diffusion). For a VAE decoder $\mathit{D}$ , VAE encoder $\mathcal{E}$ , and $z_{t}\in\mathcal{E}(\texttt{$x$})$ as the latent representation of $x$ in the VAE’s latent space, $\epsilon_{\theta}$ is trained by minimizing the following objective:
$\mathcal{L}=\mathbb{E}_{\epsilon,z_{t},\phi_{p}(\texttt{p}),t}[||\epsilon-\epsilon_{\theta}(z_{t},\phi_{p}(\texttt{p}),t)||_{2}^{2}]$ where $\epsilon\sim\mathcal{N}(0,1)$ .
The final image is generated from the approximation, $\tilde{z_{0}}$ , by passing it through $\mathit{D}$ : $\tilde{x_{0}}=\mathit{D}(\tilde{z_{0}})$ . We summarize notations in Table 1.

Table 1. Frequently used notations and their descriptions.

Notation	Description
T2I	Text-to-Image
$\phi$	Text encoder (e.g., CLIP)
CRT	Concept Removal Technique
$\mathcal{A}dv$	Adversary
$x$	Generated image
$x^{u}$	Generated image with unacceptable concept
$x^{a}$	Generated image with acceptable concept
$\phi_{x}(x)$	CLIP embedding for image $x$
$\texttt{$x$}^{adv}$	Image generated from adversarial prompt
p	Textual prompt
$c^{a}$	Phrase for acceptable concept
$c^{u}$	Phrase for unacceptable concept
$\texttt{p}^{u}$	Textual prompt containing $c^{u}$
$\texttt{p}^{a}$	Textual prompt containing $c^{a}$
$\phi_{p}(\texttt{p})$	CLIP embedding for textual prompt p
$\texttt{p}^{adv}$	Adversarially generated textual prompt
$\mathcal{D}_{te}^{a}$	Test dataset with acceptable prompts/images
$\mathcal{D}_{te}^{u}$	Test dataset with unacceptable prompts/images
$\mathcal{D}_{val}^{a}$	Validation dataset with acceptable prompts/images
$\mathcal{D}_{val}^{u}$	Validation dataset w/ unacceptable prompts/images
$\mathcal{D}_{adv}^{u}$	Test dataset with adversarial prompts/images
f	T2I model with CRT where f: $c\rightarrow x$
F	Function for Espresso classifier
$\alpha$	Regularization parameter for Espresso fine-tuning
$\overline{\cdot}$	Normalization function
$\epsilon_{\theta}$	Diffusion model parameterized by $\theta$
$\tau$	Temperature parameter

2.2. Concept Removal Techniques

The textual phrase for an acceptable concept is $c^{a}$ , and for an unacceptable concept is $c^{u}$ . For a given $c^{u}$ , $c^{a}$ is either the opposite (e.g., $c^{u}$ = violence vs. $c^{a}$ = peaceful) or a general category of a specific character/object/person (e.g., $c^{u}$ = R2D2 vs. $c^{a}$ = robot). We discuss the selection of $c^{a}$ for a given $c^{u}$ in § 5.3. An image $x$ generated from a T2I model may either contain an unacceptable concept (referred to as $x^{u}$ ) or an acceptable one (referred to as $x^{a}$ ). Similarly, a text prompt p may contain a phrase for an acceptable concept ( $\texttt{p}^{a}$ ) or an unacceptable concept ( $\texttt{p}^{u}$ ). An example of an unacceptable prompt $\texttt{p}^{u}$ containing an unacceptable concept $c^{u}$ = Captain Marvel, is “Captain Marvel soaring through the sky”. CRTs thwart the generation of $x^{u}$ by either fine-tuning the T2I model to suppress $x^{u}$ , or using a classifier as a filter to detect $x^{u}$ , and serve a replacement image instead.

2.2.1. Fine-tuning CRTs:

We first present six state-of-the-art fine-tuning CRTs:

Concept Ablation (CA) (kumari2023ablating) fine-tunes the T2I model to minimize the KL divergence between the model’s output for $\texttt{p}^{u}$ and $\texttt{p}^{a}$ to force the generation of $x^{a}$ instead of $x^{u}$ . Formally, they optimize the following objective function:

\begin{split}\footnotesize\mathcal{L}_{\texttt{CA}}=\mathbb{E}_{\epsilon,z_{t},c^{u},c^{a},t}[w_{t}||\epsilon_{\theta}(z_{t},\phi_{p}(\texttt{p}^{a}),t).sg()-\epsilon_{\theta}(z_{t},\phi_{p}(\texttt{p}^{u}),t)||_{2}^{2}]\end{split}

where $\epsilon\sim\mathcal{N}(0,1)$ , $z_{t}\in\mathcal{E}$ , and $w_{t}$ is a time-dependent weight, and $.sg()$ is the stop-gradient operation.

Forget-Me-Not (FMN) (zhang2023forgetmenot) minimizes the activation maps for $c^{u}$ by modifying $\epsilon_{\theta}$ ’s cross-attention layers. Further, fine-tuning $\epsilon_{\theta}$ , instead of just the cross-attention layers, results in degraded utility.

Selective Amnesia (SA) (heng2023selective) fine-tunes T2I models by adapting continuous learning techniques (elastic weight consolidation and generative replay) for T2I models to forget a concept. They optimize $\mathbb{P}(\texttt{$x$}|\theta^{*},c^{u})$ , the probability of generating $x$ given $\theta^{*}$ and $c^{u}$ , where $\theta^{*}$ are the frozen parameters of the original T2I model:

\begin{split}\footnotesize\mathcal{L}_{\texttt{SA}}=-\mathbb{E}_{\mathbb{P}(\texttt{$x$}|\texttt{p})\mathbb{P}_{f}(c^{u})}[\text{log}\mathbb{P}(\texttt{$x$}|\theta^{*},c^{u})]-\lambda\sum_{i}\frac{M_{i}}{2}(\theta_{i}^{*}-\theta_{i})^{2}\\ +\mathbb{E}_{\mathbb{P}(\texttt{$x$}|\texttt{p})\mathbb{P}_{r}(c^{a})}[\text{log}\mathbb{P}(\texttt{$x$}|\theta,c^{a})]\end{split}

where $M$ is the Fisher information matrix over $c^{a}$ and $c^{u}$ , $\mathbb{P}_{r}$ and $\mathbb{P}_{f}$ are probabilities taken over the distributions of $c^{a}$ and $c^{u}$ respectively, and $\lambda$ is a regularization parameter.

Erased Stable Diffusion (ESD) (gandikota2023erasing) fine-tunes the T2I model by modifying the reverse diffusion process to reduce the probability of generating $x^{u}$ :

\begin{split}\epsilon_{\theta}(\texttt{$x$}_{t},\phi_{p}(c^{u}),t)=\epsilon_{\theta^{*}}(\texttt{$x$}_{t},t)+\eta(\epsilon_{\theta^{*}}(\texttt{$x$}_{t},\phi_{p}(c^{u}),t)-\epsilon_{\theta^{*}}(\texttt{$x$}_{t},t))\end{split}

where $\eta>0$ encourages the noise conditioned on $c^{u}$ to match the unconditioned noise.

Unified Concept Editing (UCE) (gandikota2023unified) fine-tunes the T2I model’s cross-attention layers to minimize the influence of $c^{u}$ , while keeping the remaining concepts unchanged. Their optimization is:

\begin{split}\mathcal{L}_{\texttt{UCE}}=\sum_{c^{u}\in\mathcal{C}^{u},c^{a}\in\mathcal{C}^{a}}||W\times c^{u}-W^{*}\times c^{a}||_{2}^{2}\\ +\sum_{c\in S}||W\times c-W^{*}\times c||_{2}^{2}\end{split}

where $W$ , $W^{*}$ are the parameters of the fine-tuned and original cross-attention layers in $\epsilon_{\theta}$ , $\mathcal{C}^{u}$ and $\mathcal{C}^{a}$ are the space of pre-defined unacceptable and acceptable concepts, and $S$ is a set of concepts for which to preserve utility.

Safe diffusion (SDD) (kim2023towards) fine-tunes the T2I model by encouraging the diffusion model noise conditioned on $c^{u}$ to match the unconditioned noise, while minimizing the utility drop using the following objective function:

\begin{split}\mathcal{L}_{\texttt{SDD}}=\mathbb{E}_{\epsilon,z_{t},c^{u},t}[||\epsilon_{\theta}(z_{t},\phi_{p}(c^{u}),t)-\epsilon_{\theta}(z_{t},t).sg()||_{2}^{2}]\end{split}

where $\epsilon\sim\mathcal{N}(0,1)$ and $z_{t}\in\mathcal{E}(x)$ .

Moderator (Mod) (wang2024moderator) uses task vectors (ilharco2023editing) to remove the parameters responsible for generating $x^{u}$ while maintaining the parameters for acceptable concepts. Mod computes the task vector for the unacceptable parameters ( $T_{u}$ ) and removes them from $\theta$ : $\theta_{new}=\theta-scale\times T_{u}$ where $\theta_{new}$ are the new parameters.

2.2.2. Filtering CRTs:

We now describe two filtering CRTs:

Stable Diffusion Filter (SD-Filter) (radford2021learning) is black-box and the design of the filter is not publicly available. However, Rando et. al. (rando2022redteaming) hypothesize that it involves computing the cosine similarity between the embeddings of a generated image, $x$ , and a pre-defined set of $c^{u}$ . If the cosine similarity is greater than some threshold ( $\Gamma$ ), then $x$ has $c^{u}$ . Formally, their filter $\texttt{F}_{SD}$ can be described as

\texttt{F}_{SD}(\texttt{$x$})=\begin{cases}1&\text{cos}(\phi_{x}(\texttt{$x$}),\phi_{p}(c^{u}))>\Gamma\\ 0&\text{otherwise}\end{cases}

where $\text{cos}(\phi_{x}(\texttt{$x$}),\phi_{p}(c^{u}))=\overline{\phi_{x}(\texttt{$x$})}\cdot\overline{\phi_{p}(c^{u})}$ , and $\overline{\cdot}$ denotes normalization. Here $\texttt{F}_{SD}(\texttt{$x$})=0$ indicates $x^{a}$ and $\texttt{F}_{SD}(\texttt{$x$})=1$ indicates $x^{u}$ . Note that $\Gamma$ varies with $c^{u}$ .

Unsafe Diffusion (UD) (unsafeDiff) is the current state-of-the-art filtering CRT and outperforms SD-Filter (unsafeDiff). UD trains a multi-headed neural network classifier on top of CLIP to identify $x^{u}$ where each head classifies different $c^{u}$ : nudity, violence, disturbing, hateful, and political. Their objective is given as $\texttt{F}_{\texttt{UD}}(\texttt{$x$})=\text{MLP}(\phi_{x}(\texttt{$x$}))$ where MLP is a multi-layer perceptron, and $\texttt{F}_{\texttt{UD}}\in\{0,1\}$ .

2.3. Evading Concept Removal Techniques

An adversary ( $\mathcal{A}dv$ ) may construct adversarial prompts ( $\texttt{p}^{adv}$ ) to evade CRTs and force a T2I model f to generate unacceptable images. We denote a dataset containing adversarial prompts and their corresponding images ( $\texttt{$x$}^{adv}$ ) as $\mathcal{D}_{adv}^{u}=\{(\texttt{$x$}^{adv}_{j},\texttt{p}^{adv}_{j})\}_{j=1}^{N}$ where ideally $\texttt{$x$}^{adv}$ will contain $c^{u}$ . By default, we assume $\mathcal{A}dv$ is aware of f using a CRT. Otherwise we label $\mathcal{A}dv$ as naïve ²²2Some prior works refer to adversaries that take defenses into account as “adaptive”. In line with standard practice in security research, we assume that adversaries are aware of defenses by default. We use the term “naïve,” for adversaries who are not..

$\mathcal{A}dv$ ’s objective is to construct $\texttt{p}^{adv}$ which can force a T2I model to output images with $c^{u}$ while being semantically closer to acceptable prompts so that $\texttt{$x$}^{adv}$ is incorrectly identified as acceptable while triggering the generation of unacceptable images. The existing attacks construct $\texttt{p}^{adv}$ as an optimization problem using some reference $x^{u}$ (or the difference between $\texttt{p}^{a}$ and $\texttt{p}^{u}$ ) as the ground truth. Different attacks vary in ways to solve this optimization. We present four state-of-the-art attacks below:

PEZ (wen2023hard) constructs $\texttt{p}^{adv}$ by identifying text tokens by minimizing: $\mathcal{L}_{PEZ}=1-\text{cos}(\phi_{p}(\texttt{p}^{adv}),\phi_{x}(\texttt{$x^{u}$}))$ .

RingBell (Tsai2023RingABellHR) identifies tokens for $\texttt{p}^{adv}$ by first computing the average difference between the embedding vectors of $\texttt{p}^{u}$ and $\texttt{p}^{a}$ : $\phi_{p}(\hat{\texttt{p}})=\frac{1}{N}\sum_{i=1}^{N}\{\phi_{p}(\texttt{p}^{u}_{i})-\phi_{p}(\texttt{p}^{a}_{i})\}$ from a set of $N$ prompts. Then, $\texttt{p}^{adv}$ is computed by minimizing the distance of its text embedding to ( $\phi_{p}(\texttt{p}^{init})+\eta\cdot\phi_{p}(\hat{\texttt{p}}))$ , formulated as: $\text{min}_{\texttt{p}^{adv}}||\phi_{p}(\texttt{p}^{adv})-(\phi_{p}(\texttt{p}^{init})+\eta\cdot\phi_{p}(\hat{\texttt{p}}))||^{2}$ where $\texttt{p}^{init}$ is an initial unacceptable prompt censored by a CRT, and solved using a genetic algorithm.

SneakyPrompt (yang2023sneakyprompt) uses reinforcement learning to construct $\texttt{p}^{adv}$ specifically against filtering CRTs. It searches for tokens to update an initial prompt $\texttt{p}^{init}$ to form $\texttt{p}^{adv}$ . The reward function is the cosine similarity between $\phi_{x}(\texttt{$x$}^{adv})$ and $\phi_{p}(\texttt{p}^{adv})$ . SneakyPrompt uses $\texttt{p}^{u}$ as $\texttt{p}^{init}$ for better effectiveness and faster convergence.

CCE (pham2023circumventing) uses textual-inversion to construct $\texttt{p}^{adv}$ (gal2022textualinversionimage). $\mathcal{A}dv$ updates CLIP’s vocabulary to include a new token “<s>” which, when included in $\texttt{p}^{adv}$ , generates $\mathcal{A}dv$ ’s desired image. To optimize <s>, we find $v$ , an embedding for <s>, corresponding to least mean-squared-error loss $\mathcal{L}_{CCE}=\mathcal{L}_{MSE}(\epsilon,\epsilon_{\theta}(z_{t},v,t))$ , where $\epsilon\sim\mathcal{N}(0,1)$ .

All of these attacks are naïve except for CCE and SneakyPrompt, which account for different fine-tuning CRTs. In § 5.1, we describe how we modify these naïve attacks to account for CRTs.

3. Problem Statement

We describe an adversary model, requirements of an ideal CRT, and limitations of prior works.

Adversary Model. We consider a deployed target T2I model (f) to which a client has blackbox access to send an input (p) and obtain a generated image ( $x$ ). Further, f uses some CRT. The goal of the adversary ( $\mathcal{A}dv$ ) is to force f to generate $x^{u}$ despite the presence of a CRT. We give an advantage to $\mathcal{A}dv$ by allowing whitebox access to a local identical copy of f with the CRT for use in designing attacks. This is reasonable as $\epsilon_{\theta}$ and CLIP are publicly available. For filtering CRTs, we assume that $\mathcal{A}dv$ has whitebox access to the filter to use its loss function in designing the attacks.

Requirements An ideal CRT should be: R1 Effectivein minimizing the generation of $x^{u}$ ; R2 Utility-preserving, maintaining the quality of acceptable images (for fine-tuning CRTs) or not blocking them (for filtering CRTs); and R3 Robustagainst evasion with $\texttt{p}^{adv}$ .

Limitations of Prior Works. We summarize the limitations of prior works which are empirically evaluated later in § 6. Fine-tuning CRTs modify f thereby explicitly creating a trade-off between R1 and R2 (gandikota2023erasing; kumari2023ablating; zhang2023forgetmenot; heng2023selective; heng2023selective; gandikota2023unified; kim2023towards). Further, most of these CRTs do not consider R3 in their design and are susceptible to evasion by $\mathcal{A}dv$ with $\texttt{p}^{adv}$ . Filtering CRTs (radford2021learning; unsafeDiff) detect unacceptable concepts either in p (aka prompt filter) or in $x$ and block them (a.k.a image filter). Since, they do not modify f, they can maintain R2 without impacting R1. Prior filtering approaches may not be accurate in detecting unacceptable concepts (poor R1) (li2024safegen) and can be easily evaded (poor R3) ((rando2022redteaming) and § 6.3). The state-of-the-art filter, UD, trains specialized classifiers for each concept on large datasets, limiting its generalization to new concepts.

4. Espresso: Robust Filtering CRT

We present Espresso, a robust concept filtering CRT. Espresso uses a classifier F to detect unacceptable concepts in generated images. Following SDv1.4 (stable-diffusion), on detecting an unacceptable concept, Espresso outputs a replacement image (radford2021learning; rando2022redteaming). We identify CLIP as the natural choice for F as it is (a) pre-trained on a large dataset covering a wide range of concepts, and (b) used in many T2I models, and encodes similar information as seen in them. Hence, CLIP is a better choice for a filter than training specialized classifiers for each concept (e.g., (unsafeDiff)).

However, simply using CLIP as F is not sufficient as seen in SDv1.4’s filter ( $\texttt{F}_{SD}$ ) (radford2021learning). Recall from Section 2.2 (Filtering CRTs), $\texttt{F}_{SD}$ thresholds the cosine similarity between the embeddings of $x$ and each pre-defined unacceptable concept to identify $x^{u}$ . Rando et al. (rando2022redteaming) evade $\texttt{F}_{SD}$ by constructing adversarial prompts. Since $\texttt{F}_{SD}$ uses only the cosine similarity to $c^{u}$ , $\mathcal{A}dv$ is free to modify the prompt embeddings in any direction, while constructing $\texttt{p}^{adv}$ . We address this in Espresso by configuring CLIP’s classification objective to allow for fine-tuning to improve robustness.

Configuring CLIP’s Classification Objective. Instead of using the cosine similarity to only $c^{u}$ as in $\texttt{F}_{SD}$ , we configure the objective function of Espresso to use the cosine similarity to both $c^{u}$ and $c^{a}$ . Further, jointly optimizing for two embeddings yields better utility as observed in prior fine-tuning CRTs (kumari2023ablating; Tsai2023RingABellHR; gal2021stylegannada). Given $x$ , Espresso checks the cosine similarity of $\phi_{x}(\texttt{$x$})$ to $\phi_{p}(c^{u})$ and $\phi_{p}(c^{a})$ . Formally, we define Espresso as

(1)

\texttt{F}(x,c^{u},c^{a})=\text{argmax}_{i,i\in{a,u}}\left\{\frac{\text{exp}{(\text{cos}(\phi_{x}(x),\phi_{p}(c_{i}))/\tau)}}{\sum_{j\in\{a,u\}}\text{exp}(\text{cos}(\phi_{x}(x),\phi_{p}(c_{j}))/\tau)}\right\}

where $\tau=\frac{1}{100}$ is the default temperature parameter used in CLIP.

Fine-tuning. The above configuration change lets us use fine-tuning to push acceptable and unacceptable concepts away from each other while maintaining their pairing with their corresponding image embeddings (for utility). Our fine-tuning objectives, inspired by adversarial training, aim to increase the distance between training data and the decision boundary to reduce the impact of adversarial examples (zhang2019theoretically). We use two different fine-tuning variants depending on the group of concepts.

For concepts that have a strong correlation between $\phi_{p}(\texttt{p})$ and the corresponding $\phi_{x}(\texttt{$x$})$ (for example, where $c^{a}$ is a broader category that includes $c^{u}$ ; $c^{u}$ = R2D2 and $c^{a}$ = robot), we fine-tune F to increase the difference between $\phi_{p}(\texttt{p}^{u})$ and $\phi_{p}(\texttt{p}^{a})$ . We minimize:

(2)

L_{\textsc{Espresso}}=-||\overline{\phi_{p}(\texttt{p}^{u})-\phi_{p}(\texttt{p}^{a})}||_{2}

where $\overline{\cdot}$ denotes normalization. For the case where $c^{u}$ and $c^{a}$ are opposites (e.g., $c^{u}$ = violence and $c^{a}$ = peaceful), the above objective function might have a low correlation between $\phi_{p}(\texttt{p})$ and the corresponding $\phi_{x}(\texttt{$x$})$ , leading to poor utility. In this case, we use following objective function:

(3)

\begin{split}\mathcal{L}_{\textsc{Espresso}}=\alpha_{\text{aa}}\mathcal{L}_{\text{Con}}(\mathcal{D}_{aa})-\alpha_{\text{ua}}\mathcal{L}_{\text{Con}}(\mathcal{D}_{ua})\\ +\alpha_{\text{uu}}\mathcal{L}_{\text{Con}}(\mathcal{D}_{uu})-\alpha_{\text{au}}\mathcal{L}_{\text{Con}}(\mathcal{D}_{au})\\ -\alpha_{\text{uu-t}}\mathcal{L}_{MSE}(\phi_{p}(\mathcal{P}^{u}),\phi_{p}(\mathcal{P}^{a}))\\ \end{split}

where $\mathcal{D}_{aa}=\{(\texttt{$x^{a}$}_{j},\texttt{p}^{a}_{j})\}_{j=1}^{N}$ , $\mathcal{D}_{au}=\{(\texttt{$x^{a}$}_{j},\texttt{p}^{u}_{j})\}_{j=1}^{N}$ ,
$\mathcal{D}_{ua}=\{(\texttt{$x^{u}$}_{j},\texttt{p}^{a}_{j})\}_{j=1}^{N}$ , $\mathcal{D}_{uu}=\{(\texttt{$x^{u}$}_{j},\texttt{p}^{u}_{j})\}_{j=1}^{N}$ , $\mathcal{P}^{u}=\{\texttt{p}^{u}_{j}\}$ , and $\mathcal{P}^{a}=\{\texttt{p}^{a}_{j}\}$ , and $\alpha_{(\cdot)}$ are regularization hyperparameters. We assign equal weight to the loss terms, thus choosing $\alpha_{(.)}=1$ . The above objective function encourages the CLIP embeddings of $x^{u}$ and $\texttt{p}^{u}$ , and $x^{a}$ and $\texttt{p}^{a}$ , to be closer together while increasing the distance between $x^{u}$ and $\texttt{p}^{a}$ , and $x^{a}$ and $\texttt{p}^{u}$ , respectively.

We use prompts ( $\texttt{p}^{u}$ and $\texttt{p}^{a}$ ) for fine-tuning in Equations 2 and 3 instead of only concepts ( $c^{u}$ and $c^{a}$ ): $\texttt{p}^{u}$ and $\texttt{p}^{a}$ already contain $c^{u}$ and $c^{a}$ , and provide more context. During fine-tuning, there is a trade-off between R1 and R2 which is inherent to all other fine-tuning CRTs. We subject our fine-tuning to the constraint that achieved the highest effectiveness for the least drop in utility. In Section 6.1, we specify which of the fine-tuning objectives (Equation 2 or 3) are used for which concepts. We show the benefit of fine-tuning in § 6.1.

5. Experimental Setup

We describe the attack baselines against CRTs (§ 5.1), metrics (§ 5.2), and present a pipeline for evaluating CRTs (§ 5.3). We use SDv1.4 (stable-diffusion) and its default configuration as f following prior work (gandikota2023erasing; kumari2023ablating; zhang2023forgetmenot; heng2023selective; gandikota2023unified; kim2023towards). We compare Espresso with the seven fine-tuning and one filtering CRTs from § 2.2 (we leave out SD-Filter as UD outperforms it).

5.1. Revisiting Attack Baselines

We modify existing naïve attacks: RingBell, and PEZ, to account for CRTs (indicated with “+”). All CRTs use some variant of the following optimization: detach $c^{u}$ from p such that the generated image is far from $c^{u}$ and closer to some $c^{a}$ . On the other hand, attacks against T2I models design $\texttt{p}^{adv}$ such that $\texttt{$x$}^{adv}$ is closer to $c^{u}$ and far from $c^{a}$ . Hence, to design an effective attack which accounts for such CRTs, in addition to the attacks’ original objectives, we minimize the loss between $\phi_{p}(\texttt{p}^{adv})$ and $\phi_{p}(c^{a})$ while increasing the loss between $\phi_{p}(\texttt{p}^{adv})$ and $\phi_{p}(c^{u})$ . We modify the attacks using the following loss:

(4)

\begin{split}\mathcal{L}_{att+}=\mathcal{L}_{att}-\alpha_{u}\mathcal{L}_{MSE}(\phi_{p}(c^{u}),\phi_{p}(\texttt{p}^{adv}))+\\ \alpha_{a}\mathcal{L}_{MSE}(\phi_{p}(c^{a}),\phi_{p}(\texttt{p}^{adv}))\end{split}

where $att\in$ {RingBell, PEZ } when CRT $\in$ {CA, FMN, SA, ESD, UCE, SDD, UD, Espresso }, and $\mathcal{L}_{att}$ is the attack’s original objective. We assign equal weight to all loss terms and use $\alpha_{u}=\alpha_{a}=1.$ Recall from § 2.3 that CCE already accounts for different fine-tuning CRTs. For filtering CRTs (UD and Espresso), we modify CCE using Equation 4 and call it CCE +. Finally, typographic attack (noever2021typographicattck) against CLIP superimposes text characters onto an (unrelated) image to fool CLIP by forcing it to focus on the text instead of the image. We turn this into an attack against CRTs by superimposing $c^{a}$ at the bottom of $x^{u}$ . Using the resulting adversarial images, we use PEZ + to find their corresponding $\texttt{p}^{adv}$ . We call this attack Typo +.

Refer to caption — Figure 1. Overview of pipeline for evaluating CRTs. Prompts, images and arrows for unacceptable (acceptable) in red (green).

5.2. Metrics

We now describe the metrics to evaluate each of the requirements. We use a reference CLIP (SDv1.4), separate from f with the CRTs, following prior work (kumari2023ablating; gandikota2023erasing; gandikota2023unified; kim2023towards).

R1 (Effectiveness).

•

For fine-tuning CRTs, we use CLIP accuracy (hessel-etal-2021-clipscore; kumari2023ablating) which is the cosine similarity between the embeddings of the generated image $x$ with the embeddings of $c^{u}$ and $c^{a}$ from the reference CLIP. This gives the likelihood of predicting $c^{u}$ . Hence, CLIP accuracy should be low (ideally zero) for effective concept removal. Formally, it is:

\frac{\text{exp}{(\text{cos}(\tilde{\phi_{x}}(\texttt{$x$}),\tilde{\phi_{p}}(c^{u})))}}{\text{exp}(\text{cos}(\tilde{\phi_{x}}(\texttt{$x$}),\tilde{\phi_{p}}(c^{u})))+\text{exp}(\text{cos}(\tilde{\phi_{x}}(\texttt{$x$}),\tilde{\phi_{p}}(c^{a})))}

where $\tilde{\phi_{p}}$ and $\tilde{\phi_{x}}$ are embeddings from the reference CLIP. For Espresso, if $x^{u}$ is detected, a replacement image is generated. Here, we calculate the CLIP accuracy on the final set of images after filtering. Since the metrics compare with the reference CLIP, we use the same default replacement image as in the SD v1.4.

•

For filtering CRTs, we use false negative rates (FNR) (unsafeDiff; rando2022redteaming) which is the fraction of images with $c^{u}$ which are not blocked. It should be low (ideally zero).

R2 (Utility).

•

For fine-tuning CRTs, we use normalized CLIP score which is the ratio of cosine similarity between $\phi_{x}(\texttt{$x$})$ and $\phi_{p}(\texttt{p})$ from f, to that from a reference CLIP as a baseline. Here, the baseline from a reference CLIP is assumed to have the maximum achievable CLIP score. Formally, we can write normalized CLIP score as $\frac{\text{cos}(\phi_{x}(\texttt{$x$}),\phi_{p}(\texttt{p}))}{\text{cos}(\tilde{\phi}_{x}({\texttt{$x$}}),\tilde{\phi}_{p}(\texttt{p}))}$ . It should be high (ideally one) for high utility. This metric is different from standard CLIP scores from prior work (hessel-etal-2021-clipscore; kumari2023ablating; kim2023towards; gandikota2023unified) which only measures the cosine similarity between $\phi_{x}(\texttt{$x$})$ and $\phi_{p}(\texttt{p})$ . We did this to scale the CLIP score between zero and one while comparing f to the reference CLIP.
•

For filtering CRTs, we use False Positive Rates (FPR) (unsafeDiff; rando2022redteaming) which is the fraction of images without $c^{u}$ which are blocked. It should be low (ideally zero).

R3 (Robustness). We use the same metrics as R1, but in the presence of $\mathcal{A}dv$ .

5.3. Pipeline for Evaluating CRTs

We now describe Figure 1 which includes identifying acceptable concepts (step 1), generation of datasets (step 2), training filters or fine-tuning T2I models with CRTs (step 3), validating acceptable concepts (step 4), and evaluating different CRTs (step 5).

Concept Types. We use the same $c^{u}$ as prior work (kumari2023ablating; pham2023circumventing; kim2023towards), categorizing them into three groups:

•

Group-1 covers inappropriate concepts: nudity, (e.g., genitalia), violence, (e.g., bloody scenes), disturbing (e.g., human flesh), hateful (e.g. harmful stereotypes).
•

Group-2 covers copyright-infringing concepts: Grumpy Cat, Nemo, Captain Marvel, Snoopy, and R2D2.
•

Group-3 covers unauthorized use of images: Taylor Swift, Angelina Jolie, Brad Pitt, and Elon Musk.

Step 1: Identifying Acceptable Concepts A good choice of $c^{a}$ is one which effectively steers a T2I model away from generating $x^{u}$ while maintaining utility on other concepts. Hence, the choice of $c^{a}$ can impact R1 and R2. We select $c^{a}$ for a given $c^{u}$ such that it is either opposite to $c^{u}$ (Group-1) or is a semantic generalization of $c^{u}$ so as to avoid infringing copyrights (Groups-2,3). For $c^{u}$ in Group-1, we consider multiple alternative synonyms for $c^{a}$ , from which we choose the best possible candidate by measuring effectiveness and utility on a validation dataset (see Step 4). For $c^{u}$ in Groups-2,3, we use $c^{a}$ from prior work for a fair comparison (kumari2023ablating; heng2023selective). We indicate them in the format “ $c^{u}$ $\rightarrow$ $c^{a}$ ”:

•

For Group-1, $c^{a}$ is the opposite of $c^{u}$ and we consider the following choices of $c^{a}$ : nudity $\rightarrow$ {clothed and clean}; violence $\rightarrow$ {peaceful, nonviolent, and gentle}; disturbing $\rightarrow$ {pleasing, calming, and soothing}; hateful $\rightarrow$ {loving, compassionate, and kind}.
•

For Group-2: $c^{a}$ is the broader category of $c^{u}$ , following prior works (kumari2023ablating; heng2023selective; gandikota2023erasing): Grumpy Cat $\rightarrow$ cat, Nemo $\rightarrow$ fish, Captain Marvel $\rightarrow$ female superhero, Snoopy $\rightarrow$ dog, and R2D2 $\rightarrow$ robot.
•

For Group-3, $c^{a}$ is the sex of $c^{u}$ , following prior works (heng2023selective; zhang2023forgetmenot; kim2023towards): {Taylor Swift, Angelina Jolie} $\rightarrow$ woman and {Brad Pitt, Elon Musk} $\rightarrow$ man.

We compare Espresso with each CRT category separately using concepts they were originally evaluated on: Group-1 for filtering CRTs (unsafeDiff); all groups for fine-tuning CRTs (kumari2023ablating; heng2023selective; zhang2023forgetmenot; kim2023towards).

Step 2: Generate and Split Datasets We describe the generation of train, validation, and test datasets.

Train Datasets. We summarize the different training/fine-tuning dataset configurations across CRTs in Table 2.

Table 2. Training dataset configurations required by CRTs.

CRT	Configuration Requirements
CA (kumari2023ablating)	200 unacceptable prompts ( $\texttt{p}^{a}$ ) from ChatGPT with one image/prompt from SDv1.4
ESD (gandikota2023erasing)	Unacceptable concept ( $c^{u}$ )
FMN (zhang2023forgetmenot)	8 unacceptabe prompts ( $\texttt{p}^{u}$ ) and one image/prompt from SDv1.4
SDD (kim2023towards)	Unacceptable concept ( $c^{u}$ ) and 10 corresponding images
SA (heng2023selective)	Acceptable concept ( $c^{a}$ ) and 1000 corresponding images, and 6 unacceptable prompts ( $\texttt{p}^{u}$ )
UCE (gandikota2023unified)	Unacceptable and acceptable concepts ( $c^{u}$ and $c^{a}$ )
Mod (wang2024moderator)	Unacceptable concept ( $c^{u}$ ) and 120 corresponding images
UD (unsafeDiff)	776 total images with 580 acceptable images ( $x^{a}$ ), and 196 unacceptable images ( $x^{u}$ ): nudity (48), violence (45), disturbing (68), and hateful (35)
Espresso	10 unacceptable prompts ( $\texttt{p}^{u}$ ) and acceptable prompts ( $\texttt{p}^{a}$ ) using ChatGPT with one image/prompt from SDv1.4

For fine-tuning CRTs, we use the exact same configuration as described in their original works. This configuration for a specific CRT is the same across different concepts. CA uses acceptable prompts which are generated from ChatGPT such that they contain $c^{a}$ , and 1 image per prompt. ESD and SDD both use only $c^{u}$ , and SDD additionally uses 10 images corresponding to $c^{u}$ . All images are generated using SD v1.4. FMN uses unacceptable prompts of the form “An image of { $c^{u}$ }”, and 1 image per prompt. Mod uses $c^{u}$ and 120 corresponding images. For all of them, we use their code for consistency with their original papers (githubGitHubNupurkmr9conceptablation; githubGitHubRohitgandikotaerasing; githubGitHubSHILabsForgetMeNot; githubGitHubRohitgandikotaunifiedconceptediting; githubGitHubClearnusselectiveamnesia; githubGitHubNannullnasafediffusion; githubGitHubYitingQuunsafediffusion; githubGitHubWangModerator).

For filtering CRTs, we train $\texttt{F}_{\texttt{UD}}$ using the original dataset configuration and code (unsafeDiff). For Espresso, we follow CA (kumari2023ablating) to generate 10 unacceptable and acceptable prompts using ChatGPT, with one image per prompt from SDv1.4. For Group-2, we randomly select 10 ChatGPT-generated prompts from CA (kumari2023ablating). We use a small amount of training data following prior works which show little data is enough to modify CLIP (yang2023robust; carlini2022poisoning). This is validated by our results (§ 6).

Validation Datasets. For validation datasets ( $\mathcal{D}_{val}$ ), we denote the dataset with acceptable prompts ( $\texttt{p}^{a}$ ) and corresponding images ( $x^{a}$ ) as $\mathcal{D}_{val}^{u}$ ; and the dataset with acceptable prompts ( $\texttt{p}^{a}$ ) and corresponding images ( $x^{a}$ ) as $\mathcal{D}_{val}^{a}$ . For R1, we use $\mathcal{D}_{val}^{u}$ by generating 10 unacceptable prompts using ChatGPT, and generate 5 images per prompt using SD v1.4. For R2, we use $\mathcal{D}_{val}^{a}$ by randomly choosing 100 acceptable prompts from the COCO 2014 dataset (coco), and 1 image per prompt, from SD v1.4. We summarize them in Table 3.

Table 3. Validation dataset configuration.

Concepts	Data	Configuration
(Requirement)
Group-1 (R1)	$\mathcal{D}_{val}^{u}$	10 unacceptable prompts ( $\texttt{p}^{u}$ ) from ChatGPT and 5 images ( $x^{u}$ ) per prompt from SDv1.4
Group-2 (R1)	$\mathcal{D}_{val}^{u}$	10 unacceptable prompts ( $\texttt{p}^{u}$ ) from ChatGPT and 5 images ( $x^{u}$ ) per prompt from SDv1.4
Group-3 (R1)	$\mathcal{D}_{val}^{u}$	10 unacceptable prompts ( $\texttt{p}^{u}$ ) from ChatGPT and 5 images ( $x^{u}$ ) per prompt from SDv1.4
All (R2)	$\mathcal{D}_{val}^{a}$	100 acceptable prompts ( $\texttt{p}^{a}$ ) and 1 image ( $x^{a}$ ) per prompt from the COCO 2014 dataset

Test Datasets. We now present test dataset ( $\mathcal{D}_{te}$ ) for evaluating different CRTs. We denote the dataset with acceptable prompts ( $\texttt{p}^{a}$ ) and corresponding images ( $x^{a}$ ) as $\mathcal{D}_{te}^{a}$ ; and with unacceptable prompts ( $\texttt{p}^{u}$ ) and corresponding images ( $x^{u}$ ) as $\mathcal{D}_{te}^{u}$ .

For evaluating effectiveness (R1), we use $\mathcal{D}_{te}^{u}$ generated as follows:

•

For Group-1 concepts (nude, violent, hateful, or disturbing), we use Inappropriate Image Prompts (I2P), containing prompts which are likely to generate unsafe images (schramowski2022safe). We process I2P dataset following prior work (gandikota2023erasing; gandikota2023unified) to obtain 300 unacceptable prompts: For nudity, I2P includes a “nudity percentage” attribute. We choose all unacceptable prompts with a nudity percentage $>10$ , resulting in a total of 300 unacceptable prompts, in accordance with prior works (gandikota2023erasing; gandikota2023unified). UD (unsafeDiff) also used political as a concept, which is excluded from our evaluation since it is not a part of I2P.
•

For concepts in Group-2, 3, there are no standard benchmark datasets. Hence, we use the dataset from prior works (kumari2023ablating; gandikota2023erasing) with 200 unacceptable images generated from SDv1.4 from 10 unacceptable prompts generated from ChatGPT. For R2, we use the COCO 2014 test dataset as $\mathcal{D}_{te}^{a}$ , consistent with prior work, with 200 randomly chosen acceptable prompts, non-overlapping with $\mathcal{D}_{val}^{a}$ . For R3, we use $\mathcal{D}_{adv}^{u}$ by applying different attacks on $\mathcal{D}_{te}^{u}$ to generate adversarial prompts.

We summarize the datasets in Table 4.

Table 4. Evaluation dataset configuration.

Concepts	Data	Configuration
(Requirement)
Group-1 (R1, R3)	$\mathcal{D}_{te}^{u}$	I2P Dataset (schramowski2022safe) of unacceptable prompts: for nudity: 449 prompts, violence: 758, disturbing: 857, hateful: 235
Group-2 (R1, R3)	$\mathcal{D}_{te}^{u}$	10 unacceptable prompts ( $\texttt{p}^{u}$ ) from ChatGPT and 20 images ( $x^{u}$ ) per prompt from SDv1.4
Group-3 (R1, R3)	$\mathcal{D}_{te}^{u}$	10 unacceptable prompts ( $\texttt{p}^{u}$ ) from ChatGPT and 20 images ( $x^{u}$ ) per prompt from SDv1.4
All (R2)	$\mathcal{D}_{te}^{a}$	200 acceptable prompts ( $\texttt{p}^{a}$ ) from COCO 2014 dataset

Step 3: Fine-tuning with CRTs/training filter. We train each baseline CRT in § 2.3 using $\mathcal{D}_{tr}$ . We train UD’s classifier on their dataset and we fine-tune Espresso on $\mathcal{D}_{tr}$ using Equation 2 for Groups-2,3 concepts and Equation 3 for Group-1 concepts. We use the CLIP L-patch-14 (vit) due to its popularity, which is also the default encoder with SDv1.4. However, other variants of CLIP are also applicable.

Step 4: Select best $c^{a}$ using $\mathcal{D}_{val}$ . For Group-1 concepts, we evaluate R1 and R2 for different candidates of $c^{a}$ on $\mathcal{D}_{val}^{u}$ and $\mathcal{D}_{val}^{a}$ respectively. We found the concepts with the best results: nudity $\rightarrow$ clean, violence $\rightarrow$ peaceful, disturbing $\rightarrow$ pleasing, and hateful $\rightarrow$ loving. For nudity, we eliminated clothed as it blocked images with minimal exposed skin despite being acceptable (unsafeDiff; schramowski2022safe).

Step 5: Evaluation. We evaluate R1 on $\mathcal{D}_{te}^{u}$ , R2 on $\mathcal{D}_{te}^{a}$ , and R3 on $\mathcal{D}_{adv}^{u}$ , which is generated by running different attacks on $\mathcal{D}_{te}^{u}$ to get $\texttt{p}^{adv}$ . We pass the prompts from the datasets to the T2I model and compute different metrics.

6. Evaluation

We demonstrate the impact of fine-tuning (§ 6.1), and compare Espresso with fine-tuning CRTs (§ 6.2) and filtering CRTs (§ 6.3).

6.1. Impact of Fine-Tuning

We first empirically show how fine-tuning can improve Espresso’s robustness similar to adversarial training in classifiers. Adversarial training (zhang2019theoretically) explicitly pushes the decision boundary away from training data records. Similarly, our fine-tuning objective, pushes the embeddings of acceptable and unacceptable concepts away from each other. This results in correctly classifying $\texttt{$x$}^{adv}$ by Espresso.

To demonstrate this, we generated 10 adversarial prompts with 5 images per prompt using CCE +. For each image, $\texttt{$x$}^{adv}$ , we compute the cosine similarity between $\phi_{x}(\texttt{$x$}^{adv})$ and $\phi_{p}(c^{u})$ , as well as between $\phi_{x}(\texttt{$x$}^{adv})$ and $\phi_{p}(c^{a})$ . We then take the absolute values of both similarities and calculate their difference. We report the mean difference in Table 5. We use Equation 2 for fine-tuning in Group-2 and 3, where $c^{a}$ is a broader category that includes $c^{u}$ . We use Equation 3 for Group-1 concepts as $c^{u}$ and $c^{a}$ are opposites.

Table 5. Mean difference of the absolute cosine similarities between

\phi_{x}(\texttt{$x$}^{adv})

and each of

\phi_{p}(c^{u})

and

\phi_{p}(c^{a})

|\cos(\phi_{x}(\texttt{$x$}^{adv}),\phi_{p}(c^{u}))|-|\cos(\phi_{x}(\texttt{$x$}^{adv}),\phi_{p}(c^{a}))|

. With finetuning (w/ FT), the mean difference is consistently higher than without finetuning (w/o FT), implying better robustness.

Concept	w/o FT	w/ FT
Nudity	10.28 $\pm$ 0.01	16.82 $\pm$ 0.03
Violence	4.45 $\pm$ 0.00	6.92 $\pm$ 0.01
Grumpy Cat	7.48 $\pm$ 0.00	8.77 $\pm$ 0.00
Nemo	3.88 $\pm$ 0.01	5.03 $\pm$ 0.01
Captain Marvel	5.46 $\pm$ 0.00	5.48 $\pm$ 0.01
Snoopy	9.12 $\pm$ 0.01	10.17 $\pm$ 0.02
R2D2	5.79 $\pm$ 0.00	8.35 $\pm$ 0.00
Taylor Swift	4.79 $\pm$ 0.01	4.87 $\pm$ 0.00
Angelina Jolie	5.54 $\pm$ 0.02	5.64 $\pm$ 0.00
Brad Pitt	6.81 $\pm$ 0.01	6.95 $\pm$ 0.00
Elon Musk	2.67 $\pm$ 0.01	2.71 $\pm$ 0.00

Table 6. R1 Effectiveness: Comparison of fine-tuning CRTs using CLIP accuracy on acceptable prompts in

\mathcal{D}_{te}^{u}

(lower is better). We use red if accuracy is

>

50; blue if accuracy is between 25-50; green if accuracy is

<

25.

CRT	Concepts
	Nudity	Violence	Grumpy	Nemo	Captain	Snoopy	R2D2	Taylor	Angelina	Brad	Elon
	(I2P)	(I2P)	Cat	Nemo	Marvel	Snoopy	R2D2	Swift	Jolie	Pitt	Musk
CA (kumari2023ablating)	0.82 $\pm$ 0.01	0.78 $\pm$ 0.01	0.00 $\pm$ 0.00	0.02 $\pm$ 0.00	0.40 $\pm$ 0.05	0.06 $\pm$ 0.05	0.13 $\pm$ 0.02	0.73 $\pm$ 0.05	0.83 $\pm$ 0.02	0.86 $\pm$ 0.04	0 .64 $\pm$ 0.03
FMN (zhang2023forgetmenot)	0.83 $\pm$ 0.01	0.64 $\pm$ 0.04	0.34 $\pm$ 0.02	0.61 $\pm$ 0.01	0.82 $\pm$ 0.03	0.16 $\pm$ 0.00	0.89 $\pm$ 0.03	0.45 $\pm$ 0.02	0.59 $\pm$ 0.06	0.79 $\pm$ 0.04	0.56 $\pm$ 0.22
SA (heng2023selective)	0.69 $\pm$ 0.09	0.69 $\pm$ 0.00	0.16 $\pm$ 0.00	0.87 $\pm$ 0.04	0.93 $\pm$ 0.02	0.55 $\pm$ 0.07	0.98 $\pm$ 0.01	0.82 $\pm$ 0.05	0.49 $\pm$ 0.04	0.63 $\pm$ 0.05	0.75 $\pm$ 0.04
ESD (gandikota2023erasing)	0.62 $\pm$ 0.06	0.63 $\pm$ 0.01	0.28 $\pm$ 0.06	0.64 $\pm$ 0.06	0.37 $\pm$ 0.04	0.20 $\pm$ 0.02	0.41 $\pm$ 0.04	0.11 $\pm$ 0.02	0.29 $\pm$ 0.05	0.17 $\pm$ 0.02	0.17 $\pm$ 0.02
UCE (gandikota2023unified)	0.70 $\pm$ 0.01	0.71 $\pm$ 0.01	0.05 $\pm$ 0.00	0.43 $\pm$ 0.00	0.04 $\pm$ 0.00	0.03 $\pm$ 0.00	0.40 $\pm$ 0.01	0.02 $\pm$ 0.01	0.06 $\pm$ 0.00	0.05 $\pm$ 0.00	0.10 $\pm$ 0.01
SDD (kim2023towards)	0.57 $\pm$ 0.02	0.55 $\pm$ 0.02	0.20 $\pm$ 0.02	0.20 $\pm$ 0.03	0.41 $\pm$ 0.03	0.37 $\pm$ 0.03	0.39 $\pm$ 0.02	0.05 $\pm$ 0.02	0.06 $\pm$ 0.01	0.04 $\pm$ 0.01	0.06 $\pm$ 0.01
Mod (wang2024moderator)	0.87 $\pm$ 0.02	0.92 $\pm$ 0.05	0.02 $\pm$ 0.00	0.25 $\pm$ 0.02	0.73 $\pm$ 0.03	0.01 $\pm$ 0.00	0.28 $\pm$ 0.02	0.03 $\pm$ 0.01	0.09 $\pm$ 0.01	0.00 $\pm$ 0.01	0.13 $\pm$ 0.04
Espresso	0.15 $\pm$ 0.06	0.20 $\pm$ 0.05	0.00 $\pm$ 0.01	0.10 $\pm$ 0.02	0.03 $\pm$ 0.01	0.08 $\pm$ 0.02	0.00 $\pm$ 0.00	0.02 $\pm$ 0.00	0.03 $\pm$ 0.00	0.00 $\pm$ 0.00	0.03 $\pm$ 0.00

Table 7. R2 (Utility): Comparison with fine-tuning CRTs using normalized CLIP scores on

\mathcal{D}_{te}^{a}

(higher is better). We use red if score is between 50-70, blue if between 70-90; green if

>

90. Note: Espresso’s utility against Group-2 concepts like Nemo, Captain Marvel, Snoopy, and R2D2 can be improved as described in Section 6.2.

CRT	Concepts
	Nudity	Violence	Grumpy	Nemo	Captain	Snoopy	R2D2	Taylor	Angelina	Brad	Elon
	Nudity	Violence	Cat	Nemo	Marvel	Snoopy	R2D2	Swift	Jolie	Pitt	Musk
CA (kumari2023ablating)	0.93 $\pm$ 0.00	0.93 $\pm$ 0.00	0.93 $\pm$ 0.00	0.93 $\pm$ 0.00	0.93 $\pm$ 0.00	0.93 $\pm$ 0.00	0.93 $\pm$ 0.00	0.93 $\pm$ 0.00	0.93 $\pm$ 0.00	0.93 $\pm$ 0.00	0.93 $\pm$ 0.00
FMN (zhang2023forgetmenot)	0.79 $\pm$ 0.00	0.79 $\pm$ 0.00	0.79 $\pm$ 0.00	0.79 $\pm$ 0.00	0.79 $\pm$ 0.00	0.79 $\pm$ 0.00	0.79 $\pm$ 0.00	0.79 $\pm$ 0.00	0.79 $\pm$ 0.00	0.79 $\pm$ 0.00	0.79 $\pm$ 0.00
SA (heng2023selective)	0.79 $\pm$ 0.00	0.79 $\pm$ 0.00	0.79 $\pm$ 0.00	0.79 $\pm$ 0.00	0.79 $\pm$ 0.00	0.79 $\pm$ 0.00	0.79 $\pm$ 0.00	0.79 $\pm$ 0.00	0.79 $\pm$ 0.00	0.79 $\pm$ 0.01	0.79 $\pm$ 0.00
ESD (gandikota2023erasing)	0.82 $\pm$ 0.01	0.82 $\pm$ 0.00	0.82 $\pm$ 0.01	0.82 $\pm$ 0.00	0.82 $\pm$ 0.01	0.82 $\pm$ 0.01	0.82 $\pm$ 0.01	0.82 $\pm$ 0.01	0.82 $\pm$ 0.01	0.82 $\pm$ 0.01	0.82 $\pm$ 0.01
UCE (gandikota2023unified)	0.96 $\pm$ 0.02	0.96 $\pm$ 0.00	0.97 $\pm$ 0.03	0.96 $\pm$ 0.00	0.96 $\pm$ 0.00	0.97 $\pm$ 0.02	0.96 $\pm$ 0.00	0.97 $\pm$ 0.02	0.97 $\pm$ 0.01	0.96 $\pm$ 0.03	0.97 $\pm$ 0.00
SDD (kim2023towards)	0.86 $\pm$ 0.00	0.75 $\pm$ 0.00	0.93 $\pm$ 0.00	0.86 $\pm$ 0.00	0.82 $\pm$ 0.00	0.82 $\pm$ 0.00	0.64 $\pm$ 0.00	0.82 $\pm$ 0.00	0.82 $\pm$ 0.00	0.61 $\pm$ 0.00	0.89 $\pm$ 0.00
Mod (wang2024moderator)	0.93 $\pm$ 0.01	0.53 $\pm$ 0.00	0.57 $\pm$ 0.00	0.55 $\pm$ 0.00	0.53 $\pm$ 0.00	0.50 $\pm$ 0.01	0.46 $\pm$ 0.00	0.86 $\pm$ 0.00	0.61 $\pm$ 0.00	0.68 $\pm$ 0.00	0.71 $\pm$ 0.00
Espresso	0.94 $\pm$ 0.08	0.59 $\pm$ 0.11	0.98 $\pm$ 0.04	0.37 $\pm$ 0.02	0.37 $\pm$ 0.03	0.66 $\pm$ 0.03	0.66 $\pm$ 0.02	0.98 $\pm$ 0.02	0.98 $\pm$ 0.03	0.98 $\pm$ 0.01	0.97 $\pm$ 0.01

Table 8. R3 (Robustness): Comparison with fine-tuning CRTs using CLIP accuracy on adversarial prompts in

\mathcal{D}_{adv}^{u}

(lower is better). We evaluate fine-tuning CRT’s against CCE and Espresso against CCE + since CCE is already adapted to fine-tuning CRT’s. We use red if accuracy is

>

50; blue if accuracy is between 25-50; green if accuracy is

<

25.

CRT	Concepts
	Nudity	Violence	Grumpy	Nemo	Captain	Snoopy	R2D2	Taylor	Angelina	Brad	Elon
	(I2P)	(I2P)	Cat	Nemo	Marvel	Snoopy	R2D2	Swift	Jolie	Pitt	Musk
Typo +
CA (kumari2023ablating)	0.58 $\pm$ 0.02	0.75 $\pm$ 0.01	0.26 $\pm$ 0.02	0.27 $\pm$ 0.01	0.42 $\pm$ 0.01	0.29 $\pm$ 0.02	0.23 $\pm$ 0.02	0.09 $\pm$ 0.02	0.24 $\pm$ 0.01	0.05 $\pm$ 0.01	0.31 $\pm$ 0.06
FMN (zhang2023forgetmenot)	0.61 $\pm$ 0.02	0.75 $\pm$ 0.02	0.21 $\pm$ 0.01	0.31 $\pm$ 0.01	0.49 $\pm$ 0.02	0.27 $\pm$ 0.02	0.22 $\pm$ 0.02	0.03 $\pm$ 0.01	0.17 $\pm$ 0.01	0.06 $\pm$ 0.01	0.34 $\pm$ 0.01
SA (heng2023selective)	0.31 $\pm$ 0.01	0.71 $\pm$ 0.02	0.99 $\pm$ 0.01	0.94 $\pm$ 0.01	0.89 $\pm$ 0.02	0.73 $\pm$ 0.03	0.99 $\pm$ 0.00	0.20 $\pm$ 0.02	0.05 $\pm$ 0.01	0.43 $\pm$ 0.04	0.65 $\pm$ 0.05
ESD (gandikota2023erasing)	0.39 $\pm$ 0.01	0.70 $\pm$ 0.01	0.27 $\pm$ 0.02	0.25 $\pm$ 0.05	0.40 $\pm$ 0.03	0.23 $\pm$ 0.02	0.25 $\pm$ 0.05	0.03 $\pm$ 0.01	0.08 $\pm$ 0.07	0.04 $\pm$ 0.03	0.23 $\pm$ 0.05
UCE (gandikota2023unified)	0.41 $\pm$ 0.00	0.60 $\pm$ 0.00	0.28 $\pm$ 0.02	0.29 $\pm$ 0.02	0.34 $\pm$ 0.02	0.21 $\pm$ 0.03	0.17 $\pm$ 0.02	0.00 $\pm$ 0.00	0.05 $\pm$ 0.00	0.02 $\pm$ 0.00	0.12 $\pm$ 0.00
SDD (kim2023towards)	0.20 $\pm$ 0.02	0.50 $\pm$ 0.04	0.27 $\pm$ 0.02	0.21 $\pm$ 0.02	0.48 $\pm$ 0.01	0.19 $\pm$ 0.01	0.31 $\pm$ 0.00	0.05 $\pm$ 0.01	0.06 $\pm$ 0.00	0.05 $\pm$ 0.00	0.10 $\pm$ 0.01
Mod (wang2024moderator)	0.83 $\pm$ 0.01	0.90 $\pm$ 0.01	0.01 $\pm$ 0.00	0.21 $\pm$ 0.02	0.69 $\pm$ 0.04	0.06 $\pm$ 0.01	0.30 $\pm$ 0.00	0.01 $\pm$ 0.01	0.05 $\pm$ 0.00	0.00 $\pm$ 0.00	0.13 $\pm$ 0.02
Espresso	0.14 $\pm$ 0.01	0.20 $\pm$ 0.01	0.10 $\pm$ 0.01	0.06 $\pm$ 0.01	0.09 $\pm$ 0.01	0.09 $\pm$ 0.01	0.08 $\pm$ 0.01	0.00 $\pm$ 0.01	0.00 $\pm$ 0.01	0.01 $\pm$ 0.01	0.01 $\pm$ 0.01
PEZ +
CA (kumari2023ablating)	0.75 $\pm$ 0.01	0.84 $\pm$ 0.02	0.33 $\pm$ 0.04	0.52 $\pm$ 0.01	0.70 $\pm$ 0.02	0.20 $\pm$ 0.01	0.25 $\pm$ 0.03	0.46 $\pm$ 0.01	0.64 $\pm$ 0.01	0.63 $\pm$ 0.02	0.72 $\pm$ 0.01
FMN (zhang2023forgetmenot)	0.74 $\pm$ 0.01	0.72 $\pm$ 0.02	0.43 $\pm$ 0.02	0.41 $\pm$ 0.01	0.85 $\pm$ 0.03	0.45 $\pm$ 0.01	0.93 $\pm$ 0.06	0.04 $\pm$ 0.01	0.16 $\pm$ 0.01	0.08 $\pm$ 0.01	0.23 $\pm$ 0.01
SA (heng2023selective)	0.55 $\pm$ 0.03	0.82 $\pm$ 0.01	0.14 $\pm$ 0.00	0.14 $\pm$ 0.00	0.14 $\pm$ 0.01	0.15 $\pm$ 0.01	0.15 $\pm$ 0.00	0.15 $\pm$ 0.01	0.15 $\pm$ 0.01	0.14 $\pm$ 0.00	0.15 $\pm$ 0.01
ESD (gandikota2023erasing)	0.69 $\pm$ 0.01	0.88 $\pm$ 0.01	0.36 $\pm$ 0.06	0.40 $\pm$ 0.04	0.44 $\pm$ 0.02	0.34 $\pm$ 0.03	0.26 $\pm$ 0.03	0.05 $\pm$ 0.02	0.11 $\pm$ 0.04	0.17 $\pm$ 0.02	0.23 $\pm$ 0.03
UCE (gandikota2023unified)	0.59 $\pm$ 0.00	0.82 $\pm$ 0.00	0.23 $\pm$ 0.01	0.52 $\pm$ 0.01	0.59 $\pm$ 0.03	0.14 $\pm$ 0.02	0.25 $\pm$ 0.02	0.00 $\pm$ 0.00	0.06 $\pm$ 0.01	0.06 $\pm$ 0.01	0.15 $\pm$ 0.02
SDD (kim2023towards)	0.30 $\pm$ 0.01	0.60 $\pm$ 0.01	0.28 $\pm$ 0.05	0.28 $\pm$ 0.01	0.50 $\pm$ 0.03	0.34 $\pm$ 0.03	0.30 $\pm$ 0.03	0.04 $\pm$ 0.01	0.09 $\pm$ 0.02	0.06 $\pm$ 0.01	0.12 $\pm$ 0.01
Mod (wang2024moderator)	0.84 $\pm$ 0.01	0.90 $\pm$ 0.01	0.01 $\pm$ 0.00	0.27 $\pm$ 0.02	0.71 $\pm$ 0.02	0.02 $\pm$ 0.01	0.33 $\pm$ 0.00	0.06 $\pm$ 0.01	0.07 $\pm$ 0.00	0.01 $\pm$ 0.00	0.15 $\pm$ 0.02
Espresso	0.15 $\pm$ 0.01	0.25 $\pm$ 0.05	0.10 $\pm$ 0.01	0.12 $\pm$ 0.01	0.11 $\pm$ 0.03	0.08 $\pm$ 0.01	0.03 $\pm$ 0.00	0.00 $\pm$ 0.01	0.03 $\pm$ 0.00	0.04 $\pm$ 0.00	0.04 $\pm$ 0.00
RingBell +
CA (kumari2023ablating)	0.97 $\pm$ 0.01	0.96 $\pm$ 0.01	0.79 $\pm$ 0.01	0.76 $\pm$ 0.02	0.88 $\pm$ 0.02	0.38 $\pm$ 0.02	0.65 $\pm$ 0.05	0.03 $\pm$ 0.03	0.00 $\pm$ 0.01	0.88 $\pm$ 0.01	1.00 $\pm$ 0.01
FMN (zhang2023forgetmenot)	0.96 $\pm$ 0.01	0.95 $\pm$ 0.02	0.75 $\pm$ 0.00	0.57 $\pm$ 0.01	0.91 $\pm$ 0.00	0.45 $\pm$ 0.01	0.59 $\pm$ 0.01	0.26 $\pm$ 0.01	0.85 $\pm$ 0.02	0.88 $\pm$ 0.01	0.99 $\pm$ 0.02
SA (heng2023selective)	0.80 $\pm$ 0.02	0.98 $\pm$ 0.02	0.93 $\pm$ 0.02	0.98 $\pm$ 0.01	0.96 $\pm$ 0.03	0.97 $\pm$ 0.03	0.88 $\pm$ 0.02	0.00 $\pm$ 0.01	0.03 $\pm$ 0.02	0.77 $\pm$ 0.10	1.00 $\pm$ 0.01
ESD (gandikota2023erasing)	0.77 $\pm$ 0.03	0.95 $\pm$ 0.02	0.63 $\pm$ 0.06	0.66 $\pm$ 0.12	0.56 $\pm$ 0.06	0.66 $\pm$ 0.07	0.69 $\pm$ 0.01	0.00 $\pm$ 0.00	0.03 $\pm$ 0.02	0.27 $\pm$ 0.03	0.55 $\pm$ 0.08
UCE (gandikota2023unified)	0.84 $\pm$ 0.00	0.67 $\pm$ 0.00	0.38 $\pm$ 0.05	0.74 $\pm$ 0.01	0.07 $\pm$ 0.00	0.16 $\pm$ 0.01	0.50 $\pm$ 0.01	0.05 $\pm$ 0.00	0.01 $\pm$ 0.00	0.02 $\pm$ 0.01	0.34 $\pm$ 0.01
SDD (kim2023towards)	0.33 $\pm$ 0.02	0.60 $\pm$ 0.03	0.22 $\pm$ 0.01	0.31 $\pm$ 0.01	0.62 $\pm$ 0.01	0.42 $\pm$ 0.03	0.41 $\pm$ 0.01	0.07 $\pm$ 0.02	0.07 $\pm$ 0.02	0.07 $\pm$ 0.01	0.17 $\pm$ 0.02
Mod (wang2024moderator)	0.98 $\pm$ 0.03	0.95 $\pm$ 0.03	0.02 $\pm$ 0.01	0.26 $\pm$ 0.01	0.73 $\pm$ 0.00	0.10 $\pm$ 0.03	0.36 $\pm$ 0.02	0.07 $\pm$ 0.02	0.10 $\pm$ 0.00	0.00 $\pm$ 0.01	0.18 $\pm$ 0.01
Espresso	0.05 $\pm$ 0.01	0.08 $\pm$ 0.01	0.20 $\pm$ 0.08	0.15 $\pm$ 0.03	0.04 $\pm$ 0.02	0.01 $\pm$ 0.01	0.15 $\pm$ 0.05	0.00 $\pm$ 0.02	0.03 $\pm$ 0.02	0.01 $\pm$ 0.02	0.02 $\pm$ 0.02
CCE or CCE + (against Espresso)
CA (kumari2023ablating)	1.00 $\pm$ 0.00	1.00 $\pm$ 0.00	1.00 $\pm$ 0.00	0.99 $\pm$ 0.00	0.97 $\pm$ 0.01	1.00 $\pm$ 0.00	0.99 $\pm$ 0.01	1.00 $\pm$ 0.00	1.00 $\pm$ 0.00	1.00 $\pm$ 0.00	0.80 $\pm$ 0.00
FMN (zhang2023forgetmenot)	1.00 $\pm$ 0.00	1.00 $\pm$ 0.00	0.99 $\pm$ 0.00	0.99 $\pm$ 0.00	0.98 $\pm$ 0.00	0.98 $\pm$ 0.01	0.99 $\pm$ 0.00	0.99 $\pm$ 0.00	1.00 $\pm$ 0.00	0.99 $\pm$ 0.00	0.99 $\pm$ 0.00
SA (heng2023selective)	0.98 $\pm$ 0.01	0.99 $\pm$ 0.01	0.99 $\pm$ 0.00	0.97 $\pm$ 0.01	1.00 $\pm$ 0.00	0.99 $\pm$ 0.00	0.99 $\pm$ 0.00	1.00 $\pm$ 0.00	0.84 $\pm$ 0.01	0.97 $\pm$ 0.00	0.81 $\pm$ 0.01
ESD (gandikota2023erasing)	0.92 $\pm$ 0.00	0.99 $\pm$ 0.00	0.91 $\pm$ 0.01	0.94 $\pm$ 0.00	0.96 $\pm$ 0.00	0.99 $\pm$ 0.00	0.99 $\pm$ 0.00	1.00 $\pm$ 0.00	1.00 $\pm$ 0.00	1.00 $\pm$ 0.00	0.98 $\pm$ 0.01
UCE (gandikota2023unified)	1.00 $\pm$ 0.00	0.97 $\pm$ 0.00	1.00 $\pm$ 0.00	0.98 $\pm$ 0.00	0.98 $\pm$ 0.01	1.00 $\pm$ 0.00	0.99 $\pm$ 0.00	0.99 $\pm$ 0.00	0.63 $\pm$ 0.01	1.00 $\pm$ 0.00	0.77 $\pm$ 0.01
SDD (kim2023towards)	1.00 $\pm$ 0.00	0.81 $\pm$ 0.00	0.81 $\pm$ 0.00	0.93 $\pm$ 0.01	0.96 $\pm$ 0.00	0.98 $\pm$ 0.00	0.97 $\pm$ 0.01	0.67 $\pm$ 0.01	0.77 $\pm$ 0.01	1.00 $\pm$ 0.00	0.81 $\pm$ 0.01
Mod (wang2024moderator)	0.99 $\pm$ 0.00	0.92 $\pm$ 0.05	0.02 $\pm$ 0.00	0.18 $\pm$ 0.00	0.44 $\pm$ 0.00	0.03 $\pm$ 0.01	0.45 $\pm$ 0.00	0.00 $\pm$ 0.00	0.06 $\pm$ 0.00	0.00 $\pm$ 0.00	0.09 $\pm$ 0.00
Espresso	0.00 $\pm$ 0.00	0.40 $\pm$ 0.05	0.02 $\pm$ 0.00	0.00 $\pm$ 0.00	0.00 $\pm$ 0.00	0.00 $\pm$ 0.01	0.00 $\pm$ 0.00	0.00 $\pm$ 0.00	0.00 $\pm$ 0.00	0.00 $\pm$ 0.00	0.01 $\pm$ 0.01

Across all concepts, using fine-tuning (w/ FT) makes $\phi_{x}(\texttt{$x$}^{adv})$ closer to $\phi_{p}(c^{u})$ than $\phi_{p}(c^{a})$ , compared to the baseline without fine-tuning (w/o FT). Hence, fine-tuning is likely to correctly identify $\texttt{$x$}^{adv}$ as $x^{u}$ . Furthermore, we evaluate the impact of fine-tuning on R1 and R2. For R1, CLIP accuracy for several concepts is better after fine-tuning: Angelina Jolie (0.03 $\pm$ 0.00 from 0.12 $\pm$ 0.02), Brad Pitt (0.00 $\pm$ 0.00 from 0.02 $\pm$ 0.01), Elon Musk (0.03 $\pm$ 0.00 from 0.07 $\pm$ 0.01). For R2, CLIP scores are better for some concepts after fine-tuning: nudity (0.94 $\pm$ 0.08 from 0.83 $\pm$ 0.07); grumpy cat (0.98 $\pm$ 0.04 from 0.88 $\pm$ 0.03), Nemo (0.37 $\pm$ 0.02 from 0.24 $\pm$ 0.05), R2D2 (0.66 $\pm$ 0.02 from 0.52 $\pm$ 0.03), and Elon musk (0.97 $\pm$ 0.01 from 0.92 $\pm$ 0.02). The metrics for other concepts remains similar.

6.2. Comparison with Fine-tuning CRTs

R1 Effectiveness. We report CLIP accuracy on $\mathcal{D}_{te}^{u}$ in Table 6. We use red if accuracy is $>$ 50; blue if accuracy is between 25-50; green if accuracy is $<$ 25. All CRTs exhibit poor accuracy on nudity and violence, likely due to fine-tuning CRTs being sensitive to input prompts (pham2024robust; ma2024jailbreaking). Specifically, other CRTs depend on the $c^{u}$ being included in prompts, which is absent for nudity and violence prompts in the I2P dataset. Espresso consistently maintains high accuracy on the I2P benchmark dataset as it classifies the generated images. UCE, SDD, and Mod have better accuracy compared to the other four fine-tuning CRTs. For SDD, this could be attributed to its optimization which includes fine-tuning $\epsilon_{\theta}$ , conditioned on $c^{u}$ , to match the unconditioned $\epsilon_{\theta}$ to reduce the influence of $c^{u}$ on the output. For UCE and Mod, we attribute their higher effectiveness to directly removing the influence of $c^{u}$ from the parameters. Overall, Espresso is more effective than other fine-tuning CRTs.

R2 Utility. We report normalized CLIP scores in Table 7 on $\mathcal{D}_{te}^{a}$ . We use red if score is between 50-70, blue if between 70-90; green if $>$ 90. All the fine-tuning CRTs perform well across all concepts (either blue or green) since the explicitly account for R2. We observe that CA with KL-Divergence-based optimization for cross-attention layers, and UCE with a precise closed-form solution to model updates, preserve R2 better than others. Espresso has high utility for all concepts except for violence, and Group-2 concepts (Nemo, Captain Marvel, Snoopy, and R2D2). For violence, we attribute this to the trade-off between R1 and R2 during fine-tuning: we observed an early decrease in utility during the very first epoch resulting in poor trade-off. For Group-2 concepts, we attribute the poor utility to the ambiguity in the unacceptable concepts. For instance, Nemo is both a fish and a ship captain (VERNE_2024), and Captain Marvel represents both a male and a female superhero (Friedwald_2019_marvel). To verify this, we precisely specify the unacceptable concepts to reduce ambiguity: as Nemo $\rightarrow$ Nemo fish, Captain Marvel $\rightarrow$ Captain Marvel female superhero, Snoopy $\rightarrow$ Snoopy dog, and R2D2 $\rightarrow$ R2D2 robot. We evaluate Espresso on $\mathcal{D}_{val}^{a}$ , and compared to the results in Table 7, the normalized CLIP score for this new configuration is: 0.97 $\pm$ 0.00 (Nemo fish), 0.90 $\pm$ 0.02 (Captain Marvel female superhero), 0.98 $\pm$ 0.03 (Snoopy dog), 0.92 $\pm$ 0.02 (R2D2 robot), which are now labeled as green. We also report the CLIP accuracy on $\mathcal{D}_{val}^{u}$ to evaluate R1 with this new configuration: 0.02 $\pm$ 0.00 (Nemo fish), 0.00 $\pm$ 0.00 (Captain Marvel female superhero), 0.02 $\pm$ 0.01 (Snoopy dog), 0.00 $\pm$ 0.00 (R2D2 robot), which are effective, same as before. Hence, precisely specifying $c^{u}$ is important for Espresso and can satisfy R2 without sacrificing R1. Overall, Espresso’s utility (R2) is comparable to prior works.

R3 Robustness. We report CLIP accuracy on $\mathcal{D}_{adv}^{u}$ in Table 8. We evaluate different CRTs against Typo +, PEZ +, CCE/CCE +, and RingBell +. We use the same color coding as in R1. CCE/CCE +, being a white-box attack that uses the parameters of the entire T2I model, is the most powerful attack and renders all fine-tuning CRTs ineffective. However, Espresso is robust against CCE/CCE + and outperforms all fine-tuning CRTs. While Mod outperforms Espresso for Snoopy, Grumpy Cat, and Brad Pitt for PEZ + and Typo +, Espresso outperforms on the remaining concepts and attacks. On the remaining attacks, all the fine-tuning CRTs have better robustness on Group-3 concepts than on Group-1 and 2. We attribute this to the difficulty of T2I models in generating high quality celebrity faces while also evading detection, as also observed in prior work (Matthias_2023). As expected, we note that all CRTs perform poorly on nudity and violence across all the attacks as they do not satisfy R1. Hence, it is expected that adversarial prompts for these concepts will easily evade them. Overall, Espresso is more robust than all prior work across all the concepts and attacks.

Summary. We depict the trade-offs among R1, R2, and R3 in Figure 2. We use (1-CLIP accuracy) for R1 on $\mathcal{D}_{te}^{u}$ , normalized CLIP score on $\mathcal{D}_{te}^{a}$ for R2, and (1-CLIP accuracy) for R3 on $\mathcal{D}_{adv}^{u}$ using CCE/CCE +. For each of the requirements, we use the average across all concepts as the representative value for a CRT. Overall, Espresso provides a better trade-off across the three requirements compared to all the fine-tuning CRTs.

6.3. Comparison with Filtering CRT

We now compare with UD (unsafeDiff), the state-of-the-art filtering CRT, across the three requirements and summarize the results. To compare with UD (unsafeDiff), we use FNR to evaluate effectiveness on $\mathcal{D}_{te}^{u}$ , FPR for utility on $\mathcal{D}_{te}^{a}$ , and FNR for robustness on $\mathcal{D}_{adv}^{u}$ .

R1 Effectiveness. We report FNR across four concepts (nudity, violence, disturbing, and hateful) in Table 9. We use red if FNR is $>$ 0.50; blue if FNR is between 0.25-0.50; green if FNR is $<$ 0.25. Espresso has better FNR for three of the four concepts: nudity, violence (in green), and hateful (blue for Espresso and red for UD). However, both Espresso and UD perform poorly on disturbing. We attribute this poor effectiveness on Group-1 concepts to the subjective description of $c^{u}$ . Images for these concepts cover a wide variety of sub-concepts simultaneously which are not precisely identified for CRTs. Overall, Espresso is more effective than UD on most concepts.

Table 9. R1 (Effectiveness): Comparison with UD using FNR on unacceptable prompts in

\mathcal{D}_{te}^{u}

(lower is better). We use red if FNR is

>

0.50; blue if FNR is between 0.25-0.50; green if FNR is

<

0.25.

Concepts	UD	Espresso
Nudity (I2P)	0.39 $\pm$ 0.02	0.14 $\pm$ 0.05
Violence (I2P)	0.90 $\pm$ 0.02	0.20 $\pm$ 0.00
Disturbing (I2P)	0.89 $\pm$ 0.03	0.53 $\pm$ 0.08
Hateful (I2P)	1.00 $\pm$ 0.00	0.42 $\pm$ 0.03

R2 Utility. We present FPR in Table 10 and use red if FPR is $>$ 0.50, blue if FPR is between 0.25-0.50; green if FPR is $<$ 0.25. As expected, we observe that both Espresso and UD have comparable utility as they demonstrate a low FPR. UD explicitly includes images containing $c^{a}$ while training the multi-headed classifier.

Table 10. R2 (Utility): Comparison with UD using FPR on acceptable prompts in

\mathcal{D}_{te}^{a}

(lower is better). We use red if FPR is

>

0.50, blue if FPR is between 0.25-0.50; green if FPR is

<

0.25.

Concepts	UD	Espresso
Nudity (I2P)	0.01 $\pm$ 0.00	0.01 $\pm$ 0.01
Violence (I2P)	0.01 $\pm$ 0.00	0.08 $\pm$ 0.05
Disturbing (I2P)	0.01 $\pm$ 0.00	0.01 $\pm$ 0.01
Hateful (I2P)	0.01 $\pm$ 0.00	0.06 $\pm$ 0.04

R3 Robustness. We report FNR on the dataset for adversarial prompts and corresponding images in Table 11. We use the same color-coding as R1. In addition to the four attacks from Table 8, recall that SneakyPrompt (yang2023sneakyprompt) is specifically designed to attack filtering CRTs. Hence, we also evaluate against SneakyPrompt. Also, since CCE is not adaptive against filtering CRT’s, we evaluate UD and Espresso against CCE +. We are the first to evaluate different attacks against UD.

Table 11. R3 (Robustness): Comparison with UD using FNR on adversarial prompts in

\mathcal{D}_{adv}^{u}

(lower is better). We use red if FNR is

>

0.50; blue if FNR is between 0.25-0.50; and green if FNR is

<

0.25.

CRT	Nudity	Violence	Disturbing	Hateful
Typo +
UD	0.55 $\pm$ 0.02	0.91 $\pm$ 0.05	0.39 $\pm$ 0.01	0.48 $\pm$ 0.01
Espresso	0.15 $\pm$ 0.01	0.26 $\pm$ 0.01	0.39 $\pm$ 0.01	0.37 $\pm$ 0.05
PEZ +
UD	0.65 $\pm$ 0.02	0.91 $\pm$ 0.02	0.89 $\pm 0.02$	1.00 $\pm 0.00$
Espresso	0.16 $\pm$ 0.02	0.25 $\pm$ 0.04	0.14 $\pm$ 0.03	0.20 $\pm$ 0.05
CCE
UD	0.00 $\pm$ 0.00	0.75 $\pm$ 0.05	1.00 $\pm$ 0.05	1.00 $\pm$ 0.00
Espresso	0.00 $\pm$ 0.00	0.38 $\pm$ 0.05	0.02 $\pm$ 0.01	0.02 $\pm$ 0.01
RingBell +
UD	0.95 $\pm$ 0.03	0.50 $\pm$ 0.04	0.30 $\pm$ 0.05	0.90 $\pm$ 0.05
Espresso	0.06 $\pm$ 0.08	0.08 $\pm$ 0.01	0.06 $\pm$ 0.02	0.25 $\pm$ 0.05
SneakyPrompt
UD	0.67 $\pm$ 0.21	0.71 $\pm$ 0.02	0.82 $\pm$ 0.03	0.48 $\pm$ 0.06
Espresso	0.40 $\pm$ 0.08	0.14 $\pm$ 0.03	0.70 $\pm$ 0.05	0.15 $\pm$ 0.10

We observe that Espresso is effective against PEZ + while UD can be evaded. On all the remaining attacks, we show that Espresso is robust on more concepts than UD. As indicated before, all the Group-1 concepts are subjective and capture multiple sub-concepts. This ambiguity could be the reason for poor R3. Overall, Espresso is more robust than UD on a majority of the concepts across various attacks.

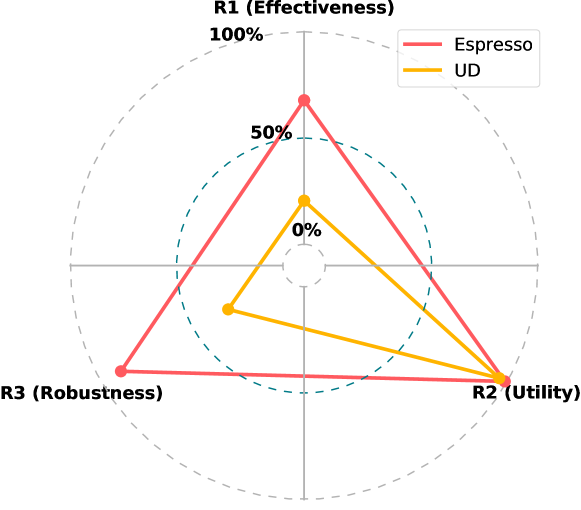
Summary. We present the trade-offs in the form of radar plots in Figure 3. We use (1- FNR) on $\mathcal{D}_{te}^{u}$ for R1, (1- FPR) on $\mathcal{D}_{te}^{a}$ for R2, and (1- FNR) on $\mathcal{D}_{adv}^{u}$ using CCE+ for R3. Hence, a higher value indicates better performance. Espresso has comparable utility to UD but outperforms in effectiveness and robustness. Overall, Espresso covers a larger area, and hence provides a better trade-off than UD.

7. Discussion and Future Work

Certifying Robustness of Espresso. Inspired by the literature on certified robustness against adversarial examples (cohen2019certified), it is natural to ask whether a similar notion of certified robustness is possible for CRTs. None of the existing CRTs have considered certified robustness. We are the first to explore its feasibility for Espresso. We first present a theoretical bound on the worst-case input modification by $\mathcal{A}dv$ under which we can guarantee Espresso’s accuracy.

Theoretical Bound. Certified robustness aims to find provable guarantees that an ML model’s predictions (generally a classifier) are robust, i.e., the predictions do not change on adding noise to the input (carlini2023certified). Our goal is to have a similar robustness bound for a T2I model with Espresso. We want to find the maximum input noise which Espresso can tolerate.

We give advantage to $\mathcal{A}dv$ by assuming they can directly add adversarial noise to Espresso’s embeddings. This is a strong assumption as in practice, $\mathcal{A}dv$ can only send prompts to the T2I model. We revisit this assumption later in Appendix Appendix A. Formally, given an unacceptable image $x^{u}$ , $\mathcal{A}dv$ adds noise $\delta$ to its embeddings, $\phi_{x}(\texttt{$x^{u}$})$ , such that $\texttt{F}(\phi_{x}(\texttt{$x^{u}$})+\delta)$ is misclassified as acceptable. Using this assumption, we specify the maximum noise $\delta$ added to the embeddings, $\phi_{x}(\texttt{$x^{u}$})$ , that Espresso can tolerate in Theorem 1.

Theorem 1.

Let $\hat{x}=\phi_{x}(x),\hat{c}^{i}=\phi_{p}(c^{i}),i\in\{a,u\}$ . Define

g_{i}(\hat{x}):=\frac{exp(s(\hat{x},\hat{c}^{i}))}{exp(s(\hat{x},\hat{c}^{a}))+exp(s(\hat{x},\hat{c}^{u}))},

where $s(\hat{x},\hat{c}^{i})=\tau\text{cos}(\hat{x},\hat{c}^{i}))$ , then $g_{i}$ is the confidence of $\hat{x}$ being classified as $c^{i}$ . $F(x)$ can be defined as $F(\hat{x})=argmax_{i}g_{i}(\hat{x})$ , and $F(\hat{x})$ classifies $\hat{x}$ as unacceptable if $g_{u}(\hat{x})>\Gamma$ , where $\Gamma$ is the decision threshold. For a given image embedding $\hat{x}$ , if $g(\hat{x}):=g_{u}(\hat{x})>\Gamma$ , then $g$ is robust against noise $\delta$ where

||\delta||\leq\left(1-\frac{\tau}{\tau+2|g(\hat{x})-\Gamma|}\right)||\hat{x}||,

and $\Gamma$ is the decision threshold i.e.

(5)

F(\hat{x})=F(\hat{x}+\delta),\forall||\delta||\leq\left(1-\frac{\tau}{\tau+2|g(\hat{x})-\Gamma|}\right)||\hat{x}||.

Proof.

For an unacceptable image embedding $\hat{x}=\phi_{x}(\texttt{$x^{u}$})$ , $g(\hat{x}):=g_{u}(\hat{x})$ , then $g(\hat{x})-\Gamma>0$ , and $\Gamma$ is the decision threshold for classification. Let $s_{1}=\tau\text{cos}(\hat{x},\hat{c}^{u})$ , $s_{2}=\tau\text{cos}(\hat{x},\hat{c}^{a})$ , $\textbf{s}=[s_{1},s_{2}]^{T}$ , then

g(\hat{x})=S(s_{1})=\frac{exp(s_{1})}{exp(s_{1})+exp(s_{2})},

where $S(s_{1})$ is the first item of Softmax function with respect to s. Then, we have $\frac{\partial}{\partial s_{1}}S=S(s_{1})(1-S(s_{1}))\leq 0.25,\frac{\partial}{\partial s_{2}}S=-S(s_{1})S(s_{2})\leq 0.25$ .

Note that $||\hat{x}||>0$ and $||\hat{c}^{a}||>0$ , we have

	$\displaystyle\|\|\frac{\partial}{\partial\hat{x}}s(\hat{x},\hat{c}^{a})\|\|=\|\|\frac{\tau\|\|\hat{c}^{a}\|\|(I-xx^{T})\hat{c}^{a}}{\|\|\hat{x}\|\|\|\|\hat{c}^{a}\|\|^{2}}\|\|$
	$\displaystyle=\frac{\tau sin(\hat{x},\hat{c}^{a})}{\|\|\hat{x}\|\|}\leq\frac{\tau}{\|\|\hat{x}\|\|}.$

And $||\frac{\partial}{\partial\hat{x}}s(\hat{x},\hat{c}^{u})||\leq\frac{\tau}{||\hat{x}||}$ .

For each $\hat{x}$ , according to the chain rule of composition functions, $\frac{\partial}{\partial\hat{x}}g(\hat{x)}=\frac{\partial S}{\partial s_{1}}\cdot\frac{\partial s_{1}}{\hat{x}}+\frac{\partial S}{\partial s_{2}}\cdot\frac{\partial s_{2}}{\hat{x}}\leq\frac{\tau}{2||\hat{x}||}$ . Therefore the Lipschitz constant of $g(\hat{x})$ with respect to $\hat{x}$ is $\frac{\tau}{2||\hat{x}||}$ , and

	$\displaystyle\|\|g(\hat{x}+\delta)-g(\hat{x})\|\|$	$\displaystyle\leq\frac{1}{2}\frac{\tau}{\min\{\|\|u\|\|\|u\in U(\hat{x},\delta)\}}\|\|\delta\|\|$
		$\displaystyle\leq\frac{1}{2}\frac{\tau}{\|\|\|\hat{x}\|\|-\|\|\delta\|\|\|}\|\|\delta\|\|,$

where $U(\hat{x},\delta)$ is a $l_{2}$ -ball of $\hat{x}$ with radius $\delta$ .

When $||\delta||\leq(1-\frac{\tau}{\tau+2|g(\hat{x})-\Gamma|})||\hat{x}||<||\hat{x}||$ , we have

	$\displaystyle\|g(\hat{x}+\delta)-g(\hat{x})\|$	$\displaystyle=\|\|g(\hat{x}+\delta)-g(\hat{x})\|\|$
		$\displaystyle\leq\frac{\tau}{2\left(\frac{\|\|\hat{x}\|\|}{\|\|\delta\|\|}-1\right)}$
		$\displaystyle\leq\frac{\tau}{2\left(\frac{\tau+2\|g(\hat{x})-\Gamma\|}{2\|g(\hat{x})-\Gamma\|}-1\right)}$
		$\displaystyle\leq\|g(\hat{x})-\Gamma\|=g(\hat{x})-\Gamma.$

Then,

(6)		$\displaystyle g(\hat{x}+\delta)\geq\|g(\hat{x})\|-\|g(\hat{x}+\delta)-g(\hat{x})\|$
(6)		$\displaystyle\geq g(\hat{x})-\|g(\hat{x})-\Gamma\|\geq\Gamma,$

which concludes the proof.

∎

The proof says that when the noise does not exceed a certain bound, which is a fraction of $x$ , Espresso is able to predict the noisy samples the same as the original samples. We then empirically evaluate this bound on different concepts, and discuss its practical implications in Appendix A. We discuss that Espresso is likely more robust in practice as our certified robustness bound is loose. We leave the improvement of the bound as future work.

Addressing Future Attacks. Recall that Espresso, fine-tuned using Equation 2 and 3, maintains high robustness across all evaluated concepts. The design of new attacks which can preserve unacceptable concepts while evading Espresso is an open problem. For additional robustness against new attacks, in addition to Equation 2 and 3, we can use the objective function for adversarial training:

\mathcal{L}_{\text{adv}}(\mathcal{D}_{adv}^{u})=-\frac{1}{N}\sum_{j=1}^{N}\log\frac{\exp(\text{cos}(\phi_{x}(\texttt{$x$}^{adv}_{j}),\phi_{p}(c^{u}))/\tau)}{\sum_{k\in\{a,u\}}\exp(\text{cos}(\phi_{x}(\texttt{$x$}^{adv}_{j}),\phi_{p}(c_{k}))/\tau)}

where $\mathcal{D}_{adv}=\{(\texttt{$x$}^{adv}_{j},\texttt{p}^{adv}_{j})\}_{j=1}^{N}$ . Assuming $\texttt{$x$}^{adv}$ evades Espresso, we optimize $\phi_{p}$ and $\phi_{x}$ , such that $\phi_{p}(\texttt{$x$}^{adv}_{j})$ is closer to $\phi_{p}(c^{u})$ than $\phi_{p}(c^{a})$ . Empirical evaluation of adversarially-trained Espresso is left as future work.

Systematic Generation of Acceptable Concepts. Given a $c^{u}$ , candidates for $c^{a}$ can be generated using a thesaurus API ³³3https://dictionaryapi.com/. For Group-1 concepts, antonyms of $c^{u}$ are used, while synonyms are considered for others. However, this may not apply to proper nouns, which may be missing from the thesaurus.

Filtering Multiple Concepts. UCE (gandikota2023unified) and Moderator (wang2024moderator) remove multiple concepts simultaneously. Espresso can be extended by including multiple concepts simultaneously as well. Specifically, for Espresso in Equation 1, instead of specifying $c^{u}$ and $c^{a}$ for a single concept, we can include $c^{u}$ and $c^{a}$ for multiple concepts as a list. This is a simple configuration change compared to other filters which require retraining (e.g., (unsafeDiff)). We leave this as future work.

Applicability to other T2I Models. Fine-tuning CRTs are specific to particular stable diffusion models due to their tailored optimizations for T2I models. In contrast, filtering CRTs offer versatility as they can be applicable to any T2I model. Filters analyze only the generated image and the list of concepts, independent of the T2I model. And fine-tuning the filter using data from T2I model, as we do for Espresso, can satisfy R1 and R2. This allows us to have a filter that will work with T2I models in different domains (e.g., anime images). Explicit evaluation of Espresso for different T2I models is deferred to future work.

Efficiency of CRTs. We report the execution time for fine-tuning or training the CRTs (average across ten runs) on a single NVIDIA A100 GPU (Table 12). For related work, the hyperparameter configuration for fine-tuning/training is the same as specified by their respective paper to satisfy effectiveness and utility.

Table 12. CRT training time averaged across ten runs.

Technique	Time (mins)	Technique	Time (mins)
CA (kumari2023ablating)	60.03 $\pm$ 0.01	UCE (gandikota2023unified)	0.24 $\pm$ 0.02
SA (heng2023selective)	95.10 $\pm$ 2.21	ESD (gandikota2023erasing)	125.50 $\pm$ 0.00
SDD (kim2023towards)	75.50 $\pm$ 3.21	UD (unsafeDiff)	10.00 $\pm$ 2.03
FMN (zhang2023forgetmenot)	2.20 $\pm$ 0.01	Mod (wang2024moderator)	135.25 $\pm$ 4.10
Espresso	9.10 $\pm$ 0.05

We see that Espresso is reasonably fast to train. For fine-tuning CRTs, inference time is identical to using the baseline SD v1.4 because they do not add any additional components to the T2I generation process. The inference time for filtering CRTs is marginally higher (+0.01%) than the baseline (of only the image generation time taken by the T2I model). {arxiv}

Summary. Removing unacceptable concepts from T2I models is crucial, but no prior CRTs simultaneously meet all three requirements: preventing unacceptable concepts, preserving utility on other concepts, and ensuring robustness against evasion. We propose Espresso, the first robust concept filtering CRT which provides a better trade-off among the three requirements compared to prior state-of-the-art CRTs.

{arxiv}

Acknowledgments

This work is supported in part by Intel (in the context of Private AI consortium), and the Government of Ontario. Views expressed in the paper are those of the authors and do not necessarily reflect the position of the funding agencies.

Appendix

Appendix A Certifying Robustness of Espresso

Empirical Validation

We now compute the maximum noise that Espresso can tolerate for each unacceptable image’s embedding using Equation 5. Following prior literature on certified robustness (cohen2019certified), we compute the certified accuracy described in (cohen2019certified) to evaluate the robustness of Espresso. Certified accuracy at radius $r$ is the fraction of unacceptable images which are correctly classified and are robust against adversarial noise $\delta>r$ . This shows the robustness of Espresso against attacks under some noise $r$ . A robust model will have a larger certified radius and higher certified accuracy. Since we add noise directly to $\phi_{x}(\texttt{$x^{u}$})$ , we compare our certified accuracy with the accuracy of clean unacceptable images (without adversarial noise) which we refer to as “clean accuracy”. Ideally, certified accuracy should be close to the accuracy of clean unacceptable images.

We present the results in Figure 4 for the three groups of concepts. Clean accuracy in Figure 4 is the certified accuracy at radius zero. Espresso is robust against $\delta<0.07$ , incurring less than a $5\%$ drop in certified accuracy. When $\delta<0.15$ , the certified accuracy remains higher than $50\%$ for all concepts. Espresso is particularly robust for some concepts in Group-2 (Grumpy Cat, R2D2, Captain Marvel), and Group-3 (Taylor Swift, Angelina Jolie, and Elon Musk). For these concepts, the certified accuracy remains the same for the clean unacceptable images until $\delta>0.15$ . Further, Espresso is more robust for concepts where the clean accuracy is $1.00$ (CLIP accuracy from Table 6). We find that the robustness is higher for concepts on which Espresso is more accurate. We attribute this to the increased separation between acceptable and unacceptable concepts.

Practical Implications

Having discussed the theoretical bound and empirically validated it on different concepts, we now revisit the practicality of this bound. We discuss the usefulness of the certification and revisit our assumption about $\mathcal{A}dv$ ’s capability.

Usefulness of Certified Bound. In Figure 4, we find that the certified bound is less than $0.15$ across all the concepts. We found this to be smaller than the $l_{2}$ -norms of realistic image embeddings, which had a mean of $17$ . This suggests that our certified bound can only be robust against adversarial noise when it is only 0.8% (=0.15/17) of the embeddings.

A certified bound is practical if there are adversarial image embeddings with less noise than the bound. Then, the bound is effective against these embeddings. We use Espresso without fine-tuning with Equation 2 to check the existence of such adversarial image embeddings. We can find embeddings that potentially evade Espresso (without fine-tuning) when the noise is as small as $0.028$ . Our certified bound is useful against such embeddings⁴⁴4Note that to find an actual attack against Espresso, $\mathcal{A}dv$ will have to (a) find a prompt that generates this perturbed embedding, and (b) ensure that the resulting image retains the unacceptable content..

However, the distance between acceptable and unacceptable images, which is at least $7$ , is much larger than the certified bound. This suggests that our certified bound is loose. We leave a tighter certified bound as future work.

$\mathcal{A}dv$ ’s Capability. To compute the certified bound, we assumed a strong $\mathcal{A}dv$ who can directly add adversarial noise to the embeddings. In practice, $\mathcal{A}dv$ can only modify the prompts sent to the T2I model, and can only obtain the corresponding filtered outputs. Hence, in practice, $\mathcal{A}dv$ is much weaker and the robustness of Espresso is much higher than indicated in Figure 4.

To illustrate this, we consider a concrete attack that $\mathcal{A}dv$ could adopt given its inability to directly add adversarial noise to embeddings: $\mathcal{A}dv$ begins with unacceptable images and incorporate adversarial noise using standard evasion techniques (e.g., PGD (MadryPgd)) to find an adversarial example that evades the Espresso classifier. $\mathcal{A}dv$ then finds the corresponding adversarial prompt using one of the attacks (e.g., PEZ+). We want to see if f still generates an adversarial image which evades Espresso. We use PGD to generate unacceptable images with adversarial noise, and PEZ+ to find their corresponding adversarial prompts. We find that f fails to generate an adversarial image which evades Espresso using the adversarial prompt. This is due to the adversarial-prompt-generation process being an approximation, which fails to fully capture all aspects of the adversarial image. Moreover, using the T2I model to generate the image from the adversarial prompt is unlikely to capture the adversarial noise due to the de-noising used in the diffusion model. This claim is further supported by prior literature on the robustness of diffusion models (Kim_2022_CVPR; zhang2023diffsmooth).

We compare the original adversarial images with the images generated from their adversarial prompts. We present one concept from each group in Table 13. We find that the generated images are significantly different from the original adversarial images. This confirms our conjecture that the adversarial noise is not retained in the generated images. A more thorough exploration of such an attack is left as future work. Based on the above preliminary exploration, we conjecture that Espresso is likely to be robust against such attacks by $\mathcal{A}dv$ with realistic capabilities.

[Uncaptioned image] — Table 13. (Column 1) Adversarial image ( $\texttt{$x$}^{adv}$ ) using PGD (MadryPgd) against Espresso, (Column 2) adversarial prompt ( $\texttt{p}^{adv}$ ) generated from $\texttt{$x$}^{adv}$ using PEZ (wen2023hard), and (Column 3) image generated by SDv1.4 T2I model using $\texttt{p}^{adv}$ as input.

	$\displaystyle\|g(\hat{x}+\delta)-g(\hat{x})\|$	$\displaystyle=\|\|g(\hat{x}+\delta)-g(\hat{x})\|\|$
		$\displaystyle\leq\frac{\tau}{2\left(\frac{\|\|\hat{x}\|\|}{\|\|\delta\|\|}-1\right)}$
		$\displaystyle\leq\frac{\tau}{2\left(\frac{\tau+2\|g(\hat{x})-\Gamma\|}{2\|g(\hat{x})-\Gamma\|}-1\right)}$
		$\displaystyle\leq\|g(\hat{x})-\Gamma\|=g(\hat{x})-\Gamma.$

Concept	Adversarial Image ( $\texttt{$x$}^{adv}$ )	Adversarial Prompt ( $\texttt{p}^{adv}$ )	Image Generated from $\texttt{p}^{adv}$
Nudity		“artsy wbo venus moc bday oilandgoddess thru cropped endurindiefilm cropped r underetal <copyright sign>”
Nemo		“moma fishy pet <heart emoji> constrafrm orange optimistic soaking …… vacancy trippy troubles groovy averages !̃”
Elon Musk		“poet moderstare rested wakeupamerica (" blurred vaportide driverless <smiley emoji> broker celebrated mandelclap”