Error Propagation and Overhead Reduced Channel Estimation for RIS-Aided Multi-User mmWave Systems
Abstract
In this paper, we propose a novel two-stage based uplink channel estimation strategy with reduced pilot overhead and error propagation for a reconfigurable intelligent surface (RIS)-aided multi-user (MU) millimeter wave (mmWave) system. Specifically, in Stage I, with the carefully designed RIS phase shift matrix and introduced matching matrices, all users jointly estimate the correlation factors between different paths of the common RIS-base station (BS) channel, which achieves significant multi-user diversity gain. Then, the inherent scaling ambiguity and angle ambiguity of the mmWave cascaded channel are utilized to construct an ambiguous common RIS-BS channel composed of the estimated correlation factors. In Stage II, with the constructed ambiguous common RIS-BS channel, each user uses reduced pilots to estimate their specific user-RIS channel independently so as to obtain the entire cascaded channel. The theoretical number of pilots required for the proposed method is analyzed and the simulation results are presented to validate the effectiveness of this strategy.
Index Terms:
Reconfigurable intelligent surface, channel estimation, multi-user systems, millimeter waveI Introduction
Reconfigurable intelligent surface (RIS) technology is envisioned to be a promising technique for enhancing the spectrum and energy efficiency of 6G-and-beyond communications with relative low hardware cost and energy consumption [1, 2, 3]. To reap the benefits promised by RIS, accurate channel state information (CSI) is required, which is challenging to achieve due to the lack of complex signal process ability of the RIS.
Recently, there have been many contributions on channel estimation for RIS-aided communication systems. Most work focused mainly on single-user system [4], but it might be not appropriate to apply the methods developed for this case to multi-user system directly since the pilot overhead would be prohibitively large, which is proportional to the number of users. On the other hand, for multi-user system, the correlation relationship among different user’s cascaded channel has been exploited to enhance the estimation performance [5] and reduce the pilot overhead of channel estimation significantly [6, 7, 8]. Specifically, for unstructured channel models, other users use reduced pilots to estimate their scaling coefficients with respect to the typical user so as to obtain the corresponding cascaded channels [6, 7]. Similarly, for structured channel models, other users’ cascaded channel can be estimated effectively with the re-parameterized common BS-RIS channel, which is constructed based on the estimated typical user’s cascaded channel [8]. However, these three methods mentioned above have a common issue that the existence of channel estimation error from the typical user in the previous stage will deteriorate the estimation accuracy of other users in the next stage, which is known as error propagation. An optional method to suppress this error propagation effect is the careful selection of the typical user. The typical user can be chosen as the closest one to the RIS for the less severe path loss. In addition, large number of pilots are usually allocated to the typical user so as to ensure the more accurate estimation performance of the typical user. However, these operations introduce the extra complexity to the system and consume excessive pilot overhead for the estimation of the typical user. Once the estimated CSI of the typical user is inaccurate, the estimation performance of the multi-user system will be severely degraded.
Motivated by the above, in this paper, we develop a two-stage based uplink cascaded channel estimation strategy without choosing the typical user for an RIS-aided millimeter wave (mmWave) multi-user system. In Stage I, with the carefully designed RIS phase shift matrix and the introduced matching matrices, all users jointly estimate the correlation factors between different paths of the common RIS-BS channel, which achieves multi-user diversity gain and suppresses the negative error propagation impact. Then, we utilize the inherent scaling ambiguity and angle ambiguity properties of the mmWave cascaded channel to construct an ambiguous common RIS-BS channel composed of the obtained correlation factors. In Stage II, based on the constructed common RIS-BS channel, each user only uses reduced pilots to estimate their specific user-RIS channel independently so as to obtain the full CSI of the cascaded channel. Lastly, we analyze the theoretical minimum number of pilots required for the strategy and present the corresponding simulation results for the proposed method.
Notations: For a matrix of arbitrary size, , , , , and stand for the conjugate, transpose, conjugate transpose, pseudo-inverse, and vectorization of . The -th row of is denoted by . Additionally, the Khatri-Rao product and Hadamard product between two matrices and are denoted by and , respectively. and denote an identity matrix and an all-zero matrix with appropriate dimensions, respectively. For a vector , denotes the subvector containing from the -th element to the -th element of , respectively. The symbol represents the Euclidean norm of . is a diagonal matrix with the entries of on its diagonal. The inner product between two vectors and is denoted by . is the imaginary unit. represents the set of complex numbers.
II System Model
We consider a narrow-band time-division duplex (TDD) mmWave system, in which single-antenna users communicate with a BS equipped with an -antenna ULA. To improve the communication performance, an RIS equipped with a passive reflecting ULA of dimension is deployed. In addition, the direct channel between the BS and users are assumed to be blocked.
II-A Transmission model
Denote as the channel matrix between the RIS and the BS, and as the channel matrix between user and the RIS, respectively. The set of users is defined as . Denote as the phase shift vector of the RIS in time slot . During the uplink transmission, the received signal from user at the BS in time slot , is expressed as
| (1) |
where is the pilot symbol of user and is the corresponding additive white Gaussian noise (AWGN) with power . represents the transmit power. is the cascaded user-RIS-BS channel of user , needed to be estimated in this work.
II-B Channel model
First, we consider a typical ULA with elements, whose steering vector can be represented by
| (2) |
The variable is regarded as the spatial frequency and there exists a one-to-one relationship between the spatial frequency and the physical angle as when assuming . Here, is the carrier wavelength and is the element spacing. In the remainder of the paper we will refer to the angle information as spatial frequency for simplicity.
Due to the limited scattering characteristics in the mmWave environment, we use the geometric channel model to rewrite the channel matrices in (1), i.e., and as
| (3) | ||||
| (4) |
where and denote the number of propagation paths (scatterers) between the BS and the RIS, and between the RIS and user , respectively. In addition, , and are the complex path gain, AoA, and AoD of the -th path in the common RIS-BS channel, respectively. Similarly, and represent the complex path gain and AoA of the -th path in the user -RIS channel, respectively. Moreover, , , and are the AoA steering (array response) matrix, AoD steering matrix and complex gain matrix of the common RIS-BS channel, respectively, and and are the AoA steering matrix and complex gain vector of the specific user -RIS channel, respectively.
III Two-Stage Based Cascaded Channel Estimation for a Multi-user System without Choosing a Typical User
In this section, a two-stage based uplink cascaded channel estimation strategy without choosing a typical user is proposed. Specifically, in Stage I, an ambiguous common RIS-BS channel is constructed by all users jointly so as to achieve multi-user diversity gain and suppress the impact of error propagation. In Stage II, each user only needs to estimate the specific user-RIS channel to obtain full CSI of the cascaded channel. Finally, the required pilot overhead is analyzed.
III-A Stage I: Estimation of the Ambiguous Common RIS-BS Channel
In this subsection, we present the details on the estimation of the ambiguous common RIS-BS channel, seen as a re-parameterized common RIS-BS channel.
During Stage I, with the carefully designed RIS phase shift coefficients, all users transmit the training pilots simultaneously so as to achieve the multi-user diversity gain. Assume the pilot symbols satisfy for , and the transmitted power of each user is the same, which equals to , so that the received signal at the BS can be expressed as
| (6) |
where is treated as the equivalent user-RIS channel, is the AWGN at the BS. Stacking time slots of (6), the received matrix is expressed as
| (7) |
where is the RIS phase shift matrix during this stage and .
III-A1 Common AoAs estimation
Estimating the AoA steering matrix of the common RIS-BS channel, i.e., , from (7) is a classical directional of arrival (DOA) estimation problem in array processing, and can be solved by many mature signal processing techniques [4]. Due to the large scale antenna arrays employed at the BS with typically , the DFT-based method in [8] can be adopted to obtain the estimate of the common AoA steering matrix.
Denote the estimate of as . Due to the property that [9], by substituting , we can obtain the equivalent received matrix as
| (8) |
where is treated as the estimation error between the common AoA and its estimate, and represents the equivalent noise matrix.
III-A2 Correlation relationship between different paths
With the estimated common AoA, i.e., , a correlation relationship between different paths in the common RIS-BS channel will be revealed, which helps us to construct the ambiguous common RIS-BS channel. Specifically, calculating the -th row and the -th row of in (8), and then taking their conjugate transpose, we have
| (9) | ||||
| (10) |
where and . Apparently, the dominant terms of and , i.e., and , contain the whole information regarding the -th path and the -th path, respectively, and there exists a relationship between these two terms, reflecting the correlation between the corresponding two paths.
To illustrate this correlation relationship, define a matching matrix for the -th path with respect to the -th path as
| (11) |
where is a complex nonlinear function of . is a DFT matrix with the -th entry given by . can be regarded as the array manifold with dimension and is an all-one vector of size . Here, the -th path is treated as the reference path.111The reference index can be chosen based on the maximum received power criterion, i.e., . and are the rotation factor and scaling factor for the -th path with respect to the -th path, respectively, which are given by
| (12) |
Clearly, . During this stage, the RIS phase shift matrix in (7) needs to be designed carefully, which should satisfy the following structure
| (13) |
Where is a DFT matrix defined in (11), satisfying the constant modulus constraint. To show how the matching matrix works intuitively, the noise terms of (9) and (10) are momentarily omitted. Then, we have
| (14) |
where the third equality is obtained using . From Eq. (14), the term can be expressed as the result of the term via the linear transformation . Thus the correlation between the -th path and the -th path is depicted by the two variables of matching matrix , i.e., and . By analogy, we conclude that the correlation relationship between any two paths in the common RIS-BS channel can be described by their rotation factors and scaling factors. Now we will show how to estimate these two kinds of factors, i.e., rotation factors and scaling factors, from the equivalent received signal .
III-A3 Estimation of the rotation factors and scaling factors
We still take the -th path and the -th path, i.e., the reference path, as an example to illustrate the method for estimating the rotation factors and scaling factors. Similar to Eq. (14), we process the received signal in (10) via the linear transformation as
| (15) |
where . By replacing and , (9) is re-expressed as
| (16) |
Here, represents the corresponding noise vector. Moreover, denote as and as , (16) can be written as
| (17) |
So our aim is to estimate the rotation factor and scaling factor with the received , which can be achieved by solving the problem shown below as
| (18) |
where is an extremely complex nonlinear function with respect to . This problem is known as a separable nonlinear least squares (SNL-LS) problem, in which the optimal and can be found via the following steps.
First, when the is fixed, the optimal is given by the least square (LS) solution, i.e., . Then, by substituting into Problem (18), the optimal can be acquired by solving the new problem as
| (19) |
where the objective function of Problem (19), i.e., , can be simplified as
| (20) |
where . With Eq. (20), Problem (19) is equivalent to the optimization problem as
| (21) |
For Problem (21), one-dimension search method can be adopted to obtain the optimal , i.e., , whose performance depends on the number of search grids. Once the rotation factor is obtained by solving Problem (21), the scaling factor is given by
| (22) |
Finally, the rotation factors and the scaling factors for any paths in the common RIS-BS channel with respect to the reference path, i.e., the -th path, can be estimated. Specifically, for , the rotation factors and the scaling factors between the -th path and the -th path, i.e., and , are obtained via the solution to Problem (21) and Eq. (22). While for , according to the definitions in (12), the corresponding rotation factor and the scaling factor are given by and .
III-A4 Construction of the common RIS-BS Channel
In previous subsections, we have shown that the rotation factors and scaling factors, i.e., and for , can be estimated effectively by all users jointly with the designed . Based on the obtained parameters, an ambiguous complex gain matrix of the common RIS-BS channel, i.e., denoted by , and an ambiguous AoD steering matrix of the common RIS-BS channel, i.e., denoted by , are constructed as
| (23) | ||||
| (24) |
It is observed that the relationship between and , and the relationship between and can be described as
| (25) | ||||
| (26) |
With the obtained , and , the corresponding ambiguous common RIS-BS channel, denoted by , is naturally constructed as
| (27) |
Then, substituting and into in (5), we have
| (28) |
where and are the corresponding ambiguous AoA steering matrix and ambiguous complex gain vector of the specific user-RIS channel for user , respectively. Accordingly, is the corresponding ambiguous specific user-RIS channel for user , that must still be found. In next subsection we will show how to estimate for with the constructed , leading to a significant reduction in the pilot overhead.
III-B Stage II: Estimation of the Ambiguous Specific User-RIS Channel
In Stage II, the users are required to transmit the pilot sequences one by one for the estimation of the ambiguous specific user-RIS channel.
Without loss of generality, we consider an arbitrary from and show how to estimate user ’s ambiguous specific user-RIS channel, i.e., . Assume pilots are allocated for user in this stage. In addition, assume the pilot symbols satisfy and the transmitted power equals to as before. Then, with Eq. (28), the received signal from user at the BS in time slot can be expressed as
| (29) |
For clear illustration, we still assume that the BS receives the pilot sequence from time slot to time slot , and thus the received matrix during user ’s pilot transmission is expressed as
| (30) |
where and .
With the estimated common AoA steering matrix , user ’s received matrix is processed similarly to what was done for (8) as
| (31) |
where . Then, vectorizing (31) and defining , we have
| (32) |
where and is the corresponding equivalent noise vector given by . The second equality is obtained via .
In particular, as illustrated in (28), where for lies within , thus we can formulate (32) as a -sparse signal recovery problem:
| (33) |
where in the third equality is the virtual angular domain (VAD) representation of . is an overcomplete dictionary matrix , and the columns of contain values for on the angle grid. is a sparse vector with nonzero entries corresponding to the ambiguous gains . Accordingly, is regarded as the equivalent measurement vector for the estimation of . Hence, the estimation problem of corresponding to (33) can be solved using CS-based techniques. To obtain the best CS-based estimation performance, the RIS phase shift matrix should be designed to ensure that the columns of the equivalent dictionary are orthogonal. A detailed design for that achieves this goal can be found in [8]. A simpler method is to choose as the random Bernoulli matrix, i.e., randomly generate the elements of from with equal probability [5].
To conclude, we obtained the estimate of and via the CS-based method, and thus the estimate of ambiguous specific user-RIS channel, denoted by , can be obtained directly. Denote the estimated common RIS-BS channel in (27) as , the estimate of the cascaded channel for user is given by . Finally, the completed estimation of for is summarized in Algorithm 1.
III-C Pilot Overhead Analysis
Now we analyze the pilot overhead required for the proposed two-stage based uplink channel emaciation strategy. For simplicity, is assumed.
In Stage I, the number of pilots is suggested to satisfy so as to ensure the vectors are linear independent. In Stage II, the number of pilots for user directly affects the estimation performance for the sparse recovery problem associated with (33), where the dimension of the equivalent sensing matrix is satisfying , and the corresponding sparsity level is . To find a -sparse complex signal with dimension , the number of measurements is on the order of . Therefore, user needs pilots. Consider users in total, the overall minimum pilot overhead is .
IV Simulation Results
In this section, we present several simulation results to validate the effectiveness of the proposed method. The channel gains and follow a complex Gaussian distribution with zero mean and variance of and , respectively. Here, , defined as the distance between the BS and the RIS, is set to m, while, , defined as the distance between the RIS and the users, is assumed to be m. The antenna spacing at the BS and the element spacing at the RIS are set to . The number of paths between the BS and the RIS, and the number of paths between the RIS and users are set to and , respectively. The normalized mean square error (NMSE) is chosen as the performance metric, which is defined by We compare the proposed method with the following three channel estimation methods: Direct-OMP Method [10], DS-OMP Method [5], and Typical User Required Method [8].
Fig. 1 illustrates the relationship between NMSE performance and pilot overhead of the various methods, where the SNR is set to dB. Since different number of pilots are allocated in different stages for the Proposed Two-Staged Method and the Typical User Required Method, we consider the users’ average pilot overhead, denoted as , and show NMSE as a function of . It can be clearly seen that an increase in the number of pilots improves the performance of all algorithms. Under the same average pilot overhead, e.g., , the estimation performance of the Proposed Two-Staged Method markedly outperforms than that of the other three methods due to the multi-user diversity gain. On the other hand, in order to achieve the same estimation performance, e.g., , the required average pilot overhead of the Proposed Two-Staged Method and the Typical User Required Method is much lower than the Direct-OMP Method and the DS-OMP Method. That is because the former two methods exploit the correlation relationship among different user’s cascaded channel, which reduces the pilot overhead.
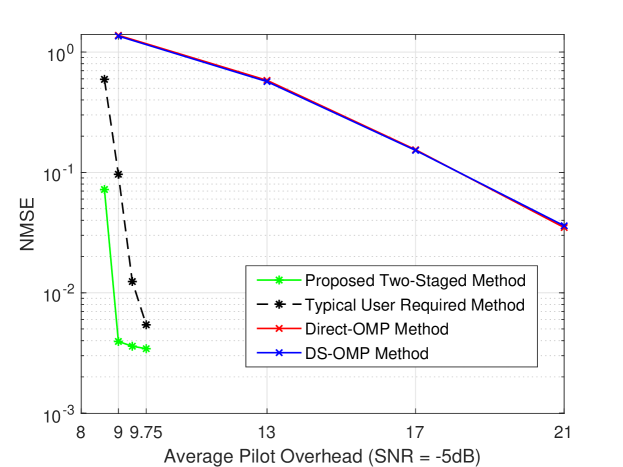
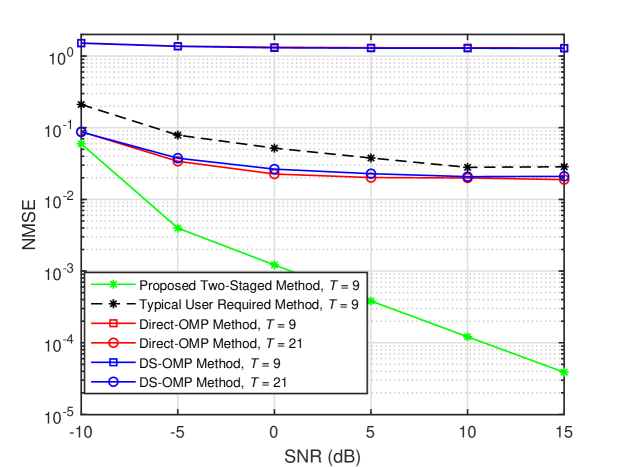
Fig. 2 displays the NMSE performance of different methods versus SNR. We observe the estimation performances of all the methods are unacceptable under low SNR case, e.g., the NMSEs are larger than with SNR = dB. Fortunately, their NMSEs are improved with the growth of the SNR. In particular, the NMSE of the Proposed Two-Staged Method decreases drastically with the SNR. By contrast, due to the shortage of measurements, the estimation accuracy of the three benchmark methods improves slightly and reaches saturation at relatively high SNR. The gap between the proposed method and the three benchmark methods becomes noticeably larger.
V Conclusions
In this paper, we proposed a novel two-stage based uplink channel estimation strategy for an RIS-aided multi-user mmWave communication system. In Stage I, all users jointly constructed the ambiguous common RIS-BS channel so as to obtain multi-user diversity gain. In Stage II, each user independently estimated their own ambiguous specific user-RIS channel with reduced pilot overhead. Additionally, theoretical overall minimum number of pilots required by the proposed strategy was analyzed. Simulation results validated that the proposed method outperforms other existing algorithms in terms of pilot overhead.
References
- [1] C. Pan, H. Ren, K. Wang et al., “Reconfigurable intelligent surfaces for 6G systems: Principles, applications, and research directions,” IEEE Commun. Mag., vol. 59, no. 6, pp. 14–20, Jun. 2021.
- [2] M. Di Renzo, A. Zappone, M. Debbah et al., “Smart radio environments empowered by reconfigurable intelligent surfaces: How it works, state of research, and the road ahead,” IEEE J. Sel. Areas Commun., vol. 38, no. 11, pp. 2450–2525, Nov. 2020.
- [3] C. Pan, H. Ren, K. Wang et al., “Intelligent reflecting surface aided MIMO broadcasting for simultaneous wireless information and power transfer,” IEEE J. Sel. Areas Commun., vol. 38, no. 8, pp. 1719–1734, Aug. 2020.
- [4] A. L. Swindlehurst, G. Zhou, R. Liu, C. Pan, and M. Li, “Channel estimation with reconfigurable intelligent surfaces–a general framework,” Proc. IEEE, early access, pp. 1–27, 2022.
- [5] X. Wei, D. Shen, and L. Dai, “Channel estimation for RIS assisted wireless communications: Part II - an improved solution based on double-structured sparsity,” IEEE Commun. Lett., vol. 25, no. 5, pp. 1403–1407, May 2021.
- [6] Z. Wang, L. Liu, and S. Cui, “Channel estimation for intelligent reflecting surface assisted multiuser communications: Framework, algorithms, and analysis,” IEEE Trans. Wireless Commun., vol. 19, no. 10, pp. 6607–6620, Oct. 2020.
- [7] Y. Wei, M.-M. Zhao, M.-J. Zhao, and Y. Cai, “Channel estimation for IRS-aided multiuser communications with reduced error propagation,” IEEE Trans. Wireless Commun, vol. 21, no. 4, pp. 2725–2741, Oct. 2022.
- [8] G. Zhou, C. Pan, H. Ren, P. Popovski, and A. L. Swindlehurst, “Channel estimation for RIS-aided multiuser millimeter-wave systems,” IEEE Trans. Signal Process., vol. 70, pp. 1478–1492, Mar. 2022.
- [9] T. Lin, X. Yu, Y. Zhu, and R. Schober, “Channel estimation for IRS-assisted millimeter-wave MIMO systems: Sparsity-inspired approaches,” IEEE Trans. Commun., vol. 70, no. 6, pp. 4078–4092, Apr. 2022.
- [10] P. Wang, J. Fang, H. Duan, and H. Li, “Compressed channel estimation for intelligent reflecting surface-assisted millimeter wave systems,” IEEE Signal Process. Lett., vol. 27, pp. 905–909, May 2020.