Error-Mitigated Quantum Simulation of Interacting Fermions with Trapped Ions
Abstract
Quantum error mitigation has been extensively explored to increase the accuracy of the quantum circuits in noisy-intermediate-scale-quantum (NISQ) computation, where quantum error correction requiring additional quantum resources is not adopted. Among various error-mitigation schemes, probabilistic error cancellation (PEC) has been proposed as a general and systematic protocol that can be applied to numerous hardware platforms and quantum algorithms. However, PEC has only been tested in two-qubit systems and a superconducting multi-qubit system by learning a sparse error model. Here, we benchmark PEC using up to four trapped-ion qubits. For the benchmark, we simulate the dynamics of interacting fermions with or without spins by applying multiple Trotter steps. By tomographically reconstructing the error model and incorporating other mitigation methods such as positive probability and symmetry constraints, we are able to increase the fidelity of simulation and faithfully observe the dynamics of the Fermi-Hubbard model, including the different behavior of charge and spin of fermions. Our demonstrations can be an essential step for further extending systematic error-mitigation schemes toward practical quantum advantages.
I Introduction
Recently, quantum computation in the noisy intermediate scale quantum (NISQ) regime has been actively developed for the possibility of reaching practical quantum advantages without quantum error correction [1, 2]. In this direction, quantum advantages with random gate sampling algorithms in superconducting systems have been demonstrated [3, 4]. The possibility of surpassing conventional classical computation in solving useful and practical problems has been seriously explored [5]. In particular, a quantum-classical hybrid method that combines the advantages of classical and quantum computation, such as the variational quantum algorithm (VQA), has been theoretically and experimentally explored to reach higher performance than with only classical computers [6, 7, 8, 9]. One of the critical issues in NISQ computation is to obtain results with high precision from quantum devices without quantum error correction [10, 11].
Various error-mitigation methods without using additional quantum resources for quantum error corrections have been proposed and applied to improve the computation results of quantum devices [12, 13, 14, 15]. Representative error-mitigation methods include zero-noise extrapolation [12, 13, 14, 15, 16, 17], probabilistic error cancellation (PEC) [12, 13, 14, 15, 18, 19, 20, 21], virtual distillation [22], etc. In particular, PEC is considered the general and systematic method for mitigating errors, which are not dependent on details of the physical implementation as long as errors are properly characterized. PEC consists of characterizing errors of each quantum gate, decomposing the inverse of the errors into combinations of basis operations, and sampling the operations with the characterized weights. In this way, we can estimate the expectation values of the desired observables without errors. PEC has been theoretically analyzed in detail and shown to be optimal for dephasing dominant noise situations [12, 13, 20, 21]. However, it has been experimentally tested with only two-qubit systems of superconducting circuits and trapped ions [18, 19] and a multi-qubit system of the superconducting circuit via fitting a sparse error model motivated by the processor topology [23].
Systematic error-mitigation schemes like PEC would enhance the performance of quantum computation in the NISQ regime drastically. Many important quantum algorithms have been developed based on the fact that quantum dynamics can be efficiently simulated in quantum computation, which also inspires VQA designs [6, 7, 8, 9]. In digital quantum simulation, the time evolution of a certain Hamiltonian is typically implemented by the Trotter-Suzuki expansion [24]. Besides the errors in the expansion, imperfect primitive quantum gates also degrade the fidelity of the quantum simulation and eventually lead to faulty results. Due to this reason, it is an essential and urgent task to design and benchmark error-mitigation techniques that are both systematic and efficient in the NISQ era. As an instance for benchmark, the Fermi-Hubbard model [25] is particularly interesting. This model is one of the fundamental models for interacting electrons, and it has been extensively studied in classical manners, either analytically [26, 27, 28] or numerically [29]. As experimental quantum technologies develop, understanding and insights for strongly-correlated quantum systems and high-temperature superconductivity [30] can be explored through quantum simulation of the Fermi-Hubbard model eventually beyond the classical computational capability. This model has been utilized in experimental demonstration of various quantum platforms [31, 32, 33, 34]. Recently, a combination of non-PEC methods has been applied to enhance simulation performance and observe the dynamics of the Fermi-Hubbard model in a superconducting system [35].

In this paper, we experimentally study the possibility and limitations of PEC by applying the method to a four-qubit system with trapped ions [36, 37]. In particular, we focus on simulating the dynamics of the 1D Fermi-Hubbard model by using multiple Trotter steps. We find the PEC method with a tomographically reconstructed error model significantly improves the fidelity of the simulation with up to three ion qubits. However, with four qubits, the improvement of fidelity by the PEC method alone is much worse than those for two- and three-qubit systems. This is because the tomographic characterization of the noisy gates is not precise enough to capture the time correlation and the cross-talk errors. With the application of total-spin and particle-number conservation [38, 39, 15] as well as positivity constraint, however, the enhanced PEC method provides recovery for the ideal dynamics of the 1D spin-Fermi-Hubbard model, where the spin and the charge behave differently.
II Fermi-Hubbard Model and Experimental Realization with Trapped ions
Here we consider the extended Fermi-Hubbard (eFH) model, which describes a system of fermions moving in a one-dimensional lattice, as illustrated in Fig. 1a and Fig. 1b for one-component and two-component fermions. The one-component fermions can be considered spinless ones. The Hamiltonian reads
| (1) | |||||
with , where () annihilates (creates) a fermion with spin () on the -th site. Here is the nearest-neighbor tunneling strength, and and respectively quantify the strength of the on-site and the nearest-neighbor interaction.
We can map the fermion system to a qubit system by using the Jordan-Wigner transformation,
| (2) | |||||
with and being the Pauli operators on the -th qubit. Thus generally speaking, we need qubits to simulate the dynamics of an -site fermionic chain.
As shown in Fig. 1c, we use ions for qubit systems. The ions are confined in a linear Paul trap. The hyperfine levels in the ground-state manifold, i.e. and , are encoded as the qubit , which can be initialized to by optical pumping and disgustingly detected by fluorescence measurement via multi-channel photo-multiplier tube [40].
The qubit-system Hamiltonian becomes
| (3) | |||||
Note that according to the orientation of the Pauli operators, we divide the qubit-system Hamiltonian into three parts, each of which contains mutually commutative terms.
To extract dynamical properties, the essential part is to simulate the evolution operator with a universal gate set available in a certain quantum computational platform. One of the well-known solutions is to use the Trotter-Suzuki decomposition. The first-order Trotter-Suzuki decomposition of reads
| (4) |
with the Trotter step being . Figs. 1d and e show examples of the circuits for simulating the dynamics of 3-site spinless and 2-site spin- fermionic systems, with the native gate set including the Mølmer-Sorensen gates, i.e. , and , and single-qubit rotations. By applying the amplitude-shaped [41] global and individual laser beams on the desired ions and driving the transverse motional modes [42, 43], we can realize the native Mølmer-Sørensen -gate (). The gate and are composed with and corresponding single qubit rotations, as shown in Fig. 1f.
In this experiment, we consider two scenarios, one for spinless fermions, and the other for two-component fermions. In the former case, the on-site interaction strength naturally vanishes, i.e. , due to the fermionic anti-commutation relation. In this case, we use ion-qubits to simulate the dynamics of a spinless fermionic chain with sites. While for the latter case, we only consider the on-site interaction, since the interaction strength decreases as the distance increases and thus in most circumstances.
III Probabilistic error cancellation in trapped ion system
Here, we introduce the PEC error-mitigation method, which systematically recovers ideal expectation values of target quantum circuits with the experimental noisy gates [14]. The essential idea is to first characterize experimental noisy gates, then identify the noise parts by comparing the ideal and the noisy gates, and then decompose the inverse of the noise parts into combinations of basis operations. Then, each of the ideal gates in target quantum circuits is replaced by a corresponding noisy one followed by basis operations sampled with probability distributions obtained from the inverse-noise decomposition. At last, the ideal expectation value can be obtained by adding up those of the sampled circuits with appropriate weights.
In circuit quantum computation, a computational task can be compiled into a quantum circuit consisting of single- and two-qubit gates. In the trapped ion system, the error of the two-qubit gate is larger than the single-qubit one [19], and we can mitigate only the errors in two-qubit gates. To characterize the experimental noisy gates, we perform quantum process tomography (QPT), under the Pauli error assumption, to obtain the Pauli transfer matrices (PTMs) of the Mølmer-Sørensen gates on different qubit pairs, i.e. for the qubit pair . Together with the ideal PTM , we can formally define an error operator for each of the noisy gates, with the PTM being
| (5) |
Note that under the Pauli-error assumption, both and its inverse can be decomposed into linear superpositions of PTMs of two-qubit Pauli operators . As a result, ideal PTMs can be rewritten in terms of the PTMs of the noisy gate and the corresponding error operators,
| (6) |
with the inverse-error decomposition
| (7) |
Here the quasi-probabilities are real and satisfy . The fact that can be negative indicates that the inverse of the error is not physical and thus can not be implemented by a deterministic quantum operation. To cancel the effect of the error operator, we rewrite the decomposition as follows
| (8) |
where are well-defined probabilities with the cost , and is the sign function.
Then, we can use the Monte-Carlo sampling to compute the PEC error-mitigated results. Here we consider a target quantum circuit consisting of number of two-qubit gates , with the -th gate labeled as , each of which is fully characterized and the inverse-error decomposition is written as with being the quasi-probability of the two-qubit Pauli operator . The full set of the random circuits to be implemented in the experimental device denoted as , contains different circuits, each of which is obtained by adding right after . To obtain the ideal expectation values, each random circuit is assigned with a probability and a sign . As it is infeasible to implement all these circuits, we use the Monte Carlo sampling to obtain average values over the random circuits. Specifically, we generate random circuits by sampling from the probability distribution and obtain the expectation value of an observable for the circuit by averaging 300 repetitions. The ideal expectation value is then calculated by
| (9) |
where the cost is given by with the cost of the -th gate being .

IV Error mitigation and simulation of two spinless fermionic modes
We now discuss the simulation of two spinless fermionic modes, where the qubit-system Hamiltonian Eq. (3) reduces to
| (10) |
With the Trotter-Suzuki expansion of Eq. (4), the evolution of Hamiltonian for two spinless fermionic modes can be experimentally realized with the specific quantum circuit shown in Fig. 2a. For the singly occupied fermion in one of the sites, the fermion oscillates between two sites caused by the nearest-neighbor tunneling. For the doubly occupied fermions, there will be no dynamics due to the Pauli exclusion principle of fermions. We apply Trotter steps and each step consists of three gates and ten single-qubit rotations. The whole quantum circuit consists of twenty-four two-qubit gates and eighty-one single-qubit gates, where the additional one is for the initial state preparation. We set the nearest-neighbor tunneling and interaction strength as .
Errors caused by gate imperfection accumulate as the number of Trotter steps increases and the fidelity of evolved dynamics would be degraded. We mitigate the errors and improve the results of dynamics. Since it is a two-qubit system, only the one native gate needs to be mitigated. The ideal gate can be decomposed as under Pauli error assumption, which is visualized as Fig. 2b. The experimental gate is characterized by QPT. The experimental results of the PTMs of the gate and the deviation from the ideal one obtained by are shown in Figs. 2c and d, where the average gate fidelity of is [44, 45]. Here, we assume the initial state preparation is perfect and apply the detection error correction method [46] for the measurement results, which makes state preparation and measurement (SPAM) errors negligible. The quasi-probabilities, i.e. the coefficients of the two-qubit Pauli operator in the decomposition of , are shown in Fig. 2e. With the values of the quasi-probabilities , we obtain the cost for .
Then, we generate random circuits by Monte-Carlo sampling illustrated in Fig. 2f. With the method described in Eq. (9), we obtain the dynamical evolutions of state populations for two spinless fermionic modes, where the observables are with occupied fermion or no occupied fermion for each mode. The error-mitigated state populations after PEC can be negative values, which are unphysical. We address this problem by imposing constraints based on general properties of probabilities, i.e. and , and obtain physical state populations by the maximum-likelihood estimation (MLE). Specifically, we minimize the norm distance between the physical populations and the PEC error-mitigated ones. On top of PEC and MLE, we also perform post-selection (PS) with respect to the symmetry constraints of the model Hamiltonian, i.e. the conservation law of the number of fermions. To demonstrate the effect of each of the error-mitigation techniques, i.e. PEC, MLE, and PS, we apply them step by step and obtain a set of error-mitigated state populations after each step.
The experimental results of fermionic dynamics are shown in Figs. 2g and h for the cases without and with error mitigation, respectively. We use the initial two-qubits state of , which contains the superposition of two occupied fermions and a single occupied fermion. The initial states simultaneously reveal the time evolutions of both single and double fermions, since no interference occurs between both dynamics. As shown in both Figs. 2g and h, the state and do not change and there is an oscillation between the state and , which is the hallmark of fermion dynamics [32]. We can see that without error mitigation, the contrast between the experimental populations (solid points) clearly decays compared with the numerical simulation under the Trotter step (hollow points) as shown in Fig. 2g, and the error-mitigated results are closer to the ideal numerical simulations as shown in Fig. 2h. The population fidelities depending on Trotter steps without and with the three error-mitigation schemes are shown in Fig. 2i. The fidelity of the gate without and with error mitigation are and , which are obtained by exponential fitting of data.
We note that the main improvement in fidelities comes from the PEC method. It is because our characterization of the gate is a good representation of the actual gate. We confirm it by simulating the dynamics of two spinless modes with the experimentally constructed PTM of . The comparisons between the simulation with the noisy PTM and experimental data clearly validate the Pauli error assumption and accuracy of measured (see Appendix B). We also note that MLE reduces the error bar of the results after PEC, which may compensate for the drawback of PEC in the aspect of variance. All the error bars are estimated by bootstrapping method (see Appendix A).

V simulation of three spinless fermionic modes
We implement the time evolution of three spinless fermionic modes as shown in Fig. 1a. The quantum circuit in Fig. 1d, obtained by the Trotter-Suzuki expansion, simulates the dynamics of the system. We initialize the three-qubit state to , which includes two fermions in three sites. The fermions propagate in the system caused by the nearest-neighbor tunneling to other sites. The dynamical evolution would be restricted in the subspace spanned by because of the conservation law of the number of fermions.
The dynamics can be different depending on the existence of nearest-neighbor interaction different from the previous case with two sites. In the experiment, we choose and for the scenarios without and with nearest-neighbor interactions, respectively. In Figs. 3a, b, d, and e, dashed-dot lines show the results of ideal numerical simulation. When , the initial state mostly evolves to the state because of the Pauli exclusion principle of fermions. On the other hand, the initial state can evolve to both and states. Therefore, in the beginning, the overall population of the state reduces, and the population of the state increases as shown in Figs. 3a and b. When , we can see the population of is not rapidly decreasing and the state is not populated compared to the case of . It is because the interaction is effectively attractive in our experiment.
In experiment, we set of the gates and apply Trotter steps for both scenarios. With nearest-neighbor interactions, each Trotter step consists of six gates and twenty single-qubit rotations. The whole quantum circuit consists of twenty-five two-qubit gates, where the additional one is for the initial state preparation, and eighty single-qubit gates. Then, we apply the error-mitigation methods to the dynamic evolution of both scenarios. There are two types of gates on different pairs of qubits, i.e., and , both of which require characterization and inverse-error decomposition. In the PEC scheme, both and gates are individually characterized by QPT and the inverse errors are decomposed independently. The average gate fidelities are for and for (see Appendix B).
For the case of , the experimental results without and with error mitigation are shown in Figs. 3a and b, respectively. We can see the error-mitigated results are more consistent with ideal numerical simulations. The fitted population fidelities per gate without and with error mitigation are and , as shown in Fig. 3c. We note that the main improvement comes from the PEC method. This is consistent with the comparison results between the simulation with the noisy PTMs of both gates and experimental data, which indicates the measured PTMs properly characterize the two-qubit gate errors (see Appendix C). Similar conclusions are obtained for the scenario with the nearest-neighbor interaction of , as shown in Figs. 3d, e and f. The fitted population fidelities per gate without and with error mitigation are and . The two-qubit gate errors in the three-qubit system are larger than that in the two-qubit system, which leads to the larger cost as and . Therefore, we sample more random circuits as to reduce the error bars of the final error-mitigated results.
We note that the fitted population fidelities after PEC could be unphysical because of the possible negative quasi-probabilities and the cost being over 1. As shown in Figs. 3c and f, fidelities greater than 1 after applying PEC exist at the beginning of the three-fermion experiments. With the help of the MLE method based on the general properties of probabilities, we can make the population fidelities physical and reasonable, which is, below 1 as shown in green dots of Figs. 3c and f. In addition, MLE reduces the error bars of the results after PEC, which may compensate for the drawback of PEC in the aspect of variance. After applying PEC, the standard deviation of the fourth Trotter step become unexpectedly large. However, the MLE method suppresses the standard deviation by a few factors in this case.

VI Simulation of four fermionic modes
We implement the simulation of four fermionic modes with spins by encoding qubits and as two fermionic sites, where each site can contain two fermionic modes with different spins, as shown in Fig. 1b. We initialize the four qubits state to , which is corresponding to the superposition state between and as shown in Fig. 1b. The two fermions interact and exchange on the four modes caused by the nearest-neighbor tunneling and on-site interaction on subspace states with conserved fermions and spins. The corresponding quantum circuit is illustrated in Fig. 1e. Here, we expect the different dynamic behaviors of spin and charge depending on the on-site interaction strength. Spin and charge of the fermions are defined as and with being the fermion number of spin-up (down) on the -th site.
To demonstrate the different behavior of spin and charge, we consider two scenarios and , which are related without and with on-site interactions, respectively. For the case of no on-site interaction, the spin and the charge of fermions should show the same dynamics. But if there is on-site interaction, the dynamics for spin and charge should show a different behavior, which is related to spin-charge separation for low energy excitation [47, 48, 35, 49]. For the case of no on-site interaction, , the dynamics of fermions with spins are similar to those without spins, which are discussed in Figs. 2g and h. The state () is going back and forth with the other state (). Likewise, the state () is oscillating with the other state (). This leads to equal amounts of charge and spin change at each site. However, when there exists on-site interaction, the dynamics of those fermionic states are no longer simple oscillations, and the state , which is not affected by the on-site interaction, and the state , which is strongly influenced by the on-site interaction, show completely different dynamics.
In experiment, we set and apply Trotter steps for both scenarios. With on-site interactions, each step consists of six gates and twenty single-qubit rotations. The whole quantum circuit consists of twenty-five two-qubit gates, where the additional one is for the initial state preparation, and eighty single-qubit gates. In order to apply error mitigations, in particular, the PEC scheme, we characterize four types of gates on different pairs of qubits, i.e., , , , and , individually and decompose their inverse errors independently. The average gate fidelities are for , for , for and for (see Appendix B).
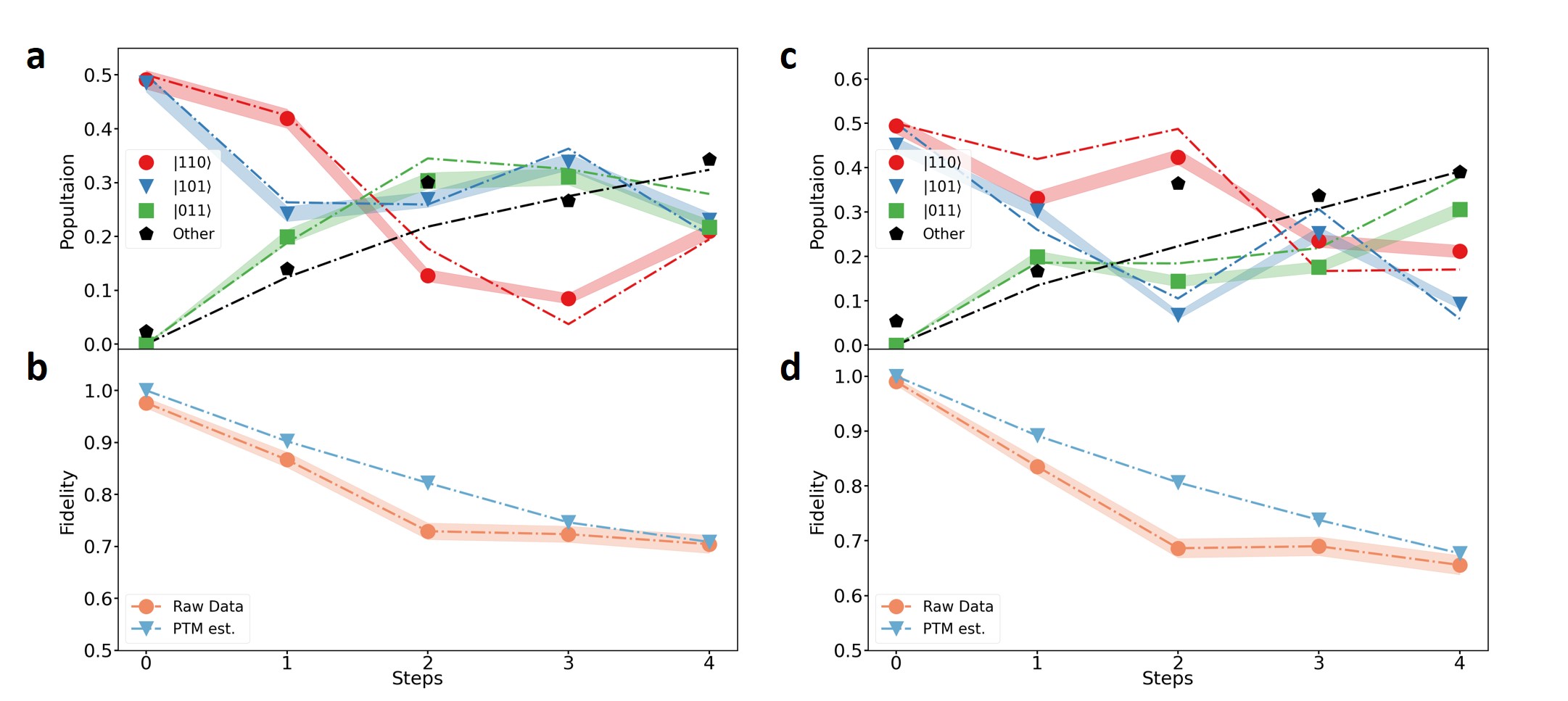
For the case of , the experimental results without and with error mitigation are shown in Figs. 4a and b, respectively. We can see the error-mitigated results are more consistent with the numerical simulation. The fitted population fidelities per gate without and with error mitigation are and , respectively, as shown in Fig. 4c. In Fig. 4d, the same behaviors of spin and charge, where the amounts of charge and spin changes are the same in the dynamics, are clearly shown with error mitigation, where the net charge and the net spin at site 1 are displayed. We can observe similar improvements in the dynamics with on-site () interaction, as shown in Figs. 4e, and f. In Fig. 4g, the fitted population fidelities per gate without and with error mitigation are and , respectively. With on-site interaction, the different behaviors of spin and charge are more clearly shown after error mitigations as shown in Fig. 4h.
We note that the PEC scheme alone does not recover the dynamics for the four fermionic modes as shown in Figs. 4c and g different from the simulations with two and three fermionic modes. The main improvements in fidelities come from the post-selection methods based on the fermion-number-conservation assumption. One reason is that the experimental PTMs of two-qubit gates in the four-qubit system do not properly characterize the imperfections of those gates. It can be seen from the inconsistency of the numerically simulated data with the PTMs of two-qubit gates and experimental results (see Appendix C). The PTMs in our experiments cannot accommodate infidelities from cross-talks between qubits and time-correlated errors, that is, the performance of the gates during characterization can be different from those of actual gates in the quantum simulation. We note that coherent errors beyond the Pauli-error model assumption also are not captured by our experimental PTMs, which partially characterize errors related to Pauli errors. However, errors from cross-talks and time-correlations would be more important factors because coherent errors have no obvious reason to be seriously worse with system size. We also note that the number of sampling is greatly increased for applying the PEC method in the four-qubit system. With the measured fidelities, the costs increase to , , and . The experimental Monte-Carlo sampling as is not sufficient, which is limited by the time-consuming running of massive random circuits in physical hardware.


VII Discussion and Outlook
We have applied the PEC method to improve the simulation of interacting fermions on up to four trapped ion qubits. We have observed the improvement of the simulation close to an order of magnitude in fidelities. With four qubits, we are able to observe the different dynamics of spin and charges for the interacting fermions.
Although PEC is the fundamental method in the experiment, several other error migration methods have been developed and applied. One of them is using the positive probability constraint. One intrinsic problem in the PEC method is that the probabilities of quantum states can be negative and not necessarily normalized. We impose constraints such that the probabilities of fermion states in the dynamics are positive and normalized, and determine the probabilities through the maximum-likelihood method. This method guarantees that observables are physically reasonable and can suppress statistical errors.
We also apply the symmetry constraint such that the total number of fermions and spins are conserved. In the simulation with four qubits, the majority of infidelity comes from the populations outside the number-conserving states. The constraints of total fermions conservation resolve the problem of population leakages. However, it is questionable if the number-conservation constraints would be scalable since the leakage can increase with the system and circuit depth.
From our experimental demonstration, although PEC incorporating constraints recoveries the dynamics of four trapped-ion qubits, it is clear that we need further improvements on the method for large-scale implementation. In particular, the drift of laser parameters and spectral crowding causes correlations resulting in remaining errors after PEC. As demonstrated in this work, combining with constraint methods can ease this issue. Recently, several proposals and experiments have been reported to tackle correlations such as using sparse Pauli-Lindblad models [23], learning-based error-mitigation [50], matrix product operator representation [51], etc. With all these techniques combined together, NISQ computers can potentially achieve the accuracy required for gaining the quantum advantage in practical applications, such as model inference for nuclear magnetic resonance (NMR) spectroscopy [52] and large-depth QAOA [53].
VIII acknowledgments
This work was supported by the Innovation Program for Quantum Science and Technology under Grants No. 2021ZD0301602, and the National Natural Science Foundation of China under Grants No. 92065205, No. 11974200, No. 12225507, No. 12088101, and No. 12204535.


IX Appendix A: Estimating error bars with the bootstrapping method
We statistically estimated the uncertainty of experimental data with and without error mitigations by using the bootstrapping method. In order to estimate the variance of experimental data, we repeatedly and randomly take out samples from our original data and apply PEC, MLE, and PS methods step by step to mitigate the population errors of each sample. In our work, the size of the samples is the same as the original data sets, and the total number of samples for each data point is usually chosen as 1000. Then we calculate the standard deviation of the state population and the population fidelities after each step with the sets of samples. In order to avoid the appearance of unphysical fidelities (larger than 100% or less than 0% after MLE and PS methods), we separated the sets of samples into two parts according to the fidelities of the original data set and calculated the standard deviation of each side, which resulted in unsymmetrical error bars. Fig. 5 shows the fidelity distribution (step 4 for the simulation of three spinless fermions, V=0) after each error-mitigation step, which indicates an increasing deviation from the normal distribution after more error-mitigation steps are applied.

X Appendix B: The PTMs and quasi-probabilities for three and four qubit system
The quantum circuits for the simulation of the three spinless fermionic modes (three-site single-component) and four fermionic modes (two-site double-component Fermi-Hubbard model) are shown in Fig. 1 (d) and (e). Here up to six two-qubit Mølmer-Sørensen gates are applied in each Trotter step. We classify the gates depending on related qubit pairs and benchmark each type of gate with the QPT method. Under Pauli error assumption, we measure 15 different components in to get the PTMs of each type of gate as shown in Fig. 6 and Fig. 7. The quasi-probabilities for gates in the simulation of three spinless fermions and two fermions with spins are shown in Fig. 8, which decides the probabilities of choosing Pauli operations in the Monte Carlo method.
XI Appendix C: The PTM simulation to understand experimental error models.
To characterize our noisy two-qubit gates, a partial QPT with Pauli error assumption is applied with 15 measurements out of 144. To verify the assumption that the errors of our gates are consistent with the increasing of Trotter steps, we perform the numerical simulation of the extended Fermi-Hubbard model with the PTMs of the noisy gates. The simulation results are shown in Figs. 9- 11 for two spinless fermions, three spinless fermions, and two fermions with spins, respectively. For the simulation of two spinless fermions, with no additional leakage to other states out of the selected subspace, we can get a consistent simulation result with the experimental data, which further convinced the significant improvement of fidelity with the PEC method as shown in the introduction of Trotter errors Fig. 2(i). For the simulation results for three spinless fermions and two fermions with spins, the population in other states out of the ideal subspace is introduced because of the Trotter errors. The leakage will be further increased by the noisy gates in the experiment, which needs to be mitigated by MLE and PS methods. As a result, the simulation results shown in Fig. 10 and 11 have obvious deviations from the experimental data, which can be considered as a result of the unexpected errors of gates such as crosstalk error.

References
- Preskill [2018] J. Preskill, Quantum computing in the nisq era and beyond, Quantum 2, 79 (2018).
- Bharti et al. [2022] K. Bharti, A. Cervera-Lierta, T. H. Kyaw, T. Haug, S. Alperin-Lea, A. Anand, M. Degroote, H. Heimonen, J. S. Kottmann, T. Menke, et al., Noisy intermediate-scale quantum algorithms, Reviews of Modern Physics 94, 015004 (2022).
- Arute et al. [2019] F. Arute, K. Arya, R. Babbush, D. Bacon, J. C. Bardin, R. Barends, R. Biswas, S. Boixo, F. G. Brandao, D. A. Buell, et al., Quantum supremacy using a programmable superconducting processor, Nature 574, 505 (2019).
- Wu et al. [2021] Y. Wu, W.-S. Bao, S. Cao, F. Chen, M.-C. Chen, X. Chen, T.-H. Chung, H. Deng, Y. Du, D. Fan, et al., Strong quantum computational advantage using a superconducting quantum processor, Physical review letters 127, 180501 (2021).
- Daley et al. [2022] A. J. Daley, I. Bloch, C. Kokail, S. Flannigan, N. Pearson, M. Troyer, and P. Zoller, Practical quantum advantage in quantum simulation, Nature 607, 667 (2022).
- Peruzzo et al. [2014] A. Peruzzo, J. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, P. J. Love, A. Aspuru-Guzik, and J. L. O’brien, A variational eigenvalue solver on a photonic quantum processor, Nat. Commun. 5, 4213 (2014).
- Shen et al. [2017] Y. Shen, X. Zhang, S. Zhang, J.-N. Zhang, M.-H. Yung, and K. Kim, Quantum implementation of the unitary coupled cluster for simulating molecular electronic structure, Phys. Rev. A 95, 020501 (2017).
- Cerezo et al. [2021] M. Cerezo, A. Arrasmith, R. Babbush, S. C. Benjamin, S. Endo, K. Fujii, J. R. McClean, K. Mitarai, X. Yuan, L. Cincio, et al., Variational quantum algorithms, Nature Reviews Physics 3, 625 (2021).
- Tilly et al. [2022] J. Tilly, H. Chen, S. Cao, D. Picozzi, K. Setia, Y. Li, E. Grant, L. Wossnig, I. Rungger, G. H. Booth, et al., The variational quantum eigensolver: a review of methods and best practices, Physics Reports 986, 1 (2022).
- Shor [1995] P. W. Shor, Scheme for reducing decoherence in quantum computer memory, Phys. Rev. A 52, R2493 (1995).
- Steane [1996] A. M. Steane, Error correcting codes in quantum theory, Phys. Rev. Lett. 77, 793 (1996).
- Temme et al. [2017] K. Temme, S. Bravyi, and J. M. Gambetta, Error mitigation for short-depth quantum circuits, Phys. Rev. Lett. 119, 180509 (2017).
- Li and Benjamin [2017] Y. Li and S. C. Benjamin, Efficient variational quantum simulator incorporating active error minimization, Phys. Rev. X 7, 021050 (2017).
- Endo et al. [2018] S. Endo, S. C. Benjamin, and Y. Li, Practical quantum error mitigation for near-future applications, Phys. Rev. X 8, 031027 (2018).
- Cai et al. [2022] Z. Cai, R. Babbush, S. C. Benjamin, S. Endo, W. J. Huggins, Y. Li, J. R. McClean, and T. E. O’Brien, Quantum error mitigation, arXiv preprint arXiv:2210.00921 (2022).
- Kandala et al. [2019] A. Kandala, K. Temme, A. D. Córcoles, A. Mezzacapo, J. M. Chow, and J. M. Gambetta, Error mitigation extends the computational reach of a noisy quantum processor, Nature 567, 491 (2019).
- Kim et al. [2021] Y. Kim, C. J. Wood, T. J. Yoder, S. T. Merkel, J. M. Gambetta, K. Temme, and A. Kandala, Scalable error mitigation for noisy quantum circuits produces competitive expectation values, arXiv preprint arXiv:2108.09197 (2021).
- Song et al. [2019] C. Song, J. Cui, H. Wang, J. Hao, H. Feng, and Y. Li, Quantum computation with universal error mitigation on a superconducting quantum processor, Science advances 5, eaaw5686 (2019).
- Zhang et al. [2020] S. Zhang, Y. Lu, K. Zhang, W. Chen, Y. Li, J.-N. Zhang, and K. Kim, Error-mitigated quantum gates exceeding phys. fidelities in a trapped-ion system, Nat. Commun. 11, 1 (2020).
- Piveteau et al. [2022] C. Piveteau, D. Sutter, and S. Woerner, Quasiprobability decompositions with reduced sampling overhead, npj Quantum Information 8, 1 (2022).
- Takagi et al. [2021] R. Takagi, S. Endo, S. Minagawa, and M. Gu, Fundamental limits of quantum error mitigation, arXiv preprint arXiv:2109.04457 (2021).
- Huggins et al. [2021] W. J. Huggins, S. McArdle, T. E. O’Brien, J. Lee, N. C. Rubin, S. Boixo, K. B. Whaley, R. Babbush, and J. R. McClean, Virtual distillation for quantum error mitigation, Physical Review X 11, 041036 (2021).
- Berg et al. [2022] E. v. d. Berg, Z. K. Minev, A. Kandala, and K. Temme, Probabilistic error cancellation with sparse pauli-lindblad models on noisy quantum processors, arXiv preprint arXiv:2201.09866 (2022).
- Suzuki [1990] M. Suzuki, Fractal decomposition of exponential operators with applications to many-body theories and monte carlo simulations, Physics Letters A 146, 319 (1990).
- Hubbard [1963] J. Hubbard, Electron correlations in narrow energy bands, Proc. R. Soc. A: Math. Phys. Eng. Sci. 276, 238 (1963).
- Lieb and Wu [1968] E. H. Lieb and F. Y. Wu, Absence of mott transition in an exact solution of the short-range, one-band model in one dimension, Phys. Rev. Lett. 20, 1445 (1968).
- Metzner and Vollhardt [1989] W. Metzner and D. Vollhardt, Correlated lattice fermions in dimensions, Phys. Rev. Lett. 62, 324 (1989).
- Müller-Hartmann [1989] E. Müller-Hartmann, Correlated fermions on a lattice in high dimensions, Zeitschrift für Physik B Condensed Matter 74, 507 (1989).
- LeBlanc et al. [2015] J. P. F. LeBlanc, A. E. Antipov, F. Becca, I. W. Bulik, G. K.-L. Chan, C.-M. Chung, Y. Deng, M. Ferrero, T. M. Henderson, C. A. Jiménez-Hoyos, E. Kozik, X.-W. Liu, A. J. Millis, N. V. Prokof’ev, M. Qin, G. E. Scuseria, H. Shi, B. V. Svistunov, L. F. Tocchio, I. S. Tupitsyn, S. R. White, S. Zhang, B.-X. Zheng, Z. Zhu, and E. Gull (Simons Collaboration on the Many-Electron Problem), Solutions of the two-dimensional hubbard model: Benchmarks and results from a wide range of numerical algorithms, Phys. Rev. X 5, 041041 (2015).
- Lee et al. [2006] P. A. Lee, N. Nagaosa, and X.-G. Wen, Doping a mott insulator: Physics of high-temperature superconductivity, Rev. Mod. Phys. 78, 17 (2006).
- Casanova et al. [2012] J. Casanova, A. Mezzacapo, L. Lamata, and E. Solano, Quantum simulation of interacting fermion lattice models in trapped ions, Physical review letters 108, 190502 (2012).
- Barends et al. [2015] R. Barends, L. Lamata, J. Kelly, L. García-Álvarez, A. G. Fowler, A. Megrant, E. Jeffrey, T. C. White, D. Sank, J. Y. Mutus, et al., Digital quantum simulation of fermionic models with a superconducting circuit, Nature communications 6, 1 (2015).
- Mazurenko et al. [2017] A. Mazurenko, C. S. Chiu, G. Ji, M. F. Parsons, M. Kanász-Nagy, R. Schmidt, F. Grusdt, E. Demler, D. Greif, and M. Greiner, A cold-atom fermi–hubbard antiferromagnet, Nature 545, 462 (2017).
- Hensgens et al. [2017] T. Hensgens, T. Fujita, L. Janssen, X. Li, C. Van Diepen, C. Reichl, W. Wegscheider, S. Das Sarma, and L. M. Vandersypen, Quantum simulation of a fermi–hubbard model using a semiconductor quantum dot array, Nature 548, 70 (2017).
- Arute et al. [2020] F. Arute, K. Arya, R. Babbush, D. Bacon, J. C. Bardin, R. Barends, A. Bengtsson, S. Boixo, M. Broughton, B. B. Buckley, et al., Observation of separated dynamics of charge and spin in the fermi-hubbard model, arXiv preprint arXiv:2010.07965 (2020).
- Lanyon et al. [2011] B. P. Lanyon, C. Hempel, D. Nigg, M. Müller, R. Gerritsma, F. Zähringer, P. Schindler, J. T. Barreiro, M. Rambach, G. Kirchmair, et al., Universal digital quantum simulation with trapped ions, Science 334, 57 (2011).
- Lu et al. [2019] Y. Lu, S. Zhang, K. Zhang, W. Chen, Y. Shen, J. Zhang, J.-N. Zhang, and K. Kim, Global entangling gates on arbitrary ion qubits, Nature 572, 363 (2019).
- Bonet-Monroig et al. [2018] X. Bonet-Monroig, R. Sagastizabal, M. Singh, and T. O’Brien, Low-cost error mitigation by symmetry verification, Physical Review A 98, 062339 (2018).
- McArdle et al. [2019] S. McArdle, X. Yuan, and S. Benjamin, Error-mitigated digital quantum simulation, Physical review letters 122, 180501 (2019).
- Olmschenk et al. [2007] S. Olmschenk, K. C. Younge, D. L. Moehring, D. N. Matsukevich, P. Maunz, and C. Monroe, Manipulation and detection of a trapped hyperfine qubit, Phys. Rev. A 76, 052314 (2007).
- Schindler [2008] P. Schindler, Frequency synthesis and pulse shaping for quantum information processing with trapped ions, Diploma thesis, Innsbruck University (2008).
- Sørensen and Mølmer [1999] A. Sørensen and K. Mølmer, Quantum computation with ions in thermal motion, Phys. Rev. Lett. 82, 1971 (1999).
- Kim et al. [2009] K. Kim, M.-S. Chang, R. Islam, S. Korenblit, L.-M. Duan, and C. Monroe, Entanglement and tunable spin-spin couplings between trapped ions using multiple transverse modes, Phys. Rev. Lett. 103, 120502 (2009).
- Nielsen [2002] M. A. Nielsen, A simple formula for the average gate fidelity of a quantum dynamical operation, Phys. Lett. A 303, 249 (2002).
- Greenbaum [2015] D. Greenbaum, Introduction to quantum gate set tomography, arXiv preprint arXiv:1509.02921 (2015).
- Shen and Duan [2012] C. Shen and L.-M. Duan, Correcting detection errors in quantum state engineering through data processing, New J. Phys. 14, 053053 (2012).
- Tarruell and Sanchez-Palencia [2018] L. Tarruell and L. Sanchez-Palencia, Quantum simulation of the hubbard model with ultracold fermions in optical lattices, C. R. Physique 19, 365 (2018).
- Vijayan et al. [2020] J. Vijayan, P. Sompet, G. Salomon, J. Koepsell, S. Hirthe, A. Bohrdt, F. Grusdt, I. Bloch, and C. Gross, Time-resolved observation of spin-charge deconfinement in fermionic hubbard chains, Science 367, 186 (2020).
- Senaratne et al. [2022] R. Senaratne, D. Cavazos-Cavazos, S. Wang, F. He, Y.-T. Chang, A. Kafle, H. Pu, X.-W. Guan, and R. G. Hulet, Spin-charge separation in a one-dimensional fermi gas with tunable interactions, Science 376, 1305 (2022).
- Strikis et al. [2021] A. Strikis, D. Qin, Y. Chen, S. C. Benjamin, and Y. Li, Learning-based quantum error mitigation, PRX Quantum 2, 040330 (2021).
- Guo and Yang [2022] Y. Guo and S. Yang, Quantum error mitigation via matrix product operators, PRX Quantum 3, 040313 (2022).
- Sels et al. [2020] D. Sels, H. Dashti, S. Mora, O. Demler, and E. Demler, Quantum approximate bayesian computation for nmr model inference, Nature machine intelligence 2, 396 (2020).
- Farhi et al. [2014] E. Farhi, J. Goldstone, and S. Gutmann, A quantum approximate optimization algorithm, arXiv preprint arXiv:1411.4028 (2014).