XX \jnumX \jyearYear
RESEARCH ARTICLE
INFORMATION SCIENCE
Corresponding authors. Email: [email protected]; [email protected]
EPR-Net: Constructing non-equilibrium potential landscape via a variational force projection formulation
Abstract
[ABSTRACT]We present EPR-Net, a novel and effective deep learning approach that tackles a crucial challenge in biophysics: constructing potential landscapes for high-dimensional non-equilibrium steady-state (NESS) systems. EPR-Net leverages a nice mathematical fact that the desired negative potential gradient is simply the orthogonal projection of the driving force of the underlying dynamics in a weighted inner-product space. Remarkably, our loss function has an intimate connection with the steady entropy production rate (EPR), enabling simultaneous landscape construction and EPR estimation. We introduce an enhanced learning strategy for systems with small noise, and extend our framework to include dimensionality reduction and state-dependent diffusion coefficient case in a unified fashion. Comparative evaluations on benchmark problems demonstrate the superior accuracy, effectiveness, and robustness of EPR-Net compared to existing methods. We apply our approach to challenging biophysical problems, such as an 8D limit cycle and a 52D multi-stability problem, which provide accurate solutions and interesting insights on constructed landscapes. With its versatility and power, EPR-Net offers a promising solution for diverse landscape construction problems in biophysics.
doi:
10.1093/nsr/XXXXkeywords:
high-dimensional potential landscape, non-equilibrium system, entropy production rate, dimensionality reduction, deep learningINTRODUCTION
Since Waddington’s famous landscape metaphor on the development of cells in the 1950s [1], the construction of potential landscape for non-equilibrium biochemical reaction systems has been recognized as an important problem in theoretical biology, as it provides insightful pictures for understanding complex dynamical mechanisms of biological processes. This problem has attracted considerable attention in recent decades in both biophysics and applied mathematics communities. Until now, different approaches have been proposed to realize Waddington’s landscape metaphor in a rational way, and its connection to computing the optimal epigenetic switching paths and switching rates in biochemical reaction systems has also been extensively studied. See [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13] and the references therein for details and [14, 15, 16, 17, 18] for reviews. Broadly speaking, these proposals can be classified into two types: (T1) the construction of potential landscape in the finite noise regime [2, 3, 4, 5] and (T2) the construction of the quasi-potential in the zero noise limit [7, 6, 8].
For low-dimensional systems (i.e., dimension less than ), the potential landscape can be numerically computed either by solving a Fokker-Planck equation (FPE) using grid-based methods until the steady solution is reached approximately as in (T1) type proposals [3, 19], or by solving a Hamilton-Jacobi-Bellman (HJB) equation using, for instance, the ordered upwind method [20] or minimum action type method [8] as in (T2) type proposals. However, these approaches suffer from the curse of dimensionality when applied to high-dimensional systems. Although methods based on mean-field approximations are able to provide a semi-quantitative description of the potential landscape for some typical systems [4, 21], direct and general approaches are still favored in applications. In this aspect, pioneering work has been done recently, which allows direct construction of a high-dimensional potential landscape using deep neural networks (DNNs), based on either the steady viscous HJB equation satisfied by the potential landscape function in the (T1) case [22, 23], or the point-wise orthogonal decomposition of the force field in (T2) case [24].
While these works have significant advanced methodological developments, these approaches are based on solving HJB equations alone and may encounter numerical difficulties due to either non-uniqueness of the weak solution to the non-viscous HJB equation in (T2) case [25], or singularity of the solution with a small noise in (T1) case. Meanwhile, the loss functions considered in [24, 22, 23] are essentially of physics-informed neural network (PINN) form [26], so are generally non-convex, and thus might encounter troubling local minimum issues in the training process.
In this work, we present a simple yet efficient DNN approach to construct the potential landscape of high-dimensional non-equilibrium steady state (NESS) systems in (T1) type with either moderate or small noise. Its intimate connection with non-equilibrium statistical mechanics, nice variational structure and superior numerical performance make it a competitive and promising approach in landscape construction methodology. Our main contributions are as follows.
-
(1)
Proposal of entropy production rate (EPR) loss. We introduce the convex EPR loss function, reveal its connection with the entropy production rate in statistical physics, and propose its enhanced version using the tempering technique.
-
(2)
Dimensionality reduction. We put forward a simple dimensionality reduction strategy when the reducing variables are prescribed, and, interestingly, the reduction formalism has a unified formulation with the EPR framework for the primitive variables. This even holds whenever the system has constant or variable diffusion coefficients.
-
(3)
Successful high-dimensional applications. We successfully apply our approach to some challenging high-dimensional biological systems including an eight-dimensional (8D) cell cycle model [4] and a 52D multi-stable system [27]. Our results reveal more delicate structure of the constructed landscapes than what mean-field approximations typically provide, yet we acknowledge that mean-field approximations are not limited by the potential challenges in SDE simulations.
Overall, EPR-Net offers a promising solution for diverse landscape construction problems in biophysics. Even its nice mathematical structure and connection with non-equilibrium statistical physics make it a unique object that deserves further theoretical and numerical exploration in the future.
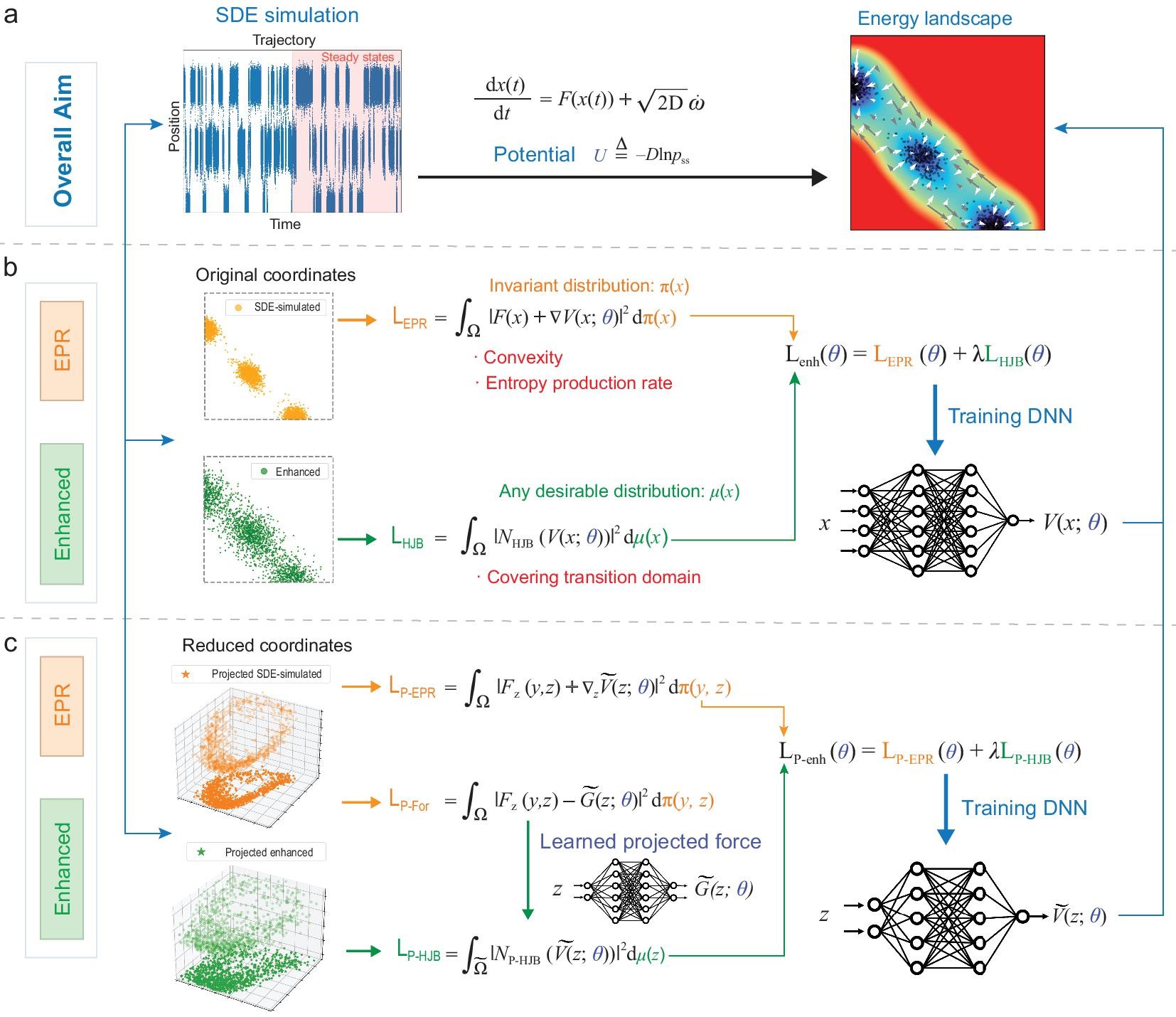
EPR FRAMEWORK
In this section, we provide an overview of the whole EPR framework, including its primitive formulation, the physical interpretation, its convex property, and the enhanced EPR version.
Overview
Consider an ergodic stochastic differential equation (SDE)
| (1) |
where , is a smooth driving force, is the -dimensional temporal Gaussian white noise with and for and . The constant specifies the noise strength, which is often proportional to the system’s temperature . We denote by its steady-state probability density function (PDF).
Following the (T1) type proposal in [3], we define the potential of (1) as and the steady probability flux in the domain , which we assume for simplicity is either or a -dimensional hyperrectangle. The steady-state PDF satisfies the Fokker-Planck equation (FPE)
| (2) |
and we assume the asymptotic boundary condition (BC) as when , or the reflecting boundary condition when is a -dimensional hyperrectangle, where is the unit outer normal. In both cases, we have and .
Here we illustrate the main EPR workflow through Fig. 1. As depicted in Fig. 1a, our primary objective is to construct the energy landscape defined for Eq. (1). Leveraging our proposed approach, the enhanced EPR method, we first simulate the considered SDEs until steady state is reached in order to get sample points (the whole ‘SDE simulation’ column of Fig. 1). We then train a neural network, representing the potential , for the landscape construction, even when confronted with challenging high-dimensional scenarios. We initially introduce the EPR loss (the middle column of Fig. 1b), which benefits from its convexity, with its minimum coinciding with the entropy production rate. Subsequently, we present the enhanced EPR loss , tailored to encompass the transition domain more effectively. Furthermore, the overall methodology can be easily extended to the dimensionality reduction problem (Fig. 1c), with a unified formulation as the EPR framework shown in Fig. 1b, but for the projected variables and corresponding loss functions and .
EPR loss
Aiming at an effective approach for high-dimensional applications, we employ NNs to approximate , and the key idea in this paper is to learn by training DNN with the loss function
| (3) |
where is a neural network function with parameters [28], and . To justify (3), we note that, for any function , satisfies the orthogonality relation
| (4) |
which follows from FPE (2), a simple integration by parts and the corresponding BC. Equation (4) means that is perpendicular to the space formed by for all possible under the -weighted inner product. Equivalently, is the orthogonal projection of the driving force onto under the -weighted inner product, which implies that is the unique minimizer (up to a constant) of the loss function (3). See Supplementary Information (SI) Section A for derivations in detail. We note that related ideas are taken in coarse-graining of molecular systems [29, 30] and generative modeling in machine learning [31, 32]. However, to the best of our knowledge, using the loss in (3) to construct the potential of NESS systems has never been considered before.
In fact, define the -weighted inner product for any square integrable functions on as
| (5) |
and the corresponding -norm by , we get a Hilbert space (see, e.g., [33, Chapter II.1]). Eq. (4) implies that the minimization of EPR loss finds the orthogonal projection of to the function gradient space , which is formed by function gradients for any , under the -weighted inner product. Choosing in (4) gives
| (6) |
However, we remark that this orthogonality holds only in the -inner product sense instead of the pointwise sense. Furthermore, the two orthogonality relations (4) and (6) can be understood as follows. Using (6), relation (4) is equivalent to for any . Integration by parts gives , which is equivalent to . When , we recover the pointwise orthogonality, which is adopted in computing quasi-potentials in [24]. In mathematical language, (6) can be understood as the Hodge-type decomposition in instead of space.
To utilize (3) in numerical computations, we replace the ensemble average (3) with respect to the unknown by the empirical average with data sampled from (1):
| (7) |
Here could be either the final states (at time ) of independent trajectories starting from different initializations, or equally spaced time series along a single long trajectory up to time , where . In both cases, the ergodicity of SDE in (1) guarantees that (7) is a good approximation of (3) as long as is large [34]. We adopt the former approach in the numerical experiments in this work, where the gradients of both (with respect to ) and the loss itself (with respect to ) in (7) are calculated by auto-differentiation through PyTorch [35]. Given the involvement of an approximation on , we perform a formal stability analysis of (3) in SI Section B to ensure its reliability and robustness. Additionally, in the following subsection, we elucidate the benefits of EPR, particularly in terms of convexity and its physical interpretation pertaining to the entropy production rate.
Physical interpretation and convexity
The minimum loss of (3), denoted as , possesses a well-defined physical interpretation. In the following discussion, we show that this minimum EPR loss aligns precisely with the steady entropy production rate as defined in the NESS theory. Following [36, 37], we have the important identity concerning the entropy production for (1):
| (8) |
Here is the entropy of the probability density function at time , is the entropy production rate (EPR)
| (9) |
and is the heat dissipation rate
| (10) |
with the probability flux at time . When , the above formulas have clear physical meaning in statistical physics.
From the loss in (3) and the steady state of (9), we get the identity
| (11) | ||||
where is the steady probability flux and denotes the steady entropy production rate (EPR) of the NESS system (1) [36, 3, 37]. Therefore, minimizing (3) is equivalent to approximating the steady Entropy Production Rate. This correspondence provides a rationale for naming our approach ‘EPR-Net’.
EPR loss has an appealing property that it is strictly convex on (up to a constant), i.e.,
| (12) |
for any and which satisfy , where . Eq. (12) can be easily verified by direct calculations. This strict convexity guarantees the uniqueness of the critical point (up to a constant) and provides theoretical guarantee on the fast convergence of the training procedure under certain assumptions [38]. It may also contribute to better convergence behavior of EPR during the training process, as mentioned in the numerical comparisons part.
Enhanced EPR loss
Substituting the relation into (2), we get the viscous HJB equation
| (13) |
with the asymptotic BC as in the case of , or the reflecting BC on when is a -dimensional hyperrectangle, respectively. As in the framework of PINNs [26], (13) motivates the HJB loss
| (14) |
where is any desirable distribution. By choosing properly, this loss allows the use of sample data that better covers the domain and, when combined with the loss in (3), leads to improvement of the training results when is small. Specifically, for small , we propose the enhanced loss which has the form
| (15) |
where is defined in (7), is an approximation of (14) using an independent data set obtained by sampling the trajectories of (1) with a larger . The weight parameter balances the contribution of the two terms in (15). While its value can be tuned based on system’s properties, in our numerical experiment we observed that the method performs well for taking values in a relatively broad range. Note that the proposed strategy is both general and easily adaptable. For instance, one can alternatively use data that contains more samples in the transition region, or employ in (15) a modification of the loss (14) [22]. We further illustrate the motivation of enhanced EPR in SI Section E.
RESULTS FOR ENERGY LANDSCAPE CONSTRUCTION
In this section, we demonstrate the superiority of the enhanced EPR over the HJB loss alone and over the normalizing flow (NF), which is a class of generative models used for density estimation that leverage invertible transformations to map between complex data distributions and simple latent distributions [39], through 2D benchmark examples. We then apply the enhanced EPR to the 3D Lorenz model and a 12D Gaussian mixture model to show its effectiveness in constructing energy landscapes in higher dimensions. We remark that alternative approaches have been investigated for potential construction in limit cycles [40] and the Lorenz system [41] distinct from our methodology.
Two-dimensional benchmark examples
Within this subsection, we undertake a comparative analysis of 2D benchmark problems. These encompass a toy model, a 2D biological system exhibiting a limit cycle [3], and a 2D multi-stable system [5], see SI Section F.1-F.4 for training details, additional results and problem settings.

Constructing landscapes
The potential function is approximated using a feedforward neural network architecture consisting of three hidden layers, employing the tanh activation function. Each hidden layer comprises 20 hidden states. Subsequently, we refer to the enhanced loss as
| (16) |
where and should be chosen to balance the corresponding loss terms. In SI Section F.1, we conduct a sensitivity analysis of , demonstrating that our methods are robust and effective across a broad spectrum of scenarios.
As illustrated in Fig. 2a-c, we initially showcase well-constructed landscapes under the EPR framework. These include the acquired potentials , the decomposition of forces, and sample points derived from the simulated invariant distribution. In the toy model (Fig. 2a), the gradient of the potential (white arrows) points directly towards the corresponding attractor, while the non-gradient part of the force field (gray arrows) shows a counter-clockwise rotation in the model with a limit cycle (Fig. 2b), and a splitting-and-back flow from the attractor in the middle to the other two attractors in the tri-stable dynamical model (Fig. 2c).
Data enhancement techniques employed to generate improved samples are flexible, as visually depicted in Fig. 2d-f. We present choices for obtaining these samples, including generating more diffusive samples with a diffusion coefficient or introducing Gaussian perturbations with a standard deviation of . We provide a more comprehensive analysis of the data enhancement in SI Section F.1, demonstrating the resilience of enhanced EPR to variations in the enhanced samples. Specifically in Fig. 2, we use for the toy model, for the multi-stable problem and for the limit-cycle problem. We use the same size of the SDE-simulated dataset and the enhanced dataset , denoted as .
Numerical comparisons
We proceed to perform a quantitative and comprehensive comparison of the performance between enhanced EPR, solving HJB alone and NF. For the toy model, the true solution is analytically known (see SI Section F.2), while for the other two 2D examples, we compute the reference solution by discretizing the steady FPE using a piecewise bilinear finite element method on a fine rectangular grid and computing the obtained sparse linear system using the least squares solver (the normalization condition is utilized to fix the additive constant). After training, we shift the minimum of the potentials to the origin and we measure their accuracy using the relative root mean square error (rRMSE) and the relative mean absolute error (rMAE):
| (17) | ||||
| (18) |
on the domain , where denotes the reference solution.
| Problem | Method | rRMSE | rMAE |
| Toy, D=0.1 | Enhanced EPR | 0.0280.010 | 0.0260.010 |
| HJB loss alone | 0.0340.016 | 0.0290.014 | |
| Normalizing Flow | 0.1240.016 | 0.0820.011 | |
| Toy, D=0.05 | Enhanced EPR | 0.0540.020 | 0.0480.019 |
| HJB loss alone | 0.1910.218 | 0.1600.179 | |
| Normalizing Flow | 0.2390.040 | 0.1740.034 | |
| Multi-stable | Enhanced EPR | 0.0670.047 | 0.0660.049 |
| HJB loss alone | 0.2490.015 | 0.2280.011 | |
| Normalizing Flow | 0.2020.029 | 0.1330.017 | |
| Limit Cycle | Enhanced EPR | 0.0700.016 | 0.0630.020 |
| HJB loss alone | 0.2310.048 | 0.1400.021 | |
| Normalizing Flow | 0.3840.021 | 0.2670.013 |

We present a detailed comparison of the 2D problems in Table 1. Our experiments involve solving HJB alone with various distributions of enhanced samples , and we report the optimal outcome as the representative entry for the table. For a fair comparison between enhanced EPR and standalone HJB, we maintain consistent network training configurations. Additionally, a detailed analysis of and in SI Section F.1 highlights the enhanced EPR’s superior performance and robustness. Concerning the flow model, we leverage the same SDE-simulated dataset as utilized in enhanced EPR. The metrics presented in Table 1 yield the same consistent result, reinforcing the superiority of enhanced EPR over other methods across all problems.
We further illustrate the learned potential landscapes obtained through different methods for the 2D toy model with in Fig. 3a-c. Furthermore, we plot the absolute error between the learned potential and the reference solution in Fig. 3d-f. These plots demonstrate that errors within enhanced EPR are consistently small. In contrast, errors in HJB alone and NF can be significantly large, leading to unfavorable outcomes and limited smoothness. Based on this study and our numerical experiences, the advantages of the enhanced EPR over both the approach using HJB loss alone and NF can be summarized into the following points.

-
•
Accuracy. As shown in Table 1, the enhanced EPR achieves the best accuracy over the HJB loss alone and normalizing flow approaches in terms of the rRMSE and rMAE metric. From Fig. 3, we can also find that the enhanced EPR presents the overall landscape more consistent with the simulated samples and the true/reference solution than the other two methods. The decomposition of the force also shows a better matching result. The learned potential by the HJB loss alone and normalizing flow tends to be rough and non-smooth near the edge of samples (Fig. 3b and c). Compared with the enhanced EPR and HJB loss alone, the normalizing flow captures the high probability domain but does not explicitly take advantage of the information of the dynamics, thus making its performance the worst.
-
•
Robustness. Without the guidance of EPR loss, minimizing HJB loss alone does not lead to a good approximation of the true solution that can closely match the heuristically chosen distribution as shown in Fig. 3b. The significant variance observed in the results for the toy model with by solving HJB alone is attributed to an exceptionally poor outlier. However, the enhanced EPR always gives reliable approximations with the introduced setup. This supports the robustness of the enhanced EPR loss. We refer to SI Section F.1 for detailed analysis of the chosen parameters and distribution of enhanced samples .
-
•
Efficiency. Our numerical experiments show that the enhanced EPR converges faster than the approach using the HJB loss alone. For instance, in the toy model with , the enhanced EPR has achieved rRMSE of and rMAE of in 2000 epochs, while training with the HJB loss alone can not attain the same accuracy level even after 3000 epochs. As we have analyzed, this efficiency might be attributed to the strict convexity of the EPR loss. Related theoretical support for this speculation can be found in [38].
-
•
Performance of single EPR. We remark that single EPR, which relies solely on the EPR loss by setting in (15), can still give acceptable results with a relatively small . Its rRMSE and rMAE are and , respectively, which are also small enough. In the limit cycle problem, single EPR is not as good as in the toy model and the multi-stable problem, since there are much fewer samples in the domain where the non-gradient force is extremely large, as shown in Fig. 2b. However, single EPR loss can achieve competitive performance as long as the samples cover the domain effectively.
Three-dimensional Lorenz system
We apply our landscape construction approach to the 3D Lorenz system [42] with isotropic temporal Gaussian white noise, i.e. the system (1) with and
| (19) | ||||
| (20) | ||||
| (21) |
where , and . We add the noise with strength . This model was also considered in [23] with . We obtain the enhanced data by adding Gaussian noises with standard deviation to the SDE-simulated data , where . We directly train the 3D potential by enhanced EPR (16) with , using Adam with a learning rate of 0.001 and batch size of 2048. A slice view of the landscape is presented in Fig. 4a and the learned 3D potential agrees well with the simulated samples.
Twelve-dimensional multi-stable system
To further validate the efficacy of EPR-Net in high-dimensional scenarios, we construct a Gaussian mixture model (GMM) in with two centers, of which the true solution can be denoted as , where , and , with normalization factor . The parameters are chosen as , , , , , , , and .
For evaluation, we first sample 10,000 points from the known GMM distribution and calculate the relative error between the learned 12D potential and the true potential . The resulting rRMSE and rMAE are 0.054 and 0.051, respectively, indicating the high accuracy of the learned potential. In addition, we denote the first two dimensions of this 12D problem as and draw samples from the corresponding conditional distribution . As depicted in Fig. 4b, we compute the cumulative measure of the absolute error between and the learned solution based on the conditional distribution as . Impressively, this integral consistently remains below 0.01, underscoring the fact that our approach yields negligible errors in the effective domain. Moreover, comparing the barrier heights (BHs) further validates the precision of our approach, with a relative error of less than 5% for both BHs. Due to the diagonal covariance matrix, the saddle point precisely lies on the line passing through and , allowing us to directly compare the BHs. As shown in Fig 4c, the true and computed slice lines coincide well. For additional details, please refer to SI Section F.5.
DIMENSIONALITY REDUCTION
When applying the approach above to high-dimensional problems, dimensionality reduction is necessary in order to visualize the results and gain physical insights. For simplicity, we consider the linear case and, with a slight abuse of notation, let , where contains the coordinates of two variables of interest, and corresponds to the remaining variables. The domain (either or a -dimensional hyperrectangle) has the decomposition , where and are the domains of and , respectively. Automatic selection of linear reduced variables and extensions to nonlinear reduced variables with general domains are also possible [43, 44]. In the current setting, the reduced potential is
| (22) |
and one can show that minimizes the loss function:
| (23) |
where is the -component of the force field .
Moreover, one can derive an enhanced loss as in (15) that could be used for systems with small . To this end, we note that satisfies the projected HJB equation
| (24) |
with asymptotic BC as , or the reflecting BC on , where is the projected force defined using the conditional distribution , and denotes the unit outer normal on . Based on (DIMENSIONALITY REDUCTION), we can formulate the projected HJB loss
| (25) |
where is any suitable distribution over , and in (DIMENSIONALITY REDUCTION) is learned beforehand by training a DNN with the loss
| (26) |
The overall enhanced loss (16) used in numerical computations comprises two terms, which are empirical estimates of (23) and (25) based on two different sets of sample data. We refer the reader to SI Section C for derivation details, SI Section G.1 for experiments of Ferrell’s cell cycle model [45] and SI Section G.2 and G.3 for details and additional results of the 8D [4] and 52D [27] models.

Eight-dimensional cell cycle: reduced potential
Subsequently, we apply our dimensionality reduction approach to construct the landscape for an 8D cell cycle model [4], which contains both a limit cycle and a stable equilibrium point. In this case, we consider CycB (a cyclin B protein) and Cdc20 (an exit protein) as the reduced variables following [4]. As shown in Fig. 5a and b, we can find that both the profile of the reduced potential and the force strength agree well with the density of projected samples. Moreover, we gain some important insights from Fig. 5b on the projection of the high-dimensional dynamics to two dimensions. One particular feature is that the limit cycle induced by the projected force (outer red circle) slightly differs from the limit cycle directly projected from high dimensions (yellow circle), and the difference is either minor or moderate depending on whether the sample density near the limit circle is high or low. This is natural in the reduction when , since the distribution involved in computing is not a Dirac -distribution, but a diffusive distribution with varying widths along the limit cycle, and the difference will disappear as . Another feature is that we unexpectedly get an additional stable limit cycle (inner red circle) and a stable point (red dot in the center) emerging inside the outer limit cycle. Though virtual in high dimensions and biologically irrelevant, the existence of such two limit sets is reminiscent of the Poincaré-Bendixson theorem in planar dynamics theory [46, Chapter 10.6], which depicts a common phenomenon when performing dimensionality reduction with limit cycles to the 2D plane. Note that this theorem does not guarantee the stability of such fixed points; they could be stable, unstable, or even saddle points, see another case in SI G.1. The emergence of these two limit sets is specific in this model due to the relatively flat landscape of the potential in the centering region. In addition, close to the saddle point of (green star), there is a barrier along the limit cycle direction, while there is a local well along the Cdc20 direction, which characterizes the region that biological cycle paths mainly go through. Last but not least, an enlarged view of the local attractive domain outside the limit cycle shows its intricate spiral structure (Fig. 5c), which has not been revealed in previous work based on mean-field approximation [4].
Fifty-two-dimensional multi-stable system: high-dimensional and reduced potentials
We compare two approaches to construct the reduced potential. One is to learn the reduced force by (26) first and then use it to construct the landscape by enhanced EPR in -space. The other is to build a high-dimensional potential by enhanced EPR first and then reduce it (see SI Section C.1). For this comparison, we apply our approach to a gene stem cell regulatory network described by an ODE in 52 dimensions [27] and take GATA6 (a major differentiation marker gene) and NANOG (a major stem cell marker gene) as the reduced variable , as suggested in [27]. We define as the set of indices for activating and as the set of indices for repressing , the corresponding relationships are defined as the 52D node network shown in [27]. For ,
| (27) |
where , , , , and . We choose the noise strength and focus on the domain .
As shown in Fig. 5d, the projected force demonstrates the reduced dynamics and the constructed potential agrees well with the SDE-simulated samples. While is learned by first obtaining the projected force, is reduced from a high-dimensional precomputed by enhanced EPR. The gray plot of the absolute error of is shown in Fig. 5e, which supports the consistency of two potentials learned by different approaches. When taking as the reference solution, we get the rRMSE 0.113 and rMAE 0.097. The minor relative errors show that these two approaches to constructing the reduced potential are quantitatively consistent, although it is difficult to know which is more accurate. It also indirectly supports the reliability of the learned high-dimensional potential . The obtained landscape shows a smoother and more delicate profile compared to the mean-field approach [27].
DISCUSSION AND CONCLUSION
The EPR-Net formulation can be extended to the case of state-dependent diffusion coefficients without difficulty. Consider the Itô SDE
| (28) |
with diffusion matrix and an -dimensional temporal Gaussian white noise . We assume that and the matrix satisfies for all , where is a positive constant. Using a similar derivation as before, we can again show that the high-dimensional landscape function of (28) minimizes the EPR loss
| (29) |
where and for . We provide derivation details of (29) in SI Section D, and we leave the numerical study of (28)–(29) for future work.
To summarize, we have demonstrated the formulation, applicability and superiority of EPR to the benchmark and real biological examples over some existing approaches. Below we make some final remarks. First, concerning the use of the steady-state distribution in (3) and its approximation by a long time series of the SDE (1) in EPR-Net, we emphasize that it is the sampling approximation of that naturally captures the important parts of the potential function, and the landscape beyond the sampled regions is not that essential in practice. Second, as is exemplified in Fig. 2 and Table 1, we found that a direct application of density estimation methods (DEM), e.g., normalizing flows [39], to the sampled time series data does not give potential landscape with satisfactory accuracy. We speculate that such deficiency of DEM is due to its over-generality and the fact that it does not take advantage of the force field information explicitly compared to (3). Finally, we remark that in our dimensionality reduction approach, we choose the reduced variables according to available biophysics prior knowledge. Our approach also exhibits the capability to be extended to incorporate a state-dependent diffusion coefficient. Automatic selection of general nonlinear reduced variables can be also studied by incorporating the idea of the identification of collected variables in molecular simulations [47, 48].
Overall, we have presented the EPR-Net, a simple yet effective DNN approach, for constructing the non-equilibrium potential landscape of NESS systems. This approach is both elegant and robust due to its variational structure and its flexibility to be combined with other types of loss functions. Further extension of dimensionality reduction to nonlinear reduced variables and numerical investigations in the case of state-dependent diffusion coefficients will be explored in future works. Moreover, we are actively considering the application of our method to single-cell RNA sequencing data, which involves systems of really high dimensionality and typically lacks analytical ODE formulations. We will explore this point in our forthcoming studies.
METHODS
Detailed methods are given in the supplementary material. The code is accessible at https://github.com/yzhao98/EPR-Net.
ACKNOWLEDGMENTS
We thank Professors Chunhe Li, Xiaoliang Wan and Dr. Yufei Ma for helpful discussions. The computation of this work was conducted on the High-performance Computing Platform of Peking University.
FUNDING
T.L. and Y.Z. acknowledge support from the National Natural Science Foundational of China (11825102 and 12288101) and the Ministry of Science and Technology of China (2021YFA1003301). The work of W.Z. was supported by the Deutsche Forschungsgemeinschaft (DFG) under Germany’s Excellence Strategy, part of the Berlin Mathematics Research Centre MATH+ (EXC-2046/1, 390685689), and the DFG through Grant CRC 1114 ‘Scaling Cascades in Complex Systems’ (235221301).
AUTHOR CONTRIBUTIONS
Y.Z., W.Z. and T.L. designed the research; Y.Z. performed the research; Y.Z., W.Z. and T.L. wrote the paper.
Conflict of interest statement. None declared.
References
- [1] Waddington C. The strategy of the genes 1957.
- [2] Ao P. Potential in stochastic differential equations: novel construction. J. Phys. A-Math. Gen. 2004; 37: L25.
- [3] Wang J, Xu L and Wang E. Potential landscape and flux framework of nonequilibrium networks: Robustness, dissipation, and coherence of biochemical oscillations. Proc. Nat. Acad. Sci. USA 2008; 105: 12271.
- [4] Wang J, Li C and Wang E. Potential and flux landscapes quantify the stability and robustness of budding yeast cell cycle network. Proc. Nat. Acad. Sci. USA 2010; 107: 8195.
- [5] Wang J, Zhang K, Xu L et al. Quantifying the Waddington landscape and biological paths for development and differentiation. Proc. Nat. Acad. Sci. USA 2011; 108: 8257.
- [6] Zhou J, Aliyu M, Aurell E et al. Quasi-potential landscape in complex multi-stable systems. J. R. Soc., Interface 2012; 9: 3539.
- [7] Ge H and Qian H. Landscapes of non-gradient dynamics without detailed balance: Stable limit cycles and multiple attractors. Chaos 2012; 22: 023140.
- [8] Lv C, Li X, Li F et al. Constructing the energy landscape for genetic switching system driven by intrinsic noise. PLoS ONE 2014; 9: e88167.
- [9] Shi J, Aihara K, Li T et al. Energy landscape decomposition for cell differentiation with proliferation effect. Nat. Sci. Rev. 2022; 9: nwac116.
- [10] Maier RS and Stein DL. Escape problem for irreversible systems. Phys. Rev. E 1993; 48: 931.
- [11] Aurell E and Sneppen K. Epigenetics as a first exit problem. Phys. Rev. Lett. 2002; 88: 048101.
- [12] Sasai M and Wolynes P. Stochastic gene expression as a many-body problem. Proc. Nat. Acad. Sci. USA 2003; 100: 2374.
- [13] Roma DM, O’Flanagan RA, Ruckenstein AE et al. Optimal path to epigenetic switching. Phys. Rev. E 2005; 71: 011902.
- [14] Ferrell JEJ. Bistability, bifurcations, and Waddington’s epigenetic landscape. Curr. Biol. 2012; 22: R458.
- [15] Wang J. Landscape and flux theory of non-equilibrium dynamical systems with application to biology. Adv. Phys. 2015; 64: 1.
- [16] Zhou P and Li T. Construction of the landscape for multi-stable systems: Potential landscape, quasi-potential, A-type integral and beyond. J. Chem. Phys. 2016; 144: 094109.
- [17] Yuan R, Zhu X, Wang G et al. Cancer as robust intrinsic state shaped by evolution: a key issues review. Rep. Prog. Phys. 2017; 80: 042701.
- [18] Fang X, Kruse K, Lu T et al. Nonequilibrium physics in biology. Rev. Mod. Phys. 2019; 91: 045004.
- [19] Li C, Hong T and Nie Q. Quantifying the landscape and kinetic paths for epithelial–mesenchymal transition from a core circuit. Phys. Chem. Chem. Phys. 2016; 18: 17949–56.
- [20] Cameron M. Finding the quasipotential for nongradient SDEs. Phys. D 2012; 241: 1532.
- [21] Li C and Wang J. Landscape and flux reveal a new global view and physical quantification of mammalian cell cycle. Proc. Nat. Acad. Sci. USA 2014; 111: 14130.
- [22] Lin B, Li Q and Ren W. Computing the invariant distribution of randomly perturbed dynamical systems using deep learning. J. Sci. Comp. 2022; 91: 77.
- [23] Lin B, Li Q and Ren W. Computing high-dimensional invariant distributions from noisy data. J. Comp. Phys. 2023; 474: 111783.
- [24] Lin B, Li Q and Ren W. A data driven method for computing quasipotentials. Proc. Mach. Learn. Res., volume 145 of 2nd Annual Conference on Mathematical and Scientific Machine Learning (2021) 652.
- [25] Crandall MG and Lions PL. Viscosity solution of Hamilton-Jacobi equations. Trans. Amer. Math. Soc. 1983; 277: 1.
- [26] Raissi M, Perdikaris P and Karniadakis GE. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comp. Phys. 2019; 378: 686.
- [27] Li C and Wang J. Quantifying cell fate decisions for differentiation and reprogramming of a human stem cell network: Landscape and biological paths. PLoS Comput. Biol. 2013; 9: e1003165.
- [28] Goodfellow I, Bengio Y and Courville A. Deep learning 2016.
- [29] Zhang L, Han J, Wang H et al. DeePCG: Constructing coarse-grained models via deep neural networks. J. Chem. Phys. 2018; 149: 034101.
- [30] Husic BE, Charron NE, Lemm D et al. Coarse graining molecular dynamics with graph neural networks. J. Chem. Phys. 2020; 153: 194101.
- [31] Hyvärinen A. Estimation of non-normalized statistical models by score matching. J. Mach. Learn. Res. 2005; 6: 695–709.
- [32] Song Y and Ermon S. Generative modeling by estimating gradients of the data distribution. Wallach H, Larochelle H, Beygelzimer A et al., editors, Advances in Neural Information Processing Systems, volume 32 of NeurIPS (2019) 11918–30.
- [33] Courant R and Hilbert D. Methods of mathematical physics 1953.
- [34] Khasminskii R. Stochastic stability of differential equations 2012.
- [35] Paszke A, Gross S, Massa F et al. Pytorch: An imperative style, high-performance deep learning library. Advances in Neural Information Processing Systems, volume 32 of NeurIPS (2019) 8024.
- [36] Qian H. Mesoscopic nonequilibrium thermodynamics of single macromolecules and dynamic entropy-energy compensation. Phys. Rev. E 2001; 65: 016102.
- [37] Zhang X, Qian H and Qian M. Stochastic theory of nonequilibrium steady states and its applications. part i. Phys. Rep. 2012; 510: 1–86.
- [38] Mei S, Montanari A and Nguyen PM. A mean field view of the landscape of two-layer neural networks. Proc. Nat. Acad. Sci. USA 2018; 115: E7665–E71.
- [39] Kobyzev I, Prince SJD and Brubaker M. Normalizing flows: An introduction and review of current methods. IEEE Trans. Patt. Anal. Mach. Intel. 2021; 43: 3964–79.
- [40] Zhu XM, Yin L and Ao P. Limit cycle and conserved dynamics. International Journal of Modern Physics B 2006; 20: 817–27.
- [41] Ma Y, Tan Q, Yuan R et al. Potential function in a continuous dissipative chaotic system: Decomposition scheme and role of strange attractor. International Journal of Bifurcation and Chaos 2014; 24: 1450015.
- [42] Lorenz EN. Deterministic nonperiodic flow. J. Atmos. Sci. 1963; 20: 130–41.
- [43] Zhang W, Hartmann C and Schütte C. Effective dynamics along given reaction coordinates, and reaction rate theory. Faraday Discuss. 2016; 195: 365–94.
- [44] Kang X and Li C. A dimension reduction approach for energy landscape: Identifying intermediate states in metabolism-emt network. Adv. Sci. 2021; 8: 2003133.
- [45] Ferrell JE, Tsai TYC and Yang Q. Modeling the cell cycle: Why do certain circuits oscillate? Cell 2011; 144: 874–85.
- [46] Hirsch MW, Smale S and Devaney RL. Differential equations, dynamical systems, and an introduction to chaos 2004.
- [47] Bonati L, Zhang YY and Parrinello M. Neural networks-based variationally enhanced sampling. Proc. Nat. Acad. Sci., USA 2019; 116: 17641–7.
- [48] Bonati L, Rizzi V and Parrinello M. Data-driven collective variables for enhanced sampling. J. Phys. Chem. Lett. 2020; 11: 2998–3004.
- [49] Evans LC. Partial differential equations 2010.
- [50] Holmes MH. Introduction to perturbation methods 2013.
- [51] Frenkel D and Smit B. Understanding molecular simulation: From algorithms to applications 2002.
- [52] Kingma DP and Ba J. Adam: a method for stochastic optimization. Proceedings of the International Conference on Learning Representations (2015) .
- [53] Durkan C, Bekasov A, Murray I et al. Neural spline flows. Advances in Neural Information Processing Systems, volume 32 of NeurIPS (2019) .
Supplementary Information for EPR-Net:
Constructing non-equilibrium potential landscape via a variational force projection formulation
In this supplementary information (SI), we will present further theoretical derivations and computational details of the contents in the main text (MT). This SI consists of two parts: theory and computation.
PART 1: THEORY
We will first provide details of theoretical derivations omitted in the MT.
Appendix A Derivation of the EPR loss
In this section, we show that, up to an additive constant, the potential function is the unique minimizer of the EPR loss in equation (1) in MT.
First, we show that the orthogonality relation
| (30) |
holds for any suitable function under both choices of the boundary conditions considered in this work, where . To see this, we note that
where we have used integration by parts, the relation , the corresponding BC, and the steady state Fokker-Planck equation (FPE) satisfied by .
Now consider the EPR loss, we have
where we have used the orthogonality relation (30) to arrive at the last equality, from which we conclude that is the unique minimizer of the EPR loss up to an additive constant.
Appendix B Stability of the EPR minimizer
In this section, we formally show that small perturbations of the invariant distribution will not introduce a disastrous change to the minimizer of the corresponding EPR loss. We only consider the case where is a -dimensional hyperrectangle. The argument for is similar.
Suppose , , and the functions and are the unique minimizers (up to a constant) of the following two EPR losses
respectively. It is not difficult to find that the Euler-Lagrange equations of are given by the following partial differential equation (PDE) with suitable BCs:
The PDEs above defined inside the domain can be converted to
Define and . We then obtain
| (31) | |||
| (32) |
Assuming that , where denotes a small constant, we have the PDE for by subtracting (32) from (31):
with BC . Since , we can obtain that
by the regularity theory of elliptic PDE [49, Section 6.3] when , or by the matched asymptotic expansion when [50, Chapter 2]. In fact, the closeness between and can be ensured as long as and are close enough in the region where and are bounded away from zero by the method of characteristics analysis [49, Section 2.1] and matched asymptotics.
The above derivations assume that the PDFs , are smooth enough. The stability analysis for general distributions and is also possible by utilizing the functional analysis tools. However, the derivations will be abstract and quite involved, and we will report it elsewhere.
Appendix C Dimensionality reduction
In this section, we study dimensionality reduction for high-dimensional problems in order to learn the projected potential. A straightforward approach is to first learn the high-dimensional potential and then find its low-dimensional representation, i.e., the reduced potential or the free energy function, using dimensionality reduction techniques. An alternative approach is to directly learn the low-dimensional reduced potential.
Denote by . As in MT Section 1.4, we assume the domain
where and are the domain of and , respectively. The reduced potential is defined as
| (33) |
One natural approach for constructing is directly integrating based on the learned with the EPR loss, i.e.,
| (34) |
However, performing this integration is not a straightforward numerical task (see, e.g., [51, Chapter 7]).
C.1 Gradient projection loss
In this subsection, we study a simple approach to approximate based on sample points, which approximately obey the invariant distribution , and the learned high dimensional potential function by EPR loss. This approach is taken in the consistency checking of the reduced potentials by different methods in SI Section G.3. The idea is to utilize the gradient projection (GP) loss on the components of :
| (35) |
To justify (35), we note that
where and denote the terms in the third and the fourth line above, respectively. The term since
and
which cancel with each other in .
Therefore, the minimization of GP loss is equivalent to minimizing
which clearly implies that is the unique minimizer (up to a constant) of the proposed GP loss.
C.2 Projected EPR loss
In this subsection, we study the projected EPR (P-EPR) loss, which has the form
| (36) |
where is the -component of the force field .
C.3 Force projection loss
In this subsection, we study the force projection (P-For) loss for approximating the projection of onto the -space.
Denote by
| (40) |
the projected force defined using the conditional distribution
| (41) |
We can learn via the following force projection loss
| (42) |
C.4 HJB equation for the reduced potential
In this subsection, we show that the reduced potential satisfies the projected HJB equation
| (44) |
with asymptotic BC as , or the reflecting BC on , where denotes the unit outer normal on . We will only consider the rectangular domain case here. The argument for the unbounded case is similar.
Recall that satisfies the FPE
| (45) |
Integrating both sides of (45) on with respect to and utilizing the boundary condition , where , we get
| (46) |
Taking (40) and (41) into account, we obtain
| (47) |
i.e., a FPE for with the reduced force field , where . The corresponding boundary condition can be also derived by integrating the original BC on with respect to for , which gives
| (48) |
Substituting the relation into (47) and (48), we get (44) and the corresponding reflecting BC after some algebraic manipulations.
Appendix D State-dependent diffusion coefficients
In this section, we study the EPR loss for NESS systems with a state-dependent diffusion coefficient.
Consider the Itô SDE
| (49) |
with the state-dependent diffusion matrix . Under the same assumptions as in MT Section 1.1, we have the FPE
| (50) |
We show that the high dimensional landscape function of (49) minimizes the EPR loss
| (51) |
where and for .
To justify (51), we first note that (50) can be rewritten as
| (52) |
which, together with the BC, implies the orthogonality relation
| (53) |
for a suitable test function . Following the same reasoning used in establishing (30) and utilizing (53), we have
The last expression implies that is the unique minimizer of up to a constant.
The above derivation for the state-dependent diffusion case will permit us to construct the landscape for the chemical Langevin dynamics, which will be studied in future works.
PART 2: COMPUTATION
Now we present the computational details omitted in the MT. We will first demonstrate the motivation for enhanced EPR, and then provide the training details and problem settings for landscape construction with original coordinates and dimension reduction. As mentioned in MT, we refer to the enhanced loss as Eq. (16).
Appendix E Motivation for enhanced EPR

We utilize enhanced samples to achieve a better coverage of the transition domain. Note that the EPR loss equation (3) in MT requires training data sampled according to . The accuracy of the learned (more precisely, the accuracy of the gradient ) using equation (3) in MT is guaranteed only in the “visible” domain of , i.e., regions that are covered by sample points. However, the enhanced EPR framework (16) combines both the EPR loss and the HJB, which allows the use of sample data that better covers the domain (e.g., more samples in the transition regions between meta-stable states and near the boundaries of the visible domain). This approach is particularly compelling when the diffusion coefficient D is relatively small.
The single EPR loss works well for the toy model with a relatively large diffusion coefficient . A slice plot of the potential at in Fig. 6a shows that the learned solution with EPR loss coincides well with the analytical solution. The relative root mean square error (rRMSE) and the relative mean absolute error (rMAE) have the mean and the standard deviation of and over 3 runs, respectively.
However, when decreasing to , the samples from the simulated invariant distribution mainly stay in the double wells (orange points in Fig. 6c) and are away from the transition region between the two wells. For this reason, as shown in Fig. 6b, the result with a single EPR loss captures the profile of the two wells, but these two parts of the profile are not accurately connected in the transition region where there are few samples, making the left well a bit higher than the right one. We then generate enhanced samples using , which have better coverage of the transition region (green points in Fig. 6a). Incorporating these enhanced samples, we learn the potential with the enhanced EPR loss and the result agrees better with the true solution (Fig. 6b).
Though the enhanced EPR is more recommended in general situations, we remark that the single EPR loss can achieve competitive performance as long as the samples cover the domain effectively. This numerical experience works for all of the considered models.
Appendix F Landscape with original coordinates
In this section, we will describe the additional setup where we utilize enhanced EPR for landscape construction with original coordinates in MT. This section includes a 2D toy model, a 2D biological system with a limit cycle [3], a 2D multi-stable system [5] and a 12D Gaussian mixture model (GMM).
F.1 Training details and additional results for benchmark problems
We begin by simulating the SDE using the Euler-Maruyama scheme with reflecting boundary conditions until time , starting from different initial states. This simulation yields final states, which are used as the training dataset to approximate the invariant distribution for EPR. For the 2D toy problem and 2D multi-stable problem, we employ a time-step size of 0.1, whereas for the 2D limit cycle problem, we use a smaller time-step size of 0.01. We train the network with a batch size of 1024 and a learning rate of 0.001 using the Adam [52] optimizer for 3000 epochs in the toy models, 5000 epochs in the multi-stable model and 10000 epochs in the limit cycle model. When focusing on single EPR loss in the toy model with , we extend to 8000 epochs to ensure adequate learning. At each training epoch, we update the dataset by performing one step Euler-Maruyama scheme to make it closer to the invariant distribution. For the comparison with normalizing flows, we train a neural spline flow [53].111https://github.com/643VincentStimper/normalizing-flows We repeat 4 blocks of the rational quadratic spline with three layers of 64 hidden units and a followed LU linear permutation. The flow model is trained by the Adam optimizer with the learning rate 0.0001 for 20000 epochs, based on the same SDE-simulated dataset as the enhanced EPR. To ensure the robustness of our results, we perform our experiments across 5 random seeds, which helps to account for variability and establish the reliability of our findings.
| Metrics | rRMSE | rMAE | |||||||
| HJB | Enhanced EPR | HJB | Enhanced EPR | ||||||
| 0.0 | 0.1 | 1.0 | 10.0 | 0.0 | 0.1 | 1.0 | 10.0 | ||
| Toy, | 0.034 0.016 | —— | —— | —— | 0.029 0.014 | —— | —— | —— | |
| 0.168 0.010 | 0.062 0.033 | 0.028 0.010 | 0.038 0.015 | 0.068 0.009 | 0.108 0.054 | 0.026 0.010 | 0.032 0.013 | ||
| 0.225 0.071 | 0.138 0.021 | 0.080 0.011 | 0.046 0.018 | 0.123 0.097 | 0.032 0.025 | 0.030 0.011 | 0.030 0.019 | ||
| 0.258 0.078 | 0.182 0.033 | 0.095 0.010 | 0.067 0.012 | 0.167 0.110 | 0.062 0.040 | 0.038 0.010 | 0.037 0.009 | ||
| Toy, | 0.191 0.218 | —— | —— | —— | 0.160 0.179 | —— | —— | —— | |
| 0.267 0.116 | 0.058 0.045 | 0.054 0.020 | 0.111 0.083 | 0.164 0.120 | 0.049 0.036 | 0.048 0.019 | 0.096 0.069 | ||
| 0.661 0.126 | 0.417 0.162 | 0.204 0.213 | 0.055 0.028 | 0.555 0.093 | 0.328 0.155 | 0.127 0.184 | 0.029 0.008 | ||
| 0.544 0.061 | 0.485 0.126 | 0.227 0.132 | 0.191 0.190 | 0.489 0.057 | 0.410 0.096 | 0.157 0.136 | 0.122 0.168 | ||
| Multi-stable | 0.255 0.007 | —— | —— | —— | 0.241 0.004 | —— | —— | —— | |
| 0.249 0.015 | 0.069 0.045 | 0.110 0.028 | 0.146 0.044 | 0.228 0.011 | 0.065 0.046 | 0.106 0.030 | 0.142 0.047 | ||
| 0.628 0.046 | 0.061 0.031 | 0.090 0.042 | 0.128 0.043 | 0.553 0.063 | 0.059 0.032 | 0.088 0.046 | 0.124 0.044 | ||
| 0.630 0.051 | 0.307 0.036 | 0.067 0.047 | 0.118 0.032 | 0.550 0.066 | 0.197 0.036 | 0.066 0.049 | 0.118 0.034 | ||
| Limit Cycle | 0.231 0.048 | —— | —— | —— | 0.140 0.021 | —— | —— | —— | |
| 0.287 0.175 | 0.256 0.181 | 0.070 0.016 | 0.136 0.002 | 0.165 0.108 | 0.149 0.107 | 0.063 0.020 | 0.108 0.003 | ||
| 0.503 0.133 | 0.372 0.173 | 0.373 0.181 | 0.122 0.008 | 0.313 0.092 | 0.222 0.119 | 0.200 0.090 | 0.101 0.006 | ||
| 0.578 0.010 | 0.556 0.013 | 0.509 0.025 | 0.298 0.055 | 0.383 0.025 | 0.355 0.030 | 0.303 0.040 | 0.175 0.029 | ||
For a fair comparison, we fix at 1.0 across all models. The parameters we use in the MT is for toy model and multi-stable model, and for the limit cycle model. As discussed in the MT, the selection of aims to balance the two terms of the loss function. Based on our experience, systems with higher entropy production rates—typically featuring more non-gradient components in their force decomposition—require a smaller , as in the limit cycle problem. However, the specific choice of is relatively robust. As demonstrated in Table 2, we scrutinize the stability of by testing its sensitivity within the enhanced EPR method. We adjust by multiplying it by a set of factors {0.0, 0.1, 1.0, 10.0} as for different experiments. Then corresponds to the scenario of using HJB alone. Despite the varying distributions of , our selected parameters typically yield satisfactory outcomes. Even with a relatively small , enhanced EPR outperforms solving by HJB alone. The performance enhancements are more pronounced when relatively large values of are used.
We also evaluate different distributions of samples using the HJB loss, i.e., . For enhanced EPR, using invariant distribution in the HJB loss term is ineffective, as HJB loss is involved to cover the transition domain. Consequently, there is no need to evaluate with or for enhanced EPR. In the case of the HJB loss, our numerical analysis suggests that overly diffusive samples can lead to significantly worse outcomes, underscoring the importance of capturing the critical domains within the loss. As shown in Table 2, the optimal results for HJB alone are achieved using the invariant distribution or a distribution slightly more extensive than that. However, with the same enhanced samples from , introducing a non-zero enhances performance compared to HJB alone, particularly when the sample domain is so diffusive that solving HJB alone performs poorly. This emphasizes the robustness of enhanced EPR to variations in and its advantage over solving HJB alone. Finally, we emphasize the optimal outcome for across various for each problem by bolding it in Table 2, serving as the result for enhanced EPR in Table 1 of the MT. While this may not be the best result among all the combinations of and , it is a commonly robust choice that can be readily achieved without dedicated tuning.
F.2 2D toy model
To verify the applicability and accuracy of our method, we initially apply it to a toy model with the driving force
| (54) |
where is a constant skew-symmetric matrix, i.e., , and is some known function. With this choice of , one can check that the true potential landscape is simply . In particular, the system becomes reversible when . We construct a 2D toy model with the double-well potential as
| (55) |
where . We take the anti-symmetric matrix
| (56) |
which introduces a counter-clockwise rotation for a focusing central force field. This sets up a simple non-equilibrium system. In this model, we have the force decomposition
and
hold in the pointwise sense. Therefore, the identity is satisfied for any and, following the discussions in MT, we have constructed a non-reversible system with analytically known double-well potential which can be used to verify the accuracy of the learned potential. We focus on the domain . To fix the extra shifting degree of freedom of the potential function, we set the minimum of the potential to be zero and only plot the result on the domain in Fig. 3 in MT since it is the domain of practical interest.
F.3 Two-dimensional limit cycle model
We apply our approach to the limit cycle dynamics with a Mexican-hat shape landscape [3].
Before introducing the concrete model, let us make the following observation. For any SDE like
| (57) |
the corresponding steady FPE is
If we make the transformation
in (57), then the steady state PDF
will not change. The transformation only changes the timescale of the dynamics (57) from to . However, the potential changes from to if we utilize the drift and noise strength in the system (57). This observation allows us to set the scale of to be by adjusting suitably for a specific problem. An alternative approach to accomplish this task is by choosing to be in the EPR loss.
F.4 Two-dimensional multi-stable model
F.5 Twelve-dimensional GMM model: high-dimensional potential
As mentioned in MT Methods 3.4, we can construct models with known potential with driving force like Eq. (54). The true solution is denoted by , where is the probability distribution of the GMM, as defined in MT Section 1.3. We randomly generate a matrix with elements uniformly in , then obtain an skew-symmetric matrix by . The non-reversible dynamics is then constructed with driving force in (54). We set the noise strength as for this problem and use for enhanced samples. We use a three-layer neural network with 80 hidden states per layer. The data size is 10000 and we use Adam with a learning rate of 0.001 and batch size of 2048. We train enhanced EPR with for 5000 epochs.
Appendix G Landscape with reduced coordinates
In this section, we provide additional details and results related to the dimension reduction problem. First, we present additional experiments of the 3D Ferrell’s cell cycle problem [45]. We then demonstrate an 8D limit cycle dynamics [4], in which interesting properties emerge with projected force and potential . Finally, we present a 52D multi-stable dynamics [27], on which we compare the reduced potential by two dimensionality reduction approaches.
G.1 Ferrell’s three-ODE model: reduced potential

We utilize the dimensionality reduction method on Ferrell’s three-ODE model for a simplified cell cycle dynamics [45], where the concentrations of the cyclin-dependent protein kinase (), Polo-like kinase 1 (), and the anaphase-promoting complex (APC), denoted by
respectively, obey the ODEs in the domain
| (62) | ||||
| (63) | ||||
| (64) |
with and . Since our focus in this paper is on the methodology of constructing the potential landscape, we refer the interested readers to the literature [45] for concrete biological meaning of the considered variables. We add the noise scale with isotropic temporal Gaussian white noise. For this particular problem, we employ three-layer neural networks with hidden units in each layer. We generate enhanced samples by simulating from a more diffusive distribution with . The projected force is trained by the loss (42) for epochs using Adam optimizer with a learning rate 0.001 and a batch size 2048. The reduced variables are utilized during this training phase. Subsequently, we train the projected potential for epochs using the enhanced EPR loss defined in (16), with the chosen values of and . As shown in Fig. 7, the obtained reduced potential shows a plateau in the centering region and a local-well tube domain along the reduced limit cycle.
G.2 Eight-dimensional complex system: reduced potential

We consider an 8D system in which the dynamics and parameters are the same as in the supplementary information of [4]. We take CycB and Cyc20 as the reduction variable , and set the mass in this problem as .
We first point out that the noise strength used in [4] is not suitable here in training neural networks since this would lead to a potential of order . Using the idea in SI Section F.3, we amplify the original force field in [4] by times, and take for the transformed force field. This amounts to setting for the original force field, which is even smaller than the parameter considered in [4]. We simulate the SDE without boundaries with timestep until , starting from initial states drawn from a uniform distribution in . The enhanced samples are obtained by adding Gaussian perturbations with a standard deviation to the SDE-simulated dataset . We only keep the data within the biologically meaningful domain of of size 25000 for computation.
We use three-layer networks with 80 hidden states in each layer for both force and potential. For the projected force, we train 2000 epochs to obtain . Then we conduct the enhanced EPR (16) with for 10000 epochs. We use Adam with a learning rate of 0.001 and batch size of 8192.
In Fig. 8, we present a more detailed picture of the reduced dynamics for the 8D model than Fig. 5c in MT. Specifically, we further show two unstable limit cycles of the projected force field obtained by reversed time integration (two green circles in Fig. 8). These two unstable limit cycles play the role of separatrices between the neighboring stable limit sets. This picture occurs due to the fact that the landscape of the considered system is very flat in the centering region. These inner limit sets are virtual in high dimensions, but they naturally appear in the reduced dynamics on the plane. Similar features might also occur in other reduced dynamics in two dimensions.
G.3 Fifty-two-dimensional multi-stable system: high-dimensional and reduced potentials
For fairness, we all use a neural network with three-layer and 20 hidden states in each layer to denote the reduced force and potential , and 80 hidden states for the 52D potential . We use enhanced samples simulated from a more diffusive distribution with . The data size is 20000 and we use Adam with a learning rate of 0.001 and batch size of 2048, still. We use in enhanced EPR (16). We train the force for 1000 epochs and conduct by enhanced EPR with for 5000 epochs. We also learn a 52D potential by enhanced EPR for 5000 epochs and then project it to by (35) for 1000 epochs.