Entropy-Regularized Process Reward Model

Hanning Zhang^♠∗, Pengcheng Wang^♡∗, Shizhe Diao^♣, Yong Lin^♢,
Rui Pan^♠, Hanze Dong^△, Dylan Zhang^♠, Pavlo Molchanov^♣, Tong Zhang^♠
^♠University of Illinois Urbana-Champaign ^♡University of Toronto
^♣NVIDIA ^♢Princeton University ^△Salesforce Research
{hanning5, ruip4, shizhuo2, tozhang}@illinois.edu
[email protected], {sdiao, pmolchanov}@nvidia.com
[email protected], [email protected]

Abstract

Large language models (LLMs) have shown promise in performing complex multi-step reasoning, yet they continue to struggle with mathematical reasoning, often making systematic errors. A promising solution is reinforcement learning (RL) guided by reward models, particularly those focusing on process rewards, which score each intermediate step rather than solely evaluating the final outcome. This approach is more effective at guiding policy models towards correct reasoning trajectories. In this work, we propose an entropy-regularized process reward model (ER-PRM) that integrates KL-regularized Markov Decision Processes (MDP) to balance policy optimization with the need to prevent the policy from shifting too far from its initial distribution. We derive a novel reward construction method based on the theoretical results. Our theoretical analysis shows that we could derive the optimal reward model from the initial policy sampling. Our empirical experiments on the MATH and GSM8K benchmarks demonstrate that ER-PRM consistently outperforms existing process reward models, achieving 1% improvement on GSM8K and 2-3% improvement on MATH under best-of-N evaluation, and more than 1% improvement under RLHF. These results highlight the efficacy of entropy-regularization in enhancing LLMs’ reasoning capabilities.¹¹1Our code is available at https://github.com/hanningzhang/ER-PRM.

\NewDocumentCommand\shizhe

mO ^shizhe[#1] \NewDocumentCommand\dylan mO ^DylanZhang[#1] \NewDocumentCommand\dylanzhangedit mO ^{DylanTentativeEdit}[#1] \NewDocumentCommand\hanning mO ^hanning[#1]

Entropy-Regularized Process Reward Model

Hanning Zhang^♠∗, Pengcheng Wang^♡∗, Shizhe Diao^♣, Yong Lin^♢, Rui Pan^♠, Hanze Dong^△, Dylan Zhang^♠, Pavlo Molchanov^♣, Tong Zhang^♠ ^♠University of Illinois Urbana-Champaign ^♡University of Toronto ^♣NVIDIA ^♢Princeton University ^△Salesforce Research {hanning5, ruip4, shizhuo2, tozhang}@illinois.edu [email protected], {sdiao, pmolchanov}@nvidia.com [email protected], [email protected]

^*^*footnotetext: Equal Contribution.

1 Introduction

Large language models (LLMs) have demonstrated remarkable performance across numerous tasks, particularly in the challenging area of mathematical reasoning (OpenAI et al., 2024; Yang et al., 2024; Dubey et al., 2024). A key factor behind these successes is the use of synthetic data, as explored in works such as Meta-MathQA (Yu et al., 2023), MAmmoTH (Yue et al., 2023), and Open-MathInstruct (Toshniwal et al., 2024b). Open-source models fine-tuned on these synthetic datasets have shown significant improvements in test accuracy on standard mathematical reasoning benchmarks such as MATH (Hendrycks et al., 2021) and GSM8K (Cobbe et al., 2021). Following supervised fine-tuning, reinforcement learning (RL) has received considerable attention as a technique for further improving models’ reasoning abilities by aligning the model’s behavior with human values and goals, especially after the release of OpenAI-o1 model²²2https://openai.com/index/introducing-openai-o1-preview/.

The RL methods used in the current literature on LLM reasoning can be broadly categorized into two approaches. The first category focuses on training-time alignment, where RL is used to fine-tune the model to maximize an RL metric evaluated by a reward model. Examples include PPO (Schulman et al., 2017), GRPO (Shao et al., 2024). More recently, scaling inference-time computation has also been shown to enhance model performance by using reward models to guide LLM decoding. Techniques such as best-of-n sampling (Dong et al., 2023) and Monte Carlo tree search (MCTS) (Xie et al., 2024) are representative examples of this approach. All these methods require an external reward model to provide a reward signal to update the model parameters or rank the candidate responses. Regardless of the specific RL method, the quality of the reward function remains the most crucial factor, as it sets the upper bound for the algorithm’s performance.

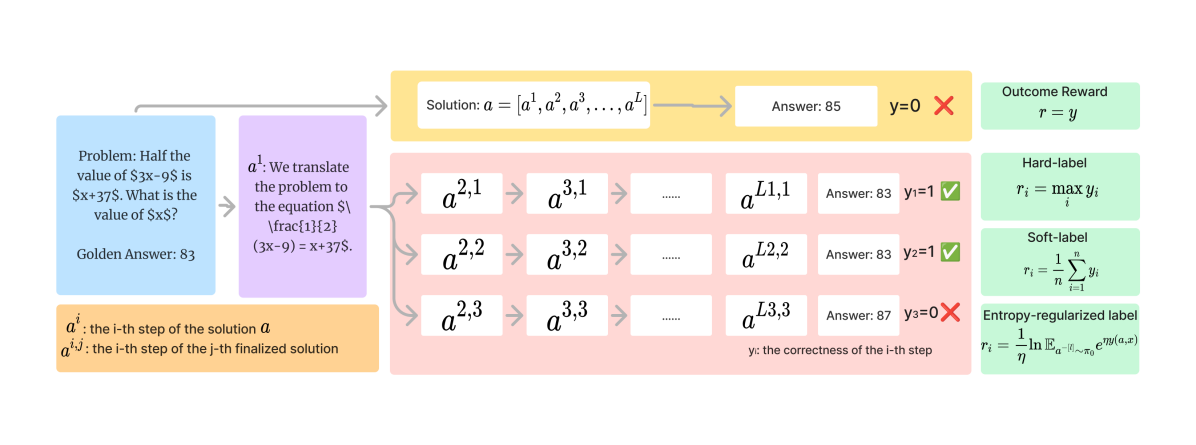
Refer to caption — Figure 1: Illustration of ER-PRM, along with other baseline methods to construct the process reward data and outcome reward data. The key idea of ER-PRM is to calculate the process reward from the sampling trajectories under entropy-regularization.

One distinct feature of complex mathematical reasoning is that models typically require multiple steps of reasoning before producing the final answer (Wei et al., 2023). Accordingly, there are generally two types of reward models in the mathematical domain: the outcome reward model (ORM) and the process reward model (PRM). ORM provides an overall score for the quality of the final answer, while PRM assigns a score to each step in the reasoning process, providing more fine-grained feedback. Existing works (Wang et al., 2024; Lightman et al., 2023) show that PRM outperforms ORM by a considerable margin. For instance, in Lightman et al. (2023), if we use the PRM to select the final output from the candidate responses, we can achieve a test accuracy of 78.2%, as compared to the ORM with 72.4% and majority voting of 69.6%. Furthermore, PRM is more interpretable because it mirrors human behavior when evaluating reasoning paths. The PRM model is able to guide the policy model’s decoding at each individual step or rerank candidate answers to enhance accuracy and consistency during generation.

Inspired by the superior performance of PRM, researchers have spent great efforts recently in the training of PRM. To get the process annotation for the PRM, one can ask humans to label the data at each step (Lightman et al., 2023), which is extremely expensive and inefficient. Since then, researchers have explored alternative labeling techniques. One representative example is the automatic labeling technique introduced by Math-Shepherd (Wang et al., 2024). The main idea of Math-Shepherd is to interpret the score of each step as its potential to deduce the correct final answer. Then, we can sample multiple trajectories starting from the intermediate step, and use the ratio of correct trajectories as a proxy for this score. The Math-Shepherd has proved as an effective way to generate high-quality process reward scores and even outperform human-labeled data.

Despite its effectiveness, Math-Shepherd considers a traditional Markov Decision Process (MDP) framework, which differs from the typical RL practice used with LLMs. Since the introduction of reinforcement learning from human feedback (RLHF), the standard approach has been using an entropy-regularized reward relative to a reference model (often the initial model) (Ouyang et al., 2022; Bai et al., 2022). This also applies to RL in reasoning tasks where we formulate the problem as an entropy-regularized MDP (Shao et al., 2024; Xiong et al., 2024b; Zhong et al., 2024b). The main goal here is to balance optimizing the reward and staying close to the original policy, which is crucial because we start with a well-trained LLM, and we do not want the model to deviate too far from this initial strong foundation policy. In recognition of this gap, in this paper, we formulate the multi-step mathematical reasoning task under the entropy-regularized MDP framework, derive the mathematical principles of the process reward construction, and propose practical algorithms. Our contributions are summarized as follows.

$\bullet$

We propose the entropy-regularized process reward, a novel method for labeling the process reward score with entropy regularization.
$\bullet$

Based on the labeled data, we train a new process reward model to improve the performance.
$\bullet$

On the MATH and GSM8K datasets, we achieve significant improvements using the best-of-N evaluation method. Furthermore, by employing the reward model with rejection sampling, we observe a substantial enhancement in the performance of the policy model.
$\bullet$

To further boost the process reward model research, we will release all the data, code, and checkpoints to the community.

2 Related Work

Mathematical Reasoning and Synthetic Data Generation.

Mathematical problem solving is crucial for evaluating LLMs’ reasoning abilities. A common approach is Chain-of-Thought (CoT) prompting, which guides LLMs to solve problems step-by-step (Wei et al., 2023; Zhou et al., 2022; Zhu et al., 2022; Tong et al., 2024). However, general chatbots still struggle with mathematical reasoning, as shown by benchmarks (Cobbe et al., 2021; Hendrycks et al., 2021). To improve performance, several works propose generating synthetic data and fine-tuning LLMs, including Meta-MathQA (Yu et al., 2023), MAmmoTH (Yue et al., 2023), MMIQC (Liu and Yao, 2024), ToRA (Gou et al., 2023), Open-MathInstruct (Toshniwal et al., 2024b), and Dart-Math (Tong et al., 2024). These datasets use teacher models to generate and filter responses, ensuring only correct answers are retained, a process known as rejection sampling or best-of-n sampling (Dong et al., 2023; Yuan et al., 2023). All these emphasize stepwise reasoning for improved task performance.

Applying RL to Mathematical Reasoning.

Inspired by the success of RL in chatbots like Chat-GPT and Claude, researchers have begun applying RL to mathematical reasoning tasks. Some works use deep RL methods like PPO (Schulman et al., 2017) and GRPO (Shao et al., 2024) to optimize external reward signals. Others apply direct preference learning algorithms, such as DPO and KTO (Jiao et al., 2024; Yuan et al., 2024), for problem-solving. Online iterative DPO, initially for chat tasks (Xiong et al., 2024a; Xu et al., 2023), has been adapted for CoT reasoning (Xie et al., 2024; Xiong et al., 2024b; Pang et al., 2024). Additionally, inference-time RL methods like best-of-n sampling (Dong et al., 2023; Lightman et al., 2023) and MCTS (Xie et al., 2024; Chen et al., 2024a; Lai et al., 2024) guide decoding or response selection using external reward models. These approaches, including deep RL, iterative preference learning, and inference-time methods, all depend on reward models and can benefit from our study.

Reward Modeling in Mathematical Reasoning.

In mathematical reasoning, reward models in RLHF are not trained via pairwise comparisons due to the availability of ground-truth answers (Bai et al., 2022; Ouyang et al., 2022; Dong et al., 2024). These models are generally divided into Outcome Reward Models (ORM) and Process Supervision Reward Models (PRM). ORM evaluates the overall quality of a response, while PRM provides feedback at each step of the reasoning process. The success of PRM approaches, like Lightman et al. (2023), has fueled interest in studying PRM construction. However, PRMs require extensive human annotation, which is challenging for open-source efforts. To mitigate this, Math-Shepherd (Wang et al., 2024) proposed a method for efficiently acquiring process reward labels by generating parallel completions and using trajectory ratios to evaluate correctness. Building on this, studies have incorporated process supervision and MCTS to improve RLHF pipelines, such as stepwise DPO with MCTS (Chen et al., 2024b), an MCTS-based PRM framework (Luo et al., 2024), MCTS Self-Refine (Zhang et al., 2024), and process generation from final answers (Chen et al., 2024a). These efforts have significantly enhanced process supervision efficiency, motivating the use of MCTS for high-quality data generation.

3 Approach

In this section, we present a novel reward formulation from an entropy perspective that utilizes KL-Regularization to derive the reward calculation of PRM, which we refer to as Entropy-Regularized PRM (ER-PRM). This formulation is followed by the derivation of obtaining the optimal policy model through RLHF using our entropy-regulated process reward calculation approach. The mathematical result is essentially from the KL-regularized RL literature, which has recently been studied in the context of DPO training in RLHF (Xiong et al., 2024b; Zhong et al., 2024a). And we move a step forward for the reward modeling. Subsequently, we compare our approach with Wang et al. (2024); Luo et al. (2024) and then demonstrate that our methodology is more robust than those proposed aggregation-based reward calculation due to their dependency on initial policy model.

3.1 Task Formulation and Optimal Policy

We consider training an LLM for reasoning. Given prompt $x$ , the LLM produces $L$ -step reasoning chain $a=[a^{1},\dots,a^{L}]$ . The reward $r(a,x)$ indicates whether the result of the reasoning chain is correct or not. We want to find LLM, denoted by a policy $\pi_{*}(a|x)$ , that optimizes $\pi\in\Pi$ with the KL-regularized loss function

\mathcal{L}(\pi)=-\mathbb{E}_{x}\mathbb{E}_{a\sim\pi(\cdot|x)}\big{[}r(a,x)-\frac{1}{\eta}\ln{\frac{\pi(a|x)}{\pi_{0}(a|x)}}\big{]}

where $\pi_{0}$ is the initial policy model, a pretrained LLM, and $\pi$ is the model being fine-tuned. According to Lemma 1, the minimizer for $\mathcal{L}$ is

\pi_{*}(a|x)=\frac{\pi_{0}(a|x)e^{\eta r(a,x)}}{\mathbb{E}_{a\sim\pi_{0}}e^{\eta r(a,x)}}\propto{\pi_{0}(a|x)e^{\eta r(a,x)}}.

3.2 Multi-step Reasoning

We refer to multi-step reasoning as over partial chains by adopting these definitions in appendix H, and our partial reward score assesses the correctness for one step beyond the current partial chain context. Let $a^{[l]}=[a^{1},\dots,a^{l}]$ , be partial reasoning chain up to step $l$ , and $a^{-[l]}=[a^{l+1},\dots,a^{L}]$ be the completion of the partial reasoning chain from step $l+1$ . We define the intermediate reward by $e^{\eta r(a^{[l]},x)}=\mathbb{E}_{a^{-[l]}\sim\pi_{0}}e^{\eta r(a,x)}$ . Thus, we have

\pi_{*}(a^{-[l]}|x,a^{[l]})=\frac{\pi_{0}(a^{-[l]}|x,a^{[l]})e^{\eta r(a,x)}}{\mathbb{E}_{a^{-[l]}\sim\pi_{0}(\cdot|x,a^{[l]})}e^{\eta r(a,x)}},

and we obtain

\pi_{*}(a^{[l]}|x)=\frac{\pi_{0}(a^{[l]}|x)e^{\eta r(a^{[l]},x)}}{\mathbb{E}_{a^{[l]}\sim\pi_{0}}e^{\eta r(a^{[l]},x)}}.

r(a^{[l]},x)=\frac{1}{\eta}\ln\mathbb{E}_{a^{-[l]}\sim\pi_{0}}e^{\eta r(a,x)}.

(1)

The partial reward according to this formula is our definition of entropy regularized process reward. We can optimize partial reasoning step $\pi(a^{[l]}|x)$ using this process reward.

An important property of this formulation is that our process reward model can be computed by using the reference policy $\pi_{0}$ to generate the completion. In comparison, in traditional RL, the reward depends on the optimal policy that generates the completion. Therefore in the traditional RL, one has to learn reward and policy simultaneously. This is not necessary in our entropy-based approach. As one can see, equation 1 employs soft optimism over paths generated by the reference policy. More generally, the reward can be computed using any policy including the optimal policy. In this case, the equivalent formula becomes

r(a^{[l]},x)=-\frac{1}{\eta}\ln{\mathbb{E}}_{a^{-[l]}\sim\pi_{*}}e^{-\eta r(a,x)},

(2)

where we have used the following fact to express equation 1 using $\pi_{*}$ :

\pi_{0}(a^{-[l]}|x,a^{[l]})=\frac{\pi_{*}(a^{-[l]}|x,a^{[l]})e^{-\eta r(a,x)}}{\mathbb{E}_{a^{-[l]}\sim\pi_{*}}e^{-\eta r(a,x)}}.

Intuitively, equation 2 implements soft pessimism over paths generated by the optimal policy. It can be shown that the reward of this model is equivalent to the reward computed using the reference policy in equation 1. As we have already pointed out, the fact that entropy-regularized process reward model can be computed using the reference policy is a key advantage of entropy regularization approach. In this paper, we will use equation 1 to compute our process reward models, and demonstrate its advantage over previous approaches empirically.

We note that the process reward has two formulations: when completions are generated from the initial policy $\pi_{0}$ , it is soft-max, and when completions are generated from the optimal policy, it is soft-min. If one trains LLM and reward model simultaneously using examples generated by the updated LLM, then one needs to gradually turn from soft max to soft min during the training process.

4 Experimental Settings

Process Reward Model

We use two widely adopted mathematical datasets, GSM8K (Cobbe et al., 2021) and MATH (Hendrycks et al., 2021) in our experiments. We generate and label our process reward data using automatic labeling with entropy regularization, similar to Math-Shepherd (Wang et al., 2024), inspired by Monto Carlo Tree Search (MCTS). In the automatic labeling, the quality of a step is defined as the potential to deduce the final correct answer. For each problem in the training dataset, we use the generator to sample 15 solutions with step-by-step rationale for automatic labeling to increase the diversity of data. For each step, we use the completer to sample 16 paths to reach the final answer. By evaluating the number of correct final answers, the quality of the current step could be reflected. The process reward score for each step is calculated by Equation 1, using initial policy $\pi_{0}$ , where $y(a,x)=1$ if the step reaches the correct answer otherwise $y(a,x)=0$ .

We use Mistral-7b (Jiang et al., 2023) fine-tuned on MetaMath (Yu et al., 2024) and deepseek-math-7b-instruct (Shao et al., 2024) in our experiments. We use them as the generator and the completer to collect data. For each model, we have around 260K data and 1.5 million step annotations. We train our reward models using Llama-3.1-8B (Dubey et al., 2024). The reward models trained on data from Mistral and deepseek are denoted as Mistral-data Models and deepseek-data Models respectively. The hyper-parameter settings are discussed in Appendix B.

We use the whole test set of GSM8K, and the MATH500 introduced in Lightman et al. (2023) for evaluation. We use the best-of-N strategy to evaluate our reward models. For each problem in the test set, we randomly sample N solutions from the Mistral-MetaMath-7b (Yu et al., 2023) and the deepseek-math-7b-instruct (Shao et al., 2024) generators. Each step in each response is given a score by the reward model. We select the response with the highest score as the final answer. The score for each response is represented using the lowest score among all the steps.

To demonstrate the effectiveness of our method, we compare our models with the hard-label process reward model (Hard-label PRM), vanilla soft-label process reward model (Soft-label PRM), and outcome reward model (ORM). For Hard-label PRM, one reasoning step will be labeled good as long as it can reach the final correct answer. For Soft-label PRM, the step score is approximated by the probability of reaching the final correct answer. For the ORM, it will assign an overall score for the entire mathematical reasoning. The reward calculations are shown and compared in Figure 1. We train the Hard-label PRM, Soft-label PRM, and ORM using the next token prediction, also known as auto-regressive training. We train the PRM to predict the probability of a special token ${}^{\prime}+^{\prime}$ after each reasoning step, and ORM to predict after the entire response. The reward models are trained on these tokens with cross-entropy loss between the prediction and the ground-truth reward The prediction scores would be in the range of $(0,1)$ . The dataset format is similar to Math-Shepherd (Wang et al., 2024). We also explore regression training where the reward model is trained to predict a real number as the score given the question and current steps with mean-square error (MSE) loss. The results for regression training are in Section 6.2. We also explore reward models with various sizes in Appendix D, OOD performance with stronger policy models as generators in Appendix E and Appendix F.

Improving Policy Model with PRM

We also design experiments to improve our policy model Mistral-MetaMath-7b using RLHF where we adopt the rejection sampling fine-tuning strategy (Dong et al., 2023) on the MATH training set and OpenMathInstruct-2 dataset (Toshniwal et al., 2024b). For each question, we sample 16 responses and rank them with the reward model. We select the responses with the highest reward score and fine-tune our policy models on these data. The fine-tuned policy models are evaluated on GSM8K and MATH using Top-1 accuracy under a zero-shot CoT setting. We compare different policy models guided by our reward model and guided by other baseline reward models.

5 Experimental Results

Models	Methods	GSM8K	MATH
Mistral	Baseline	77.9	28.6
	Soft-Label	78.7	30.1
	Hard-Label	79.0	32.0
	ER-PRM	79.5	32.8
deepseek	Baseline	82.0	42.8
	Soft-Label	82.8	43.2
	Hard-Label	82.7	43.6
	ER-PRM	83.1	44.2

Table 1: Zero-shot CoT evaluation for policy model Mistral-MetaMath-7b and deepseek-math-7b-instruct improved via Rejection Sampling Fine-tuning. Mistral and deepseek in the table denote Mistral-MetaMath-7b and deepseek-math-7b-instruct.

5.1 Auto-Regressive Training Results

The results of our model compared with several baseline methods are shown in Figure LABEL:fig:mistral-policy-best-of-n and Figure LABEL:fig:deepseek-instruct-policy-best-of-n, which are trained in an auto-regressive way.

When the policy model is Mistral-MetaMath-7b, as N increases, the best-of-N accuracy for most of the models keeps increasing except the Outcome Reward Model (ORM). In particular, ER-PRM outperforms other baselines in all evaluation settings. Our model demonstrates consistent improvements, with more substantial gains observed on the more challenging datasets. Concretely, on MATH, which presents harder questions compared with GSM8K, the gap widens significantly, highlighting our method’s more pronounced effectiveness in tackling complex datasets.

When the models are trained on deepseek data and evaluate on deepseek-math-7b-instruct, the results are similar, where the accuracy is boosted by a large margin. And ER-PRM outperforms Soft-label PRM and Hard-label PRM on GSM8K and MATH500. However, we notice that on MATH500, the increment from $N=4$ to $N=64$ is not very significant. And there are reward hacking problems with large $N$ . Similar Observations are also reflected in Section F. Interestingly, we observe a very strong performance of ORM on GSM8K, demonstrating the potential of training a powerful ORM with high-quality data.

We notice that the Hard-label PRM also demonstrates similar strong performance for best-of-N evaluation, and is effective as Soft-label PRM in some cases, especially when N is large. We attribute this to the semi-supervised learning process during the hard-label training. The labels during the Markov Decision Process are only an estimation of the process reward instead of a precise value. The Hard-label setting is a way to reduce the noise during the training.

We note that here the Hard-label setting adopts the same labeling strategy with Math-Shepherd (Wang et al., 2024), trained with the same base model as ER-PRM to ensure a fair comparison. Our model outperforms Math-Shepherd in all settings on GSM8K and MATH, demonstrating the ability to better rank and select candidate responses. It shows that ours are intrinsically competent reward models compared to the open-source models with high consistency and robustness.

5.2 RLHF Results

We choose to verify the effectiveness of our auto-regressive Entropy-Regularized Process Reward Model (ER-PRM) by comparing it against the Soft-Label PRM and Hard-Label PRM in RLHF via RAFT algorithm (Dong et al., 2023). We use the Mistral-MetaMath-7b and the deepseek-Math-7B-Instruct as the initial baseline policy models, and the reward models trained on Mistral data and deepseek data.

During initial tests, we observed that the baseline policy model exhibited signs of overfitting to the training data from GSM8K and MATH, resulting in only marginal performance gains after RLHF on the original training set, particularly for deepseek-Math-7B-Instruct. To address this, we incorporated out-of-domain data from OpenMathInstruct-2 (Toshniwal et al., 2024a), augmenting GSM8K and MATH with 12,500 additional new questions each. For each question, the initial policy model generated 16 candidate rationales, which were then evaluated by both ER-PRM and baseline PRMs to select the highest-scoring rationale as training data for RLHF.

Table 1 summarizes the performance improvements using RLHF enhanced via ER-PRM and baseline PRMs. Compared to the baselines, Our ER-PRM outperformed by surpassing Soft-Label PRM 0.8% and 2.7% on GSM8K and MATH, and Hard-Label PRM 0.5% and 0.8%, respectively for the Mistral model. We also observe a larger improvement for the deepseek model with respect to the baselines, indicating ER-PRM’s superior capability in guiding the optimal policy model and its robustness in handling more complex task settings. We also notice that the Hard-Label setting consistently outperforms the Soft-Label setting in RLHF. The surprisingly strong performance for Hard-Label indicates its feasibility, also a different discovery compared to Luo et al. (2024).

In general, our RLHF approach achieved superior performance in evaluating the policy model in GSM8K and MATH. The reason is that our ER-PRM consistently having 1-2% higher best-of-N accuracy in selecting data from both in-domain and out-of-domain datasets than the baselines, showcasing the stability and effectiveness of our entropy-regularized reward formulation in selecting accurate rationales from varying quality data sources.

6 Analysis

6.1 Entropy-Regularized Reward Analysis

To better interpret our entropy-regularized method, we change the hyper-parameter $\eta$ to regularize the penalty of the entropy during automatic process reward labeling. We train the reward model on GSM8K and MATH dataset separately, instead of training on both datasets in the main experiments. We then evaluate our models using the best-of-N strategy on each dataset. Note that when $\eta\to 0$ , the labeling strategy is vanilla soft labeling. When $\eta\to\infty$ , the labeling strategy is hard labeling. We show the performance change as $\eta$ changes, and intend to find the optimal $\eta$ for these two datasets.

The result is shown in Figure LABEL:fig:mistral-policy-best-of-n-eta for best-of-N performance on each $\eta$ . We observe that there is a peak performance for each dataset and then the performance drops when $\eta$ is too large or small. The experiments show that $\eta=1$ or $\eta=2$ is the best for hard dataset MATH. $\eta=15$ is the best for easy dataset GSM8K. Larger $\eta$ represents a larger penalty on the entropy for the process rewards where they are pushed higher and closer to the hard label estimation, while smaller $\eta$ represents a small penalty on the entropy for the process rewards. We conclude that to achieve the best performance on automatic process reward labeling, a more fine-grained estimation of the reward scores should be applied. Simply applying hard label estimation may introduce too much noise for reward model training. We also notice that vanilla soft label estimation may not be an optimal strategy, as the performance is relatively bad when $\eta$ is small ( $\eta=0.1$ ) for both datasets.

Considering the difficulty of the GSM8K and MATH datasets, We may need a larger entropy penalty for the process reward for the hard dataset, and a relatively smaller entropy penalty estimation for the easy dataset.

6.2 Regression Training Strategy

In addition to training the reward model in an auto-regressive way, we also explore the reward models with the regression training strategy, where we train the model to output a score directly given a problem and current steps. The best-of-N evaluation results are shown in Figure LABEL:fig:regression. The performance of best-of-N increases as N becomes larger. Our reward model still outperforms the Soft-label and Hard-label settings. We also identify it as a method to train reward models. However, we notice that auto-regressive training could yield better results for reward models than regression training. On both GSM8K and MATH datasets, the best-of-N accuracies are consistently lower than the models trained using the auto-regressive strategy. Especially on MATH, there is a significant gap of the accuracy between the two training methods. One hypothesis is that auto-regressive training integrates the steps, reducing the total number of training steps, which in turn leads to less forgetting. For the MATH dataset, since there are more reasoning steps per question, splitting them into multiple training samples increases the difficulty for the reward models to learn. It is also possible that the reasoning steps in auto-regressive training are continuous and coherent, allowing the reward model to better learn the process of assigning rewards.

7 Conclusion

In this paper, we demonstrate the potential of process reward models (PRMs) in enhancing the performance of large language models (LLMs) on complex mathematical reasoning tasks. By leveraging the fine-grained feedback provided by PRMs, we achieve a notable improvement over traditional outcome reward models (ORMs), as PRMs better capture the multi-step reasoning required for such tasks. To enhance the process reward model, we formulate the multi-step reasoning in the entropy perspective and then derive the process reward score by a new aggregation method. The effectiveness of our automatic labeling process rewards, coupled with entropy-regularized reinforcement learning techniques, highlights the importance of balancing reward optimization with policy stability. Our model outperforms baseline ORMs and PRMs by a large margin on the MATH and GSM8K benchmarks. Furthermore, we apply our process reward model to improve the policy model under RLHF experiments and observe a significant improvement after rejection sampling.

8 Limitations

Although our method demonstrates the potential to improve the reward models and the policy models with rejection fine-tuning, we have not conducted large-scale online RLHF experiments such as PPO (Schulman et al., 2017), due to the limitation of the computational resources. Future work could explore more policy models training for mathematical reasoning using more RLHF methods, combined with ER-PRM.

References

Bai et al. (2022) Yuntao Bai, Andy Jones, Kamal Ndousse, Amanda Askell, Anna Chen, Nova DasSarma, Dawn Drain, Stanislav Fort, Deep Ganguli, Tom Henighan, Nicholas Joseph, Saurav Kadavath, Jackson Kernion, Tom Conerly, Sheer El-Showk, Nelson Elhage, Zac Hatfield-Dodds, Danny Hernandez, Tristan Hume, Scott Johnston, Shauna Kravec, Liane Lovitt, Neel Nanda, Catherine Olsson, Dario Amodei, Tom Brown, Jack Clark, Sam McCandlish, Chris Olah, Ben Mann, and Jared Kaplan. 2022. Training a helpful and harmless assistant with reinforcement learning from human feedback. Preprint, arXiv:2204.05862.
Chen et al. (2024a) Guoxin Chen, Minpeng Liao, Chengxi Li, and Kai Fan. 2024a. Alphamath almost zero: process supervision without process. Preprint, arXiv:2405.03553.
Chen et al. (2024b) Guoxin Chen, Minpeng Liao, Chengxi Li, and Kai Fan. 2024b. Step-level value preference optimization for mathematical reasoning. Preprint, arXiv:2406.10858.
Cobbe et al. (2021) Karl Cobbe, Vineet Kosaraju, Mohammad Bavarian, Mark Chen, Heewoo Jun, Lukasz Kaiser, Matthias Plappert, Jerry Tworek, Jacob Hilton, Reiichiro Nakano, Christopher Hesse, and John Schulman. 2021. Training verifiers to solve math word problems. Preprint, arXiv:2110.14168.
Dong et al. (2023) Hanze Dong, Wei Xiong, Deepanshu Goyal, Yihan Zhang, Winnie Chow, Rui Pan, Shizhe Diao, Jipeng Zhang, Kashun Shum, and Tong Zhang. 2023. Raft: Reward ranked finetuning for generative foundation model alignment. arXiv preprint arXiv:2304.06767.
Dong et al. (2024) Hanze Dong, Wei Xiong, Bo Pang, Haoxiang Wang, Han Zhao, Yingbo Zhou, Nan Jiang, Doyen Sahoo, Caiming Xiong, and Tong Zhang. 2024. Rlhf workflow: From reward modeling to online rlhf. arXiv preprint arXiv:2405.07863.
Dubey et al. (2024) Abhimanyu Dubey, Abhinav Jauhri, Abhinav Pandey, Abhishek Kadian, Ahmad Al-Dahle, Aiesha Letman, Akhil Mathur, Alan Schelten, Amy Yang, Angela Fan, Anirudh Goyal, Anthony Hartshorn, Aobo Yang, Archi Mitra, Archie Sravankumar, Artem Korenev, Arthur Hinsvark, Arun Rao, Aston Zhang, Aurelien Rodriguez, Austen Gregerson, Ava Spataru, Baptiste Roziere, Bethany Biron, Binh Tang, Bobbie Chern, Charlotte Caucheteux, Chaya Nayak, Chloe Bi, Chris Marra, Chris McConnell, Christian Keller, Christophe Touret, Chunyang Wu, Corinne Wong, Cristian Canton Ferrer, Cyrus Nikolaidis, Damien Allonsius, Daniel Song, Danielle Pintz, Danny Livshits, David Esiobu, Dhruv Choudhary, Dhruv Mahajan, Diego Garcia-Olano, Diego Perino, Dieuwke Hupkes, Egor Lakomkin, Ehab AlBadawy, Elina Lobanova, Emily Dinan, Eric Michael Smith, Filip Radenovic, Frank Zhang, Gabriel Synnaeve, Gabrielle Lee, Georgia Lewis Anderson, Graeme Nail, Gregoire Mialon, Guan Pang, Guillem Cucurell, Hailey Nguyen, Hannah Korevaar, Hu Xu, Hugo Touvron, Iliyan Zarov, Imanol Arrieta Ibarra, Isabel Kloumann, Ishan Misra, Ivan Evtimov, Jade Copet, Jaewon Lee, Jan Geffert, Jana Vranes, Jason Park, Jay Mahadeokar, Jeet Shah, Jelmer van der Linde, Jennifer Billock, Jenny Hong, Jenya Lee, Jeremy Fu, Jianfeng Chi, Jianyu Huang, Jiawen Liu, Jie Wang, Jiecao Yu, Joanna Bitton, Joe Spisak, Jongsoo Park, Joseph Rocca, Joshua Johnstun, Joshua Saxe, Junteng Jia, Kalyan Vasuden Alwala, Kartikeya Upasani, Kate Plawiak, Ke Li, Kenneth Heafield, Kevin Stone, Khalid El-Arini, Krithika Iyer, Kshitiz Malik, Kuenley Chiu, Kunal Bhalla, Lauren Rantala-Yeary, Laurens van der Maaten, Lawrence Chen, Liang Tan, Liz Jenkins, Louis Martin, Lovish Madaan, Lubo Malo, Lukas Blecher, Lukas Landzaat, Luke de Oliveira, Madeline Muzzi, Mahesh Pasupuleti, Mannat Singh, Manohar Paluri, Marcin Kardas, Mathew Oldham, Mathieu Rita, Maya Pavlova, Melanie Kambadur, Mike Lewis, Min Si, Mitesh Kumar Singh, Mona Hassan, Naman Goyal, Narjes Torabi, Nikolay Bashlykov, Nikolay Bogoychev, Niladri Chatterji, Olivier Duchenne, Onur Çelebi, Patrick Alrassy, Pengchuan Zhang, Pengwei Li, Petar Vasic, Peter Weng, Prajjwal Bhargava, Pratik Dubal, Praveen Krishnan, Punit Singh Koura, Puxin Xu, Qing He, Qingxiao Dong, Ragavan Srinivasan, Raj Ganapathy, Ramon Calderer, Ricardo Silveira Cabral, Robert Stojnic, Roberta Raileanu, Rohit Girdhar, Rohit Patel, Romain Sauvestre, Ronnie Polidoro, Roshan Sumbaly, Ross Taylor, Ruan Silva, Rui Hou, Rui Wang, Saghar Hosseini, Sahana Chennabasappa, Sanjay Singh, Sean Bell, Seohyun Sonia Kim, Sergey Edunov, Shaoliang Nie, Sharan Narang, Sharath Raparthy, Sheng Shen, Shengye Wan, Shruti Bhosale, Shun Zhang, Simon Vandenhende, Soumya Batra, Spencer Whitman, Sten Sootla, Stephane Collot, Suchin Gururangan, Sydney Borodinsky, Tamar Herman, Tara Fowler, Tarek Sheasha, Thomas Georgiou, Thomas Scialom, Tobias Speckbacher, Todor Mihaylov, Tong Xiao, Ujjwal Karn, Vedanuj Goswami, Vibhor Gupta, Vignesh Ramanathan, Viktor Kerkez, Vincent Gonguet, Virginie Do, Vish Vogeti, Vladan Petrovic, Weiwei Chu, Wenhan Xiong, Wenyin Fu, Whitney Meers, Xavier Martinet, Xiaodong Wang, Xiaoqing Ellen Tan, Xinfeng Xie, Xuchao Jia, Xuewei Wang, Yaelle Goldschlag, Yashesh Gaur, Yasmine Babaei, Yi Wen, Yiwen Song, Yuchen Zhang, Yue Li, Yuning Mao, Zacharie Delpierre Coudert, Zheng Yan, Zhengxing Chen, Zoe Papakipos, Aaditya Singh, Aaron Grattafiori, Abha Jain, Adam Kelsey, Adam Shajnfeld, Adithya Gangidi, Adolfo Victoria, Ahuva Goldstand, Ajay Menon, Ajay Sharma, Alex Boesenberg, Alex Vaughan, Alexei Baevski, Allie Feinstein, Amanda Kallet, Amit Sangani, Anam Yunus, Andrei Lupu, Andres Alvarado, Andrew Caples, Andrew Gu, Andrew Ho, Andrew Poulton, Andrew Ryan, Ankit Ramchandani, Annie Franco, Aparajita Saraf, Arkabandhu Chowdhury, Ashley Gabriel, Ashwin Bharambe, Assaf Eisenman, Azadeh Yazdan, Beau James, Ben Maurer, Benjamin Leonhardi, Bernie Huang, Beth Loyd, Beto De Paola, Bhargavi Paranjape, Bing Liu, Bo Wu, Boyu Ni, Braden Hancock, Bram Wasti, Brandon Spence, Brani Stojkovic, Brian Gamido, Britt Montalvo, Carl Parker, Carly Burton, Catalina Mejia, Changhan Wang, Changkyu Kim, Chao Zhou, Chester Hu, Ching-Hsiang Chu, Chris Cai, Chris Tindal, Christoph Feichtenhofer, Damon Civin, Dana Beaty, Daniel Kreymer, Daniel Li, Danny Wyatt, David Adkins, David Xu, Davide Testuggine, Delia David, Devi Parikh, Diana Liskovich, Didem Foss, Dingkang Wang, Duc Le, Dustin Holland, Edward Dowling, Eissa Jamil, Elaine Montgomery, Eleonora Presani, Emily Hahn, Emily Wood, Erik Brinkman, Esteban Arcaute, Evan Dunbar, Evan Smothers, Fei Sun, Felix Kreuk, Feng Tian, Firat Ozgenel, Francesco Caggioni, Francisco Guzmán, Frank Kanayet, Frank Seide, Gabriela Medina Florez, Gabriella Schwarz, Gada Badeer, Georgia Swee, Gil Halpern, Govind Thattai, Grant Herman, Grigory Sizov, Guangyi, Zhang, Guna Lakshminarayanan, Hamid Shojanazeri, Han Zou, Hannah Wang, Hanwen Zha, Haroun Habeeb, Harrison Rudolph, Helen Suk, Henry Aspegren, Hunter Goldman, Ibrahim Damlaj, Igor Molybog, Igor Tufanov, Irina-Elena Veliche, Itai Gat, Jake Weissman, James Geboski, James Kohli, Japhet Asher, Jean-Baptiste Gaya, Jeff Marcus, Jeff Tang, Jennifer Chan, Jenny Zhen, Jeremy Reizenstein, Jeremy Teboul, Jessica Zhong, Jian Jin, Jingyi Yang, Joe Cummings, Jon Carvill, Jon Shepard, Jonathan McPhie, Jonathan Torres, Josh Ginsburg, Junjie Wang, Kai Wu, Kam Hou U, Karan Saxena, Karthik Prasad, Kartikay Khandelwal, Katayoun Zand, Kathy Matosich, Kaushik Veeraraghavan, Kelly Michelena, Keqian Li, Kun Huang, Kunal Chawla, Kushal Lakhotia, Kyle Huang, Lailin Chen, Lakshya Garg, Lavender A, Leandro Silva, Lee Bell, Lei Zhang, Liangpeng Guo, Licheng Yu, Liron Moshkovich, Luca Wehrstedt, Madian Khabsa, Manav Avalani, Manish Bhatt, Maria Tsimpoukelli, Martynas Mankus, Matan Hasson, Matthew Lennie, Matthias Reso, Maxim Groshev, Maxim Naumov, Maya Lathi, Meghan Keneally, Michael L. Seltzer, Michal Valko, Michelle Restrepo, Mihir Patel, Mik Vyatskov, Mikayel Samvelyan, Mike Clark, Mike Macey, Mike Wang, Miquel Jubert Hermoso, Mo Metanat, Mohammad Rastegari, Munish Bansal, Nandhini Santhanam, Natascha Parks, Natasha White, Navyata Bawa, Nayan Singhal, Nick Egebo, Nicolas Usunier, Nikolay Pavlovich Laptev, Ning Dong, Ning Zhang, Norman Cheng, Oleg Chernoguz, Olivia Hart, Omkar Salpekar, Ozlem Kalinli, Parkin Kent, Parth Parekh, Paul Saab, Pavan Balaji, Pedro Rittner, Philip Bontrager, Pierre Roux, Piotr Dollar, Polina Zvyagina, Prashant Ratanchandani, Pritish Yuvraj, Qian Liang, Rachad Alao, Rachel Rodriguez, Rafi Ayub, Raghotham Murthy, Raghu Nayani, Rahul Mitra, Raymond Li, Rebekkah Hogan, Robin Battey, Rocky Wang, Rohan Maheswari, Russ Howes, Ruty Rinott, Sai Jayesh Bondu, Samyak Datta, Sara Chugh, Sara Hunt, Sargun Dhillon, Sasha Sidorov, Satadru Pan, Saurabh Verma, Seiji Yamamoto, Sharadh Ramaswamy, Shaun Lindsay, Shaun Lindsay, Sheng Feng, Shenghao Lin, Shengxin Cindy Zha, Shiva Shankar, Shuqiang Zhang, Shuqiang Zhang, Sinong Wang, Sneha Agarwal, Soji Sajuyigbe, Soumith Chintala, Stephanie Max, Stephen Chen, Steve Kehoe, Steve Satterfield, Sudarshan Govindaprasad, Sumit Gupta, Sungmin Cho, Sunny Virk, Suraj Subramanian, Sy Choudhury, Sydney Goldman, Tal Remez, Tamar Glaser, Tamara Best, Thilo Kohler, Thomas Robinson, Tianhe Li, Tianjun Zhang, Tim Matthews, Timothy Chou, Tzook Shaked, Varun Vontimitta, Victoria Ajayi, Victoria Montanez, Vijai Mohan, Vinay Satish Kumar, Vishal Mangla, Vítor Albiero, Vlad Ionescu, Vlad Poenaru, Vlad Tiberiu Mihailescu, Vladimir Ivanov, Wei Li, Wenchen Wang, Wenwen Jiang, Wes Bouaziz, Will Constable, Xiaocheng Tang, Xiaofang Wang, Xiaojian Wu, Xiaolan Wang, Xide Xia, Xilun Wu, Xinbo Gao, Yanjun Chen, Ye Hu, Ye Jia, Ye Qi, Yenda Li, Yilin Zhang, Ying Zhang, Yossi Adi, Youngjin Nam, Yu, Wang, Yuchen Hao, Yundi Qian, Yuzi He, Zach Rait, Zachary DeVito, Zef Rosnbrick, Zhaoduo Wen, Zhenyu Yang, and Zhiwei Zhao. 2024. The llama 3 herd of models. Preprint, arXiv:2407.21783.
Gou et al. (2023) Zhibin Gou, Zhihong Shao, Yeyun Gong, Yujiu Yang, Minlie Huang, Nan Duan, Weizhu Chen, et al. 2023. Tora: A tool-integrated reasoning agent for mathematical problem solving. arXiv preprint arXiv:2309.17452.
Hendrycks et al. (2021) Dan Hendrycks, Collin Burns, Saurav Kadavath, Akul Arora, Steven Basart, Eric Tang, Dawn Song, and Jacob Steinhardt. 2021. Measuring mathematical problem solving with the math dataset. Preprint, arXiv:2103.03874.
Jiang et al. (2023) Albert Q. Jiang, Alexandre Sablayrolles, Arthur Mensch, Chris Bamford, Devendra Singh Chaplot, Diego de las Casas, Florian Bressand, Gianna Lengyel, Guillaume Lample, Lucile Saulnier, Lélio Renard Lavaud, Marie-Anne Lachaux, Pierre Stock, Teven Le Scao, Thibaut Lavril, Thomas Wang, Timothée Lacroix, and William El Sayed. 2023. Mistral 7b. Preprint, arXiv:2310.06825.
Jiao et al. (2024) Fangkai Jiao, Chengwei Qin, Zhengyuan Liu, Nancy F Chen, and Shafiq Joty. 2024. Learning planning-based reasoning by trajectories collection and process reward synthesizing. arXiv preprint arXiv:2402.00658.
Lai et al. (2024) Xin Lai, Zhuotao Tian, Yukang Chen, Senqiao Yang, Xiangru Peng, and Jiaya Jia. 2024. Step-dpo: Step-wise preference optimization for long-chain reasoning of llms. arXiv preprint arXiv:2406.18629.
Lightman et al. (2023) Hunter Lightman, Vineet Kosaraju, Yura Burda, Harri Edwards, Bowen Baker, Teddy Lee, Jan Leike, John Schulman, Ilya Sutskever, and Karl Cobbe. 2023. Let’s verify step by step. Preprint, arXiv:2305.20050.
Liu and Yao (2024) Haoxiong Liu and Andrew Chi-Chih Yao. 2024. Augmenting math word problems via iterative question composing. arXiv preprint arXiv:2401.09003.
Luo et al. (2024) Liangchen Luo, Yinxiao Liu, Rosanne Liu, Samrat Phatale, Harsh Lara, Yunxuan Li, Lei Shu, Yun Zhu, Lei Meng, Jiao Sun, and Abhinav Rastogi. 2024. Improve mathematical reasoning in language models by automated process supervision. Preprint, arXiv:2406.06592.
OpenAI et al. (2024) OpenAI, Josh Achiam, Steven Adler, Sandhini Agarwal, Lama Ahmad, Ilge Akkaya, Florencia Leoni Aleman, Diogo Almeida, Janko Altenschmidt, Sam Altman, Shyamal Anadkat, Red Avila, Igor Babuschkin, Suchir Balaji, Valerie Balcom, Paul Baltescu, Haiming Bao, Mohammad Bavarian, Jeff Belgum, Irwan Bello, Jake Berdine, Gabriel Bernadett-Shapiro, Christopher Berner, Lenny Bogdonoff, Oleg Boiko, Madelaine Boyd, Anna-Luisa Brakman, Greg Brockman, Tim Brooks, Miles Brundage, Kevin Button, Trevor Cai, Rosie Campbell, Andrew Cann, Brittany Carey, Chelsea Carlson, Rory Carmichael, Brooke Chan, Che Chang, Fotis Chantzis, Derek Chen, Sully Chen, Ruby Chen, Jason Chen, Mark Chen, Ben Chess, Chester Cho, Casey Chu, Hyung Won Chung, Dave Cummings, Jeremiah Currier, Yunxing Dai, Cory Decareaux, Thomas Degry, Noah Deutsch, Damien Deville, Arka Dhar, David Dohan, Steve Dowling, Sheila Dunning, Adrien Ecoffet, Atty Eleti, Tyna Eloundou, David Farhi, Liam Fedus, Niko Felix, Simón Posada Fishman, Juston Forte, Isabella Fulford, Leo Gao, Elie Georges, Christian Gibson, Vik Goel, Tarun Gogineni, Gabriel Goh, Rapha Gontijo-Lopes, Jonathan Gordon, Morgan Grafstein, Scott Gray, Ryan Greene, Joshua Gross, Shixiang Shane Gu, Yufei Guo, Chris Hallacy, Jesse Han, Jeff Harris, Yuchen He, Mike Heaton, Johannes Heidecke, Chris Hesse, Alan Hickey, Wade Hickey, Peter Hoeschele, Brandon Houghton, Kenny Hsu, Shengli Hu, Xin Hu, Joost Huizinga, Shantanu Jain, Shawn Jain, Joanne Jang, Angela Jiang, Roger Jiang, Haozhun Jin, Denny Jin, Shino Jomoto, Billie Jonn, Heewoo Jun, Tomer Kaftan, Łukasz Kaiser, Ali Kamali, Ingmar Kanitscheider, Nitish Shirish Keskar, Tabarak Khan, Logan Kilpatrick, Jong Wook Kim, Christina Kim, Yongjik Kim, Jan Hendrik Kirchner, Jamie Kiros, Matt Knight, Daniel Kokotajlo, Łukasz Kondraciuk, Andrew Kondrich, Aris Konstantinidis, Kyle Kosic, Gretchen Krueger, Vishal Kuo, Michael Lampe, Ikai Lan, Teddy Lee, Jan Leike, Jade Leung, Daniel Levy, Chak Ming Li, Rachel Lim, Molly Lin, Stephanie Lin, Mateusz Litwin, Theresa Lopez, Ryan Lowe, Patricia Lue, Anna Makanju, Kim Malfacini, Sam Manning, Todor Markov, Yaniv Markovski, Bianca Martin, Katie Mayer, Andrew Mayne, Bob McGrew, Scott Mayer McKinney, Christine McLeavey, Paul McMillan, Jake McNeil, David Medina, Aalok Mehta, Jacob Menick, Luke Metz, Andrey Mishchenko, Pamela Mishkin, Vinnie Monaco, Evan Morikawa, Daniel Mossing, Tong Mu, Mira Murati, Oleg Murk, David Mély, Ashvin Nair, Reiichiro Nakano, Rajeev Nayak, Arvind Neelakantan, Richard Ngo, Hyeonwoo Noh, Long Ouyang, Cullen O’Keefe, Jakub Pachocki, Alex Paino, Joe Palermo, Ashley Pantuliano, Giambattista Parascandolo, Joel Parish, Emy Parparita, Alex Passos, Mikhail Pavlov, Andrew Peng, Adam Perelman, Filipe de Avila Belbute Peres, Michael Petrov, Henrique Ponde de Oliveira Pinto, Michael, Pokorny, Michelle Pokrass, Vitchyr H. Pong, Tolly Powell, Alethea Power, Boris Power, Elizabeth Proehl, Raul Puri, Alec Radford, Jack Rae, Aditya Ramesh, Cameron Raymond, Francis Real, Kendra Rimbach, Carl Ross, Bob Rotsted, Henri Roussez, Nick Ryder, Mario Saltarelli, Ted Sanders, Shibani Santurkar, Girish Sastry, Heather Schmidt, David Schnurr, John Schulman, Daniel Selsam, Kyla Sheppard, Toki Sherbakov, Jessica Shieh, Sarah Shoker, Pranav Shyam, Szymon Sidor, Eric Sigler, Maddie Simens, Jordan Sitkin, Katarina Slama, Ian Sohl, Benjamin Sokolowsky, Yang Song, Natalie Staudacher, Felipe Petroski Such, Natalie Summers, Ilya Sutskever, Jie Tang, Nikolas Tezak, Madeleine B. Thompson, Phil Tillet, Amin Tootoonchian, Elizabeth Tseng, Preston Tuggle, Nick Turley, Jerry Tworek, Juan Felipe Cerón Uribe, Andrea Vallone, Arun Vijayvergiya, Chelsea Voss, Carroll Wainwright, Justin Jay Wang, Alvin Wang, Ben Wang, Jonathan Ward, Jason Wei, CJ Weinmann, Akila Welihinda, Peter Welinder, Jiayi Weng, Lilian Weng, Matt Wiethoff, Dave Willner, Clemens Winter, Samuel Wolrich, Hannah Wong, Lauren Workman, Sherwin Wu, Jeff Wu, Michael Wu, Kai Xiao, Tao Xu, Sarah Yoo, Kevin Yu, Qiming Yuan, Wojciech Zaremba, Rowan Zellers, Chong Zhang, Marvin Zhang, Shengjia Zhao, Tianhao Zheng, Juntang Zhuang, William Zhuk, and Barret Zoph. 2024. Gpt-4 technical report. Preprint, arXiv:2303.08774.
Ouyang et al. (2022) Long Ouyang, Jeff Wu, Xu Jiang, Diogo Almeida, Carroll L. Wainwright, Pamela Mishkin, Chong Zhang, Sandhini Agarwal, Katarina Slama, Alex Ray, John Schulman, Jacob Hilton, Fraser Kelton, Luke Miller, Maddie Simens, Amanda Askell, Peter Welinder, Paul Christiano, Jan Leike, and Ryan Lowe. 2022. Training language models to follow instructions with human feedback. Preprint, arXiv:2203.02155.
Pang et al. (2024) Richard Yuanzhe Pang, Weizhe Yuan, Kyunghyun Cho, He He, Sainbayar Sukhbaatar, and Jason Weston. 2024. Iterative reasoning preference optimization. arXiv preprint arXiv:2404.19733.
Schulman et al. (2017) John Schulman, Filip Wolski, Prafulla Dhariwal, Alec Radford, and Oleg Klimov. 2017. Proximal policy optimization algorithms. arXiv preprint arXiv:1707.06347.
Shao et al. (2024) Zhihong Shao, Peiyi Wang, Qihao Zhu, Runxin Xu, Junxiao Song, Xiao Bi, Haowei Zhang, Mingchuan Zhang, Y. K. Li, Y. Wu, and Daya Guo. 2024. Deepseekmath: Pushing the limits of mathematical reasoning in open language models. Preprint, arXiv:2402.03300.
Tong et al. (2024) Yuxuan Tong, Xiwen Zhang, Rui Wang, Ruidong Wu, and Junxian He. 2024. Dart-math: Difficulty-aware rejection tuning for mathematical problem-solving.
Toshniwal et al. (2024a) Shubham Toshniwal, Wei Du, Ivan Moshkov, Branislav Kisacanin, Alexan Ayrapetyan, and Igor Gitman. 2024a. Openmathinstruct-2: Accelerating ai for math with massive open-source instruction data. arXiv preprint arXiv:2410.01560.
Toshniwal et al. (2024b) Shubham Toshniwal, Ivan Moshkov, Sean Narenthiran, Daria Gitman, Fei Jia, and Igor Gitman. 2024b. Openmathinstruct-1: A 1.8 million math instruction tuning dataset. arXiv preprint arXiv:2402.10176.
Wang et al. (2024) Peiyi Wang, Lei Li, Zhihong Shao, R. X. Xu, Damai Dai, Yifei Li, Deli Chen, Y. Wu, and Zhifang Sui. 2024. Math-shepherd: Verify and reinforce llms step-by-step without human annotations. Preprint, arXiv:2312.08935.
Wei et al. (2023) Jason Wei, Xuezhi Wang, Dale Schuurmans, Maarten Bosma, Brian Ichter, Fei Xia, Ed Chi, Quoc Le, and Denny Zhou. 2023. Chain-of-thought prompting elicits reasoning in large language models. Preprint, arXiv:2201.11903.
Xie et al. (2024) Yuxi Xie, Anirudh Goyal, Wenyue Zheng, Min-Yen Kan, Timothy P Lillicrap, Kenji Kawaguchi, and Michael Shieh. 2024. Monte carlo tree search boosts reasoning via iterative preference learning. arXiv preprint arXiv:2405.00451.
Xiong et al. (2024a) Wei Xiong, Hanze Dong, Chenlu Ye, Ziqi Wang, Han Zhong, Heng Ji, Nan Jiang, and Tong Zhang. 2024a. Iterative preference learning from human feedback: Bridging theory and practice for rlhf under kl-constraint. Preprint, arXiv:2312.11456.
Xiong et al. (2024b) Wei Xiong, Chengshuai Shi, Jiaming Shen, Aviv Rosenberg, Zhen Qin, Daniele Calandriello, Misha Khalman, Rishabh Joshi, Bilal Piot, Mohammad Saleh, Chi Jin, Tong Zhang, and Tianqi Liu. 2024b. Building math agents with multi-turn iterative preference learning. Preprint, arXiv:2409.02392.
Xu et al. (2023) Jing Xu, Andrew Lee, Sainbayar Sukhbaatar, and Jason Weston. 2023. Some things are more cringe than others: Preference optimization with the pairwise cringe loss. arXiv preprint arXiv:2312.16682.
Yang et al. (2024) An Yang, Beichen Zhang, Binyuan Hui, Bofei Gao, Bowen Yu, Chengpeng Li, Dayiheng Liu, Jianhong Tu, Jingren Zhou, Junyang Lin, Keming Lu, Mingfeng Xue, Runji Lin, Tianyu Liu, Xingzhang Ren, and Zhenru Zhang. 2024. Qwen2.5-math technical report: Toward mathematical expert model via self-improvement. Preprint, arXiv:2409.12122.
Yu et al. (2023) Longhui Yu, Weisen Jiang, Han Shi, Jincheng Yu, Zhengying Liu, Yu Zhang, James T Kwok, Zhenguo Li, Adrian Weller, and Weiyang Liu. 2023. Metamath: Bootstrap your own mathematical questions for large language models. arXiv preprint arXiv:2309.12284.
Yu et al. (2024) Longhui Yu, Weisen Jiang, Han Shi, Jincheng Yu, Zhengying Liu, Yu Zhang, James T. Kwok, Zhenguo Li, Adrian Weller, and Weiyang Liu. 2024. Metamath: Bootstrap your own mathematical questions for large language models. Preprint, arXiv:2309.12284.
Yuan et al. (2024) Lifan Yuan, Ganqu Cui, Hanbin Wang, Ning Ding, Xingyao Wang, Jia Deng, Boji Shan, Huimin Chen, Ruobing Xie, Yankai Lin, et al. 2024. Advancing llm reasoning generalists with preference trees. arXiv preprint arXiv:2404.02078.
Yuan et al. (2023) Zheng Yuan, Hongyi Yuan, Chengpeng Li, Guanting Dong, Keming Lu, Chuanqi Tan, Chang Zhou, and Jingren Zhou. 2023. Scaling relationship on learning mathematical reasoning with large language models. arXiv preprint arXiv:2308.01825.
Yue et al. (2023) Xiang Yue, Ge Zhang Xingwei Qu, Yao Fu, Wenhao Huang, Huan Sun, Yu Su, and Wenhu Chen. 2023. Mammoth: Building math generalist models through hybrid instruction tuning. arXiv preprint arXiv:2309.05653.
Zhang et al. (2024) Di Zhang, Xiaoshui Huang, Dongzhan Zhou, Yuqiang Li, and Wanli Ouyang. 2024. Accessing gpt-4 level mathematical olympiad solutions via monte carlo tree self-refine with llama-3 8b. Preprint, arXiv:2406.07394.
Zhang (2023) Tong Zhang. 2023. Mathematical analysis of machine learning algorithms. Cambridge University Press.
Zhong et al. (2024a) Han Zhong, Guhao Feng, Wei Xiong, Xinle Cheng, Li Zhao, Di He, Jiang Bian, and Liwei Wang. 2024a. Dpo meets ppo: Reinforced token optimization for rlhf. Preprint, arXiv:2404.18922.
Zhong et al. (2024b) Han Zhong, Guhao Feng, Wei Xiong, Li Zhao, Di He, Jiang Bian, and Liwei Wang. 2024b. Dpo meets ppo: Reinforced token optimization for rlhf. arXiv preprint arXiv:2404.18922.
Zhou et al. (2022) Denny Zhou, Nathanael Schärli, Le Hou, Jason Wei, Nathan Scales, Xuezhi Wang, Dale Schuurmans, Claire Cui, Olivier Bousquet, Quoc Le, et al. 2022. Least-to-most prompting enables complex reasoning in large language models. arXiv preprint arXiv:2205.10625.
Zhu et al. (2022) Xinyu Zhu, Junjie Wang, Lin Zhang, Yuxiang Zhang, Yongfeng Huang, Ruyi Gan, Jiaxing Zhang, and Yujiu Yang. 2022. Solving math word problems via cooperative reasoning induced language models. arXiv preprint arXiv:2210.16257.

Appendix A Technical Lemma

Lemma 1 (Solution of KL-regularized Optimization)

Given a loss functional with respect to $p(\cdot|x)$ , written as

	$\displaystyle\mathbb{E}_{w\sim p(\cdot)}\Big{[}-U(w)+\eta D_{\mathrm{KL}}\big{(}p(\cdot),p_{0}(\cdot)\big{)}\Big{]}$
	$\displaystyle=\eta D_{\mathrm{KL}}\Big{(}p(\cdot),p_{0}(\cdot)\exp\Big{(}\frac{1}{\eta}U(\cdot)\Big{)}\Big{)}$
	$\displaystyle\qquad-\eta\cdot\log\underbrace{\mathbb{E}_{w\sim p_{0}(\cdot)}\exp\big{(}\frac{1}{\eta}U(w)\big{)}}_{C_{r}},$

where the minimizer of the loss functional is $p^{*}(w)=\frac{1}{C_{r}}p_{0}(w)\exp\Big{(}\frac{1}{\eta}U(w)\Big{)}$ , also known as Gibbs distribution.

See Proposition 7.16 and Theorem 15.3 of Zhang (2023) for a detailed proof.

Appendix B Hyper-parameter Settings

We train the reward models using meta-llama/Llama-3.1-8B Dubey et al. (2024) as the base model. The reward models are trained with a global batch size of 64, a learning rate of 1e-6, a max length of 512, and an epoch of 1 on 4 H100 GPUs. We have conducted hyper-parameter searching on the learning rate on { $5e^{-6}$ , $2e^{-6}$ , $1e^{-6}$ , $5e^{-7}$ }. During the automatic labeling process, we use an $\eta$ of 2 in our main experiments for Mitral data, and an $\eta$ of 10 for deepseek data. We also conducted hyper-parameter searching on the $\eta$ on { $0.1$ , $1$ , $2$ , $5$ , $8$ , $10$ , $15$ }.

Appendix C Best-of-N Evaluation Results in Tables

In this section, we list the performance of the best-of-N evaluation of ER-PRM and other baselines in Tables. The results for the reward models with policy model Mistral-MetaMath-7b are shown in Table 2, which corresponds to Figure LABEL:fig:mistral-policy-best-of-n. The results for the reward models with policy model deepseek-math-7b-instruct are shown in Table 3, which corresponds to Figure LABEL:fig:deepseek-instruct-policy-best-of-n.

The results for Section 6.1 in Analysis are shown in Table 4 and Table 5, corresponding to the GSM8K and MATH datasets. The results for Section 6.2 are shown in Table 6.

	GSM8K				MATH500
Best-of-N	Ours	Soft-label PRM	Hard-label PRM	ORM	Ours	Soft-label PRM	Hard-label PRM	ORM
N=4	86.05	85.97	85.44	84.54	35.0	33.6	34.0	34.4
N=8	87.79	86.88	87.19	86.20	37.2	37.0	34.0	36.2
N=16	88.78	87.11	88.48	86.88	39.2	38.6	38.4	37.4
N=32	89.23	88.25	89.01	86.66	40.8	38.6	38.4	39.0
N=64	89.54	88.10	89.16	85.90	41.8	38.4	39.8	39.2
Top1@acc	78.09				29.4

Table 2: Best-of-N evaluation for policy model Mistral-MetaMath-7b. The reward models are trained using auto-regressive strategy from Llama-3.1-8B on Mistral data (GSM8K and MATH).

	GSM8K				MATH500
Best-of-N	Ours	Soft-label PRM	Hard-label PRM	ORM	Ours	Soft-label PRM	Hard-label PRM	ORM
N=4	86.73	86.28	86.66	86.88	51.0	50.2	50.4	48.8
N=8	87.33	86.81	87.19	87.26	52.2	49.6	52.0	49.4
N=16	88.55	88.25	88.10	88.40	53.2	50.0	53.2	51.0
N=32	89.23	88.63	88.63	89.08	53.2	49.8	52.8	51.2
N=64	90.22	88.55	89.04	90.06	53.0	50.4	52.6	51.2
Top1@acc	82.03				42.8

Table 3: Best-of-N evaluation for policy model deepseek-math-7b-instruct, The reward models are trained from Llama-3.1-8B on deepseek data (GSM8K and MATH).

	GSM8K
Best-of-N	$\bm{\eta=0.1}$	$\bm{\eta=1}$	$\bm{\eta=2}$	$\bm{\eta=5}$	$\bm{\eta=8}$	$\bm{\eta=10}$	$\bm{\eta=15}$	$\bm{\eta=20}$
N=4	83.93	84.69	84.99	84.38	85.22	84.69	84.91	84.53
N=8	85.14	85.82	86.43	86.35	86.73	86.28	86.66	86.43
N=16	85.29	85.75	86.05	87.11	87.57	87.04	87.72	87.04
N=32	86.13	85.52	86.43	87.72	87.87	88.02	88.78	87.11
N=64	86.13	85.90	86.35	88.17	88.25	88.48	88.78	87.19

Table 4: Best-of-N evaluation for different

\eta

values on GSM8K dataset. The reward models are trained from Llama-3.1-8B solely on GSM8K.

	MATH
Best-of-N	$\bm{\eta=0.1}$	$\bm{\eta=1}$	$\bm{\eta=2}$	$\bm{\eta=5}$	$\bm{\eta=8}$	$\bm{\eta=10}$	$\bm{\eta=15}$	$\bm{\eta=20}$
N=4	35.0	34.0	35.0	33.2	32.4	33.2	33.2	31.8
N=8	35.8	37.2	39.0	35.0	36.0	35.8	35.6	33.8
N=16	39.0	38.6	40.0	37.0	39.4	38.6	39.0	37.4
N=32	39.8	39.8	40.2	38.6	39.2	39.4	38.6	38.8
N=64	38.6	41.0	40.2	37.4	38.2	40.0	40.2	39.4

Table 5: Best-of-N evaluation for different

\eta

values on MATH dataset. The reward models are trained from Llama-3.1-8B solely on MATH.

	GSM8K			MATH500
Best-of-N	Ours	Soft-label PRM	Hard-label PRM	Ours	Soft-label PRM	Hard-label PRM
N=4	84.84	84.60	84.60	33.6	31.4	31.8
N=8	86.80	86.05	86.73	33.6	33.0	33.0
N=16	87.95	87.41	87.41	36.2	35.0	35.6
N=32	88.40	87.87	87.71	37.0	35.0	36.6
N=64	88.40	88.24	88.17	36.8	34.2	36.4

Table 6: Best-of-N evaluation for policy model Mistral-MetaMath-7b, The reward models are trained using regression strategy from Llama-3.1-8B on Mistral data (GSM8K and MATH).

Appendix D Reward Models with Various Sizes

In addition to training the reward model with Llama-3.1-8B, we also explore training on various sizes. In this section, we train the reward model with Llama-3.2-3B-Instruct and Llama-3.2-1B-Instruct (Dubey et al., 2024). We hope to increase the performance of smaller-size models so we use the instruct-version for them instead of base models. We train them using the Mistral data, the same as the training data used in the main experiments.

The experiment results are shown in Table 7 and Table 8. Although we change into models of smaller sizes, the best-of-N accuracy still outperforms the Top 1 accuracy by a large margin. For example, for the 1B size model, the best-of-4 accuracy outperforms Top 1 accuracy by 4% and the best-of-64 accuracy outperforms by 5 $\sim$ 6% on GSM8K dataset. We observe that the performance gain from best-of-4 to best-of-64 for the 1B model is much smaller than the 8B model shown in Table 2, which has 4 $\sim$ 6% performance gain while 1B model has only 2 $\sim$ 3% performance gain. The comparison demonstrates that larger models have higher chances of selecting the gold answer from candidates when $N$ is large. We also discover that the 1B model suffers from severe reward hacking problems on the MATH test set. For ER-PRM and Hard-label PRM, they both achieve an accuracy of 37.6% on best-of-16 evaluation. However, their accuracy drops about 2% on best-of-64 evaluation, showing that they are distracted by the wrong answers and could not effectively select the gold responses. The reward hacking problem becomes less severe for the easy dataset GSM8K, which probably due to the less number of wrong candidate answers.

For the 3B size model, it consistently outperforms the 1B size model, showing that training with larger-size reward models would generally achieve better performance. The 3B reward model on MATH shows a competent performance as the 8B reward model (Table 2), demonstrating the feasibility of training small-size but powerful models. We also discover that the reward hacking problem is largely mitigated for the 3B size model, as the best-of-N accuracy keeps increasing on MATH as $N$ increases, and does not drop much on GSM8K from best-of-32 to best-of-64. However, we still notice that on the GSM8K test set, the performance gain from $N=4$ to $N=64$ is still little compared to the 8B case. We may conclude that a larger model size reward model would generally have a larger performance gain when $N$ increases.

In both 1B and 3B size settings, ER-PRM consistently outperforms the Soft-label PRM and Hard-label PRM, demonstrating the effectiveness of our methods across various model sizes.

	GSM8K			MATH500
Best-of-N	Ours	Soft-label PRM	Hard-label PRM	Ours	Soft-label PRM	Hard-label PRM
N=4	82.41	82.56	82.18	32.6	32.8	31.4
N=8	82.56	82.56	82.41	34.8	33.0	33.6
N=16	83.70	82.94	83.54	37.6	35.2	37.6
N=32	84.31	84.00	83.47	36.4	35.8	36.2
N=64	84.08	83.93	83.47	35.8	35.0	35.4
Top1@acc	78.09			29.4

Table 7: Best-of-N evaluation for policy model Mistral-MetaMath-7b, The reward models are trained from Llama-3.2-1B-Instruct on Mistral data (GSM8K and MATH).

	GSM8K			MATH500
Best-of-N	Ours	Soft-label PRM	Hard-label PRM	Ours	Soft-label PRM	Hard-label PRM
N=4	83.54	83.32	83.39	36.0	36.0	35.4
N=8	83.92	83.47	83.47	37.8	37.2	37.2
N=16	84.23	84.00	83.92	38.4	38.2	37.4
N=32	84.91	84.68	84.38	41.8	39.2	40.2
N=64	85.36	85.06	84.68	41.8	39.6	41.0
Top1@acc	78.09			29.4

Table 8: Best-of-N evaluation for policy model Mistral-MetaMath-7b, The reward models are trained from Llama-3.2-3B-Instruct on Mistral data (GSM8K and MATH).

Appendix E OOD Performance of PRMs

In this section, we examine the OOD performance of the PRMs. We use deepseek-math-7b-rl (Shao et al., 2024) as the policy model for best-of-N generation. We train the reward model from Llama-3.1-8b on Mistral data.

The results are shown in Figure LABEL:fig:deepseek-policy-best-of-n and Table 9. The accuracy increases slowly when N increases from 4 to 64 on GSM8K. And the increment on the MATH dataset is also slower than in the case where we use Mistral as the policy model. We observe the performance drop for ORM reward models, indicating its instability for out-of-distribution generated data. The reason for the smaller performance gain is that, our process reward data is generated from a weaker model Mistral-MetaMath-7b. The reward model might only understand the behavior of the weak model. For certain steps where the weak model fails to produce the correct answer, the reward model is likely to assign these steps a low score. However, a stronger model may be capable of deriving the correct answer in such cases.

	GSM8K				MATH500
Best-of-N	Ours	Soft-label PRM	Hard-label PRM	ORM	Ours	Soft-label PRM	Hard-label PRM	ORM
N=4	89.46	89.39	88.70	88.77	52.6	51.4	51.8	52.6
N=8	89.91	89.61	88.93	89.09	55.8	54.8	55.4	55.0
N=16	90.22	90.22	89.76	89.01	55.6	54.8	55.4	55.2
N=32	90.45	90.45	89.84	89.01	56.0	55.0	55.0	55.0
N=64	90.67	90.45	89.84	88.10	57.0	55.4	55.6	53.4
Top1@acc	88.17				51.0

Table 9: Best-of-N evaluation for policy model deepseek-math-7b-rl. The reward models are trained using auto-regressive strategy from Llama-3.1-8B on Mistral data (GSM8K and MATH).

Appendix F OpenMath2-Llama3.1-8B as the Policy Model on MATH

In this section, We want to examine the reward model performance paired with one of the most powerful open-source policy models fine-tuned from open-source data. We could also see the reward model performance on the Out-of-Distribution Scenario. We use OpenMath2-Llama3.1-8B (Toshniwal et al., 2024b) as the generator, which is fine-tuned from 14 million mathematical problems and excellent in mathematical reasoning. It achieves a Top 1 accuracy of 66.2% of the MATH500 test set. We evaluate the best-of-N performance on the MATH500 test dataset. For each question, we use OpenMath2-Llama3.1-8B to generate N candidate solutions and use the reward model to select the response. We use the reward model trained from Llama-3.1-8B on deepseek data.

The results are shown in Table 10. We first observe a satisfactory performance gain compared to the Top 1 accuracy (66.2%) for all 3 reward models. It could increase the accuracy by more than 4%. The results show that even the reward model trained with data from a weaker model, it could still guide the decoding process during the inference time. We also observe the reward hacking problem when we use the weak reward model to improve the inference of the strong policy model. As shown in the table, there is not much performance gain from $N=4$ to $N=64$ . And $N=64$ does not perform the best. We discover that the ER-PRM method still improves the policy model most, demonstrating the feasibility of our method when implemented with strong models.

	MATH
Best-of-N	Ours	Soft-label PRM	Hard-label PRM
N=4	69.0	67.2	69.2
N=8	70.6	68.6	68.8
N=16	70.4	69.2	69.4
N=32	70.2	68.4	69.8
N=64	70.4	67.6	68.6

Table 10: Best-of-N evaluation on the MATH500 test set. The reward models are trained from Llama-3.1-8B on deepseek data. The policy model for generation is OpenMath2-Llama3.1-8B.

Appendix G Experiments on Entire MATH Test Set

In our previous experiments, we evaluate the best-of-N performance on the MATH500 test sets to align with previous works (Wang et al., 2024; Lightman et al., 2023) and save computation cost. In this section, we evaluate our reward models on the entire MATH test set which contains 5000 questions. The reward models are trained from Llama-3.1-8B on Mistral data. And the Policy model for best-of-N generation is Mistral-MetaMath-7b.

The results are shown in Table 11. When evaluated on the MATH test set, we could still observe an increasing trend in the accuracy as N increases. Compared to Hard-label and Soft-label settings, our model consistently outperforms them. When N is larger, the increment for Soft-label and Hard-label PRM is less noticeable while the increment for ER-PRM is still significant.

	MATH
Best-of-N	Ours	Soft-label PRM	Hard-label PRM
N=4	32.94	32.80	33.38
N=8	34.72	33.80	34.28
N=16	36.24	35.00	36.18
N=32	37.80	36.12	37.46
N=64	38.62	36.74	37.50

Table 11: Best-of-N evaluation on the entire MATH test set. The reward models are trained from Llama-3.1-8B on Mistral data. The policy model for generation is Mistral-MetaMath-7b.

Appendix H Definition of Step, Partial Chain, and Chain

Step:
A step refers to the smallest unit of operation in a reasoning process. Each step performs a single operation (e.g., a single calculation or logical deduction) and represents one incremental action within the overall reasoning process.

Chain:
A chain represents the complete series of operations that culminate in the final result or target solution. It consists of multiple sequential steps, forming the full reasoning process.

Partial Chain:
A partial chain is a subset of a complete chain, consisting of a sequence of intermediate steps leading toward (but not necessarily reaching) the final result. Partial chains are used in our work to compute intermediate reward scores that guide the reasoning process step-by-step.

In our paper, when we refer to “step-level derivation,” we are specifically describing the last step reward score associated with partial chains. These scores are step-level reward scores and not chain-level reward scores, as they evaluate the contributions of individual steps (or intermediate sequences) rather than the final output of the entire chain. The distinction is important because step-level scores are critical for guiding the model at each reasoning step, while chain-level scores evaluate the overall success of the complete reasoning process.