Enhancing teleportation via noisy channels: effects of the induced multipartite entanglement

Quantum teleportation stands out as one of the most fascinating applications of quantum entanglement. It allows the transmission of quantum information between two spatially separated agents, Alice and Bob, by means of local operations, classical communication, and a key element: a shared correlated state known as resource state ¹¹1Some authors refer also to the resource state as quantum channel. Here we will keep the term ‘quantum channel’ to denote a completely positive trace-preserving map, that in the present context gives the reduced dynamics of an open system.. The original standard teleportation protocol [2] uses a (pure, maximally entangled, two-qubit) Bell state as the resource state. Subsequent investigations extended the scheme noticing that there exist resource states that are useful for teleportation yet are neither maximally entangled [3] nor pure, and their relation with violations of Bell inequalities [4, 5] and discord-like correlations [6] has been discussed.

A mixed rather than a pure resource state is more realistic, particularly when taking into consideration the interaction of the (Alice and Bob’s) entangled pair with its surroundings, resulting in mixing of the resource state. There has been extensive research on such noisy quantum teleportation schemes [7, 8, 9, 10, 11, 12, 13, 14, 15, 16], e.g., resorting to the Lindblad formalism to explore the fidelity of teleportation in terms of decoherence rates [7], or to determine the optimal Bell resource state under different local Pauli noises [8]. Recent methods for protecting teleportation against some decoherence channels have also been advanced [9, 10]. The effect on the teleportation fidelity of different noisy channels acting on the resource state —typically representing the interaction of Alices’s and Bob’s particles with additional subsystems (which in the present case are regarded as local environments)—, has been studied considering the Kraus operators corresponding to dissipative interactions via an amplitude damping channel [11, 12], together with other paradigmatic noise or decoherence channels on qubits such as bit flip, phase flip, depolarizing [13], and phase damping [14]. Also, the teleportation protocol under noisy channels in higher dimensional systems has been explored [15]. A general theoretical and experimental [16] conclusion that ensues from these investigations is that there exist appropriate channels (acting on suitable initially pure resource states) for which the detrimental effects of noise on the teleportation fidelity are minimal, compared to other noisy channels.

Further extensions of the original teleportation protocol have also been advanced that consider multi-party resource states exhibiting some type of multipartite entanglement. This has led to the development of strategies that exploit multipartite entanglement to teleport multiple qubit states, as e.g. in [17, 18, 19, 20, 21]. Multi-directional teleportation, allowing quantum information transmission between several agents, has also been explored [22, 23, 24, 25], including the effect of noisy channels [26, 27, 28, 29].

Despite the advances achieved regarding the teleportation success under noisy channels, whether acting on bipartite or multipartite resource states, the relation between the teleportation fidelity and the multipartite entanglement generated among the resource qubits and the environment, has been much less explored. Such an analysis would allow us to identify the type of processes —characterized by the type of entanglement they induce—, that favor a more successful teleportation, and to possibly explain the fidelity improvement as an effect assisted by the created multipartite entanglement. In [30, 31] some progress has been made, by relating the teleportation fidelity with the 3-partite entanglement resulting from the local interaction of one qubit of the resource state with a two-level environment. Here we contribute along these lines, by focusing on the standard teleportation protocol in the presence of noisy channels acting on the bipartite resource state. We consider a generalized noisy quantum channel that can be continuously transformed from the amplitude damping to the dephasing channel [32], and explore the correlation between the maximal average fidelity and the amount of 3- and 4-partite entanglement, distributed among the pair of qubits that conform the resource state and the qubits that represent the corresponding local environments.

We first revisit the standard teleportation protocol and the notion of maximal average fidelity $F_{\max}$ as a quantifier of the teleportation success (Sec. II), and express the latter in terms of the Kraus operators of an arbitrary quantum channel acting on the (arbitrary yet initially pure) resource state, conformed by two qubits $A$ and $B$ (Sec. III). After these preliminary sections, we relate the maximal average fidelity above the classical threshold value, $\mathbb{F}_{\max}$, with the bipartite entanglement between $A$ and $B$, considering $A+B$ as an ideal closed system (Sec. IV). Assuming then that $B$ interacts with a local, two-level environment $E_{B}$ via the generalized channel, we investigate the relation between $\mathbb{F}_{\max}$ and the 3-partite entanglement distributed among $A,B$ and $E_{B}$ (Sec. V). The analysis is extended to the 4-partite case by considering that both $A$ and $B$ locally interact with their respective environments $E_{A}$ and $E_{B}$ under independent generalized channels, and a non-trivial correlation between $\mathbb{F}_{\max}$ and the 4-partite entanglement is disclosed (Sec. VI). Finally, some concluding remarks are presented (Sec. VII).

The main idea behind the standard teleportation protocol is that Alice wants to send to Bob an arbitrary input state, $\rho_{\textrm{in}}$, encoded in a qubit $a$ in her possession. For this task, they share a pair of qubits $A$ and $B$ (in Alice and Bob’s possession, respectively) in an entangled state $\rho_{AB}$, called resource state. Alice then performs a Bell measurement [33, 34, 35] on her pair of qubits $a$ and $A$, and communicates the outcome to Bob via a classical channel. Upon receiving this information —and knowing $\rho_{AB}$ [36]—, Bob performs a unitary operation $\sigma^{(i)}\in\{\mathsf{I}_{2},\sigma^{x},\sigma^{y},\sigma^{z}\}$ on his qubit $B$, thus putting it into the output state $\rho_{\textrm{out}}$ ($\sigma^{x,y,z}$ stand for the Pauli matrices, and $\mathsf{I}_{n}$ denotes the $n\times n$ identity operator).

Figure 1 shows a schematic generalization of the standard teleportation protocol. The qubits $A$ and $B$ are initially in the state $\left|{0}\right\rangle$, whereas $a$ is already in $\rho_{\textrm{in}}$, the state to be teleported. Vertical dashed lines separate the different stages of the protocol corresponding, from left to right, to:

• •

  A unitary transformation $U(\phi,\varphi)$ rotates the qubit $A$, and a cnot gate is employed to prepare the initial resource state

  $$\left|{\phi_{0}}\right\rangle_{AB}=\cos\phi\left|{00}\right\rangle+e^{i\varphi}\sin\phi\left|{11}\right\rangle,$$

  (1)

  with $\phi\in[0,\pi/2]$, and $\varphi\in[-\pi/2,3\pi/2]$. (This generalizes the application of the Hadamard gate, resulting in the Bell state $\frac{1}{\sqrt{2}}(\left|{00}\right\rangle+\left|{11}\right\rangle)$).

• •

  Alice applies a cnot and a Hadamard gate to the qubits in her possession, then performs a measurement in the Bell basis and communicates the outcome to Bob via classical channels.

• •

  Depending on Alice’s measurement outcome, Bob applies appropriate unitary operations on his qubit $B$, so the output state of $B$ coincides with the input state of $a$. The whole strategy leads to perfect teleportation if the resource state (1) is the Bell state $\frac{1}{\sqrt{2}}(\left|{00}\right\rangle+\left|{11}\right\rangle)$ (if $\left|{\phi_{0}}\right\rangle$ was another Bell state, then the operations in Bob’s strategy must be changed).

For pure input states, $\rho_{\textrm{in}}=\left|{\chi}\right\rangle\!\left\langle{\chi}\right|$, the success of the teleportation can be quantified by means of the maximal average fidelity $F_{\max}$, which measures the probability that $\rho_{\textrm{out}}$ coincides with the (unknown) $\rho_{\textrm{in}}$, averaged over all input states, provided the appropriate $\sigma^{(i)}$ is chosen. The maximal average fidelity for an arbitrary 2-qubit resource state $\rho_{AB}$ can be written as [37]

where $\mathcal{F}_{\max}$ is the maximal singlet fraction [38]

corresponding to the maximum fidelity between the resource state and any of the Bell states ²²2In Ref. [38] the maximal singlet fraction is defined considering the maximum over all the maximally entangled states. Here we maximize only over those states that can be obtained from Bell states by means of unitary transformations of the form $\mathsf{I}_{2}\otimes\sigma^{(i)}$. With this restriction we adhere to the standard teleportation protocol (in which Bob’s operations are implemented via Pauli operators).

Putting $\sigma^{(0)}=\mathsf{I}_{2}$, and $\sigma^{(1),(2),(3)}=\sigma^{x,y,z}$, we get

Therefore, $\mathcal{F}_{\max}$ picks out the optimal Bell state, i.e., the Bell state that is closest to $\rho_{AB}$. The above expressions show that if $\rho_{AB}$ is a Bell state, the protocol guarantees the complete reconstruction of the input state.

For the quantum teleportation to be considered successful $F_{\max}$ must be greater than $2/3$, which is the value of the maximal average fidelity corresponding to the best possible reconstruction through a purely classical channel [40]. Throughout this paper we will be interested in the success of non-classical teleportation, hence we will focus on those regimes in which $F_{\max}\geq 2/3$, and accordingly pay attention to the quantity

Let us assume that $A$ and $B$ are initially prepared in the state $\left|{\phi_{0}}\right\rangle_{AB}$, given by Eq. (1), which then passes through a quantum channel $\Lambda_{AB}$ represented by a set of Kraus operators $\{\Pi_{\mu}\}$, acting on $\mathcal{H}_{A}\otimes\mathcal{H}_{B}$ [41]. A scheme of this process is shown in Fig. 2.

The channel thus transforms $\left|{\phi_{0}}\right\rangle\!\left\langle{\phi_{0}}\right|$ into an effective (typically mixed) resource state $\rho_{AB}$ given by

Since Alice and Bob are typically spatially separated, we will focus on cases in which $A$ and $B$ undergo independent local channels, so $\Lambda_{AB}=\Lambda_{A}\otimes\Lambda_{B}$ and

where $\{Q_{\alpha}\}$ and $\{K_{\beta}\}$ stand for the sets of Kraus operators associated to $\Lambda_{A}$ and $\Lambda_{B}$, respectively, each set having at most $(\dim\mathcal{H}_{A(B)})^{2}=4$ elements. Equation (8) becomes then

The channel $\Lambda_{A}\otimes\Lambda_{B}$ acts as if $A$ and $B$ interact locally with a corresponding party $E_{A}$ and $E_{B}$. Assuming that the systems $(A+B)$, $E_{A}$ and $E_{B}$ are initially uncorrelated, and that $E_{A}$ and $E_{B}$ are qubits in the initial state $\left|{0}\right\rangle$, we may write

for the initial 4-partite state. Further, if the interaction between $A$ and $E_{A}$ is represented by the unitary operator $U_{AE_{A}}$ (and similarly for $B$ and $E_{B}$), then

with $\{\left|{\alpha}\right\rangle\}$ and $\{\left|{\beta}\right\rangle\}$ basis of $\mathcal{H}_{E_{A}}$ and $\mathcal{H}_{E_{B}}$, respectively. In addition, the (unitary) evolution of the complete system can be obtained from these Kraus operators as

A particular family of local channels, that involves a 3-party system instead of a 4-partite one, is that in which one of the resource qubits, say $A$, remains unaffected so $\Lambda_{A}=\mathsf{I}_{2}$, while $B$ goes through an arbitrary channel $\Lambda_{B}$. In this case $Q_{\alpha}=\mathsf{I}_{2}\,\delta_{\alpha 0}$, and from Eq. (10) we are led to

Clearly for $\Lambda_{AB}=\mathsf{I}_{2}\otimes\Lambda_{B}$ the subsystem $E_{A}$ is superfluous, and Eq. (11) reduces to the 3-qubit initial state

The standard protocol, depicted in the circuit of Fig. 1, corresponds to $\Lambda_{AB}=\mathsf{I}_{4}$. Equation (8) thus becomes

With $\left|{\phi_{0}}\right\rangle$ given by (1), the optimal strategy corresponds to the state $\left|{\Phi^{+}}\right\rangle$ for $\varphi\in[-\frac{\pi}{2},\frac{\pi}{2}]$, and $\left|{\Phi^{-}}\right\rangle$ for $\varphi\in[\frac{\pi}{2},\frac{3\pi}{2}]$, so (16) reduces to $F_{\max}=\frac{2}{3}+\frac{1}{3}\,\mathcal{E}_{0}\,|\!\cos\varphi|$, and consequently, in the non-interacting case, Eq. (6) gives

where $\mathcal{E}_{0}$ stands for the entanglement of the initial resource state

Here $C$ is the concurrence, quantifying the amount of qubit-qubit entanglement [42]. For an arbitrary (in general mixed) 2-qubit state $\rho_{AB}$ it is defined as

where $\{\lambda_{n}\}$ are the eigenvalues of the matrix $\rho_{AB}(\sigma^{y}\otimes\sigma^{y})\rho^{*}_{AB}(\sigma^{y}\otimes\sigma^{y})$ ordered in decreasing order, and $\rho^{*}_{AB}$ stands for the complex conjugate of $\rho_{AB}$ expressed in the computational basis. When the state is pure ($\rho_{AB}=\left|{\chi}\right\rangle\!\left\langle{\chi}\right|$), the expression for the concurrence simplifies and reads

with $\rho_{A(B)}=\textrm{Tr}_{B(A)}\rho_{AB}$ the reduced density matrix of either one of the qubits.

Equation (17) makes explicit that the teleportation success enhances as the resource state’s entanglement $\mathcal{E}_{0}$ increases. It also shows that as $\varphi$ tends to $\pm\pi/2$, the fidelity decreases up to its minimal —classically attainable— value $2/3$, irrespective of the initial entanglement, as can be seen in Fig. 3.

That is, there are maximally entangled resource states for which the maximal average fidelity does not exceed its classical limit, and the relative phase $\varphi$ determines the fraction of $\mathcal{E}_{0}$ that ultimately improves the fidelity.

We now focus on the case in which only $B$ undergoes through a quantum channel, effectively representing an interaction with an additional qubit $E_{B}$. Figure 4 illustrates this situation, leading to a mixed resource state $\rho_{AB}$ before the measurement stage of the protocol.

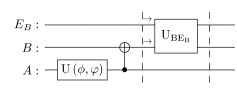
The scenario under consideration corresponds to that in which $\left|{\phi_{0}}\right\rangle\!\left\langle{\phi_{0}}\right|$ is subject to a channel $\Lambda_{AB}=\mathsf{I}_{2}\otimes\Lambda_{B}$, where $\Lambda_{B}$ encodes the interaction between $B$ and $E_{B}$, giving rise to the possible creation of tripartite entanglement in the system $A+B+E_{B}$. The channel thus transforms the initial state (15)

into the 3-qubit state (see Eq. (13) with $Q_{\alpha}=\mathsf{I}_{2}\,\delta_{\alpha 0}$)

In [43] necessary and sufficient conditions on the Kraus operators $K_{\beta}=\left\langle{\beta}\right|U_{BE_{B}}\left|{0}\right\rangle$ were established, that ensure the emergence of bipartite and tripartite entanglement among the parties $A,B,E_{B}$. For the present analysis we concentrate on the dynamics of the resource state’s (bipartite) entanglement $C_{AB}=C(\rho_{AB})$, and the tripartite entanglement, as measured by the so-called 3-tangle. The latter stands as a legitimate measure of residual entanglement in a 3-qubit pure state $\left|{\psi}\right\rangle_{ijk}$, and quantifies the amount of three-way ghz-type entanglement in the state [44]. The 3-tangle is defined as [45]

where $C_{ij}$ is given by Eq. (19), and $C_{i|jk}$ by

The last expression generalizes (20) for a 3-party pure state and quantifies the entanglement across the bipartition $i|(j+k)$ [46].

In [43] it is found that for $\Lambda_{AB}=\mathsf{I}_{2}\otimes\Lambda_{B}$, $C_{AB}$ and $\tau_{ABE_{B}}$ evolve according to

and

where $u=4\det K_{0}K_{1}$ and $v=g^{2}(K_{0},K_{1})$, with $g(M,N)=\textrm{Tr}M\,\textrm{Tr}N-\textrm{Tr}(MN)$. The evolution parameter is encoded in the Kraus operators and is not explicitly written in the above expressions.

We now consider that both qubits $A$ and $B$ undergo local channels $\Lambda_{A}$ and $\Lambda_{B}$, as a result of their separate interaction with initially uncorrelated qubits, $E_{A}$ and $E_{B}$. The initial resource state is thus (see Eqs. (1) and (11))

and the Kraus operators of the local channels are generically given by Eq. (12). Figure 8 shows the first two stages of the corresponding teleportation protocol.

Different forms of multipartite entanglement may arise in this 4-qubit system [50]. Here we will focus on the multipartite entanglement as measured by the 4-tangle $\tau_{4}$, defined for a 4-qubit pure state $\left|{\psi}\right\rangle$ as [51]

This quantity becomes maximal ($\tau_{4}=1$) for the 4-partite ghz state $\frac{1}{\sqrt{2}}(\left|{0000}\right\rangle+\left|{1111}\right\rangle)$, and vanishes for the 4-partite w state $\frac{1}{\sqrt{4}}(\left|{1000}\right\rangle+\left|{0100}\right\rangle+\left|{0010}\right\rangle+\left|{0001}\right\rangle)$.