Enhancing Dynamic-Mode Decomposition via Multi-Scale Analysis
1 Introduction
In recent years, beginning with the now seminal papers [1, 2], a large body of literature has emerged around the modal decomposition technique known as Dynamic-Mode Decomposition (DMD); see [3] for a comprehensive review of the literature, and the recent reviews in [4] and [5] for the most recent summaries and extensions. The primary advantage of DMD is that it is a completely model free data processing tool, allowing for the ready determination of results from arbitrarily complicated data sets. However, this advantage comes at the cost of introducing an infinite dimensional framework by way of determining the spectral properties of the affiliated Koopman operator [6].
As shown in [7, 8], by making thoughtful choices of affiliated observables of the given data set which best explore the affiliated infinite dimensional spaces associated with the Koopman operator, one can get vastly superior results from the DMD approach. This then shows that even low dimensional data sets must be examined essentially from a Hilbert space perspective, thus making controlling for error and describing features of the DMD decomposition a difficult task. Some remedies to this can be found in the rigorous work presented in [9], which presents systematic ways to determine the spectra and eigenspaces of the Koopman operators. The methods developed are computationally intensive and thus restricted to relatively low dimensional dynamical systems.
Koopman Operators and Dynamic-Mode Decomposition
While finite-dimensional dynamical systems are certainly of interest in their own right, we often wish to study nonlinear partial-differential equations (PDEs) of the general form
where is some reasonably chosen Hilbert space. Frequently, the only recourse to solving the above initial-value problem is through numerical simulation, which is often facilitated by expanding the solution along an orthonormal basis of so that
This generates a system of equations describing the evolution of the coefficients .
We are therefore motivated to study nonlinear dynamical systems of the generic form
where we suppose . We denote the affiliated flow of this equation as . We define the associated Hilbert space of observables, say , so that if
where is some appropriately chosen measure. A great deal of insight can be gained from looking at the affiliated linear representation of the problem given via the infinite-dimensional Koopman operator , where
so that if , then
Note, throughout the remainder of the paper, we refer to the space of observables as .
The power in this approach is that by moving to a linear-operator framework, the affiliated dynamics of the nonlinear system as measured via observables is captured via the eigenvalues of . Thus, assuming for the moment that has only discrete spectra, then if we can find a basis of via the Koopman modes where
then for any other observable , we should have
However, as one would imagine, determining the modes of the Koopman operator is in general impossible in an analytic way. The Dynamic-Mode Decomposition (DMD) method [2, 1, 7, 3] has been developed which allows for the determination of a finite number of the Koopman modes.
To wit, if we sample the flow at a discrete set of times , where , thereby generating the data set , and if we select some set of observables , then the DMD method approximates by computing the spectra of the finite-dimensional operator , which solves the the finite-dimensional least-squares problem
| (1) |
where and are the matrices of the past and future states respectively, i.e.
For example, if we chose the observable where
which just finds the approximation of the solution to the PDE of interest at the point of the computational mesh, then the Koopman operator provides a linear framework to describe the dynamics of a coordinate which evolves along an otherwise nonlinear flow. Note, this particular choice of observation function is called the canonical observation throughout the remainder of this paper.
The efficacy of this approach though is contingent on the choice of observables one makes, and to date no general strategy for observable choosing strategies has been made. Some success has been had by trying to use kernel based means allowing for the efficient exploration of more complicated, nonlinear observables; see [10]. However, as shown in [8], for infinite dimensional problems, or at least the relatively high-dimensional dynamical systems which approximate them, kernel based techniques can be of very limited utility. By using various reproducing kernel techniques from machine learning, [11], more robust methods for determining effective observables can be found. While effective, the methodology in [11] is computationally intensive requiring the manipulation of large matrices.
In this paper we propose a relatively stream-lined, and in some sense, more physically motivated approach to constructing nonlinear observables . We do this by making use of wavelet based, multi-scale approximations of various function space norms. By doing so, we are able to create a more robust implementation of the DMD algorithm without creating a significantly larger computational burden. We likewise show that the greater degrees of freedom introduced by our approach allow for more optimal decomposition strategies than would be available otherwise. Thus our work should be of use in helping to enhance current DMD based approaches as well as the next way of methodologies under current development [12, 13].
The outline of the paper is as follows. In Section 2 we explain our wavelet based multi-scale generation of observables. In Section 3 we present our results on a model test case. Section 4 collects the conclusions of our work.
2 Multi-Scale Analysis and Norm-Based Observables
To remedy this issue of effective observable selection, we make use multi-scale approximations by way of wavelets. Discrete wavelet analysis begins with a scaling function , such that relative to some length scale , the set of functions
forms an orthonormal set, where
We define the subspace so that
By introducing the corresponding wavelet function , one is able to seperate the space such that
where
so that represents the parts of functions in which vary on double the length scale, while represents the details of the functions in . In turn, one can then look at longer scales by separating and so forth. This collection of separated spaces represents a multi-resolution approximation (MRA).
Thus, for a given function , or some high-order numerically generated approximation to it, we can decompose in an MRA consisting of levels such that
where
and where denotes the detail coefficients at the scale while denotes the approximation coefficients at the terminal scale . To use the MRA to build observables , we note that because of orthonormality, we can readily show that
Thus, we can define affiliated observables say where
From an analytic point of view, one of the most significant applications of orthonormal wavelets is their ability to readily characterize complicated function spaces in terms of the detail and approximation coefficients described above. In particular, following [14], if we choose a function , where is the space of functions of rapid decay [15], such that for its Fourier transform , we have for some positive constant that
then the Besov space , for , is characterized by the norm
where
and refers to the standard norm for the Lebesgue space , i.e.
Here the parameter acts as a regularity paramater measuring the degree of differentiability of the function . To wit, if we let , then for , , where is defined via the norm
Thus the homogeneous Besov spaces are in some sense spaces but with regularity. It is a nontrivial yet powerful result, see [14], that if has a wavelet expansion in the form
then
Thus, by using one wavelet decomposition, we can generate an arbitrary number of observables of the form , where
in the same way that we separated the norm into a sequence of observables reflecting the different wavelet scales.
3 Implementation and Results
Model Problem
We take as our prototypical example of a nonlinear PDE the Nonlinear Schrödinger Equation (NLS) which is
While we cannot simulate this equation on all of , by taking , , we can generate a highly accurate numerical approximation to the above equation by using a standard periodic pseudo-spectral approximation in space coupled to a 4th-order Runge-Kutta scheme with integrating factor in time. Thus, we decompose so that
where , , thereby generating a -dimensional dynamical system describing the evolution of . In general, we expect this system to be Hamiltonian, which implies the Koopman operator is unitary, and thus has strictly imaginary spectra ; see [6, 9, 16].
As an initial condition, we take
where is a continuous random-walk generated from the uniform distribution , and . Thus for nonzero , we look at an inital condition in which we have a central peak at and a secondary one at all on a background of normally distributed perturbations. In the limit as , we should have
Using the canonical observation in the limit, we see that if the time step in the numerical integrator is then we have
where and are and diagonal matrices respectively such that
and is a matrix of ones, i.e.
Thus, in the vanishing limit, we see that the approximation to the Koopman operator found via DMD given by is
where denotes the Moore–Penrose pseudoinverse of the matrix . If the Singular Value Decomposition (SVD) of is
we readily see that
where is a matrix of ones. Thus the eigenvalues of are and , repeated times, so ignoring the null-space of , we find the affiliated Koopman eigenvalue . Thus in all future computations we anticipate that the computed spectra should reflect some degree of perturbation away from .
DMD: Details and Implementation
Following the approach in [2], the practical implementation of the DMD starts with a SVD of the past matrix so that Equation (1) becomes
Motivated by the previous example though, we should anticipate the possibility that could be of relatively small rank, which is to say that the conditioning inherent in trying to compute the Moore–Penrose pseudoinverse of could compromise the accuracy of any results one might try to compute. Thus, letting be the descending ordered vector of the non-negative primary diagonal entries of , we define the index to be the largest index of such that
Thus the non-negative integer tol sets the relative accuracy of any computations and allows for the omission of spurious modes computed by the DMD. This in turn defines a reduced SVD of so that
and thus becomes the matrix
Finding the affiliated eigenvalues and eigenvectors of , i.e.
then gives us the affiliated approximation formula at
where the coefficients reflect the initial values of the observables .
With regards to our choice of Besov norms and corresponding multiscale decompositions, we choose to add to the list of canonical observables the decompositions of the quantities
This corresponds to the first conserved quantity of the NLSE, i.e. the energy , while the next two quantities reflect the nonlinearity and dispersion of the NLSE as reflected in the Hamiltonian where
This adds an overall observables to the canonical observables corresponding to finding , which we collectively denote as . Then the extended observables are given by
We denote the Besov-norm enhanced, multiscale DMD as the MDMD. Note, while we have relied on knowing the model to make our decisions, one would very naturally choose these two Besov norms in so far as their affiliated variational derivatives naturally lead one to cubic nonlinearities and Laplacian based dispersion terms, which from a Ginzburg–Landau analysis are very natural leading order effects which emerge across a wide range of models.
At this point, with the choice of and the number of levels across which to perform a wavelet decomposition of the data, it is a nontrivial question to determine parameter choices for optimal performance of the DMD decomposition. To measure this performance, we use two criteria. The first is accuracy of the reconstruction of the given data. The second is that we know the underlying model is a Hamiltonian dynamical system, and thus the affiliated spectra should lie entirely on the imaginary unit circle. We thus define an affiliated error where
where the reconstruction error is given by
and the spectral error is given by
where are the canonical observables not including those computed by Besov Norms measured at the final sampled time point, is the affiliated DMD generated approximation of those same observables computed at the final sampled time point, and is a relative weighting parameter between the two criteria. Thus for , we favor reconstruction accuracy, while for , we favor adherance of the spectra to the unit circle.
Throughout the simulations below then, for given choice of , we use an optimization strategy of sweeping through different choices of and until a minimal error is found. The parameters are swept out over the intervals
Since we examine the role of noise, we also do ensemble runs of where the number of members , which was the largest number of runs which allowed for practical run times of the simulations. Each simulation is run with and for a time step of and up to a time of so that since in this case we have that . The secondary peak in the initial condition is centered at .
Results
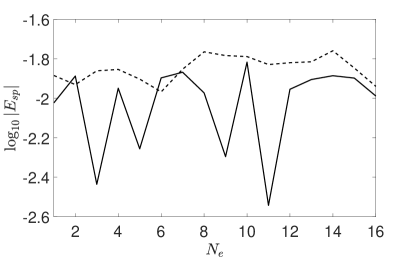
We first look at weighting the error norm in favor of approximation accuracy by choosing for relatively weak perturbations, , and stronger perturbations in which . These results are seen respectively in Figures 1 and 2. For the relatively weak perturbation case, we see the reconstruction error is at times almost an order of magnitude better for the MDMD, while only making a modest sacrifice in the spectral error; see Figures 1 (a) and (b). Moreover, looking at Figures 1 (a) and (b), we see that the MDMD method is able to create a more uniform error in the approximation across the 16 different simulations. As we see in Figure 1 (c), this is done in part by allowing for a higher value of , thereby allowing for the use of more modes emerging from the DMD decomposition, and in part by using to adjust to varying noise profiles in an adaptive way as seen in Figure 1 (d).
For the larger perturbation when , as seen in Figure 2 (a), the classic DMD approach often is incapable of maintaining reconstruction accuracy. While the multiscale approach also can suffer, it is far more reliable than its traditional counterpart. As seen in Figure 2 (b), this better reconstruction accuracy comes at a modest loss of spectral accuracy relative to the traditional DMD, though it should be noted that the reconstruction errors of the traditional DMD are , thus bringing into question the value of it maintaing spectral accuracy. Again, as seen in Figures 2 (b)-(d), the error profile using Besov-norms is slightly better and more uniform, the Besov approach uses more DMD modes, and is chosen in a highly adaptive manner.
 |
 |
| (a) | (b) |
 |
 |
| (c) | (d) |
 |
 |
| (a) | (b) |
 |
 |
| (c) | (d) |
By instead looking at prioritizing the spectral accuracy of the DMD decomposition by setting , we see for both levels of perturbations that the Besov based approach provides strong improvements over standard DMD. While for both levels of the perturbation the MDMD approach provides both better and more uniform levels of reconstruction error, again for the largest perturbation, the standard DMD approach completely breaks down while the multiscale approach is markedly more robust; see Figures 3 (a) and 4 (a). Again this comes at a modest loss of spectral accuracy; see Figures 3 (b) and 4 (b). Thus, the MDMD based approach does not compromise approximation fidelity to the extent that the traditional DMD method does through the enhanced adaptability and better capturing of the dynamics facilitated by the Besov norms which help capture the key nonlinear features of the flow.
 |
 |
| (a) | (b) |
 |
 |
| (c) | (d) |
 |
 |
| (a) | (b) |
 |
 |
| (c) | (d) |
4 Conclusion
As we show, by introducing well chosen norms with ready multiscale decompositions to stand in for various nonlinear effects in a given model, we are able to produce a more robust implementation of the Dynamic-Mode Decomposition. This is done with only a modest increase in computational time and complexity, while the benefits can be an order of magnitude better than otherwise obtainable using standard approaches. Likewise, the added degrees of freedom allow for a greater degree of optimization in choosing a decomposition scheme. How our approach would enhance other DMD approaches currently under development is a question of future research.
References
- [1] I. Mezić. Spectral properties of dynamical systems, model reduction, and decompositions. Nonlinear Dyn., 41:309–325, 2005.
- [2] P. Schmid. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech., 656:5–28, 2010.
- [3] J.N. Kutz, S.L. Brunton, B.W. Brunton, and J.L. Proctor. Dynamic Mode Decomposition: Data-driven modeling of complex systems. SIAM, Philadelphia, PA, 2016.
- [4] K. Taira, S.L. Brunton, S.T.M. Dawson, C.W. Rowley, T. Colonius, B.J. McKeon, O.T. Schmidt, S. Gordeyev, V. Theofilis, and L.S. Ukeiley. Modal analysis of fluid flows: An overview. AIAA, 55:4013–4041, 2017.
- [5] S. Le Clainche and J. M. Vega. Analyzing nonlinear dynamics via data-driven dynamic mode decomposition-like methods. Complexity, 2018:1–21, 2018.
- [6] B.O. Koopman. Hamiltonian systems and transformation in Hilbert space. Proc. Nat. Acad. Sci., 17:315–318, 1931.
- [7] M.O. Williams, I. G. Kevrekidis, and C. W. Rowley. A data-driven approximation of the Koopman operator: extending dynamic mode decomposition. J. Nonlin. Sci., 25:1307–1346, 2015.
- [8] J.N. Kutz, J.L. Proctor, and S.L. Brunton. Applied Koopman theory for partial differential equations and data-driven modeling of spatio-temporal systems. Complexity, 2018:1–16, 2018.
- [9] M. Korda and I. Mezić. On convergence of extended dynamic mode decomposition to the Koopman operator. J. Nonlinear Sci., 28:687–710, 2018.
- [10] M.O. Williams, C. W. Rowley, and I. G. Kevrekidis. A kernel-based method for data driven Koopman spectral analysis. J. Comp. Dyn., 2:247–265, 2015.
- [11] A. M. Degenarro and N. M. Urban. Scalable extended dynamic-mode decomposition using random kernel approximation. SIAM J. Sci. Comp., 41:1482–1499, 2019.
- [12] O. Azencot, W. Yin, and A. Bertozzi. Consistent dynamic mode decomposition. SIAM J. Appl. Dyn. Sys., to appear, 2019.
- [13] T. Askham and J.N. Kutz. Variable projection methods for an optimized dynamic mode decomposition. SIAM J. Appl. Dyn. Sys., 2018:380–416, 2018.
- [14] M. Frazier, B. Jawerth, and G. Weiss. Littlewood–Paley Theory and the Study of Function Spaces. AMS, Providence, RI, 1991.
- [15] G. Folland. Real Analysis: Modern Techniques and Applications. Wiley Interscience, New York, NY, 1999.
- [16] C.W. Curtis, R. Carretero-Gonzalez, and M. Polimeno. Characterizing coherent structures in Bose-Einstein condensates through dynamic-mode decomposition. Phys. Rev. E, 99:062215, 2019.