Enhancing Deep Traffic Forecasting Models with Dynamic Regression
Abstract
Deep learning models for traffic forecasting often assume the residual is independent and isotropic across time and space. This assumption simplifies loss functions such as mean absolute error, but real-world residual processes often exhibit significant autocorrelation and structured spatiotemporal correlation. This paper introduces a dynamic regression (DR) framework to enhance existing spatiotemporal traffic forecasting models by incorporating structured learning for the residual process. We assume the residual of the base model (i.e., a well-developed traffic forecasting model) follows a matrix-variate seasonal autoregressive (AR) model, which is seamlessly integrated into the training process through the redesign of the loss function. Importantly, the parameters of the DR framework are jointly optimized alongside the base model. We evaluate the effectiveness of the proposed framework on state-of-the-art (SOTA) deep traffic forecasting models using both speed and flow datasets, demonstrating improved performance and providing interpretable AR coefficients and spatiotemporal covariance matrices.
Introduction
Traffic forecasting stands as a pivotal task within intelligent transportation systems (ITS), boasting a myriad of applications, including trip planning, travel time estimation, and traffic flow management, among others (Vlahogianni, Karlaftis, and Golias 2014). At its core, this task entails a multivariate and multistep time series forecasting challenge. Imagine a traffic network equipped with sensors, capturing traffic data within a matrix of dimensions over an observation span of . The ultimate objective of traffic forecasting is to anticipate the traffic conditions for future intervals based on the most recent historical intervals.
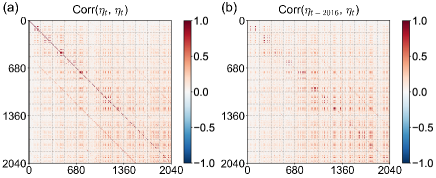
Deep learning (DL) models have gained extensive traction in traffic forecasting due to their adeptness in capturing the intricate nonlinearity and spatiotemporal structures present in traffic data. Noteworthy spatiotemporal forecasting models, including STGCN (Yu, Yin, and Zhu 2018), DCRNN (Li et al. 2018), Graph Wavenet (Wu et al. 2019), and STSGCN (Song et al. 2020), have showcased their prowess. These DL models typically employ mean absolute error (MAE) or mean squared error (MSE) for training, rooted in the assumption that: (i) temporal correlation doesn’t exist among residuals at distinct time points, and (ii) entries within the residual matrix are both independent and isotropic, lacking concurrent correlations. However, these assumptions do not align with real-world datasets. On one hand, the exclusion of pertinent features often leads to time-correlated residuals. For instance, in traffic speed forecasting, significant time-varying factors like weather conditions and vehicle flow rates are frequently disregarded, resulting in temporally correlated residuals. On the other hand, multistep-ahead forecasting implies spatiotemporal correlations within the residual process, contrary to the assumption of independent and isotropic entries. A clear example is the increased variance from the 5-minute-ahead prediction to the 60-minute-ahead prediction. Neglecting these factors could detrimentally impact DL model performance. Demonstrated in Figure 1, the concurrent spatiotemporal correlations, , and the lag-2016 autocorrelation, , extracted from STSGCN (Song et al. 2020) trained on the PEMS08 traffic flow dataset with MAE loss, exhibit clear correlation structures. Notably, significant autocorrelation within could result from the omission of influential covariates, such as traffic congestion information, which has a profound impact on the observed flow (Cheng, Trépanier, and Sun 2021). Incorporating these additional covariates into DL-based traffic forecasting models might seem appealing, but it could introduce an extensive and often unavailable set of covariates, complicating model training. Leveraging the statistical attributes of the residual process presents opportunities to enhance these DL models.
In this study, we introduce a direct and efficacious approach to adjust residual correlations using a dynamic regression framework, flexible for integration with any DL model used in spatiotemporal traffic forecasting. We assume the residual follows a matrix-variate AR process that can be integrated into the original DL model’s training. In addition to learning the AR coefficients, we also effectively learn the full covariance matrix for the error, which is assumed to follow a matrix normal distribution. The parameters of the residual regression module and the error covariance matrices are jointly optimized with the parameters of the base model. The key contributions of this study are summarized as follows:
-
•
We propose to use a bi-linear AR structure for the matrix-valued residuals to address autocorrelation. The interpretability of the AR coefficient matrices allows us to unveil the connection between the current and past residuals.
-
•
We model the error term in the residual AR model using a matrix normal distribution. Its negative log-likelihood is integrated into the loss function for joint optimization. The resulting covariance matrices are interpretable and can be further used to perform probabilistic forecasting with uncertainty quantification.
-
•
The proposed method is model-agnostic. We assess our method across diverse traffic datasets and consistently observe enhancements in several SOTA DL-based traffic forecasting models.
Related Work
Deep Learning for Traffic Forecasting
Here, we review some signature frameworks for DL-based spatiotemporal traffic forecasting models. Starting from the DCRNN framework (Li et al. 2018), modern deep learning models are generally featured with a combination of different neural networks to process the spatial and temporal dependencies in traffic data. For example, DCRNN uses a diffusion convolution operation to model the spatial dependency. The convolution process is integrated into Gated Recurrent Units (GRUs) for modeling temporal dependency. The STGCN framework (Yu, Yin, and Zhu 2018) uses Graph Convolutional Networks (GCNs) to extract spatial correlations and Convolutional Neural Networks (CNNs) to extract temporal correlations. GCNs have the advantage of incorporating graph structure into the spatial modeling process. CNNs can reduce the training time through parallel computing since it avoids the recurrent process in Recurrent Neural Networks (RNNs). Building on STGCN, the ASTGCN framework (Guo et al. 2019) integrates a spatiotemporal attention mechanism to pre-process the traffic data before being fed to the convolutional layers. Both STGCN and ASTGCN use a pre-calibrated adjacency matrix that cannot be jointly learned with the model. The Graph WaveNet framework (Wu et al. 2019) uses an adaptive adjacency matrix to learn the graph structure. The entries in the adjacency matrix are treated as trainable parameters in the optimization. Dilated causal convolution is used as Temporal Convolutional Networks (TCNs) to model temporal dependency and GCNs are used to model spatial dependency. Prior GCN-based architectures process spatial information and temporal information separately. Song et al. proposed the STSGCN framework (Song et al. 2020) to learn spatial and temporal information simultaneously by connecting individual spatial graphs of adjacent time steps into one graph. STSGCN has shown superior performance to the previous GCN-based frameworks. Other SOTA models include GMAN (Zheng et al. 2020), N-BEATS (Oreshkin et al. 2020), and FC-GAGA (Oreshkin et al. 2021), to name a few.
Adjusting for Correlated Residuals
Autocorrelated residuals in time series data have been extensively studied in econometrics, utilizing models with exact forms (Durbin and Watson 1950; Ljung and Box 1978; Breusch 1978; Godfrey 1978; Cochrane and Orcutt 1949; Prais and Winsten 1954; Beach and MacKinnon 1978). As DL models advance rapidly, the matter of how to learn and adapt the residual process has garnered notable attention in recent research. Two primary statistical approaches exist for modeling the residual process: (i) capturing autocorrelation, and (ii) learning concurrent correlation in independent errors.
To address autocorrelation, Sun, Lang, and Boning (2021) proposed a reparametrization strategy for the input and output of a neural network used in time series forecasting. This reparametrization inherently employs a first-order residual AR process through a linear regression framework. The method effectively enhances performance for various DL-based one-step-ahead forecasting models across a diverse range of time series datasets, enabling joint parameter optimization of both base and residual regressors. Additionally, Kim et al. (2022) introduced a lightweight DL module designed to calibrate residual autocorrelation within predictions from pre-trained traffic forecasting models. This calibration module employs recent observed residuals and predictions to anticipate future residuals, ultimately enhancing the performance of numerous traffic forecasting models, especially on traffic speed datasets.
Regarding learning concurrent correlation, Jia and Benson (2020) emphasized that assuming independence in residuals of a node regression problem is unwarranted. They advocated modeling concurrent correlation using a multivariate Gaussian distribution. This method, termed residual propagation in Graph Neural Networks (GNNs), adjusts predictions of unknown nodes based on known node labels. Similarly, Huang et al. (2021) introduced a correct-and-smooth approach, serving as a post-processing scheme to rectify correlated residuals in GNNs, focusing on a classification task. Additionally, Choi et al. (2022) proposed a dynamic mixture of matrix normal Gaussian as a regularization technique to address concurrent spatiotemporal correlation within residuals.
Traffic forecasting entails a multivariate sequence-to-sequence (Seq2Seq) framework entwined with strong seasonality, rendering direct applicability challenging. The primary obstacle lies in the residual process, which transforms into an matrix-variate time series, characterized by conspicuous temporal dynamics and a structured error covariance. The cohesive learning of this process and the base DL model constitutes a pivotal challenge.
Our work differs from Sun, Lang, and Boning (2021) and Kim et al. (2022) in several important ways. Firstly, we extend the scope of Sun, Lang, and Boning (2021) to encompass multivariate Seq2Seq forecasting, while also bypassing the need for input and output reparametrization. Secondly, our approach allows for the concurrent optimization of both the residual regression module and the base model, in contrast to the post-hoc adjustment presented by Kim et al. (2022). Lastly, we investigate the presence of seasonal autocorrelation, a substantial element in traffic forecasting, setting our work apart from the aforementioned studies.
Methodology
This section introduces the formulation of a multivariate Seq2Seq traffic forecasting problem and outlines the dynamic regression framework for characterizing residual autocorrelation.
Traffic Forecasting
A traffic network can be defined as a directed graph , where with is a set of nodes representing traffic sensors; is a set of links connecting these nodes; is a weighted adjacency matrix characterizing the proximity of nodes. Denote by the vector of observed traffic states at time . The traffic forecasting problem aims to learn a function that maps data from past steps to the prediction of future steps.
Denote by and , we have
| (1) |
where is a Seq2Seq DL model that generates the predicted mean and is a zero-mean residual process. In many cases, is trained with MSE as the loss function:
| (2) |
This loss function simply assumes: (i) is temporally independent, i.e., there is no correlation between and when ; and (ii) entries in follow an isotropic Gaussian with no concurrent correlations, i.e., . Likewise, using MAE as the loss function corresponds to assuming entries in follow a Laplacian distribution.
Modeling Residual with Matrix-valued Autoregression
Following the idea of dynamic regression (Hyndman and Athanasopoulos 2018), we assume that the relationship between the input and the output has not been fully captured by , and the unexplained residual is governed by a temporal process. For example, for a one-step-ahead prediction model (i.e., as ), it is straightforward to model using a -th order vector autoregressive model:
| (3) |
where () are the regression coefficient, and is an independent white-noise process.
However, for a Seq2Seq model with , the residual at time cannot be directly modeled using Eq. (3), as the residuals, , will not be entirely accessible due to overlapping. To address this issue, we instead try to model the relation between and those lagged residuals that are accessible, i.e., for as long as . Therefore, we have the model for the vector as:
| (4) |
where and the size of the white-noise covariance matrix is also of size . As traffic data often shows strong day-to-day and week-to-week similarity, for simplicity we only introduce a single lagged residual component , where is a predetermined seasonal lag (e.g., one day or one week) showcasing pronounced correlations with the present time.
However, a notable limitation of the aforementioned formulation is the introduction of an excessive number of parameters within and . For improved scalability of this approach, we assume the follows a bi-linear autoregressive model (Chen, Xiao, and Yang 2021; Hsu, Huang, and Tsay 2021):
| (5) |
where and are regression coefficients, and follows an independent matrix white-noise process. The vectorized version of Eq. (5) becomes
| (6) |
and we can see that the bi-linear formulation is equivalent to imposing a Kronecker product structure on the coefficient matrix in Eq. (4), leading to a significant reduction in the parameters. Combining Eqs. (1) and (5), we can construct an improved loss function, such as MAE, on instead of :
| (7) |
| (8) |
where and , as trainable parameters, can be jointly updated with the base model . When and have no relations (e.g., when ), collapse to the default MAE loss used in existing DL models. If both and are identity matrices, the model corresponds to assuming the residual process follows a seasonal random walk. To promote sparsity in and , we also introduce an regularization term into the loss function:
| (9) |
Once and coefficients and are learned, prediction at time can be made by:
| (10) |
Spatiotemporal Covariance Structure for the Matrix White Noise
We next try to consider the concurrent spatiotemporal correlation among entries in the white noise through learning its covariance matrix . The key challenge here is the large size (i.e., ) of . For model scalability, we follow Choi et al. (2022) and assume to follow a zero-mean matrix normal distribution with
| (11) |
where and are covariance matrices of the matrix normal distribution capturing the correlation across forecasting steps and spatial locations. The negative log-likelihood of this distribution is included in the loss function to facilitate joint optimization:
| (12) | ||||
As we have to calculate the inverse and determinant of , , we parameterize the precision matrix (i.e., the inverse of the covariance matrix) directly to circumvent numerical problems. Another benefit of parameterizing precision matrices lies in their ability to model conditional independence between two variables, based on the observations of other variables. This modeling introduces zero elements in precision matrices when two variables are conditionally independent, resulting in significantly sparse matrices that augment the scalability of our approach. The tangible interpretation of a precision matrix signifies the lack of an edge connecting two nodes in a graph when they are conditionally independent (Adametz and Roth 2014). This characteristic holds special importance in the realm of traffic forecasting, where each traffic sensor is typically connected to a limited number of other sensors.
In this paper, we consider the Cholesky decomposition of the precision matrix as trainable parameters following Choi et al. (2022):
| (13) |
where and are lower-triangular Cholesky factors (as trainable parameters) that can be jointly optimized with other model parameters. The determinant can be conveniently calculated by summing the logarithm of diagonal entries of the lower triangular Cholesky factors:
| (14) |
In addition, the trace can be simplified into
| (15) | ||||
where . Substitute Eq. (14) and Eq. (15) into Eq. (12), we obtain a probabilistic loss function to learn the correlation structure in :
| (16) |
As the covariance matrix determines the concurrent spatiotemporal correlations in , we posit that it will not only improve model accuracy but also provide better uncertainty quantification when performing probabilistic forecasting.
Experiments
To assess the effectiveness of our proposed approach, we conduct experiments on three distinct traffic datasets: PEMSD7 (M), PEMS03, and PEMS08. PEMSD7 (M) is a highway traffic speed dataset initially employed in STGCN (Yu, Yin, and Zhu 2018). PEMS03 and PEMS08 represent highway traffic flow data originally utilized in ASTGCN (Guo et al. 2019) and STSGCN (Song et al. 2020), respectively. We follow the identical data processing procedures outlined in the original studies. For PEMS03 and PEMS08, we allocate 60% of the data for training, 20% for validation, and the remaining 20% for testing. As for PEMSD7 (M), the split ratio is 7:1:2. Across all datasets, we apply z-score normalization using statistics derived from the training set. Further details regarding the datasets are summarized in Table 1.
| Datasets | #Nodes | #Time Steps | Resolution |
|---|---|---|---|
| PEMSD7 (M) | 228 | 12,672 | 5 min |
| PEMS03 | 358 | 26,208 | 5 min |
| PEMS08 | 170 | 17,856 | 5 min |
Baselines
Aligned with the chosen datasets for method validation, we assess our approach using the following models as the base model .
-
•
STGCN (Yu, Yin, and Zhu 2018): Spatiotemporal graph convolutional network, which uses ChebNet to process spatial correlation and CNNs to process temporal correlation.
-
•
ASTGCN (Guo et al. 2019): Attention-based spatiotemporal graph convolutional network, which attaches spatial and temporal attention mechanisms to STGCN for learning dynamic spatial-temporal correlations of traffic data.
-
•
STSGCN (Song et al. 2020): Spatial-temporal synchronous graph convolutional network that captures spatial-temporal correlations over the time axis.
-
•
Graph WaveNet (Wu et al. 2019): A spatiotemporal forecasting model that combines dilated 1D convolution for modeling temporal dynamics and graph convolution for modeling spatial dynamics.
Experimental Setup
Our experimental setup involved a computer environment featuring an Intel(R) Xeon(R) CPU E5-2698 v4 @ 2.20GHz and four NVIDIA Tesla V100 GPUs. Baseline models were implemented using either the original source code or their PyTorch versions. All models were configured to employ 12 historical observation steps () for predicting 12 future steps (). During training, the Adam optimizer was utilized with an initial learning rate of 0.001 and a weight decay of 0.0001. To prevent overfitting, early stopping was employed when the validation loss showed consistent increase over 30 epochs. All reported outcomes are based on the average of evaluation metrics derived from three independent runs.
For the residual AR process, we need to determine the lag length and the initialization of the regression coefficients and . Since traffic data is featured with strong local correlation and seasonality, we mainly consider the correlation between the current residual and its 1) most recent available predecessor (); 2) counterpart one day apart (); and 3) counterpart one week apart (). The inclusion of seasonal residual correlation is novel to prior works (Sun, Lang, and Boning 2021; Kim et al. 2022). Regarding the initialization of and , we attempt three different settings: 1) random. and consist of random numbers sampled from a normal distribution with mean 0 and variance 1; 2) zeros. and are zero matrices; 3) diagonal. and are diagonal matrices. The initial values of parameters in these settings are scaled down to very small numbers so that the model is nearly equivalent to the original model at the beginning of the training stage. Based on the preliminary observation of autocorrelation matrices, we used for PEMSD7 (M), for PEMS03, and for PEMS08. For the initialization, we chose “random” and “zeros” for STGCN and Graph WaveNet on PEMSD7 (M), “diagonal” for PEMS03, and “random” for PEMS08. For the parameters of the matrix normal distribution in section Spatiotemporal Covariance Structure for the Matrix White Noise, the matrices and consist of random numbers sampled from a normal distribution with mean 0 and variance 1. The Softplus function is applied to enforce positive diagonals of and .
The final loss function is composed of three parts:
| (17) |
where and are the MAE loss built on Eq. (8) and the regularization in Eq. (9), respectively, is the probabilistic loss term in Eq. (16), and and are weight parameters. We set , and use for PEMSD7 (M) and PEMS03, for PEMS08. The evaluation metrics are MAE and RMSE. Missing values are excluded from both training and testing.
In comparison to the base model, the proposed method introduces four additional learnable parameters, i.e., , , and two lower-triangular Cholesky factors and . Nevertheless, the size of additional parameters is almost negligible compared to the overall size of the base model.
Experimental Results

We begin by demonstrating both the autocorrelation and the concurrent spatiotemporal correlations of the residuals from an original traffic forecasting model. We calculate two types of correlation: and . is the concurrent spatiotemporal correlation of the variables in , while is the autocorrelation at lag . Ideally, if the residuals are independently sampled from an isotropic distribution, should be an identity matrix and should be a zero matrix. In Figure 2, we present the residual correlation matrices of PEMS08 using the results from Graph WaveNet. We can observe that is not diagonal, suggesting there exists spatial and across-step correlations in the residuals. In terms of , we examine different values including (1 hour), (1 day), and (1 week). Interestingly, we find that provides the strongest autocorrelation patterns, while correlations with and are weak. We believe this is mainly due to the fact that traffic flow is heavily determined by travel demand, which often exhibits prominent weekly periodicity. Therefore, we choose for the residual AR process for PEMS08.
| Data | Model | 1-step | 3-step | 6-step | 12-step | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | |||
| PEMSD7 | STGCN | w/o | 2.70 | 5.01 | 3.03 | 5.61 | 3.49 | 6.54 | 4.26 | 8.04 |
| w/ | 2.39 | 3.65 | 2.78 | 4.53 | 3.35 | 5.80 | 4.41 | 7.72 | ||
| Graph WaveNet | w/o | 1.29 | 2.20 | 2.12 | 3.97 | 2.74 | 5.37 | 3.33 | 6.58 | |
| w/ | 1.28 | 2.17 | 2.12 | 3.96 | 2.72 | 5.33 | 3.26 | 6.43 | ||
| PEMS03 | STSGCN | w/o | 13.49 | 21.93 | 15.54 | 25.44 | 17.63 | 29.00 | 21.73 | 35.26 |
| w/ | 13.38 | 21.55 | 15.31 | 24.82 | 17.34 | 28.00 | 21.15 | 33.66 | ||
| Graph WaveNet | w/o | 12.44 | 21.03 | 13.77 | 23.91 | 14.94 | 25.99 | 16.68 | 28.52 | |
| w/ | 12.25 | 20.56 | 13.54 | 23.22 | 14.67 | 25.35 | 16.42 | 28.03 | ||
| PEMS08 | STSGCN | w/o | 13.84 | 21.29 | 15.74 | 24.47 | 17.61 | 27.70 | 21.50 | 33.66 |
| w/ | 13.81 | 21.22 | 15.61 | 24.26 | 17.36 | 27.21 | 20.82 | 32.15 | ||
| ASTGCN | w/o | 13.97 | 21.21 | 16.12 | 24.60 | 17.95 | 27.38 | 21.57 | 32.50 | |
| w/ | 13.79 | 21.13 | 15.36 | 23.87 | 16.27 | 25.77 | 17.99 | 28.87 | ||
| Graph WaveNet | w/o | 12.81 | 19.95 | 13.92 | 22.17 | 15.04 | 24.29 | 16.74 | 26.80 | |
| w/ | 11.66 | 19.45 | 12.58 | 21.45 | 13.46 | 23.24 | 14.76 | 25.49 | ||

Table 2 presents a comprehensive summary of our approach’s performance across diverse DL models and datasets, spanning prediction horizons of 1-step, 3-step, 6-step, and 12-step ahead. Notably, our method consistently yields superior outcomes across nearly all scenarios. Graph WaveNet’s exceptional performance is particularly noteworthy, primarily stemming from its implementation of the adaptive adjacency matrix. Upon adopting our approach, Graph WaveNet demonstrates substantial additional enhancement, even in scenarios where the original models already excel, such as the 1-step ahead prediction. A case in point is the 1-step MAE of Graph WaveNet on PEMS08, which decreases from 12.81 to 11.66, signifying the presence of explainable factors eluding the original model’s grasp.
Figure 3 visually illustrates the marked reduction in both concurrent spatiotemporal correlation and autocorrelation, when compared to Figure 2. Notably, our approach exhibits amplified enhancement for models manifesting stronger residual correlations, such as STSGCN and ASTGCN, with particularly pronounced benefits observed for the 12-step ahead prediction. For example, the 12-step MAE of ASTGCN on PEMS08 decreases from 21.57 to 17.99. These diverse yet discernible improvements underscore that our method’s efficacy is contingent upon the degree of autocorrelation inherent in the original models’ residuals, alongside the suitability of the matrix normal distribution assumption in characterizing errors.
Ablation Study
| Model | 1-step | 3-step | 6-step | 12-step | ||||
|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | |
| Graph WaveNet | 12.81 | 19.95 | 13.92 | 22.17 | 15.04 | 24.29 | 16.74 | 26.80 |
| Our method | 11.66 | 19.45 | 12.58 | 21.45 | 13.46 | 23.24 | 14.76 | 25.49 |
| Our method w/o | 11.79 | 19.59 | 12.73 | 21.61 | 13.65 | 23.46 | 15.04 | 25.78 |
| Our method w/o AR | 12.66 | 19.76 | 13.79 | 21.89 | 14.85 | 23.79 | 16.50 | 26.31 |
To dissect the individual impact of the two components of our proposed DR framework, we conducted comparative analyses using either the residual AR module or the error covariance learning module in isolation (Table 3). “w/o ” represents the variant excluding the negative log-likelihood loss of the error from the loss function. “w/o AR” denotes the variant employing matrix normal distribution to characterize directly, bypassing the application of the residual AR process. Using Graph WaveNet and PEMS08 as an example, where both autocorrelation and spatiotemporal correlation are prominent (Figure 2), we observe from Table 3 that the model attains its optimal performance when both components are employed. While model variants featuring a single component still surpass the original model, the outcomes substantiate the concurrent efficacy of the two components in collectively refining model accuracy. Notably, in this specific context, the model derives more pronounced benefits from the residual AR process, as evidenced by the higher accuracy of the ”w/o ” variant compared to the ”w/o AR” model.
Model Interpretation


We proceed by explaining our findings through visualizations of the coefficient matrices ( and ) along with the covariance matrices ( and ). Figure 4 showcases the coefficient matrices of the residual AR module in Graph WaveNet on PEMS08. In Figure 4 (a), the correlations between residuals from different spatial locations are depicted, revealing that most spatial locations exhibit strong self-correlations, as indicated by the prominent diagonal. Intriguingly, certain locations display strong correlations with residuals from other locations. Figure 4 (b) further highlights a pronounced diagonal in matrix . Given that signifies the column effect of the past residual on , the current residual showcases the highest correlation with the past residual at the corresponding forecasting step.
Figure 5 presents the acquired covariance matrices based on the precision matrices obtained for Graph WaveNet on PEMSD7 (M). The covariance matrix (Figure 5 (a)) encapsulates the covariance across the prediction horizon, which we can observe that the diagonal elements of progressively expand with the prediction step, an intuitively rational behavior for multistep prediction tasks. Furthermore, the visualization reveals a discernible propagation of errors in the extended prediction period, evidenced by the elevated covariance between consecutive prediction steps. In Figure 5 (b), the covariance of residuals from different spatial locations is depicted. Evidently, specific covariance structures materialize among adjacent locations, underscoring the existence of inherent relationships. Such characterization of inter-step and spatial correlations plays a pivotal role in regularizing the optimization process, ultimately enhancing the capacity to effectively model the residual distribution.
Conclusion
In this paper, we present a DR framework to enhance existing deep spatiotemporal models for traffic forecasting, which assumes that the residual is independent with no concurrent spatiotemporal correlation. Our key idea is to properly account for the temporal dependencies in the residual process by modifying the loss function, and this method can be easily integrated into any existing DL model. For simplicity, we model the residual process as a first-order matrix-variate seasonal autoregressive model. This method introduces several additional parameters in DR, including , , and , which can be jointly learned with the base forecasting model. Through extensive experiments on several SOTA traffic forecasting models using real-world traffic speed and traffic flow datasets, we demonstrate the effectiveness of the proposed methods. We also show that the learned parameters in DR are interpretable with clear physical and statistical meaning, and the learned covariance matrix can also facilitate probabilistic forecasting with uncertainty quantification. To our knowledge, the proposed method represents an initial effort in concurrently addressing the spatiotemporal correlation of residuals within Seq2Seq DL models for multistep traffic forecasting. Despite being primarily designed for traffic forecasting, we believe this method can be adapted for a wide range of spatiotemporal forecasting problems characterized by datasets showcasing specific seasonal patterns, such as predicting daily weather and climatology variables.
Acknowledgments
We acknowledge the support of the Natural Sciences and Engineering Research Council of Canada (NSERC). V. Z. Zheng acknowledges the support received from the FRQNT B2X Doctoral Scholarship Program.
References
- Adametz and Roth (2014) Adametz, D.; and Roth, V. 2014. Distance-based network recovery under feature correlation. Advances in Neural Information Processing Systems, 27.
- Beach and MacKinnon (1978) Beach, C. M.; and MacKinnon, J. G. 1978. A maximum likelihood procedure for regression with autocorrelated errors. Econometrica: journal of the Econometric Society, 51–58.
- Breusch (1978) Breusch, T. S. 1978. Testing for autocorrelation in dynamic linear models. Australian Economic Papers, 17(31): 334–355.
- Chen, Xiao, and Yang (2021) Chen, R.; Xiao, H.; and Yang, D. 2021. Autoregressive models for matrix-valued time series. Journal of Econometrics, 222(1): 539–560.
- Cheng, Trépanier, and Sun (2021) Cheng, Z.; Trépanier, M.; and Sun, L. 2021. Incorporating travel behavior regularity into passenger flow forecasting. Transportation Research Part C: Emerging Technologies, 128: 103200.
- Choi et al. (2022) Choi, S.; Saunier, N.; Zheng, V. Z.; Trepanier, M.; and Sun, L. 2022. Scalable Dynamic Mixture Model with Full Covariance for Probabilistic Traffic Forecasting. arXiv preprint arXiv:2212.06653.
- Cochrane and Orcutt (1949) Cochrane, D.; and Orcutt, G. H. 1949. Application of least squares regression to relationships containing auto-correlated error terms. Journal of the American Statistical Association, 44(245): 32–61.
- Durbin and Watson (1950) Durbin, J.; and Watson, G. S. 1950. Testing for serial correlation in least squares regression: I. Biometrika, 37(3/4): 409–428.
- Godfrey (1978) Godfrey, L. G. 1978. Testing against general autoregressive and moving average error models when the regressors include lagged dependent variables. Econometrica: Journal of the Econometric Society, 1293–1301.
- Guo et al. (2019) Guo, S.; Lin, Y.; Feng, N.; Song, C.; and Wan, H. 2019. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting. In AAAI Conference on Artificial Intelligence, volume 33, 922–929.
- Hsu, Huang, and Tsay (2021) Hsu, N.-J.; Huang, H.-C.; and Tsay, R. S. 2021. Matrix autoregressive spatio-temporal models. Journal of Computational and Graphical Statistics, 30(4): 1143–1155.
- Huang et al. (2021) Huang, Q.; He, H.; Singh, A.; Lim, S.-N.; and Benson, A. R. 2021. Combining label propagation and simple models out-performs graph neural networks. In International Conference on Learning Representations.
- Hyndman and Athanasopoulos (2018) Hyndman, R. J.; and Athanasopoulos, G. 2018. Forecasting: Principles and Practice. OTexts.
- Jia and Benson (2020) Jia, J.; and Benson, A. R. 2020. Residual correlation in graph neural network regression. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, 588–598.
- Kim et al. (2022) Kim, D.; Cho, Y.; Kim, D.; Park, C.; and Choo, J. 2022. Residual Correction in Real-Time Traffic Forecasting. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management, 962–971.
- Li et al. (2018) Li, Y.; Yu, R.; Shahabi, C.; and Liu, Y. 2018. Diffusion convolutional recurrent neural network: Data-driven traffic forecasting. In International Conference on Learning Representations.
- Ljung and Box (1978) Ljung, G. M.; and Box, G. E. 1978. On a measure of lack of fit in time series models. Biometrika, 65(2): 297–303.
- Oreshkin et al. (2021) Oreshkin, B. N.; Amini, A.; Coyle, L.; and Coates, M. J. 2021. FC-GAGA: Fully Connected Gated Graph Architecture for spatio-temporal traffic forecasting. In AAAI Conference on Artificial Intelligence.
- Oreshkin et al. (2020) Oreshkin, B. N.; Carpov, D.; Chapados, N.; and Bengio, Y. 2020. N-BEATS: Neural basis expansion analysis for interpretable time series forecasting. In International Conference on Learning Representations.
- Prais and Winsten (1954) Prais, S. J.; and Winsten, C. B. 1954. Trend estimators and serial correlation. Technical report, Cowles Commission discussion paper Chicago.
- Song et al. (2020) Song, C.; Lin, Y.; Guo, S.; and Wan, H. 2020. Spatial-temporal synchronous graph convolutional networks: A new framework for spatial-temporal network data forecasting. In AAAI Conference on Artificial Intelligence, volume 34, 914–921.
- Sun, Lang, and Boning (2021) Sun, F.-K.; Lang, C.; and Boning, D. 2021. Adjusting for autocorrelated errors in neural networks for time series. Advances in Neural Information Processing Systems, 34: 29806–29819.
- Vlahogianni, Karlaftis, and Golias (2014) Vlahogianni, E. I.; Karlaftis, M. G.; and Golias, J. C. 2014. Short-term traffic forecasting: Where we are and where we’re going. Transportation Research Part C: Emerging Technologies, 43: 3–19.
- Wu et al. (2019) Wu, Z.; Pan, S.; Long, G.; Jiang, J.; and Zhang, C. 2019. Graph wavenet for deep spatial-temporal graph modeling. In Proceedings of the 28th International Joint Conference on Artificial Intelligence, 1907–1913. AAAI Press.
- Yu, Yin, and Zhu (2018) Yu, B.; Yin, H.; and Zhu, Z. 2018. Spatio-temporal graph convolutional networks: a deep learning framework for traffic forecasting. In Proceedings of the 27th International Joint Conference on Artificial Intelligence, 3634–3640. AAAI Press.
- Zheng et al. (2020) Zheng, C.; Fan, X.; Wang, C.; and Qi, J. 2020. Gman: A graph multi-attention network for traffic prediction. In AAAI Conference on Artificial Intelligence, volume 34, 1234–1241.