Enhancement of superconductivity and its relation to lattice expansion in InTe

Superconductivity has been the subject of continuous research since its discovery more than a century ago in 1911 by Kammerling-Onnes [1]. Despite its long history, the question of what governs and how to control the superconducting transition temperature $T_{\rm c}$ is still a tempting issue. Even in conventional Bardeen-Cooper-Schrieffer (BCS) superconductors, while seemingly well understood theoretically, there are various strategies how to enhance $T_{\rm c}$ discussed in the literature. According to the BCS theory [2], larger $T_{\rm c}$ values are expected for enhanced phonon frequencies involved in Cooper pairing, an enhanced density of states (DOS) at the Fermi level $E_{\rm F}$, and an increased electron-phonon interaction. Soon after, Anderson pointed out that $T_{\rm c}$ in conventional superconductors is barely affected by nonmagnetic impurity scattering and weak disorder [3]. Nevertheless, there are theoretical works where such imperfections are discussed to bear the potential to enhance $T_{\rm c}$ [4, 5]. Also, the valence-skipping feature of some elements is considered to be capable of improving the superconducting pairing interaction via the so-called negative-$U$ mechanism, as pointed out by Varma [6, 7]. Doping is one common approach to exploit these mechanisms, which all work within a BCS framework. Another versatile way to control $T_{\rm c}$ is by applying physical pressure $p$, which may enhance or suppress $T_{\rm c}$, depending on the particular system. Physical pressure is an experimental tool to manipulate solely the unit-cell volume without introducing disorder into the system, which was already phenomenologically discussed by Matthias and others in the 1950s [8, 9]: Arguably, an expanded lattice is often in favor of yielding larger $T_{\rm c}$ values as compared to compressed lattices.

Against this background, cubic InTe is an interesting superconductor: In is one of these valence-skipping elements found in the periodic table. At first glance, it should take its divalent state here, given the strong electron affinity of Te which tends to be in its $2-$ state. However, In²⁺ is energetically unstable [10, 7, 11, 12] and usually takes its $1+$ or $3+$ state. A direct correlation between changes in $T_{\rm c}$ and the In content $x$ in In_xTe was reported in the past but only phenomenologically explained in terms of a changing ratio of In¹⁺ and In³⁺ ions with $x$ [10, 13]. As reported recently [12], the overall In valence state is likely to be close to $1+$ in InTe.

In this paper, to elucidate the microscopic mechanism that governs $T_{\rm c}$, we vary the In concentration $0.84\leq x\leq 1$ in In_xTe. This enables a very fine-tuned and systematic control of $T_{\rm c}$ from around 1.3 K to about 3.5 K. This composition control allows to study the interrelation of DOS, phonon frequencies, electron-phonon interaction, and lattice expansion by simply changing $x$. Here, we observe an interesting crossover in the nature of the superconductivity around $x\sim 0.92$ where $T_{\rm c}$ has increased to about 2.2 K: Initially this enhancement can be traced back to a concomitant increase of DOS with $x$ as it is often seen in conventional superconductors. However, above $x\gtrsim 0.92$, the DOS enhancement becomes gradual and, hence, solely DOS-based arguments cannot explain the observed continued enhancement of $T_{\rm c}$ up to $x=1$. The only material parameter which keeps changing is the cubic InTe lattice constant $a_{c}$, as presented in Fig. 1(b). This suggests that the lattice expansion is dominant for the $T_{\rm c}$ enhancement for $x\gtrsim 0.92$ in In_xTe. For this In concentration range $0.92<x\leq 1$, we develop a simple model with the cubic lattice parameter as only variable. It successfully reproduces qualitatively and quantitatively the experimental evolution of DOS, electron-phonon coupling constant $\lambda_{\rm el-ph}$, and $T_{\rm c}$ with $x$. A lattice-expansion-induced enhancement of the electron-phonon coupling strength is proposed to be responsible for the observed enhancement of $T_{\rm c}$ in this $x$ range.

This paper is organized as follows: After summarizing the experimental and computational methods in the next Section II, we present experimental results in Section III. Our theoretical model is introduced in Section IV. In Section V, theoretical and experimental results for $x>0.92$ are compared and we discuss possible origins of the continuous enhancement of $T_{\rm c}$ and its fine-tuned controllability via the composition ratio. We conclude with summarizing this work. Additional data and discussions are provided in the accompanying Supplemental Materials (SM) [14].

In_xTe batches with $0.84\leq x\leq 1$ were grown by melting stoichiometric amounts of In and Te shots in evacuated quartz glass tubes at 950^∘C for 24 – 48 h, and subsequently quenching into water. The resulting tetragonal InTe material was ground again and approximately 400 mg powder of each batch were used for high-pressure synthesis (5 GPa, 600^∘C, 1 h) to obtain the metastable superconducting phase of InTe with cubic structure at ambient conditions.

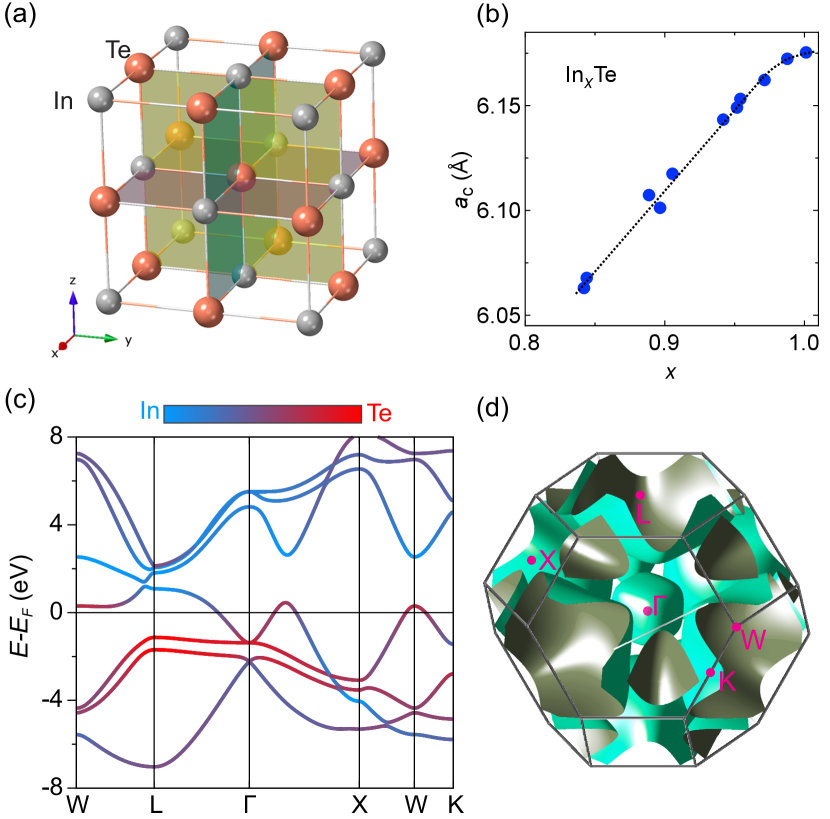
X-ray diffraction patterns were taken on these batches with an in-house x-ray diffractometer (Rigaku). All batches with $x>0.85$ were found to be single-phase cubic InTe (space group 225; $Fm\bar{3}m$) with sharp reflection peaks, see Figs. S1 and S2 in [14]. Estimated cubic lattice constants $a_{c}$ are plotted against $x$ in Fig. 1(b), exhibiting a linear variation with a saturation tendency when approaching $x=1$. Only for the lowest In concentration $x=0.84$ very tiny impurity peaks are seen, possibly indicating the start of the formation of other phases. To further check this, we also made one test specimen with $x=0.79$, where these and additional impurity peaks are more pronounced. This apparently indicates the lower border of stability of cubic In_xTe, which seems also reflected in a slight broadening of the peak widths, cf. Section S1 in [14] for a brief discussion. One might also suspect that reducing the In content in In_xTe causes antisite defects. However, a careful analysis of our XRD data shows that even for large In deficiency, Te remains on its regular lattice sites without forming antisite defects down to $x=0.84$, see Fig. S3 in [14].

The In concentration of all batches was checked by inductively coupled plasma atomic-emission spectroscopy (ICP-AES) chemical analyses. The results are close to the nominal values, cf. Section S2 in [14]. Throughout the paper, the ICP results are used when referring to samples.

The superconducting critical temperatures $T_{\rm c}$ of all samples were determined by temperature-dependent magnetization $M(T)$ measurements (magnetic property measurement system MPMS3 equipped with a ³He insert, Quantum Design). Data were taken upon heating in $B=10$ G after zero-field cooling to the base temperature. All samples exhibit sharp single superconducting transitions. The shielding fractions were roughly corrected for the demagnetization effect according to Ref. [15]. Our data suggest large superconducting phase fractions close to 100%. In magnetization measurements, $T_{\rm c}$ is defined as the intersection of a linear extrapolation of the transition in $M(T)$ with the normal-state signal, cf. Section S3 in [14].

Resistivity $\rho_{xx}$ and specific heat $c_{p}$ were measured on selected samples by a standard four-probe technique and relaxation method, respectively (physical property measurement system PPMS equipped with a ³He insert, Quantum Design). In these measurements, $T_{\rm c}$ is either defined as the temperature at which the resistivity drops to zero, or as midpoint of the superconducting transition in the electronic specific heat divided by temperature $c_{\rm el}/T$, cf. Section S4 in [14]. Measurements of the resistivity under hydrostatic pressure up to approximately 2.25 GPa were performed with a clamp-type pressure cell mounted to a PPMS sample puck (pressure cell HPC-33, ElectroLab Corporation, pressure medium: Daphne 7373 oil). The applied pressure was determined from the suppression of the superconducting $T_{\rm c}$ of a simultaneously measured Pb standard sample.

The electronic and vibrational properties of InTe were calculated within density functional theory [16] using Perdew-Burke-Ernzerhof exchange-correlation functional [17] and ultrasoft pseudo-potentials as implemented in the Quantum Espresso program package [18, 19, 20]. The plane-wave cut-off energy was set to 35 Ry. The relativistic effects, including spin-orbit coupling, were fully considered. An fcc lattice with a variable lattice constant was chosen for InTe. The corresponding Brillouin zone (BZ) was sampled by a 24$\times$24$\times$24 $k$-mesh. The phonon modes, Eliashberg spectral function $\alpha^{2}F(\omega)$, and electron-phonon coupling constant $\lambda_{\rm el-ph}$ were computed using density-functional perturbation theory employing a $4\times 4\times 4$ $q$-mesh. The calculation of the superconducting transition temperature $T_{\rm c}$ was done by means of Mc-Millan’s equation modified by Allen and Dynes [21, 22] using the screened Coulomb potential $\mu^{*}=0.1$.

A schematic plot of the face-centered cubic structure of superconducting InTe is shown in Fig. 1(a) [23, 24]. Each Te is octahedrally coordinated with six In ions as its first-nearest neighbors (1NN). The second-nearest neighbors are twelve Te ions, forming cuboctahedral coordination. Te as an anion needs two electrons to complete its $5p$ shell. The In cations can afford to transfer one electron to their 1NN [12]. To satisfy this situation, hybridization takes place and InTe forms a metallic band structure with a mixed ionic character at and near the Fermi level $E_{\rm F}$, cf. Fig. 1(c). Due to the significant In – Te hybridization, many bands exhibit sizable bonding-antibonding dispersions. Accordingly, this creates several energy valleys, appearing as separated electron and hole pockets in the BZ of InTe as sketched in Fig. 1(d). The only electron pocket is centered at the $\Gamma$ point, whereas the major hole pockets span the BZ around its L points.

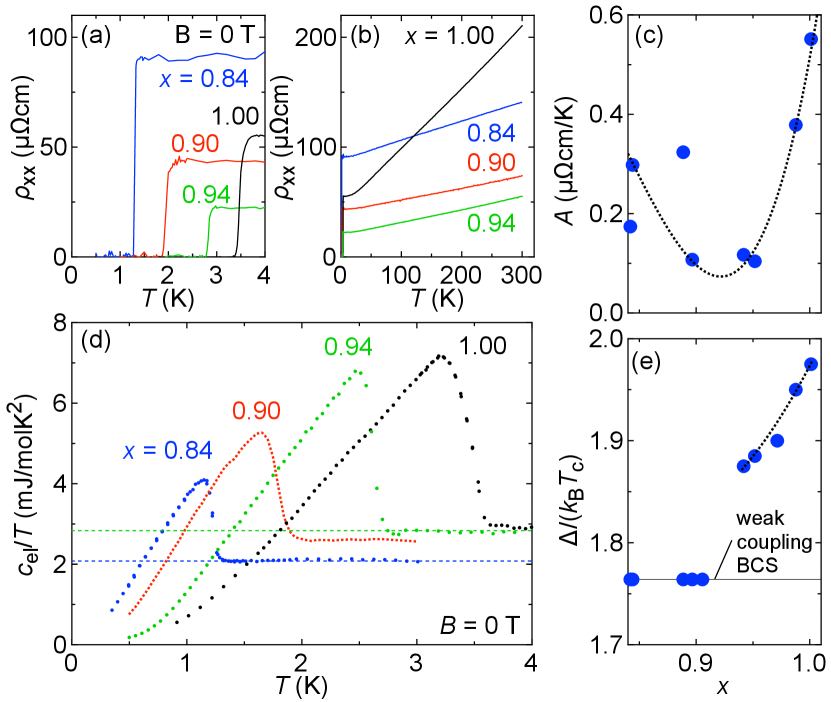
Figure 2 summarizes resistivity and specific-heat data along with fitting results of these quantities on selected samples In_xTe with $0.84\leq x\leq 1$. Resistivity data are presented in Figs. 2(a) and (b) for $T\leq 4$ K and up to room temperature, respectively. We find sharp drops to zero resistivity for all samples examined. In the normal state, all samples exhibit a linear temperature dependence over a wide temperature range $\sim 40~{}{\rm K}<T\leq 300$ K. The $T$-linear slope $A$ estimated from fits $\rho_{xx}(T)\propto AT$ to the data in this temperature range is plotted as a function of $x$ in Fig. 2(c). Although there is some scatter among the data points in the low-$x$ region, $A$ exhibits a steep increase for $x\gtrsim 0.92$, clearly indicating an enhancement of the electron-phonon scattering toward stoichiometric InTe.

Figure 2(d) presents zero-field electronic specific-heat data displayed as $c_{\rm el}/T$ vs $T$ for $T\leq 4$ K for selected samples. All samples exhibit a clear and sharp jump-like anomaly at $T_{\rm c}$, indicating bulk superconductivity in In_xTe. The lower and upper dotted horizontal lines represent the normal-state electronic specific-heat coefficient $\gamma_{\rm n}$ for $x=0.84$ (blue data) and $x=0.94$ (green), respectively. Apparently there is a strong enhancement of $\gamma_{\rm n}$ when increasing the In content from $x=0.84$, but this enhancement saturates for $x>0.9$. For larger $x$ there is no appreciable increase any more. The electronic specific heat is further analyzed in a BCS framework employing the $\alpha$ model [25, 26], see Section S4 in [14]. Herein, $\alpha=\Delta/k_{\rm B}T_{\rm c}$ is a measure of the superconducting coupling strength with the superconducting energy gap $\Delta$ (at 0 K), cf. Section S4 in [14] for a detailed description of this approach. Figure 2(e) summarizes $\alpha(x)$. In accord with the observed changes in the slope $A$ of the linear resistivity and the flattening of $\gamma_{\rm n}$, $\alpha$ starts to increase beyond the weak-coupling BCS limit for $x\gtrsim 0.92$, reaching almost $\alpha=2$ when $x$ approaches $1$. The most striking experimental result here is the clear change in the superconducting response of the system across $x\sim 0.92$: $A$, $\alpha$, and $T_{\rm c}$ increase toward $x=1$, while $\gamma_{\rm n}$ saturates, suggesting a change in the dominant ingredients governing the superconductivity in In_xTe.

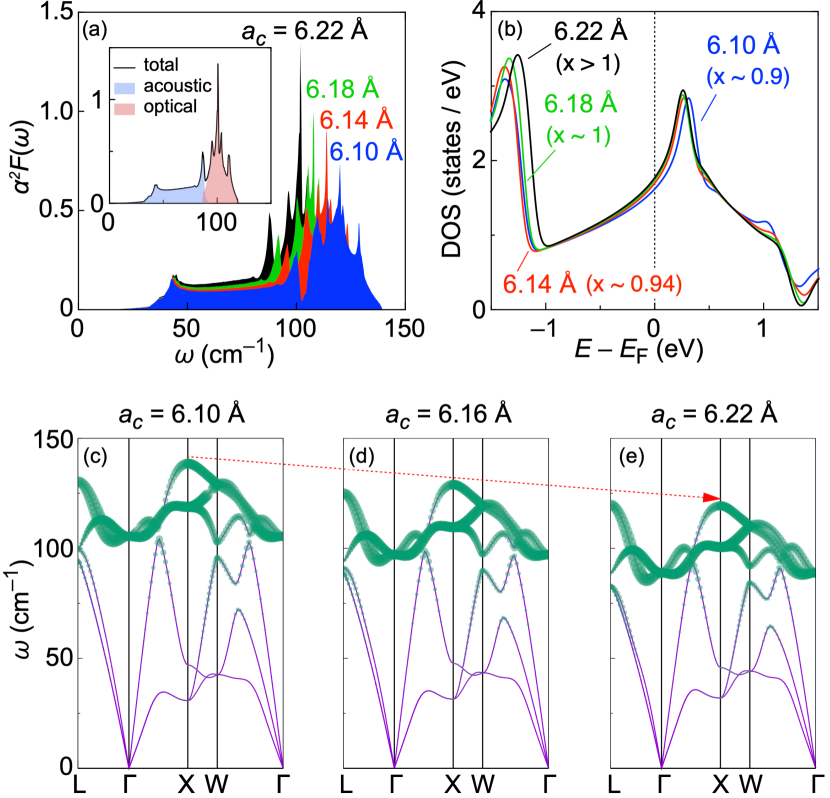
To shed light on this issue, we have developed a mean-field model which successfully reproduces our observations for $x\gtrsim 0.92$. The results are summarized in Fig. 3. Starting with Fig. 3(a), we have calculated the Eliashberg function $\alpha^{2}F(\omega)$ as a function of the phonon frequency $\omega$ for InTe with cubic lattice constants $a_{c}=6.10$ Å (blue), 6.14 Å (red), 6.18 Å (green), and hypothetical 6.22 Å (black), corresponding to $x\sim 0.9$, 0.94, 1, and $x>1$, respectively. The spectral weight of $\alpha^{2}F$ increases with $a_{c}$, already suggesting a possible increase in $\lambda_{\rm el-ph}$ upon expanding the crystal lattice of In_xTe, which will become clearer in the next Section. As highlighted in the inset, the optical phonons are the main source of this enhancement. Figure 3(b) shows the calculated electronic DOS data for the same lattice constants.

Figures 3(c) – (e) summarize the calculated energy dispersions of phonon frequencies in InTe for $a_{c}=6.10$ Å, 6.16 Å, and 6.22 Å, respectively. As indicated by the red arrow, the optical phonon frequencies, which are the dominant source of $\lambda_{\rm el-ph}$, are strongly softened upon increasing $a_{c}$. This points towards a scenario of the superconductivity where the lattice expansion in In_xTe may play a significant role.

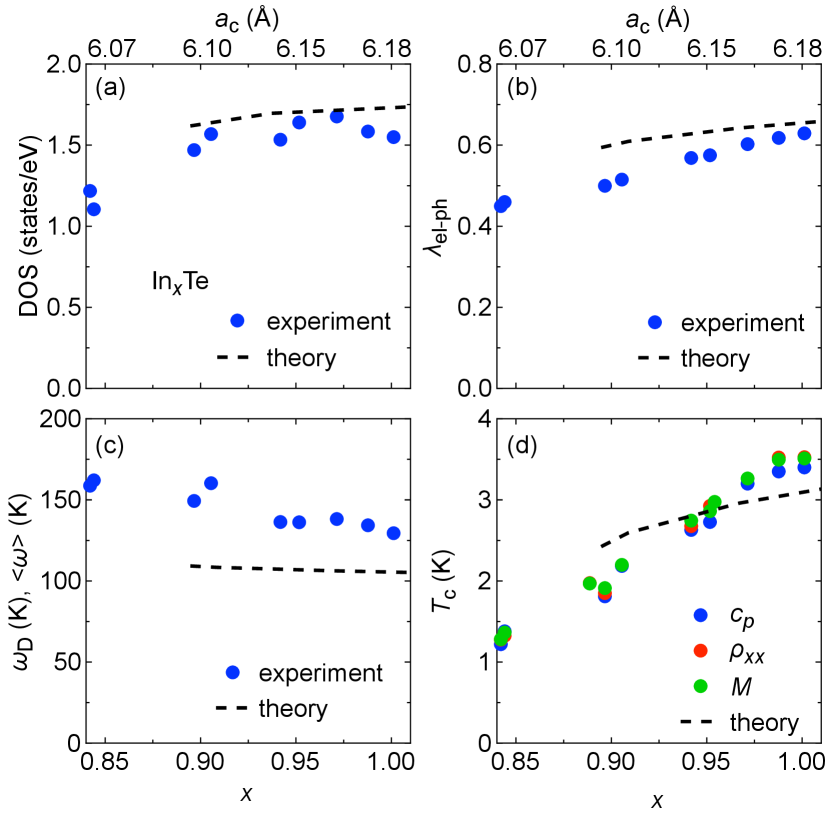
Figure 4 compares experimental and theoretical data of In_xTe. Blue data points in all panels are estimated from specific-heat data. Red and green data points in Fig. 4(d) refer to $T_{\rm c}$ values deduced from resistivity and magnetization data, respectively. The procedure how experimental DOS, $\lambda_{\rm el-ph}$, and $\omega_{\rm D}$ data were deduced from specific-heat measurements is described in Section S4 in [14]. The theoretical values are calculated as a function of the lattice constant $a_{c}$ and are plotted in Fig. 4 as black dashed lines against the corresponding In concentration $x$.

Density-of-states data are shown in Fig. 4(a) as a function of $x$. Since theoretical calculations yield the bare DOS without electron-phonon interaction, therein the experimental DOS results are divided by $1+\lambda_{\rm el-ph}$ to allow a quantitative comparison. In accordance with the electronic specific-heat data shown in Fig. 2(d), there is an enhancement of DOS upon increasing $x$ from 0.84 to 0.92, which amounts to almost $\sim 0.5$ states/eV. However, above $x\sim 0.92$, the enhancement becomes gradual and DOS seems to saturate. The latter is very well reproduced by our theoretical modeling: the black dashed line is DOS from Fig. 3(b) replotted as a function of $x$, matching well with the experimental data. Figure 4(b) shows the corresponding electron-phonon coupling strength $\lambda_{\rm el-ph}$, which increases from 0.45 to 0.63 when varying the In content from $x=0.84$ to 1.0. The black dotted line therein represents integrated Eliashberg functions $\lambda_{\rm el-ph}=2\int d\omega\,\alpha^{2}F(\omega)/\omega$ [22] shown in Fig. 3(a) which again agrees well with experimental data.

The $x$ dependences of the experimental Debye frequency $\omega_{\rm D}$ and its theoretical counterpart $\textless\omega\textgreater=2/\lambda_{\rm el-ph}\int d\omega\alpha^{2}F(\omega)$ [22] are given in Fig. 4(c). Experimentally we observe a decrease of $\omega_{\rm D}$ with $x$, indicating a softening of the lattice vibrations as suggested by Figs. 3(c) – (e). The negative slope of $\omega_{\rm D}(x)$ is reproduced in our model calculations.

Theoretical and experimental $T_{\rm c}$ values are summarized in Fig. 4(d). For $x=0.84$, the smallest $T_{\rm c}\sim 1.3$ K in this study is found [27]. Upon increasing $x$, $T_{\rm c}$ enhances linearly in accord with Refs. [10, 13]. Close to stoichiometric InTe, the slope decreases and $T_{\rm c}$ seems to saturate. Again, our theoretical model catches the $T_{\rm c}$ values for $x>0.92$ well.

Finally, we will propose a possible scenario of this change in the superconductivity in In_xTe. Below $x\sim 0.92$, an interpretation of our data in terms of a mainly DOS-driven enhancement of $\lambda_{\rm el-ph}$ and $T_{\rm c}$ seems obvious, as suggested by the concomitant increase of DOS with $x$, when comparing Figs. 4(a), (b), and (d). However, above $x\sim 0.92$, DOS flattens while $\lambda_{\rm el-ph}$ and $T_{\rm c}$ keep increasing. The continuous increase of $\lambda_{\rm el-ph}$ is ascribed to the softening of phonons in the higher $x$ region.

A phenomenological explanation can be given when considering the observed expansion of the cubic lattice with $x$ as shown in Fig. 1(b). The lattice expansion is reasonable because more and more voids in the InTe matrix get filled with $x$. The shorter lattice constants at low $x$ imply a more rigid lattice than for larger $x$. As a consequence, the electron-phonon interaction is relatively weak at small $x$, and therefore, $T_{\rm c}$ is small. Upon filling voids in the In sublattice, the crystal lattice expands and atoms are shifted more apart from each other. This allows for an easier vibration of the constituent atoms, leading to softer phonon modes as seen in Figs. 3(c) to (e). This can be regarded as a “negative pressure” effect (lattice expansion) in analogy to the physical pressure effect (lattice contraction). Note that changes in $\lambda_{\rm el-ph}$ and $T_{\rm c}$ are induced mainly by DOS changes in conventional cases while these are governed by phonon softening in the present case. A similar phonon-softening induced enhancement of superconductivity is discussed in literature [28].

To further test this hypothesis, we converted the “negative pressure” effect into physical pressure, which is shown with blue circle symbols in Fig. 5. The $T_{\rm c}$ values are normalized with respect to the largest $T_{\rm c}=3.51$ K (for $x=1.00$; all $T_{\rm c}$ values are from magnetization measurements) and plotted against physical pressure $p$. The latter values are calculated from the change of each sample’s unit-cell volume $V$ again with respect to the sample with $x=1.00$ by using the known bulk modulus [29], cf. Section S5 in [14] for a detailed description of the conversion process. For comparison, we also determined the phyical pressure dependence $T_{\rm c}(p)$ from resistivity measurements on a sample with $x=1.00$. These data are shown with red square symbols in Fig. 5 and are normalized to the ambient-pressure zero-resistance $T_{\rm c}=3.53$ K of this sample, cf. Section S6 in [14]. The agreement between converted $T_{\rm c}(x)$ and measured $T_{\rm c}(p)$ is very good and indeed pointing towards a scenario where the lattice expansion plays a significant role.

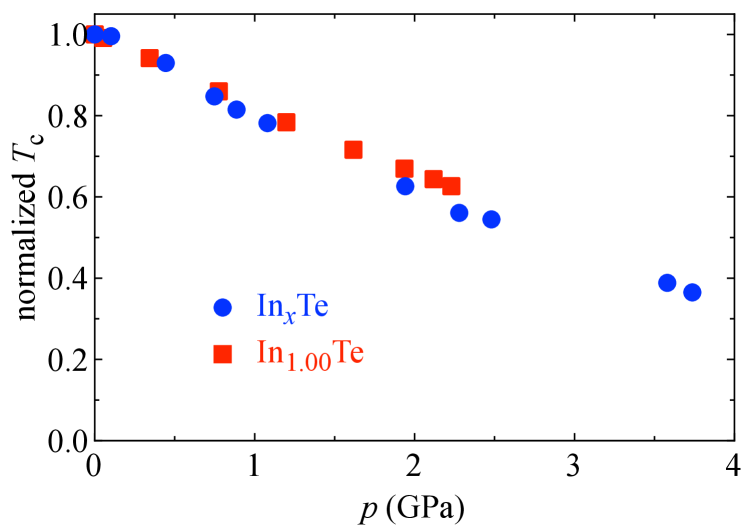
The total change of $T_{\rm c}$ in In_xTe for $0.84\leq x\leq 1.00$ corresponds to an applied physical pressure of $p\sim 3.75$ GPa. To further contextualize this value, a comparison between the case of In_xTe and several superconducting elements is shown in Section S5 in [14]. It turns out that In_xTe exhibits one of the strongest pressure effects observed in such chemically simple BCS superconductors, emphasizing that the soft lattice in In_xTe is indeed in favor of its superconductivity. This may be related to the valence-fluctuation feature of In in the present compound which could be an interesting starting point for future studies.

To summarize, we demonstrate that controlling and fine-tuning superconductivity can be achieved by simply changing the In concentration $x$ in In_xTe. For $x<0.92$, the enhancement of the superconductivity can be straight-forwardly understood as a consequence of an enhanced density of states at the Fermi level. Upon further increasing $x$, this enhancement fades out and the observed continued increase of the superconducting $T_{\rm c}$ cannot be attributed exclusively to a density-of-states effect any more. Therefore, we modeled this In concentration range theoretically and reproduced well the experimental data of density of states, electron-phonon coupling constant, and superconducting transition temperature for $0.92<x\leq 1$ by solely changing the cubic lattice constant. Together with the outcome of our physical pressure experiment, our results suggest that the enhanced superconductivity in this system is closely related to the soft lattice of this simple chalcogenide.

This work was partly supported by Grants-In-Aid for Scientific Research (S) from the Japan Society for the Promotion of Science (JSPS, No. 24224009), JST (No. JP16H00924), and PRESTO (JPMJPR15N5) and Grants-In-Aid for Scientific Research (B) (JSPS, No. 17H02770). We thank the RIKEN Materials Characterization Team for compositional analyses. M.K. thanks D. Hashizume, T. Kikitsu, D. Inoue, T. Nakajima, and D. Maryenko for fruitful discussions. M.K. and M.S.B. contributed equally to this work.