Enhanced Urban Region Profiling with Adversarial Contrastive Learning
Abstract.
Urban region profiling is influential for smart cities and sustainable development. However, extracting fine-grained semantics and generating robust urban region embeddings from noisy and incomplete urban data is challenging. In response, we present EUPAC (Enhanced Urban Region Profiling with Adversarial Contrastive Learning), a novel framework that enhances the robustness of urban region embeddings through joint optimization of attentive supervised and adversarial contrastive modules. Specifically, region heterogeneous graphs containing human mobility data, point of interest information, and geographic neighborhood details for each region are fed into our model, which generates region embeddings that preserve intra-region and inter-region dependencies through graph convolutional networks and multi-head attention. Meanwhile, we introduce spatially learnable augmentation to generate positive samples that are semantically similar and spatially close to the anchor, preparing for subsequent contrastive learning. Furthermore, we propose an adversarial training method to construct an effective pretext task by generating strong positive pairs and mining hard negative pairs for the region embeddings. Finally, we jointly optimize attentive supervised and adversarial contrastive learning to encourage the model to capture the high-level semantics of region embeddings while ignoring the noisy and irrelevant details. Extensive experiments on real-world datasets demonstrate the superiority of our model over state-of-the-art methods.
1. Introduction
Urban regions play a pivotal role in shaping the dynamics and functionality of cities. As cities grow and evolve, understanding the characteristics and interconnections of different urban regions becomes essential for effective urban planning, transportation management, and social policy development. Urban region profiling is a crucial technique that maps urban regions into a lower-dimensional space, which aims to systematically analyze and interpret attributes, relationships, and dynamics inherent in these regions, thereby acquiring profound insights into the intricate complexities of the urban landscape (Zhang et al., 2017; Huang et al., 2023).
Recently, many deep learning models have shown promising results in urban region profiling. MV-PN(Fu et al., 2019) proposed a region embedding model that learns intra and inter-regional similarities by using intra-regional point of interest (POI) networks and spatial autocorrelation layers. CGAL(Zhang et al., 2019a) extends the idea proposed in (Fu et al., 2019) by introducing a collective adversarial training strategy. MVGRE(Zhang et al., 2020) develops a multi-view joint learning model for learning region representations. MGFN(Wu et al., 2022) extracts traffic patterns for learning region representations, but it only considers mobility data and ignores POIs data, which is essential for capturing region functionalities. ROMER(Chan and Ren, 2023) excels in urban region embedding by capturing potential dependencies from distant regions with an improved global attention graph network and incorporating a two-stage fusion module. HREP(Zhou et al., 2023) applies the prefix-tuning to replace the direct use of region embedding in the downstream tasks. However, they overlook the suboptimal embeddings caused by the inevitable noise and incompleteness in urban region data. To address this challenge, contrastive learning has emerged as a promising solution.


challenge
Contrastive learning is one of the categories of self-supervised learning (SSL) that aims at grouping similar samples closer and diverse samples far from each other (Liu et al., 2023). The study of contrastive learning has made significant progress in natural language processing (NLP) (Radford et al., 2021; Giorgi et al., 2021; Rethmeier and Augenstein, 2023) and computer vision (CV) (He et al., 2020; Grill et al., 2020; Chen et al., 2020). Inspired by the success of contrastive learning in images, recent studies propose similar contrastive frameworks to enable self-supervised training on graph data (Qiu et al., 2020; Wang et al., 2022). However, the key to successfully incorporating contrastive learning into urban region embedding tasks lies in designing an effective data augmentation strategy that encourages the encoder to capture the high-level semantics of the region embedding. Existing data augmentation methods, including those specifically designed for sequential data and spatiotemporal data, fail to meet the requirements. There are two specific reasons for this:
-
(1)
In the spatial dimension, each POI is discrete, highly semantic, and information-dense. The set of geographical region neighbors is fixed in urban, as shown in Fig. 1(a). Therefore, directly adopting existing data augmentation methods (Hou et al., 2022; He et al., 2020; Wei et al., 2019; You et al., 2020) e.g., masking, replacement, disruption, and cropping to disturb the POIs and neighbors sets fail to generate high-level semantically similar positive samples.
-
(2)
Each human mobility trip has unique characteristics, (e.g., length, origins, and destinations), making them easily distinguishable. As depicted in Fig. 1(b), replacing the POIs of a mobility trip, e.g. a café with a nearby restaurant or shopping center, changes the moving purpose of a trip.
To tackle these challenges, we propose an urban region profiling model called EUPAC, which combines attentive supervised and adversarial contrastive learning to comprehend high-level semantics in noisy or incomplete urban data. Specifically, region heterogeneous graphs containing human mobility data, POIs information, and geographic neighborhood details for each region are fed into the model, which generates region embeddings that preserve intra-region and inter-region dependencies through graph convolutional network (GCN) and multi-head attention. Meanwhile, we introduce a spatial learnable augmentation layer to generate positive samples that are semantically similar and spatially close to the anchor for subsequent contrastive learning. To enhance contrastive learning, adversarial training is employed to generate ’hard’ negative samples through minor perturbations, minimizing semantic-level conditional likelihood. In contrast, ’strong’ positive samples result from larger perturbations while maintaining high conditional likelihood. This strategy ensures that negative samples are closely aligned with anchors in the latent embedding space, but are semantically different (e.g., travel purpose), while positive samples are farther away from the anchor, but are semantically similar. Finally, we jointly optimize attentive supervised and adversarial contrastive learning to facilitate the model in generating powerful region embeddings. In summary, our work has the following contributions:
-
•
To address the noise problem in urban data and effectively mine potential correlations between regions, we propose a joint supervised learning and self-supervised learning framework for urban region profiling.
-
•
To avoid tedious manual adjustments, we propose a spatial learnable augmentation strategy to generate meaningful positive samples based on the specificity of urban region embedding for subsequent contrastive learning.
-
•
To further enhance contrastive learning, we introduce an adversarial strategy to automatically generate hard positive-negative pairs, which encourages the model to comprehend the high-level semantics for the urban region embeddings.
-
•
We extensively evaluate our approach using real-world data through a series of experiments. The results demonstrate the superiority of our method compared to state-of-the-art baselines.
In the rest of this paper, we first present some preliminary definitions and define the problem. Then, we detail the proposed model and show the experimental settings and results. Finally, we conclude the paper.
2. Related Work
Graph neural networks (GNNs) are designed to learn graph embeddings from graph structures. With the rapid development of GNNs (Kipf and Welling, 2016, 2017; Xu et al., 2019; Liu et al., 2020a; Defferrard et al., 2017), their basic components (Gao et al., 2018; Ying et al., 2019; Gao et al., 2021; Wang and Ji, 2023; Yuan and Ji, 2020; Gao and Ji, 2019) and related fields (Yuan et al., 2020; Liu et al., 2020b) have been extensively studied and significantly advanced. Notably, GCN (Kipf and Welling, 2017) introduces convolutional concepts from computer vision into GNNs. GraphSage (Hamilton et al., 2018) enables inductive representation learning in GNNs. GAT (Veličković et al., 2018a) incorporates the attention mechanism into neighbor aggregation. GIN (Xu et al., 2019) demonstrates that GNNs can match the performance of the Weisfeiler-Lehman graph isomorphism test. Efforts to extend GNNs to heterogeneous graphs include RGCN (Schlichtkrull et al., 2018) for modeling knowledge graphs, HetGNN (Zhang et al., 2019b) which uses different RNNs for different node types, and HGT (Hu et al., 2020a) which introduces transformers into GNNs. In contrast, applying SSL to GNNs is still emerging. Many SSL methods for GNNs draw inspiration from image domain techniques due to structural similarities, such as DGI (Veličković et al., 2018b) and GPT-GNN (Hu et al., 2020b). For contrastive models, the main challenge is obtaining good graph views and selecting appropriate graph encoders for different models and datasets.
With the increasing availability and scale of urban data sources, research on learning urban region representations has flourished, primarily categorized into single and multiple data sources. Regional human mobility data is commonly used as a single data source to mine inter-regional correlations. For instance, HDGE (Wang and Li, 2017) constructs flow and spatial graphs to learn region embeddings through human mobility. ZE-Mob (Yao et al., 2018) extracts mobility patterns from taxi trajectories and learns region embeddings using source-destination co-occurrences. MGFN (Wu et al., 2022) analyzes mobility data from different periods to build mobility patterns for region embedding. In contrast, methods integrating multiple urban data sources provide more comprehensive regional attribute information, resulting in richer region embeddings. Specifically, MV-PN (Fu et al., 2019) constructs two graph flattenings of inter-region human mobility data and intra-region POIs, using them as initial region vectors fed into an AutoEncoder to learn the final region embeddings. CGAL (Zhang et al., 2019a) incorporates generative adversarial networks into the AutoEncoder, using a similar strategy to connect different graphs. MVGRE (Zhang et al., 2020) improves performance by building different region-based graphs from multiple data sources and employing a multi-view fusion mechanism. Region2Vec (Luo et al., 2022) leverages knowledge graphs to explore global and local correlations in multi-source data, enhancing region representation learning. ROMER (Chan and Ren, 2023) excels in urban region embedding by capturing multi-view dependencies from diverse data sources, using global graph attention networks, and incorporating a dual-stage fusion module. Recently, HREP (Zhou et al., 2023) introduced prefix prompt learning from NLP to automatically optimize and guide downstream tasks. These methods have achieved commendable results in urban region embedding. However, their effectiveness heavily depends on generating high-quality region graphs. Learning high-quality region representations may be challenging with noisy and incomplete urban region data.
According to the design of the pretext training task, SSL methods can be categorized into two types: contrastive models and predictive models (Xie et al., 2023; Liu et al., 2023). Contrastive learning, successful in NLP (Radford et al., 2021; Giorgi et al., 2021; Gao et al., 2022; Rethmeier and Augenstein, 2023; Lee et al., 2021; Yan et al., 2021) and CV (He et al., 2020; Grill et al., 2020; Caron et al., 2021; Chen et al., 2020; Ramesh et al., 2022), has been extended to enable self-supervised training on graph data (Wang et al., 2022; Wu et al., 2018). Contrastive learning enables the model to capture high-level semantics meanwhile ignoring the noisy details of the graph. Commonly employed contrastive transformations include node attribute masking as feature transformation(Zhu et al., 2021), edge perturbation and diffusion as structure transformations(Qiu et al., 2020; You et al., 2020), and uniform sampling, ego-nets sampling, and random walk sampling as sample-based transformations(Veličković et al., 2018b; Sun et al., 2020; Wang et al., 2021). Although there is no theoretical analysis to guide contrastive graph generation, some studies(Tian et al., 2020; Suresh et al., 2021; Xu et al., 2021) have shown that both stronger divergence between samples and utilizing adversarial graph enhancement strategies lead to better contrast learning. Importantly, adopting appropriate data enhancement methods according to the characteristics of different data samples is also key to improving contrast learning(You et al., 2020; Gong et al., 2023).
Motivated by the studies mentioned above, considering the characteristics of urban region information, we will investigate how to design a robust and universal contrastive learning model for urban region profiling with the help of adversarial perturbations.
3. Preliminaries
In this section, we first give some notations and define the urban region embedding problem. Suppose that a city is divided into a set of non-overlapping regions , where denotes the -th region and denotes the number of the regions.
Definition 3.1 (Human Mobility).
Let represent a travel record, where is the origin region and is the target region with . Human mobility is defined as a set of trips occurring in urban areas, where is the number of trips.
Definition 3.2 (Regional POIs Information).
Region function features are characterized by POIs in the city. We represent the region information as , where and is the number of categories.
Definition 3.3 (Geographic Neighbor Information).
The geographical neighbor information signifies the spatial relationships between a region and its neighboring areas. Specifically, the set of geographical neighbors can be expressed as , where is the geographical neighbor vector for the urban region .
Definition 3.4 (Region Heterogeneous Graph).
A region heterogeneous graph is denoted as , where denotes the set of region nodes, with each node corresponding to a specific urban region. is the set of edges connecting the nodes, and represents the set of different edge types. Here, denotes the origin edge type, represents the target edge type, corresponds to the POI edge type, and corresponds to the geographic neighbor edge type. The edge types and are constructed based on correlations of human mobility data, while the edge type is constructed using POIs information. Regarding the edge type , each node is connected to all of its geographic neighbors.
Definition 3.5 (Urban Region Embedding).
Given a set of regions , human mobility , POIs information , and geographic neighbor information , our goal is to learn low-dimensional embeddings , where represents the -dimensional embedding for the region . These embeddings in should capture movement patterns, geographic neighborhoods, and POI-related details for various urban downstream tasks.
| the number of the regions | |
| different data sources similarity matrix | |
| the relation embedding | |
| relation-focused region embedding | |
| relation-aware region embedding (Anchor) | |
| final task embedding | |
| positive samples | |
| spatial learnable augmentation positive samples (LA-Pos) | |
| hard negative samples (Trickster) | |
| strong positive samples (DevCopy) |
4. Methodology
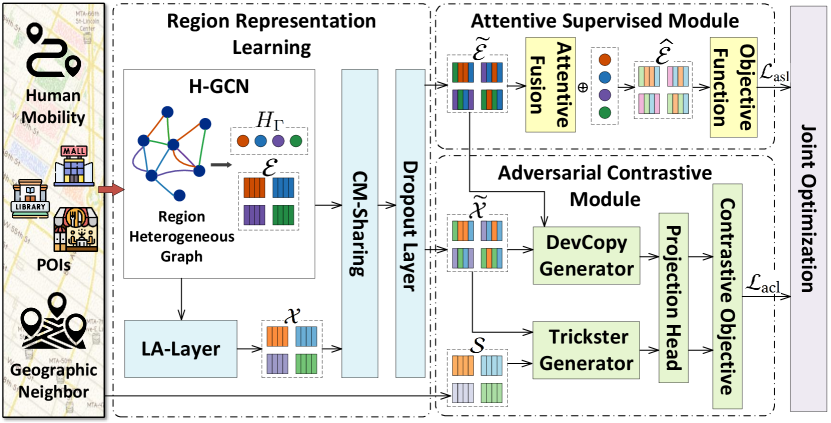
In this section, we present the technical details of our EUPAC framework. The overall model architecture is illustrated in Fig. 2, which mainly consists of three components, region representation learning, attentive supervised module, and adversarial self-supervised module. The important notations are listed in Table. 1.
4.1. Region Representation Learning
In this module, our focus is on leveraging the region’s heterogeneous graph to learn embeddings that capture multi-level urban features and inter-region semantic correlations. We generate effective positive samples based on the acquired region embeddings in preparation for subsequent contrastive learning.
4.1.1. Heterogeneous GCN Layers (H-GCN)
To capture both intra-view and inter-view region dependencies, we conduct message passing on the heterogeneous region graph . Our model integrates relation embeddings into the GCN for enhanced graph learning. Let and denote the node and relation embeddings at the -th layer, respectively. Here, , , , and represent the relation embeddings for origin, target, POIs, and geographic neighbor relationships, respectively. Then, given the initial node embedding and relation embedding , we update them at the layer as follows:
| (1) |
| (2) |
where , , and denotes a specific relation type. Here, represents the LeakyReLU activation function, and is the element-wise product. The learnable parameter for node embedding update in the -th layer is denoted as . Additionally, stands for the neighbor set of the region under relation type . To quantify the correlation between region vertex pair , we define the normalization weight , determined by the degrees of the vertices. Moreover, and are layer-specific parameters projecting relation embeddings from the previous layer to the same embedding space for subsequent use.
In addition, to mitigate feature smoothing in graph neural networks, we incorporate ResNet(He et al., 2016) into H-GCN for multi-layer graph aggregation. At the th layer, the aggregation process is expressed as follows:
| (3) |
where denotes the adjacency matrix, and is the corresponding diagonal matrix. The geographic neighbor similarity and adjacency matrices are constructed based on neighbor relationships. To build the adjacency matrix based on human mobility data and POIs, we follow (Zhang et al., 2020) to build the POI similarity matrix , mobility origin similarity matrix and mobility target similarity matrix . Subsequently, we employ the Top- method with set to 10 to construct these three adjacency matrices. Finally, we obtain the relation-focused region embeddings and the relation embeddings under each relation type.
4.1.2. Spatial Learnable Augmentation Layer (LA-Layer)
To autonomously generate effective positive samples based on the specificity of urban region embeddings for subsequent contrastive learning preparation, we perturb the region embeddings in latent space. In particular, given the region representations from relation-focused region embeddings as , we use to denote the positive example, where . Formally,
| (4) |
where is sampled from a Gaussian distribution with zero mean and standard deviation . represents the scale factor for perturbation magnitude, with and serving as hyper-parameters. The result is then fed into CM-sharing to obtain spatial learnable augmentation positive samples (LA-Pos), denoted as .
4.1.3. Cross-network Message Sharing Layer (CM-Sharing)
Generally, different attributes within the same region are interrelated. For instance, factors like unemployment, poverty, and educational levels in neighboring areas may influence crime rates in certain regions. To capture global information, we employ the multi-head self-attention mechanism(Vaswani et al., 2017). Formally, given the region representations from relation-focused region embeddings as . For each representation , we associate a key matrix , a query matrix and a value matrix with it as follows:
| (5) |
where , , and are learnable parameters for the -th head. Then, compute multi-head self-attention by the following equation:
| (6) |
where is the learnable parameter for transformation, denotes concatenation, and is the number of heads. So far, we obtain which is considered as the relevant global region information. Subsequently, we introduce the learning-based linear interpolation to improve the embedding, formulated as follows:
| (7) |
where , , and denotes the learning parameters. Finally, we obtain the relation-aware region embedding, denoted by . To ensure the model’s generalization ability, dropout layers are further employed.

4.2. Attentive Supervised Module
For the learned region embeddings to maintain the regional similarity of different region attributes and to consider the strength of the influence of different types of regions, we propose an attentive supervised learning module that introduces attention vectors to compute the attention weights.
First, a nonlinear transformation is employed to transform each relation-focused region embedding into hidden space. Subsequently, an attention vector, denoted by , is introduced to compute a relation-based weight. In particular, given a relation-aware region embedding, denoted by , where , the weight of each node embedding is averaged to obtain the attention coefficient, as follows:
| (8) |
where indicates the LeakyReLU activation function. For meaningful fusion, parameters , , and are shared across all relation-aware region embeddings. This sharing projects all embeddings into the same space, allowing for the computation of the attention coefficient. And then, we use learned region embedding and learned relation embedding to generate multi-task embedding as follows:
| (9) |
where . So far, we obtain the final task embedding for the downstream tasks.
To effectively train our model, we formulate multi-task learning to design our supervised learning objective function for the attentive supervised learning module, as follows:
| (10) |
where , , and are losses for geographic predictor, mobility predictor, and POI predictor respectively.
We construct the geographic predictor to protect the neighborhood region property, as geographically adjacent regions in general may have higher similarity. Formally, given the fusion embedding , geographic predictor loss by Triplet Margin Loss function be defined as follows:
| (11) |
where (resp. ) is a positive (resp. negative) sample of geographic neighbors (resp. non-geographic neighbors) from the -th region, is the anchor.
Through the mobility predictor, we can predict the target (resp. origin) region when the origin (resp. target) region is provided. Given the mobility embeddings , and human mobility , we first compute original mobility distribution as follows:
| (12) |
Consequently, reconstruct origin and target region distributions as follows:
| (13) |
Hence, mobility predictor loss by KL divergence can be defined as follows:
| (14) |
The purpose of the POI predictor is to ensure that the POI information is retained in the final region representation. Given POI embedding and POI similarity matrix , we have the POI loss formulated by:
| (15) |
4.3. Adversarial Contrastive Module
To avoid perturbations to the region embeddings producing positive samples with semantic biases, we employ adversarial perturbations for spatial augmentation to generate strong negative and positive pairs, which encourages our model to effectively capture the semantics of region embeddings and enjoy satisfactory generalization ability and robustness.
4.3.1. Adversarial Perturbations Layer
Considering that the strong distinguishable properties of different region embeddings hinder the effectiveness of contrast training, inspired by (Suresh et al., 2021), stronger divergence and adversarial graph augmentation can improve contrast learning. As a result, we propose adversarial perturbations to generate hard negative pairs and hard positive pairs. This strategy facilitates overcoming noise while extracting high-level semantics in region embeddings, thus ensuring strong generalization. The studies suggest stronger divergence and adversarial graph enhancements improve contrast learning. The adversarial perturbation layer comprises the Trickster Generator and Deviation Copy Generator, with the detailed implementation processes depicted in Figure. 3.
The Trickster Generator aims to produce hard negative samples, denoted as , that exhibit proximity to anchor in the latent embedding space while maintaining semantic distinctions. In particular, is derived by introducing a slight perturbation to the anchor , where the Euclidean norm of is constrained within the limit of . Simultaneously, to alter the inherent semantics as extensively as feasible, we aim to minimize the conditional likelihood of to the original similarity matrix . Formally,
| (16) |
where has the same size with relation-aware region embedding . Due to the intractability of exact minimization for neural networks, we implement it as follows:
| (17) |
Algorithm 1 presents the trickster generator’s pseudo code. is an adversarial sample that puts pressure on the urban region embedding contrastive learning task, enhancing the robustness and generalization of the model.

In addition, we propose the Deviation Copy Generator intending to generate strong positive samples , referred to as DevCopy. It is intended to exhibit semantics similar to the anchor while maintaining a far distance in the latent space. The relationship between them is illustrated in Figure 4. Specifically, a well-suited perturbation is introduced to to minimize its cosine similarity with . However, the exact computation of under these constraints is intractable. To address this, we use two computational phases to approximate it. In the first stage, a perturbation is added to to minimize the contrastive learning loss (refer to Eq.21, where can be viewed as and as ). Formally,
| (18) |
In the second step, we aim to maintain semantics by minimizing the KL divergence between the conditional likelihood and , pulling them closer together. Formally,
| (19) |
| (20) |
Algorithm 2 presents the Deviation Copy Generator’s pseudo code. Finally, we also applied linear projections to and to obtain better results by applying separate projections(Xie et al., 2023) to the representations of different types of nodes.
4.3.2. Contrastive Objective Optimization for Augmentation
In the contrastive learning layer, we utilize the InfoNCE Loss (van den Oord et al., 2019) to maximize the similarity between the anchor and DevCopy, while minimizing the similarity between the anchor and Trickster:
| (21) |
where measures the correlation between two embeddings, represents the spatially augmented positive sample (i.e., LA-Pos), and is a set of randomly selected negative samples from the same batch.
As explained previously, incorporating the contrastive learning framework into urban region embeddings makes no sense if random non-targeted region representations are utilized as negative examples to train the model, since these fictitious negative examples are located far away from the positive examples in the embedding space, even if the positive examples are semantically irrelevant to the anchor. To make the contrast process more effective in guiding the training of the model, we additionally used the generated ”hard” negative and positive examples to optimize the contrastive learning loss. Firstly, we design the Trickster contrastive loss by introducing the Trickster as an extra negative example to Eq. 21. Formally,
| (22) |
where denotes . We further enhance the training process by adding the hard positive sample as follows,
| (23) |
Finally, the total contrastive loss is expressed as:
| (24) |
where is a hyper-parameter.
4.4. Joint Optimization
To combine the attentive supervised module and adversarial contrastive module, we jointly optimize the urban region profiling model, which is as below,
| (25) |
where denotes the trainable parameters for regularization with the strength of . is a hyper-parameter that controls the proportion of supervised and self-supervised learning.
5. Experiments
In this section, extensive experiments are conducted to verify the superiority of the proposed model.
5.1. Datasets
Experiments are conducted on several real-world datasets of New York City from the NYC open data website111https://opendata.cityofnewyork.us/. We have chosen the borough of Manhattan in New York City as our study area, which serves as a benchmark dataset in the field of research. The study area is divided into 180 regions for comprehensive analysis. We have obtained authentic and diverse datasets, such as census block shapefiles, taxi trip data, POIs data, and check-in data, from the renowned NYC Open Data platform for our research efforts. The description of each dataset can be found in Table. 2.
5.2. Experimental Settings
EUPAC has been implemented based on the Pytorch framework. All the experiments have been carried out on an Intel(R) Xeon(R) CPU E5-2680 v4 hardware platform equipped with NVIDIA GeForce RTX 3090 Ti-24G. In particular, the model is optimized using Adam with a learning rate of 0.001. For this implementation, the dimension of our model is 144. The layer of heterogeneous GCN is set as 3. In the multi-head self-attention, we set the number of heads as 4. As for the hyperparameter settings, the standard deviation = 0.01, = 0.80, the scale factor = 1, = 1, the scale factor = 1, = 0.50, = 0.15 and = 4.
| Dataset | Details |
|---|---|
| Regions | 180 regions based on the Manhattan community boards. |
| Taxi trips | 10 million taxicab trips during one month. |
| Check-in data | 100,000 check-in points with 200 categories. |
| POIs data | 20,000 PoIs in 13 categories in the studied areas. |
| Crime data | 40,000 criminal records in a year |
5.3. Baselines
This paper compares the EUPAC model with the following baselines.
-
•
LINE(Tang et al., 2015): It is applied to preserve both the local and global network structures while optimizing the objective function.
-
•
node2vec(Grover and Leskovec, 2016): It is applied to concatenate the embedding of each graph to obtain the region embedding.
-
•
HDGE (Wang and Li, 2017): It is applied to traffic flow graphs and spatial graphs for path sampling to jointly learn region representations.
-
•
ZE-Mob(Yao et al., 2018) : It is applied to the learning of region embeddings by taking into account the co-currency relation of the regions in human mobility trips.
-
•
MV-PN(Fu et al., 2019) : It is used to learn region embeddings with a region-wise multi-view POI network. We denote it as MV-PN.
-
•
CGAL(Zhang et al., 2019a) : It is used to encode region embeddings utilizing unsupervised methods on both the constructed POIs and mobility graphs. The adversarial learning is adopted to integrate the intra-region structures and inter-region dependencies.
-
•
MVGRE(Zhang et al., 2020) : It is used to implement cross-view information sharing, and weighted multi-view fusion to extract region embeddings based on both the mobility of people and the inherent properties of regions (e.g. POI, check-in).
-
•
MGFN (Wu et al., 2022): It utilizes multi-graph fusion networks with a multi-level cross-attention mechanism to learn comprehensive region embeddings from multiple mobility patterns, integrated via a mobility graph fusion module.
-
•
ROMER (Chan and Ren, 2023): It excels in urban region embedding by capturing multi-view dependencies from diverse data sources, employing global graph attention networks, and incorporating a two-stage fusion module.
-
•
HREP (Zhou et al., 2023): It applies the continuous prompt method prefix-tuning to replace the direct use of region embedding in the downstream tasks, which can have different guiding effects in different downstream tasks and therefore can achieve better performance.
5.4. Experimental Results
| Models | Check-in Prediction | Crime Prediction | ||||
|---|---|---|---|---|---|---|
| MAE | RMSE | MAE | RMSE | |||
| LINE | 564.59 | 853.82 | 0.08 | 117.53 | 152.43 | 0.06 |
| node2vec | 372.83 | 609.47 | 0.44 | 75.09 | 104.97 | 0.49 |
| HDGE | 399.28 | 536.27 | 0.57 | 72.65 | 96.36 | 0.58 |
| ZE-Mob | 360.71 | 592.92 | 0.47 | 101.98 | 132.16 | 0.20 |
| MV-PN | 476.14 | 784.25 | 0.08 | 92.30 | 123.96 | 0.30 |
| CGAL | 315.58 | 524.98 | 0.59 | 69.59 | 93.49 | 0.60 |
| MVGRE | 297.72 | 495.27 | 0.63 | 65.16 | 88.19 | 0.64 |
| MGFN | 280.91 | 436.58 | 0.72 | 59.45 | 77.60 | 0.72 |
| ROMER | 252.14 | 413.96 | 0.74 | 64.47 | 85.46 | 0.72 |
| HREP | 270.28 | 406.53 | 0.75 | 65.66 | 84.59 | 0.68 |
| EUPAC (Ours) | 251.70 | 394.68 | 0.77 | 58.56 | 77.41 | 0.73 |

5.4.1. Check-in and crime prediction
In check-in and crime prediction tasks, we predict the number of crime and check-in events in each region for one year with the learned region embeddings. In practice, we apply the Lasso regression (Tibshirani, 1996) with metrics of Mean Absolute Error (MAE), Root Mean Square Error (RMSE), and coefficient of determination () to measure the performance of the models. Table 3 reports the comparison results of the check-in and the crime prediction task. In particular, our approach improves MAE, RMSE, and in the check-in prediction task by 6.8%, 2.9%, 2.6%, and in the crime prediction task by 10.8%, 8.2%, 7.3% on dataset compared to the HREP approach which highlights the strength of our joint attentive supervised and contrastive learning framework. This framework encourages the encoder to extract region nonlinear dependency and capture high-level semantics in urban region embeddings that suffer from noise problems.
In contrast, traditional graph embedding methods (i.e. LINE, node2vec) perform poorly because of the local sampling approach, which can not fully express the relationships between nodes. The deep learning methods perform better than the traditional graph embedding methods in all three data sources. Models such as HDGE, ZE-Mob, and MV-PN utilize multi-scale graph structures and embedding methods to capture the multi-level features and complex relationships within urban areas. They do not consider the varying importance of nodes for modeling dependencies, which influences the performance. Furthermore, graph representation methods such as MVGRE, MGFN, and ROMER perform better than others. As they employ a multi-view fusion and attention mechanism that captures the dependencies between nodes, allowing the model to strike a good balance between local perception and information aggregation. While the HRPE model has demonstrated promising results by incorporating prompt learning to guide downstream tasks, none of the aforementioned models consider the impact of noise and incompleteness in urban region data on region representation learning.
5.4.2. Land usage classification
We employ K-means to cluster the region embeddings and present the outcomes visually for intuitive interpretation. Fig. 6(a) illustrates that the community boards (Berg, 2007) partition the Manhattan administrative district into 12 regions based on land use. Accordingly, we split the study area into 12 clusters as well. The clustering outcomes should group regions with identical land use types. To further measure the region clustering results, inspired by (Yao et al., 2018), we use normalized mutual information (NMI) and adjusted Rand index (ARI). Figure 5 reports the comparison results of the land use classification task. Compared to the ROMER approach, more than 3.7% improvement in NMI and more than 4.4% improvement in ARI are achieved in the land classification task.






For visual evaluation of the land use classification task, we depict the clustering results of five baselines and our model in Fig. 6, where regions in the same cluster are marked with the same color. Notably, the clustering results obtained by our method show the most ideal degree of consistency with the real boundaries of the ground conditions. This observation suggests that the region embeddings learned by our model better represent regional functions. The reason is that our method performs well at exploiting high-level semantics in noisy or incomplete urban data, capturing universal human mobility patterns, and generating accurate urban region embeddings.

5.4.3. Ablation Study
To better verify the role of each component, this paper conducts an ablation study in land usage classification, check-in prediction tasks, and crime prediction. We have designed the variants of EUPAC in the following way:
-
•
w/o Spatial Augmentation (w/o SA): The spatial learnable augmentation layer using the replacement data augmentation approach to generate positive samples.
-
•
w/o Adversarial Contrastive Learning (w/o ACL): We remove the adversarial contrastive module from EUPAC.
-
•
w/o Attentive Supervised Learning (w/o ASL): We remove the attentive supervised module from EUPAC.
-
•
w/o Trickster (w/o T): is removed from EUPAC, with all other settings unchanged.
-
•
w/o DevCopy (w/o D): is removed from EUPAC, with all other settings unchanged.
Fig. 7 shows the ablation results of EUPAC and its variants. These results highlight the critical importance of effective data augmentation for graph contrastive learning. Without our proposed spatial learnable augmentation layer, the performance is worse than when adversarial contrastive learning is excluded. This indicates that the model’s robustness is significantly improved by adding appropriate spatially augmented perturbations to the latent space. Additionally, using only adversarial contrastive learning yields unsatisfactory results, underscoring the necessity of our framework, which combines attentive supervised and adversarial contrastive learning. Moreover, the model’s discriminative performance is enhanced by dynamically adding Trickster and DevCopy. As training progresses, the difficulty of augmented samples increases, further strengthening the model’s discriminative ability. Finally, the integration of these modules in our final model produces the best outcomes.
5.4.4. Impact of noise
To further validate the contribution of our proposed adversarial contrastive learning in addressing noise issues, rather than merely complicating the structure, we added noise to the data through replacement and compared the performance of different methods under the influence of noise in downstream tasks. As shown in Table 4, although some of the state-of-the-art methods in recent years are structurally simpler, they perform very poorly when confronted with noisy data, with ROMER’s performance decreasing by approximately 9%. In contrast, our EUPAC model is very robust, with a performance degradation of only about 2.5%. Additionally, the ablation results indicate that within the adversarial contrastive module, the Trickster Generator exhibits stronger noise resistance than the Deviation Copy Generator.
| Methods | Check-in Prediction | Crime Prediction |
|---|---|---|
| RMSE | MAE | |
| MVGRE | 532.41 (7.5% +37.15) | 69.85 (7.2% +4.69) |
| ROMER | 450.80 (8.9% +36.84) | 70.45 (9.4% +5.98) |
| HREP | 431.33 (6.1% +24.80) | 69.53 (5.9% +3.87) |
| w/o T | 447.09 (3.5% +15.16) | 61.64 (3.6% +2.14) |
| w/o D | 447.68 (2.8% +12.19) | 62.41 (2.9% +1.76) |
| EUPAC (Ours) | 405.33 (2.5% +10.66) | 60.14 (2.7% +1.58) |

5.4.5. Hyperparameter studies
We systematically tune important hyperparameters in EUPAC. The weighting parameter in Eq. 24 affects the sum of positive and negative sample losses in contrastive learning, which we explored within , with =0.50 yielding the best performance. This balance turns out to be crucial for effective contrastive learning within our designed adversarial self-supervised module. For the joint optimization parameter in Eq. 25, varying within , the model excels with = 0.15, highlighting the dominant role of contrastive learning in mining high-level region semantics from noisy urban data.
6. Conclusion
In this paper, we propose a novel approach to urban region profiling that effectively addresses the data noise problems of existing urban region embedding models by integrating attentive supervised learning and adversarial contrastive learning paradigms. We conduct extensive experiments on three urban downstream tasks with real-world datasets, to validate the effectiveness and versatility of our proposed EUPAC in different settings. In particular, the designed Trickster Generator showed exceptional resistance to noise. For future research, we aim to incorporate causal inference and expand the dataset to include various aspects of urban regions, such as healthcare, economics, and weather. Our goal is to design an interpretability and explainability urban region representation paradigm and delve into more granular urban regional semantics.
Acknowledgments
This work was supported by National Key RD Program of China under Grant No.2020YFB1710200, the China Postdoctoral Science Foundation under Grant No.2022M711088, the National Natural Science Foundation of China under Grant No.62172243.
References
- (1)
- Berg (2007) B.F. Berg. 2007. New York City Politics: Governing Gotham. Rutgers University Press, New york. https://books.google.com/books?id=N3OiWo5DkfMC
- Caron et al. (2021) Mathilde Caron, Ishan Misra, Julien Mairal, Priya Goyal, Piotr Bojanowski, and Armand Joulin. 2021. Unsupervised Learning of Visual Features by Contrasting Cluster Assignments. arXiv:2006.09882 [cs.CV]
- Chan and Ren (2023) Weiliang Chan and Qianqian Ren. 2023. Region-Wise Attentive Multi-View Representation Learning For Urban Region Embedding. In Proceedings of the 32nd ACM International Conference on Information and Knowledge Management (Birmingham, United Kingdom) (CIKM ’23). Association for Computing Machinery, New York, NY, USA, 3763–3767. https://doi.org/10.1145/3583780.3615194
- Chen et al. (2020) Ting Chen, Simon Kornblith, Mohammad Norouzi, and Geoffrey Hinton. 2020. A Simple Framework for Contrastive Learning of Visual Representations. In Proceedings of the 37th International Conference on Machine Learning (ICML’20). JMLR.org, Vienna, Article 149, 11 pages.
- Defferrard et al. (2017) Michaël Defferrard, Xavier Bresson, and Pierre Vandergheynst. 2017. Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering. arXiv:1606.09375 [cs, stat]
- Fu et al. (2019) Yanjie Fu, Pengyang Wang, Jiadi Du, Le Wu, and Xiaolin Li. 2019. Efficient Region Embedding with Multi-View Spatial Networks: A Perspective of Locality-Constrained Spatial Autocorrelations. Proceedings of the AAAI Conference on Artificial Intelligence 33, 01 (July 2019), 906–913. https://doi.org/10.1609/aaai.v33i01.3301906
- Gao and Ji (2019) Hongyang Gao and Shuiwang Ji. 2019. Graph Representation Learning via Hard and Channel-Wise Attention Networks. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (Anchorage, AK, USA) (KDD ’19). Association for Computing Machinery, New York, NY, USA, 741–749. https://doi.org/10.1145/3292500.3330897
- Gao et al. (2021) Hongyang Gao, Yi Liu, and Shuiwang Ji. 2021. Topology-Aware Graph Pooling Networks. IEEE Trans. Pattern Anal. Mach. Intell. 43, 12 (dec 2021), 4512–4518. https://doi.org/10.1109/TPAMI.2021.3062794
- Gao et al. (2018) Hongyang Gao, Zhengyang Wang, and Shuiwang Ji. 2018. Large-Scale Learnable Graph Convolutional Networks. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (London, United Kingdom) (KDD ’18). Association for Computing Machinery, New York, NY, USA, 1416–1424. https://doi.org/10.1145/3219819.3219947
- Gao et al. (2022) Tianyu Gao, Xingcheng Yao, and Danqi Chen. 2022. SimCSE: Simple Contrastive Learning of Sentence Embeddings. arXiv:2104.08821 [cs.CL]
- Giorgi et al. (2021) John Giorgi, Osvald Nitski, Bo Wang, and Gary Bader. 2021. DeCLUTR: Deep Contrastive Learning for Unsupervised Textual Representations. In Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing (Volume 1: Long Papers), Chengqing Zong, Fei Xia, Wenjie Li, and Roberto Navigli (Eds.). Association for Computational Linguistics, Online, 879–895. https://doi.org/10.18653/v1/2021.acl-long.72
- Gong et al. (2023) Letian Gong, Youfang Lin, Shengnan Guo, Yan Lin, Tianyi Wang, Erwen Zheng, Zeyu Zhou, and Huaiyu Wan. 2023. Contrastive Pre-training with Adversarial Perturbations for Check-In Sequence Representation Learning. Proceedings of the AAAI Conference on Artificial Intelligence 37, 4 (June 2023), 4276–4283. https://doi.org/10.1609/aaai.v37i4.25546
- Grill et al. (2020) Jean-Bastien Grill, Florian Strub, Florent Altché, Corentin Tallec, Pierre H. Richemond, Elena Buchatskaya, Carl Doersch, Bernardo Avila Pires, Zhaohan Daniel Guo, Mohammad Gheshlaghi Azar, Bilal Piot, Koray Kavukcuoglu, Rémi Munos, and Michal Valko. 2020. Bootstrap your own latent: A new approach to self-supervised Learning. arXiv:2006.07733 [cs.LG]
- Grover and Leskovec (2016) Aditya Grover and Jure Leskovec. 2016. Node2vec: Scalable Feature Learning for Networks. arXiv:1607.00653 [cs, stat]
- Hamilton et al. (2018) William L. Hamilton, Rex Ying, and Jure Leskovec. 2018. Inductive Representation Learning on Large Graphs. arXiv:1706.02216 [cs, stat]
- He et al. (2020) Kaiming He, Haoqi Fan, Yuxin Wu, Saining Xie, and Ross Girshick. 2020. Momentum Contrast for Unsupervised Visual Representation Learning. In 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). IEEE, Seattle, WA, USA, 9726–9735. https://doi.org/10.1109/CVPR42600.2020.00975
- He et al. (2016) Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. 2016. Deep Residual Learning for Image Recognition. In 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). IEEE, Las Vegas, 770–778. https://doi.org/10.1109/CVPR.2016.90
- Hou et al. (2022) Zhenyu Hou, Xiao Liu, Yukuo Cen, Yuxiao Dong, Hongxia Yang, Chunjie Wang, and Jie Tang. 2022. GraphMAE: Self-Supervised Masked Graph Autoencoders. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (Washington DC, USA) (KDD ’22). Association for Computing Machinery, New York, NY, USA, 594–604. https://doi.org/10.1145/3534678.3539321
- Hu et al. (2020b) Ziniu Hu, Yuxiao Dong, Kuansan Wang, Kai-Wei Chang, and Yizhou Sun. 2020b. GPT-GNN: Generative Pre-Training of Graph Neural Networks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (Virtual Event, CA, USA) (KDD ’20). Association for Computing Machinery, New York, NY, USA, 1857–1867. https://doi.org/10.1145/3394486.3403237
- Hu et al. (2020a) Ziniu Hu, Yuxiao Dong, Kuansan Wang, and Yizhou Sun. 2020a. Heterogeneous Graph Transformer. In Proceedings of The Web Conference 2020 (Taipei, Taiwan) (WWW ’20). Association for Computing Machinery, New York, NY, USA, 2704–2710. https://doi.org/10.1145/3366423.3380027
- Huang et al. (2023) Weiming Huang, Daokun Zhang, Gengchen Mai, Xu Guo, and Lizhen Cui. 2023. Learning Urban Region Representations with POIs and Hierarchical Graph Infomax. ISPRS Journal of Photogrammetry and Remote Sensing 196 (Feb. 2023), 134–145. https://doi.org/10.1016/j.isprsjprs.2022.11.021
- Kipf and Welling (2016) Thomas N. Kipf and Max Welling. 2016. Variational Graph Auto-Encoders. arXiv:1611.07308 [cs, stat]
- Kipf and Welling (2017) Thomas N. Kipf and Max Welling. 2017. Semi-Supervised Classification with Graph Convolutional Networks. arXiv:1609.02907 [cs, stat]
- Lee et al. (2021) Seanie Lee, Dong Bok Lee, and Sung Ju Hwang. 2021. Contrastive Learning with Adversarial Perturbations for Conditional Text Generation. arXiv:2012.07280 [cs]
- Liu et al. (2020a) Meng Liu, Hongyang Gao, and Shuiwang Ji. 2020a. Towards Deeper Graph Neural Networks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. Association for Computing Machinery, Portland, 338–348. https://doi.org/10.1145/3394486.3403076 arXiv:2007.09296 [cs, stat]
- Liu et al. (2023) Xiao Liu, Fanjin Zhang, Zhenyu Hou, Li Mian, Zhaoyu Wang, Jing Zhang, and Jie Tang. 2023. Self-Supervised Learning: Generative or Contrastive. IEEE Transactions on Knowledge and Data Engineering 35, 1 (2023), 857–876. https://doi.org/10.1109/TKDE.2021.3090866
- Liu et al. (2020b) Yi Liu, Hao Yuan, Lei Cai, and Shuiwang Ji. 2020b. Deep Learning of High-Order Interactions for Protein Interface Prediction. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (Virtual Event, CA, USA) (KDD ’20). Association for Computing Machinery, New York, NY, USA, 679–687. https://doi.org/10.1145/3394486.3403110
- Luo et al. (2022) Yan Luo, Fu-lai Chung, and Kai Chen. 2022. Urban Region Profiling via Multi-Graph Representation Learning. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management (Atlanta, GA, USA) (CIKM ’22). Association for Computing Machinery, New York, NY, USA, 4294–4298. https://doi.org/10.1145/3511808.3557720
- Qiu et al. (2020) Jiezhong Qiu, Qibin Chen, Yuxiao Dong, Jing Zhang, Hongxia Yang, Ming Ding, Kuansan Wang, and Jie Tang. 2020. GCC: Graph Contrastive Coding for Graph Neural Network Pre-Training. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (Virtual Event, CA, USA) (KDD ’20). Association for Computing Machinery, New York, NY, USA, 1150–1160. https://doi.org/10.1145/3394486.3403168
- Radford et al. (2021) Alec Radford, Jong Wook Kim, Chris Hallacy, Aditya Ramesh, Gabriel Goh, Sandhini Agarwal, Girish Sastry, Amanda Askell, Pamela Mishkin, Jack Clark, Gretchen Krueger, and Ilya Sutskever. 2021. Learning Transferable Visual Models From Natural Language Supervision. arXiv:2103.00020 [cs]
- Ramesh et al. (2022) Aditya Ramesh, Prafulla Dhariwal, Alex Nichol, Casey Chu, and Mark Chen. 2022. Hierarchical Text-Conditional Image Generation with CLIP Latents. arXiv:2204.06125 [cs]
- Rethmeier and Augenstein (2023) Nils Rethmeier and Isabelle Augenstein. 2023. A Primer on Contrastive Pretraining in Language Processing: Methods, Lessons Learned, and Perspectives. ACM Comput. Surv. 55, 10, Article 203 (feb 2023), 17 pages. https://doi.org/10.1145/3561970
- Schlichtkrull et al. (2018) Michael Schlichtkrull, Thomas N. Kipf, Peter Bloem, Rianne van den Berg, Ivan Titov, and Max Welling. 2018. Modeling Relational Data with Graph Convolutional Networks. In The Semantic Web: 15th International Conference, ESWC 2018, Heraklion, Crete, Greece, June 3–7, 2018, Proceedings (Heraklion, Greece). Springer-Verlag, Berlin, Heidelberg, 593–607. https://doi.org/10.1007/978-3-319-93417-4_38
- Sun et al. (2020) Fan-Yun Sun, Jordan Hoffmann, Vikas Verma, and Jian Tang. 2020. InfoGraph: Unsupervised and Semi-supervised Graph-Level Representation Learning via Mutual Information Maximization. arXiv:1908.01000 [cs.LG]
- Suresh et al. (2021) Susheel Suresh, Pan Li, Cong Hao, and Jennifer Neville. 2021. Adversarial Graph Augmentation to Improve Graph Contrastive Learning. In Advances in Neural Information Processing Systems, M. Ranzato, A. Beygelzimer, Y. Dauphin, P.S. Liang, and J. Wortman Vaughan (Eds.), Vol. 34. Curran Associates, Inc., Online, 15920–15933. https://proceedings.neurips.cc/paper_files/paper/2021/file/854f1fb6f65734d9e49f708d6cd84ad6-Paper.pdf
- Tang et al. (2015) Jian Tang, Meng Qu, Mingzhe Wang, Ming Zhang, Jun Yan, and Qiaozhu Mei. 2015. LINE: Large-Scale Information Network Embedding. In Proceedings of the 24th International Conference on World Wide Web (Florence, Italy) (WWW ’15). International World Wide Web Conferences Steering Committee, Republic and Canton of Geneva, CHE, 1067–1077. https://doi.org/10.1145/2736277.2741093
- Tian et al. (2020) Yonglong Tian, Chen Sun, Ben Poole, Dilip Krishnan, Cordelia Schmid, and Phillip Isola. 2020. What makes for good views for contrastive learning?. In Proceedings of the 34th International Conference on Neural Information Processing Systems (¡conf-loc¿, ¡city¿Vancouver¡/city¿, ¡state¿BC¡/state¿, ¡country¿Canada¡/country¿, ¡/conf-loc¿) (NIPS ’20). Curran Associates Inc., Red Hook, NY, USA, Article 573, 13 pages.
- Tibshirani (1996) Robert Tibshirani. 1996. Regression Shrinkage and Selection via the Lasso. Journal of the Royal Statistical Society. Series B (Methodological) 58, 1 (1996), 267–288. https://doi.org/10.1111/j.2517-6161.1996.tb02080.x arXiv:2346178
- van den Oord et al. (2019) Aaron van den Oord, Yazhe Li, and Oriol Vinyals. 2019. Representation Learning with Contrastive Predictive Coding. arXiv:1807.03748 [cs.LG]
- Vaswani et al. (2017) Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, and Illia Polosukhin. 2017. Attention Is All You Need. arXiv:1706.03762 [cs]
- Veličković et al. (2018a) Petar Veličković, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Liò, and Yoshua Bengio. 2018a. Graph Attention Networks. arXiv:1710.10903 [cs, stat]
- Veličković et al. (2018b) Petar Veličković, William Fedus, William L. Hamilton, Pietro Liò, Yoshua Bengio, and R. Devon Hjelm. 2018b. Deep Graph Infomax. arXiv:1809.10341 [cs, math, stat]
- Wang and Li (2017) Hongjian Wang and Zhenhui Li. 2017. Region Representation Learning via Mobility Flow. In Proceedings of the 2017 ACM on Conference on Information and Knowledge Management. ACM, Singapore Singapore, 237–246. https://doi.org/10.1145/3132847.3133006
- Wang et al. (2021) Xiao Wang, Nian Liu, Hui Han, and Chuan Shi. 2021. Self-Supervised Heterogeneous Graph Neural Network with Co-Contrastive Learning. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining (Virtual Event, Singapore) (KDD ’21). Association for Computing Machinery, New York, NY, USA, 1726–1736. https://doi.org/10.1145/3447548.3467415
- Wang et al. (2022) Yuyang Wang, Jianren Wang, Zhonglin Cao, and Amir Barati Farimani. 2022. Molecular Contrastive Learning of Representations via Graph Neural Networks. Nat Mach Intell 4, 3 (March 2022), 279–287. https://doi.org/10.1038/s42256-022-00447-x
- Wang and Ji (2023) Zhengyang Wang and Shuiwang Ji. 2023. Second-Order Pooling for Graph Neural Networks. IEEE Transactions on Pattern Analysis and Machine Intelligence 45, 6 (2023), 6870–6880. https://doi.org/10.1109/TPAMI.2020.2999032
- Wei et al. (2019) Chen Wei, Lingxi Xie, Xutong Ren, Yingda Xia, Chi Su, Jiaying Liu, Qi Tian, and Alan L. Yuille. 2019. Iterative Reorganization With Weak Spatial Constraints: Solving Arbitrary Jigsaw Puzzles for Unsupervised Representation Learning. In 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). IEEE, Long Beach, 1910–1919. https://doi.org/10.1109/CVPR.2019.00201
- Wu et al. (2022) Shangbin Wu, Xu Yan, Xiaoliang Fan, Shirui Pan, Shichao Zhu, Chuanpan Zheng, Ming Cheng, and Cheng Wang. 2022. Multi-Graph Fusion Networks for Urban Region Embedding. arXiv:2201.09760 [cs]
- Wu et al. (2018) Zhenqin Wu, Bharath Ramsundar, Evan N. Feinberg, Joseph Gomes, Caleb Geniesse, Aneesh S. Pappu, Karl Leswing, and Vijay Pande. 2018. MoleculeNet: A Benchmark for Molecular Machine Learning. Chem. Sci. 9, 2 (2018), 513–530. https://doi.org/10.1039/C7SC02664A
- Xie et al. (2023) Yaochen Xie, Zhao Xu, Jingtun Zhang, Zhengyang Wang, and Shuiwang Ji. 2023. Self-Supervised Learning of Graph Neural Networks: A Unified Review. IEEE Transactions on Pattern Analysis and Machine Intelligence 45, 2 (2023), 2412–2429. https://doi.org/10.1109/TPAMI.2022.3170559
- Xu et al. (2021) Dongkuan Xu, Wei Cheng, Dongsheng Luo, Haifeng Chen, and Xiang Zhang. 2021. InfoGCL: Information-Aware Graph Contrastive Learning. In Advances in Neural Information Processing Systems, A. Beygelzimer, Y. Dauphin, P. Liang, and J. Wortman Vaughan (Eds.). Curran Associates, Inc., online, 1. https://openreview.net/forum?id=519VBzfEaKW
- Xu et al. (2019) Keyulu Xu, Weihua Hu, Jure Leskovec, and Stefanie Jegelka. 2019. How Powerful Are Graph Neural Networks? arXiv:1810.00826 [cs, stat]
- Yan et al. (2021) Yuanmeng Yan, Rumei Li, Sirui Wang, Fuzheng Zhang, Wei Wu, and Weiran Xu. 2021. ConSERT: A Contrastive Framework for Self-Supervised Sentence Representation Transfer. arXiv:2105.11741 [cs.CL]
- Yao et al. (2018) Zijun Yao, Yanjie Fu, Bin Liu, Wangsu Hu, and Hui Xiong. 2018. Representing Urban Functions through Zone Embedding with Human Mobility Patterns. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence. International Joint Conferences on Artificial Intelligence Organization, Stockholm, Sweden, 3919–3925. https://doi.org/10.24963/ijcai.2018/545
- Ying et al. (2019) Rex Ying, Jiaxuan You, Christopher Morris, Xiang Ren, William L. Hamilton, and Jure Leskovec. 2019. Hierarchical Graph Representation Learning with Differentiable Pooling. arXiv:1806.08804 [cs.LG]
- You et al. (2020) Yuning You, Tianlong Chen, Yongduo Sui, Ting Chen, Zhangyang Wang, and Yang Shen. 2020. Graph Contrastive Learning with Augmentations. In Advances in Neural Information Processing Systems, H. Larochelle, M. Ranzato, R. Hadsell, M.F. Balcan, and H. Lin (Eds.), Vol. 33. Curran Associates, Inc., Online, 5812–5823. https://proceedings.neurips.cc/paper_files/paper/2020/file/3fe230348e9a12c13120749e3f9fa4cd-Paper.pdf
- Yuan and Ji (2020) Hao Yuan and Shuiwang Ji. 2020. StructPool: Structured Graph Pooling via Conditional Random Fields. In 8th International Conference on Learning Representations, ICLR 2020, Addis Ababa, Ethiopia, April 26-30, 2020. OpenReview.net, Online, 1. https://openreview.net/forum?id=BJxg_hVtwH
- Yuan et al. (2020) Hao Yuan, Jiliang Tang, Xia Hu, and Shuiwang Ji. 2020. XGNN: Towards Model-Level Explanations of Graph Neural Networks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (Virtual Event, CA, USA) (KDD ’20). Association for Computing Machinery, New York, NY, USA, 430–438. https://doi.org/10.1145/3394486.3403085
- Zhang et al. (2019b) Chuxu Zhang, Dongjin Song, Chao Huang, Ananthram Swami, and Nitesh V. Chawla. 2019b. Heterogeneous Graph Neural Network. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (Anchorage, AK, USA) (KDD ’19). Association for Computing Machinery, New York, NY, USA, 793–803. https://doi.org/10.1145/3292500.3330961
- Zhang et al. (2017) Chao Zhang, Keyang Zhang, Quan Yuan, Haoruo Peng, Yu Zheng, Tim Hanratty, Shaowen Wang, and Jiawei Han. 2017. Regions, Periods, Activities: Uncovering Urban Dynamics via Cross-Modal Representation Learning. In Proceedings of the 26th International Conference on World Wide Web. International World Wide Web Conferences Steering Committee, Perth Australia, 361–370. https://doi.org/10.1145/3038912.3052601
- Zhang et al. (2020) Mingyang Zhang, Tong Li, Yong Li, and Pan Hui. 2020. Multi-View Joint Graph Representation Learning for Urban Region Embedding. In Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence. International Joint Conferences on Artificial Intelligence Organization, Yokohama, Japan, 4431–4437. https://doi.org/10.24963/ijcai.2020/611
- Zhang et al. (2019a) Yunchao Zhang, Yanjie Fu, Pengyang Wang, Xiaolin Li, and Yu Zheng. 2019a. Unifying Inter-region Autocorrelation and Intra-region Structures for Spatial Embedding via Collective Adversarial Learning. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. ACM, Anchorage AK USA, 1700–1708. https://doi.org/10.1145/3292500.3330972
- Zhou et al. (2023) Silin Zhou, Dan He, Lisi Chen, Shuo Shang, and Peng Han. 2023. Heterogeneous Region Embedding with Prompt Learning. AAAI 37, 4 (June 2023), 4981–4989. https://doi.org/10.1609/aaai.v37i4.25625
- Zhu et al. (2021) Yanqiao Zhu, Yichen Xu, Feng Yu, Qiang Liu, Shu Wu, and Liang Wang. 2021. Graph Contrastive Learning with Adaptive Augmentation. In Proceedings of the Web Conference 2021 (Ljubljana, Slovenia) (WWW ’21). Association for Computing Machinery, New York, NY, USA, 2069–2080. https://doi.org/10.1145/3442381.3449802