Enhanced symmetry energy bears universality of the r-process
Abstract
The abundance of about half of the stable nuclei heavier than iron via the rapid neutron capture process or -process is intimately related to the competition between neutron capture and -decay rates, which ultimately depends on the binding energy of neutron-rich nuclei. The well-known Bethe-Weizsäcker semi-empirical mass formula[1, 2] describes the binding energy of ground states – i.e. nuclei with temperatures of MeV – with the symmetry energy parameter converging between MeV for heavy nuclei. Here we find an unexpected enhancement of the symmetry energy at higher temperatures, MeV, from the available data of giant dipole resonances built on excited states. Although these are likely the temperatures where seed elements are created – during the cooling down of the ejecta following neutron-star mergers[3] or collapsars[4] – the fact that the symmetry energy remains constant between MeV, suggests a similar trend down to MeV, where neutron-capture may start occurring. Calculations using this relatively larger symmetry energy yield a reduction of the binding energy per nucleon for heavy neutron-rich nuclei and inhibits radiative neutron-capture rates. This results in a substantial close in of the neutron dripline – where nuclei become unbound – which elucidates the long sought universality of heavy-element abundances through the -process; as inferred from the similar abundances found in extremely metal-poor stars and the Sun.
keywords:
symmetry energy , dipole polarizability , photo-absorption cross sections , r-process , neutron driplineurl]https://nuclear.uwc.ac.za
The binding energy of a nucleus with protons and neutrons can be described by the well-known Bethe-Weizsäcker semi-empirical mass formula (SEMF) [1, 2],
| (1) | |||||
where is the mass number and and are the volume, surface, Coulomb, symmetry energy and pairing coefficients, respectively. The symmetry energy, , reduces the total binding energy of a nucleus as the neutron-proton asymmetry becomes larger, i.e. for , and yields the typical negative slope of the binding energy curve[5] for . It is divided by A to reduce its importance for heavy nuclei, and it depends on the mass dependency of . Its convergence for heavy nuclei establishes the frontiers of the neutron dripline for particle-unbound nuclei and eventually leads to the disappearance of protons at extreme nuclear densities[6].
Furthermore, is relevant to understanding neutron skins[7], the effect of three-nucleon forces[8] and – through the equation of state (EoS) – supernovae cores, neutron stars and binary mergers[9, 10, 11]. The latter are the first known astrophysical site where heavy elements are created through the rapid neutron-capture or -process[12, 13]. The identification of heavy elements in neutron star mergers is supported by the short duration gamma-ray bursts via their infrared afterglow[14] – only understood by the opacities of heavy nuclei – as well as blueshifted Sr II absorption lines[15], following the expansion speed of the ejecta gas at . Mergers are expected to be the only source for the creation of elements above lead and bismuth, as inferred from the very scarce abundance of actinides in the solar system[16].
The universality of the -process for the heaviest elements with is further inferred from the similar abundance patterns observed in both extremely metal-poor stars and the Sun[17, 18]. Other potential sources of heavy elements involve different types of supernova (e.g. collapsars [4] – the supernova-triggering collapse of rapidly rotating massive stars – and type-II supernova[12]), which need to be considered in order to explain all neutron-capture abundances[19, 20].
It is the motivation of this work to understanding the limits of the neutron dripline and heavy-element production by investigating at different temperatures using available data of potential interest to the -process; namely, data from photoabsorption cross sections, binding energies and giant dipole resonances.
Generally, is parametrized using the leptodermous approximation of Myers and Swiatecki, where [21],
| (2) |
which considers the modification of the volume symmetry energy, , by the surface symmetry energy . This particular leptodermous parametrization was chosen on the account of its better fit to the masses of isobaric nuclei [22]. Constraints on these parameters have been investigated using experimental and theoretical information concerning properties of ground states, i.e. at MeV[23, 24].
The giant dipole resonance (GDR) represents the main contribution to the absorption and emission of electromagnetic radiation (photons) in nuclei[25]. The dynamics of this quantum collective excitation is characterized by the inter-penetrating motion of proton and neutron fluids out of phase[26], which results from the density-dependent symmetry energy, , acting as a restoring force[25]; where , and are the neutron, proton and total density, respectively, which spread uniformly throughout the nucleus.
The ratio of the induced dipole moment to an applied constant electric field yields the static nuclear polarizability, . Using the hydrodynamic model and assuming inter-penetrating proton and neutron fluids with a well-defined nuclear surface of radius fm and as the potential energy of the liquid drop, Migdal[26] obtains the following relation between the static nuclear polarizability, , and ,
| (3) |
where fm, MeV fm in the c.g.s. system, and a constant value of MeV was utilized.
Alternatively, can be calculated for the ground states of nuclei using second-order perturbation theory[27] following the sum rule,
| (4) | |||||
| (5) | |||||
| (6) |
where is the -ray energy corresponding to a transition connecting the ground state and an excited state , the nucleon mass, the dimensionless oscillator strength for transitions [27] and the second moment of the total electric-dipole photo-absorption cross section,
| (7) |
where is the total photo-absorption cross section, which generally includes photoneutron and available photoproton and photofission cross sections [28], in competition in the GDR region [29, 30]. By comparing Eqs. 3 and 6, a mass-dependent symmetry energy, (A), is extracted in units of MeV,
| (8) |
Empirical evaluations reveal that can also be approximated by , where the dipole polarizability parameter measures GDR deviations between experimental and hydrodynamic model predictions[31].
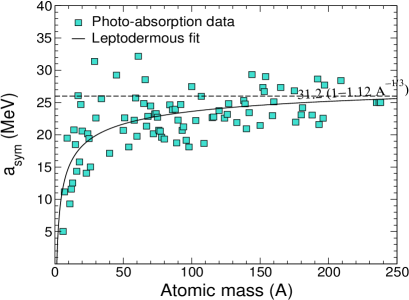
Figure 1 shows the distribution of for the ground state of stable isotopes, along the nuclear landscape, determined from empirical values. Data include all available emission channels. The contribution of cross sections are evident in light nuclei, which significantly reduces the symmetry energy. For heavy nuclei, cross sections are dominant because of the higher Coulomb barrier. A fit to the data using Eq. 2 (solid line) yields MeV, with an RMS deviation of 22%[34]. Unfortunately, cross-section data are very scarce, which directly affects the trend for in Fig. 1.
In addition, Tian and co-workers determined MeV from a global fit to the binding energies of isobaric nuclei with mass number [22] – extracted from the 2012 atomic mass evaluation[35] – with MeV being the bulk symmetry energy coefficient and the surface-to-volume ratio. Similar coefficients are calculated in Refs.[9, 36]. Within this approach, the extraction of only depends on the Coulomb energy term in the SEMF and shell effects[37] – which are both included [22] – and presents a maximum energy around 23 MeV. This description of has been used to explain the enhanced values observed for low-mass nuclei[34].
The symmetry energy is the fundamental parameter that characterizes the energy of the GDR, , within the Steinwedel-Jensen (SJ) model of proton and neutron compressible fluids moving within the rigid surface of the nucleus[38]. Danos improved the SJ model by including the GDR width, [39, 25] in the second-sound hydrodynamic model[39, 25], where and are related to as[30],
| (9) | |||||
where is the real eigenvalue of , with the boundary condition , and has a value of for a spherical nucleus[40]. For quadrupole deformed nuclei with an eccentricity of , where and are the half axes and the deformation parameter, the GDR lineshape splits into two peaks with similar values of and [39]. For deformed nuclei, we estimate a similar equation to Eq. 9, but using the average centroid energy and the FWHM of the total Lorentzian (see e.g.[41]). Uncertainties in the quoted values arise from the error propagation of Eq. 9.
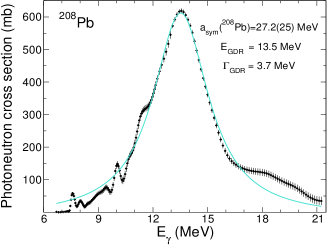
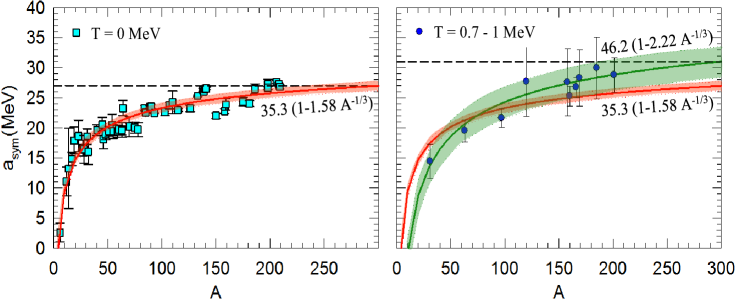
The GDR cross-section data for each nucleus were obtained from the EXFOR and ENDF databases [32, 33] and fitted with one or two Lorentzian curves to extract and , as shown e.g. in Fig. 2 for 208Pb. The data set for each nucleus was selected based on the number of data points, experimental method and energy range. In this work, the maximum integrated -ray energy, E, was in the range 20–50 MeV, therefore excluding contributions resulting from high energy effects such as pion exchange and other meson resonances. The resulting distribution of is shown in the left panel of Fig. 3, which converges at approximately 27 MeV for heavy nuclei. It is reassuring that the two methods based on photoabsorption cross-section data — namely extracted from values and parameters of GDRs built on ground states – present similar trends.
Data obtained from GDR parameters at can also be fitted to Eq. 2, which yields MeV (red solid band in Fig. 3), with an RMS deviation of 15%. Larger values of and were determined by Berman using Eq. 9 for 29 nuclei ranging from to 209 [42]. Furthermore, Berman argued that assuming a surface binding energy coefficient of MeV in the SEMF, the large symmetry to surface energy ratio, , favors – as a result of a steeper slope of the binding energy curve for heavy nuclei – a close-in neutron dripline for heavy elements; hence, constraining the reaction network that produces heavy elements by the -process in neutron mergers and supernovae. Using our value of and MeV, a more reasonable ratio of is determined. Slightly smaller values of MeV are also found in the literature[5, 36], yielding .
Furthermore, it is interesting to investigate the behavior of using the available information on GDRs built on excited states, below the critical temperatures and spins where the GDR width starts broadening; i.e. for moderate average temperatures of MeV and spins below the critical angular momentum . In fact, similar centroid energies, , and resonance strengths, – relative to the Thomas–Reiche–Kuhn sum rule [27] – to those found for the ground-state counterparts [29, 43] indicate a common physical origin for all GDRs, in concordance with the Brink–Axel hypothesis that assumes that a GDR can be built on every state in a nucleus [44, 45].
Applying again Eq. 9, the right panel of Fig. 3 shows values for GDRs built on excited states in slightly-deformed nuclei 31P [46], 63Cu [47], 97Tc [48], 120Sn [49] and 201Tl [50], as well as for well-deformed nuclei in the mass region (158,160,166Er, 169Tm and 185Re [41, 51, 52]). With an average temperature between and 1.0 MeV and below , these nuclei were selected to investigate the symmetry energy at temperatures relevant to the r-process nucleosynthesis. Surprisingly, values for heavy nuclei are relatively larger than previously observed at MeV. A fit to the data using Eq. 2 (green solid line in Fig. 3) yields MeV, with an RMS deviation of 6%. A value of MeV for heavy nuclei yields larger values of , and (again for MeV). Two bands showing the loci limits of the two fitting curves at and MeV are shown for comparison. Such a distinct behaviour could clearly affect nucleosynthesis of heavy elements via the -process during the cooling down of the ejecta.
Lighter or heavier seed nuclei are generally produced depending on the density and temperature of the ejecta gas. Assuming nuclear-statistical equilibrium – when forward and reverse reactions are balanced – abundances follow a Maxwell-Boltzmann distribution where lighter seed nuclei are favoured at very high temperatures () and heavier nuclei are favoured at very high densities (), as those found in the ejecta of neutron-star mergers [3]. At temperatures below MeV (or K), seed nuclei are produced before charge reactions freeze out – impeded by the Coulomb barrier – at about MeV (or K). Thereafter, heavy nuclei are produced through subsequent neutron capture until neutron reactions freeze out – as neutrons are finally consumed – at a few 108 K.
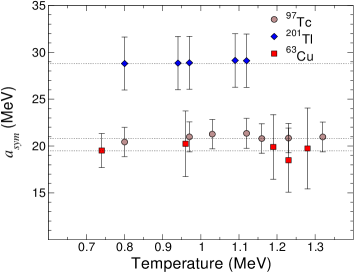
Our work may not be sensitive to the lower temperatures occurring during neutron capture in neutron-star mergers, which likely range from K [53] to K [54] (i.e. in the range from to 0.43 MeV, respectively). Nevertheless, Fig. 4 shows that the symmetry energy does not change with temperature in the [0.74,1.3] MeV range, which suggests that this relation may still hold at lower temperatures.
Such an increase in the symmetry energy results from the change in the effective mass of the nucleon, which decreases as increases in the temperature interval MeV [55]. The temperature dependence of the symmetry energy has been studied within the liquid-drop and Fermi gas models [56], where an effective nucleon mass – the so-called ‘’ mass – is introduced to account for the non-locality of the Hartree-Fock potential. This leads to an increase in the centroid energy of the GDR and, hence, the symmetry energy of medium and heavy mass nuclei also increases by approximately 8% at MeV [55]. In the current work, we notice a slight increase of 3-5% in the centroid energy at MeV as compared with the ground-state values for nearly-spherical 120Sn [57], 208Pb [58] and 201Tl [50] nuclei as well as for the deformed nuclei in the mass region [41, 51, 52]. Although such an increase is within the experimental errors, it leads to a distinct systematic behaviour, as shown in the right panel of Fig. 3.
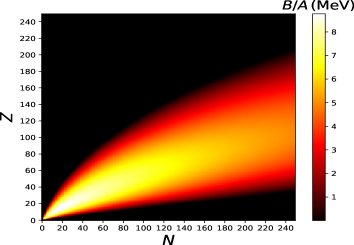
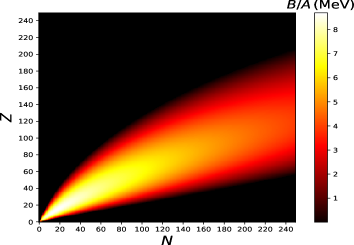
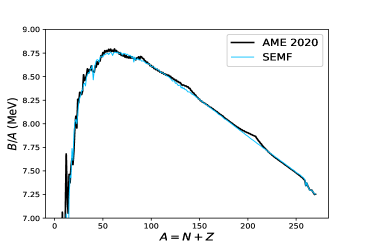
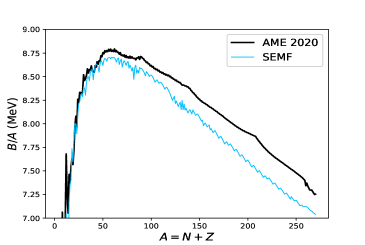
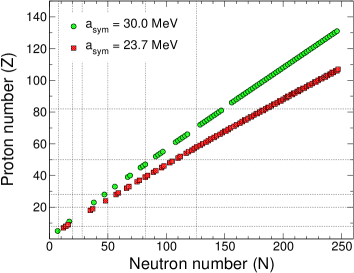
Finally, the effects from the larger symmetry energy at MeV are illustrated in Fig. 5, which shows the corresponding nuclear charts (top) and binding energy curves (bottom) using MeV[60] (left) and MeV (right), respectively. The nuclear chart determined using MeV illustrates a substantial close-in of the neutron dripline, as a result of the decreasing binding energy per nucleon in neutron-rich nuclei. For instance, the dripline closes in from 254Pt to 220Pt for and MeV, respectively. Figure 6 shows the respective neutron driplines and clearly illustrates the dramatic effect of an enhanced symmetry energy in the production of heavy elements, which constrains exotic -process paths and plausibly explains the universality of -process abundances inferred from the observation of extremely metal-poor stars and our Sun.
Consequently, such an increase in the symmetry energy leads to the reduction of radiative neutron capture rates as neutron-rich nuclei become less bound. The corresponding change in the capture cross section has been calculated using TALYS [61] and EMPIRE [62] codes by changing only the mass excess with standard input parameters. Both codes yield similar results with a reduction of the neutron-capture cross section by a factor of the order of 102 in the mass region relevant to the -process. More detailed calculations will be presented in a separate manuscript. These findings support the rapid drop of the neutron capture rates at increasing neutron excesses inferred from Goriely’s microscopic calculations at K [12].
More experimental data regarding GDRs built on excited states below MeV are crucially needed in order to elucidate the nature of the symmetry energy as a function of temperature. Modern high-efficient spectrometers such as GAMKA in South Africa [63] – with up to 30 HPGe clover and LaBr3 detectors – may provide such data.
References
- [1] C. F. von Weizsäcker, Zur Theorie der Kernmassen. Z. Phys. 96 (1935) 431.
- [2] H. A. Bethe and R. F. Bacher, Stationary States of Nuclei, Rev. Mod. Phys. 8 (1936) 82.
- [3] F. -K. Thielemann, M. Eichler, I. V. Panov, and B. Wehmeyer, Neutron Star Mergers and Nucleosynthesis of Heavy Elements, Annu. Rev. Nucl. Part. Sci. 67 (2017) 253.
- [4] D. M. Siegel, J. Barnes, and B. D. Metzger, Collapsars as a major source of r-process elements, Nature 569 (2019) 241.
- [5] K. S. Krane, Introductory Nuclear Physics, Wiley (1987).
- [6] M. Kutschera, Nuclear symmetry energy and structure of dense matter in neutron stars, Phys. Lett. B 340 (1994) 1.
- [7] J. Piekarewicz, B. K. Agrawal, G. Colò, W. Nazarewicz, N. Paar, P.-G. Reinhard, X. Roca-Maza, and D. Vretenar, Electric dipole polarizability and the neutron skin, Phys. Rev. C 85 (2012) 041302(R).
- [8] K. Hebeler and A. Schwenk, Symmetry energy, neutron skin, and neutron star radius from chiral effective field theory interactions, Eur. Phys. J. A 50 (2014) 11.
- [9] A. W. Steiner, M. Prakash, J. M. Lattimer, and P. J. Ellis, Isospin asymmetry in nuclei and neutron stars, Phys. Rep. 411 (2005) 325.
- [10] J. M. Latimer, Symmetry energy in nuclei and neutron stars, Nucl. Phys. A 928 (2014) 276.
- [11] J. M. Pearson, N. Chamel, A. F. Fantina, and S. Goriely, Symmetry energy: nuclear masses and neutron stars, Eur. Phys. J. A 50 (2014) 43.
- [12] S. Goriely, The r-process nucleosynthesis: a continued challenge for nuclear physics, Nucl. Phys. A 718 (2003) 287c.
- [13] J. J. Cowan, C. Sneden, J. E. Lawler, A. Aprahamian, M. Wiescher, K. Langanke, G. Martínez-Pinedo, and F. -K. Thielemann, Origin of the heaviest elements: The rapid neutron-capture process, Rev. Mod. Phys. 93 (2021) 015002.
- [14] B. D. Metzger, Kilonova, Living Reviews in Relativity 20 (2017) 3.
- [15] D. Watson et al., Identification of strontium in the merger of two neutron stars, Nature 574 (2019) 497.
- [16] I. Bartos and S. Marka, A nearby neutron-star merger explains the actinide abundances in the early Solar System. Nature 569 (2019) 85.
- [17] N. Christlieb et al., A stellar relic from the early Milky Way, Nature 419 (2002) 904.
- [18] C. Sneden, J. J. Cowan, and R. Gallino, Neutron-capture elements in the early galaxy, Annu. Rev. Astron. Astrophys. 46 (2008) 241.
- [19] Y.-Z. Qian, Supernovae versus neutron star mergers as the major r-process sources, Astrophys. J. 534 (2000) L67.
- [20] W. Aoki, S. Honda, T. C. Beers, T. Kajino, H. Ando, J. E. Norris, S. G. Ryan, H. Izumiura, K. Sadakane, and M. Takada-Hidai, Spectroscopic studies of very metal-poor stars with the Subaru high dispersion spectrograph. III. Light neutron-capture elements, ApJ 632 (2005) 611.
- [21] W. D. Myers and W. J. Swiatecki, Average nuclear properties, Ann. Phys. 55 (1969) 395.
- [22] J. Tian, H. Cui, K. Zheng, and N. Wang, Effect of Coulomb energy on the symmetry energy coefficients of finite nuclei, Phys. Rev. C 90 (2014) 024313.
- [23] J. M. Lattimer and Y. Lim, Constraining the symmetry parameters of the nuclear interaction, ApJ 771 (2013) 51.
- [24] L. Trippa, G. Colò, and E. Vigezzi, Giant dipole resonance as a quantitative constraint on the symmetry energy, Phys. Rev. C 77 (2008) 061304(R).
- [25] B. L. Berman and S. C. Fultz, Measurements of the giant dipole resonance with monoenergetic photons, Rev. Mod. Phys. 47 (1975) 713.
- [26] A. B. Migdal, Quadrupole and dipole gamma-radiation of nuclei, J. Exptl. Theoret. Phys. U.S.S.R. 15 (1945) 81.
- [27] J. S. Levinger, Nuclear Photo-Disintegration. Oxford University Press, Oxford (1960).
- [28] T. Kawano et al., IAEA Photonuclear Data Library 2019, Nucl. Data Sheets 163 (2020) 109.
- [29] K. A. Snover, Giant Resonances in Excited Nuclei, Ann. Rev. Nucl. Part. Sci. 36 (1986) 545.
- [30] R. Bergere, Lecture Notes in Physics 61, Photonuclear Reactions I, (Springer-Verlag, 1977).
- [31] J. N. Orce, Polarizability effects in atomic nuclei, Int. J. Mod. Phys. E 29 (2020) 2030002.
- [32] EXFOR: Experimental Nuclear Reaction Data. https://www-nds.iaea.org/exfor/exfor.htm
- [33] ENDF: Evaluated Nuclear Data File. https://www-nds.iaea.org/exfor/endf.htm (iaea.org)
- [34] J. N. Orce, New formulas for the moment of the photoabsorption cross section, , Phys. Rev. C 91 (2015) 064602.
- [35] M. Wang, G. Audi, A. H. Wapstra, and F. G. Kondev, The AME2016 atomic mass evaluation (II), Chin. Phys. C 36 (2012) 1603.
- [36] P. Danielewicz, Surface symmetry energy, Nucl. Phys. A 727 (2003) 233.
- [37] H. Koura, T. Tachibana, M. Uno, and M. Yamada, Nuclidic mass formula on a spherical basis with an improved even-odd term, Prog. Theor. Phys. 113 (2005) 305.
- [38] H. Steinwedel, J. H. D. Jensen, and P. Jensen, Nuclear dipole vibrations, Phys. Rev. 79 (1950) 1019.
- [39] M. Danos, On the long-range correlation model of the photonuclear effect, Nucl. Phys. 5 (1958) 23.
- [40] Lord Rayleigh, The Theory of Sound, second edition (MacMillan Co., London, 1896) Chapter XVII.
- [41] J. J. Gaardhøje, A. M. Bruce, and B. Herskind, Nuclear collective motion under extreme conditions: the GDR at very high spin and temperature, Nucl. Phys. A 482 (1988) 121c.
- [42] B. L. Berman, Mass variation of the nuclear symmetry energy. Proceedings of the International Conference on Photonuclear Reactions and Applications, Pacific Grove, California, ed. by B. L. Berman (Lawrence Livermore Laboratory, Livermore) (1973) 569.
- [43] J. J. Gaardhøje, Nuclear structure at high excitation energy studied with giant resonances, Annu. Rev. Nucl. Part. Sci. 42 (1992) 483.
- [44] D. Brink, Some aspects of the interaction of light with matter. Doctoral thesis, Oxford University, 1955 (unpublished).
- [45] P. Axel, Electric dipole ground-state transition width strength function and 7-Mev photon interactions, Phys. Rev. 126 (1962) 671.
- [46] D. Mondal et al. Study of giant dipole resonance in hot rotating light mass nucleus 31P, Phys. Lett. B 784 (2018) 423.
- [47] M. Kicińska-Habior, K. A. Snover, C. A. Gossett, J. A. Behr, G. Feldman, H. K. Glatzel, J. H. Gundlach, and E. F. Garman, Statistical giant dipole resonance decay of highly excited states of 63Cu, Phys. Rev. C 36 (1987) 612.
- [48] B. Dey et al., Probing the critical behavior in the evolution of GDR width at very low temperatures in A100 mass region, Phys. Lett. B 731 (2014) 92.
- [49] P. Heckman et al., Low-temperature measurement of the giant dipole resonance width, Phys. Lett. B 555 (2003) 43.
- [50] D. Pandit, S. Mukhopadhyay, S. Pal, A. De, and S. R. Banerjee, Critical behavior in the variation of GDR width at low temperature, Phys. Lett. B 713 (2012) 434.
- [51] C. A. Gossett, K. A. Snover, J. A. Behr, G. Feldman, and J. L. Osborne, Deformation of heated nuclei observed in the statistical decay of the giant dipole resonance, Phys. Rev. Lett. 54 (1985) 1486.
- [52] D. Pandit et al., Puzzle of collective enhancement in the nuclear level density, Phys. Lett. B 816 (2021) 136173.
- [53] S. Goriely, A. Bauswein, and H. -T. Janka, r-process nucleosynthesis in dynamically ejected matter of neutron star mergers, ApJ Lett. 732 (2011) L32.
- [54] Meng-Ru Wu, R. Fernández, G. Martínez-Pinedo, and B. D. Metzger, Production of the entire range of r-process nuclides by black hole accretion disc outflows from neutron star mergers, MNRAS 463 (2016) 2323.
- [55] P. Donati, P. M. Pizzochero, P. F. Bortignon, and R. A. Broglia, Temperature dependence of the nucleon effective mass and the physics of stellar collapse, Phys. Rev. Lett. 72 (1994) 2835.
- [56] P. F. Bortignon, A. Bracco, and R. A. Broglia, Giant Resonances: Nuclear structure at finite temperature, Contemporary Concepts in Physics (Routledge, 1998).
- [57] P. Heckman et al., Low-temperature measurement of the giant dipole resonance width, Phys. Lett. B 555 (2003) 43.
- [58] T. Baumann et al., Evolution of the giant dipole resonance in excited 120Sn and 208Pb nuclei populated by inelastic alpha scattering, Nucl. Phys. A 635 (1998) 428.
- [59] M. Wang, W. J. Huang, F. G. Kondev, G. Audi, and S. Naim, The AME 2020 atomic mass evaluation (II), Chinese Phys. C 45 (2021) 030003.
- [60] J. W. Rohlf, "Modern Physics from alpha to Z0", Wiley (1994).
- [61] A. J. Koning, S. Hilaire, and S. Goriely, (2015) Talys User Manual, http:// www.talys.eu/en/download-talys/
- [62] M. Herman, et al (2007) EMPIRE: nuclear reaction model code system for data evaluation. Nucl Data Sheets. https ://doi. org/10.1016/j.nds.2007.11.00310 8:2655-2715
- [63] https://www.nrf.ac.za/media-room/news/nrf-funds-state-art-nuclear-spectrometer-uwc