Enhanced Superconductivity in Bilayer PtTe2 by Alkali-Metal Intercalations
Abstract
Layered platinum tellurium (PtTe2) were recently synthesized with controllable layer numbers down to monolayer limit. Using calculation based on anisotropic Midgal-Eliashberg formalism, we show that by rubidium (Rb) intercalation, weak superconductivity in bilayer PtTe2 can be significantly boosted with superconducting = 8 K in the presence of spin-orbit coupling (SOC). The intercalant on one hand mediates the interlayer coupling and serve as an electron donor, leading to large density of states at Fermi energy. On the other hand, it increases the mass-enhancement parameter with electron-phonon coupling strength comparable to that of Pt. The potassium intercalated bilayer PtTe2 has a comparable to the case of Rb intercalation. The relatively high with SOC combined with experimental accessible crystal structures suggest that these superconductors are promising platforms to study the novel quantum physics associated with two-dimensional superconductivity, such as the recently proposed type-II Ising superconductivity.
I Introduction
Transition metal dichalcogenides (TMDCs) exhibit intriguing physical properties including superconductivity, charge-density wave, Dirac semimetals, among which the two-dimensional (2D) superconductivity has received growing attention, where the reduced dimensionality leads to unique behaviors compared to their bulk counterparts. One notable example is monolayer NbSe2: (1) the enhanced charge-density wave and reduced superconductivity in going from bulk to the monolayer [1]; (2) the transition from a two-gap superconductor (bulk) to a single-gap one (monolayer) [2, 3], owning to the competition between charge-density wave and superconductivity [4]; (3) suppressed magnetic instability by charge-density wave [5]; (4) Ising superconductivity, where the inversion-symmetry-broken crystal leads to large Zeeman type spin-orbit coupling (SOC), resulting in the extremely large in-plane upper critical field [6, 7]. Besides the inversion-symmetry-broken Ising superconductivity, the large critical fields were also observed in 2D centrosymmetric systems known as type-II Ising superconductivity, arising from multiple degenerate orbitals with spin-orbital locking [8, 9, 10]. Clearly, realizing 2D superconductivity in layered TMDCs is desirable to offer potential platforms for studying the novel quantum physics and the interplay among different orders in 2D limit.
The group VIII TMDCs, MTe2, where M=Ni, Pd, Pt, recently attach increasing attentions for the experimentally verified type-II Dirac semimetal [11, 12, 13], pressure induced superconductivity in their bulk phases [14, 15], and novel physics in their ultrathin films [9, 16, 17, 18, 19, 20, 21]. In particular, monolayer NiTe2 was predicted to be an intrinsic superconductor, and lithium intercalation can boost the superconducting transition temperature (henceforth ) of bilayer NiTe2 up to 11.3 K [16]. Few-layer PdTe2 were experimentally verified to be type-II Ising superconductors though with 1 K [21]. Very recently, their homologues PtTe2 crystals were reported to be synthesized with controllable thickness down to monolayer limit [18]. Different from NiTe2, monolayer PtTe2 is an intrinsic semiconductor with band gap about 0.8 eV. Interlayer coupling in PtTe2 is expected to be stronger, due to the smaller interlayer spacing in bulk PtTe2. Furthermore, SOC is supposed to be stronger in PtTe2, as Pt element is much heavier than Pd and Ni. The above differences, combined with the longing for the 2D superconductor motivate us to study the possibility of the emergence of superconductivity in 2D PtTe2 crystals.
This Letter reports an study on electron-phonon coupling (EPC) and superconducting properties of PtTe2. We show that the weak superconductivity in bilayer PtTe2(Pt2Te4) can be significantly boosted by alkali-metal intercalations. In particular, rubidium (Rb) intercalation leads to the formation of a thermodynamically stable crystal with the stoichiometry of RbPt2Te4, where the Rb occupy all the octahedral sites. Based on anisotropic Midgal-Eliashberg formalism, the of the RbPt2Te4 is computed to be 8 K with SOC, which is very high among TMDCs. The homologues KPt2Te4 is shown to have comparable to RbPt2Te4. The mechanism of the remarkable boosted superconductivity and the effect of SOC are systematically analyzed.
II Computational methods
Density-functional theory and density-functional perturbation theory calculations were performed with the exchange-correlation functional of PBE [22] to study the crystal structures, electronic structures, EPC of bulk, and few-layer PtTe2 before and after alkali-metal intercalations [23, 24]. The norm-conserving pseudopotentials of FHI98 [25] and ONCV [26] were used to describe the interaction between valance and core electrons. The Kohn-shame valance states were expanded as plane waves below 80 Rydberg. A 1818 (181812) -mesh and a 66 (664) -mesh were adopted to calculate the ground states of charge density and phonons for few-layer (bulk) systems, whereupon the electron-phonon coupling (EPC) matrix element are calculated, which quantifies the scattering amplitude between the electronic states with wavevector , band index (, ), and (+, ) via a phonon with branch and wavevector . Then above quantities are interpolated to the -grid of 120120 (606036) and -grid of (303020) [28, 27], based on which the mass-enhancement parameter [] are computed, where is the Eliashberg spectrum, defined as:
| (1) |
where are phonon-momentum-resolved EPC constant [27], is the volume of the 1st Brillouin zone, and is replaced with a gaussian function with a broadening of 0.5 meV. Using the same - and -grids, the temperature-dependent superconducting gaps [] are obtained by solving the anisotropic Midgal-Eliashberg equations with the Matsubara frequencies below 0.23 eV on imaginary axis [27, 29], followed by performing analytic continuation to the real axis with Padé functions.
III results and discussions
Monolayer PtTe2 is composed of Te-Pt-Te triatomic layers, where each Pt is octahedral-coordinated by six Te atoms. Its bulk counterpart, 1-PtTe2 is formed by the AA stacking of such monolayers along direction, separated by an interlayer spacing Å [30], with the hexagonal lattice constants = 4.01 and Å [18]. The optimized lattice constants are =4.08, and = 5.27 Å using the FHI98 pseudopotential [25], in nice agreement with the experiment. To study the SOC effect on EPC and superconducting properties, we also adopt the ONCV pseudopotential [26], which yields the optimized , and Å, slightly larger the experimental one. Nonetheless, we found that the above two pseudopotentials yield consistent computational results (see Sec. S1 [31] for details). In addition to the different pseudopotentials, the van der Waals (vdW) correlations [32, 33, 34] are also found to have little influence on the electronic structures (see Sec. S1[31]). Therefore, we mainly report in the main text, the results of the ONCV without vdW correction. It should also be mentioned that we involve the projector augmented wave type of pseudopotentials for more efficient calculations of molecular dynamic (AIMD), and the determination of convex hull for the Rb intercalated bilayer PtTe2, which will be discussed soon. More details of the motivation of using the above methods can be found [35]. The interlayer distance Å of the bulk PtTe2 is much smaller than that of other layered TMDCs (e.g., 2.90 Å for 2-NbSe2 [36], 2.89 Å for -WTe2 [37]) and even smaller than its homologues NiTe2 (2.63 Å) [38], indicating the potential strong interlayer coupling. Indeed, it was reported that the dispersive bandstructure along suppresses its superconductivity in bulk PtTe2 [39]. Besides, our computational results show that the electron-doped monolayer PtTe2 can exhibit overall large EPC strength () and isotropic superconducting as shown in Sec. S2 [31]. Therefore, it is expected that the superconductivity can be emerged in PtTe2 by electron doping and weakening the interlayer coupling. Thus, to enhance the superconductivity in layered PtTe2, the intercalation of alkali-metal atoms should be a reasonable way, as the intercalants can act as electron donors and relieve the interlayer coupling by expanding the interlayer spacing. To realize 2D superconductivity in PtTe2, we then study the alkali-metal intercalated bilayer PtTe2.

We begin by studying the energy favorable geometry structures of Rb-intercalated bilayer PtTe2, whose stoichiometry can be generated as Rbm(Pt2Te4)n, where and are integers, counting the number of Rb and Pt2Te4 units, respectively. We use a 33 supercell to calculate the formation energies with respect to the Rb concentration fraction , defined as = [Rbx(Pt2Te4)1-x] - E [Rb] - (1-) [Pt2Te4], where [Rb] and [Pt2Te4] are the energies of a body-center cubic Rb crystal per atom and a bilayer PtTe2 per Pt2Te4 unit, respectively. Fig. 1(b) displays the corresponding results, where decrease as the increase of and reach the minimum at , corresponding to the crystal with the stoichiometry RbPt2Te4. Further increasing the number of Rb, the begins to increase. The resultant convex hull shown in Fig. 1(b) suggests that the RbPt2Te4 crystal is thermodynamically stable with respect to any other stoichiometry. Fig. 1(a) displays the crystal structure of the RbPt2Te4, where the Rb atoms occupy all the octahedral sites at the midpoints of the nearest pairs of Pt atoms in the adjacent monolayers, which is similar to the case of lithium intercalated bilayer NiTe2 [16]. AIMD simulations [24, 40] further suggest that the RbPt2Te4 crystal is stable at room temperature without structure distortion in 10 picoseconds (see Sec. S3 [31]).

Figs. 2(a) and S4(a) display the electronic bandstructures of bilayer (henceforth Pt2Te4) and monolayer PtTe2, respectively. The monolayer is computed to have a band gap of 0.8 eV, which agrees well with the experiment [18]. On going from the monolayer to the bilayer, a semiconductor-to-metal transition is seen with the strong modification of the electronic structure around Fermi energy (). The mostly remarkable change is a band derived mainly from the -like orbitals of Te drops down and crosses (see Sec. S4 for the projected bandstructures [31]). This can be assigned to the overlap between the -like orbitals of the Te atoms in the bilayer, suggesting the strong interlayer coupling. The calculated bandstructure of the Pt2Te4 is again consistent with the ARPES measurements [18]. After Rb intercalation, the interlayer spacing expands and the interlayer coupling weakens, accompanied by the electrons transfer from Rb to its adjacent Te layers. The synergy effects of Rb-mediated interlayer coupling and electron doping make the bandstructure of the RbPt2Te4 resemble that of the electron doped monolayer PtTe2, but with slight band splitting [compare Figs. 2(b) and S4(a)]. One can see from Fig. 2(b) that without SOC, there are two conduction bands crossing the , leading to the formation of several electron pockets depicted by the solid black circles in Figs. 2(c)– 2(d). The two bands intersect at the Brillouin zone corners, K and K’, at the energy 12 meV above , which is responsible for the emergent tiny cirles centered at K and K’. When the SOC is included, though the Kramers degeneracy is preserved due to the inversion symmetry at the site of Rb, the double degenerated bands at K and K’ are split, leading to the avoided crossing near and a 57 meV gap opening at K and K’, giving rise to a slight reduced density of states at []. In addition to the small Fermi circles, the clover-shaped pockets centered at K and K’ are also noted, each of them consists of three separate petals. Centered at M and points, there are also two electron pockets. The calculated projected electronic density of states (DOS) [right panel of Fig. 2(b)] and the momentum-resolved DOS for the states near [Figs. 2(c)–2(d)] suggest that these states near K, K’ are significantly contributed by the -like orbitals, and the remaining states are assigned to the hybridization of the - and -like orbitals.

The computed phonon dispersions () of the RbPt2Te4 [Figs. 3(a) and S5(b)] and Pt2Te4 [Fig. S5(a)] show that all the , suggesting the dynamically stabilities of the crystals. The SOC is found to have little influence on of RbPt2Te4 [Fig. S5(b)], and slightly decrease the intensity of the mass-enhancement parameter [; see Fig. 3(b)], but the main features of the is similar to the case without SOC. For easier analysis, we first focus on the case without SOC. Fig. 3(b) displays the comparison of the and the corresponding accumulated EPC strength (dashed lines) between RbPt2Te4 and Pt2Te4. It is found that after the intercalation of Rb, the are remarkably enhanced in the energy region between 5 – 13 meV. Particularly, three intensive peaks are found located at 6.6, 9.6 and 12.3 meV, respectively. To further study the mechanism of the enhanced EPC, we decomposed the into the contributions from in-plane () and out-of-plane () vibrations of each atom by computing
| (2) |
where is the component of atom (Pt, Rb, Te) in the eigenvector of the dynamic matrix with phonon momentum and modes , and is the unit projection direction vector, which is chosen along in-plane () and out-of-plane () directions. The computed and the corresponding accumulated EPC constants are shown in Figs. 3(c) and 3(e), respectively. The most remarkable change is the doubled to 0.56 after the Rb intercalation [Fig. 3(e)]. This is consistent with the computed [Fig. 3(c)], where dominates the total spectrum of in 5 – 13 meV, suggesting the strongly coupling of the in-plane vibration of Te atoms with the electrons. In particular, the two pairs of double degenerated modes Eg and Eu can be seen at with energy of 12.08 and 12.11 meV, respectively [Fig. 3(a)], which are derived from Texy vibrations [see Fig. S6(a) [31]]. Among them, the two Eg modes exhibit large . The vibrational pattern for one of the Eg is shown in the inset of Fig. 3(d). By comparing the bandstructures with and without such phonon displacements imposed on the equilibrant RbPt2Te4 crystal, one can see that the Texy displacements have strong influences on the bands near , especially around K, where a Lifshitz transition is noted [Fig. 3(d)]. The secondary contributions to arise from the Tez, Ptxy and Rbxy vibrations as shown in Fig. 3(e). By further examining the corresponding spectra in Fig. 3(c), one can see that the contribution of Tez vibration is mainly associated with the peaks at 6.6 and 12.3 meV, while Ptxy exhibits a relatively uniform contribution in the whole energy region. Interestingly, the Rb also exhibits moderate contribution to , as the computed is comparable to = 0.31 [see Fig. 3(e)]. The Rb vibrations promote the peak at 9.6 meV [Fig. 3(c)], being on par with the contribution of Texy at the same energy.
We turn to study the mechanism of the enhanced EPC in RbPt2Te4 by analyzing the electronic states involved in EPC. We computed the -resolved EPC constant , defined as follow in this work:
| (3) | |||
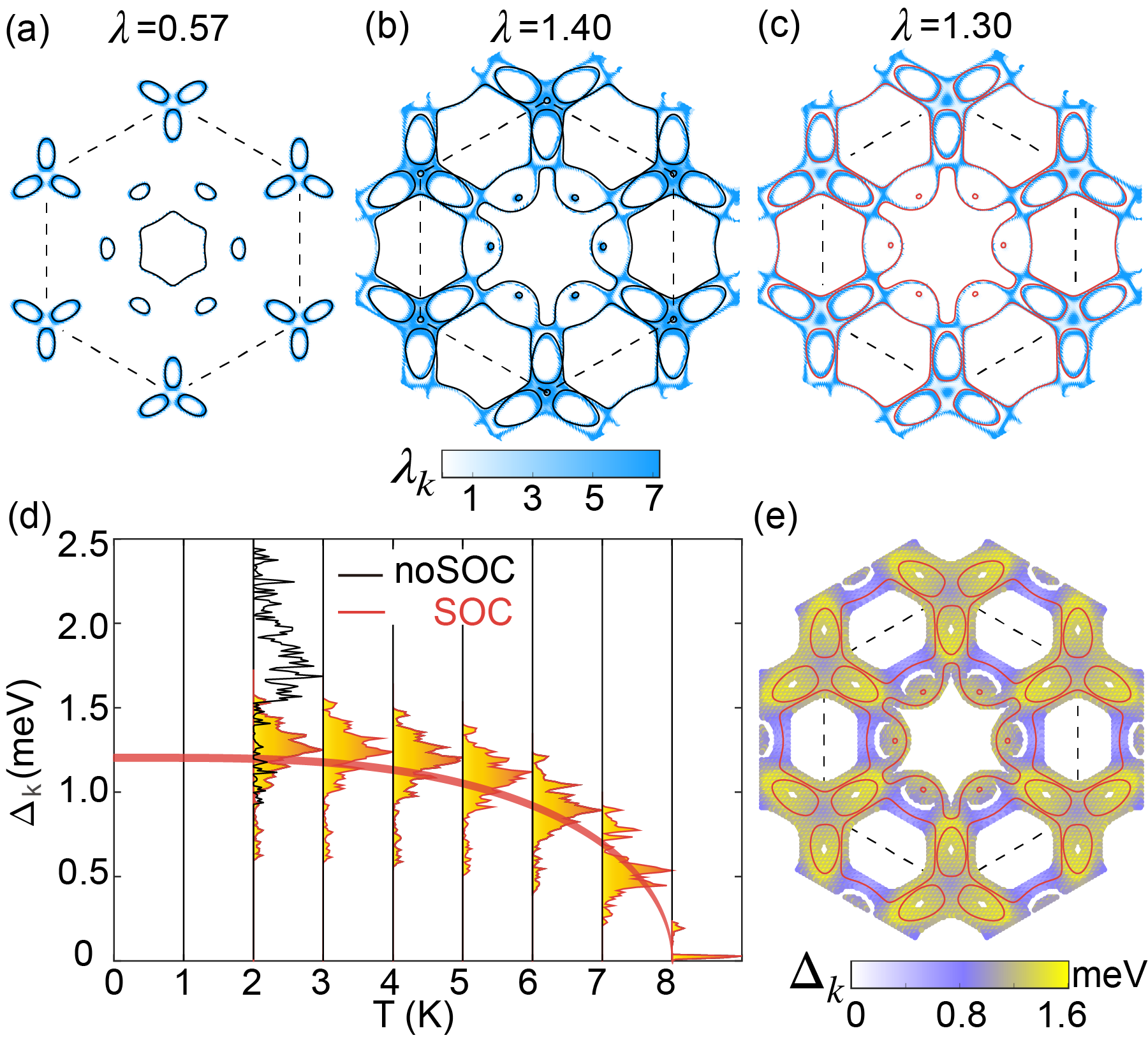
where is the volume of the first Brillouin zone, is the EPC matrix element, and the functions related to electron and phonon energies are replaced by gaussian functions with broadening of 10 and 0.5 meV, respectively. The is related to total EPC constant by . By comparing of Pt2Te4 and RbPt2Te4 shown in Figs. 4(a) and 4(b), one can see the clover-shaped circles at K and K’ are expanded, and the additional Fermi circles emerge after Rb intercalation, promoting the from 1.54 to 4.09 states/eV/Pt. Consequently, the in RbPt2Te4 is remarkably boosted to 1.4, as more pairs of electronic states can be involved in the EPC. Furthermore, the contribution of the of RbPt2Te4 are almost arising from the near K and K’ as shown in Fig. 4(b), which are mainly derived from the electronic states of Te atoms [Fig. 2(d)]. By similar analysis, the states in the remaining sections of the Fermi surface, derived from the - hybridization of Te and Pt atoms, also contribute to . The SOC is found to reduce the near K, K’ [Fig. 4(c)], attributable to the reduced arising from band splitting at K, K’[Fig. 2(b)]. Consequently, decreases to 1.3 with SOC. Except that, the main feature of the computed is unchanged. Therefore, it is evident that the large in RbPt2Te4 is mainly contributed by the pairing of electronic states of Te atoms near K, K’ Fermi pockets.
The significantly enhanced indicates the boost of the superconducting . Indeed, using McMillan-Allen-Dynes approach [41, 42, 43] based on the calculated = 1.30, the logarithmic average of the phonon frequencies K, and evaluated by [44], the isotropic superconducting of RbPt2Te4 is calculated to be 6.6 K with SOC. In contrast, the computed for Pt2Te4 are only 1.1 K. The reliability of the computed isotropic is also examined by computing bulk PtTe2 as discussed in Sec. S7, where one can see the computed for bulk PtTe2 is 0.35 and the corresponding is 0 K, in nice agreement with previous study that the bulk PtTe2 is non-superconducting with [39]. To obtain more reliable superconducting for the systems with reduced dimensionality and anisotropic Fermi surface [29, 45, 46], we further evaluate the of RbPt2Te4 by solving the full Midgal-Eliashberg gap equation [29, 45]. Compared to the slight decrease of the aforementioned isotropic , the SOC has relatively noticeable influences on the anisotropic superconducting properties. Fig. 4(d) shows the evolution of the energy distribution of superconducting gaps () with respect to temperatures. At = 2 K without SOC, the are distributed in the energy range between 0.9 – 2.4 meV with an average value of 1.6 meV, showing strong anisotropy. When SOC is involved, the overall decreased and the suppressed anisotropic distribution of are seen, as the average value of decreases to 1.2 meV, and the energy distribution range is reduced to 0.6 – 1.6 meV. The corresponding distribution of in an extended Brillouin zone is shown in Fig. 4(e), where one can see that the exhibit anisotropic distribution to some extents, in which the relatively large comes from the Fermi pockets around K and K’, dominated by the electronic states of Te atoms as analyzed before. As the temperature increases, the values of gradually reduce and finally vanish at , suggesting the of the RbPt2Te4 is 8 K, which is higher than the isotropic one (6.6 K) due to the anisotropic . We also study the intercalation of other alkali metal elements including lithium (Li), sodium(Na), potassium(K) and caesium(Cs), in which the KPt2Te4 is expected to have comparable to the RbPt2Te4, followed by the of CsPt2Te4, whereas the LiPt2Te4 and NaPt2Te4 are with relatively low [see Sec. S8 for details].
IV conclusion
In summary, we have predicted the enhanced EPC and superconducting in RbPt2Te4 and understood the corresponding mechanisms from calculations. Firstly, according to the computed convex hull, phonon dispersions and molecular dynamic simulations, the intercalated Rb are energetically favorable to occupy all the octahedral sites in the interlayer gallery, forming the thermodynamically stable RbPt2Te4 crystal. The of RbPt2Te4 is computed to be 8 K with the anisotropic superconducting gaps based on the anisotropic Midgal-Eliashberg formalism in the presence of SOC, though the pristine Pt2Te4 have a very low . Such a remarkable enhancement is assigned to the effects of the Rb intercalations from two sides. On one hand, the synergy effect of Rb-mediated interlayer coupling and electron doping lead to the significant promotion of , accompanied by the markedly enhanced EPC of Te phonons. On the other hand, the Rb directly contributes to the EPC by significantly increasing the intensity of peak at 9.6 meV. The SOC reduces the and the anisotropic superconducting gaps by splitting the band degeneracy near . The KPt2Te4 is proposed to have comparable to the RbPt2Te4. The reliability of our predictions is supported by the consistent computational results of electronic structures of few-layer PtTe2, and the EPC and superconductivity of bulk PtTe2 with previous studies.
Considering bilayer PtTe2 has been experimentally synthesized [18], and the intercalation of alkali-metal atoms therein can be experimentally realized [47, 48, 49, 50], our predictions can be straightforwardly probed. Therefore, the experimental accessibility, combined with the relatively high superconducting with SOC will make these superconductors promising platforms to investigate intriguing novel quantum physics associated with 2D superconductivity. For example, as we have shown before, the RbPt2Te4 crystal has three-fold rotational symmetries, which are preserved at high symmetry momenta of K and K’, at which the double degenerated electronic bands very close to are noted without SOC, and they will be further split by SOC [Fig. 2(b)]. The KPt2Te4 also exhibits similar results (Fig. S10). The above results suggest that the alkali-metal intercalated bilayer PtTe2 are potential candidates for realizing the type-II Ising superconductivity with relatively high superconducting [8], which calls for further studies.
Acknowledgements.
This work is supported by National Natural Science Foundation of China (Grants No. 11804118), Guangdong Basic and Applied Basic Research Foundation (Grants No. 2021A1515010041), open project funding of Guangzhou Key Laboratory of Vacuum Coating Technologies and New Energy Materials (KFVEKFVE20200001). The Calculations were performed on high-performance computation cluster of Jinan University, and Tianhe Supercomputer System. D.H. Wu, Y.P. Lin and L.X. Xiong contribute equally to this work.References
- Xi et al. [2015] X. Xi, L. Zhao, Z. Wang, H. Berger, L. Forró, J. Shan, and K. F. Mak, Nat. Nanotechnol. 10, 765 (2015).
- Noat et al. [2015] Y. Noat, J. A. Silva-Guillén, T. Cren, V. Cherkez, C. Brun, S. Pons, F. Debontridder, D. Roditchev, W. Sacks, L. Cario, P. Ordejón, A. García, and E. Canadell, Phys. Rev. B 92, 134510 (2015).
- Khestanova et al. [2018] E. Khestanova, J. Birkbeck, M. Zhu, Y. Cao, G. L. Yu, D. Ghazaryan, J. Yin, H. Berger, L. Forró, T. Taniguchi, K. Watanabe, R. V. Gorbachev, A. Mishchenko, A. K. Geim, and I. V. Grigorieva, Nano Lett. 18, 2623 (2018), .
- Zheng and Feng [2019] F. Zheng and J. Feng, Phys. Rev. B 99, 161119 (2019).
- Zheng et al. [2018] F. Zheng, Z. Zhou, X. Liu, and J. Feng, Phys. Rev. B 97, 081101(R) (2018).
- Xi et al. [2016] X. Xi, Z. Wang, W. Zhao, J.-H. Park, K. T. Law, H. Berger, L. Forró, J. Shan, and K. F. Mak, Nat. Phys. 12, 139 (2016), .
- Xing et al. [2017] Y. Xing, K. Zhao, P. Shan, F. Zheng, Y. Zhang, H. Fu, Y. Liu, M. Tian, C. Xi, H. Liu, J. Feng, X. Lin, S. Ji, X. Chen, Q. K. Xue, and J. Wang, Nano Lett. 17, 6802 (2017), .
- Wang et al. [2019] C. Wang, B. Lian, X. Guo, J. Mao, Z. Zhang, D. Zhang, B. L. Gu, Y. Xu, and W. Duan, Phys. Rev. Lett. 123, 126402 (2019), .
- Liu et al. [2020a] M. Liu, C. Wu, Z. Liu, Z. Wang, D. X. Yao, and D. Zhong, Nano Res. 13, 1733 (2020a), .
- Falson et al. [2020] J. Falson, Y. Xu, M. Liao, Y. Zang, K. Zhu, C. Wang, Z. Zhang, H. Liu, W. Duan, K. He, H. Liu, J. H. Smet, D. Zhang, and Q. K. Xue, Science 367, 1454 (2020).
- Zhang et al. [2017] K. Zhang, M. Yan, H. Zhang, H. Huang, M. Arita, Z. Sun, W. Duan, Y. Wu, and S. Zhou, Phys. Rev. B 96, 125102 (2017).
- Yan et al. [2017] M. Yan, H. Huang, K. Zhang, E. Wang, W. Yao, K. Deng, G. Wan, H. Zhang, M. Arita, and H. Yang, Nat. Commun. 8, 257 (2017).
- Huang et al. [2016] H. Huang, S. Zhou, and W. Duan, Phys. Rev. B 94, 121117 (2016).
- Qi et al. [2020] M. Qi, C. An, Y. Zhou, H. Wu, B. Zhang, C. Chen, Y. Yuan, S. Wang, Y. Zhou, X. Chen, R. Zhang, and Z. Yang, Phys. Rev. B 101, 1 (2020).
- Xiao et al. [2017] R. C. Xiao, P. L. Gong, Q. S. Wu, W. J. Lu, M. J. Wei, J. Y. Li, H. Y. Lv, X. Luo, P. Tong, X. B. Zhu, and Y. P. Sun, Phys. Rev. B 96, 075101 (2017).
- Zheng et al. [2020] F. Zheng, X.-B. Li, Y. Lin, L. Xiong, and J. Feng, Phys. Rev. B 101, 100505(R) (2020), .
- Zhao et al. [2018] B. Zhao, W. Dang, Y. Liu, B. Li, J. Li, J. Luo, Z. Zhang, R. Wu, H. Ma, and G. Sun, J. Am. Chem. Soc. 140, 14217 (2018).
- Lin et al. [2020] M. K. Lin, R. A. B. Villaos, J. A. Hlevyack, P. Chen, R. Y. Liu, C. H. Hsu, J. Avila, S. K. Mo, F. C. Chuang, and T. C. Chiang, Phys. Rev. Lett. 124, 036402 (2020).
- Deng et al. [2019] K. Deng, M. Yan, C. P. Yu, J. Li, X. Zhou, K. Zhang, Y. Zhao, K. Miyamoto, T. Okuda, W. Duan, Y. Wu, X. Zhong, and S. Zhou, Sci. Bull. 64, 1044 (2019).
- Liu et al. [2018] C. Liu, C. S. Lian, M. H. Liao, Y. Wang, Y. Zhong, C. Ding, W. Li, C. L. Song, K. He, X. C. Ma, W. Duan, D. Zhang, Y. Xu, L. Wang, and Q. K. Xue, Phys. Rev. Mater. 2, 094001 (2018).
- Liu et al. [2020b] Y. Liu, Y. Xu, J. Sun, C. Liu, Y. Liu, C. Wang, Z. Zhang, K. Gu, Y. Tang, C. Ding, H. Liu, H. Yao, X. Lin, L. Wang, Q. K. Xue, and J. Wang, Nano Lett. 20, 5728 (2020b).
- Perdew et al. [1996] J. P. Perdew, K. Burke, and M. Ernzerhof, Phys. Rev. Lett. 77, 3865 (1996), .
- Giannozzi et al. [2009] P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari, and R. M. Wentzcovitch, J. Phys. Condens. Matter 21, 395502 (2009).
- Kresse and Furthmüller [1996] G. Kresse and J. Furthmüller, Phys. Rev. B 54, 11169 (1996).
- Fuchs and Scheffler [1999] M. Fuchs and M. Scheffler, Comput. Phys. Commun. 119, 67 (1999).
- Hamann [2013] D. R. Hamann, Phys. Rev. B 88, 85117 (2013).
- Poncé et al. [2016] S. Poncé, E. R. Margine, C. Verdi, and F. Giustino, Comput. Phys. Commun. 209, 116 (2016), .
- Mostofi et al. [2008] A. A. Mostofi, J. R. Yates, Y.-S. Lee, I. Souza, D. Vanderbilt, and N. Marzari, Comput. Phys. Commun. 178, 685 (2008).
- Margine and Giustino [2013] E. R. Margine and F. Giustino, Phys. Rev. B 87, 024505 (2013), .
- [30] Furuseth, S., K. Selte, and A. Kjekshus, Acta Chemica Scandinavica 19, 257 (1965).
- [31] Supplemental Materials.
- Thonhauser et al. [2007] T. Thonhauser, V. R. Cooper, S. Li, A. Puzder, P. Hyldgaard, and D. C. Langreth, Phys. Rev. B 76, 125112 (2007).
- Sabatini et al. [2012] R. Sabatini, E. Küçükbenli, B. Kolb, T. Thonhauser, and S. De Gironcoli, J. Phys. Condens. Matter 24, 424209 (2012).
- Hamada [2014] I. Hamada, Phys. Rev. B 89, 121103 (2014).
- [35] The optimized structure parameters of bulk PtTe2 using the FHI98 (without vdW), which is a type of norm-conserving pseudopotential, are in nice agreement with experiment (see Table S1 [31]). Therefore, it is the best choice to using the FHI98 for all the calculations. However, we did not find the fully relativistic version of the FHI98, so that the SOC effect cannot be taken into account. Therefore, we turn to the ONCV pseudopotential, another type of norm-conserving pseudopotential, which has both the versions, so that the calculations with and without SOC can be performed, and the comparison of the results with and without SOC can be made. Therefore, we report the results of the ONCV (Figs. 2, 3 and 4) in the main text. Regarding the vdW correction, we find that the structure parameters optimized using ONCV with and without vdW are both reasonable and the former ones are closer to experiment (Table S1 [31]). On the other hand, we find that the density functional perturbation theory calculations are hard to converge when the vdW is included in the phonon calculations for the Pt2Te4 and RbPt2Te4. Therefore, the calculations of phonons, electron-phonon coupling and superconducting properties are using ONCV without vdW in the main text. We also examined the electronic structures computed using the ONCV with and without vdW and found that the vdW correlation has little influence on the electronic structure of RbPt2Te4, especially for the DOS at Fermi energy (Sec. 1 [31]). Futhermore, we also find the consistent results of superconducting of RbPt2Te4 using the ONCV (11 K, Fig. S13[31]) and FHI98 (11.5 K, Fig. S11[31]) without vdW and SOC. Therefore, we believe that the results obtained using ONCV without vdW correction, which we report in the main text, are reliable. It should also be mentioned that for more efficient calculations of the systems containing large numbers of atoms and electrons, we adopt projector augmented wave pseudopotentials with an energy truncation of 29.4 Rydberg, in cooperation with vdW correction, for the molecular dynamic simulations of RbPt2Te4 using a 551 supercell (see Sec. S3 [31]), and for determining the convex hull of Rbx(Pt2Te4)1-x in a 331 supercell [see Fig. 1(b)]. This type of pseudopotential also yields reasonable structure parameters as shown in Table S1 [31].
- [36] K. Selte and A. Kjekshus, Acta chem. scand. 18, 697 (1964).
- Zheng et al. [2016] F. Zheng, C. Cai, S. Ge, X. Zhang, X. Liu, H. Lu, Y. Zhang, J. Qiu, T. Taniguchi, K. Watanabe, S. Jia, J. Qi, J.-H. Chen, D. Sun, and J. Feng, Adv. Mater. 28, 4845 (2016).
- [38] Peacock, M. A., Thompson, R. M., American Mineralogist, 31, 204 (1946).
- Kim et al. [2018] K. Kim, S. Kim, J. S. Kim, H. Kim, J. H. Park, and B. I. Min, Phys. Rev. B 97, 165102 (2018).
- Allen and Tildesley [1989] M. P. Allen and D. J. Tildesley, Computer simulation of liquids (Oxford university press, 1989).
- Giustino [2017] F. Giustino, Rev. Mod. Phys. 89, 015003 (2017), .
- McMillan [1968] W. L. McMillan, Phys. Rev. 167, 331 (1968).
- Allen and Dynes [1975] P. B. Allen and R. C. Dynes, Phys. Rev. B 12, 905 (1975).
- Bennemann and Garland [1972] K. H. Bennemann and J. W. Garland, in AIP Conf. Proc., Vol. 4 (AIP, 1972) pp. 103–137.
- Choi et al. [2002] H. J. Choi, D. Roundy, H. Sun, M. L. Cohen, and S. G. Louie, Nature 418, 758 (2002).
- Sanna et al. [2012] A. Sanna, S. Pittalis, J. K. Dewhurst, M. Monni, S. Sharma, G. Ummarino, S. Massidda, and E. K. Gross, Phys. Rev. B 85, 184514 (2012).
- Sajadi et al. [2018] E. Sajadi, T. Palomaki, Z. Fei, W. Zhao, P. Bement, C. Olsen, S. Luescher, X. Xu, J. A. Folk, and D. H. Cobden, Science 362, 922 (2018).
- Fan et al. [2019] X. Fan, H. Chen, J. Deng, X. Sun, L. Zhao, L. Chen, S. Jin, G. Wang, and X. Chen, Inorg. Chem. 58, 7564 (2019).
- Nakata et al. [2019] Y. Nakata, K. Sugawara, A. Chainani, K. Yamauchi, K. Nakayama, S. Souma, P.-Y. Chuang, C.-M. Cheng, T. Oguchi, and K. Ueno, Phys. Rev. Mater. 3, 71001 (2019).
- Bianchi et al. [2012] M. Bianchi, R. C. Hatch, Z. Li, P. Hofmann, F. Song, J. Mi, B. B. Iversen, Z. M. Abd El-Fattah, P. Löptien, L. Zhou, A. A. Khajetoorians, J. Wiebe, R. Wiesendanger, and J. W. Wells, ACS Nano 6, 7009 (2012).