The MicroBooNE Collaboration ††thanks: [email protected]
Enhanced Search for Neutral Current Radiative Single-Photon Production in MicroBooNE
Abstract
We report results from an updated search for neutral current (NC) resonant (1232) baryon production and subsequent radiative decay (NC ). We consider events with and without final state protons; events with a proton can be compared with the kinematics of a baryon decay, while events without a visible proton represent a more generic phase space. In order to maximize sensitivity to each topology, we simultaneously make use of two different reconstruction paradigms, Pandora and Wire-Cell, which have complementary strengths, and select mostly orthogonal sets of events. Considering an overall scaling of the NC rate as an explanation of the MiniBooNE anomaly, our data exclude this hypothesis at 94.4% CL. When we decouple the expected correlations between NC events with and without final state protons, and allow independent scaling of both types of events, our data exclude explanations in which excess events have associated protons, and do not exclude explanations in which excess events have no associated protons.
The 4.8 MiniBooNE low-energy excess (LEE) of electron-like neutrino interactions [1] remains an important unexplained result in particle physics [2]. There have been many attempts to explain this excess as additional electrons, photons, or electron-positron pairs, produced by standard-model (SM) or beyond-the-standard-model (BSM) hypotheses [3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]. As a Cherenkov detector, MiniBooNE was largely unable to differentiate these different hypotheses, and therefore each possibility must be investigated. In contrast, the MicroBooNE liquid argon time projection chamber [14] has high-resolution 3D imaging and calorimetry, allowing for excellent electron-photon separation. MicroBooNE operated in the same Booster Neutrino Beam (BNB) at approximately the same baseline as MiniBooNE, giving it the capability to investigate the LEE in detail.
In this letter, we present an updated test of a single-photon interpretation of the MiniBooNE LEE. This builds on a previous result [15] that searched for neutrino-induced neutral current radiative decay to a nucleon and a photon (NC ); an anomalous enhancement of this interaction rate by a factor of 3.18, which could explain the MiniBooNE LEE [1], was disfavored at 94.8% confidence level (CL). The previous result had significant sensitivity to events containing just one visible photon and one visible proton (), but limited sensitivity to events containing just one visible photon and zero visible protons (). We expand the previous result by incorporating similar selections using different reconstruction tools, targeting a broader signal category with enhanced sensitivity to the signal hypothesis. The analysis presented in this letter features significantly enhanced sensitivity to events.
Although the PDG [16] assigns only an 8.3% uncertainty to the branching fraction, the possibility of an enhancement in the NC rate remains an interesting hypothesis. This process has never been observed in neutrino scattering, and it is the only significant expected source of single photons in MiniBooNE and MicroBooNE. Thus, it is a natural process to consider when trying to connect observations between the two detectors. The NC process allows for a comparison of single photon event rates between MiniBooNE and MicroBooNE, accounting for beam exposure, nuclear modeling, and selection efficiencies. Additionally, a scaling of NC events is the only quantitative measure of a single photon excess reported by the MiniBooNE collaboration [1], allowing for a direct comparison between MicroBooNE and MiniBooNE photon observations. A search for NC events can also be sensitive to other types of neutrino-induced neutral current single-photon production [17].
We use the same selections as Ref. [15] using Pandora [18] reconstruction, and we add new selections developed using Wire-Cell (WC) [19] reconstruction. Pandora and Wire-Cell are complementary approaches to event reconstruction, with Pandora performing provisional clustering of 2D hits in each wire plane before correlating features across planes to produce 3D particles, while Wire-Cell uses a tomographic approach to first correlate 2D hits across planes before proceeding with 3D pattern recognition to produce 3D particles. In each case, selections were developed in order to maximize the number of signal NC events while minimizing all other backgrounds. The Pandora selections which are unchanged relative to Ref. [15] use pre-selections targeting a specific topology, or , and then use ensembles of Boosted Decision Trees (BDTs) targeting different background types. The Wire-Cell selections use a generic neutrino pre-selection [20] followed by a single BDT trained to select NC events from all topologies. The Wire-Cell BDT is trained on a large number of reconstructed variables, in a similar method as the charged-current (CC) BDT in Ref. [21]. After applying the Wire-Cell BDT requirement, we split the selection into and using a 35 MeV reconstructed proton kinetic energy threshold. This choice is comparable to the corresponding effective threshold in Pandora proton track reconstruction, and corresponds to a proton that travels about one centimeter, a few wire spacings, the minimum range necessary to perform particle identification using reconstructed measurements. Unlike the Pandora selections, which contain only events with zero or one reconstructed proton and zero reconstructed charged pions , the Wire-Cell selections do not reject events with two or more reconstructed protons or events with one or more reconstructed charged pions in the final state, making the reconstructed topology , where refers to any number of particles. These relaxed particle multiplicity requirements increase the relative NC selection efficiency over a combined and Wire-Cell selection by 9%, and could increase sensitivity to more complex single-photon hypotheses, for example those involving two nucleons as described in Ref. [22].
We investigate events with () and without () reconstructed protons separately because these selections can point towards different types of physics effects. NC events with no hadronic activity represent a phase space with only two degrees of freedom, shower energy and shower angle. Therefore, our selection is not as sensitive to the underlying physical source of the photon as our selection, which preferentially selects events with photon-proton invariant mass near the resonance. Because of this, the channel can be tied to a broader set of alternative excess hypotheses, whether from SM backgrounds or BSM signatures.
Each selection results in a single-bin sample in reconstructed shower energy. The bins are 0-600 MeV, 100-700 MeV, and 0-1500 MeV for the Pandora , Pandora , and both Wire-Cell selections ( and ), respectively. All selections were developed according to a blinding policy, where only a small sample of data corresponding to protons-on-target (POT) was examined before the selections were finalized. The Pandora and Wire-Cell samples used for the reported results correspond to and POT, respectively, due to different data processing campaigns.
Table 1 shows a summary of the efficiency and purity of each selection. The purity in each selection is limited by events containing two photons from a decay in which only one photon was reconstructed. In particular, note the improvement in the Wire-Cell channel relative to the Pandora channel, and the large increase in total efficiency when all selections are combined.
| WC | Pandora | WC | Pandora | Combined | |||
| NC efficiency | 4.09% | 4.24% | 8.79% | 5.52% | 19.64% | ||
| NC purity | 9.60% | 14.84% | 7.50% | 3.98% | 6.37% |
Signal and background predictions for each selection are generated with Monte Carlo simulations. These model the neutrino flux, neutrino-argon interactions, and detector response. The simulated detector response is overlaid on cosmic ray backgrounds measured in-situ with dedicated samples collected without the neutrino beam. Simulated data samples were reprocessed for this analysis, leading to some differences between this work and the result reported in Ref. [15]; these differences fall within the statistical uncertainties of the simulated data sample.
It is worth noting that the Pandora and Wire-Cell selections are almost orthogonal. Of the 175.6 predicted events in the Wire-Cell selection, only 21.9 are found in the 194.4-event Pandora selection. This small rate of overlap indicates that there is significant room for future improvements in single-photon reconstruction and selection, and also highlights the benefit from this analysis which combines the selected events from these two independent workflows.
We determine systematic uncertainties by following the same procedure as outlined in Ref. [21].
(1) We consider BNB flux uncertainties by varying , , and production rates, altering the beam line configuration modeling within its uncertainties, and fluctuating the pion and nucleon total, inelastic, and quasi-elastic scattering cross sections on beryllium and aluminum [23].
(2) Neutrino-argon interaction cross section uncertainties are modeled using GENIE v3.0.6 tune G18_10a_02_11a, (“MicroBooNE tune”), varying 46 underlying model parameters, including those related to the quasi-elastic, meson-exchange-current, resonance, deep-inelastic-scattering, coherent scattering, neutral current, and final state interaction models [24, 25]. No GENIE NC branching ratio uncertainty was considered, as this was a free parameter in this analysis; this matches the systematic uncertainty treatment in Ref. [15].
(3) Uncertainties on hadron-argon interactions outside of the struck nucleus are modeled by considering inelastic collisions of protons, positive pions, and negative pions with argon, varying each cross section around its mean Geant4 prediction [26] by 20%.
(4) We consider detector uncertainties related to the electronic response to ionization charge, the light yield and propagation, the space charge effect, and the recombination model [27].
(5) We consider Monte Carlo statistical uncertainties. Statistical uncertainty correlations from events selected by both Wire-Cell and Pandora are accounted for by a repeated sampling bootstrapping procedure [21].
(6) We add an additional 50% uncertainty for events with a true neutrino vertex outside the cryostat in order to consider any possible mis-modeling of external materials.
Additional systematic uncertainties associated with higher mass resonance radiative decays, photonuclear absorption, and coherent single-photon production are negligible in this analysis. The relative sizes of all uncertainties on our signal channels are shown in Table 2.
| Uncertainty Type | WC | WC | Pandora | Pandora |
| Flux model | 6.58% | 6.29% | 7.39% | 6.66% |
| GENIE cross section | 19.49% | 17.09% | 25.96% | 17.87% |
| Hadron re-interaction | 1.27% | 0.70% | 2.22% | 0.89% |
| Detector modeling | 17.58% | 23.35% | 15.69% | 10.96% |
| Monte Carlo statistics | 5.64% | 3.67% | 10.40% | 5.47% |
| Out-of-cryostat interactions | 0.00% | 0.33% | 0.00% | 1.02% |
| Total uncertainty (unconstrained) | 27.65% | 29.85% | 32.94% | 22.61% |
| Total uncertainty (constrained) | 16.80% | 12.39% | 23.96% | 15.02% |
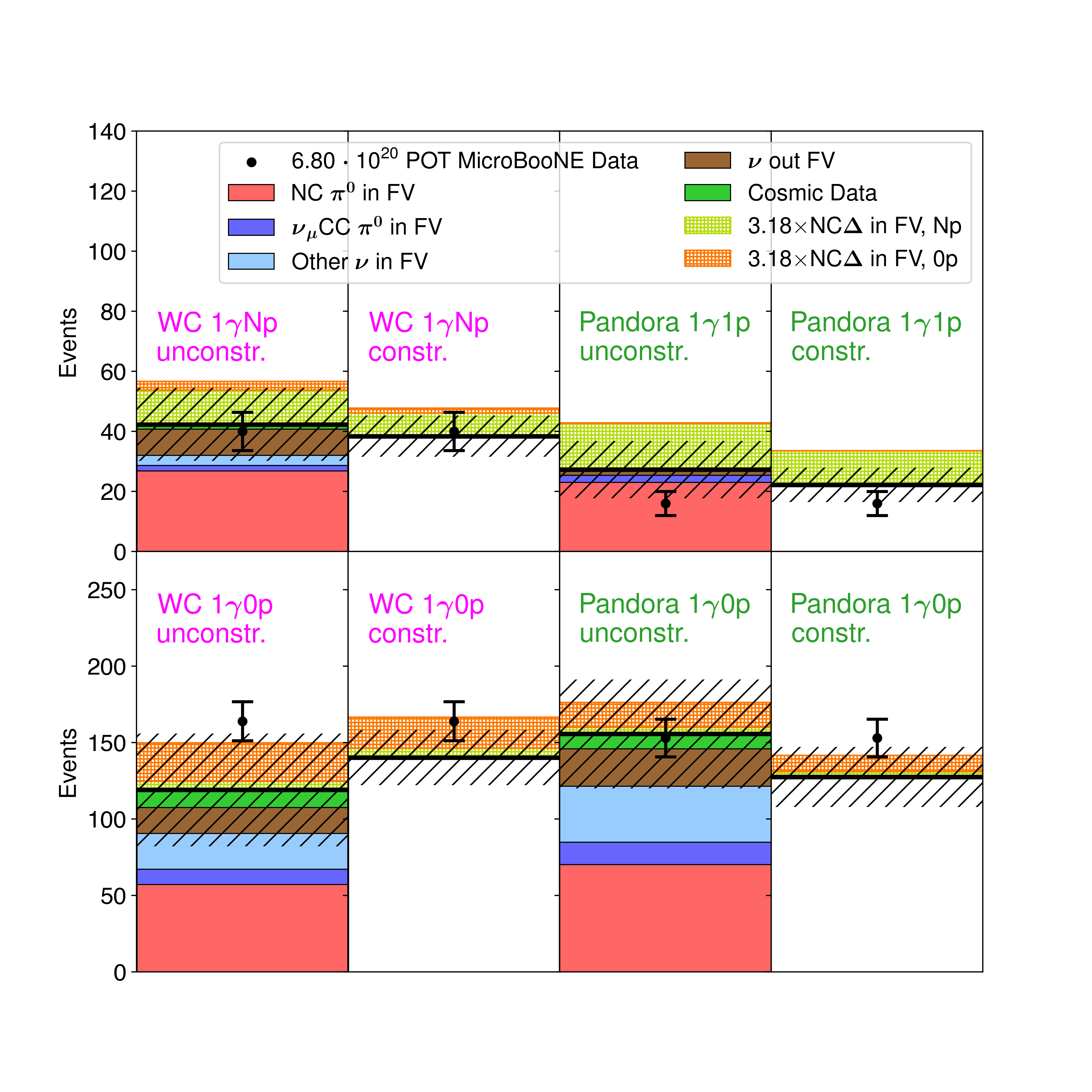
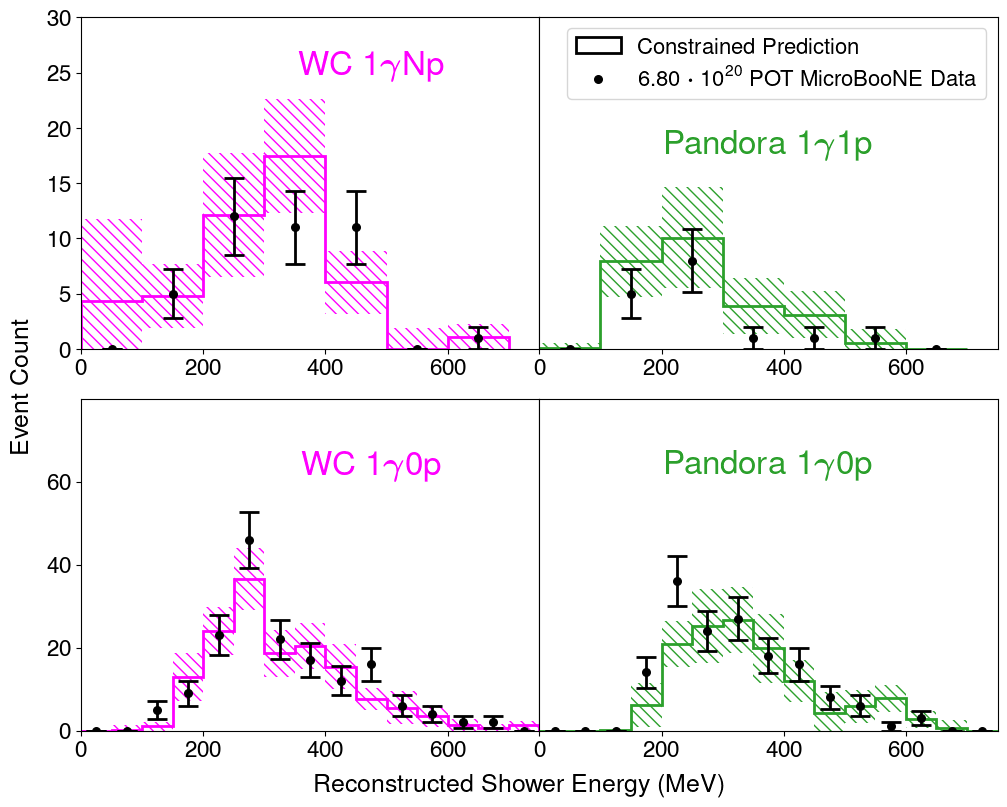
In order to reduce systematic uncertainties and adjust the central-value prediction in a data-driven way, we apply a conditional constraint based on the measurement of NC and CC events from dedicated sidebands. This constraint considers all statistical and systematic uncertainties and follows the same procedure as the constraint applied in Ref. [21]. We use the same sideband channels to constrain all four signal channels. The constraining NC selections use Wire-Cell reconstruction, and are updated relative to the NC selection in Ref. [21] by utilizing a BDT, described in Ref. [28]. The constraining CC selections also use Wire-Cell reconstruction, and are identical to those in Ref. [21]. As shown in Table 3, the largest background contribution to our signal channels come from NC interactions, and this component is significantly constrained by the observation in the NC selections. The NC selections also constrain the signal NC events, which have large correlations with many NC interactions because of the common resonance parentage. The CC selections further constrain some uncertainties. These constraining channels are split into reconstructed energy distributions with and without reconstructed protons, which can be found in the Supplemental Material. Our four signal channels are shown with and without the conditional constraint in Table 3 and Fig. 1, and the resulting constrained shower energy distributions are shown in Fig. 2. The signal channel uncertainties before and after constraint are shown in Table 2. The constraints generally act to lower the prediction, due to an observed over-prediction of NC events containing at least one proton. However, the observed under-prediction of low energy NC events with no protons acts to increase the prediction for the Wire-Cell channel. Wire-Cell selected events with multiple protons and selected events with charged pions each agree with our nominal predictions within uncertainties.
| Process | WC | WC | Pandora | Pandora |
| NC in FV | 26.8 | 57.2 | 23.0 | 70.1 |
| CC in FV | 1.9 | 10.0 | 2.4 | 14.7 |
| Other in FV | 8.7 | 16.9 | 1.9 | 24.6 |
| Out FV | 3.4 | 23.3 | 0.0 | 36.6 |
| Cosmic Beam-off Data | 1.6 | 11.7 | 0.0 | 9.8 |
| NC in FV | 4.5 | 9.7 | 4.9 | 6.5 |
| Unconstrained total prediction | 46.8 | 128.7 | 32.2 | 162.2 |
| Constrained total prediction | 38.4 | 140.2 | 22.2 | 127.5 |
| Observed data | 40 | 164 | 16 | 153 |
We consider two types of MiniBooNE LEE hypotheses. We first consider a simple scaling where we vary the total NC cross section equally across all samples. This is the same procedure employed in MicroBooNE’s previous NC search [15]. In this analysis, we also consider a second scaling that allows for the possibility of different rates of NC for the final states with and without protons. In this model, the rates of these two sub-processes are allowed to vary independently, leading to a model with two degrees of freedom.
For the one dimensional LEE hypothesis, we fit the signal and constraining channels with a single free parameter , corresponding to the normalization of the nominal rate of NC events. A value of one corresponds to the standard GENIE prediction, and a value of 3.18 corresponds to the MiniBooNE LEE under a NC scaling hypothesis [1]. To compare with MiniBooNE visually in Fig. 3, we assign a confidence interval for the scaling parameter of , which has been estimated from the significance of the MiniBooNE LEE. The scaling parameter is also interpreted as a scaling of the effective branching fraction and as a scaling of the flux-averaged cross section for NC interactions on argon .
We form confidence intervals using the Feldman-Cousins approach [29]. We use a Combined-Neyman-Pearson [30] and use a covariance matrix that includes systematic uncertainties and correlations between our four one-bin signal channels and all of our constraining bins. This test is essentially the same performed in Ref. [15], with different signal channels and constraining channels, and small differences in the systematic uncertainty treatment. With the combination of Wire-Cell and Pandora selections, our expected 90% CL upper limit exclusion is at , indicating notably higher sensitivity than either Pandora alone at , or Wire-Cell alone at . More details can be found in the Supplemental Material. The result is shown in Fig. 3. We see consistency with both the standard GENIE prediction and with the MiniBooNE LEE under an hypothesis within 90% CL. This is the case for all three sets of data considered: Wire-Cell, Pandora, and Wire-Cell + Pandora. The Wire-Cell + Pandora result has a best fit that lies slightly below the GENIE prediction, includes at 68% CL, and includes at 90% CL. The Pandora selections prefer lower scale factors, while the Wire-Cell selections prefer higher scale factors. The result for the Pandora-only exclusion is consistent with the result in Ref. [15], but these are not identical due to the different sideband constraints in this work.
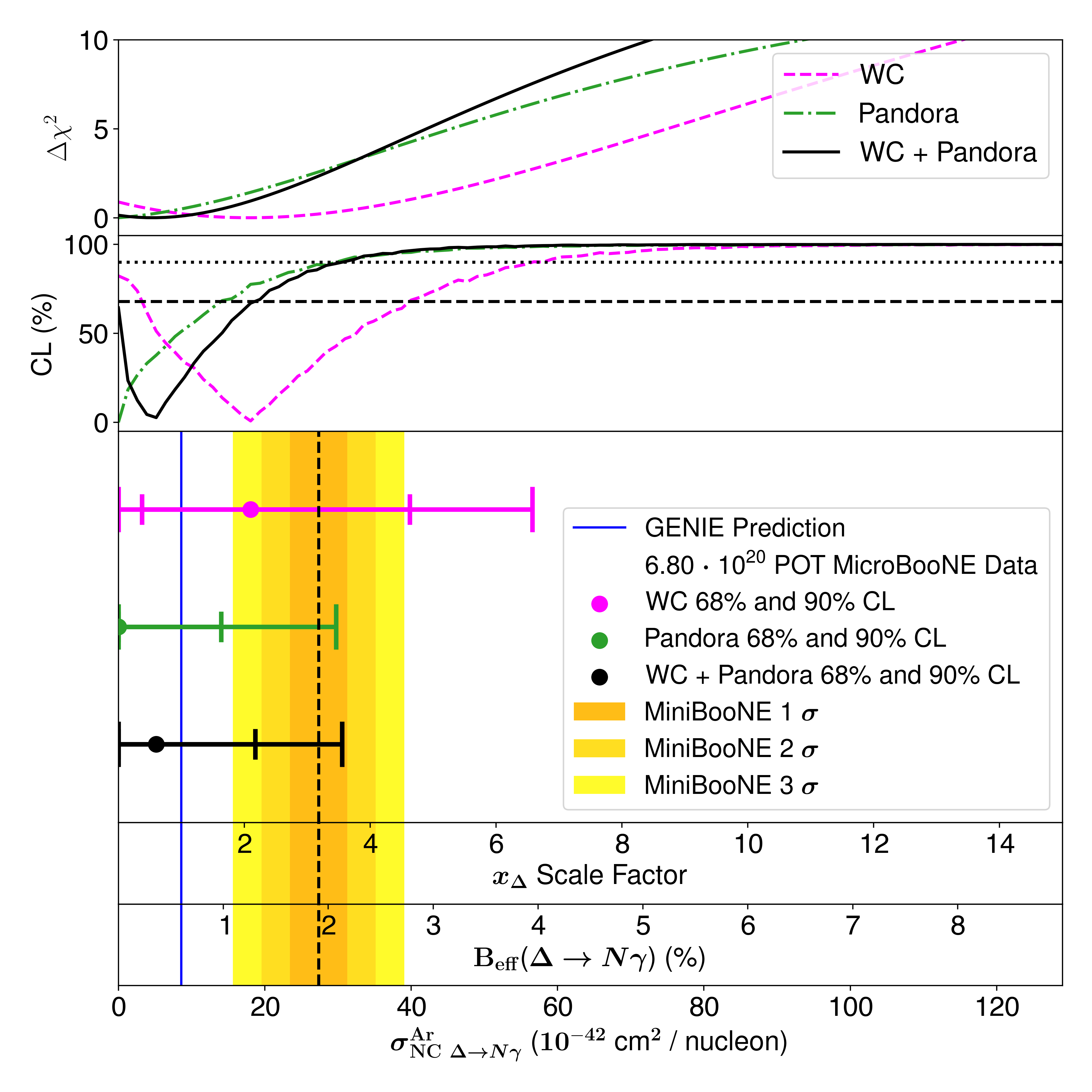
We also perform a two-hypothesis test, using a test statistic comparing the MiniBooNE LEE under an hypothesis and the standard GENIE prediction. We exclude the LEE hypothesis with 1.91, a p-value of 94.4% CL. This is consistent with our prior NC search, which excluded the LEE hypothesis at a p-value of 94.8% [15].
With a two dimensional LEE hypothesis, we can consider each final state separately, and decouple the search for an excess in NC events from the predicted breakdown of hadronic activity as modeled in the GENIE neutrino interaction generator. We test this quantitatively by considering separate scalings of signal NC events with and without true primary protons with kinetic energy greater than 35 MeV. We call these scaling parameters and , respectively.
In order to translate the inclusive NC excess at each point in the space, we split signal events according to the formula , based on our modeling of the make up of and signatures for signal events in MicroBooNE. We then estimate the significance at each point in this 2D space using the same method as for the 1D fit. Note that we do not make any assumptions about true proton multiplicities for NC events in MiniBooNE and instead only consider the total predicted count.
We apply a Feldman-Cousins procedure, the same as was used to obtain the results in Fig. 3, on a two-dimensional space of hypotheses to extract the exclusion contours. The expected sensitivities are shown in Fig. 5, while the exclusions using real data are shown in Fig. 5. The Wire-Cell-only contour in pink excludes large and large scalings about equally well. The Pandora-only contour in green excludes scalings well, but provides a weaker constraint on scalings. This is expected due to the slight over-prediction in the Pandora channel and the weak sensitivity of the Pandora channel. The Wire-Cell+Pandora combined result disfavors higher scaling values for true events, but does not exclude higher scaling values for true events. This behavior is explained by the over-prediction in the Pandora channel, and the under-prediction in the Wire-Cell and Pandora channels. Due to the weaker correlations between and signal predictions, this two-dimensional test leads to weaker exclusions than the one-dimensional test. The resulting exclusion and the sensitivity are stronger for the combined Wire-Cell+Pandora result than the exclusions with either reconstruction alone.
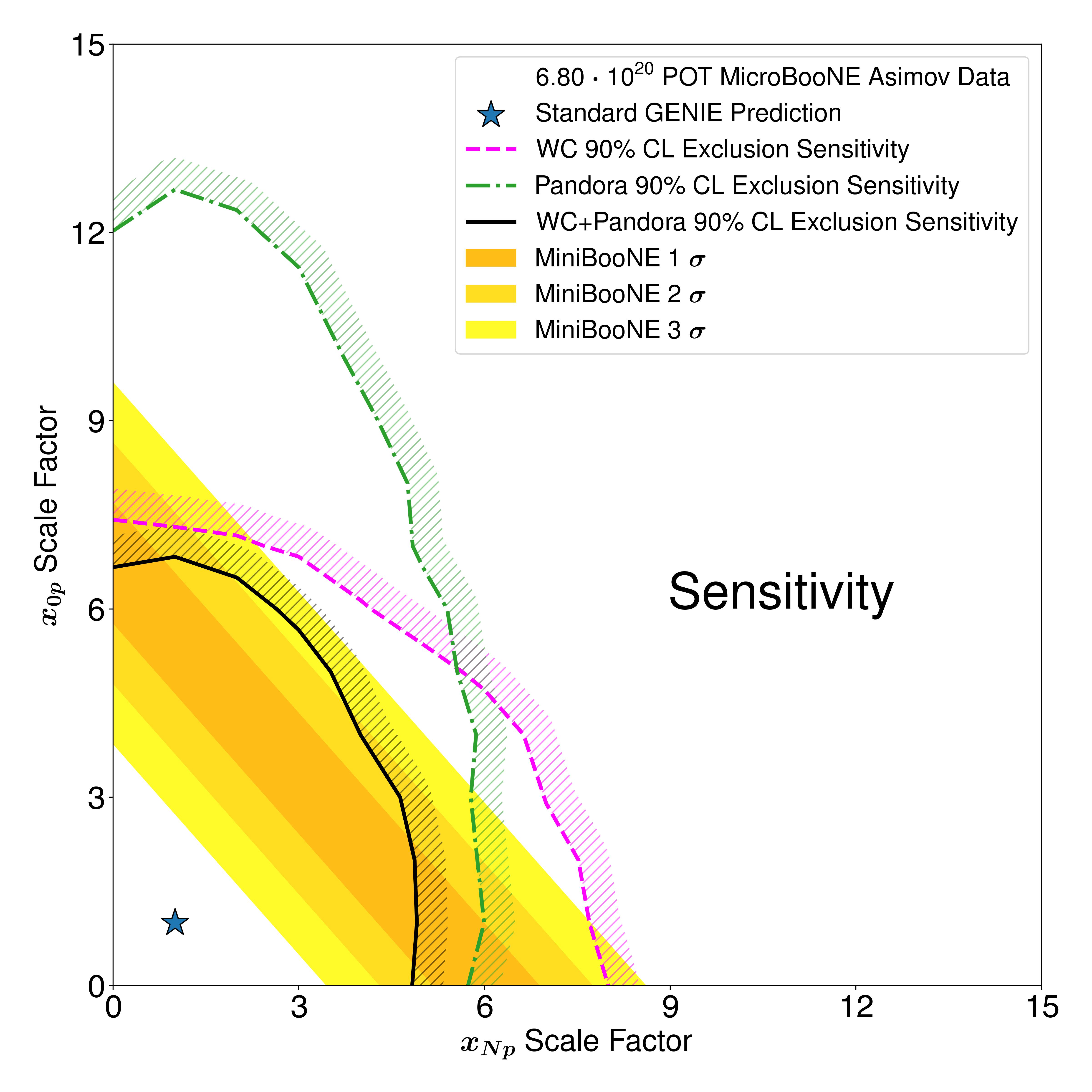
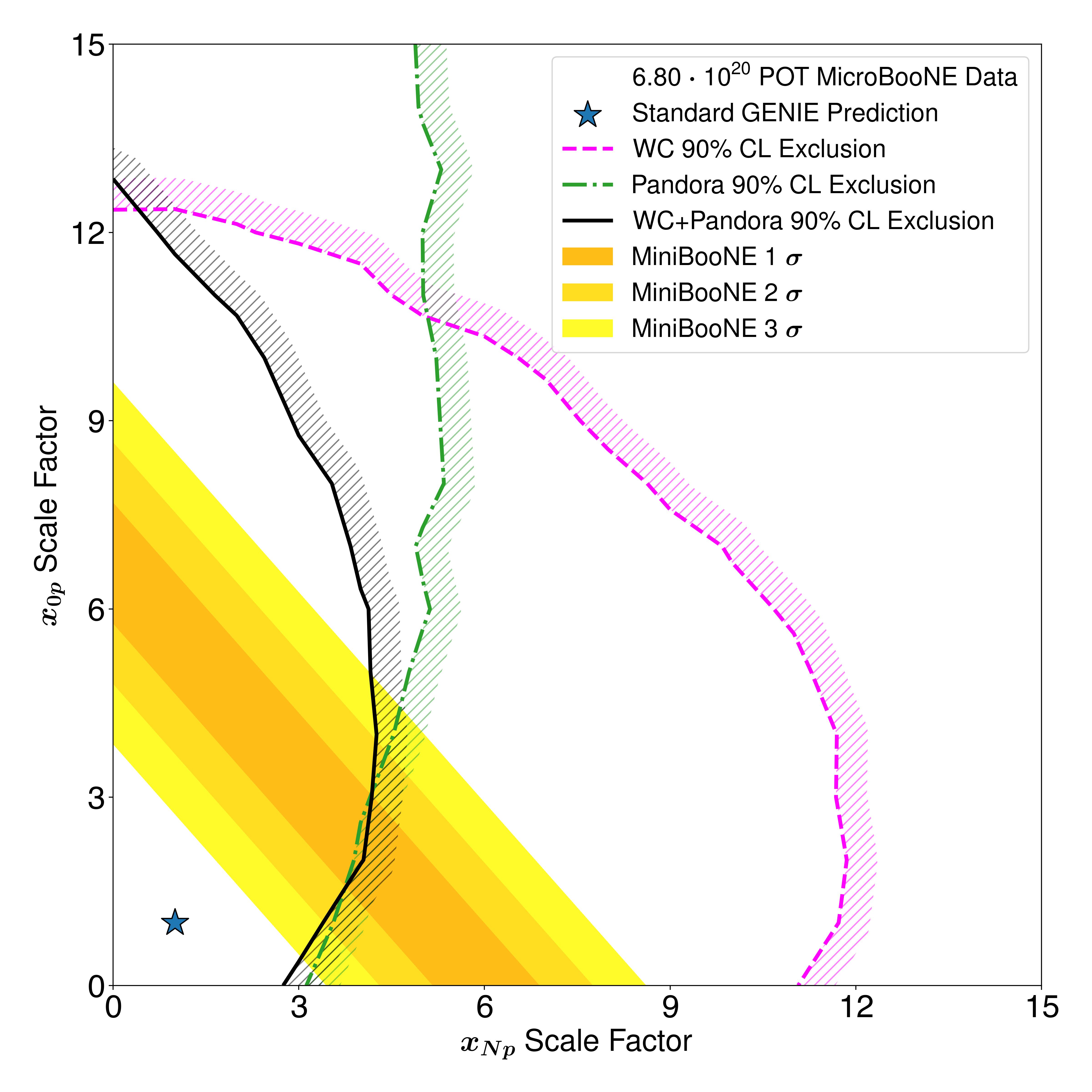
In simple scalings of the NC rate, the data are found to be consistent with the nominal prediction and disfavors the NC scaling LEE prediction. Meanwhile, with a more general LEE model which considers different scalings for and events, our data are consistent with the nominal prediction and exclude NC -like explanations of the MiniBooNE LEE where all single photon events are assumed to have associated proton activity. Our data are consistent with NC -like explanations of the MiniBooNE LEE where all single photon events are assumed to have no associated proton activity and for NC -like explanations of the MiniBooNE LEE consisting of a mixture of single photon events with and without proton activity, but which are not subject to the predicted NC branching ratio correlations for single photon events with and without proton activity. The majority of the LEE exclusion power comes from the Pandora channel with its data deficit. However, the Wire-Cell channels increase the sensitivity and exclusion power, most notably for events with no visible protons.
In summary, our updated search for NC resonant production and subsequent radiative decay, utilizing both the Pandora and Wire-Cell reconstruction techniques, yields significant constraints on interpretations of the MiniBooNE LEE. Under the assumption of a uniform scaling of the NC rate, our analysis excludes this hypothesis at 94.4% CL, consistent with our previous result [15]. Furthermore, when considering a model that permits independent scaling for events with and without final state protons, our results rule out scenarios where the majority of the excess events are associated with protons, while remaining compatible with cases where most excess events occur without a visible proton. MicroBooNE has also investigated other types of single photons, including NC coherent single photon production [31] and an inclusive search for single photons [32]. The analysis presented here uses approximately half of MicroBooNE’s collected BNB data set, and future analyses will use increased statistics, improved reconstructions, and different signal models to further advance our understanding of single photon events in MicroBooNE.
This document was prepared by the MicroBooNE collaboration using the resources of the Fermi National Accelerator Laboratory (Fermilab), a U.S. Department of Energy, Office of Science, Office of High Energy Physics HEP User Facility. Fermilab is managed by Fermi Forward Discovery Group, LLC, acting under Contract No. 89243024CSC000002. MicroBooNE is supported by the following: the U.S. Department of Energy, Office of Science, Offices of High Energy Physics and Nuclear Physics; the U.S. National Science Foundation; the Swiss National Science Foundation; the Science and Technology Facilities Council (STFC), part of the United Kingdom Research and Innovation; the Royal Society (United Kingdom); the UK Research and Innovation (UKRI) Future Leaders Fellowship; and the NSF AI Institute for Artificial Intelligence and Fundamental Interactions. Additional support for the laser calibration system and cosmic ray tagger was provided by the Albert Einstein Center for Fundamental Physics, Bern, Switzerland. We also acknowledge the contributions of technical and scientific staff to the design, construction, and operation of the MicroBooNE detector as well as the contributions of past collaborators to the development of MicroBooNE analyses, without whom this work would not have been possible. For the purpose of open access, the authors have applied a Creative Commons Attribution (CC BY) public copyright license to any Author Accepted Manuscript version arising from this submission.
References
- Aguilar-Arevalo et al. [2021] A. A. Aguilar-Arevalo et al. (MiniBooNE Collaboration), Updated MiniBooNE neutrino oscillation results with increased data and new background studies, Phys. Rev. D 103, 052002 (2021).
- Acero et al. [2024] M. A. Acero et al., White paper on light sterile neutrino searches and related phenomenology, J. Phys. G 51, 120501 (2024).
- Gninenko [2011] S. N. Gninenko, LSND/MiniBooNE excess events and heavy neutrino from and decays, Phys. Rev. D 83, 093010 (2011).
- Fischer et al. [2020] O. Fischer, A. Hernández-Cabezudo, and T. Schwetz, Explaining the MiniBooNE excess by a decaying sterile neutrino with mass in the 250 MeV range, Phys. Rev. D 101, 075045 (2020).
- [5] L. Alvarez-Ruso and E. Saul-Sala, Radiative decay of heavy neutrinos at MiniBooNE and MicroBooNE, arXiv:1705.00353 .
- Vergani et al. [2021] S. Vergani, N. W. Kamp, A. Diaz, C. A. Argüelles, J. M. Conrad, M. H. Shaevitz, and M. A. Uchida, Explaining the MiniBooNE excess through a mixed model of neutrino oscillation and decay, Phys. Rev. D 104, 095005 (2021).
- Bertuzzo et al. [2018] E. Bertuzzo, S. Jana, P. A. N. Machado, and R. Zukanovich Funchal, Dark neutrino portal to explain MiniBooNE excess, Phys. Rev. Lett. 121, 241801 (2018).
- Abdullahi et al. [2021] A. Abdullahi, M. Hostert, and S. Pascoli, A dark seesaw solution to low energy anomalies: MiniBooNE, the muon (), and BaBar, Phys. Lett. B 820, 136531 (2021).
- Ballett et al. [2019] P. Ballett, S. Pascoli, and M. Ross-Lonergan, ′ mediated decays of heavy sterile neutrinos in MiniBooNE, Phys. Rev. D 99, 071701 (2019).
- Abdallah et al. [2021] W. Abdallah, R. Gandhi, and S. Roy, Two-Higgs doublet solution to the LSND, MiniBooNE and muon anomalies, Phys. Rev. D 104, 055028 (2021).
- Dutta et al. [2020] B. Dutta, S. Ghosh, and T. Li, Explaining , the KOTO anomaly, and the MiniBooNE excess in an extended Higgs model with sterile neutrinos, Phys. Rev. D 102, 055017 (2020).
- Chang et al. [2021] C.-H. V. Chang, C.-R. Chen, S.-Y. Ho, and S.-Y. Tseng, Explaining the MiniBooNE anomalous excess via a leptophilic ALP-sterile neutrino coupling, Phys. Rev. D 104, 015030 (2021).
- [13] W. Abdallah, R. Gandhi, T. Ghosh, N. Khan, S. Roy, and S. Roy, A 17 MeV pseudoscalar and the LSND, MiniBooNE and ATOMKI anomalies, arXiv:2406.07643 .
- Acciarri et al. [2017] R. Acciarri et al. (MicroBooNE Collaboration), Design and construction of the MicroBooNE detector, JINST 12 (02), P02017 (2017).
- Abratenko et al. [2022a] P. Abratenko et al. (MicroBooNE Collaboration), Search for neutrino-induced neutral-current radiative decay in MicroBooNE and a first test of the MiniBooNE low energy excess under a single-photon hypothesis, Phys. Rev. Lett. 128, 111801 (2022a).
- Navas et al. [2024] S. Navas et al. (Particle Data Group Collaboration), Review of particle physics, Phys. Rev. D 110, 030001 (2024).
- Wang et al. [2014] E. Wang, L. Alvarez-Ruso, and J. Nieves, Photon emission in neutral-current interactions at intermediate energies, Phys. Rev. C 89, 015503 (2014).
- Acciarri et al. [2018] R. Acciarri et al. (MicroBooNE Collaboration), The Pandora multi-algorithm approach to automated pattern recognition of cosmic-ray muon and neutrino events in the MicroBooNE detector, Eur. Phys. J. C 78, 82 (2018).
- Abratenko et al. [2021a] P. Abratenko et al. (MicroBooNE Collaboration), Neutrino event selection in the MicroBooNE liquid argon time projection chamber using Wire-Cell 3D imaging, clustering, and charge-light matching, JINST 16 (06), P06043 (2021).
- Abratenko et al. [2021b] P. Abratenko et al. (MicroBooNE Collaboration), Cosmic ray background rejection with Wire-Cell LArTPC event reconstruction in the MicroBooNE detector, Phys. Rev. Appl. 15, 064071 (2021b).
- Abratenko et al. [2022b] P. Abratenko et al. (MicroBooNE Collaboration), Search for an anomalous excess of inclusive charged-current interactions in the MicroBooNE experiment using Wire-Cell reconstruction, Phys. Rev. D 105, 112005 (2022b).
- Kelly and Kopp [2023] K. J. Kelly and J. Kopp, More ingredients for an Altarelli cocktail at MiniBooNE, J. High Energy Phys. 2023 (5), 113.
- [23] “Booster Neutrino Flux Prediction at MicroBooNE”, MicroBooNE public-note 1031, http://microboone.fnal.gov/wp-content/uploads/MICROBOONE-NOTE-1031-PUB.pdf.
- Alvarez-Ruso et al. [2021] L. Alvarez-Ruso et al. (GENIE Collaboration), Recent highlights from GENIE v3, Eur. Phys. J.: Spec. Top. 230, 4449 (2021).
- Abratenko et al. [2022c] P. Abratenko et al. (MicroBooNE Collaboration), New GENIE model tune for MicroBooNE, Phys. Rev. D 105, 072001 (2022c).
- Agostinelli et al. [2003] S. Agostinelli et al. (GEANT4 Collaboration), GEANT4–a simulation toolkit, Nucl. Instrum. Meth. A 506, 250 (2003).
- Abratenko et al. [2022d] P. Abratenko et al. (MicroBooNE Collaboration), Novel approach for evaluating detector-related uncertainties in a LArTPC using MicroBooNE data, Eur. Phys. J. C 82, 454 (2022d).
- [28] P. Abratenko et al. (MicroBooNE Collaboration), First double-differential cross section measurement of neutral-current production in neutrino-argon scattering in the MicroBooNE detector, arXiv:2404.10948 .
- Feldman and Cousins [1998] G. J. Feldman and R. D. Cousins, Unified approach to the classical statistical analysis of small signals, Phys. Rev. D 57, 3873 (1998).
- Ji et al. [2020] X. Ji, W. Gu, X. Qian, H. Wei, and C. Zhang, Combined Neyman–Pearson chi-square: an improved approximation to the Poisson-likelihood chi-square, Nucl. Instrum. Meth. A 961, 163677 (2020).
- Abratenko et al. [2025a] P. Abratenko et al. (MicroBooNE Collaboration), First Search for Neutral Current Coherent Single-Photon Production in MicroBooNE (2025a), https://microboone.fnal.gov/coherent-single-photon-2025/.
- Abratenko et al. [2025b] P. Abratenko et al. (MicroBooNE Collaboration), Inclusive Search for Anomalous Single-Photon Production in MicroBooNE (2025b), https://microboone.fnal.gov/inclusive-single-photon-2025/.