Enhanced Quantum State Transfer and Bell State Generation over Long-Range Multimode Interconnects via Superadiabatic Transitionless Driving
Abstract
Achieving high-fidelity direct two-qubit gates over meter-scale long quantum interconnects is challenging in part due to the multimode nature of such systems. One alternative scheme is to combine local operations with remote quantum state transfer or remote entanglement. Here, we study quantum state transfer and entanglement generation for two distant qubits, equipped with tunable interactions, over a common multimode interconnect. We employ the SuperAdiabatic Transitionless Driving (SATD) solutions for adiabatic passage and demonstrate various favorable improvements over the standard protocol. In particular, by suppressing leakage to a select (resonant) interconnect mode, SATD breaks the speed-limit relation imposed by the qubit-interconnect interaction , where instead the operation time is limited by leakage to the adjacent modes, i.e. free spectral range of the interconnect, allowing for fast operations even with weak . Furthermore, we identify a multimode error mechanism for Bell state generation using such adiabatic protocols, in which the even/odd modal dependence of qubit-interconnect interaction breaks down the dark state symmetry, leading to detrimental adiabatic overlap with the odd modes growing as . Therefore, adopting a weak coupling, imposed by a multimode interconnect, SATD provides a significant improvement in terms of operation speed and consequently sensitivity to incoherent error.
I Introduction
Modular design of quantum computers Devitt_Architectural_2009 ; Monroe_Large_2014 ; Bravyi_Future_2022 relaxes wiring and control complexity, as well as cryogenic cooling power requirements, of the underlying Quantum Processing Units (QPU), and is the path forward for the required scaling Fowler_High_2009 ; Fowler_Surface_2012 ; Bravyi_High_2023 towards quantum error correction Knill_Theory_1997 ; Gottesman_Stabilizer_1997 ; Knill_Theory_2000 ; Lidar_Quantum_2013 ; Terhal_Quantum_2015 . For superconducting qubits, this vision necessitates developing interconnects at various levels of modularity Bravyi_Future_2022 , such as dense short-range interconnects Gold_Entanglement_2021 ; Conner_Superconducting_2021 to extend the effective size of QPUs, and sparse meter-range interconnects to enable parallelization of multiple QPUs within a dilution fridge. The short-range interconnect length is comparable to the distance between the qubits within a single chip and behaves effectively as a single mode system. While standard two-qubit gates could potentially work across a short interconnect, the multimode nature of long-range interconnects makes direct two-qubit gates more difficult. Two alternatives are to use the interconnect to perform state transfer, or to generate remote entanglement such as a Bell state. In conjunction with local operations and classical communication, either of these operations can be used as a resource to implement indirect remote two-qubit gates Gottesman_Demonstrating_1999 ; Eisert_Optimal_2000 ; Huang_Experimental_2004 .
The past few years have seen a recent surge into numerous superconducting circuit realizations of remote entanglement generation and quantum state transfer Kurpiers_Deterministic_2018 ; Axline_Demand_2018 ; Campagne_Deterministic_2018 ; Leung_Deterministic_2019 ; Zhong_Violating_2019 ; Bienfait_Phonon_2019 ; Chang_Remote_2020 ; Zhong_Deterministic_2021 ; Yan_entanglement_2022 ; Kannan_Demand_2023 ; Niu_Low_2023 ; Qiu_Deterministic_2023 . These protocols can be broadly categorized as either employing time-symmetric emission and capture of itinerant photons Kurpiers_Deterministic_2018 ; Axline_Demand_2018 ; Campagne_Deterministic_2018 ; Zhong_Violating_2019 ; Bienfait_Phonon_2019 ; Kannan_Demand_2023 ; Niu_Low_2023 ; Qiu_Deterministic_2023 , or using qubit interactions with the standing-wave modes of meter-long scale interconnects Leung_Deterministic_2019 ; Zhong_Violating_2019 ; Chang_Remote_2020 ; Zhong_Deterministic_2021 ; Qiu_Deterministic_2023 . Among protocols based on standing-wave modes, Stimulated Raman Adiabatic Passage (STIRAP) Gaubatz_Population_1990 ; Vitanov_Stimulated_2017 ; Bergmann_Roadmap_2019 achieves better fidelity Chang_Remote_2020 compared to a qubit-interconnect-qubit direct excitation exchange, also referred to as the relay protocol Zhong_Violating_2019 , by protection against interconnect loss.
In STIRAP Gaubatz_Population_1990 ; Vitanov_Stimulated_2017 ; Bergmann_Roadmap_2019 , we evolve the dark eigenstate of a Lambda system adiabatically towards a desired target state, applicable to quantum state transfer and entanglement generation. One advantage is the suppression of potential relaxation through the intermediate lossy interconnect. The operation speed is, however, limited by leakage to the bright lossy eigenstates whose transition frequency is set by the coupling strength. Transitionless Driving (TD) methods Demirplak_Adiabatic_2003 ; Demirplak2008consistency ; Berry_Transitionless_2009 ; Ibanez_Multiple_2012 ; Zheng_Optimal_2022 cancel out non-adiabatic transitions exactly via a modified control Hamiltonian, similar in spirit to the perturbative Derivative Removal by Adiabatic Gate (DRAG) technique Motzoi_Simple_2009 ; Gambetta_Analytic_2011 ; Malekakhlagh_Mitigating_2022 ; Li_Suppression_2023 . One potential practical drawback can however be the need for a control knob not accessible by the original Hamiltonian. SuperAdiabatic Transition Driving (SATD) Baksic_Speeding_2016 ; Zhou_Accelerated_2017 redefines the evolution path, connecting the original source and target states, such that in the dressed frame the non-adiabatic transitions are canceled out exactly without the need for additional control knobs. SATD solutions for STIRAP have also been generalized to single-qubit tripod gates Ribeiro_Accelerated_2019 ; Setiawan_Analytic_2021 and more recently to two-qubit gates Setiawan_Fast_2023 for fluxonium qubits Manucharyan_Fluxonium_2009 .
In this paper, we characterize the performance improvements of the SATD protocol against STIRAP, and promote its usage for quantum state transfer and Bell state generation in a multimode interconnect setting. By removing leakage to the resonant interconnect mode, the operation speed for SATD is not limited by the qubit-interconnect coupling anymore, but determined by the interconnect Free Spectral Range (FSR) , leading to a significant speedup as well as a robustness to variation in compared to STIRAP. We show that the single-mode SATD solutions work reasonably well for a multimode interconnect with sufficiently large FSR (), and quantify the deviations from expected behavior due to multimode effects. In particular, we find that the even-odd mode dependence of the interaction breaks the dark-state symmetry, which is in principle detrimental to such dark-state-based adiabatic protocols. This impacts the Bell state generation more by an adiabatic overlap error proportional to , and can be mitigated only via a weaker . This weaker requirement due to multimode effects, and the robustness of SATD makes its application very advantageous especially for Bell state generation. Furthermore, we observe improvements by SATD in suppressing the incoherent error due to qubits relaxation, pure dephasing, and the interconnect quality factor.
The remainder of this work is organized as follows. Section II describes the system under consideration with two quantum modules connected via a multimode interconnect, and a Lindblad model introduced for our analytical and numerical analyses. In Sec. III, we revisit the ideal single-mode STIRAP protocol, used for quantum state transfer and entanglement generation, and discuss potential detrimental multimode sources of error. In Sec. IV, we present extensive simulations investigating the numerous advantages of SATD compared to regular STIRAP in such a multimode context. We further assess the performance of indirect two-qubit gates achieved by combining quantum state transfer and remote entanglement with local operations. Appendix A discusses the details of our Lindblad model and simulations, and provides a numerical convergence test. Appendices B and C review the single-mode STIRAP, and complications that arise due to a multimode interconnect, respectively. In Appendix D, we review the derivation of SATD solutions for single-mode STIRAP following Ref. Baksic_Speeding_2016 .
II system and model
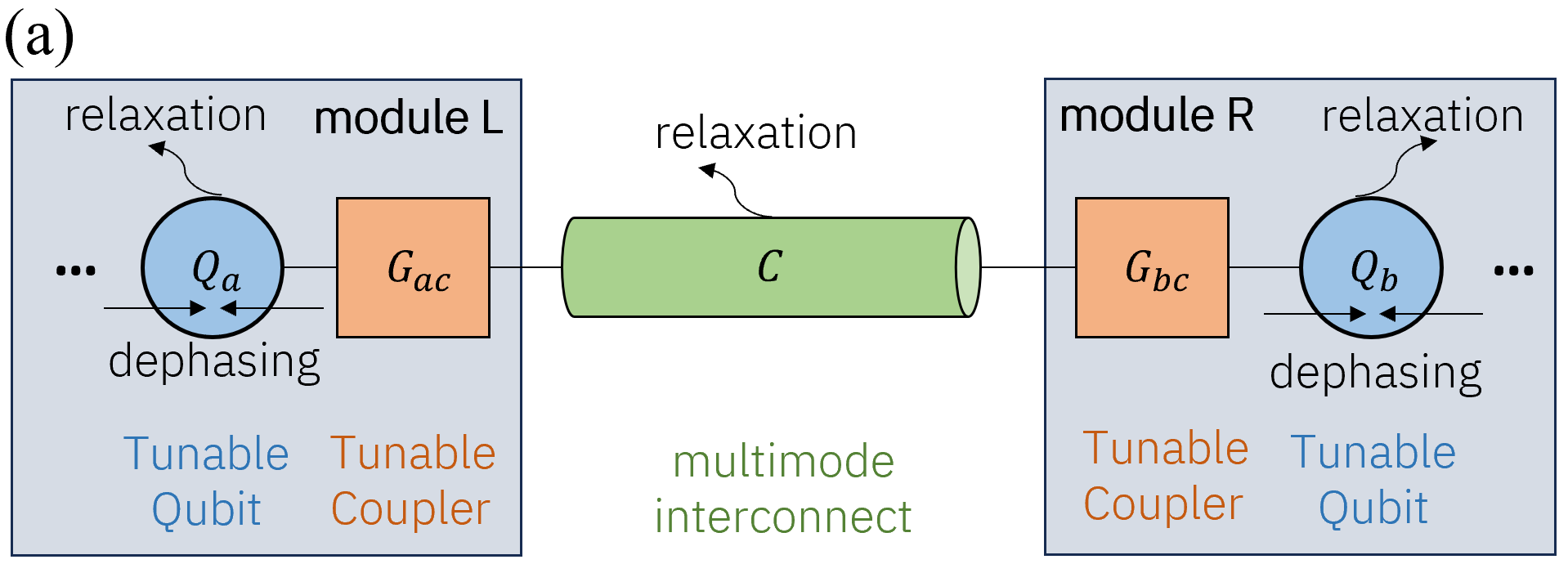
We consider a system consisting of two tunable-frequency qubits that have tunable interactions to a common long-range multimode interconnect as depicted in Fig. 1(a). The standard motivation for such a setup is to perform remote quantum operations between two modules (chips) connected via a long interconnect such as a coaxial cable. This can, however, be also relevant to on-chip transmission lines between distant qubits Sundaresan_Beyond_2015 . Notable experimental studies have employed tunable grounded Transmon qubits with tunable RF SQUID couplers Barends_Coherent_2013 ; Chen_Qubit_2014 ; Geller_Tunable_2015 connected via an on-chip transmission line Chang_Remote_2020 or a cable Qiu_Deterministic_2023 . Although this work is motivated by superconducting architectures, the following analysis and characterization of remote operations is presented in a system-agnostic manner.
We characterize the performance of STIRAP and SATD protocols for quantum state transfer and Bell state generation via a Lindblad simulation that accounts for qubit relaxation (), pure dephasing () and cable relaxation ():
| (1) | ||||
where is the system density matrix, and is the dissipator for the collapse operator . We model the qubits as weakly anharmonic, and the interconnect as a collection of harmonic quantum oscillators, with time-dependent (controllable) qubit-interconnect interaction as:
| (2) | ||||
where , , and are the qubit frequency, anharmonicity, evenly spaced mode frequency with FSR , and qubit-interconnect interaction rates for , respectively. Moreover, is the center mode index, and is the additional modes kept on each side. In writing Hamiltonian (2), we have made certain approximations, motivated by the physics of multimode interconnects (see Appendix A), similar to Ref. Chang_Remote_2020 . An important feature of Hamiltonian (2) is the even-odd mode-dependent relative sign for the qubit-interconnect interaction, which accounts for the distinct spatial profile of even and odd interconnect modes Chang_Remote_2020 .
III STIRAP via a multimode interconnect
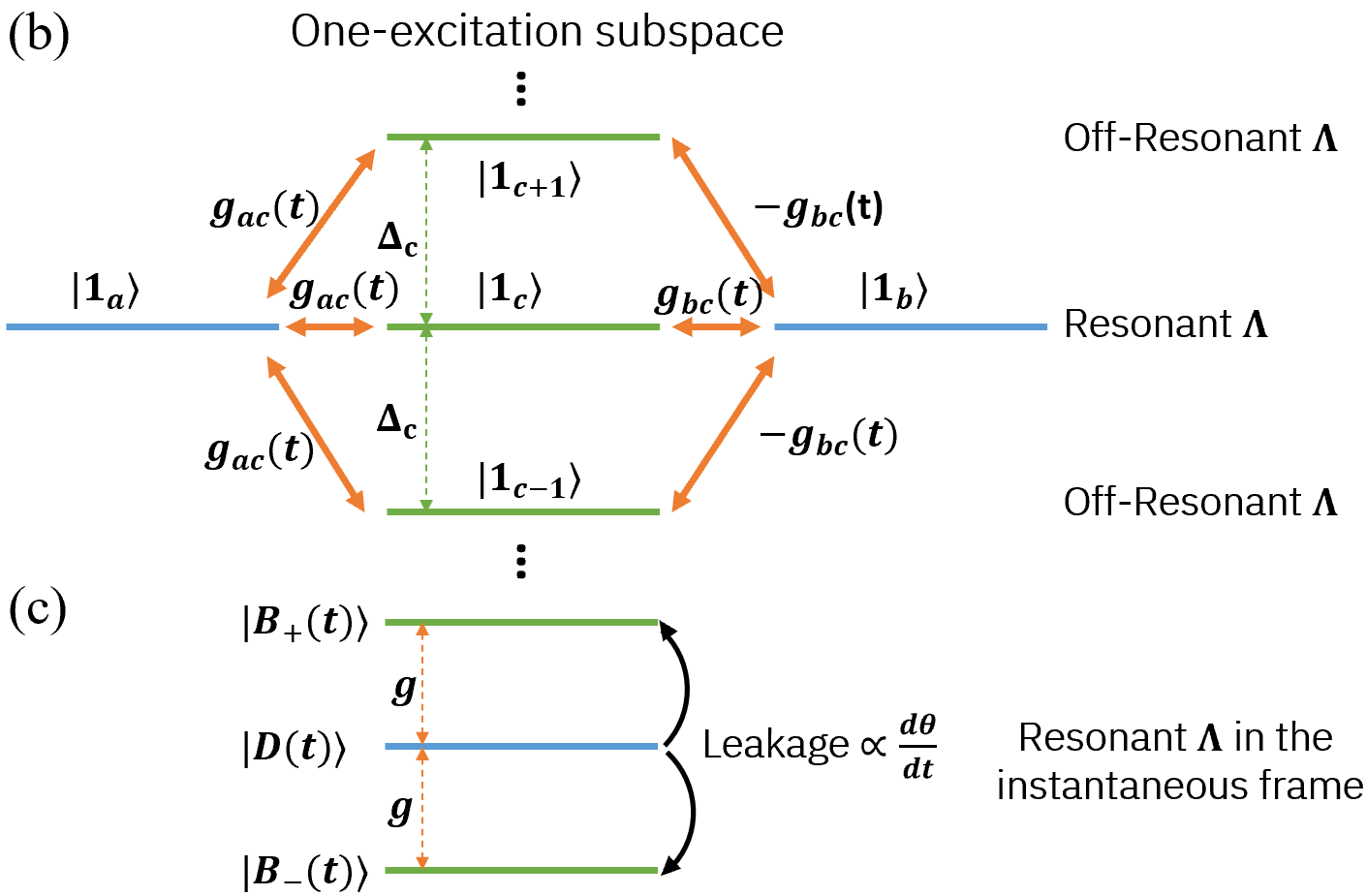
STIRAP is a protocol for adiabatic transfer of population in a Lambda system, i.e. between two quantum states coupled through a common intermediate state, via temporal control of the interactions [Fig. 1(b)]. Under the single-mode (ideal) case, the Hamiltonian reads
| (3) | ||||
where we assume all levels are resonant. This resonant Lambda system has a dark eigenstate
| (4) |
and two bright eigenstates
| (5) | ||||
with the mixing angle defined as .
The dark eigenstate, having no overlap with the intermediate (possibly) lossy interconnect state, therefore allows for an adiabatic quantum state transfer by arbitrarily evolving the mixing angle . A common choice for the controls are and with for . For instance, sweeping from 0 to or should ideally implement (full state transfer), or (Bell state), respectively. Note, however, that unwanted non-adiabatic transitions, whose probabilities grow with , impose a limit on the STIRAP speed (Fig. 1(c) and Appendix B).
For a multimode interconnect, with the interaction comparable to the FSR , the adjacent modes impact the fidelity of STIRAP detrimentally by (i) breaking the dark-symmetry condition, (ii) introducing additional leakage, and (iii) additional decay channels. Regarding item (i), each adjacent mode forms an effective off-resonant Lambda system with the qubits [Fig. 1(b)]. Our extended multimode STIRAP analysis suggests that for a hypothetical interconnect with same-sign interactions the Hamiltonian supports the original dark eigenstate, while for the physical case of mode-dependent interactions, one instead finds a pseudo dark eigenstate having a non-zero overlap with the one-excitation subspace of the odd (opposite-sign) modes (Appendix C). Such an adiabatic error vanishes for quantum state transfer with , but is maximized for Bell state generation with requiring a weaker for better fidelity.
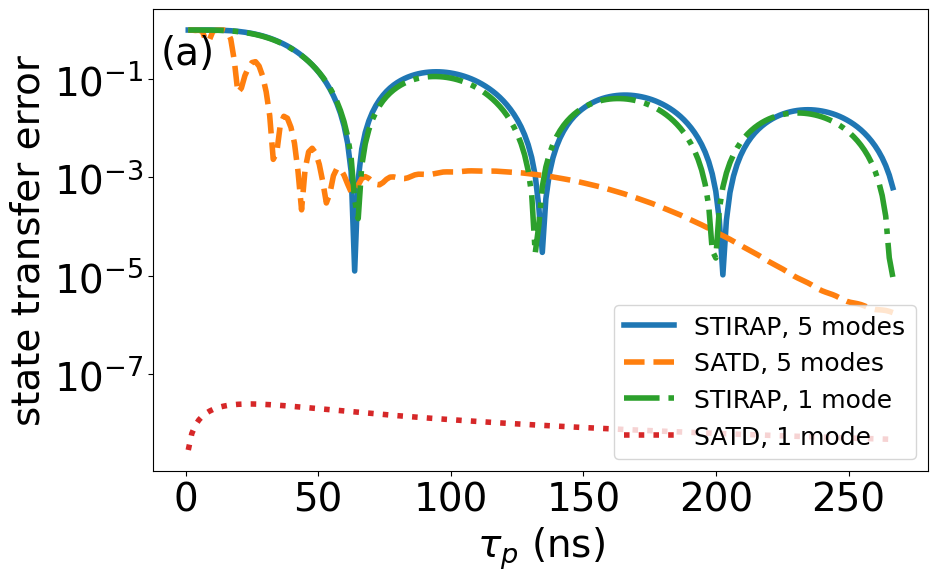
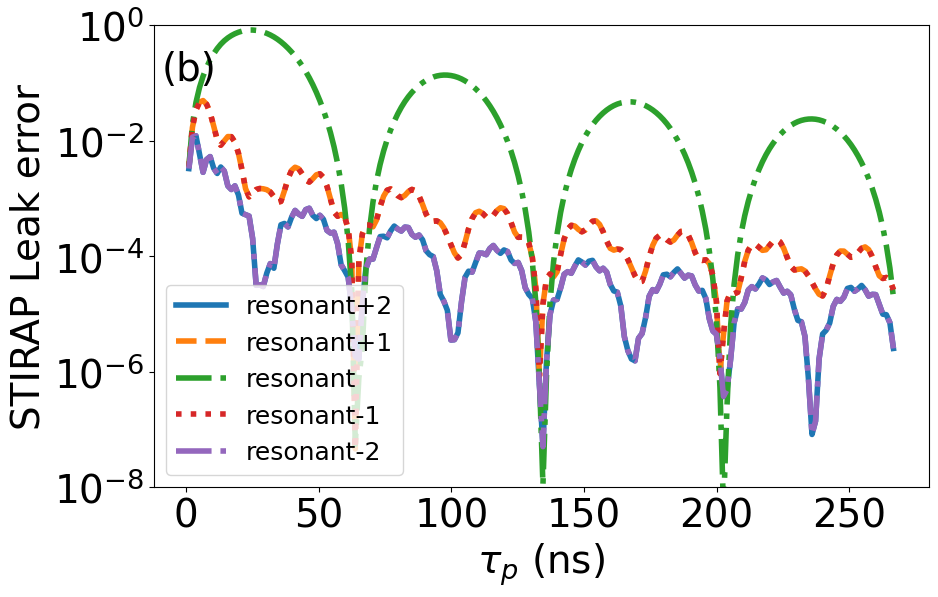
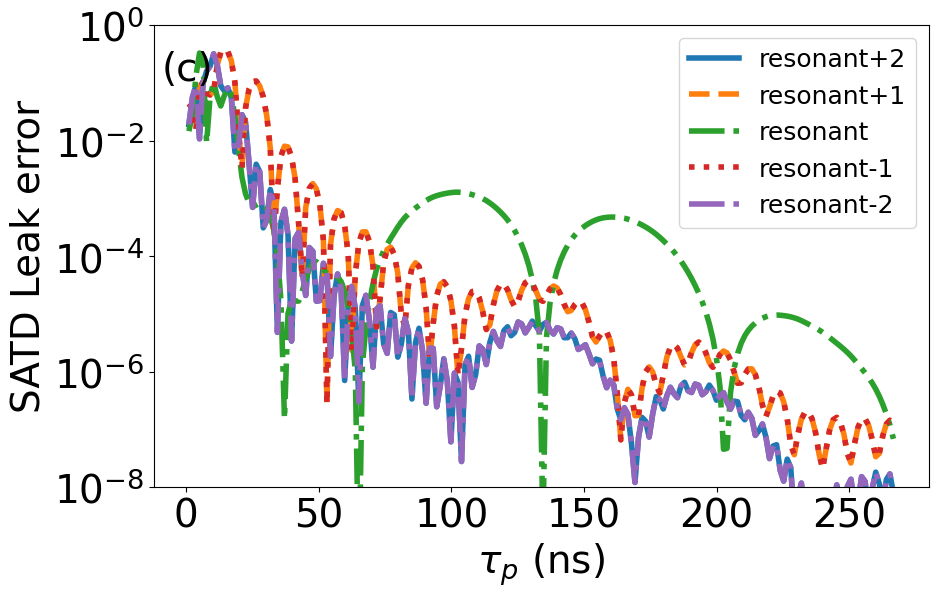
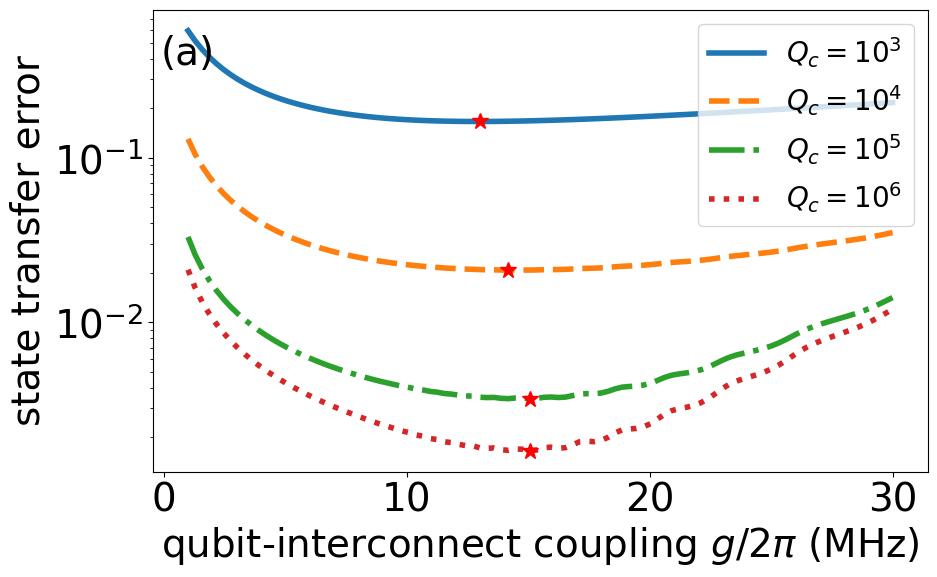
Figure 2 characterizes the performance of STIRAP in such a multimode context, where we simulate the Lindblad Eqs. (1)–(2) numerically with five interconnect modes evenly spaced about the qubit frequency for the common sine/cosine STIRAP controls and initial pure state . We define error,
| (6) |
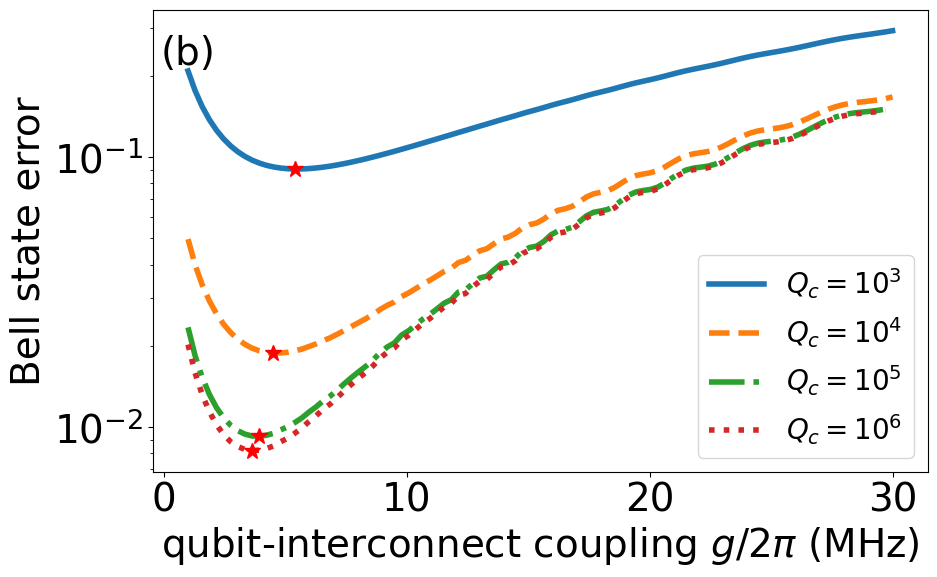
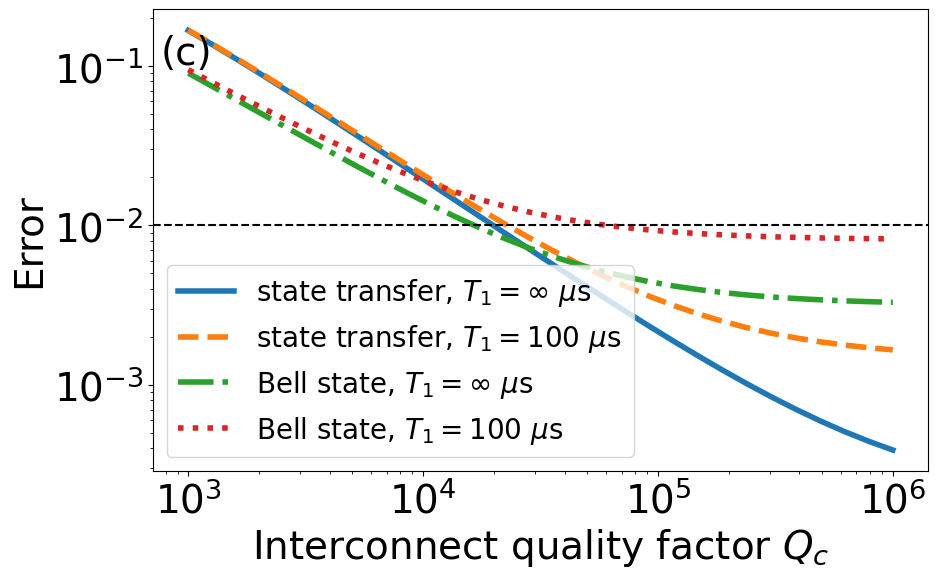
in terms of the overlap of the final density matrix with the ideal target states for state transfer and Bell states as and , respectively. Panels (a) and (b) show the corresponding error as a function of for fixed FSR of MHz and various interconnect quality factors, where we observe distinct approximate optimal ratio of and for state transfer and Bell state, respectively, at and s. The optimal couplings are a balance between more leakage to the neighboring modes at stronger (faster operation) and more incoherent error at weaker (slower operation). The Bell state generation also suffers from a non-zero adiabatic overlap with the odd interconnect modes due to dark-state symmetry breakdown (Appendix C and Sec. IV.2). Using the optimal couplings in panel (c), we find that in order to reach sub-percent error the interconnect must approximately exceed and for state transfer and Bell state, respectively.
IV Improved STIRAP via SuperAdiabatic Transitionless Driving
TD is a control technique for cancelling out non-adiabatic transitions via a corrected control Hamiltonian Demirplak_Adiabatic_2003 ; Demirplak2008consistency ; Berry_Transitionless_2009 ; Ibanez_Multiple_2012 . In an ideal case, from the hardware perspective, the correction can be simply implemented via a modification of the original control pulses. The superadiabatic aspect refers to implementing the cancellation in a dressed frame, i.e. effectively evolving the initial state in a modified path in the Hilbert space towards the target state. The standard single-mode STIRAP problem allows for a family of exact SATD solutions Baksic_Speeding_2016 . A commonly employed SATD solution dresses the evolution path along the spin-1 operator, yielding the explicit results Baksic_Speeding_2016 ; Ribeiro_Accelerated_2019 ; Setiawan_Analytic_2021 ; Setiawan_Fast_2023 (see also Appendix D)
| (7) | |||
| (8) |
where the corrections depend on both the first and the second derivative of the mixing angle (check Appendix D for a comparison of pulse shapes).
In the following, we characterize and compare the performance of regular STIRAP and SATD protocols, and dissect various favorable aspects of SATD usage in the context of multimode interconnects for quantum state transfer and Bell state generation. Some advantages of the SATD protocol can be summarized as follows:
-
(i)
The speed of standard STIRAP is limited by the darkbright transitions, whose effective transition frequency is equivalent to the resonant interaction rate (Appendix B). SATD, however, removes the darkbright leakage, and allows for faster operations whose speed limit is set by leakage to the adjacent interconnect modes (Appendix D, Figs. 3 and 7).
-
(ii)
One crucial practical consequence of (i) is the SATD robustness to qubit-interconnect interaction , and the possibility of performing fast high-fidelity operations even with weak interactions (Fig. 4).
-
(iii)
SATD provides a more pronounced speedup over STIRAP for the Bell state generation. This is the case as Bell state generation is more sensitive to the even/odd sign dependence of the interaction, compared to state transfer, and requires a weaker coupling to mitigate adiabatic overlap with the odd modes (Appendix C and Fig. 7).
- (iv)
IV.1 Quantum state transfer
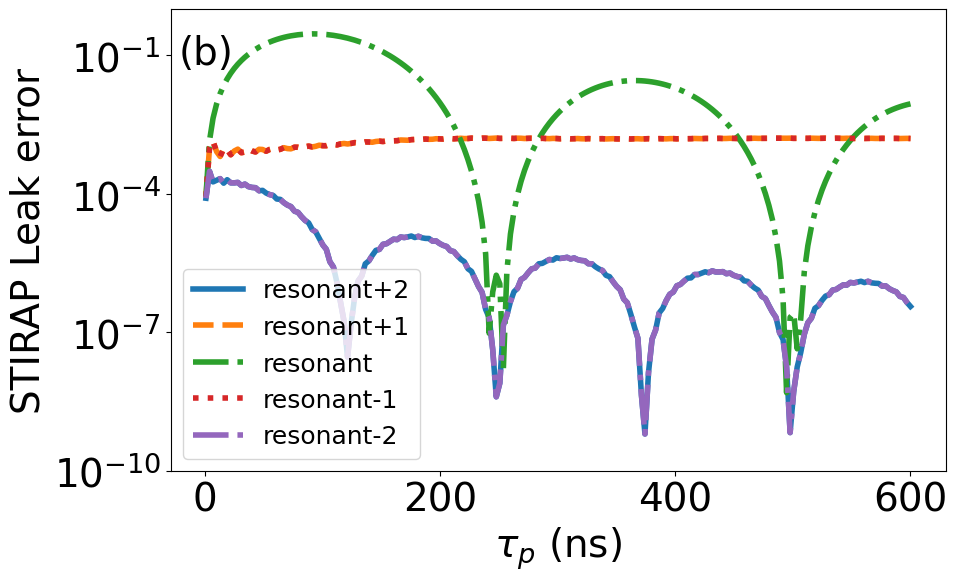
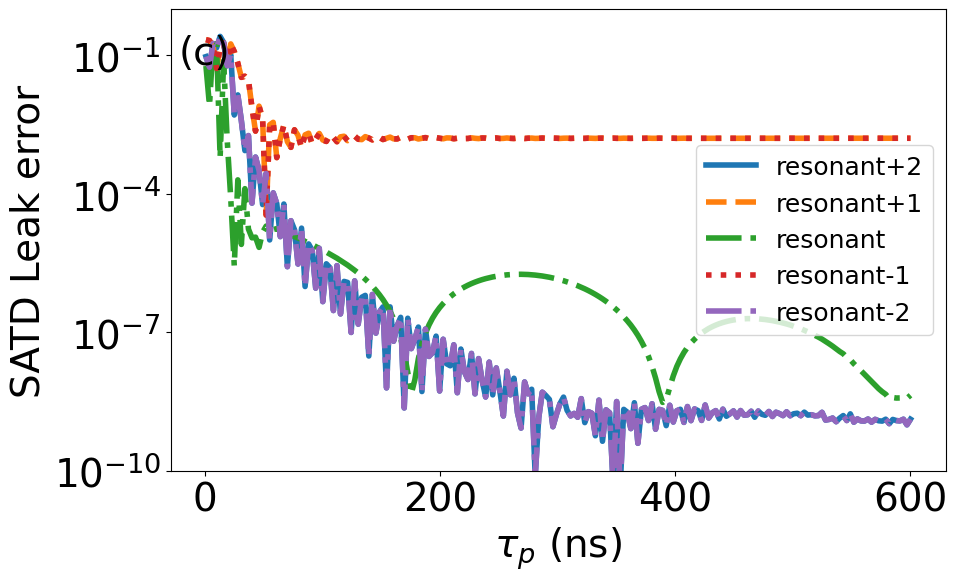
We begin by analyzing the performance of SATD for quantum state transfer. Figure 3 shows a comparison and breakdown of quantum state transfer error between regular STIRAP and SATD protocols. To emphasize the corrections provided by adopting the single-mode SATD solutions in this multimode setting, here we present the results considering both single and five interconnect modes and for zero qubit pure dephasing and qubit/interconnect relaxation. Panel (a) shows that for regular STIRAP, the single- and five-mode curves agree indicating that state-transfer error is limited mainly by leakage to the resonant interconnect mode. The single-mode SATD simulation confirms the elimination of this leakage down to numerical error as expected. Applying the single-mode SATD solutions (7)–(8) in the multimode setting is still advantageous in terms of operation time (orange curve). Panels (b)–(c) show the breakdown of final-time leakage to individual interconnect modes, where for SATD the error is mainly limited by leakage to the adjacent interconnect modes at shorter times.
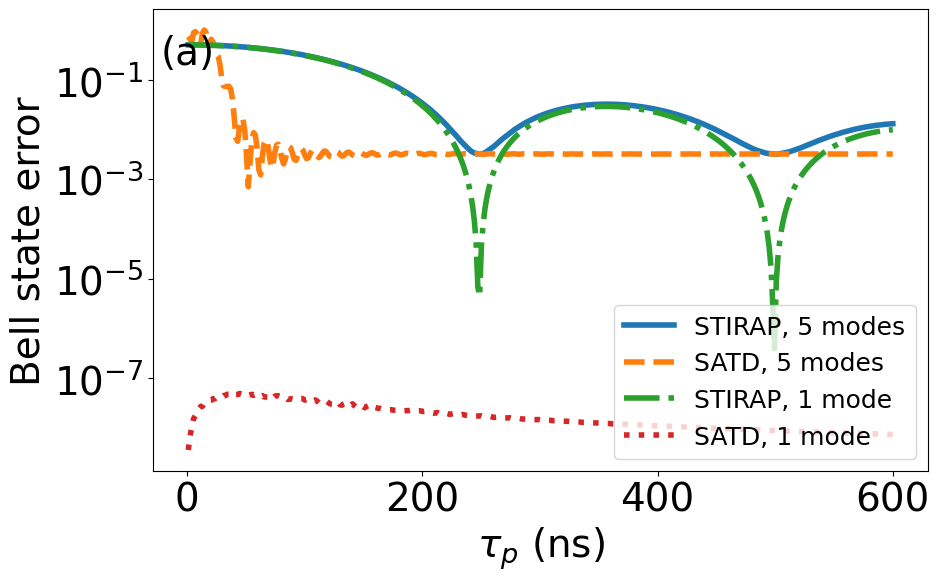
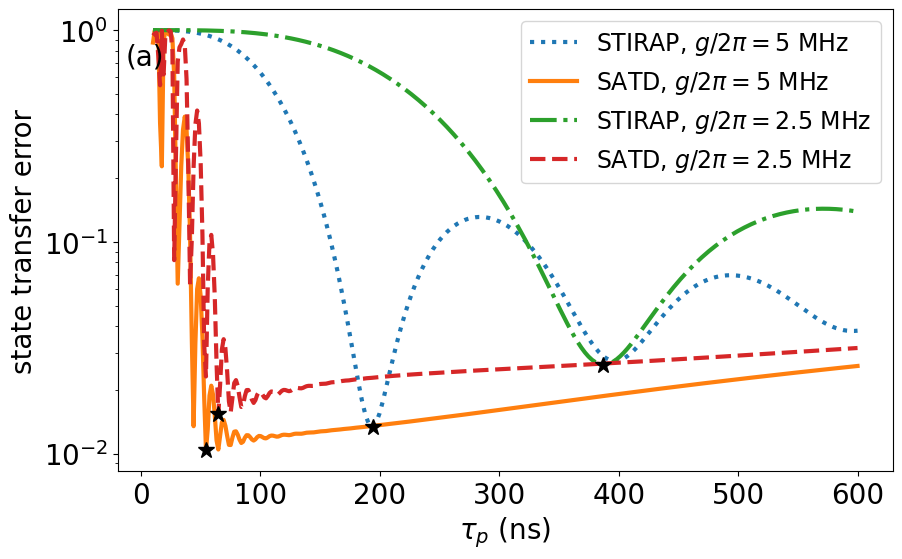
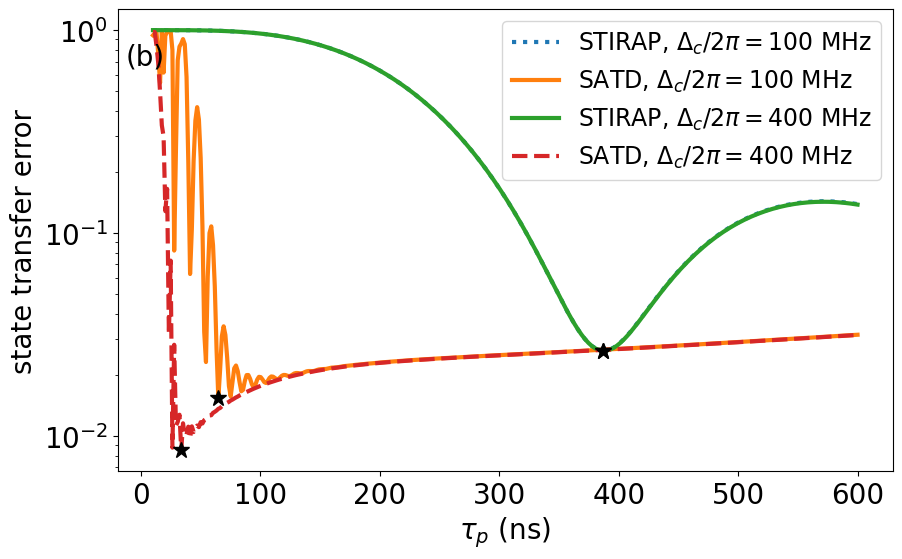
To demonstrate the robustness of the SATD protocol with respect to , and the interplay with FSR , we compare STIRAP and SATD performance for weaker-than-optimal couplings in Fig. 4. Comparing the state transfer error for fixed MHz and two choices of and MHz in panel (a) reveals a robustness of the SATD protocol, in which the two couplings provide comparable optimal error (black stars) of 0.015 and 0.01 at 64 ns and 54 ns, respectively. On the other hand, the standard STIRAP’s time is inversely proportional to , where we find optimal error of approximately 0.013 and 0.026 at 194 ns and 387 ns (double), respectively. This feature of SATD is very beneficial as it allows to run high-fidelity fast operations even at weak coupling rates. In panel (b), we run a similar comparison but for a fixed weak MHz and two interconnect FSR (inversely proportional to length) choices of and MHz. By the same token, SATD provides faster and improved error for the larger FSR case, 0.009 at 34 ns compared to 0.015 at 65 ns, while regular STIRAP’s error/speed is 0.026 at 387 ns and the same for the two cases.
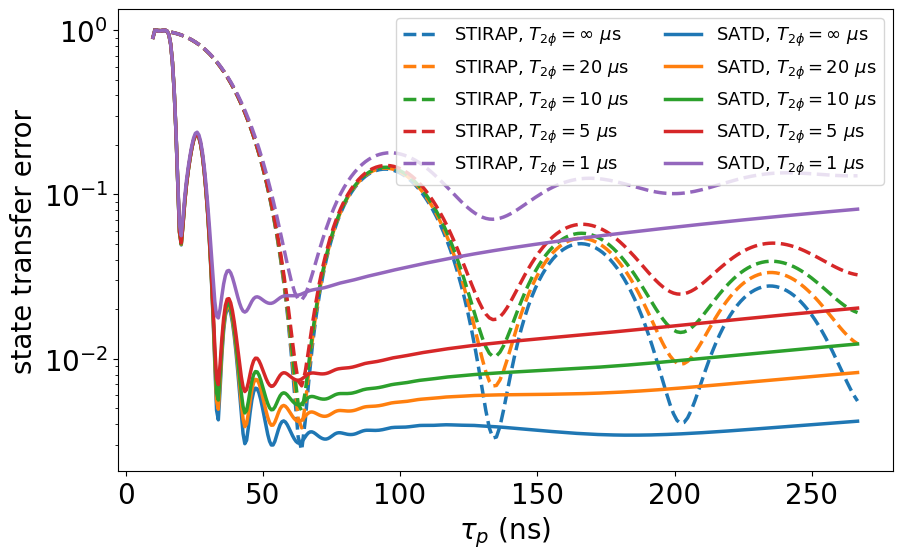
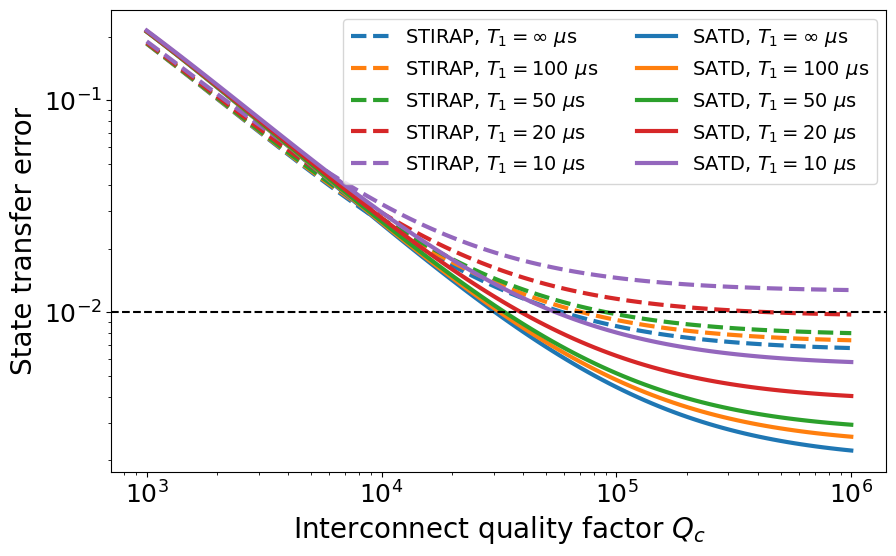
We also assess the improvement by SATD, compared to STIRAP, in error sensitivity to pure dephasing and qubit/interconnect relaxation in Figs. 5–6 with the approximately optimal MHz for state transfer (Fig. 2(a)). We find that the incoherent errors due to dephasing and relaxation are approximately additive. Figure 5 shows the state transfer error as a function of for various ranging in s. First, due to the expedited transfer, the pure dephasing error, , for SATD is substantially reduced, where at ns we find . Moreover, at longer (standard) STIRAP time of ns, SATD demonstrates a substantial improvement of dephasing error as compared to . Furthermore, Fig. 6 shows the error as a function of the quality factor for various relaxation times s. We observe that SATD offers substantial improvement in sensitivity with respect to qubit as compared to at sufficiently large .
IV.2 Bell state generation
We next discuss the advantages of the SATD protocol for Bell state (entanglement) generation. The trade-offs/benefits demonstrated in Sec. IV.1 for state transfer carry on to Bell state generation as well. In addition, Bell state generation is more prone to the even/odd sign of interaction, and hence requires a weaker qubit-interconnect as found in Fig. 2(b). The use of regular STIRAP, however, means the operation time will be set by and hence would become very slow. Therefore, SATD, whose speed is limited by , provides a larger speedup for Bell state generation compared to state transfer.
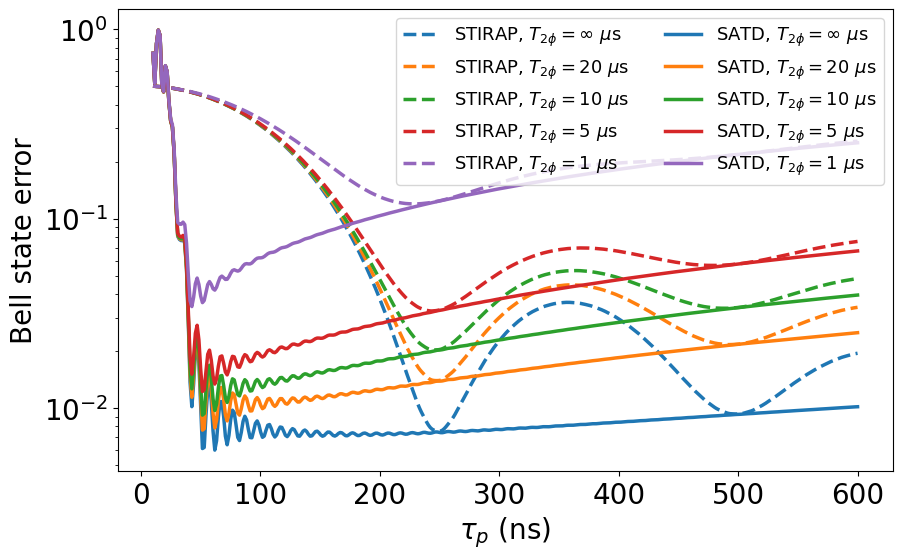
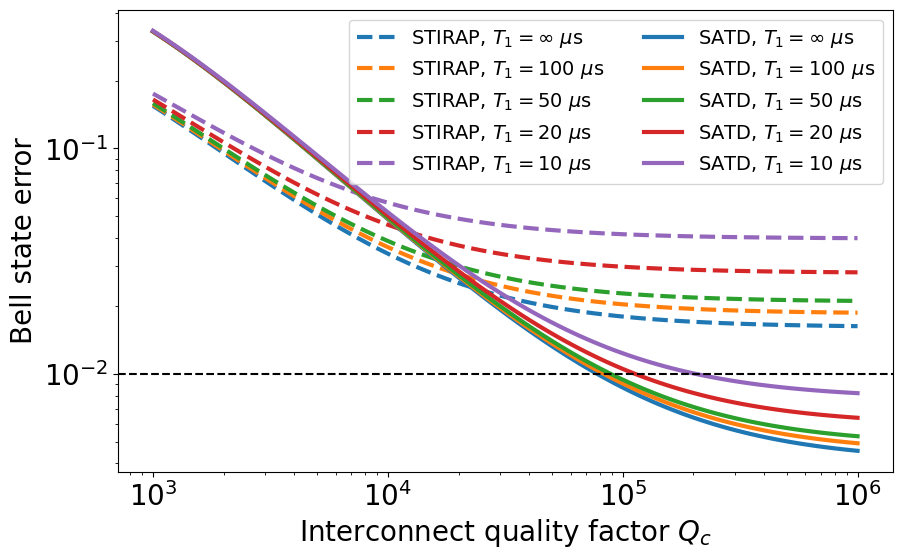
Figure 7 shows a comparison between STIRAP and SATD, similar to that of Fig. 3 with zero relaxation and dephasing, for Bell state generation. Panel (a) shows that the SATD solution cancels out the non-adiabatic error entirely. The five mode simulation, however, manifests a constant floor for the error at sufficiently long times independent of . The breakdown of interconnect mode populations in panels (b)–(c) reveals the source of this error as loss of qubit population to the odd modes which is almost equal between STIRAP and SATD. We find this adiabatic overlap of the supposedly dark state with the odd modes to scale approximately as . Here, we have picked a weak coupling of MHz, which suppresses the overlap error down to . In this regime, SATD gives a substantial speedup, where the fastest operation times for STIRAP and SATD are approximately 250 ns and 86 ns, respectively. Furthermore, Figs. 8 and 9 characterize the sensitivity of Bell state generation error to pure dephasing and qubit/interconnect relaxation in a similar format as in Figs. 5–6 but for MHz. In this weak coupling limit, SATD leads to a noticeable reduction in error sensitivity to pure dephasing, where at ns we find , compared to at ns. Moreover, based on Fig. 9, SATD achieves improved error sensitivity with respect to both and , where compared to at sufficiently large .
IV.3 Practical impacts of SATD on indirect remote two-qubit gate schemes
To put the SATD improvements into perspective, we revisit two indirect two-qubit gate schemes shown in Fig. 10. Imagine two QPU units with qubits A and B on the left, and D and E on the right. In each unit, we can perform a native two-qubit gate . However, assume that between the interface qubits B and D across the interconnect C, we can only perform quantum state transfer or generate entanglement.
The first scheme in Fig. 10(b) allows the arbitrary native two-qubit gate to act between an interface qubit and the qubit adjacent to the interface qubit on the other side. For instance, to perform a remote gate between qubits A and D we need to: (i) initialize qubit B in the ground state , (ii) transfer the state of D to B, (iii) perform the local native gate , and (iv) transfer the state of B back to D. In another words, . A similar gate could be implemented between qubits B and E. Assuming sufficiently high fidelity for each individual operation, the average gate error Pedersen_Fidelity_2007 up to the leading order is roughly . Given the requirement for two state transfers, we expect the use of SATD to give noticeable improvement in both the gate speed and the average error. For instance, with MHz, Ref. Chang_Remote_2020 calibrates a 130 ns state transfer using STIRAP, while with SATD we expect a ns transfer time for FSR of MHz.
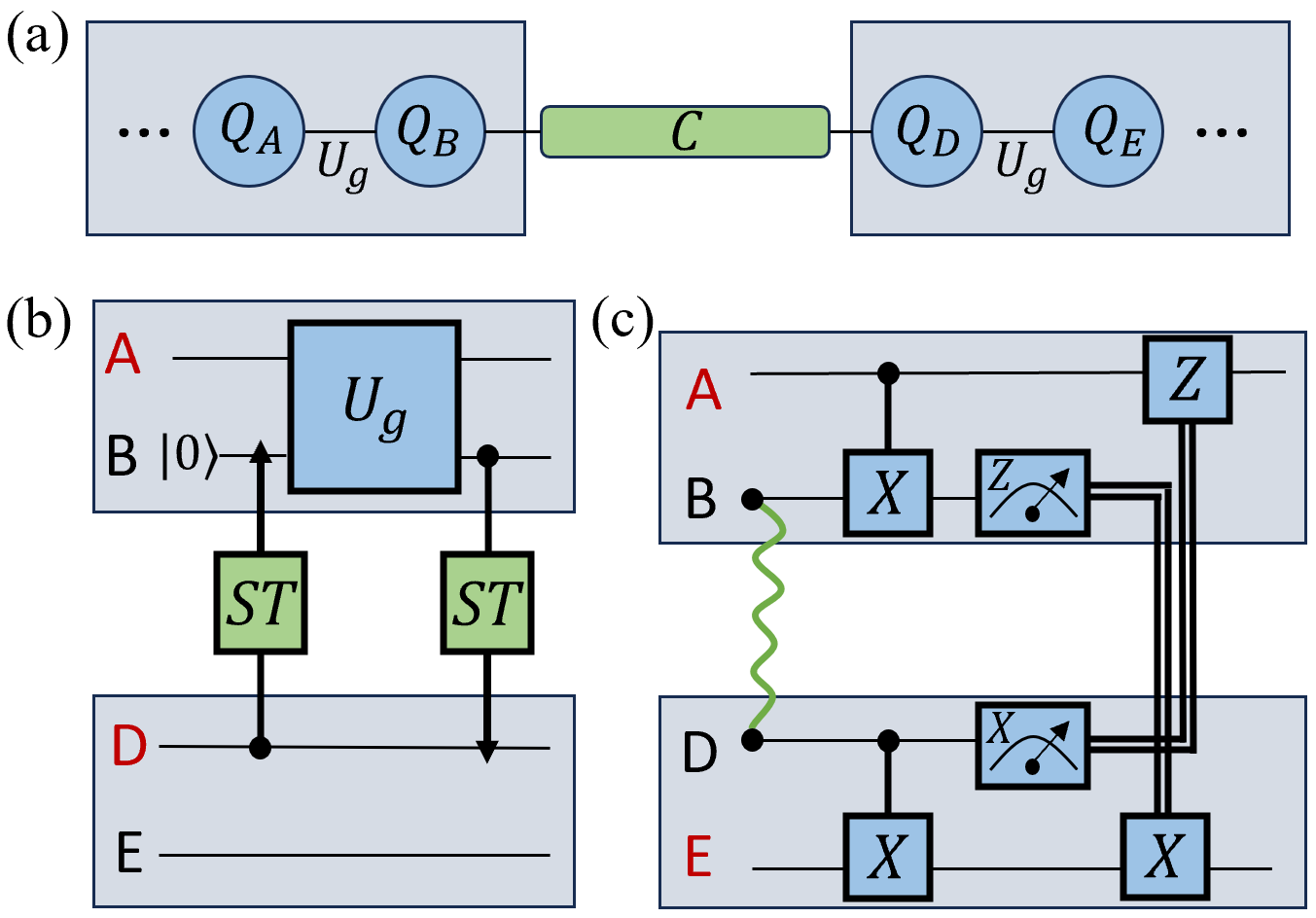
Figure 10(c) shows the well-known CNOT teleportation scheme Eisert_Optimal_2000 ; Huang_Experimental_2004 ; Chou_Deterministic_2018 ; Wan_Quantum_2019 . The protocol requires an initial entangled Bell pair between the interface qubits B and D, which can be prepared using STIRAP or SATD. Applying two local CNOT gates and two mid-circuit measurements and feedforward operations across the interconnect yields an effective CNOT gate between the outer qubits A and E. We expect the fidelity of the protocol to be mainly limited by the relatively long mid-circuit measurements and feedforward operations. The requirement for a weaker optimal MHz, however, makes the use of SATD more crucial, which can expedite the Bell generation substantially e.g. from 250 ns down to ns (see Fig. 8).
V Conclusion and outlook
In this work, we promote the general application of shortcuts to adiabaticity methods Jarzynski_Generating_2013 ; Deffner_Classical_2014 ; Guery_Shortcuts_2019 , in particular SATD for STIRAP Baksic_Speeding_2016 ; Ribeiro_Accelerated_2019 ; Setiawan_Analytic_2021 ; Setiawan_Fast_2023 , in improving remote entanglement generation and quantum state transfer in multimode interconnects. Our results have applications to both long-range QPU-QPU and potential on-chip connections. Besides introducing new leakage and decay channels, we find the multimode nature of an interconnect violates the dark state symmetry required for adiabatic passage by an adiabatic overlap error with the odd modes that grows as , which impacts entanglement generation more strongly. This observation makes SATD a great fit in this multimode context, since due to its robustness against it allows for fast quantum operations at a sufficiently weak that suppresses the overlap error as well. For a meter-long interconnect with FSR of 100 MHz, we can calibrate ns quantum state transfer and Bell state with sub-percent error.
We find the single-interconnect-mode SATD solutions Baksic_Speeding_2016 ; Ribeiro_Accelerated_2019 ; Setiawan_Analytic_2021 ; Setiawan_Fast_2023 to work approximately as intended in the weak limit such that only leakage in the resonant subspace (dark-bright transitions) is cancelled out, and the operation speed is limited by leakage to the adjacent modes, which is set by the interconnect FSR. A potential future research direction is expediting the operation even further by suppressing leakage to the off-resonant modes. One could ask whether precise or approximate SATD solutions exist in the multimode case, and whether they can be implemented via the same control knobs. Also, the single-mode SATD solutions can potentially serve as a reasonable initial guess for numerical optimal control techniques Khaneja_Optimal_2005 ; Koch_Quantum_2022 for further leakage improvement.
VI Acknowledgements
We appreciate helpful discussions with the IBM Quantum members Vikesh Siddhu, Theodore J. Yoder, Alireza Seif, Luke C. G. Govia, Muir Kumph, Jerry M. Chow, and Jay M. Gambetta. The authors acknowledge the IBM Research Cognitive Computing Cluster (CCC) service for providing resources that have contributed to the research results reported within this paper.
Appendix A Lindblad simulation
For our numerical modeling of STIRAP and SATD, we run Lindbald simulations with two qubits and a finite number of interconnect modes. The Hamiltonian can be approximately described as
| (9) | ||||
with , and denoting the qubits and the interconnect modes, respectively. Moreover, , and represent mode frequency, anharmonicity and exchange interaction, respectively. The multimode interconnect is modeled as a set of linear quantum harmonic oscillators as with the center frequency and FSR .
We account for various incoherent error sources such as qubit relaxation, cable relaxation, and qubit pure dephasing, by numerically solving the following Lindblad equation for the system density matrix :
| (10) | ||||
where and are the relaxation and pure dephasing times for qubit , respectively, and is the decay rate of the interconnect mode. Furthermore, is the dissipator for the collapse operator .
A few remarks are in order. First, the qubit Hamiltonian is expressed as a multi-level Kerr oscillator. For the purpose of modeling state transfer and Bell state generation, however, the time-evolution is fairly accurately described by the one-excitation subspace. Therefore, the two-level approximation works well. Second, we have preformed RWA on the qubit-interconnect interactions given the experimentally relevant realizations where MHz, and GHz. Third, the qubit-interconnect interaction rates for in principle depend on the mode number approximately as Houck_Controlling_2008 ; Malekakhlagh_Origin_2016 ; Gely_Convergence_2017 ; Malekakhlagh_Cutoff-Free_2017 . For a long coupler, however, qubits are resonant with a high-order interconnect mode, making the modal dependence of the interaction less pronounced. Fourth, the phase factor for qubit interaction rate accounts for the opposite amplitude sign of even and odd spatial modes at the two ends of the interconnect.
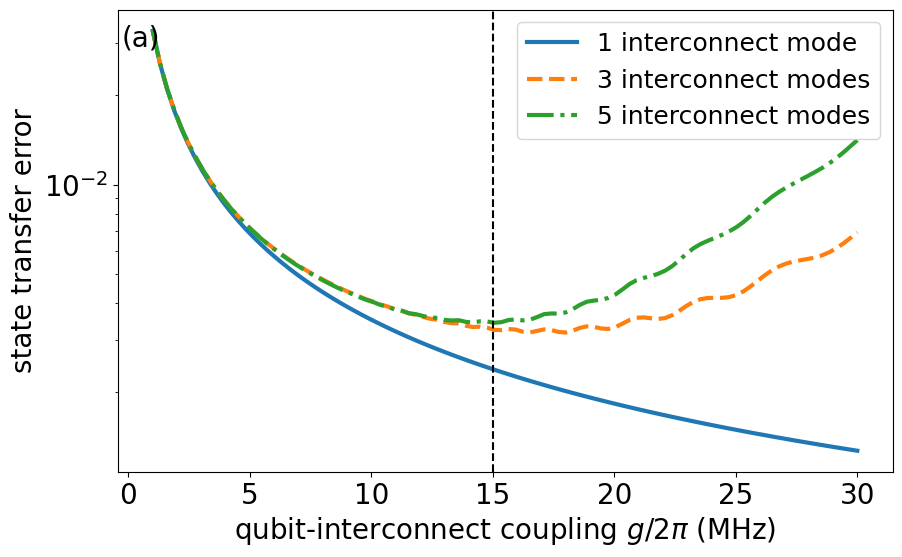
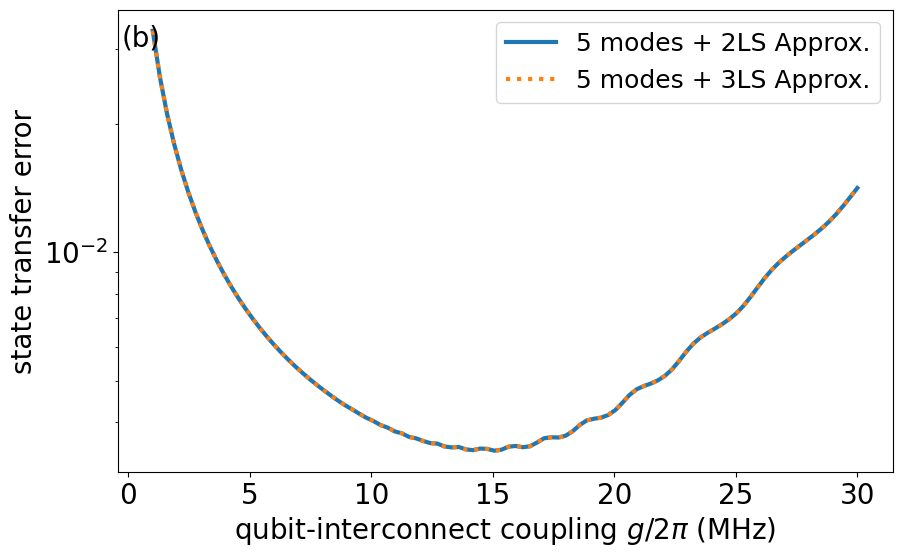
For all results in the main text, we have accounted for five interconnect modes; one resonant with the qubits and two on each side. Even under two-level approximation for the qubits and the modes, this constitutes a large density matrix of dimension 128128 (). Figure 11(a) shows a convergence test of state transfer error with one, three and five interconnect modes. Generally speaking, stronger leads to more pronounced multimode effects involving further detuned modes. Our choice of five interconnect modes is a balance between simulation precision and speed for of up to approximately 15 MHz used in the main text. Furthermore, since STIRAP is excitation preserving, higher-levels of the qubits would not impact the dynamics as shown in Fig. 11(b).
Lastly, we note that our numerical simulation of the Lindblad dynamics (9)–(10) was performed using Qiskit Dynamics Puzzuoli_Algorithms_2023 ; Puzzuoli_Qiskit_2023 , along with standard Python scientific computing packages including numpy Harris_Array_2020 and scipy Virtanen_Scipy_2020 . We used the DOP853 ODE solver with absolute and relative tolerances set to atol=rtol=1e-10. The simulations were parallelized over multiple CPU cores (up to 250) on IBM’s Cognitive Computing Cluster.
Appendix B Single-mode STIRAP
Consider a resonant Lambda system with tunable interaction rates between the qubit states and coupler state as:
| (11) | ||||
where in the second step we have re-expressed the interactions as and . This resonant system contains two bright and one dark instantaneous eigenstates, where dark refers to no overlap with the intermediate interconnect state. Explicitly, Hamiltonian (11) can be diagonalized as
| (12) | ||||
via the unitary transformation
| (13) |
where the rows of Eq. (13) represent the bright and dark eigenstates, having eigenergies and , respectively.
Under STIRAP, we adiabatically evolve the dark state of the system by sweeping the angle . Starting with , we can create a Bell state or perform state transfer at final angle and , respectively. Common control pulse shapes are
| (14) | |||
| (15) | |||
| (16) |
which keeps the bright-dark transition frequency constant in time equal to . The non-adiabatic error of STIRAP is explicitly found by the time-dependent transformation of the Schrödinger equation in the instantaneous frame as:
| (17) | ||||
which is responsible for dark-bright state transitions whose strength is determined by the STIRAP speed .
We can derive leading-order expressions for the dark-bright transitions using Magnus expansion Magnus_Exponential_1954 ; Blanes_Magnus_2009 ; Blanes_Pedagogical_2010 . Employing the control pulse shapes (14)–(15), and in the frame rotating with the instantaneous Hamiltonian (12), the non-adiabatic Hamiltonian is transformed to
| (18) | ||||
Up to the lowest order, the Magnus generator and the time-evolution operator are found as Blanes_Pedagogical_2010 :
| (19) | |||
| (20) |
We finally compute the dark-bright transition probability up to the leading order as:
| (21) | ||||
Based on Eq.(21), for constant , such a leakage can be minimized if the operation time satisfies for , explaining the regular STIRAP lobes as e.g. in Fig. 3(a).
Appendix C STIRAP considerations for a multimode interconnect
In a multimode setting, where is a non-negligible fraction of the interconnect’s FSR , the off-resonant modes have a detrimental effect on the STIRAP protocol. Here, we provide a simplified argument on why using STIRAP for entanglement generation is more prone to multimode error compared to state transfer.
Note the qubits also form off-resonant Lambda systems with the adjacent interconnect modes. To study the role of off-resonant modes, and the even-odd sign-dependent interactions, consider the simplest multimode extension of Eq. (11) as:
| (22) | ||||
where we add two adjacent interconnect modes with detunings .
Due to the sign-dependent interactions, Hamiltonian (22) only supports a pseudo-dark eigenstate of the form:
| (23) |
where and .
According to Eq. (23), for the case of alternating interaction sign, the pseudo dark eigenstate has a non-zero overlap of magnitude with the one-excitation subspace of the odd interconnect modes. For a hypothetical case of same-sign interaction, however, we find the original dark state is supported with zero overlap with all interconnect modes. First, we emphasize that this unwanted overlap is an adiabatic error, which is independent of the STIRAP speed , and can only be mitigated by weaker interaction . Second, when sweeping the mixing angle from to for state transfer, the unwanted end overlap is zero given that . This is, however, not the case for arbitrary entanglement generation and Bell state generation with in particular, making it more susceptible to such an adiabatic error.
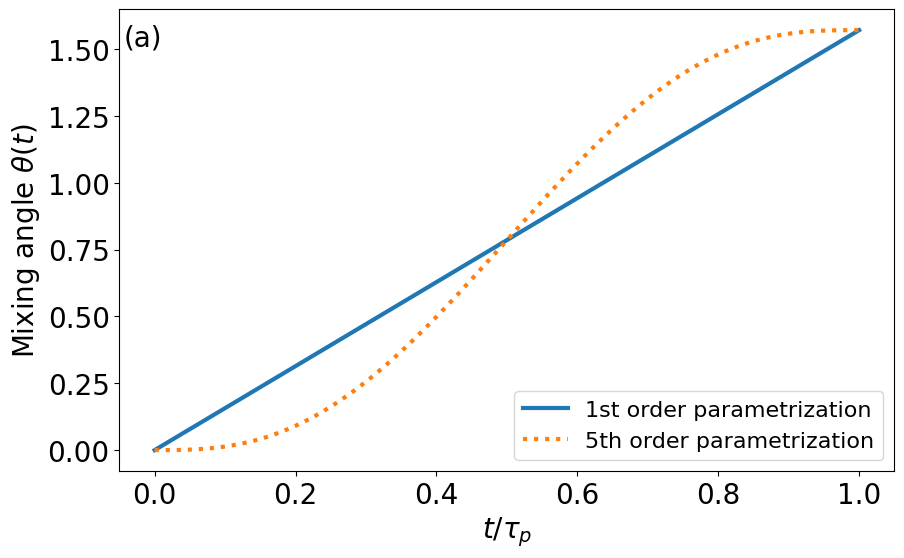
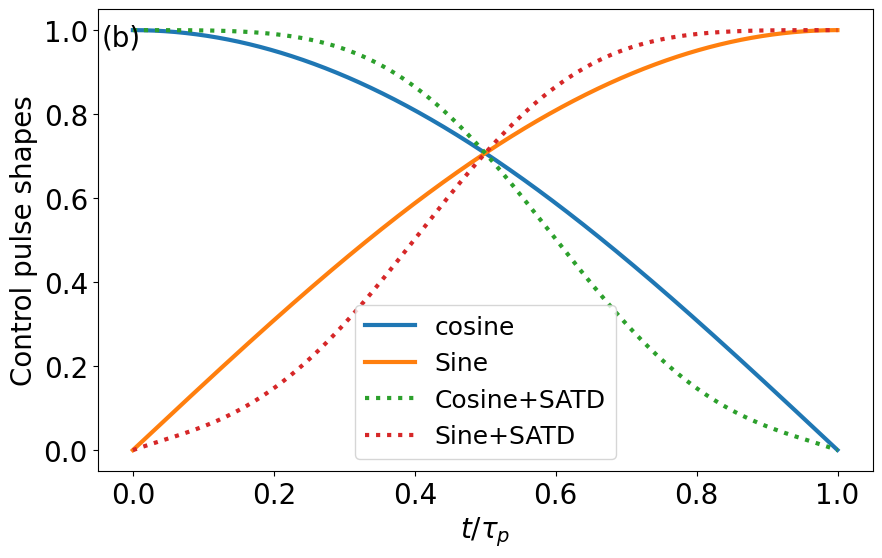
Appendix D SATD correction for STIRAP
Here, we review the derivation of SATD solutions for the STIRAP problem Baksic_Speeding_2016 ; Ribeiro_Accelerated_2019 ; Setiawan_Analytic_2021 ; Setiawan_Fast_2023 . Under the SATD method, we actively cancel out the non-adiabatic contribution by (i) correcting the controls, and (ii) dressing the adiabatic evolution path. Here, we review the derivation of a special SATD solution in which both the control and the dressing is along the direction:
| (24) | |||
| (25) |
where and are the x-control amplitude and x-dressing angle, respectively (to be determined), and for is the spin-1 operator.
We then solve for and such that in the frame dressed by , given by
| (26) | ||||
the off-diagonal non-adiabatic transitions are cancelled out at arbitrary time . Enforcing the cancellation results in the following equations:
| (27) | ||||
| (28) |
with an explicit solution for as:
| (29) |
Transforming the corrected control back to the lab frame according to Eq. (24) one finds the SATD solutions as:
| (30) | |||
| (31) |
To ensure that the initial and final points of the adiabatic evolution remains unchanged we further enforce , in addition to and . The lowest-order polynomial satisfying these conditions is then found as:
| (32) |
Figure 12 shows a comparison between the modified SATD control pulse shapes (30)–(32) and the standard STIRAP control in Eqs. (14)–(16).
References
- [1] Simon J Devitt, Austin G Fowler, Ashley M Stephens, Andrew D Greentree, Lloyd CL Hollenberg, William J Munro, and Kae Nemoto. “architectural design for a topological cluster state quantum computer”. New Journal of Physics, 11(8):083032, 2009.
- [2] Christopher Monroe, Robert Raussendorf, Alex Ruthven, Kenneth R Brown, Peter Maunz, L-M Duan, and Jungsang Kim. “large-scale modular quantum-computer architecture with atomic memory and photonic interconnects”. Physical Review A, 89(2):022317, 2014.
- [3] Sergey Bravyi, Oliver Dial, Jay M Gambetta, Darío Gil, and Zaira Nazario. “the future of quantum computing with superconducting qubits”. Journal of Applied Physics, 132(16), 2022.
- [4] Austin G Fowler, Ashley M Stephens, and Peter Groszkowski. “high-threshold universal quantum computation on the surface code”. Physical Review A, 80(5):052312, 2009.
- [5] Austin G Fowler, Matteo Mariantoni, John M Martinis, and Andrew N Cleland. “surface codes: Towards practical large-scale quantum computation”. Physical Review A, 86(3):032324, 2012.
- [6] Sergey Bravyi, Andrew W Cross, Jay M Gambetta, Dmitri Maslov, Patrick Rall, and Theodore J Yoder. “high-threshold and low-overhead fault-tolerant quantum memory”. arXiv preprint arXiv:2308.07915, 2023.
- [7] Emanuel Knill and Raymond Laflamme. “theory of quantum error-correcting codes”. Physical Review A, 55(2):900, 1997.
- [8] Daniel Gottesman. “Stabilizer codes and quantum error correction”. California Institute of Technology, 1997.
- [9] Emanuel Knill, Raymond Laflamme, and Lorenza Viola. “theory of quantum error correction for general noise”. Physical Review Letters, 84(11):2525, 2000.
- [10] Daniel A Lidar and Todd A Brun. “Quantum error correction”. Cambridge university press, 2013.
- [11] Barbara M Terhal. “quantum error correction for quantum memories”. Reviews of Modern Physics, 87(2):307, 2015.
- [12] Alysson Gold, JP Paquette, Anna Stockklauser, Matthew J Reagor, M Sohaib Alam, Andrew Bestwick, Nicolas Didier, Ani Nersisyan, Feyza Oruc, Armin Razavi, et al. Entanglement across separate silicon dies in a modular superconducting qubit device. npj Quantum Information, 7(1):142, 2021.
- [13] CR Conner, A Bienfait, H-S Chang, M-H Chou, É Dumur, J Grebel, GA Peairs, RG Povey, H Yan, YP Zhong, et al. “superconducting qubits in a flip-chip architecture”. Applied Physics Letters, 118(23), 2021.
- [14] Daniel Gottesman and Isaac L Chuang. “demonstrating the viability of universal quantum computation using teleportation and single-qubit operations”. Nature, 402(6760):390–393, 1999.
- [15] Jens Eisert, Kurt Jacobs, Polykarpos Papadopoulos, and Martin B Plenio. “optimal local implementation of nonlocal quantum gates”. Physical Review A, 62(5):052317, 2000.
- [16] Yun-Feng Huang, Xi-Feng Ren, Yong-Sheng Zhang, Lu-Ming Duan, and Guang-Can Guo. “experimental teleportation of a quantum controlled-not gate”. Physical review letters, 93(24):240501, 2004.
- [17] Alexandre Baksic, Hugo Ribeiro, and Aashish A Clerk. “speeding up adiabatic quantum state transfer by using dressed states”. Physical review letters, 116(23):230503, 2016.
- [18] Philipp Kurpiers, Paul Magnard, Theo Walter, Baptiste Royer, Marek Pechal, Johannes Heinsoo, Yves Salathé, Abdulkadir Akin, Simon Storz, J-C Besse, et al. “deterministic quantum state transfer and remote entanglement using microwave photons”. Nature, 558(7709):264–267, 2018.
- [19] Christopher J Axline, Luke D Burkhart, Wolfgang Pfaff, Mengzhen Zhang, Kevin Chou, Philippe Campagne-Ibarcq, Philip Reinhold, Luigi Frunzio, SM Girvin, Liang Jiang, et al. “on-demand quantum state transfer and entanglement between remote microwave cavity memories”. Nature Physics, 14(7):705–710, 2018.
- [20] P Campagne-Ibarcq, E Zalys-Geller, A Narla, S Shankar, P Reinhold, L Burkhart, C Axline, W Pfaff, L Frunzio, RJ Schoelkopf, et al. “deterministic remote entanglement of superconducting circuits through microwave two-photon transitions”. Physical review letters, 120(20):200501, 2018.
- [21] N Leung, Y Lu, S Chakram, RK Naik, N Earnest, R Ma, K Jacobs, AN Cleland, and DI Schuster. “deterministic bidirectional communication and remote entanglement generation between superconducting qubits”. npj quantum information, 5(1):18, 2019.
- [22] YP Zhong, H-S Chang, KJ Satzinger, M-H Chou, Audrey Bienfait, CR Conner, É Dumur, Joel Grebel, GA Peairs, RG Povey, et al. “violating bell’s inequality with remotely connected superconducting qubits”. Nature Physics, 15(8):741–744, 2019.
- [23] Audrey Bienfait, Kevin J Satzinger, YP Zhong, H-S Chang, M-H Chou, Chris R Conner, É Dumur, Joel Grebel, Gregory A Peairs, Rhys G Povey, et al. “phonon-mediated quantum state transfer and remote qubit entanglement”. Science, 364(6438):368–371, 2019.
- [24] H-S Chang, YP Zhong, Audrey Bienfait, M-H Chou, Christopher R Conner, Étienne Dumur, Joel Grebel, Gregory A Peairs, Rhys G Povey, Kevin J Satzinger, et al. “remote entanglement via adiabatic passage using a tunably dissipative quantum communication system”. Physical Review Letters, 124(24):240502, 2020.
- [25] Youpeng Zhong, Hung-Shen Chang, Audrey Bienfait, Étienne Dumur, Ming-Han Chou, Christopher R Conner, Joel Grebel, Rhys G Povey, Haoxiong Yan, David I Schuster, et al. “deterministic multi-qubit entanglement in a quantum network”. Nature, 590(7847):571–575, 2021.
- [26] Haoxiong Yan, Youpeng Zhong, Hung-Shen Chang, Audrey Bienfait, Ming-Han Chou, Christopher R Conner, Étienne Dumur, Joel Grebel, Rhys G Povey, and Andrew N Cleland. “entanglement purification and protection in a superconducting quantum network”. Physical Review Letters, 128(8):080504, 2022.
- [27] Bharath Kannan, Aziza Almanakly, Youngkyu Sung, Agustin Di Paolo, David A Rower, Jochen Braumüller, Alexander Melville, Bethany M Niedzielski, Amir Karamlou, Kyle Serniak, et al. “on-demand directional microwave photon emission using waveguide quantum electrodynamics”. Nature Physics, 19(3):394–400, 2023.
- [28] Jingjing Niu, Libo Zhang, Yang Liu, Jiawei Qiu, Wenhui Huang, Jiaxiang Huang, Hao Jia, Jiawei Liu, Ziyu Tao, Weiwei Wei, et al. “low-loss interconnects for modular superconducting quantum processors”. Nature Electronics, 6(3):235–241, 2023.
- [29] Jiawei Qiu, Yang Liu, Jingjing Niu, Ling Hu, Yukai Wu, Libo Zhang, Wenhui Huang, Yuanzhen Chen, Jian Li, Song Liu, et al. “deterministic quantum teleportation between distant superconducting chips”. arXiv preprint arXiv:2302.08756, 2023.
- [30] U Gaubatz, P Rudecki, S Schiemann, and K Bergmann. “population transfer between molecular vibrational levels by stimulated raman scattering with partially overlapping laser fields. a new concept and experimental results”. The Journal of Chemical Physics, 92(9):5363–5376, 1990.
- [31] Nikolay V Vitanov, Andon A Rangelov, Bruce W Shore, and Klaas Bergmann. “stimulated raman adiabatic passage in physics, chemistry, and beyond”. Reviews of Modern Physics, 89(1):015006, 2017.
- [32] Klaas Bergmann, Hanns-Christoph Nägerl, Cristian Panda, Gerald Gabrielse, Eduard Miloglyadov, Martin Quack, Georg Seyfang, Gunther Wichmann, Silke Ospelkaus, Axel Kuhn, et al. “roadmap on stirap applications”. Journal of Physics B: Atomic, Molecular and Optical Physics, 52(20):202001, 2019.
- [33] Mustafa Demirplak and Stuart A Rice. “adiabatic population transfer with control fields”. The Journal of Physical Chemistry A, 107(46):9937–9945, 2003.
- [34] Mustafa Demirplak and Stuart A Rice. “on the consistency, extremal, and global properties of counterdiabatic fields”. The Journal of chemical physics, 129(15), 2008.
- [35] Michael Victor Berry. “transitionless quantum driving”. Journal of Physics A: Mathematical and Theoretical, 42(36):365303, 2009.
- [36] Sara Ibáñez, Xi Chen, E Torrontegui, Juan Gonzalo Muga, and Andreas Ruschhaupt. “multiple schrödinger pictures and dynamics in shortcuts to adiabaticity”. Physical review letters, 109(10):100403, 2012.
- [37] Wen Zheng, Yu Zhang, Yuqian Dong, Jianwen Xu, Zhimin Wang, Xiaohan Wang, Yong Li, Dong Lan, Jie Zhao, Shaoxiong Li, et al. “optimal control of stimulated raman adiabatic passage in a superconducting qudit”. npj Quantum Information, 8(1):9, 2022.
- [38] F. Motzoi, J. M. Gambetta, P. Rebentrost, and F. K. Wilhelm. “simple pulses for elimination of leakage in weakly nonlinear qubits”. Phys. Rev. Lett., 103:110501, Sep 2009.
- [39] Jay M Gambetta, F Motzoi, ST Merkel, and Frank K Wilhelm. “analytic control methods for high-fidelity unitary operations in a weakly nonlinear oscillator”. Physical Review A, 83(1):012308, 2011.
- [40] Moein Malekakhlagh and Easwar Magesan. “mitigating off-resonant error in the cross-resonance gate”. Phys. Rev. A, 105:012602, Jan 2022.
- [41] Boxi Li, Tommaso Calarco, and Felix Motzoi. “suppression of coherent errors in cross-resonance gates via recursive drag”’. arXiv preprint arXiv:2303.01427, 2023.
- [42] Brian B Zhou, Alexandre Baksic, Hugo Ribeiro, Christopher G Yale, F Joseph Heremans, Paul C Jerger, Adrian Auer, Guido Burkard, Aashish A Clerk, and David D Awschalom. “accelerated quantum control using superadiabatic dynamics in a solid-state lambda system”. Nature Physics, 13(4):330–334, 2017.
- [43] Hugo Ribeiro and Aashish A Clerk. “accelerated adiabatic quantum gates: optimizing speed versus robustness”. Physical Review A, 100(3):032323, 2019.
- [44] F Setiawan, Peter Groszkowski, Hugo Ribeiro, and Aashish A Clerk. “analytic design of accelerated adiabatic gates in realistic qubits: General theory and applications to superconducting circuits”. PRX Quantum, 2(3):030306, 2021.
- [45] Fnu Setiawan, Peter Groszkowski, and Aashish A Clerk. “fast and robust geometric two-qubit gates for superconducting qubits and beyond”. Physical Review Applied, 19(3):034071, 2023.
- [46] Vladimir E Manucharyan, Jens Koch, Leonid I Glazman, and Michel H Devoret. Fluxonium: Single cooper-pair circuit free of charge offsets. Science, 326(5949):113–116, 2009.
- [47] Neereja M. Sundaresan, Yanbing Liu, Darius Sadri, László J. Szőcs, Devin L. Underwood, Moein Malekakhlagh, Hakan E. Türeci, and Andrew A. Houck. Beyond strong coupling in a multimode cavity. Phys. Rev. X, 5:021035, Jun 2015.
- [48] Rami Barends, Julian Kelly, Anthony Megrant, Daniel Sank, Evan Jeffrey, Yu Chen, Yi Yin, Ben Chiaro, Josh Mutus, Charles Neill, et al. “coherent josephson qubit suitable for scalable quantum integrated circuits”. Physical review letters, 111(8):080502, 2013.
- [49] Yu Chen, C Neill, P Roushan, N Leung, M Fang, R Barends, J Kelly, B Campbell, Z Chen, B Chiaro, et al. “qubit architecture with high coherence and fast tunable coupling”. Physical review letters, 113(22):220502, 2014.
- [50] Michael R Geller, Emmanuel Donate, Yu Chen, Michael T Fang, Nelson Leung, Charles Neill, Pedram Roushan, and John M Martinis. “tunable coupler for superconducting xmon qubits: Perturbative nonlinear model”. Physical Review A, 92(1):012320, 2015.
- [51] Line Hjortshøj Pedersen, Niels Martin Møller, and Klaus Mølmer. “fidelity of quantum operations”. Physics Letters A, 367(1-2):47–51, 2007.
- [52] Kevin S Chou, Jacob Z Blumoff, Christopher S Wang, Philip C Reinhold, Christopher J Axline, Yvonne Y Gao, Luigi Frunzio, MH Devoret, Liang Jiang, and RJ Schoelkopf. “deterministic teleportation of a quantum gate between two logical qubits”. Nature, 561(7723):368–373, 2018.
- [53] Yong Wan, Daniel Kienzler, Stephen D Erickson, Karl H Mayer, Ting Rei Tan, Jenny J Wu, Hilma M Vasconcelos, Scott Glancy, Emanuel Knill, David J Wineland, et al. “quantum gate teleportation between separated qubits in a trapped-ion processor”. Science, 364(6443):875–878, 2019.
- [54] Christopher Jarzynski. “generating shortcuts to adiabaticity in quantum and classical dynamics”. Physical Review A, 88(4):040101, 2013.
- [55] Sebastian Deffner, Christopher Jarzynski, and Adolfo del Campo. “classical and quantum shortcuts to adiabaticity for scale-invariant driving”. Physical Review X, 4(2):021013, 2014.
- [56] David Guéry-Odelin, Andreas Ruschhaupt, Anthony Kiely, Erik Torrontegui, Sofia Martínez-Garaot, and Juan Gonzalo Muga. “shortcuts to adiabaticity: Concepts, methods, and applications”’. Reviews of Modern Physics, 91(4):045001, 2019.
- [57] Navin Khaneja, Timo Reiss, Cindie Kehlet, Thomas Schulte-Herbrüggen, and Steffen J Glaser. “optimal control of coupled spin dynamics: design of nmr pulse sequences by gradient ascent algorithms”. Journal of magnetic resonance, 172(2):296–305, 2005.
- [58] Christiane P Koch, Ugo Boscain, Tommaso Calarco, Gunther Dirr, Stefan Filipp, Steffen J Glaser, Ronnie Kosloff, Simone Montangero, Thomas Schulte-Herbrüggen, Dominique Sugny, et al. “quantum optimal control in quantum technologies. strategic report on current status, visions and goals for research in europe”’. EPJ Quantum Technology, 9(1):19, 2022.
- [59] A. A. Houck, J. A. Schreier, B. R. Johnson, J. M. Chow, Jens Koch, J. M. Gambetta, D. I. Schuster, L. Frunzio, M. H. Devoret, S. M. Girvin, and R. J. Schoelkopf. “controlling the spontaneous emission of a superconducting transmon qubit”. Phys. Rev. Lett., 101:080502, Aug 2008.
- [60] Moein Malekakhlagh and Hakan E. Türeci. “origin and implications of an -like contribution in the quantization of circuit-qed systems”. Phys. Rev. A, 93:012120, Jan 2016.
- [61] Mario F Gely, Adrian Parra-Rodriguez, Daniel Bothner, Ya M Blanter, Sal J Bosman, Enrique Solano, and Gary A Steele. “convergence of the multimode quantum rabi model of circuit quantum electrodynamics”. Physical Review B, 95(24):245115, 2017.
- [62] Moein Malekakhlagh, Alexandru Petrescu, and Hakan E. Türeci. “cutoff-free circuit quantum electrodynamics”. Phys. Rev. Lett., 119:073601, Aug 2017.
- [63] Daniel Puzzuoli, Sophia Fuhui Lin, Moein Malekakhlagh, Emily Pritchett, Benjamin Rosand, and Christopher J Wood. “algorithms for perturbative analysis and simulation of quantum dynamics”. Journal of Computational Physics, page 112262, 2023.
- [64] Daniel Puzzuoli, Christopher J Wood, Daniel J Egger, Benjamin Rosand, and Kento Ueda. “qiskit dynamics: A python package for simulating the time dynamics of quantum systems”. Journal of Open Source Software, 8(90):5853, 2023.
- [65] Charles R Harris, K Jarrod Millman, Stéfan J van der Walt, Ralf Gommers, Pauli Virtanen, David Cournapeau, Eric Wieser, Julian Taylor, Sebastian Berg, Nathaniel J Smith, et al. “array programming with numpy”. Nature, 585(7825):357–362, 2020.
- [66] Pauli Virtanen, Ralf Gommers, Travis E Oliphant, Matt Haberland, Tyler Reddy, David Cournapeau, Evgeni Burovski, Pearu Peterson, Warren Weckesser, Jonathan Bright, et al. “scipy 1.0: fundamental algorithms for scientific computing in python”. Nature methods, 17(3):261–272, 2020.
- [67] Wilhelm Magnus. “on the exponential solution of differential equations for a linear operator”. Communications on pure and applied mathematics, 7(4):649–673, 1954.
- [68] Sergio Blanes, Fernando Casas, Jose-Angel Oteo, and José Ros. “the magnus expansion and some of its applications”. Physics reports, 470(5-6):151–238, 2009.
- [69] Sergio Blanes, Fernando Casas, JA Oteo, and J Ros. “a pedagogical approach to the magnus expansion”. European journal of physics, 31(4):907, 2010.