Enhanced optical trapping via structured scattering

Interferometry can completely redirect light, providing the potential for strong and controllable optical forces. However, small particles do not naturally act like interferometric beamsplitters, and the optical scattering from them is not generally thought to allow efficient interference. Instead, optical trapping is typically achieved via deflection of the incident field. Here we show that a suitably structured incident field can achieve beamsplitter-like interactions with scattering particles. The resulting trap offers order-of-magnitude higher stiffness than the usual Gaussian trap in one axis, even when constrained to phase-only structuring. We demonstrate trapping of 3.5 to 10.0 $\mu$m silica spheres, achieving stiffness up to 27.5$\pm$4.1 times higher than is possible using Gaussian traps, and two orders of magnitude higher measurement signal-to-noise ratio. These results are highly relevant to many applications, including cellular manipulation[1, 2], fluid dynamics[3, 4], micro-robotics[5], and tests of fundamental physics[6, 7].

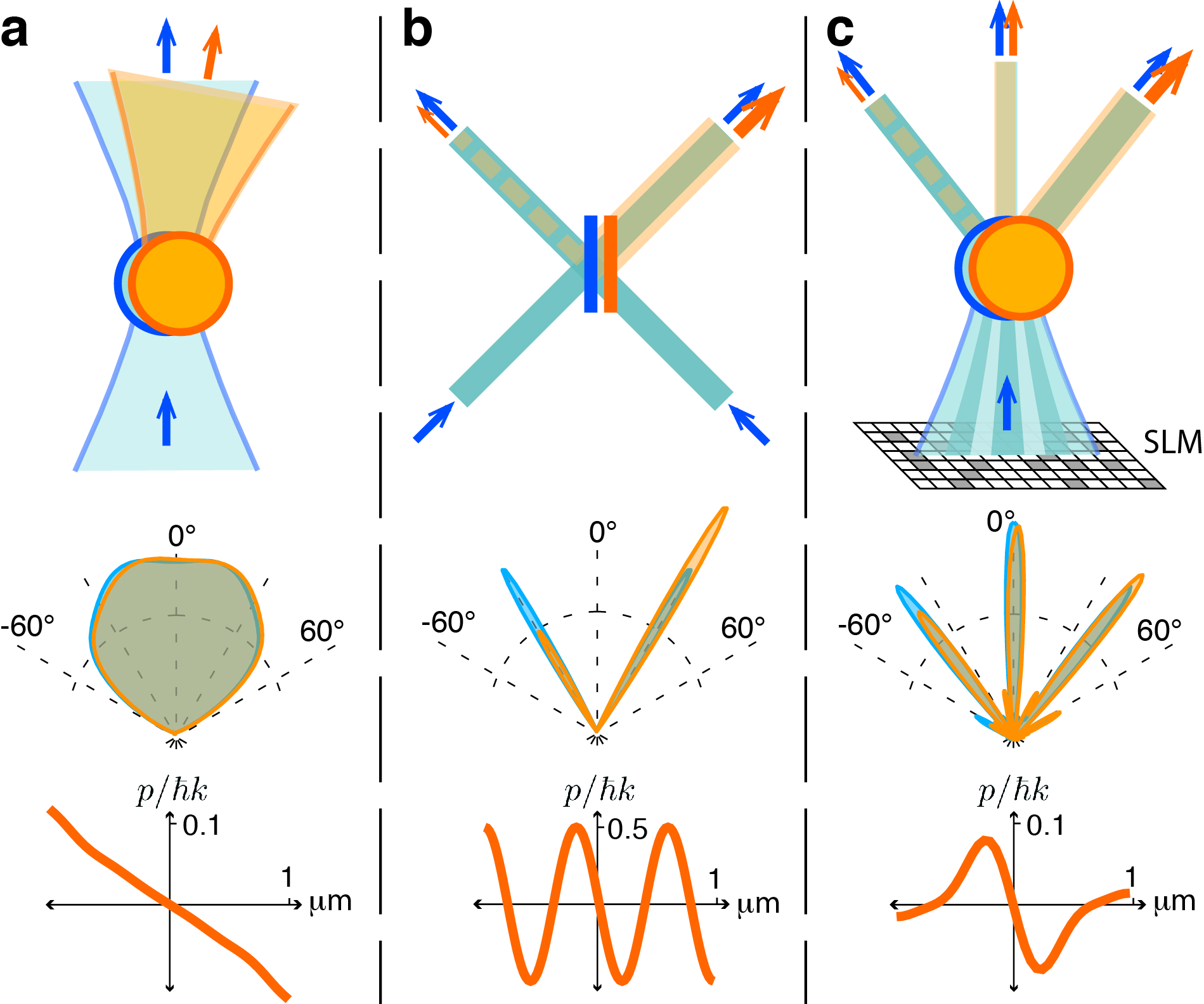
Optical forces are exerted when a particle changes the propagation direction of light. In optical tweezers this typically involves deflection of the light in proportion to the particle displacement, with minimal changes in its spatial structure (Fig. 1a). Similarly, a beamsplitter which combines two fields will also experience an optical force (Fig. 1b). In this case, the force arises because a relative phase shift between the incident fields redirects power between the outputs. Since the phase changes with beamsplitter displacement, interferometry can be used to stably trap. Here, in contrast to deflection-based trapping, the interference redirects light between two discrete propagation directions. Displacements as small as $\lambda/(4n_{m})$ are capable of completely rerouting the light, where $\lambda$ is the wavelength and $n_{m}$ the medium refractive index. This far greater sensitivity can in principle allow trap stiffness that exceeds all previous experiments[8] by over an order of magnitude. However, the beamsplitters which are traditionally used to interfere fields are poorly suited to optical micromanipulation experiments. Such experiments instead rely almost exclusively on scattering particles.

Recent works have shown that precise knowledge of scattering together with wavefront shaping allows particles to act as near-arbitrary optical elements, such as a mirror or lens [9]. In a similar way, we use non-trivial spatial structure in Mie scattering to convert particles to effective beamsplitters which separate a phase-structured input field into distinct output fringes (Fig. 1c). Rather than deflecting the fringes, particle displacements act to redirect optical power between them. This enables a new form of beamsplitter-like optical trapping, which we term enhanced trapping via structured scattering (ENTRAPS).

To understand the forces achieved with ENTRAPS, it is useful to first review the force on an interferometer beamsplitter. When the incident fields have equal power $P/2$ and phase difference $\phi$, the power imbalance $\Delta P$ between the two output ports is $\Delta P=P\,{\rm cos}\phi$. This results in an optical force

$$F=\frac{P\,n_{m}}{c}\,{\rm cos}\phi\,{\rm sin}\theta,$$

(1)

with $c$ the speed of light and $\theta$ the incident angle on the beamsplitter. Lateral movement of the beamsplitter by a distance $x$ causes a relative phase shift $\Delta\phi=4\pi n_{m}(x/\lambda)\,{\rm sin}\theta$ between the input fields, and changes the force on the beamsplitter. If the initial phase is set to $\phi=\pi/2$ and the light is normally incident ($\theta=\pi/2$), this achieves a stable trap of the form $F=-\kappa x$, with trap stiffness $\kappa=\frac{4\pi n_{m}^{2}P}{c\lambda}$. As discussed in the supplementary information, without recourse to non-propagating fields or quantum states of light that exhibit non-classical photon correlations, this represents a fundamental upper limit on the achievable stiffness of any optical trap.

ENTRAPS achieves strong trapping through similar principles, though instead using a scattering microparticle to interfere the fields. The particle can have any geometry, though here we restrict our discussion to homogeneous dielectric spheres for which the scattered light is described with Mie theory. It is well known that Mie scattering preferentially occurs into fringes at distinct scattering angles. However, the intensity of these fringes is usually much lower than the forward-scattering. Furthermore, neighbouring fringes are $\pi$ rad out-of-phase and destructively interfere if the incident illumination is homogeneous over a broad angular range, as is the case for a Gaussian trap. This further suppresses the fringe intensities (see Fig. 1a (middle)). As a consequence, Mie scattering fringes can usually be ignored in optical traps. However, we show here that they can be controllably populated using structured illumination (Fig. 1c (middle)). As such, the incident phase controls interference in Mie scattering fringes in a similar manner to the output of a beamsplitter. In ENTRAPS, the fringes are populated with fields that have near-orthogonal phase, such that a small phase shift can lead to constructive or destructive interference and redirect light between interference lobes on either side of the particle. This provides a beamsplitter-like trapping force (see Fig. 1c (bottom)).

One might expect that full control of both the amplitude and phase is required to achieve ENTRAPS. However, the phase alone determines whether interference is constructive or destructive, while the amplitude profile determines the efficiency of the interference. As such, ENTRAPS can be achieved using phase-only control of the incident light. Henceforth in this paper, we focus on these phase-only implementations. While the restriction to phase-only control can be expected to limit the achievable stiffness, it makes the protocol easily accessible to widely used holographic optical tweezers and, as we show here, still allows order-of-magnitude enhancements.

To identify appropriately structured incident optical fields for phase-only ENTRAPS and predict the performance of the protocol, we numerically optimised the phase profile of the incident field to maximize trap stiffness (see Methods and Supplement section S3). Particles with radius $R>\lambda$ were found to converge on profiles that achieve ENTRAPS, as evidenced by a particle-position-dependent redirection of power between distinct scattering fringes with fixed propagation directions (see polar plots in Fig. 3a and Supplementary section S3). We therefore postulate that, for particles that exhibit significant Mie scattering fringes, any trapping field that is near-optimized for trap stiffness will exhibit ENTRAPS.

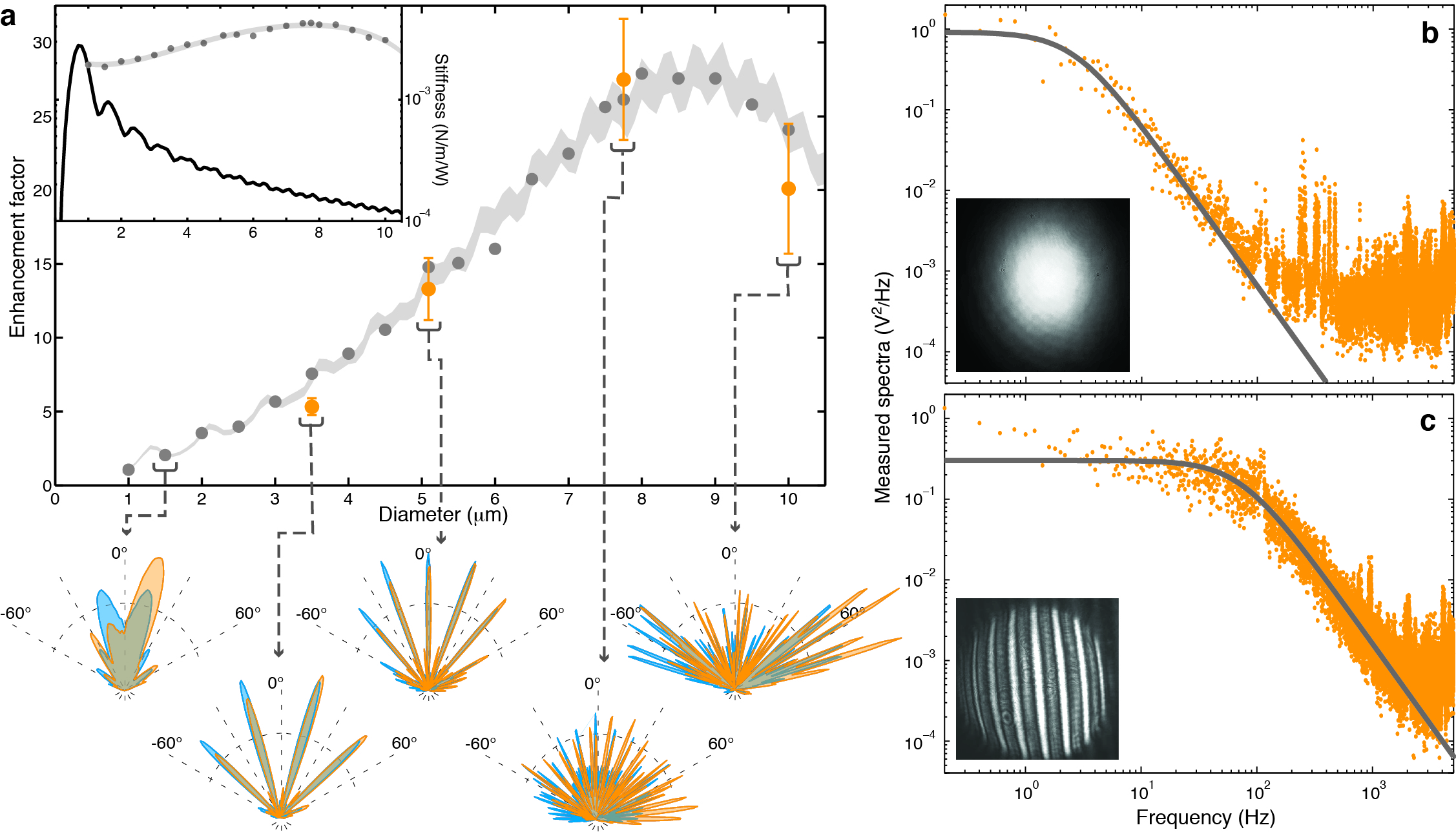
In general, Mie scattering profiles become increasingly complex as the particle size increases. This is apparent in the transmitted intensity patterns of ENTRAPS, which feature an increasing number of bright fringes as the particle size increases (Fig. 3a). ENTRAPS relies on this complexity, and uses it to control the transmitted wavefront. Consequently, we find that the achievable enhancement in trap stiffness increases with the particle size, and exceeds an order of magnitude for sizes above 5 $\mu$m (Fig. 3a). A drop in stiffness enhancement is evident above 8 $\mu$m, which may indicate that the calculated holograms are not fully optimal. For particles between 7 and 10 $\mu$m in size, the predicted trap stiffness exceeds 3 mN m^-1W^-1. This is comparable to the current record demonstrated with anti-reflection coated high refractive index particles[8], even though the particles considered here are silica and thus low contrast.

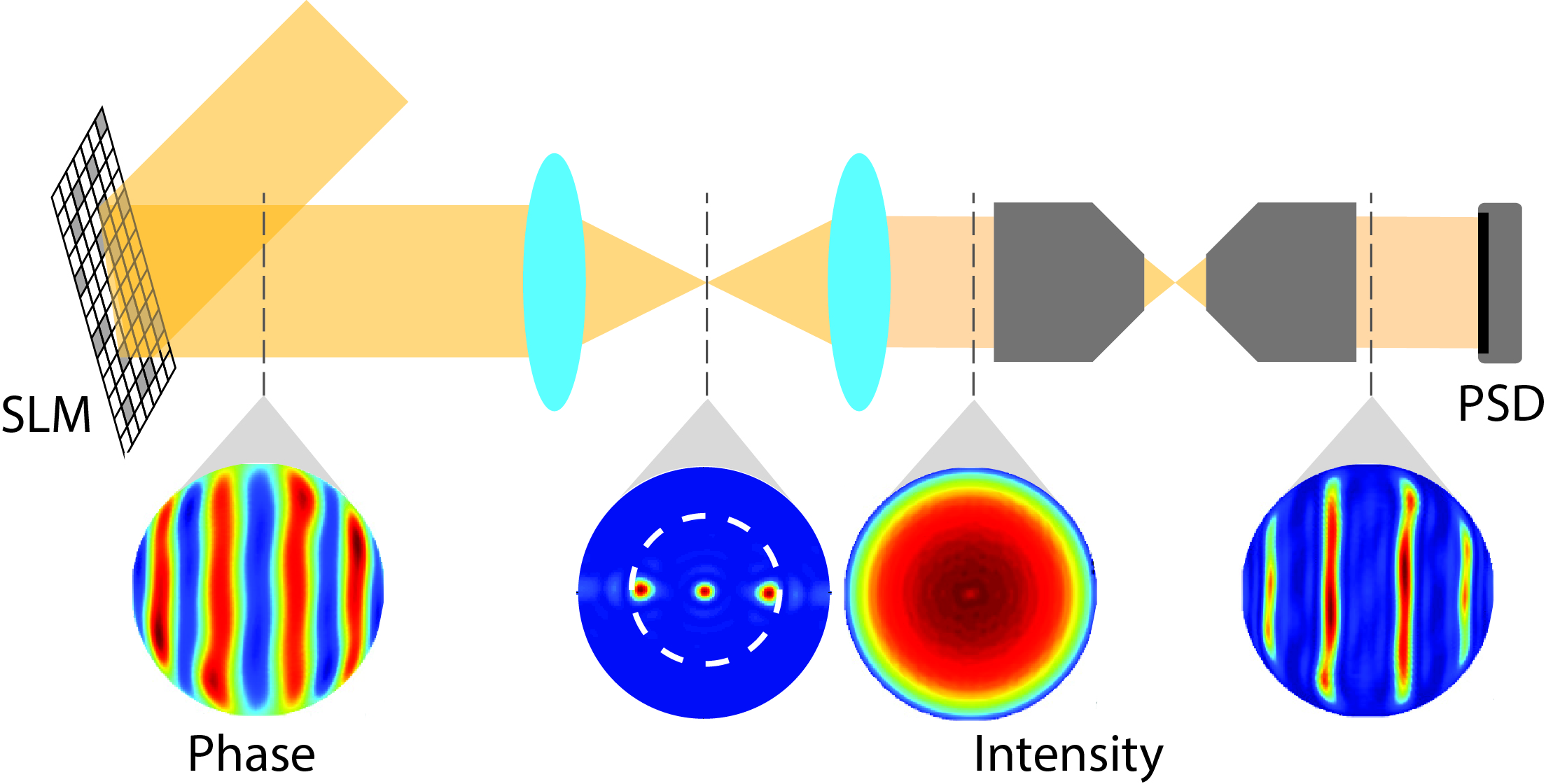
To test the predictions described above we implemented a holographic optical tweezer (see Fig. 2 and methods). Silica microspheres were trapped either with Gaussian input light or with the pre-calculated ENTRAPS holograms. Thermal position fluctuations of the trapped beads were monitored using a position sensitive detector (PSD). Freely moving beads in water exhibit Brownian motion, which has a mechanical power spectrum that scales with the inverse-square of frequency. The optical trap suppresses low frequency motion, resulting in a spectrally flat region at low frequency[2]. The corner frequency quantifies the transition between these two spectral regions, and is directly proportional to the trap stiffness $\kappa$. The ENTRAPS enhancement factor could therefore be determined by comparing the corner frequencies obtained with ENTRAPS and Gaussian traps.

Experiments were performed with particles of 3.48 $\mu$m, 5.09 $\mu$m, 7.75 $\mu$m, and 10.0 $\mu$m diameter. These sizes are relatively large for optical tweezers, with 10 $\mu$m near the upper limit for particles that are regularly trapped[5, 10]. To illustrate these measurements, Fig. 3 shows mechanical power spectra measured with 7.75 $\mu$m particles. The corner frequency measured with ENTRAPS is 73.2$\pm 2.8$ Hz, compared to 2.66$\pm 0.38$ Hz for the Gaussian trap (Fig. 3b and c). This constitutes an increase in trap stiffness by a factor of 27.5$\pm 4.1$, consistent with the predicted enhancement of 26.1. The enhancement was close to theory for all particle sizes, as shown in Fig. 3a, with mechanical spectra given in Supplementary section S4.

In addition to improving the trap stiffness, ENTRAPS also provides a dramatic improvement in the measurement signal-to-noise ratio (SNR). Laser tracking in optical tweezers is based on measurements of the centroid position of the transmitted light. This centroid is proportional to the applied optical force. As such, the observed signal at a given displacement is enhanced as the trap stiffness increases. When using 7.75 $\mu$m particles, ENTRAPS improved the SNR by a factor of 249, which allowed the thermal motion of the particle to be measured with an order of magnitude higher bandwidth (see Fig. 3b and c). Substantial SNR enhancements were observed for all particle sizes, and exceeded two orders of magnitude for both 5.09 and 10.0 $\mu$m beads.

ENTRAPS complements a range of novel approaches to optical micromanipulation that have only recently been demonstrated. It has been shown that the direction of optical forces need not align with the propagation of light, including a lateral force applied with Airy beams[11] and pulling force applied with a Bessel beam[12] and an interference-based tractor beam[13]. Recently, negative torque which opposes the optical angular momentum has also been demonstrated[14].

While it has been known for over two decades that structured light fields can be used to improve optical traps[15], no previous proposal or experiment has made use of the spatial structure of scattering to improve trap stiffness. As such, ENTRAPS represents a fundamentally different approach. Furthermore, compared to the order-of-magnitude enhancements possible with ENTRAPS, previous experiments have only allowed relatively modest enhancements. Higher order Laguerre-Gaussian modes have been shown to increase the axial restoring force on 5 $\mu$m particles by a factor of 1.60[16]; while radially and axially polarized modes have been predicted to provide even better trapping strengths[17], with experimental realisations enhancing the axial and lateral trapping forces by factors of 1.30 and 1.16, respectively[18].

To date the most powerful method to improve trapping forces has been to engineer the particle rather than structure the light. Most notably, anti-reflection coated high refractive index titania particles allow transverse trapping forces double that achieved with polystyrene microspheres[8], which remain the strongest trapping forces and trap stiffness ever reported. The axial trapping was simultaneously improved, though with a smaller (1.3-fold) enhancement. Alternatively, back-scatter can be minimized for a homogeneous sphere by careful choice of diameter, which also improves trap stiffness[19]. Another recent demonstration achieved strong static optical forces, though not optical trapping, on a bent waveguide structure that redirects the light with near-perfect efficiency[20].

Even while achieving substantial enhancements in trap stiffness and measurement signal-to-noise, we note that our currently implementation of ENTRAPS has significant limitations. Firstly, compared to the three-axis enhancement achieved, for example, in Ref. [8]; its achieves enhancement only along a single axis. It is possible that this could be overcome in future using three-axis-optimised phase profiles. Secondly, it can be seen from Fig. 1a and c (bottom) that ENTRAPS has a reduced trapping region compared to a Gaussian trap. In the case of a 10.0 $\mu$m particle, for instance, our theory and experimental force calibration (see Fig. 4 in the Supplementary information) show a reduction from 10 $\mu$m to approximately 500 nm. Indeed, a general trade-off exists between trap stiffness and trapping region. The scattering force on a trapped particle initially increases linearly with displacement in proportion to the trap stiffness. However, since photon scattering events cannot exert transverse momentum kicks larger than $\hbar k$ this cannot continue indefinitely, with the region of linear response reducing as the trap stiffness increases. In our experiments the momentum kick per photon reaches a maximum of approximately $\hbar k/7$. It is therefore concievable that the trapping region could be enlarged by a factor of seven without compromising stiffness. Finally, due to the presence of intricate phase structure ENTRAPS favours particles with volumes large enough to accommodate interference. ENTRAPS is therefore best achieved using particles larger than an optical wavelength.

Optical trapping has many important applications for particles larger than the wavelength. However, these applications are much less well explored than the small particle regime, as Gaussian traps lose trap stiffness with increasing diameter[21] (see Fig. 3a (inset)). For instance, cells are often manipulated optically, though in many cases they are too large to efficiently use a single-beam optical trap and require counter-propagating fields[1, 2]. Likewise, aerosols up to 10 $\mu$m are regularly trapped and studied in optical tweezers to gain insights into pollution, vapour based drug delivery, and atmospheric physics [10]. Micro-robotics also often relies on optical control of large spherical particles; either as handles that are attached to larger compound structures, or with the microsphere itself acting as the micro-robot[5]. Microspheres are also levitated in vacuum, where high mass can be important in studies of gravitational forces and particle physics[7, 22, 23]. The improved stiffness and measurement precision of ENTRAPS could greatly improve such applications.

Studies of hydrodynamics could also greatly benefit from ENTRAPS, since large particles couple more strongly to fluid flow[6, 4]. For instance, particle motion is expected to decouple from its surrounding fluid envelope only at very short time-scales, beyond the reach of state-of-the-art technology for a 1 $\mu$m sphere[24] but accessible with ultraprecise tracking of 10 $\mu$m particles. Hydrodynamic resonances are predicted to allow coherent energy exchange between the particle and fluid flow. Such resonances have recently been observed[3, 4], though with trap stiffness a factor of five beneath the strong resonance condition. ENTRAPS may allow this condition to be met, which would provide a test of hydrodynamic theory in a previously uncharted regime. The highly localized fluid flow generated near the particle could also provide a new avenue for non-contact and low-damage manipulation of cells, similar to experiments utilizing fluid flow near rotating particles[25]. It may also allow mechanical sensing of the fluid properties within the localized flow region, thus allowing nanoscale microrheology[3]. We envision that ENTRAPS could greatly improve these applications and others like them, and thus play an important part in the future of optical manipulation.