^†^†thanks: These two authors contributed equally.^†^†thanks: These two authors contributed equally.

Engineering exotic second-order topological semimetals by periodic driving

Bao-Qin Wang Lanzhou Center for Theoretical Physics, Key Laboratory of Theoretical Physics of Gansu Province, Lanzhou University, Lanzhou 730000, China Hong Wu Lanzhou Center for Theoretical Physics, Key Laboratory of Theoretical Physics of Gansu Province, Lanzhou University, Lanzhou 730000, China Jun-Hong An [email protected] Lanzhou Center for Theoretical Physics, Key Laboratory of Theoretical Physics of Gansu Province, Lanzhou University, Lanzhou 730000, China

Abstract

Second-order topological semimetals (SOTSMs) are featured with hinge Fermi arcs. How to generate them in different systems has attracted much attention. We propose a scheme to create exotic SOTSMs by periodic driving. Novel Dirac SOTSMs, with a widely tunable number of nodes and hinge Fermi arcs, the adjacent nodes having the same chirality, and the coexisting nodal points and loops, are generated at ease by the periodic driving. When the time-reversal symmetry is broken, our scheme permits us to realize hybrid-order Weyl semimetals with the coexisting hinge and surface Fermi arcs. Our Weyl semimetals possess a rich hybrid of 2D sliced zero- and $\pi/T$ -mode topological phases, which may be any combination of the normal insulator, Chern insulator, and second-order topological insulator. Enriching the family of topological semimetals, our scheme supplies a convenient way to artificially synthesize exotic topological phases by periodic driving.

I Introduction

Topological quantum matters [1, 2, 3, 4, 5] including topological insulator, superconductor, and semimetal enrich the paradigm of condensed matter physics. The finding of higher-order topological phases opens up a new frontier of topological physics [6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19]. Featured with hinge and corner states for three (3D)- and two-dimensional (2D) systems, second-order topological insulators (SOTIs) with some fantastic applications [20] have been realized in various systems [21, 22, 23, 24, 25, 26, 27, 28, 26, 29, 30]. On the other hand, topological Dirac [31, 32, 33, 34, 35, 36, 37, 38, 39] and Weyl [40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54] semimetals also have been widely studied due to their chiral anomaly and close connection with diverse topological phases [55, 56, 57, 58, 59, 54]. Second-order topological semimetals (SOTSMs) in both Dirac [60, 61, 62, 63, 64] and Weyl types [65, 66] were recently proposed. Different from surface Fermi arc in first-order semimetals, SOTSMs manifest in hinge Fermi arc [65, 66, 64]. Although they have been simulated in classical acoustic metamaterials [67, 68], their observation of SOTSMs in electronic materials is hard. One of the difficulties is that the control ways to various of interactions in natural materials are limited because their features would not be switched once they are fabricated.

Coherent control via periodic driving dubbed Floquet engineering has become a versatile tool in creating topological phases in systems of ultracold atoms [69, 70], photonics [71, 72], superconductor qubits [73], and graphene [74]. It permits us to artificially synthesize a variety of exotic topological phases [75, 76, 77, 78, 79]. Greatly increasing the controllability and reducing the realistic difficulty in generating topological phases by adjusting intrinsic parameters of static systems, Floquet engineering supplies an extra dimension in exploring topological matters. Following the theme of condensed-matter physics in discovering novel quantum matter, one generally desires to know what exotic features can be created in the recently proposed SOTSMs by this novel dimension. Further, one also expects Floquet engineering to enrich the control way to complicated interactions in natural materials such that the difficulty in observing SOTSMs there could be reduced. Although some studies on Floquet engineering to SOTIs have been performed [80, 81, 82, 83, 84, 85, 86, 85, 87, 88, 89], those for SOTSMs are still lacking. A challenge is how to establish the bulk-corner correspondence (BCC) under the fact that the periodic-driving induced symmetry breaking and the presence of novel $\pi/T$ -mode corner states invalidates the BCC of the original static system.

Refer to caption — Figure 1: (a) Schematics of SOTSM on a cubic lattice with an intracell hopping rate $\gamma$ , and intercell ones $\lambda$ in the single layer and $a/2$ between two neighboring layers, respectively. The dashed lines denote the hopping rates with a $\pi$ -phase difference from their solid counterparts. (b) Static phase diagram described by the winding number $\mathcal{W}$ . (c) Energy spectrum and (d) hinge Fermi arcs under the $x,y$ -direction open boundary condition when $\gamma=0.8f$ . The red solid (dashed) lines in (b) and (c) are the dispersion relations of $\theta=\pi$ ( $0$ ). We use $\lambda=0.2f$ , $a=1.5f$ , and the lattice numbers $L_{x}=L_{y}=30$ .

We propose a scheme to artificially create exotic SOTSMs by Floquet engineering. A complete BCC to the SOTSMs induced by periodic driving is established. Taking a system of spinless fermions moving on a cubic lattice as an example, we find diverse Dirac SOTSMs with a widely tunable number of nodes and hinge Fermi arcs, the adjacent nodes appearing in pair of same chirality, and the coexisting second-order nodal points and lines, which are absent in the static system. By adding a perturbation to break the time-reversal symmetry, hybrid-order Weyl SOTSMs manifesting in the coexisting hinge and surface Fermi arcs are created by the driving. Our work highlights Floquet engineering as a convenient way to control and explore novel SOTSMs.

II Static system

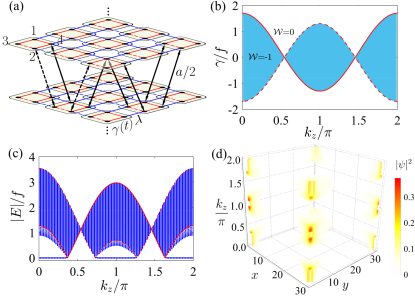
We investigate a system of spinless fermions moving on a 3D lattice [see Fig. 1(a)]. Its Hamiltonian [90] reads $\hat{H}=\sum_{\bf k}\hat{\bf C}_{\bf k}^{\dagger}\mathcal{H}({\bf k})\hat{\bf C}_{\bf k}$ , with $\hat{\bf C}^{\dagger}_{\bf k}=(\begin{array}[]{cccc}\hat{c}_{{\bf k},1}^{\dagger}&\hat{c}_{{\bf k},2}^{\dagger}&\hat{c}_{{\bf k},3}^{\dagger}&\hat{c}_{{\bf k},4}^{\dagger}\end{array})$ and [6]

	$\displaystyle\mathcal{H}(\mathbf{k})$	$\displaystyle=$	$\displaystyle[\gamma+\chi(k_{z})\cos k_{x}]\Gamma_{5}-\chi(k_{z})\sin k_{x}\Gamma_{3}$		(1)
			$\displaystyle-[\gamma+\chi(k_{z})\cos k_{y}]\Gamma_{2}-\chi(k_{z})\sin k_{y}\Gamma_{1},$		(1)

where $\lambda$ , $\gamma$ , and $a$ are, respectively, the intercell, intracell, and interlayer hopping rates, $\chi(k_{z})=\lambda+a\cos k_{z}$ , $\Gamma_{1/2/3}=\tau_{y}\sigma_{x/y/z}$ , $\Gamma_{4}=\tau_{z}\sigma_{0}$ , and $\Gamma_{5}=\tau_{x}\sigma_{0}$ , with $\tau_{i}$ and $\sigma_{i}$ being Pauli matrices, $\tau_{0}$ and $\sigma_{0}$ being identity matrices. It is a 3D generalization of 2D SOTIs in the Benalcazar-Bernevig-Hughes model [91] by considering the interlayer hopping. It is different from the one of Ref. [66] only in the interlayer-hopping way.

The SOTSM is sliced into a family of 2D $k_{z}$ -dependent SOTIs and normal insulators. As a prerequisite for Dirac semimetal, the time-reversal $\mathcal{T}=K$ , with $K$ being the complex conjugation, and inversion $\mathcal{P}=\tau_{0}\sigma_{y}$ symmetries are respected. The system also has the mirror-rotation $\mathcal{M}_{xy}=[(\tau_{0}-\tau_{z})\sigma_{x}-(\tau_{0}+\tau_{z})\sigma_{z}]/2$ and chiral $\mathcal{S}=\tau_{z}\sigma_{0}$ symmetries. Thus, the 2D SOTIs are well described by $\mathcal{H}(\theta,\theta,k_{z})$ along the high-symmetry line $k_{x}=k_{y}\equiv\theta$ , which is diagonalized into $\text{diag}[\mathcal{H}^{+}(\theta,k_{z}),\mathcal{H}^{-}(\theta,k_{z})]$ with $\mathcal{H}^{\pm}(\theta,k_{z})={\bf h}^{\pm}\cdot{\boldsymbol{\sigma}}$ and ${\bf h}^{\pm}=\sqrt{2}[\gamma+\chi(k_{z})\cos\theta,\pm\chi(k_{z})\sin\theta,0]$ . Its topology is characterized by the mirror-graded winding numbers $\mathcal{W}(k_{z})=(\mathcal{W}_{+}-\mathcal{W}_{-})/2$ , where $\mathcal{W}_{\pm}$ are the winding numbers of $\mathcal{H}^{\pm}(\theta,k_{z})$ [24, 90]. The phase diagram in Fig. 1(b) reveals a phase transition at $|\gamma|=|\chi(k_{z})|$ , where $\mathcal{W}(k_{z})=-1$ signifies the formation of a SOTI. The energy spectrum in Fig. 1(c) confirms the presence of a $4|\mathcal{W}(k_{z})|$ -fold degenerate zero-mode state distributing at the corners. The corner state contributes to the hinge Fermi arcs [see Fig. 1(d)]. The family of 2D SOTIs forms a 3D SOTSM which hosts the Dirac nodes at the critical points $k_{z}=\arccos[-(\lambda\pm\gamma)/a]$ of 2D SOTI transition. Each Dirac node carries a chirality $\mathcal{Q}$ [55]. The chirality of the Dirac node $k_{z,0}$ equals to the difference of the winding numbers of its separated phases, i.e., $\mathcal{Q}=\mathcal{W}(k_{z,0}+\delta)-\mathcal{W}(k_{z,0}-\delta)$ , with $\delta>0$ being an infinitesimal [90]. Figure 1(b) shows the adjacent Dirac nodes have the opposite $\mathcal{Q}$ , which explains that only one four-fold degenerate corner state at most is formed.

III Periodic-driving induced exotic SOTSMs

III.1 Dirac SOTSMs via Floquet engineering

We consider that the intracell hopping $\gamma$ periodically changes its strength in a step-like manner within the respective time duration $T_{1}$ and $T_{2}$ as

\gamma(t)=\begin{cases}\gamma_{1}=q_{1}f,~{}t\in[mT,mT+T_{1})\\ \gamma_{2}=q_{2}f,~{}t\in[mT+T_{1},(m+1)T),\end{cases}

(2)

where $m\in\mathbb{Z}$ , $T=T_{1}+T_{2}$ is the driving period, and $f$ is an energy scale to make the amplitudes $q_{j}$ dimensionless. Determined by the overlap of spatial wave-function of the fermion on the relevant sites, $\gamma(t)$ could be realized by applying electric field via gate voltage. A periodic system $\hat{H}(t)$ does not have well-defined energies. According to Floquet theorem, the one-period evolution operator $\hat{U}_{T}=\mathbb{T}e^{-i\int_{0}^{T}\hat{H}(t)dt}$ defines an effective Hamiltonian $\hat{H}_{\text{eff}}\equiv{i\over T}\ln\hat{U}_{T}$ whose eigenvalues are called the quasienergies [92, 93]. The SOTSMs of our periodic system are defined in such quasienergy spectrum. Applying Floquet theorem on a general four-band $\mathcal{H}_{j}({\bf k})=\mathbf{n}_{j}\cdot\mathbf{\Gamma}$ , we have $\mathcal{H}_{\text{eff}}({\bf k})={i\over T}\ln[e^{-i\mathcal{H}_{2}({\bf k})T_{2}}e^{-i\mathcal{H}_{1}({\bf k})T_{1}}]$ [90]. First, we obtain from $\mathcal{H}_{\text{eff}}({\bf k})$ that the bands close for $\mathbf{k}$ and driving parameters satisfying either

			$\displaystyle T_{j}E_{j}=z_{j}\pi,$		(3)
	or		$\displaystyle\begin{cases}\underline{\mathbf{n}}_{1}\cdot\underline{\mathbf{n}}_{2}=\pm 1,\\ T_{1}{E}_{1}\pm T_{2}{E}_{2}=z\pi,\end{cases}$		(4)

with $\underline{\mathbf{n}}_{j}\equiv\mathbf{n}_{j}/|\mathbf{n}_{j}|$ , at the quasienergy zero (or $\pi/T$ ) when $z_{j}$ are integers with same (or different) parities and $z$ is even (or odd) number. Giving the positions of Dirac nodes, Eqs. (3) and (4) provide a guideline to control the driving parameters for engineering various Dirac nodes at will. Deriving ${\bf n}_{j}$ from Eq. (1) with $\gamma$ driven as Eq. (2), we obtain the conditions for the Dirac nodes as follows.
Case I: Equation (3) results in that the Dirac nodes present at ${\bf k}$ satisfying

\sqrt{2}[\gamma^{2}_{j}+\chi^{2}(k_{z})+\gamma_{j}\chi(k_{z})(\cos k_{x}+\cos k_{y})]^{1\over 2}T_{j}=z_{j}\pi.

(5)

Satisfied by three independent parameters $(k_{x},k_{y},k_{z})$ , the two constraints in Eqs. (5) result in the band-touching points to form a loop instead of discrete points. Thus, it generally gives a nodal-line semimetal. Defined in the full Brillouin zone (BZ), Eqs. (5) describe the physics beyond the high-symmetry lines.
Case II: $\underline{\mathbf{n}}_{1}\cdot\underline{\mathbf{n}}_{2}=\pm 1$ needs the high-symmetry line $\theta=0$ or $\pi$ . According to Eq. (4), the Dirac nodes present when

\sqrt{2}\big{[}|\gamma_{1}+\chi(k_{z})e^{i\theta}|T_{1}\pm|\gamma_{2}+\chi(k_{z})e^{i\theta}|T_{2}\big{]}=z_{\theta,\pm}\pi,

(6)

for sgn[ $\prod_{j=1}^{2}(\gamma_{j}+\chi(k_{z})e^{i\theta})$ ] $=\pm 1$ . Satisfied by discrete $\theta$ and $k_{z}$ , it gives a nodal-point semimetal.

It is interesting to see that we not only can control the number and the position of the Dirac nodes but also can create nodal-line semimetal from the static nodal-point one by virtue of the periodic driving.

Second, we establish the BCC from $\mathcal{H}_{\text{eff}}({\bf k})$ for our system. Although $\mathcal{H}_{\text{eff}}({\bf k})$ inherits the inversion and mirror-rotation symmetries, it does not have the time-reversal and chiral symmetries [90]. To recover the symmetries, we make two unitary transformations $G_{j}({\bf k})=e^{i(-1)^{j}\mathcal{H}_{j}({\bf k})T_{j}/2}$ and obtain $\tilde{\mathcal{H}}_{\text{eff},j}({\bf k})=G_{j}({\bf k})\mathcal{H}_{\text{eff}}({\bf k})G_{j}^{-1}({\bf k})$ [76]. Respecting the time-reversal and chiral symmetries, $\tilde{\mathcal{H}}_{\text{eff},j}({\bf k})$ have well-defined mirror-graded winding numbers $\mathcal{W}_{j}$ . Since the transformations do not change the quasienergies, the SOTIs in $\mathcal{H}_{\text{eff}}({\bf k})$ at the quasienergies zero and $\pi/T$ are described by $\mathcal{W}_{j}$ as

\mathcal{W}_{0}=(\mathcal{W}_{1}+\mathcal{W}_{2})/2,~{}~{}\mathcal{W}_{\pi/T}=(\mathcal{W}_{1}-\mathcal{W}_{2})/2.

(7)

Reflecting the firm BCC, the numbers of the zero- and $\pi/T$ -mode corner states equal to $4|\mathcal{W}_{0}|$ and $4|\mathcal{W}_{\pi/T}|$ . The $k_{z}$ -dependent SOTIs form a 3D SOTSMs, which hosts second-order Dirac nodes at the critical points of a 2D topological phase transition and hinge Fermi arcs from the distribution of the corner states. Note that it is equivalent to deem that $\mathcal{H}_{\text{eff}}({\bf k})$ has hidden time-reversal and chiral symmetries under the redefined operations $G^{-1}_{j}(-{\bf k})\mathcal{T}G_{j}({\bf k})$ and $G^{-1}_{j}({\bf k})\mathcal{S}G_{j}({\bf k})$ [90].

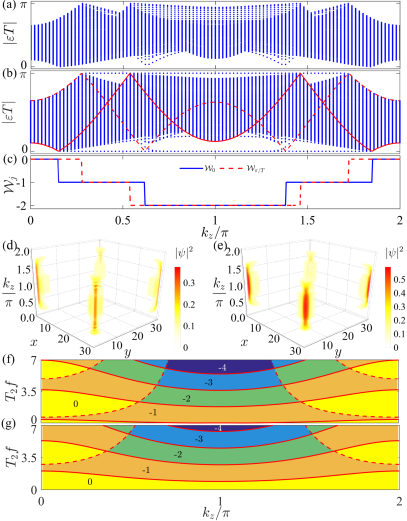
We demonstrate the constructive role of the periodic driving in generating novel Dirac nodal-point SOTSMs in Fig. 2. The quasienergy spectrum under the $x$ -direction open boundary in Fig. 2(a) shows a topologically trivial phase, while the one under the $x,y$ -direction open boundary in Fig. 2(b) shows rich topological phases in both the quasienergies zero and $\pi/T$ . It signifies the diverse topological phases trivial in the first order but nontrivial in the second order. The Dirac nodal points in Fig. 2(b) at $k_{z}=0.15\pi$ , $0.54\pi$ , $0.28\pi$ , and $0.62\pi$ are well explained by Eq. (6) with $z_{\pi,-}=-2$ , $-3$ , $z_{0,-}=-1$ and 0, respectively. Compared with the static case, the number of the nodal points is dramatically enhanced. It verifies the periodic driving as a useful way to manipulate the nodal points. The 2D SOTIs are completely characterized by the winding number $\mathcal{W}_{j}$ defined in $\tilde{\mathcal{H}}_{\text{eff},j}$ . The numbers $4|\mathcal{W}_{0}|$ and $4|\mathcal{W}_{\pi/T}|$ correctly count the zero- and $\pi/T$ -mode corner states [see Fig. 2(c)]. Another interesting result is that the chiralities of the adjacent Dirac nodal points possess the same sign instead of the opposite sign in the static case. This explains why more corner states than the static case are created by the periodic driving. It also endows the Dirac nodal points in our periodic system with robustness to the perturbation-induced annihilation, which is only sensitive to the nodal points with opposite chiralities [55]. Both of the zero- and $\pi/T$ -mode corner states contribute the hinge Fermi arcs [see Figs. 2(d) and 2(e)] of the SOTSMs.

To give a global picture of the Dirac nodal-point SOTSMs in our periodic system, we plot in Figs. 2(f) and 2(g) the phase diagram characterized by $\mathcal{W}_{0}$ and $\mathcal{W}_{\pi/T}$ in the $k_{z}$ - $T_{2}$ plane. Much richer 2D-sliced SOTIs with a widely tunable number of zero- and $\pi/T$ -mode corner states than the static case in Fig. 1(b) are created by the periodic driving. The phase boundaries well described by Eq. (6) correspond to the Dirac nodal points of the SOTSMs. Different from the static case, where the Dirac nodal points separate the trivial and SOTIs, the ones in our periodic system also separate the SOTIs with a different number of corner states. A clear tendency with the increase of the period $T_{2}$ is that the number of the Dirac nodal points increases, which can be analytically understood from Eq. (6).

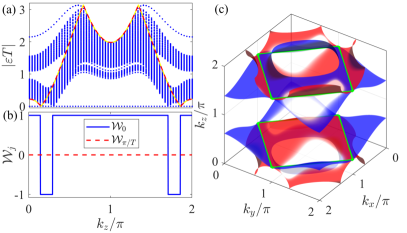
Next, we create the Dirac nodal-loop SOTSMs from the static nodal-point ones via engineering the periodic driving to satisfy Eqs. (5). The quasienergy spectrum in Fig. 3(a) reveals that, besides the zero-mode Dirac nodal points at $k_{z}=0.14\pi$ and $1.86\pi$ , recoverable by Eq. (6) with $z_{\pi/0,+}=2$ , and the $\pi/T$ -mode ones at $k_{z}=0.66\pi$ and $1.34\pi$ , recoverable by Eq. (6) with $z_{\pi/0,+}=1$ , there are two extra band-touching points at $k_{z}=0.29\pi$ and $1.71\pi$ . Plotting the two surfaces governed by Eqs. (5) in the BZ in Fig. 3(c), we really see two closed intersecting lines at $k_{z}=0.29\pi$ and $1.71\pi$ . It confirms the presence of two parallel nodal loops. The associated mirror-graded winding numbers in Fig. 3(b) show that both of the nodal points and loops cause the second-order topological phase transition, which endows them with the second-order feature. All these results verify the formation of a novel SOTSM with coexisting nodal points and loops via periodically driving a static Dirac nodal-point one. Such phase has not been found in static systems. Although a similar semimetal with coexisting nodal points and loops was reported in the static system [94], it is in the first-order Weyl type. However, ours is in the second-order Dirac type and protected by both $\mathcal{P}$ and $\mathcal{T}$ symmetries. The result proves the distinguished role of the periodic driving in creating exotic matters absent in static systems.

III.2 Weyl SOTSMs via Floquet engineering

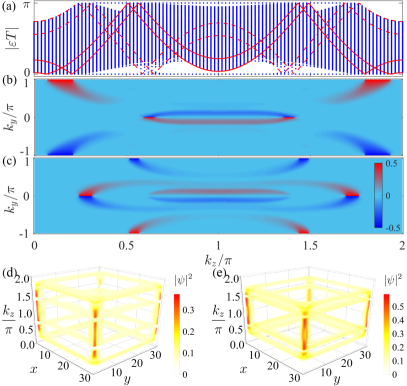
Our periodic driving scheme (2) can be used to create novel Weyl SOTSMs by introducing a perturbation $\Delta\mathcal{H}=ip\Gamma_{1}\Gamma_{3}$ to break the $\mathcal{T}$ symmetry. The quasienergy spectrum in Fig. 4(a) reveals that each Dirac point in Fig. 2(a) splits into two Weyl points with a Chern insulator formed between them. Each Weyl point can be analytically explained by our band-touching condition [90]. The Chern insulator is signified by the gapless chiral boundary states, which can be topologically witnessed by the Wannier center [65]. The Wannier center of the zero- and $\pi/T$ -mode gaps jumping from $-0.5$ to $0.5$ when $k_{y}$ runs from $-\pi$ to $\pi$ verifies the formation of a Chern band [see Figs. 4(b) and 4(c)], which contributes the surface Fermi arcs. Therefore, we have realized a hybrid-order Weyl semimetal, which is featured with the coexisting first- and second-order Weyl points as well as the surface and hinge Fermi arcs [see Figs. 4(d) and 4(e)]. This result dramatically enriches the family of the recently proposed purely second-order Weyl semimetal in static systems [65, 66]. Another novel character of our periodic system is that it possesses a rich hybrid of topological phases in the zero and $\pi/T$ modes for a given $k_{z}$ in the 2D-sliced subsystem, which can be any combination of normal insulator, Chern insulator, and SOTI in the zero and $\pi/T$ modes. This is also absent in static systems. All of these results confirm again the superiority of the periodic driving in freely tuning and synthesizing exotic topological matters. Note that the hybrid-order nature of the Weyl semimetal in our periodic system does not depend on the form of the $\mathcal{T}$ -symmetry breaking perturbation. To other forms, the explicit locations on forming the Weyl points may be different, but the conclusion that a Chern band is present between each pair of Weyl points does not change.

IV Discussion and conclusion

Although we only show the generation of the same order of semimetals as the static case, the periodic driving also has the ability to create the SOTSMs from the static first-order semimetal or even normal insulator [90]. The step like driving protocol is considered just for analytical solvability. Our scheme is generalizable to other driving forms. The SOTSMs have been predicted in Cd₃As₂, KMgBi, and PtO₂ [95, 61] and realized in classical acoustic metamaterials [67, 68]. Periodic driving has exhibited its power in engineering exotic phases in electronic material [96, 74], ultracold atoms [97], superconductor qubits [73], and photonics [71, 98, 99, 72]. The progress indicates that our result is realizable in the recent experimental state of the art.

In summary, we have investigated the exotic SOTSMs induced by periodic driving. It is revealed that the periodic driving provides a sufficient freedom in creating novel SOTSMs absent in static systems. The discovered widely tunable number of nodes and hinge Fermi arcs, the adjacent nodes with same chirality, and the coexisting nodal points and nodal loops in Dirac SOTSMs and the hybrid-order Weyl semimetals with the coexisting hinge and surface Fermi arcs dramatically enrich the family of topological semimetals in natural materials. Our result indicates that the periodic driving supplies a feasible and convenient way to explore the exotic semimetal physics by adding the time periodicity as a novel control dimension. This significantly reduces the difficulties in fabricating specific material structure in static systems.

Acknowledgments

The work is supported by the National Natural Science Foundation (Grants No. 11875150, No. 11834005, and No. 12047501).

References

Hasan and Kane [2010] M. Z. Hasan and C. L. Kane, Colloquium: Topological insulators, Rev. Mod. Phys. 82, 3045 (2010).
Qi and Zhang [2011] X.-L. Qi and S.-C. Zhang, Topological insulators and superconductors, Rev. Mod. Phys. 83, 1057 (2011).
Chiu et al. [2016] C.-K. Chiu, J. C. Y. Teo, A. P. Schnyder, and S. Ryu, Classification of topological quantum matter with symmetries, Rev. Mod. Phys. 88, 035005 (2016).
Armitage et al. [2018] N. P. Armitage, E. J. Mele, and A. Vishwanath, Weyl and Dirac semimetals in three-dimensional solids, Rev. Mod. Phys. 90, 015001 (2018).
Lv et al. [2021] B. Q. Lv, T. Qian, and H. Ding, Experimental perspective on three-dimensional topological semimetals, Rev. Mod. Phys. 93, 025002 (2021).
Benalcazar et al. [2017a] W. A. Benalcazar, B. A. Bernevig, and T. L. Hughes, Quantized electric multipole insulators, Science 357, 61 (2017a).
Langbehn et al. [2017] J. Langbehn, Y. Peng, L. Trifunovic, F. von Oppen, and P. W. Brouwer, Reflection-symmetric second-order topological insulators and superconductors, Phys. Rev. Lett. 119, 246401 (2017).
Song et al. [2017] Z. Song, Z. Fang, and C. Fang, $(d-2)$ -dimensional edge states of rotation symmetry protected topological states, Phys. Rev. Lett. 119, 246402 (2017).
Schindler et al. [2018a] F. Schindler, A. M. Cook, M. G. Vergniory, Z. Wang, S. S. P. Parkin, B. A. Bernevig, and T. Neupert, Higher-order topological insulators, Science Advances 4, eaat0346 (2018a).
Yan et al. [2018] Z. Yan, F. Song, and Z. Wang, Majorana corner modes in a high-temperature platform, Phys. Rev. Lett. 121, 096803 (2018).
Ezawa [2018] M. Ezawa, Topological switch between second-order topological insulators and topological crystalline insulators, Phys. Rev. Lett. 121, 116801 (2018).
Liu et al. [2019a] F. Liu, H.-Y. Deng, and K. Wakabayashi, Helical topological edge states in a quadrupole phase, Phys. Rev. Lett. 122, 086804 (2019a).
Zhang et al. [2019] R.-X. Zhang, W. S. Cole, X. Wu, and S. Das Sarma, Higher-order topology and nodal topological superconductivity in Fe(Se,Te) heterostructures, Phys. Rev. Lett. 123, 167001 (2019).
Park et al. [2019] M. J. Park, Y. Kim, G. Y. Cho, and S. Lee, Higher-order topological insulator in twisted bilayer graphene, Phys. Rev. Lett. 123, 216803 (2019).
Sheng et al. [2019] X.-L. Sheng, C. Chen, H. Liu, Z. Chen, Z.-M. Yu, Y. X. Zhao, and S. A. Yang, Two-dimensional second-order topological insulator in graphdiyne, Phys. Rev. Lett. 123, 256402 (2019).
Tiwari et al. [2020] A. Tiwari, M.-H. Li, B. A. Bernevig, T. Neupert, and S. A. Parameswaran, Unhinging the surfaces of higher-order topological insulators and superconductors, Phys. Rev. Lett. 124, 046801 (2020).
Ren et al. [2020] Y. Ren, Z. Qiao, and Q. Niu, Engineering corner states from two-dimensional topological insulators, Phys. Rev. Lett. 124, 166804 (2020).
Zeng et al. [2020] Q.-B. Zeng, Y.-B. Yang, and Y. Xu, Higher-order topological insulators and semimetals in generalized Aubry-André-Harper models, Phys. Rev. B 101, 241104(R) (2020).
Slager et al. [2015] R.-J. Slager, L. Rademaker, J. Zaanen, and L. Balents, Impurity-bound states and Green’s function zeros as local signatures of topology, Phys. Rev. B 92, 085126 (2015).
Zhang et al. [2020] W. Zhang, X. Xie, H. Hao, J. Dang, S. Xiao, S. Shi, H. Ni, Z. Niu, C. Wang, K. Jin, X. Zhang, and X. Xu, Low-threshold topological nanolasers based on the second-order corner state, Light. Sci. Appl. 9, 109 (2020).
Serra-Garcia et al. [2018] M. Serra-Garcia, V. Peri, R. Süsstrunk, O. R. Bilal, T. Larsen, L. G. Villanueva, and S. D. Huber, Observation of a phononic quadrupole topological insulator, Nature 555, 342 (2018).
Peterson et al. [2018] C. W. Peterson, W. A. Benalcazar, T. L. Hughes, and G. Bahl, A quantized microwave quadrupole insulator with topologically protected corner states, Nature 555, 346 (2018).
Schindler et al. [2018b] F. Schindler, Z. Wang, M. G. Vergniory, A. M. Cook, A. Murani, S. Sengupta, A. Y. Kasumov, R. Deblock, S. Jeon, I. Drozdov, H. Bouchiat, S. Guéron, A. Yazdani, B. A. Bernevig, and T. Neupert, Higher-order topology in bismuth, Nature Physics 14, 918 (2018b).
Imhof et al. [2018] S. Imhof, C. Berger, F. Bayer, J. Brehm, L. W. Molenkamp, T. Kiessling, F. Schindler, C. H. Lee, M. Greiter, T. Neupert, and R. Thomale, Topolectrical-circuit realization of topological corner modes, Nature Physics 14, 925 (2018).
Wu et al. [2020a] J. Wu, X. Huang, J. Lu, Y. Wu, W. Deng, F. Li, and Z. Liu, Observation of corner states in second-order topological electric circuits, Phys. Rev. B 102, 104109 (2020a).
Fan et al. [2019] H. Fan, B. Xia, L. Tong, S. Zheng, and D. Yu, Elastic higher-order topological insulator with topologically protected corner states, Phys. Rev. Lett. 122, 204301 (2019).
Chen et al. [2019] X.-D. Chen, W.-M. Deng, F.-L. Shi, F.-L. Zhao, M. Chen, and J.-W. Dong, Direct observation of corner states in second-order topological photonic crystal slabs, Phys. Rev. Lett. 122, 233902 (2019).
Xie et al. [2019] B.-Y. Xie, G.-X. Su, H.-F. Wang, H. Su, X.-P. Shen, P. Zhan, M.-H. Lu, Z.-L. Wang, and Y.-F. Chen, Visualization of higher-order topological insulating phases in two-dimensional dielectric photonic crystals, Phys. Rev. Lett. 122, 233903 (2019).
Yang et al. [2020] Z.-Z. Yang, X. Li, Y.-Y. Peng, X.-Y. Zou, and J.-C. Cheng, Helical higher-order topological states in an acoustic crystalline insulator, Phys. Rev. Lett. 125, 255502 (2020).
Yang et al. [2021] Y. Yang, J. Lu, M. Yan, X. Huang, W. Deng, and Z. Liu, Hybrid-order topological insulators in a phononic crystal, Phys. Rev. Lett. 126, 156801 (2021).
Liu et al. [2014] Z. K. Liu, B. Zhou, Y. Zhang, Z. J. Wang, H. M. Weng, D. Prabhakaran, S.-K. Mo, Z. X. Shen, Z. Fang, X. Dai, Z. Hussain, and Y. L. Chen, Discovery of a three-dimensional topological Dirac semimetal, Na₃Bi, Science 343, 864 (2014).
Neupane et al. [2014] M. Neupane, S.-Y. Xu, R. Sankar, N. Alidoust, G. Bian, C. Liu, I. Belopolski, T.-R. Chang, H.-T. Jeng, H. Lin, A. Bansil, F. Chou, and M. Z. Hasan, Observation of a three-dimensional topological Dirac semimetal phase in high-mobility Cd₃As₂, Nature Communications 5, 3786 (2014).
Borisenko et al. [2014] S. Borisenko, Q. Gibson, D. Evtushinsky, V. Zabolotnyy, B. Büchner, and R. J. Cava, Experimental realization of a three-dimensional Dirac semimetal, Phys. Rev. Lett. 113, 027603 (2014).
Xu et al. [2015a] S.-Y. Xu, C. Liu, S. K. Kushwaha, R. Sankar, J. W. Krizan, I. Belopolski, M. Neupane, G. Bian, N. Alidoust, T.-R. Chang, H.-T. Jeng, C.-Y. Huang, W.-F. Tsai, H. Lin, P. P. Shibayev, F.-C. Chou, R. J. Cava, and M. Z. Hasan, Observation of Fermi arc surface states in a topological metal, Science 347, 294 (2015a).
Young et al. [2012] S. M. Young, S. Zaheer, J. C. Y. Teo, C. L. Kane, E. J. Mele, and A. M. Rappe, Dirac semimetal in three dimensions, Phys. Rev. Lett. 108, 140405 (2012).
Wang et al. [2012] Z. Wang, Y. Sun, X.-Q. Chen, C. Franchini, G. Xu, H. Weng, X. Dai, and Z. Fang, Dirac semimetal and topological phase transitions in ${A}_{3}$ Bi ( ${A}=\text{Na}$ , K, Rb), Phys. Rev. B 85, 195320 (2012).
Wang et al. [2013] Z. Wang, H. Weng, Q. Wu, X. Dai, and Z. Fang, Three-dimensional Dirac semimetal and quantum transport in Cd₃As₂, Phys. Rev. B 88, 125427 (2013).
Chen et al. [2015a] R. Y. Chen, Z. G. Chen, X.-Y. Song, J. A. Schneeloch, G. D. Gu, F. Wang, and N. L. Wang, Magnetoinfrared spectroscopy of landau levels and zeeman splitting of three-dimensional massless Dirac Fermions in ZrTe₅, Phys. Rev. Lett. 115, 176404 (2015a).
Liu et al. [2016] Y. Liu, X. Yuan, C. Zhang, Z. Jin, A. Narayan, C. Luo, Z. Chen, L. Yang, J. Zou, X. Wu, S. Sanvito, Z. Xia, L. Li, Z. Wang, and F. Xiu, Zeeman splitting and dynamical mass generation in Dirac semimetal ZrTe₅, Nature Communications 7, 12516 (2016).
Wan et al. [2011] X. Wan, A. M. Turner, A. Vishwanath, and S. Y. Savrasov, Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates, Phys. Rev. B 83, 205101 (2011).
Burkov and Balents [2011] A. A. Burkov and L. Balents, Weyl semimetal in a topological insulator multilayer, Phys. Rev. Lett. 107, 127205 (2011).
Weng et al. [2015] H. Weng, C. Fang, Z. Fang, B. A. Bernevig, and X. Dai, Weyl semimetal phase in noncentrosymmetric transition-metal monophosphides, Phys. Rev. X 5, 011029 (2015).
Huang et al. [2015a] S.-M. Huang, S.-Y. Xu, I. Belopolski, C.-C. Lee, G. Chang, B. Wang, N. Alidoust, G. Bian, M. Neupane, C. Zhang, S. Jia, A. Bansil, H. Lin, and M. Z. Hasan, A Weyl Fermion semimetal with surface Fermi arcs in the transition metal monopnictide TaAs class, Nature Communications 6, 7373 (2015a).
Xu et al. [2015b] S.-Y. Xu, I. Belopolski, N. Alidoust, M. Neupane, G. Bian, C. Zhang, R. Sankar, G. Chang, Z. Yuan, C.-C. Lee, S.-M. Huang, H. Zheng, J. Ma, D. S. Sanchez, B. Wang, A. Bansil, F. Chou, P. P. Shibayev, H. Lin, S. Jia, and M. Z. Hasan, Discovery of a Weyl Fermion semimetal and topological Fermi arcs, Science 349, 613 (2015b).
Lv et al. [2015] B. Q. Lv, H. M. Weng, B. B. Fu, X. P. Wang, H. Miao, J. Ma, P. Richard, X. C. Huang, L. X. Zhao, G. F. Chen, Z. Fang, X. Dai, T. Qian, and H. Ding, Experimental discovery of Weyl semimetal TaAs, Phys. Rev. X 5, 031013 (2015).
Yang et al. [2015] L. X. Yang, Z. K. Liu, Y. Sun, H. Peng, H. F. Yang, T. Zhang, B. Zhou, Y. Zhang, Y. F. Guo, M. Rahn, D. Prabhakaran, Z. Hussain, S.-K. Mo, C. Felser, B. Yan, and Y. L. Chen, Weyl semimetal phase in the non-centrosymmetric compound taas, Nature Physics 11, 728 (2015).
Huang et al. [2015b] X. Huang, L. Zhao, Y. Long, P. Wang, D. Chen, Z. Yang, H. Liang, M. Xue, H. Weng, Z. Fang, X. Dai, and G. Chen, Observation of the chiral-anomaly-induced negative magnetoresistance in 3d Weyl semimetal TaAs, Phys. Rev. X 5, 031023 (2015b).
Xu et al. [2015c] S.-Y. Xu, N. Alidoust, I. Belopolski, Z. Yuan, G. Bian, T.-R. Chang, H. Zheng, V. N. Strocov, D. S. Sanchez, G. Chang, C. Zhang, D. Mou, Y. Wu, L. Huang, C.-C. Lee, S.-M. Huang, B. Wang, A. Bansil, H.-T. Jeng, T. Neupert, A. Kaminski, H. Lin, S. Jia, and M. Zahid Hasan, Discovery of a Weyl Fermion state with Fermi arcs in niobium arsenide, Nature Physics 11, 748 (2015c).
Shekhar et al. [2015] C. Shekhar, A. K. Nayak, Y. Sun, M. Schmidt, M. Nicklas, I. Leermakers, U. Zeitler, Y. Skourski, J. Wosnitza, Z. Liu, Y. Chen, W. Schnelle, H. Borrmann, Y. Grin, C. Felser, and B. Yan, Extremely large magnetoresistance and ultrahigh mobility in the topological Weyl semimetal candidate NbP, Nature Physics 11, 645 (2015).
Lu et al. [2013] L. Lu, L. Fu, J. D. Joannopoulos, and M. Soljačić, Weyl points and line nodes in gyroid photonic crystals, Nature Photonics 7, 294 (2013).
Lu et al. [2015] L. Lu, Z. Wang, D. Ye, L. Ran, L. Fu, J. D. Joannopoulos, and M. Soljačić, Experimental observation of Weyl points, Science 349, 622 (2015).
Soluyanov et al. [2015] A. A. Soluyanov, D. Gresch, Z. Wang, Q. Wu, M. Troyer, X. Dai, and B. A. Bernevig, Type-II Weyl semimetals, Nature 527, 495 (2015).
Xu et al. [2015d] Y. Xu, F. Zhang, and C. Zhang, Structured Weyl points in spin-orbit coupled fermionic superfluids, Phys. Rev. Lett. 115, 265304 (2015d).
Nguyen et al. [2020] T. Nguyen, F. Han, N. Andrejevic, R. Pablo-Pedro, A. Apte, Y. Tsurimaki, Z. Ding, K. Zhang, A. Alatas, E. E. Alp, S. Chi, J. Fernandez-Baca, M. Matsuda, D. A. Tennant, Y. Zhao, Z. Xu, J. W. Lynn, S. Huang, and M. Li, Topological singularity induced chiral Kohn anomaly in a Weyl semimetal, Phys. Rev. Lett. 124, 236401 (2020).
Burkov et al. [2011] A. A. Burkov, M. D. Hook, and L. Balents, Topological nodal semimetals, Phys. Rev. B 84, 235126 (2011).
Yan et al. [2017] Z. Yan, R. Bi, H. Shen, L. Lu, S.-C. Zhang, and Z. Wang, Nodal-link semimetals, Phys. Rev. B 96, 041103(R) (2017).
Bi et al. [2017] R. Bi, Z. Yan, L. Lu, and Z. Wang, Nodal-knot semimetals, Phys. Rev. B 96, 201305(R) (2017).
Samanta et al. [2021] A. Samanta, D. P. Arovas, and A. Auerbach, Hall coefficient of semimetals, Phys. Rev. Lett. 126, 076603 (2021).
Sengupta et al. [2020] S. Sengupta, M. N. Y. Lhachemi, and I. Garate, Phonon magnetochiral effect of band-geometric origin in Weyl semimetals, Phys. Rev. Lett. 125, 146402 (2020).
Lin and Hughes [2018] M. Lin and T. L. Hughes, Topological quadrupolar semimetals, Phys. Rev. B 98, 241103(R) (2018).
Wieder et al. [2020] B. J. Wieder, Z. Wang, J. Cano, X. Dai, L. M. Schoop, B. Bradlyn, and B. A. Bernevig, Strong and fragile topological dirac semimetals with higher-order fermi arcs, Nature Communications 11, 627 (2020).
Wu et al. [2020b] W. Wu, Z.-M. Yu, X. Zhou, Y. X. Zhao, and S. A. Yang, Higher-order Dirac Fermions in three dimensions, Phys. Rev. B 101, 205134 (2020b).
Roy [2020] B. Roy, Higher-order topological superconductors in $\mathcal{P}$ -, $\mathcal{T}$ -odd quadrupolar Dirac materials, Phys. Rev. B 101, 220506(R) (2020).
Wang et al. [2020a] K. Wang, J.-X. Dai, L. B. Shao, S. A. Yang, and Y. X. Zhao, Boundary criticality of $\mathcal{PT}$ -invariant topology and second-order nodal-line semimetals, Phys. Rev. Lett. 125, 126403 (2020a).
Wang et al. [2020b] H.-X. Wang, Z.-K. Lin, B. Jiang, G.-Y. Guo, and J.-H. Jiang, Higher-order Weyl semimetals, Phys. Rev. Lett. 125, 146401 (2020b).
Ghorashi et al. [2020] S. A. A. Ghorashi, T. Li, and T. L. Hughes, Higher-order Weyl semimetals, Phys. Rev. Lett. 125, 266804 (2020).
Luo et al. [2021] L. Luo, H.-X. Wang, Z.-K. Lin, B. Jiang, Y. Wu, F. Li, and J.-H. Jiang, Observation of a phononic higher-order Weyl semimetal, Nature Materials 20, 794 (2021).
Wei et al. [2021] Q. Wei, X. Zhang, W. Deng, J. Lu, X. Huang, M. Yan, G. Chen, Z. Liu, and S. Jia, Higher-order topological semimetal in acoustic crystals, Nature Materials 20, 812 (2021).
Eckardt [2017] A. Eckardt, Colloquium: Atomic quantum gases in periodically driven optical lattices, Rev. Mod. Phys. 89, 011004 (2017).
Meinert et al. [2016] F. Meinert, M. J. Mark, K. Lauber, A. J. Daley, and H.-C. Nägerl, Floquet engineering of correlated tunneling in the Bose-Hubbard model with ultracold atoms, Phys. Rev. Lett. 116, 205301 (2016).
Rechtsman et al. [2013] M. C. Rechtsman, J. M. Zeuner, Y. Plotnik, Y. Lumer, D. Podolsky, F. Dreisow, S. Nolte, M. Segev, and A. Szameit, Photonic Floquet topological insulators, Nature (London) 496, 196 (2013).
Cheng et al. [2019] Q. Cheng, Y. Pan, H. Wang, C. Zhang, D. Yu, A. Gover, H. Zhang, T. Li, L. Zhou, and S. Zhu, Observation of anomalous $\pi$ modes in photonic Floquet engineering, Phys. Rev. Lett. 122, 173901 (2019).
Roushan et al. [2017] P. Roushan, C. Neill, A. Megrant, Y. Chen, R. Babbush, R. Barends, B. Campbell, Z. Chen, B. Chiaro, A. Dunsworth, A. Fowler, E. Jeffrey, J. Kelly, E. Lucero, J. Mutus, P. J. J. OHuo Heng alley, M. Neeley, C. Quintana, D. Sank, A. Vainsencher, J. Wenner, T. White, E. Kapit, H. Neven, and J. Martinis, Chiral ground-state currents of interacting photons in a synthetic magnetic field, Nature Physics 13, 146 (2017).
McIver et al. [2020] J. W. McIver, B. Schulte, F.-U. Stein, T. Matsuyama, G. Jotzu, G. Meier, and A. Cavalleri, Light-induced anomalous Hall effect in graphene, Nature Physics 16, 38 (2020).
Xiong et al. [2016] T.-S. Xiong, J. Gong, and J.-H. An, Towards large-Chern-number topological phases by periodic quenching, Phys. Rev. B 93, 184306 (2016).
Liu et al. [2019b] H. Liu, T.-S. Xiong, W. Zhang, and J.-H. An, Floquet engineering of exotic topological phases in systems of cold atoms, Phys. Rev. A 100, 023622 (2019b).
Li et al. [2018] L. Li, C. H. Lee, and J. Gong, Realistic Floquet semimetal with exotic topological linkages between arbitrarily many nodal loops, Phys. Rev. Lett. 121, 036401 (2018).
Wu and An [2020] H. Wu and J.-H. An, Floquet topological phases of non-Hermitian systems, Phys. Rev. B 102, 041119(R) (2020).
Kundu et al. [2014] A. Kundu, H. A. Fertig, and B. Seradjeh, Effective theory of Floquet topological transitions, Phys. Rev. Lett. 113, 236803 (2014).
Wu et al. [2021] H. Wu, B.-Q. Wang, and J.-H. An, Floquet second-order topological insulators in non-Hermitian systems, Phys. Rev. B 103, L041115 (2021).
Peng and Refael [2019] Y. Peng and G. Refael, Floquet second-order topological insulators from nonsymmorphic space-time symmetries, Phys. Rev. Lett. 123, 016806 (2019).
Bomantara et al. [2019] R. W. Bomantara, L. Zhou, J. Pan, and J. Gong, Coupled-wire construction of static and Floquet second-order topological insulators, Phys. Rev. B 99, 045441 (2019).
Seshadri et al. [2019] R. Seshadri, A. Dutta, and D. Sen, Generating a second-order topological insulator with multiple corner states by periodic driving, Phys. Rev. B 100, 115403 (2019).
Hu et al. [2020] H. Hu, B. Huang, E. Zhao, and W. V. Liu, Dynamical singularities of Floquet higher-order topological insulators, Phys. Rev. Lett. 124, 057001 (2020).
Huang and Liu [2020] B. Huang and W. V. Liu, Floquet higher-order topological insulators with anomalous dynamical polarization, Phys. Rev. Lett. 124, 216601 (2020).
Ghosh et al. [2021] A. K. Ghosh, T. Nag, and A. Saha, Floquet generation of a second-order topological superconductor, Phys. Rev. B 103, 045424 (2021).
Nag et al. [2021] T. Nag, V. Juričić, and B. Roy, Hierarchy of higher-order Floquet topological phases in three dimensions, Phys. Rev. B 103, 115308 (2021).
Rodriguez-Vega et al. [2019] M. Rodriguez-Vega, A. Kumar, and B. Seradjeh, Higher-order Floquet topological phases with corner and bulk bound states, Phys. Rev. B 100, 085138 (2019).
Rui et al. [2021] W. B. Rui, S.-B. Zhang, M. M. Hirschmann, Z. Zheng, A. P. Schnyder, B. Trauzettel, and Z. D. Wang, Higher-order Weyl superconductors with anisotropic Weyl-point connectivity, Phys. Rev. B 103, 184510 (2021).
[90] See the Supplemental Material for the real-space Hamiltonian, the definitions of the mirror-graded winding number and the chirality, the symmetry analysis, the derivation of the condition to form the Dirac/Weyl nodes, and the definition of Wilson loop.
Benalcazar et al. [2017b] W. A. Benalcazar, B. A. Bernevig, and T. L. Hughes, Electric multipole moments, topological multipole moment pumping, and chiral hinge states in crystalline insulators, Phys. Rev. B 96, 245115 (2017b).
Sambe [1973] H. Sambe, Steady states and quasienergies of a quantum-mechanical system in an oscillating field, Phys. Rev. A 7, 2203 (1973).
Chen et al. [2015b] C. Chen, J.-H. An, H.-G. Luo, C. P. Sun, and C. H. Oh, Floquet control of quantum dissipation in spin chains, Phys. Rev. A 91, 052122 (2015b).
Lu et al. [2020] Y.-H. Lu, B.-Z. Wang, and X.-J. Liu, Ideal Weyl semimetal with 3d spin-orbit coupled ultracold quantum gas, Science Bulletin 65, 2080 (2020).
Li et al. [2020] C.-Z. Li, A.-Q. Wang, C. Li, W.-Z. Zheng, A. Brinkman, D.-P. Yu, and Z.-M. Liao, Reducing electronic transport dimension to topological hinge states by increasing geometry size of dirac semimetal josephson junctions, Phys. Rev. Lett. 124, 156601 (2020).
Mahmood et al. [2016] F. Mahmood, C.-K. Chan, Z. Alpichshev, D. Gardner, Y. Lee, P. A. Lee, and N. Gedik, Selective scattering between floquet-bloch and volkov states in a topological insulator, Nat. Phys. 12, 306 (2016).
Wintersperger et al. [2020] K. Wintersperger, C. Braun, F. N. Ünal, A. Eckardt, M. D. Liberto, N. Goldman, I. Bloch, and M. Aidelsburger, Realization of an anomalous floquet topological system with ultracold atoms, Nat. Phys. 16, 1058 (2020).
Mukherjee et al. [2017] S. Mukherjee, A. Spracklen, M. Valiente, E. Andersson, P. Öhberg, N. Goldman, and R. R. Thomson, Experimental observation of anomalous topological edge modes in a slowly driven photonic lattice, Nature Communications 8, 13918 (2017).
Maczewsky et al. [2017] L. J. Maczewsky, J. M. Zeuner, S. Nolte, and A. Szameit, Observation of photonic anomalous floquet topological insulators, Nat. Commun. 8, 13756 (2017).