Enantio-detection of cyclic three-level chiral molecules in a driven cavity

Yu-Yuan Chen Beijing Computational Science Research Center, Beijing 100193, China Jian-Jian Cheng Beijing Computational Science Research Center, Beijing 100193, China Chong Ye Beijing Key Laboratory of Nanophotonics and Ultrafine Optoelectronic Systems, School of Physics, Beijing Institute of Technology, 100081 Beijing, China Yong Li [email protected] Beijing Computational Science Research Center, Beijing 100193, China

Abstract

We propose an enantio-detection method of chiral molecules in a cavity with external drive. The chiral molecules are coupled with a quantized cavity field and two classical light fields to form the cyclic three-level systems. The chirality-dependent cavity-assisted three-photon process in the three-level systems leads to the generation of intracavity photons. Simultaneously, the drive field also results in the chirality-independent process of the generation of intracavity photons. Based on the interference between the intracavity photons generated from these two processes, one can detect the enantiomeric excess of chiral mixture via monitoring the transmission rate of the drive field.

I Introduction

The existence of two molecular structural forms known as enantiomers (left- and right- handed chiral molecules) is one of the most important manifestations of symmetry breaking in nature MolecularStructure . Chiral molecules refer to the molecules that cannot be superposed on their mirror images via translations and rotations. They play crucial roles in various enantio-selective biological activities and chemical reactions EnantioEffect-Chiralitye2012 ; EnantioEffect-Science1996 . Thus, enantio-detection Barron-MolecularScatter ; Discrimination-JSepSci2007 ; Discrimination-OR ; Discrimination-VCD ; Discrimination-JiaWZ ; Discrimination-ZhangXD ; Discrimination-Lehmann ; Discrimination-YeC ; Discrimination-XuXW ; Discrimination-ChenYY ; Discrimination-Lehmann-Arxiv1 ; Microwave-Doyle-Nature ; Microwave-Doyle-PRL ; Microwave-Lehmann-JPCL ; Microwave-Schnell-ACIE ; Microwave-Schnell-JPCL ; Discrimination-ZhangX of chiral molecules is an important and challenging work. Most conventional spectroscopic methods Barron-MolecularScatter ; Discrimination-JSepSci2007 ; Discrimination-OR ; Discrimination-VCD for enantio-detection of chiral molecules are based on the interference between the electric-dipole and magnetic-dipole (or electric-quadrupole) transitions, and thus, the chiral signals are weak since the magnetic-dipole and electric-quadrupole transition moments are usually weak compared with the electric-dipole transition moments.

On the other hand, cavity quantum electrodynamics (CQED) systems with a single molecule or many molecules confined in a cavity have received considerable interest CQEDMolecule2 ; CQEDtransfer1 ; CQEDtransfer2 ; CQEDtransfer3 ; CQEDMoleculeSpectra1 ; CQEDMoleculeSpectra2 ; CQEDMoleculeSpectra3 ; CQEDReaction1 ; CQEDReaction2 ; CQEDReaction3 ; CQEDMoleculeXia ; CQEDMoleculeWe . In such CQED systems, the electromagnetic environment of the molecule(s) is modified by the quantized cavity field. This can strengthen the interaction between light fields and molecule(s) dramatically. Thus, the CQED systems have shown promising applications in the fields of energy transfer CQEDtransfer1 ; CQEDtransfer2 ; CQEDtransfer3 , molecular spectra CQEDMoleculeSpectra1 ; CQEDMoleculeSpectra2 ; CQEDMoleculeSpectra3 , and control of chemical reactions CQEDReaction1 ; CQEDReaction2 ; CQEDReaction3 for molecules.

Most recently, the enantio-detection of single chiral molecule CQEDMoleculeXia or many chiral molecules CQEDMoleculeWe has been investigated theoretically in the CQED systems. In Ref. CQEDMoleculeXia , it has been proposed to distinguish the chirality of single chiral molecule by using the single-molecule model of cyclic three-level system. However, in realistic case, the systems of enantio-detection Barron-MolecularScatter ; Discrimination-JSepSci2007 ; Discrimination-OR ; Discrimination-VCD ; Discrimination-JiaWZ ; Discrimination-ZhangXD ; Discrimination-Lehmann ; Discrimination-YeC ; Discrimination-XuXW ; Discrimination-ChenYY ; Discrimination-Lehmann-Arxiv1 ; Microwave-Doyle-Nature ; Microwave-Doyle-PRL ; Microwave-Lehmann-JPCL ; Microwave-Schnell-ACIE ; Microwave-Schnell-JPCL (as well as enantio-specific state transfer Seperation-Shapiro-PRL ; Seperation-JiaWZ-JPB ; Seperation-Koch-JCP ; Seperation-LiY-PRA ; Seperation-Schnell-ACIE ; Seperation-SepDoyle-PRL ; Seperation-Vitanov-PRR ; Seperation-YeC-PRA ; Seperation-ZhangQS-JPB , spatial enantio-separation Spatial-Separation-LiY-PRL ; Spatial-Seperation-Hornberger-JCP ; Spatial-Seperation-Shapiro-JCP ; Spatial-Seperation-LiuB ; Spatial-Seperation-Kravets-PRL ; Spatial-Seperation-Cipparrone-LSAppl , and enantio-conversion Conversion-Cohen-PRL ; Conversion-Shapiro-JCP ; Conversion-Shapiro-PRL ; Conversion-YeC-PRR ; Conversion-YeC1 ; Conversion-YeC2 ; Conversion-Shapiro-PRA ) of chiral molecules commonly contain a large number of molecules. In the case of the quantized cavity field(s) coupling with many molecules, one should resort to the multi-molecules treatment CQEDtransfer1 ; CQEDtransfer2 ; CQEDMoleculeSpectra1 ; CQEDMoleculeSpectra2 ; CQEDMoleculeSpectra3 ; CQEDReaction1 ; CQEDReaction2 ; CQEDMoleculeSpectra2 ; CQEDReaction3 ; CQEDtransfer3 , rather than the single-molecule one, which is only appropriate in the case of classical field(s) interacting with many molecules Barron-MolecularScatter ; Discrimination-JSepSci2007 ; Discrimination-OR ; Discrimination-VCD ; Discrimination-JiaWZ ; Discrimination-ZhangXD ; Discrimination-Lehmann ; Discrimination-YeC ; Discrimination-XuXW ; Discrimination-ChenYY ; Discrimination-Lehmann-Arxiv1 ; Microwave-Doyle-Nature ; Microwave-Doyle-PRL ; Microwave-Lehmann-JPCL ; Microwave-Schnell-ACIE ; Microwave-Schnell-JPCL . In Ref. CQEDMoleculeWe , the enantio-detection of chiral mixture has been achieved with the multi-molecule treatment in the CQED system for cyclic three-level chiral molecules in a cavity without external drive. The chirality-dependent cavity-assisted three-photon process leads to the generation of intracavity photons (even in the absence of external drive to the cavity). Thus it provided a promising way to detect the enantiomeric excess of chiral mixture by measuring the output field of the cavity.

In this paper, we propose an enantio-detection method based on the CQED system for cyclic three-level chiral molecules, which locate in a traveling-wave cavity RingCavity-Xiao-2001 ; RingCavity-Xiao-2008 ; RingCavity-Culver-2016 with external drive. Each molecule is described by the cyclic three-level system coupled with the quantized cavity field and two classical light fields. In the absence of the external drive, due to the existence of the two classical light fields, the intracavity photons can be generated via the chirality-dependent cavity-assisted three-photon process CQEDMoleculeWe . In the presence of the external drive, the drive field enters the cavity and also results in the chirality-independent process of generation of intracavity photons. There exists the interference between the intracavity photons resulting from these two processes. Based on this, we demonstrate that the enantiomeric excess can be detected by monitoring the steady-state transmission rate of the drive field.

We remark that in the previous system CQEDMoleculeWe where the cyclic three-level model is designed in the standing-wave cavity, the size of sample is required to be much smaller than the wavelengths of all the light fields to evade the influence of the phase-mismatching and the spatial dependence of the coupling strength. In our current system, however, such a strict requirement is not necessary since the present cyclic three-level model is specially-designed in the traveling-wave cavity. On the other hand, there is no external drive to the cavity in the previous system CQEDMoleculeWe and thus the enantiopure samples are required in the enantio-detection therein. In contrast, the existence of the external drive to the cavity in our system ensures our present method works without requiring the enantiopure samples. Therefore, the present method has advantages in enantio-detection of chiral molecules compared with the previous one in Ref. CQEDMoleculeWe .

This paper is organized as follows. In Sec. II, we give the model and Hamiltonian of the CQED system for cyclic three-level chiral molecules. Then the steady-state transmission of the drive field is investigated in Sec. III. Further, we present the results for enantio-detection of chiral molecules in Sec. IV, and then give the discussions about our investigations in Sec. V. Finally, the conclusion is given in Sec. VI.

II Model and Hamiltonian

We consider the CQED system for cyclic three-level chiral molecules as shown in Fig. 1. The system consists of a driven traveling-wave cavity and a ensemble of chiral mixture confined in the cavity. The drive field with amplitude $\varepsilon_{d}$ and angular frequency $\nu_{d}$ enters the cavity from mirror $M_{\rm{I}}$ and exits from mirror $M_{\rm{II}}$ . The chiral mixture contains $N=N_{L}+N_{R}$ molecules with $N_{L}$ and $N_{R}$ denoting the numbers of left- and right- handed molecules, respectively. The subscript $Q~{}(=L,R)$ is introduced to represent the molecular chirality. Each molecule in the chiral mixture is modeled as the cyclic three-level system, where the ground state $\left|1\right\rangle_{Q}$ is coupled to the state $\left|2\right\rangle_{Q}$ by the quantized cavity field with angular frequency $\omega_{a}$ and the state $\left|1\right\rangle_{Q}$ ( $\left|2\right\rangle_{Q}$ ) is coupled to the state $\left|3\right\rangle_{Q}$ by the classical light field with angular frequency $\nu_{31}$ ( $\nu_{32}$ ). Here, we focus on the three-photon resonant condition

\displaystyle\nu_{31}=\nu_{d}+\nu_{32}.

(1)

Under the dipole approximation and rotating-wave approximation, the Hamiltonian in the interaction picture with respect to ${H_{0}}={\nu_{d}}{a^{\dagger}}a+{\nu_{d}}(S_{22}^{L}+S_{22}^{R})+{\nu_{31}}(S_{33}^{L}+S_{33}^{R})$ is written in the time-independent form as ( $\hbar=1$ )

$\displaystyle{H_{I}}=$	$\displaystyle\,{\Delta_{a}}{a^{\dagger}}a+i\sqrt{{\kappa_{a}}}({\varepsilon_{d}}{a^{\dagger}}-\varepsilon_{d}^{*}a)$
	$\displaystyle+{\Delta_{21}}(S_{22}^{L}+S_{22}^{R})+{\Delta_{31}}(S_{33}^{L}+S_{33}^{R})$
	$\displaystyle+[{g_{a}}a(S_{21}^{L}+S_{21}^{R})+{\Omega_{31}}(S_{31}^{L}+S_{31}^{R})$
	$\displaystyle+{\Omega_{32}}({e^{i{\phi_{L}}}}S_{32}^{L}+{e^{i{\phi_{R}}}}S_{32}^{R})+{\rm{H.c.}}],$	(2)

where $\Delta_{a}=\omega_{a}-\nu_{d}$ , $\Delta_{21}=\omega_{21}-\nu_{d}$ , and $\Delta_{31}=\omega_{31}-\nu_{31}$ are the detunings, with $\omega_{21}$ and $\omega_{31}$ denoting the transition angular frequencies. $a$ ( $a^{\dagger}$ ) is the annihilation (creation) operator of the quantized cavity field. Here, both the cavity decay rates from mirror $M_{\rm{I}}$ and mirror $M_{\rm{I}}$ are assumed to be $\kappa_{a}/{2}$ , while other cavity decay rates have been neglected. Thus, the total cavity decay rate is equal to $\kappa_{a}$ . For simplicity but without loss of generality, the amplitude of the drive field, $\varepsilon_{d}$ , is taken as real. $S_{jk}^{Q}=\sum_{m=1}^{N_{Q}}|j\rangle_{m\,m}^{Q\,Q}\langle k|$ ( $j,k=1,2,3$ ) are introduced to denote the collective operators for the chiral molecules. $g_{a}$ represents the coupling strength between the quantized cavity field and single molecules, $\Omega_{31}$ and $\Omega_{32}e^{i{\phi_{Q}}}$ denote the coupling strengths between the two classical light fields and single molecules. Here, $g_{a}$ , $\Omega_{31}$ , and $\Omega_{32}$ are assumed to be identical for all the molecules and are taken as real. $\phi_{L}$ and $\phi_{R}$ are the overall phases of the three coupling strengths in the cyclic three-level systems of the left- and right- handed molecules, and the chirality of the cyclic three-level system is specified as

\displaystyle\phi_{L}=\phi,\,\phi_{R}=\phi+\pi.

(3)

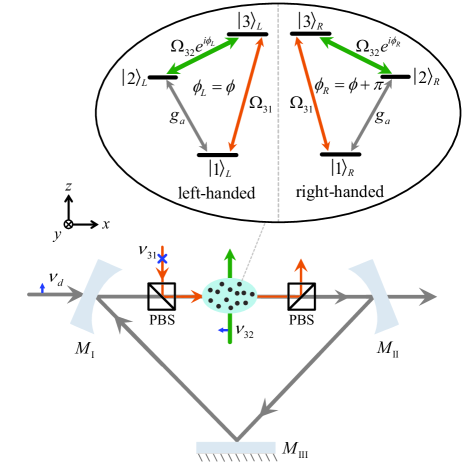
Refer to caption — Figure 1: The model of the CQED system for cyclic three-level chiral molecules under consideration. The cavity is composed of three mirrors $M_{\rm{I}}$ , $M_{\rm{II}}$ , and $M_{\rm{III}}$ . Here, the mirrors $M_{\rm{I}}$ and $M_{\rm{II}}$ are partially reflective and have the same reflection coefficients, while the mirror $M_{\rm{III}}$ is assumed to be perfectly reflective. The chiral molecules are coupled with the quantized cavity field and two classical light fields to form the cyclic three-level systems. The polarization directions of the light fields are shown in blue. The classical light field with angular frequency $\nu_{31}$ is introduced through the polarizing beam splitter (PBS) to interact with the molecules.

In our CQED system, when the chiral molecules confined in the cavity are coupled with the two classical light fields, the cavity-assisted three-photon process can result in the generation of intracavity photons CQEDMoleculeWe . Meanwhile, the drive field can also lead to the process of the generation of intracavity photons. The interference between the intracavity photons resulting from these two processes determines the output field of the cavity, which provides a way to detect the enantiomeric excess by monitoring the output field (e.g. the transmission rate of the drive field). Therefore, our method is different from that in Ref. CQEDMoleculeWe , wherein only the intracavity photons generated from the cavity-assisted three-photon process determine the output field of the cavity due to the absence of external drive.

Furthermore, these collective operators $S_{jk}^{Q}$ can be expressed by introducing the generalized Holstein-Primakoff transformation HPT-Brandes-PRL2003 ; HPT-Pioneer1940 ; HPT-RMP1991 ; HPT-Sun-PRL2003 as

	$\displaystyle S_{11}^{Q}=N_{Q}-A_{Q}^{\dagger}A_{Q}-B_{Q}^{\dagger}B_{Q},\ \ S_{22}^{Q}=A_{Q}^{\dagger}A_{Q},\ \ S_{33}^{Q}=B_{Q}^{\dagger}B_{Q},$
	$\displaystyle S_{21}^{Q}=A_{Q}^{\dagger}\sqrt{S_{11}^{Q}},\ \ S_{31}^{Q}=B_{Q}^{\dagger}\sqrt{S_{11}^{Q}},\ \ S_{32}^{Q}=B_{Q}^{\dagger}A_{Q},$		(4)

where $A_{Q}$ ( $A_{Q}^{\dagger}$ ) and $B_{Q}$ ( $B_{Q}^{\dagger}$ ) obey the standard bosonic commutation relations $[A_{Q},A_{Q}^{\dagger}]=[B_{Q},B_{Q}^{\dagger}]=1$ and $[A_{Q},B_{Q}]=[A_{Q},B_{Q}^{\dagger}]=0$ . In the low-excitation limit of molecules with large $N_{Q}$ limit (i.e., most molecules stay at their ground states: $\langle{A_{Q}^{\dagger}A_{Q}+B_{Q}^{\dagger}B_{Q}}\rangle\ll N_{Q}$ ) HPT-3level-2003 ; ThreeLevel-LiY ; HPT-3level-2010 ; HPT-3level-2013 , Hamiltonian (2) is rewritten as

$\displaystyle H_{I}\simeq$	$\displaystyle\,\Delta_{a}a^{\dagger}a+i\sqrt{\kappa_{a}}\varepsilon_{d}(a^{\dagger}-a)$
	$\displaystyle+\Delta_{21}(A_{L}^{\dagger}A_{L}+A_{R}^{\dagger}A_{R})+{\Delta_{31}}(B_{L}^{\dagger}B_{L}+B_{R}^{\dagger}B_{R})$
	$\displaystyle+[g_{a}a(\sqrt{N_{L}}A_{L}^{\dagger}+\sqrt{N_{R}}A_{R}^{\dagger})+\Omega_{31}(\sqrt{N_{L}}B_{L}^{\dagger}+\sqrt{N_{R}}B_{R}^{\dagger})$
	$\displaystyle+\Omega_{32}(B_{L}^{\dagger}A_{L}e^{i\phi_{L}}+B_{R}^{\dagger}A_{R}e^{i\phi_{R}})+\mathrm{H.c.}].$	(5)

In the following discussions, we will use 1,2-propanediol as an example to demonstrate our method. The working states of the cyclic three-level system are chosen as $|1\rangle=|g\rangle\left|0_{000}\right\rangle$ , $|2\rangle=|e\rangle\left|1_{110}\right\rangle$ , and $|3\rangle=(|e\rangle\left|1_{101}\right\rangle+|e\rangle\left|1_{10-1}\right\rangle)/\sqrt{2}$ , with $|g\rangle$ ( $|e\rangle$ ) denoting the vibrational ground (first-excited) state for the motion of OH-stretch with the transition angular frequency $\omega_{\text{vib}}=2\pi\times 100.950\,\text{THz}$ PropanediolParameter1994 . The rotational states are marked in the $\left|J_{K_{a}K_{c}M}\right\rangle$ notation Seperation-Koch-JCP ; anglemomentum . Correspondingly, as shown in Fig. 1, the state $\left|1\right\rangle$ is coupled to the state $\left|2\right\rangle$ by the $z$ -polarized quantized field in the cavity, which is driven by the $z$ -polarized classical light field. The state $\left|1\right\rangle$ ( $\left|2\right\rangle$ ) is coupled to the state $\left|3\right\rangle$ by the $y$ -polarized ( $x$ -polarized) classical light field. According to the rotational constants for 1,2-propanediol $A=2\pi\times 8524.405\,\text{MHz}$ , $B=2\pi\times 3635.492\,\text{MHz}$ , and $C=2\pi\times 2788.699\,\text{MHz}$ PropanediolParameter2017 , the bare transition angular frequencies are obtained as $\omega_{21}=2\pi\times 100.961\,\text{THz}$ , $\omega_{31}=2\pi\times 100.962\,\text{THz}$ , and $\omega_{32}=2\pi\times 0.847\,\text{GHz}$ anglemomentum . We would like to remark that our model and method are applicable for general (asymmetric-top) gaseous chiral molecules though we take 1,2-propanediol as an example in the discussions.

III Steady-state transmission

In this section, we study the transmission of the drive field in the steady state and explore its potential applications in enantio-detection of chiral mixture.

According to Hamiltonian (5), one can obtain the quantum Langevin equations for the system as

$\displaystyle\dot{a}=$	$\displaystyle-K_{a}a-ig_{a}(\sqrt{N_{L}}A_{L}+\sqrt{N_{R}}A_{R})+\sqrt{\kappa_{a}}(\varepsilon_{d}+a_{\rm{in}}^{\rm{I}}+a_{\rm{in}}^{\rm{II}}),$
$\displaystyle\dot{A}_{Q}=$	$\displaystyle-K_{A}A_{Q}-ig_{a}\sqrt{N_{Q}}a-i\Omega_{32}e^{-i\phi_{Q}}B_{Q}+F_{A}^{Q},$
$\displaystyle\dot{B}_{Q}=$	$\displaystyle-K_{B}B_{Q}-i\Omega_{31}\sqrt{N_{Q}}-i\Omega_{32}e^{i\phi_{Q}}A_{Q}+F_{B}^{Q},$	(6)

where $K_{a}=i\Delta_{a}+\kappa_{a}$ , $K_{A}=i\Delta_{21}+\Gamma_{A}$ , and $K_{B}=i{\Delta_{31}}+\Gamma_{B}$ . $a_{\rm{in}}^{\rm{I}}$ ( $a_{\rm{in}}^{\rm{II}}$ ) is the quantum input noise operator from mirror $M_{\rm{I}}$ ( $M_{\rm{II}}$ ) of the cavity, and has zero-mean value (i.e., $\langle a_{\rm{in}}^{\rm{I}}\rangle=\langle a_{\rm{in}}^{\rm{II}}\rangle=0$ ). $\Gamma_{A}$ ( $\Gamma_{B}$ ) is introduced to denote the decay rate of the collective mode $A_{Q}$ ( $B_{Q}$ ). $F_{A}^{Q}$ ( $F_{B}^{Q}$ ) is the quantum input noise term of the collective operator $A_{Q}$ ( $B_{Q}$ ), and has zero-mean value (i.e., $\langle F_{A}^{Q}\rangle=\langle F_{B}^{Q}\rangle=0$ ). Therefore, we obtain the following steady-state equations

$\displaystyle 0=$	$\displaystyle-K_{a}\langle a\rangle-ig_{a}(\sqrt{N_{L}}\langle A_{L}\rangle+\sqrt{N_{R}}\langle A_{R}\rangle)+\sqrt{\kappa_{a}}\varepsilon_{d},$
$\displaystyle 0=$	$\displaystyle-K_{A}\langle A_{Q}\rangle-ig\sqrt{N_{Q}}\langle a\rangle-i\Omega_{32}e^{-i\phi_{Q}}\langle B_{Q}\rangle,$
$\displaystyle 0=$	$\displaystyle-K_{B}\langle B_{Q}\rangle-i\Omega_{31}\sqrt{N_{Q}}-i\Omega_{32}e^{i\phi_{Q}}\langle A_{Q}\rangle,$	(7)

where $\langle O\rangle$ (with $O=a,\,A_{Q},\,B_{Q}$ ) represents the mean value of the operator $O$ . Thus, the steady-state value of $\langle a\rangle$ is given by

\displaystyle\langle a\rangle=

\displaystyle\frac{i\left(N_{L}-N_{R}\right)g_{a}\Omega_{31}\Omega_{32}e^{-i\phi}+\sqrt{\kappa_{a}}\varepsilon_{d}\left(K_{A}K_{B}+\Omega_{32}^{2}\right)}{K_{a}\left(K_{A}K_{B}+\Omega_{32}^{2}\right)+g_{a}^{2}NK_{B}}.

(8)

From Eq. (8), one can understand the physical mechanism underlying our method as follows. In the absence of the external drive (i.e., $\varepsilon_{d}=0$ ), only the first term in the numerator, which results from the chirality-dependent cavity-assisted three-photon process for the chiral mixture CQEDMoleculeWe , contributes to the intracavity photons. This term is proportional to $N_{L}-N_{R}$ since $g_{a}\Omega_{31}\Omega_{32}e^{-i\phi_{Q}}$ changes sign with enantiomer. When the external drive is applied (i.e., $\varepsilon_{d}\neq 0$ ), the second term in the numerator of Eq. (8) appears, resulting from the chirality-independent generation process of intracavity photons due to the drive field. Consequently, the interference between the intracavity photons generated from these two processes determines the output field of the cavity, which depends on the enantiomeric excess Discrimination-YeC ; Discrimination-XuXW ; Discrimination-ChenYY $\eta\equiv(N_{L}-N_{R})/{N}$ .

According to the input-output relation at mirrors $M_{\rm{I}}$ and $M_{\rm{II}}$ of the cavity QuantumNoise ; QuantumOpticsBook1 ; QuantumOpticsBook2

	$\displaystyle\sqrt{\kappa_{a}}a$	$\displaystyle=a_{\rm{in}}^{\rm{I}}+a_{\rm{out}}^{\rm{I}}+\varepsilon_{d},$
	$\displaystyle\sqrt{\kappa_{a}}a$	$\displaystyle=a_{\rm{in}}^{\rm{II}}+a_{\rm{out}}^{\rm{II}},$		(9)

one can obtain the mean output field from mirror $M_{\rm{II}}$ of the cavity $\left\langle a_{\rm{out}}^{\rm{II}}\right\rangle=\sqrt{\kappa_{a}}\left\langle a\right\rangle$ . Therefore, the steady-state transmission rate of the drive field $T\equiv\left|\left\langle a_{\rm{out}}^{\rm{II}}\right\rangle/\varepsilon_{d}\right|^{2}$ is given by

\displaystyle T=\frac{\kappa_{a}}{\varepsilon_{d}^{2}}\left|\frac{{iNg_{a}\Omega_{31}\Omega_{32}e^{-i\phi}}\eta+\sqrt{\kappa_{a}}\varepsilon_{d}\left(K_{A}K_{B}+\Omega_{32}^{2}\right)}{g_{a}^{2}NK_{B}+K_{a}\left(K_{A}K_{B}+\Omega_{32}^{2}\right)}\right|^{2}.

(10)

In what follows, we further assume that the quantized cavity field is resonantly coupled with the transition $\left|2\right\rangle_{Q}$ $\leftrightarrow$ $\left|1\right\rangle_{Q}$ , which means $\Delta_{a}=\Delta_{21}$ . And we assume the total number of chiral molecules $N=10^{8}$ CQEDMolecule2 ; CQEDReaction1 , the decay rates of molecules $\Gamma_{A}/2\pi=\Gamma_{B}/2\pi=0.1\,\text{MHz}$ Microwave-Doyle-Nature ; Microwave-Doyle-PRL , and the total cavity decay rate $\kappa_{a}/2\pi=1\,\text{MHz}$ CavityCouplingDecay-Kampschulte-2018 ; CavityDecay-Hoghooghi-2019 . Here, we take the weak coupling strength $\Omega_{31}/2\pi=8\,\text{kHz}$ since such a weak coupling strength usually ensures the low-excitation limit of molecules.

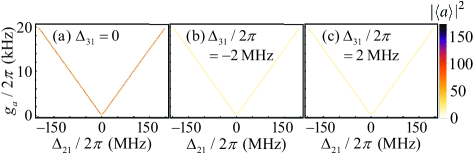
In the present work, the chirality-dependent cavity-assisted three-photon process is essential in the detection of the enantiomeric excess. Thus, we first consider the case in the absence of the external drive (i.e., $\varepsilon_{d}=0$ ) and display the corresponding steady-state intracavity mean photon number $\left|\langle a\rangle\right|^{2}$ versus the detuning $\Delta_{21}$ and the coupling strength $g_{a}$ for different detunings $\Delta_{31}$ in Fig. 2. As can be seen from Fig. 2(a), the intracavity mean photon number reaches the maximum $\left|\langle a\rangle\right|^{2}\simeq 180$ at the detunings $\Delta_{21}\simeq\pm g_{a}\sqrt{N}$ . This is the result of the vacuum Rabi splitting induced by the quantized cavity field in the strong collective coupling condition QuantumOpticsBook2 ; RabiSplit1 ; CQEDtransfer2 ; CQEDReaction1 . Here, it is worth mentioning that since the molecules are collectively coupled to the common quantized cavity field in our system, the collective coupling strength (between the quantized cavity field and the collective mode $A_{Q}$ ) $g_{a}\sqrt{N}$ can be strong even the single-molecule coupling strength (between the quantized cavity field and single molecules) $g_{a}$ is weak. Such a collectively-enhanced coupling strength, which depends on the total number of the molecules $N$ , can release the technical requirements for single-molecule strong coupling strength CQEDtransfer2 ; CQEDReaction1 . Moreover, it is found that there are more intracavity photons in the resonant case $\Delta_{31}=0$ compared with the non-resonant case $\Delta_{31}\neq 0$ [see Figs. 2(a)-2(c)]. In the further discussions, we take the coupling strength $g_{a}/2\pi=10\,\text{kHz}$ and the detuning $\Delta_{31}=0$ .

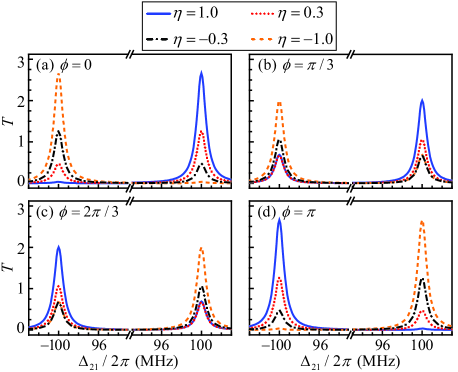
Furthermore, we consider the case in the presence of the external drive (i.e., $\varepsilon_{d}\neq 0$ ). In order to investigate the influence of the overall phase $\phi$ on the transmission rate of the drive field $T$ , we choose different $\phi$ to give $T$ versus the detuning $\Delta_{21}$ in Fig. 3. Here, only the results within the region $\phi\in[0,\,\pi]$ (e.g., $\phi=0$ , $\phi=\pi/3$ , $\phi=2\pi/3$ , and $\phi=\pi$ ) are displayed since the results corresponding to left- and right- handed molecules will exchange when replacing the overall phase $\phi$ in the region $\phi\in[0,\,\pi]$ by $\phi+\pi$ . Here, we find the transmission rate can be larger than one (i.e., $T>1$ ). This is the result of the constructive interference between the intracavity photons resulting from the cavity-assisted three-photon process and those generated from the drive field. Moreover, it is also shown that the transmission rate of the drive field is dependent on the overall phase. The underlying physics is that the interference between the intracavity photons generated from the cavity-assisted three-photon process and those resulting from the drive field strongly depends on the overall phase $\phi$ [see Eq. (8)]. Specially, for the overall phase $\phi=n\pi$ (with $n$ an arbitrary integer) [see Figs. 3(a) and 3(d)], $T$ becomes relatively sensitive to $\eta$ compared with the case of other values of $\phi$ .

IV Detection of enantiomeric excess

In this work, we focus on detecting the enantiomeric excess $\eta$ via measuring the transmission rate of the drive field $T$ . On one hand, we expect that a given $T$ corresponds to only a unique $\eta$ . That means $\eta$ can be detected via monitoring $T$ without requiring the enantiopure samples. On the other hand, we expect to achieve high resolution of detection, which requires that $T$ varies significantly with $\eta$ .

In the following simulations of this section, the detuning $\Delta_{a}$ , the total number of chiral molecules $N$ , the decay rates of molecules ( $\Gamma_{A}$ and $\Gamma_{B}$ ), and the coupling strength $\Omega_{31}$ are taken as the same values as those in Sec. III. Moreover, we assume the coupling strength $g_{a}/2\pi=10\,\text{kHz}$ and the detuning $\Delta_{31}=0$ .

As discussed above (see Fig. 3), at the detunings $\Delta_{21}\simeq\pm g_{a}\sqrt{N}$ , the transmission rate of the drive field for $\phi=n\pi$ is relatively sensitive to the enantiomeric excess compared with the case of other values of $\Delta_{21}$ . Therefore, for simplicity, we here focus on the optimal transmission rate at $\Delta_{21}=g_{a}\sqrt{N}$ :

T_{\rm{op}}\simeq\frac{\kappa_{a}}{\varepsilon_{d}^{2}}\left(\frac{\sqrt{\kappa_{a}}\varepsilon_{d}\Gamma_{B}\pm\sqrt{N}\Omega_{31}\Omega_{32}{\eta}}{\Gamma_{A}\Gamma_{B}+\kappa_{a}\Gamma_{B}+\Omega_{32}^{2}}\right)^{2},

(11)

which is obtained by substituting $\Delta_{21}=g_{a}\sqrt{N}$ into Eq. (10) and considering the approximation $g_{a}\sqrt{N}\gg\{\kappa_{a},\Gamma_{A},\Gamma_{B},\Omega_{32},\Omega_{31}\}$ . In the numerator of Eq. (11), “ $+$ ” and “ $-$ ” correspond respectively to the case of $\phi=2n\pi$ and $\phi=(2n+1)\pi$ . It is found from Eq. (11) that, when the parameters satisfy the condition

\displaystyle\sqrt{\kappa_{a}}\varepsilon_{d}\Gamma_{B}\geq\sqrt{N}\Omega_{31}\Omega_{32},

(12)

$T_{\rm{op}}$ varies with $\eta$ monotonically. That means, a given transmission rate corresponds to only a unique enantiomeric excess.

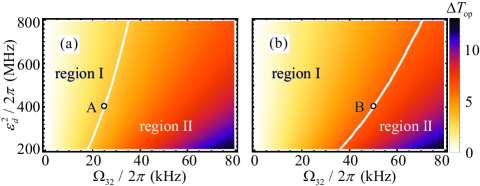
According to Eqs. (11) and (12), we further introduce the difference between the optimal transmission rates for purely left-handed ( $\eta=1$ ) and purely right-handed ( $\eta=-1$ ) chiral mixtures

\Delta T_{\rm{op}}=T_{\rm{op}}\lvert_{\eta=1}-T_{\rm{op}}\lvert_{\eta=-1}

(13)

to evaluate the resolution of detection, where $T_{\rm{op}}\lvert_{\eta=1}$ ( $T_{\rm{op}}\lvert_{\eta=-1}$ ) is obtained by substituting $\eta=1$ ( $\eta=-1$ ) into Eq. (11). In Fig. 4(a), we display $\Delta T_{\rm{op}}$ versus the coupling strength $\Omega_{32}$ and the intensity of the drive field $\varepsilon_{d}^{2}$ . Here, we take the overall phase $\phi=0$ . It is shown that $\Delta T_{\rm{op}}$ strongly depends on $\Omega_{32}$ and $\varepsilon_{d}^{2}$ . Specially, for the total cavity decay rate $\kappa_{a}/2\pi=1\,\text{MHz}$ , one finds $\Delta T_{\rm{op}}\simeq 3$ when taking $\Omega_{32}/2\pi\simeq 25\,\text{kHz}$ and $\varepsilon_{d}^{2}/2\pi\simeq 400\,\text{MHz}$ [see point A in Fig. 4(a)]. For the larger total cavity decay rate $\kappa_{a}/2\pi=4\,\text{MHz}$ , one obtains $\Delta T_{\rm{op}}\simeq 3.8$ when taking $\Omega_{32}/2\pi\simeq 50\,\text{kHz}$ and $\varepsilon_{d}^{2}/2\pi\simeq 400\,\text{MHz}$ [see point B in Fig. 4(b)].

Based on the results in Fig. 4, we further take $\kappa_{a}/2\pi=4\,\text{MHz}$ , $\Omega_{32}/2\pi=50\,\text{kHz}$ , and $\varepsilon_{d}^{2}/2\pi=400\,\text{MHz}$ to display the optimal transmission rate $T_{\rm{op}}$ as a function of the enantiomeric excess $\eta$ for different overall phases. It is found in Fig. 5(a) that, for $\phi=0$ ( $\phi=\pi$ ), $T_{\rm{op}}$ is relatively sensitive to $\eta$ in the region $\eta\in(0,\,1)$ [ $\eta\in(-1,\,0)$ ] compared with the case in the region $\eta\in(-1,\,0)$ [ $\eta\in(0,\,1)$ ]. Therefore, to ensure that the enantiomeric excess can be detected accurately via monitoring the transmission rate, the overall phase should be adjusted as $\phi=0$ ( $\phi=\pi$ ) when the left-handed (right-handed) molecules are dominant in the chiral mixture.

V Discussions

Here, it is worth mentioning that the above results are based on the low-excitation limit of molecules with large $N_{Q}$ limit (i.e., $\langle{A_{Q}^{\dagger}A_{Q}+B_{Q}^{\dagger}B_{Q}}\rangle\ll N_{Q}$ ). Thus, we introduce the factor

\displaystyle P_{e}=\frac{\langle A_{L}^{\dagger}A_{L}+B_{L}^{\dagger}B_{L}\rangle}{N_{L}}+\frac{\langle A_{R}^{\dagger}A_{R}+B_{R}^{\dagger}B_{R}\rangle}{N_{R}}

(14)

to verify whether or not the parameters used for simulations meet such a limit. The first (second) term in Eq. (14) denotes the proportion of left- (right-) handed molecules occupying their excited states to the total ones $N_{L}$ ( $N_{R}$ ). Here, we take the mean-field approximation QuantumOpticsBook2 $\langle A_{Q}^{\dagger}A_{Q}\rangle\simeq\langle A_{Q}^{\dagger}\rangle\langle A_{Q}\rangle$ and $\langle B_{Q}^{\dagger}B_{Q}\rangle\simeq\langle B_{Q}^{\dagger}\rangle\langle B_{Q}\rangle$ . The steady-state solutions $\langle A_{Q}\rangle$ , $\langle A_{Q}^{\dagger}\rangle$ , $\langle B_{Q}\rangle$ , and $\langle B_{Q}^{\dagger}\rangle$ are obtained by solving the steady-state Eq. (7). For the parameters in Fig. 5(a), we find $P_{e}\simeq 1.28\times 10^{-2}$ [see Fig. 5(b)]. This implies that most molecules stay at their ground states, and thus, the results meet the requirement for the low-excitation limit of molecules.

Note that in the previous CQED system for cyclic three-level chiral molecules in the standing-wave cavity CQEDMoleculeWe , the finite size of the sample usually would lead to the phase-mismatching problem Discrimination-Lehmann and the space-dependent coupling strength QuantumOpticsBook1 between the quantized cavity field and single molecules. In order to evade the influence of the phase-mismatching and the spatial dependence of the coupling strength, the size of sample $l$ should be much smaller than the wavelengths of all the light fields, that is, $\{|\vec{k}_{a}|,\,|\vec{k}_{32}|,\,|\vec{k}_{31}|\}l\ll 2\pi$ . In the present method, we use the system for three-level chiral molecules confined in the traveling-wave cavity RingCavity-Xiao-2001 ; RingCavity-Xiao-2008 ; RingCavity-Culver-2016 . When the spatial distribution of molecules is considered, only $g_{a}$ should be replaced by $g_{a}e^{i\Delta\vec{k}\cdot\vec{r}_{m}}$ (with the coupling strengths $\Omega_{31}$ and $\Omega_{32}$ remaining unchanged) to investigate the influence of the phase-mismatching with $\Delta\vec{k}=\vec{k}_{31}-\vec{k}_{a}-\vec{k}_{32}$ , where $\vec{r}_{m}$ is the position of the $m$ -th molecule. To ensure that the influence of the phase-mismatching is negligible, the size of sample $l$ should meet the requirement $|\Delta\vec{k}|l\ll 2\pi$ . In the present system, $\vec{k}_{32}$ is the smallest one among the three vectors. Thus, with taking $\vec{k}_{31}$ and $\vec{k}_{a}$ to be parallel and $\vec{k}_{32}$ to be perpendicular to them (see Fig. 1), one can minimize the effect of the phase-mismatching. Here, we obtain $|\Delta\vec{k}|\simeq 2\pi\times 4.277\,\text{m}^{-1}$ for the present model of 1,2-propanediol. That means, when the sample is fixed in a volume with its size $l\ll{2\pi}/{|\Delta\vec{k}|}\simeq 0.234\,\text{m}$ , the influence of the phase-mismatching can be neglected reasonably. Therefore, the requirement (i.e., the size of sample should be much smaller than the wavelengths of all the light fields) in the previous CQED method CQEDMoleculeWe is released in our current method since the related cyclic three-level model is specially-designed in the traveling-wave cavity.

VI Conclusion

In conclusion, we have proposed an enantio-detection method based on the CQED system for cyclic three-level chiral molecules. The key idea is to achieve the interference between the intracavity photons generated via the cavity-assisted three-photon process and those arising from the drive field. Our results show that the enantiomeric excess can be detected via measuring the steady-state transmission rate of the drive field. In the previous CQED method CQEDMoleculeWe and enantiomer-specific microwave spectroscopic methods Microwave-Doyle-Nature ; Microwave-Doyle-PRL ; Microwave-Lehmann-JPCL ; Microwave-Schnell-ACIE ; Microwave-Schnell-JPCL for enantio-detection of chiral molecules, usually the enantiopure samples are required to indicate the sign of the enantiomeric excess. Note that the preparation of enantiopure samples remains a challenging work for many chiral molecules Spatial-Separation-LiY-PRL ; Spatial-Seperation-Hornberger-JCP ; Spatial-Seperation-Shapiro-JCP ; Spatial-Seperation-LiuB ; Seperation-JiaWZ-JPB ; Seperation-Koch-JCP ; Seperation-LiY-PRA ; Seperation-Schnell-ACIE ; Seperation-SepDoyle-PRL ; Seperation-Vitanov-PRR ; Seperation-YeC-PRA ; Seperation-ZhangQS-JPB ; Conversion-Cohen-PRL ; Conversion-Shapiro-JCP ; Conversion-Shapiro-PRL ; Conversion-YeC-PRR ; Conversion-YeC1 ; Conversion-YeC2 ; Conversion-Shapiro-PRA ; Seperation-Shapiro-PRL ; Spatial-Seperation-Kravets-PRL ; Spatial-Seperation-Cipparrone-LSAppl . In our method, however, such enantiopure samples are not necessary since our method is based on the interference between the intracavity photons generated via the chirality-dependent cavity-assisted three-photon process and those arising from the chirality-independent drive field. Therefore, our method provides promising applications in the detection of enantiomeric excess for the chiral molecules whose enantiopure samples are still difficult to prepare.

Moreover, we note that besides enantio-detection of chiral molecules CQEDMoleculeXia ; CQEDMoleculeWe , the CQED systems had also been used in studying energy transfer CQEDtransfer1 ; CQEDtransfer2 ; CQEDtransfer3 and control of chemical reactions CQEDReaction1 ; CQEDReaction2 ; CQEDReaction3 for molecules due to their potential applications in manipulating the molecular dynamical evolution. Therefore, in future investigations, we will further focus on the ambitious issues related to chiral molecules involving molecular dynamical evolution (such as enantio-specific state transfer, spatial enantio-separation, and enantio-conversion of chiral molecules) based on the CQED systems for cyclic three-level chiral molecules.

Acknowledgements.

This work was supported by the Natural Science Foundation of China (Grants No. 12074030 and No. U1930402), National Science Foundation for Young Scientists of China (No. 12105011), and Beijing Institute of Technology Research Fund Program for Young Scholars.

References

(1) R. G. Wooley, “Quantum theory and molecular structure,” Adv. Phys. 25, 27 (1976).
(2) A. J. Hutt and S. C. Tan, “Drug chirality and its clinical significance,” Drugs 52, 1 (1996).
(3) J. Gal, “The Discovery of Stereoselectivity at Biological Receptors: Arnaldo Piutti and the Taste of the Asparagine Enantiomers—History and Analysis on the 125th Anniversary,” Chirality 12, 959 (2012).
(4) L. D. Barron, Molecular Light Scattering and Optical Activity (Cambridge University Press, Cambridge, UK, 1982).
(5) P. J. Stephens, “Theory of Vibrational Circular Dichroism,” J. Phys. Chem. 89, 748 (1985).
(6) R. K. Kondru, Peter Wipf, and D. N. Beratan, “Atomic contributions to the optical rotation angle as a quantitative probe of molecular chirality,” Science 282, 2247 (1998).
(7) R. Bielski and M. Tencer, “Absolute enantioselective separation: Optical activity ex machina,” J. Sep. Sci. 28, 2325 (2005).
(8) D. Zhai, P. Wang, R.-Y. Wang, X. Tian, Y. Ji, W. Zhao, L. Wang, H. Wei, X. Wu, and X. Zhang, “Plasmonic polymers with strong chiroptical response for sensing molecular chirality,” Nanoscale 7, 10690 (2015).
(9) W. Z. Jia and L. F. Wei, “Probing molecular chirality by coherent optical absorption spectra,” Phys. Rev. A 84, 053849 (2011).
(10) D. Patterson, M. Schnell, and J. M. Doyle, “Enantiomer-specific detection of chiral molecules via microwave spectroscopy,” Nature (London) 497, 475 (2013).
(11) D. Patterson and J. M. Doyle, “Sensitive Chiral Analysis via Microwave Three-Wave Mixing,” Phys. Rev. Lett. 111, 023008 (2013).
(12) V. A. Shubert, D. Schmitz, D. Patterson, J. M. Doyle, and M. Schnell, “Identifying Enantiomers in Mixtures of Chiral Molecules with Broadband Microwave Spectroscopy,” Angew. Chem. Int. Ed. 53, 1152 (2014).
(13) S. Lobsiger, C. Pérez, L. Evangelisti, K. K. Lehmann, and B. H. Pate, “Molecular Structure and Chirality Detection by Fourier Transform Microwave Spectroscopy,” J. Phys. Chem. Lett. 6, 196 (2015).
(14) V. A. Shubert, D. Schmitz, C. Pérez, C. Medcraft, A. Krin, S. R. Domingos, D. Patterson, and M. Schnell, “Chiral Analysis Using Broadband Rotational Spectroscopy,” J. Phys. Chem. Lett. 7, 341 (2015).
(15) K. K. Lehmann, “Proposal for Chiral Detection by the AC Stark-Effect,” arXiv: 1501.05282 (2015); K. K. Lehmann, “Stark Field Modulated Microwave Detection of Molecular Chirality,” arXiv: 1501.07874 (2015).
(16) K. K. Lehmann, “Influence of spatial degeneracy on rotational spectroscopy: Three-wave mixing and enantiomeric state separation of chiral molecules,” J. Chem. Phys. 149, 094201 (2018).
(17) C. Ye, Q. Zhang, Y.-Y. Chen, and Y. Li, “Determination of enantiomeric excess with chirality-dependent ac Stark effects in cyclic three-level models,” Phys. Rev. A 100, 033411 (2019).
(18) X.-W. Xu, C. Ye, Y. Li, and A.-X. Chen, “Enantiomeric-excess determination based on nonreciprocal-transition-induced spectral-line elimination,” Phys. Rev. A 102, 033727 (2020).
(19) Y.-Y. Chen, C. Ye. Q. Zhang, and Y. Li, “Enantio-discrimination via light deflection effect,” J. Chem. Phys. 152, 204305 (2020).
(20) C. Ye. Y. Sun, and X. Zhang, “Entanglement-Assisted Quantum Chiral Spectroscopy,” J. Phys. Chem. Lett. 52, 8591 (2021).
(21) Y.-x. Liu, J. Q. You, L. F. Wei, C. P. Sun, and F. Nori, “Optical Selection Rules and Phase-Dependent Adiabatic State Control in a Superconducting Quantum Circuit,” Phys. Rev. Lett. 95, 087001 (2005).
(22) Y. Li, L. Zheng, Y.-x. Liu, and C. P. Sun, “Correlated photons and collective excitations of a cyclic atomic ensemble,” Phys. Rev. A 73, 043805 (2006).
(23) E. Hirota, “Triple resonance for a three-level system of a chiral molecule,” Proc. Jpn. Acad. Ser. B 88, 120 (2012).
(24) L. Zhou, L.-P. Yang, Y. Li, and C. P. Sun, “Quantum Routing of Single Photons with a Cyclic Three-Level System,” Phys. Rev. Lett. 111, 103604 (2013).
(25) C. Ye, Q. Zhang, and Y. Li, “Real single-loop cyclic three-level configuration of chiral molecules,” Phys. Rev. A 98, 063401 (2018).
(26) N. V. Vitanov and M. Drewsen, “Highly Efficient Detection and Separation of Chiral Molecules through Shortcuts to Adiabaticity,” Phys. Rev. Lett. 122, 173202 (2019).
(27) J.-L. Wu, Y. Wang, J.-X. Han, C. Wang, S.-L. Su, Y. Xia, Y.-Y. Jiang, and J. Song, “Two-Path Interference for Enantiomer-Selective State Transfer of Chiral Molecules,” Phys. Rev. Appl. 13, 044021 (2020).
(28) P. Král and M. Shapiro, “Cyclic Population Transfer in Quantum Systems with Broken Symmetry,” Phys. Rev. Lett. 87, 183002 (2001).
(29) Y. Li and C. Bruder, “Dynamic method to distinguish between left- and right-handed chiral molecules,” Phys. Rev. A 77, 015403 (2008).
(30) W. Z. Jia and L. F. Wei, “Distinguishing left- and right-handed molecules using two-step coherent pulses,” J. Phys. B: At. Mol. Opt. Phys. 43, 185402 (2010).
(31) S. Eibenberger, J. M. Doyle, and D. Patterson, “Enantiomer-Specific State Transfer of Chiral Molecules,” Phys. Rev. Lett. 118, 123002 (2017).
(32) C. Pérez, A. L. Steber, S. R. Domingos, A. Krin, D. Schmitz, and M. Schnell, “Coherent Enantiomer-Selective Population Enrichment Using Tailored Microwave Fields,” Angew. Chem. Int. Ed. 56, 12512 (2017).
(33) C. Ye, Q. Zhang, Y.-Y. Chen, and Y. Li, “Effective two-level models for highly efficient inner-state enantioseparation based on cyclic three-level systems of chiral molecules,” Phys. Rev. A 100, 043403 (2019).
(34) M. Leibscher, T. F. Giesen, and C. P. Koch, “Principles of enantio-selective excitation in three-wave mixing spectroscopy of chiral molecules,” J. Chem. Phys. 151, 014302 (2019).
(35) Q. Zhang, Y.-Y. Chen, C. Ye, and Y. Li, “Evading thermal population influence on enantiomeric-specific state transfer based on a cyclic three-level system via ro-vibrational transitions,” J. Phys. B: At. Mol. Opt. Phys. 53, 235103 (2020).
(36) B. T. Torosov, M. Drewsen, and N. V. Vitanov, “Chiral resolution by composite Raman pulses,” Phys. Rev. Research 2, 043235 (2020).
(37) Y. Li, C. Bruder, and C. P. Sun, “Generalized Stern-Gerlach Effect for Chiral Molecules,” Phys. Rev. Lett. 99, 130403 (2007).
(38) X. Li and M. Shapiro, “Theory of the optical spatial separation of racemic mixtures of chiral molecules,” J. Chem. Phys. 132, 194315 (2010).
(39) A. Jacob and K. Hornberger, “Effect of molecular rotation on enantioseparation,” J. Chem. Phys. 137, 044313 (2012).
(40) N. Kravets, A. Aleksanyan, and E. Brasselet, “Chiral Optical Stern-Gerlach Newtonian Experiment,” Phys. Rev. Lett. 122, 024301 (2019).
(41) Y. Shi, T. Zhu, T. Zhang, A. Mazzulla, D. P. Tsai, W. Ding, A. Q. Liu, G. Cipparrone, J. J. Sáenz, and C.-W. Qiu, “Chirality-assisted lateral momentum transfer for bidirectional enantioselective separation,” Light Sci. Appl. 9, 62 (2020).
(42) B. Liu, C. Ye, C. P. Sun, and Y. Li, “Spatial enantioseparation of gas chiral molecules,” Phys. Rev. A 104, 013113 (2021).
(43) R. Bennett, D. Steinbrecht, Y. Gorbachev, and S. Y. Buhmann, “Symmetry Breaking in a Condensate of Light and its Use as a Quantum Sensor,” Phys. Rev. Appl. 13, 044031 (2020).
(44) X. Zhong, T. Chervy, S. Wang, J. George, A. Thomas, J. A. Hutchison, E. Devaux, C. Genet, and T. W. Ebbesen, “Non-Radiative Energy Transfer Mediated by Hybrid Light-Matter States,” Angew. Chem. Int. Ed. 55, 6202 (2016).
(45) R. Sáez-Blázquez, J. Feist, A. I. Fernández-Domínguez, and F. J. García-Vidal, “Organic polaritons enable local vibrations to drive long-range energy transfer,” Phys. Rev. B 97, 241407(R) (2018).
(46) A. D. Dunkelberger, B. T. Spann, K. P. Fears, B. S. Simpkins, and J. C. Owrutsky, “Modified relaxation dynamics and coherent energy exchange in coupled vibration-cavity polaritons,” Nat. Commun. 7, 13504 (2016).
(47) F. Herrera1 and F. C. Spano, “Dark Vibronic Polaritons and the Spectroscopy of Organic Microcavities,” Phys. Rev. Lett. 118, 223601 (2017).
(48) T. Neuman and J. Aizpurua, “Origin of the asymmetric light emission from molecular exciton-polaritons,” Optica 5, 1247 (2018).
(49) Z. Zhang, K. Wang, Z. Yi, M. S. Zubairy, M. O. Scully, and S. Mukamel, “Polariton-Assisted Cooperativity of Molecules in Microcavities Monitored by Two-Dimensional Infrared Spectroscopy,” J. Phys. Chem. Lett. 10, 4448 (2019).
(50) F. Herreral and F. C. Spano, “Cavity-Controlled Chemistry in Molecular Ensembles,” Phys. Rev. Lett. 116, 238301 (2016).
(51) J. A. Campos, R. F. Ribeiro, and J. Yuen-Zhou, “Resonant catalysis of thermally activated chemical reactions with vibrational polaritons,” Nat. Commun. 10, 4685 (2019).
(52) J. Lather, P. Bhatt, A. Thomas, T. W. Ebbesen, and J. George, “Cavity Catalysis by Cooperative Vibrational Strong Coupling of Reactant and Solvent Molecules,” Angew. Chem. Int. Ed. 58, 10635 (2019).
(53) Y.-H. Kang, Z.-C. Shi, J. Song, and Y. Xia, “Effective discrimination of chiral molecules in a cavity,” Opt. Lett. 45, 4952 (2020).
(54) Y.-Y. Chen, C. Ye, and Y. Li, “Enantio-detection via cavity-assisted three-photon processes,” Opt. Express 29, 36132 (2021).
(55) M. Shapiro, E. Frishman, and P. Brumer, “Coherently Controlled Asymmetric Synthesis with Achiral Light,” Phys. Rev. Lett. 84, 1669 (2000).
(56) D. Gerbasi, M. Shapiro, and P. Brumer, “Theory of enantiomeric control in dimethylallene using achiral light,” J. Chem. Phys. 115, 5349 (2001).
(57) P. Brumer, E. Frishman, and M. Shapiro, “Principles of electric-dipole-allowed optical control of molecular chirality,” Phys. Rev. A 65, 015401 (2001).
(58) P. Král, I. Thannopulos, M. Shapiro, and D. Cohen, “Two-Step Enantio-Selective Optical Switch,” Phys. Rev. Lett. 90, 033001 (2003).
(59) C. Ye, Q. Zhang, Y.-Y. Chen, and Y. Li, “Fast enantioconversion of chiral mixtures based on a four-level double- $\Delta$ model,” Phys. Rev. Research 2, 033064 (2020).
(60) C. Ye, Q. Zhang, Y.-Y. Chen, and Y. Li, “Improved laser-distillation method for complete enantio-conversion of chiral mixtures,” J. Phys. B: At. Mol. Opt. Phys. 54, 145102 (2021).
(61) C. Ye, B. Liu, Y.-Y. Chen, and Y. Li, “Enantio-conversion of chiral mixtures via optical pumping,” Phys. Rev. A 103, 022830 (2021).
(62) H. Wang, D. J. Goorskey, and M. Xiao, “Bistability and instability of three-level atoms inside an optical cavity,” Phys. Rev. A 65, 011801(R) (2001).
(63) H. Wu, J. Gea-Banacloche, and M. Xiao, “Observation of Intracavity Electromagnetically Induced Transparency and Polariton Resonances in a Doppler-Broadened Medium,” Phys. Rev. Lett. 100, 173602 (2008).
(64) R. Culver, A. Lampis, B. Megyeri, K. Pahwa, L. Mudarikwa, M. Holynski, P. W. Courteille, and J. Goldwin, “Collective strong coupling of cold potassium atoms in a ring cavity,” New J. Phys. 18, 113043 (2016).
(65) T. Holstein and H. Primakoff, “Field Dependence of the Intrinsic Domain Magnetization of a Ferromagnet,” Phys. Rev. 58, 1098 (1940).
(66) A. Klein and E. R. Marshalek, “Boson realizations of Lie algebras with applications to nuclear physics,” Rev. Mod. Phys. 63, 375 (1991).
(67) C. P. Sun, Y. Li, and X. F. Liu, “Quasi-Spin-Wave Quantum Memories with a Dynamical Symmetry,” Phys. Rev. Lett. 91, 147903 (2003).
(68) C. Emary and T. Brandes, “Quantum Chaos Triggered by Precursors of a Quantum Phase Transition: The Dicke Model,” Phys. Rev. Lett. 90, 044101 (2003).
(69) G. R. Jin, P. Zhang, Y.-x. Liu, and C. P. Sun, “Superradiance of low-density Frenkel excitons in a crystal slab of three-level atoms: The quantum interference effect,” Phys. Rev. B 68, 134301 (2003).
(70) Z. Kurucz and K. Mølmer, “Multilevel Holstein-Primakoff approximation and its application to atomic spin squeezing and ensemble quantum memories,” Phys. Rev. A 81, 032314 (2010).
(71) A. Baksic, P. Nataf, and C. Ciuti, “Superradiant phase transitions with three-level systems,” Phys. Rev. A 87, 023813 (2013).
(72) C. R. Ayrea and R. J. Madix, “The adsorption and reaction of 1,2-propanediol on Ag(110) under oxygen lean conditions,” Surf. Sci. 303, 279 (1994).
(73) R. N. Zare, Angular Momentum (Wiley, New York, 1988).
(74) B. E. Arenas, S. Gruet, A. L. Steber, and M. Schnell, “A global study of the conformers of 1,2-propanediol and new vibrationally excited states,” J. Mol. Spec. 337, 9 (2017).
(75) C. Gardiner and P. Joller, Quantum Noise (Springer, Berlin, 2004).
(76) D. F. Walls and G. J. Milburn, Quantum Optics, 2nd ed. (Springer, Berlin, 2008).
(77) G. S. Agarwal, Quantum Optics (Cambridge University Press, Cambridge, 2013).
(78) T. Kampschulte and J. H. Denschlag, “Cavity-controlled formation of ultracold molecules,” New J. Phys. 20, 123015 (2018).
(79) N. Hoghooghi, R. J. Wright, A. S. Makowiecki, W. C. Swann, E. M. Waxman, I. Coddington, and G. B. Rieker, “Broadband coherent cavity-enhanced dual-comb spectroscopy,” Optica 6, 28 (2019).
(80) M. Tavis and F. W. Cummings, “Exact Solution for an N-Molecule-Radiation-Field Hamiltonian,” Phys. Rev. 170, 379 (1968).