Enabling low threshold laser through an asymmetric tetramer metasurface harnessing polarization-independent quasi-BICs
Abstract
We propose and numerically demonstrate a novel strategy to achieve dual-band symmetry-protected bound states in the continuum (BICs) based on a nanodisk tetramer metasurface for lasing generation. The method involves breaking the in-plane symmetry along the diagonal of the metasurface unit cell by introducing air holes in the tetramers. Through our simulations, we show that this flexible approach enables the support of dual-band BICs in the telecom-band range, with these modes evolving into quasi-BICs with remarkably high quality factors by breaking the symmetry of the system. Furthermore, the ultracompact device exhibits the unique characteristic of being polarization-independent across all viewing angles. Finally, the optically pumped gain medium provides sufficient optical gain to compensate the quasi-BIC mode losses, enabling two mode lasing with ultra-low pump threshold and very narrow optical linewidth in the telecom-band range. Our adaptable device paves the way for polarization-insensitive metasurfaces with multiple lasing resonances. This innovation holds the potential to transform areas like low-threshold lasing and biosensing by delivering improved performance and broader capabilities.
I Introduction
Bound states in the continuum (BICs) are localized states that exist alongside a continuous spectrum of radiating waves, appearing as resonances not interacting with any of the continuum states Wang2024 ; Hsu2016 ; Hu2021 ; Romano2019 . Since their first experimental demonstration in 2013, optical BICs have captured significant interest within various photonic systems Hsu2013 . Optical BICs are considered dark states with an infinite radiative lifetime, allowing them to achieve infinitely Q resonances and facilitating enhanced interactions between light and matter Zhang2024 . This unique characteristic allows for the exploration of distinctive and robust light-matter interactions through the engineering and utilization of BICs Gao2023 . Consequently, researchers can investigate topological photonics and create innovative photonic devices with exceptional properties, such as low-threshold lasing and highly sensitive sensing capabilities Sun2024 ; Schiattarella2024 ; Mohamed2022 ; Zhang2021 .
Based on the physical mechanisms underlying their formation, BICs can be broadly classified into two groups Koshelev2019 ; Han2024 . The most straightforward type is the symmetry-protected BIC (SP-BIC), which are formed due to the symmetry or separability restricted out-coupling Joseph2021 ; Lee2012 . In periodic photonic structures such as gratings Zhang2021 , photonic crystals Kang2022 , and even other kinds of metasurfaces Fan2023 ; Campione2016 ; Liu2019 , the SP-BICs can be found as discrete modes in the Brillouin zone near the gamma () point. In theory, ideal BICs cannot be observed because they have zero linewidth and infinite Q-factor in the continuum. However, in real structure or fabricated systems, the Q factor of the BIC is finite due to the restricted dimension, losses, and imperfection in the fabricated system Joseph2021 . Therefore, only the quasi-BICs can be experimentally realized. Alternatively, people can either slightly break the excitation field symmetry through oblique incidences, or break the in-plane or out-of-plane structural symmetry under normal incidence Xiang2020 . In-plane symmetry breaking is a typical approach which involves altering the shape or the structure of the meta-atom, or by introducing a relative tile between paired meta-atoms, whereas the out-of-plane symmetry breaking relies on disturbing the heights of a dimer or trimer cluster Feng2023 .
In this paper, we propose a new method to break the symmetry of a tetramer metasurface by introducing air holes for the elements along the inner diagonals. Using this asymmetric array, we numerically explore the excitation of BIC and the evolution of the resulting Fano resonances. Then, we verify the distinct property of the polarization-independence of our design. Finally, by introducing optical gain medium to compensate for system losses, we successfully achieve dual-BIC mode lasing with ultra-low threshold and very narrow optical spectrum linewidth. In particular, the dominating mode of the laser is switched from one state to another when the pump power is higher than a certain value. Therefore, this novel symmetry-breaking technique opens up new possibilities for manipulating the behavior and properties of tetramer metasurfaces, offering promising applications in various fields such as efficient lasing, harmonic generation, biosensing, optical imaging, and entangled photon generation Liang2024 .
II Structure design
Fig. 1 displays the schematic of the proposed structure, which is composed of a square lattice of InGaAsP disk tetramers on a SiO2 substrate. The tetramer cluster is made up of four InGaAsP disks, each having the same geometry parameters and a periodicity of , as shown in Fig. 1a. The 3D view of the tetramer cluster is shown in Fig. 1b, allowing for a more immersive and realistic visualization of the structure. The disks possess radius and thickness , while the tetramer cluster is defined by periodicity . To break the in-plane geometric symmetry, an air hole with radius is introduced in the tetramer cluster as shown in Fig. 1a. Here, we shall introduce the parameter defining the degree of asymmetry of the overall system.

The quasi-BIC resonance can be detected and studied by analyzing either the transmission or reflection spectrum of the system Li2022 ; Quaranta2018 ; Yang2023 ; Novotny2012 . If the system contains quasi-BIC resonances, they will manifest as narrow peaks or dips in the transmission and reflection spectra, indicating resonant modes that enhance or suppress these wave components. This is especially true in the present case, where an all-dielectric structure has been considered, hence providing results free from any broad feature possibly related to the occurrence of absorption. In terms of the adopted computational approach, the finite difference time domain (FDTD) has been selected. In this respect, to guarantee accurate results, the boundary conditions are set to be periodic along the - and -direction to emulate the infinite planar wave and structural periodicity. Vice-versa perfectly matched layer (PML) is employed along the -direction to avoid that the outgoing electromagnetic field could reenter into the structure, hence determining misleading results. As light source was selected a transverse-electric (TE) plane wave impinging on the structure along the -axis (see Fig. 1c) having the electric field vector oriented along the -direction.
The tetramer cluster chosen for the present analysis is characterized by a period = 1200 nm and a height = 250 nm. Furthermore, the refractive index associated with the InGaAsP disks and the SiO2 substrate is set to 3.47 and 1.45, respectively. Importantly, the proposed structure can be experimentally fabricated owing to the well established fabrication techniques involving InGaAsP, a commonly used semiconductor material. In particular, electron-beam lithography (EBL) and molecular-beam epitaxy (MBE) Hwang2021 ; Kodigala2017 , can be employed to realize the structure shown in Fig. 1. Furthermore, the bandgap of InGaAsP can be tailored to specific wavelengths, thereby making this material one of the best candidates for the development of highly efficient lasers, such as edge-emitting lasers and vertical-cavity surface-emitting lasers (VCSELs) Yang1990 ; Behrend1998 .
III Results and discussions
III.1 Evolution of Fano resonance dominated by SP-BIC
Fig. 2a shows the mapping of the reflection spectra while changing the radius from 0 to 150 nm (correspondingly, ) while keeping R constant at 260 nm. When , the reflection spectrum in the range of 1400 to 1600 nm is close to zero, therefore presenting a high transmittance (none of the adopted materials is lossy). This result can be attributed to the presence of SP-BICs, which display resonances with infinitely narrow linewidth Zhang2018 ; Doeleman2018 . This is further confirmed by the observation that, as increases, the symmetry of the structure is disturbed and two resonances gradually appear in the reflection spectrum. This particular phenomenon can be attributed to the coupling of bound states to radiative channels, resulting in the excitation of two quasi-BICs. These modes have been marked by QBIC1 and QBIC2, the latter with a longer emission wavelength.
Interestingly, we notice a blue-shift of both BIC1 and BIC2 upon increase of , possibly due to the decrease of the effective refractive index of the structure Zhou2018 ; Lustig2023 . At the same time, their line widths become larger, indicating the degradation of the Q-factors of these two quasi-BIC modes. Finally, when the size of the air hole is increased even further, these two modes merge into one another, resulting in a phenomenon known as “degeneracy”. This implies that the characteristics of the two individual modes become indistinguishable or interchangeable. This merging of the modes can occur due to the increasing similarity in their respective wavelengths, allowing them to overlap and share common features Wang2020 . Fig. 2b shows the representative reflection spectra of the metasurface of the tetramer when 0 (black line), 0.15 (pink line), 0.32 (blue line) and 0.58 (green line), which confirms the analysis of Fig. 2a.

To confirm the resonance and calculate the Q-factor of BIC modes , we employ the conventional Fano formula Saadatmand2023 :
| (1) |
where represents the resonant frequency, a1, a2, and b are constants, and indicates the total damping rate and characterizes the Q-factor of the QBIC modes. The fitting reflection spectra for QBIC1 and QBIC2 modes, corresponding to = 0.15, are shown in Fig. 2c and d, respectively. Specifically, QBIC1 exhibits a resonance at 1511 nm with a Q-factor of 6946, while QBIC2 is centered at 1562 nm and possesses a Q-factor of 7800. These results are consistent with the numerical simulation outcomes, which are illustrated by the black solid lines in Fig. 2c and d, respectively.
Fig. 2e and f show the dependence of the Q factor of the two quasi-BIC modes on the asymmetry parameter (in log-log scale). The Q factors of these two resonant modes become very similar when , suggesting a mode degradation possibly leading to a loss of confinement. This is confirmed by the green line in Fig. 2b (), clearly showing two very broad linewidths associated to the two resonance modes. For this reason, here we shall focus on the region where . Furthermore, the two figures further stress the enhanced radiation loss occurring for high alpha values, by showing a steady Q factor decrease upon increase. When , both modes are BIC resonances and exhibit infinite Q factors. When a degree of asymmetry is introduced, the Q factors of both QBIC1 and QBIC2 remain high with values above . However, for a larger degree of asymmetry , the Q factor substantially decreases to , suggesting an augmented radiation loss of the tetramer metasurface. Furthermore, our study reveals that the Q factors of both modes exhibit a clear dependence on following an inverse quadratic law when , which is in line with the findings of previous studies Koshelev2018 ; Liu2019 , hence suggesting to be in the presence of SP-BICs.
Fig. 3 shows the simulated intensity distributions of the electromagnetic field of QBIC1 and QBIC2 in the (, )-plane, providing a clear visual representation of the spatial distribution of both modes under asymmetric conditions (). This visualization provides a better understanding of the resonances QBIC1 and QBIC2. As shown in Fig. 3a, for the QBIC1 mode we observe high electromagnetic intensity especially within the InGaAsP disks, with a distribution clearly resulting from a x-polarized impinging radiation. Conversely, for the QBIC2 mode, the electromagnetic radiation is primarily concentrated within the air holes (highlighted by dashed lines) and in the air region surrounding the InGaAsP disks. As already depicted in Fig. 2a, this results in the QBIC1 resonance being blue-shifted compared to the QBIC2 resonance (InGaAsP refractive index ) Vaity2021 ; Algorri2024 .

To better understand the properties of QBIC modes, the cartesian multipole decomposition method is employed to compute the scattering power for diverse multipole excitations. By integrating the displacement current density across the unit cell, a comprehensive portrayal of the far-field responses of electromagnetic sources is achieved. Subsequently, for a specified frequency, the total far-field scattered power is determined for all multipoles. Among these, the eight multipoles including the electric dipole (ED), the magnetic dipole (MD), the magnetic toroidal dipole (MTD), the electric toroidal dipole (ETD), the electric quadrupole (EQ), the magnetic quadrupole (MQ), the electric toroidal quadrupole (ETQ), and the magnetic toroidal quadrupole (MTQ), are defined by the following equations respectively Saadatmand2023 ; Tang2017 :
| (2) | |||
| (3) | |||
| (4) | |||
| (5) | |||
| (6) | |||
| (7) | |||
| (8) | |||
| (9) | |||
where represents the angular frequency, , and denote the position vectors and the speed of light, respectively. is the Dirac delta function, and the subscripts , take values , , . The scattered power associated with each multipole moment can be calculated from Ref. Huang2012 . They are expressed as
| (10) | |||
| (11) | |||
| (12) | |||
| (13) | |||
| (14) | |||
| (15) |
where , , , , , and denote the scattering power from the electric dipole, the magnetic dipole, the toroidal dipole, the electric quadrupole, the electric toroidal quadrupole, and the magnetic quadrupole, respectively Huang2012 .
The multipole decompositions of the structure for alpha=0.15 are depicted in Fig. 4. Specifically, Fig. 4a illustrates that for QBIC1 mode, the MQ is the dominant multipole, accompanied by partial contributions from the TD and MD. Notably, the contributions from other higher-order multipoles are significantly suppressed in this instance. Analogously, QBIC2 mode presents a similar property, with the MTQ remaining the dominant multipole and the TD contributing partially. In this case as well, the contributions from other higher-order multipoles are negligible, as shown in Fig. 4b.
The multipole analysis provides insights into the underlying mechanisms responsible for the dark mode behaviour associated with QBIC1 and QBIC2 at = 0 and for small values (see Fig. 2a). Specifically, from Fig. Fig. 4c, the evolution of the electric dipole (ED) multipole to QBIC1 and QBIC2 with changing is evident. The analysis reveals that the ED multipole increases with , which explains why a linearly polarized incident radiation cannot effectively excite the structure at = 0 or for small values, as observed in Fig. 2a. This is because linearly polarized radiation corresponds to an ED-like mode. Considering that, in addition to energy and momentum parallel to the structure surface, the symmetry of the incident radiation must also be conserved during mode transformation (such as when an incident radiation excites a mode), it becomes apparent that a linearly polarized radiation can best excite ED modes Algorri2022 . In turn, this means that a linearly polarized radiation can properly couple to the structure shown in Fig. 1 only at high values. This finding is confirmed by Fig. 4d, where the evolution of the MQ multipole is shown. The results say that at = 0 the main multipole is MQ (see Fig. 4a and Fig. 4b), a contribution that decreases by increasing , exactly the opposite found for the ED multipole.

In order to gain an even deeper understanding of the impact of the asymmetry, we further conduct an analysis on the electromagnetic field distributions of the QBIC1 and QBIC2 modes in (, )-plane for the structures with air hole size of 0.08, 0.23, and 0.39. As shown in Fig. 5a-c, we find that the maximum intensity of QBIC1 mode decreases with the size of the air holes (similar behaviour occurs also for QBIC2, as shown in Fig. 5d-f). The decreasing trend can be attributed to the reduction in the factor of the QBIC1 mode as already observed in Fig. 2c and d. Indeed, a lower -factor implies a weaker confinement for the electromagnetic field within the structure, thus resulting in the observed weakening of the field intensity. Furthermore, when comparing Fig. 5c and f, it is observed that the two resonances tend to converge towards a similar pattern, namely QBIC1 and QBIC2 somehow merge in a unique kind of mode, a behaviour matching with the results of Fig. 2a.

III.2 Polarization independent behaviour
To verify the polarization independent behaviour of the quasi-BIC resonances in the metasurface, it was calculated their reflection spectra with different excitation angles and for 0.15. The direction of polarization of the incident linearly polarized beam is defined by the angle () between the incident electric field and the -axis (see Fig. 6a). As shown in Fig. 6b, when the incident beam is polarized along the axis (i.e., ), the resonant wavelengths of QBIC1 and QBIC2 are 1512 nm and 1557 nm, respectively. As the polarization angle varies from to (see dashed arrow in the figure), the resonant wavelengths of both quasi-BIC modes remain nearly unchanged. This observation clearly indicates that the proposed metasurface shows polarization insensitivity when exciting the quasi-BIC resonances. This unique characteristic can be exploited to reduce, if not eliminate, the need for polarization calibration, thus offering greater flexibility for practical applications such as wireless communication systems, radar technology, and optical sensing Cui2024 ; Zhang2023 .

III.3 Dual mode lasing and characterization
Lasing action based on BICs or quasi-BICs in two-dimensional metasurface structures has recently garnered significant attention in the field of photonics Kodigala2017 ; Zhang2022 ; Heilmann2022 . These unique structures exhibit remarkable properties that enable the confinement and manipulation of light at the nanoscale, leading to potential advancements in lasers and optical devices Pavlov2018 . In the present context, the selected structure for realizing lasing from both the quasi-BIC modes is defined by = 0.15. Furthermore, since InGaAsP is a natural gain material, the imaginary part of its refractive index is considered through all the numerical simulations.
The gain medium can be well described as a four-energy-level system, and a semi-quantum framework is adopted to simulate the interaction between the electromagnetic fields and gain medium. Details about the population dynamics of each energy level within the gain medium, including the ground state and the three excited states, can be found in the Ref. Di2023 ; Zhang2022 . Similarly to the calculation of the quasi-BIC modes, the FDTD method is employed also for simulating the lasing effect, where a 4 ps plane wave pump pulse is deployed on the metasurface along -direction. The detailed parameters used in the simulation are described in Di2023 .
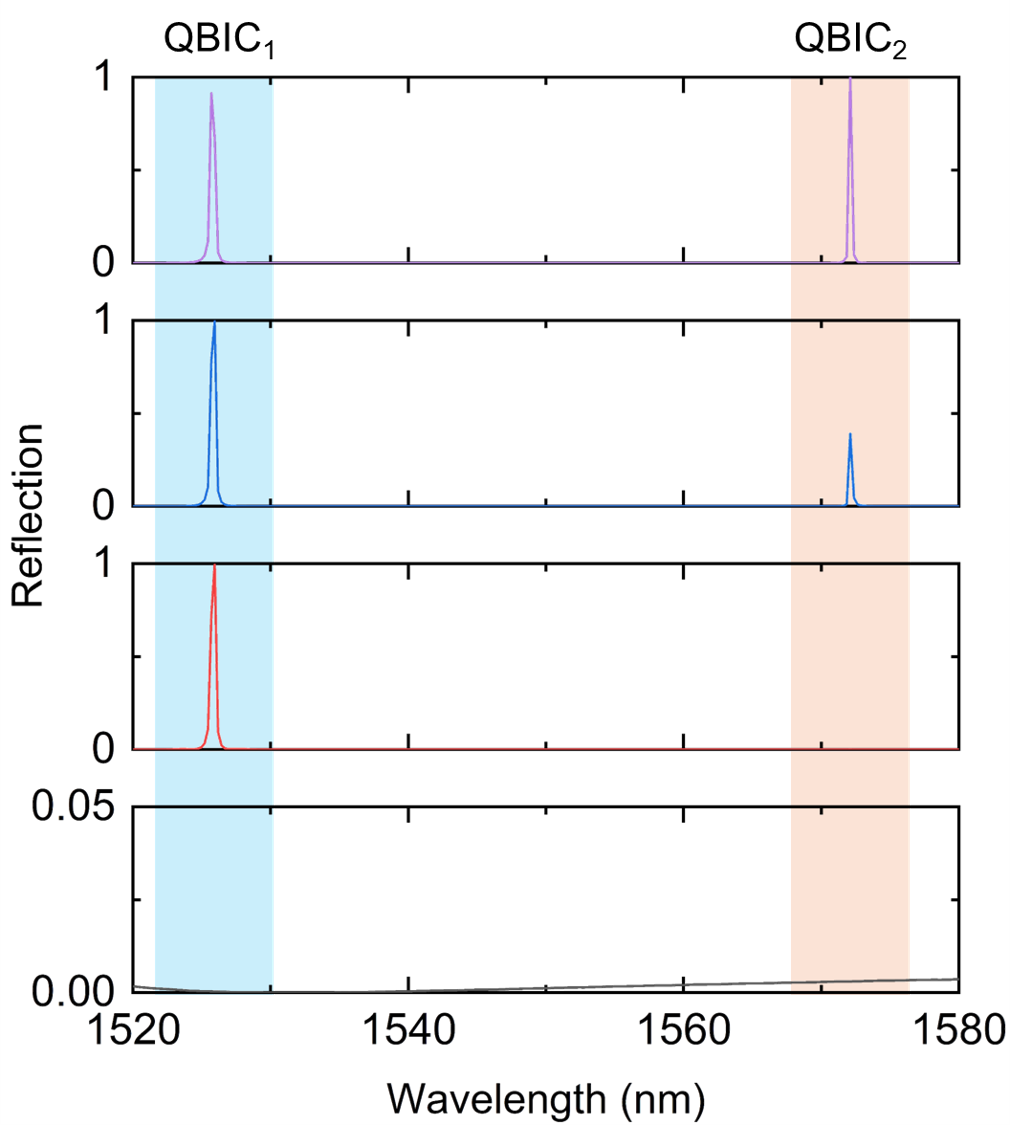
Fig. 7 shows the gain spectrum of the designed metasurface (black curve), the QBIC modes reflection spectra (blue curve) and their lasing emission (red curve), the latter being red-shifted against the reflection spectra due to the quantum efficiency of the gain medium. It is evident that the gain spectrum exhibits a wide linewidth, and its central region overlaps the peaks associated to the QBIC modes. So, this characteristic can guarantee that cavity losses are effectively compensated, enabling optimal laser operation Wang2017 ; Sun2021 .

Fig. 8 shows the normalized (i.e., divided by the maximum output value) input-output function curves of the QBIC1 (a) and QBIC2 (b) modes, providing a comprehensive understanding of their characteristic lasing behaviors. From these results, it is clear that the QBIC1 mode has a significantly lower lasing threshold compared to the QBIC2 mode, indicating that the QBIC1 mode requires substantially less input power to initiate the lasing action. In addition, both modes exhibit a consistent and proportionate growth with input power within the specified power range. This implies that the output of the system experiences a steady and uniform increase as the input power surpasses a certain threshold. The linear increment in output power enhances the overall performance of both modes and reaffirms their reliability and effectiveness in practical applications.

Fig. 9 presents the variation of lasing emission peaks with respect to pump power. These spectra provide valuable insights into the dynamic evolution of the lasing behavior of QBIC1 and QBIC2 modes. Specifically, when the laser operates below threshold at a pump power of V/m, no discernible mode is observed. As the pump power increases to V/m, the peak describing the lasing effect associated to the QBIC1 mode can be clearly observed, whereas no lasing effect associated to the QBIC2 mode is noticed due to the insufficient input power. The result is consistent with input-output function curves in Fig. 8. As the pump power is further elevated to V/m, the QBIC2 mode starts lasing as well, yet the QBIC1 mode remains the dominant mode, with its intensity continuously increasing and linewidth steadily decreasing (as indicated by the blue curve, representing the spectrum of the device at a pump power of V/m). Finally, when the pump power reaches V/m, the intensity of the QBIC2 mode surpasses that of the QBIC1 mode, signifying a mode-switching event.
IV Conclusions
In conclusion, we have demonstrated a polarization-independent laser emitter, working in the telecom-band, based on a tetramer metasurface capable of sustaining asymmetric BICs. This designed metasurface consists of four dielectric nanodisks with air holes positioned along the diagonal of the tetramer cluster, showing a symmetry-breaking effect in both vertical and horizontal directions. By gradually increasing the air hole diameter, two high Q-factor quasi-BIC modes were successfully generated. Finally, the effect of a gain medium inserted in the metasurface was analyzed in terms of lasing behaviour. Indeed, it was shown that by compensating the tetramer metasurface losses, an ultracompact laser device emitting in the telecom-band was achieved. In particular, the laser could operate at two different frequencies, corresponding to the two BICs modes sustained by the tetramer metasurface. This result is a significant achievement in the field of laser technology, as it opens up new possibilities for compact and efficient laser devices in the telecom-band range.
Acknowledgment
The authors would like to thank Prof. Yang Li and Dr. Yueyang Liu for their insightful discussion. T. W. was supported by Key Research and Development Plan of Shaanxi Province, China (Grant No. 2024GH-ZDXM-42), National Natural Science Foundation of China (Grant No. 61804036). R. P. Z. was supported by National Natural Science Foundation of China (Grant No. 32071317).
References
- (1) Jiajun Wang, Peishen Li, Xingqi Zhao, Dezhuan Han, Chao Peng, Lei Shi, Zhiyuan Qian, Xinhao Wang, Feifan Wang, Xinyi Zhou, and Jian Zi, “Optical bound states in the continuum in periodic structures: mechanisms, effects, and applications,” Photonics Insights, 3, R01, (2024).
- (2) C. W. Hsu, B. Zhen, A. D. Stone, J. D. Joannopoulos, and M. Soljačić, ”Bound states in the continuum,” Nature Reviews Materials, 1, 16048, (2016).
- (3) Z. Hu, D. Bongiovanni, D. Jukić, E. Jajtić, S. Xia, D. Song, J. Xu, R. Morandotti, H. Buljan, and Z. Chen, ”Nonlinear control of photonic higher-order topological bound states in the continuum,” Laser Photonics Rev., 10, 164 (2021).
- (4) S. Romano, G. Zito, S. N. Lara Yépez, S. Cabrini, E. Penzo, G. Coppola, I. Rendina, and V. Mocellaark, “Tuning the exponential sensitivity of a bound-state-in-continuum optical sensor,” Opt. Express, 27, 18776-18786, (2019)
- (5) C. W. Hsu, B. Zhen, J. Lee, S. L. Chua, S. G. Johnson, J. D. Joannopoulos, and M. Soljačić, “Observation of trapped light within the radiation continuum,” Nature, 499, 188-191, (2013).
- (6) S. Zhang, M. Zong, Y. Liu, Z. Wu, J. Lv, and Z. Xu, ”Independent dual-band bound states in the continuum supported by double asymmetric periodic gratings in germanium-based structure,” Laser Photonics Rev., 18, 2301206, (2024).
- (7) J. Y. Gao, J. Liu, H. M. Yang, H. S. Liu, G. Zeng, and B. Huang, “Anisotropic medium sensing controlled by bound states in the continuum in polarization-independent metasurfaces,” Opt. Express, 31, 44703-44719, (2023).
- (8) G. Sun, Y. Wang, Y. Li, Z. Cui, W. Chen, and K. Zhang, ”Tailoring topological nature of merging bound states in the continuum by manipulating structure symmetry of the all-dielectric metasurface,” Phys. Rev. B, 109, 035406, (2024).
- (9) C. Schiattarella, S. Romano, L. Sirleto, V. Mocella, I. Rendina, V. Lanzio, F. Riminucci, A. Schwartzberg, S. Cabrini, J. Chen, L. Liang, X. Liu, and G. Zito, “Directive giant upconversion by supercritical bound states in the continuum,” Nature, 626, 765-771, (2024).
- (10) S. Mohamed, J. Wang, H. Rekola, J. Heikkinen, B. Asamoah, L. Shi, and T. K. Hakala, “Controlling topology and polarization state of lasing photonic bound states in continuum,” Laser Photonics Rev., 16, 2100574, (2022).
- (11) H. Zhang, T. Wang, J. Tian, J. Sun, S. Li, I. De Leon, R. P. Zaccaria, L. Peng, F. Gao, X. Lin, H. Chen and G. Wang, “Quasi-BIC laser enabled by high-contrast grating resonator for gas detection,” Nanophotonics, 11, 297-304, (2022).
- (12) K. Koshelev, A. Bogdanov, and Y. Kivshar, “Meta-optics and bound states in the continuum,” Sci. Bull., 64, 836-842, (2019).
- (13) Y. Han, L. Xiong, J. Shi and G. Li, “Observation of tunable accidental bound state in the continuum in silicon nanodisk array,” Nanophotonics, 13(9), 1603-1609, (2024).
- (14) S. Joseph, S. Sarkar, S. Khan, and J. Joseph, “Exploring the optical bound state in the continuum in a dielectric grating coupled plasmonic hybrid system,” Adv. Optical Mater., 9, 2001895, (2021).
- (15) J. Lee, B. Zhen, S. L. Chua, W. Qiu, J. D. Joannopoulos, M. Soljačić, O. Shapira, “Observation and differentiation of unique high-Q optical resonances near zero wave vector in macroscopic photonic crystal slabs,” Phys. Rev. Lett., 109, 067401, (2012).
- (16) M. Kang, Z. Zhang, T. Wu, X. Zhang, Q. Xu, A. Krasnok, J. Han, and A. Alú, “Coherent full polarization control based on bound states in the continuum,” Nature Communications, 13, 4536, 2022.
- (17) H. Fan, J. Li, Y. Sun, X. Wang, T. Wu, and Y. Liu, “Asymmetric cross metasurfaces with multiple resonances governed by bound states in the continuum,” Materials, 16, 2227, (2023).
- (18) S. Campione, S. Liu, L. I. Basilio, L. K. Warne, W. L. Langston, T. S. Luk, J. R. Wendt, J. L. Reno, G. A. Keeler, I. Brener, and M. B. Sinclair, Broken symmetry dielectric resonators for high quality factor Fano metasurfaces,” ACS Photonics, 3, 2362-2367, (2016).
- (19) Z. Liu, Y. Xu, Y. Lin, J. Xiang, T. Feng, Q. Cao, J. Li, S. Lan, and J. Liu, “High-Q quasibound states in the continuum for nonlinear metasurfaces,” Phys. Rev. Lett., 123, 253901, (2019).
- (20) J. Xiang, Y. Xu, J. D. Chen and S. Lan, “Tailoring the spatial localization of bound state in the continuum in plasmonic-dielectric hybrid system,” Nanophotonics, 9(1), 133-142, 2020.
- (21) J. Feng, X. Wang, J. Cheng, and M. Zeng, “Polarization-independent bound state in the continuum without the help of rotational symmetry,” Opt. Lett., 48, 4829-4832, (2023).
- (22) Y. Liang, D. P. Tsai, and Y. Kivshar, “From local to nonlocal high-Q plasmonic metasurfaces,” Phys. Rev. Lett. 133, 053801, (2024).
- (23) Z. Li, Y. Xiang, S. Xu, and X. Dai, “Ultrasensitive terahertz sensing in all-dielectric asymmetric metasurfaces based on quasi-BIC,” J Opt. Soc. Am. B, 39, 286-291, (2022).
- (24) G. Quaranta, G. Basset, O. J. F. Martin, B. Gallinet, “Recent advances in resonant waveguide gratings,” Laser & Photonics Reviews, 12, 1800017, (2018).
- (25) H. Yang, X. Chen, E. Wu, P. Tang, L. Jing, F. Gao, H. Chen, and Z. Wang, “Off-resonance spin-locked metasurfaces empowered by quasi-bound states in the Continuum for optical analog computing,” Adv. Funct. Mater. 33, 2305110, (2023).
- (26) L. Novotny and B. Hecht, Principles of Nano-Optics, Cambridge University Press, (2006).
- (27) M. S. Hwang1, H. C. Lee1, K. H. Kim, K. Y. Jeong, S. H. Kwon, K. Koshelev, Y. Kivshar, and H. G. Park, “Ultralow-threshold laser using super-bound states in the continuum,” Nature Communications, 12, 4135, (2021).
- (28) A. Kodigala, T. Lepetit, Q. Gu, B. Bahari, Y. Fainman, and B. Kanté, “Lasing action from photonic bound states in continuum,” Nature, 541, 196-199, (2017).
- (29) L. Yang, M. C. Wu, K. Tai, T. TanbunEk, and R. A. Logan, “InGaAsP(1.3 m)/InP vertical-cavity surface-emitting laser grown by metalorganic vapor phase epitaxy,” Applied Physics Letters, 56, 889, (1990).
- (30) J. Behrend, J. F. Carlin, A. V. Sirbu, C. A. Berseth, A. Rudra, E. Kapon, “InAsP/InGaAsP periodic gain structure for 1.5 m vertical cavity surface emitting laser applications,” Journal of Crystal Growth, 188, 295-299, (1998).
- (31) Y. Zhang, A. Chen, W. Liu, C. W. Hsu, B. Wang, F. Guan, X. Liu, L. Shi, L. Lu, and J. Zi, “Observation of polarization vortices in momentum space,” Phys. Rev. Lett., 120, 186103, (2018).
- (32) H. M. Doeleman, F. Monticone, W. den Hollander, A. Alú, and A. F. Koenderink, “Experimental observation of a polarization vortex at an optical bound state in the continuum,” Nat. Photonics, 12, 397, (2018).
- (33) C. Zhou, G. Liu, G. Ban, S. Li, Q. Huang, J. Xia, Y. Wang, and M. Zhan, “Tunable fano resonator using multilayer graphene in the near-infrared region,” Appl. Phys. Lett., 112(10), 101904, (2018).
- (34) E. Lustig, O. Segal, S. Saha, E. Bordo, S. N. Chowdhury, Y. Sharabi, A. Fleischer, A. Boltasseva, O. Cohen, V. M. Shalaev, and M. Segev, “Time-refraction optics with single cycle modulation,” Nanophotonics, 12(12), 2221-2230, (2023).
- (35) X. Wang, S. Li, and C. Zhou, “Polarization-independent toroidal dipole resonances driven by symmetry-protected BIC in ultraviolet region,” Opt. Express, 28, 11983-11989, (2020).
- (36) S, B. Saadatmand, V. Ahmadi, and S. M. Hamidi, “Quasi-BIC based all-dielectric metasurfaces for ultra-sensitive refractive index and temperature sensing,” Sci Rep, 13, 20625, (2023).
- (37) K. Koshelev, S. Lepeshov, M. Liu, A. Bogdanov, and Y. Kivshar, “Asymmetric metasurfaces with high-Q resonances governed by bound states in the continuum,” Phys. Rev. Lett., 121, 193903, (2018).
- (38) P. Vaity, H. Gupta, A. Kala, S. D. Gupta, Y. S. Kivshar, V. R. Tuz, and V. G. Achanta, “Polarization-independent quasibound states in the continuum,” Adv. Photonics Res., 3, 2100144, (2022).
- (39) T. J. Cui, S. Zhang, A. Al, et al., “Roadmap on electromagnetic metamaterials and metasurfaces,” J. Phys. Photonics, 6, 032502, (2024).
- (40) X. Zhang, M. Dai, W. Deng, Y. Zhang and Q. J. Wang, “A broadband, self-powered, and polarization-sensitive PdSe2 photodetector based on asymmetric van der Waals contacts,” Nanophotonics, 12, 607-618, (2023).
- (41) J. F. Algorri, V. Dmitriev, H. E. Herná ndez-Figueroa, L. Rodrí guez-Cobo, F. Dell’Olio, A. Cusano, J. M. Løpez-Higuera, D. C. Zografopoulos, ”Polarization-independent hollow nanocuboid metasurfaces with robust quasi-bound states in the continuum,” Optical Materials, 147, 114631, (2024).
- (42) C. Tang, B. Yan, Q.Wang, J. Chen, Z. Yan, F. Liu, N. Chen, and C. Sui, “Toroidal dipolar excitation in metamaterials consisting of metal nanodisks and a dielectrc spacer on metal substrate.” Sci. Rep. 7, 582, (2017).
- (43) Y. W. Huang, W. T. Chen, P. C. Wu, V. Fedotov, V. Savinov, Y. Z. Ho, Y. F. Chau, N. I. Zheludev, and D. P. Tsai, “Design of plasmonic toroidal metamaterials at optical frequencies,” Opt. Express, 20, 1760-1768, (2012).
- (44) J. F. Algorri, F. Dell’Olio, P. Roldán-Varona, L. Rodrĺguez-Cobo, J. M. López-Higuera, J. M. Sánchez-Pena, V. Dmitriev, and D. C. Zografopoulos, “Analogue of electromagnetically induced transparency in square slotted silicon metasurfaces supporting bound states in the continuum,” Opt. Express, 30, 4615-4630, (2022).
- (45) H. Zhang , T. Wang, J. Tian , J. Sun , S. Li , I. De Leon , R. P. Zaccaria , L. Peng , F. Gao , X. Lin , H. Chen and G. Wang, “Quasi-BIC laser enabled by high-contrast grating resonator for gas detection,” Nanophotonics, 11, 297-304, (2022).
- (46) R. Heilmann, G. Salerno, J. Cuerda, T. K. Hakala, P. Törmä, “Quasi-BIC mode lasing in a quadrumer plasmonic lattice,” ACS Photonics, 19, 9, 224-232, (2022).
- (47) A. Pavlov, I. Zabkov, and V. Klimov, “Lasing threshold of the bound states in the continuum in the plasmonic lattices,” Opt. Express, 26, 28948-28962, (2018).
- (48) W. Di, T. Wang, X. Gao, H. Wang, Q. Fang, C. Qian, H. Qian, H. Chen, and T. Wang “Quasi-BIC lasing at telecom wavelengths and its potential application in biosensing,” IEEE Sensors Journal, 24, 238-245, (2024).
- (49) X. Y. Wang , Y. L. Wang , S. Wang , B. Li , X. W. Zhang , L. Dai, and R. M. Ma, “Lasing enhanced surface plasmon resonance sensing,” Nanophotonics, 6(2), 472-478, (2017).
- (50) J. Sun, T. Wang, Z. Jafari, F. Gao, X. Lin, H. Chen, G. Wang, and I. De Leon, “High-Q plasmonic crystal laser for ultra-sensitive biomolecule detection,” IEEE Journal of Selected Topics in Quantum Electronics, 27, 4601407, (2021).