Emitter-Optomechanical Interaction in Ultra-High-Q hBN Nanocavities

Light-matter coupling between one or more quantum emitters and the photonic mode in a nanocavity is the central pillar of cavity QED experiments. This coupling provides the spin-photon interface as the basic building block from which nanophotonic quantum devices and circuits are built [1, 2, 3, 4]. Recently, cavity optomechanics has emerged in which the coupling between photonic and mechanical (phononic) modes allows coherent phonons to be controlled via photons, or vice versa [5, 6, 7, 8, 9]. Such cavity optomechanics opens up entirely new perspectives for applications in ultra-precise sensing and meteorology, as well as building nano-opto-electro-mechanical devices with novel functionalities [10, 11, 12].

In particular, quantum emitters simultaneously coupled to cavity photonic and mechanical modes realize an interface between spin, photons and phonons as a hybrid quantum node. However, the experimental exploration of such multi-modal systems remains a challenge. For traditional emitters such as quantum dot and transition metal dichalcogenides, the coupling of electronic and mechanical degrees of freedom is weak, and thereby, typically studied in acoustic cavities [13, 14, 15]. In such system, the mechanical vibration is controlled by extrinsic driving, rather than the intrinsic light-matter coupling. This limits the exploration of coupled mode physics and transduction between different degrees of freedom.

The light-matter coupling for traditional emitters can be described by the Jaynes-Cummings model [16] where the electronic transition couples directly to the optical field without the participation of phonons. In contrast, the charged boron vacancy $V_{B}^{-}$ in hexagonal boron nitride hBN is a recently explored quantum emitter [17, 18, 19, 20, 21] that has a weak zero-phonon line, emission instead being dominated by phonon-induced processes [22, 23, 24, 25]. This is indicative of robust electron-phonon polarons that couple to the optical field, thereby intertwining electronic, phononic and photonic degrees of freedom. By creating $V_{B}^{-}$ centers in an hBN nanobeam cavity [26, 27], we realize a novel emitter-optomechanical system for which $V_{B}^{-}$ related phonon polaritons couple electronic transitions, cavity photonic modes and cavity mechanical modes.

We investigate the emitter-optomechanical system using spatially resolved photoluminescence (PL) and Raman spectroscopy. A pronounced spectral asymmetry is observed in the PL from the cavity photonic mode, only when the Q-factor is above a threshold of $\sim$10⁴. To explain this asymmetry, we construct a numerical model based on $V_{B}^{-}$ [22, 23, 24, 25] for which the light-matter coupling is induced by the phonons. Our model accounts well for the experiment, in contrast to expectations based on the Jaynes-Cummings model. Furthermore, we demonstrate the strong interaction between phonon-induced $V_{B}^{-}$ emission and optomechanical cavity modes by spatially correlating luminescence in freely suspended structures [28] and resonantly exciting the cavity photonic mode [7]. In position-dependent measurements, we observe anticrossings and phonon polaritons induced by the nanomechanical vibrations. When subject to resonant excitation, the Raman signals arising from $V_{B}^{-}$ phonons exhibit an asymmetric enhancement for red and blue detunings, corresponding to cooling and heating of the cavity mechanical modes, respectively [7]. This reveals that the cavity mechanical modes induce the coupling between cavity photons and $V_{B}^{-}$ phonons.

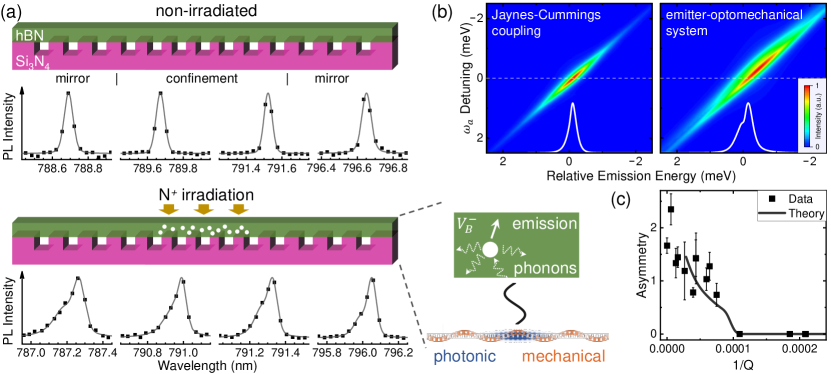
The structure of our hBN/Si₃N₄ nanobeam cavity is schematically depicted in Fig. 1(a). Fabrication procedures are presented in supplement Sec. I A. The confinement for nanophotonic modes is achieved by locally chirping the photonic crystal periodicity around the cavity center. Besides the photonic modes, the cavity also supports nanomechanical modes, since the hBN/Si₃N₄ nanobeam is freely suspended but clamped at both ends [27]. Representative photonic and mechanical modes are depicted in Fig. 1(a) in blue and orange, respectively. We investigate two samples in this work that differ with respect to the area over which $V_{B}^{-}$ centers are created. In Sample-A, a 30 keV N⁺ ion beam of $10^{13}$ $\mathrm{ions/cm^{2}}$ fluence (dose) creates $V_{B}^{-}$ centers only within the volume of photonic mode (Fig. 1(a) bottom). The phonon-induced emission of $V_{B}^{-}$ [22, 23, 24, 25] gives rise to a spectrally broad emission, even at low temperature [17], and coupling of local phonon modes to the optical transitions of $V_{B}^{-}$ center. Thereby, phonons of the cavity mechanical modes may reasonably be expected to impact on the $V_{B}^{-}$ emission. This cavity-$V_{B}^{-}$ system involves couplings between electronic transitions, $V_{B}^{-}$ phonons, cavity photons and cavity nanomechanical vibrations, as a multi-modal emitter-optomechanical system depicted schematically in Fig. 1(a).

We continue by comparing the emission spectral form observed from the cavities with and without irradiation. All cavities are excited using a 532nm cw-laser having a spot size $\sim 1\ \mathrm{\mu m}$ and a power $\sim 120\ \mathrm{\mu W}$. The cavity photonic mode is hence excited by the emission of $V_{B}^{-}$ centers in hBN (irradiated) and/or filtered light arising from other native luminescent defects in the hBN and underlying Si₃N₄ (non-irradiated). The cavity mode exhibits high Q-factor $\sim 10^{5}$ limited only by the spectral resolution of our detection system [26]. Remarkably, for the N⁺ irradiated cavities we observe a strongly asymmetric lineshape of cavity emission that is broadened on the short wavelength (high energy) side. Typical spectra recorded from four representative cavities without and with irradiation are presented in the upper and lower panels of Fig. 1(a), respectively. We identify this asymmetry as arising from strong photon-phonon coupling [7, 30, 8]. To quantitatively account for this spectral asymmetry, we construct a model in which a 2-level emitter simultaneously couples to cavity photons and local phonons. The Hamiltonian of the multi-modal cavity QED system can then be written as

including the 6 terms corresponding to the emitter, photon, phonon, emitter-phonon coupling with a strength $\lambda_{e\text{-}q}$, photon-phonon coupling with a strength $\lambda_{p\text{-}q}$, and emitter-photon coupling, respectively [16]. $\sigma_{A,B}$ ($A,B\in\{X,G\}$) is the Dirac operator for the emitter with the ground ($G$) and excited ($X$) state, $a^{+}$/$a$ are the ladder operators for cavity photons, and $q^{+}$/$q$ are the ladder operators for phonons. Since the $V_{B}^{-}$ emission is dominated by phonon-induced processes [22, 23, 24, 25], we introduce an effective phonon-induced emitter-photon coupling

where $g$ is the coupling strength and $k$ is the number of phonons involved the coupling. $k=0$ corresponds to the conventional Jaynes-Cummings model applied for usual emitters dominated by zero-phonon line emission, where the phonons only introduce vibronic sublevels to mediate the emitter-photon coupling, but do not directly participate. In contrast, $\textit{H}_{e\text{-}p}$ with $k\geq 1$ represents an entirely different but coherent interface of emitter, photon and phonon, in which the phonon is necessary to induce the emitter-photon coupling.

We calculated the spectral form of the emission from the cavity photonic mode by solving the master equation (for details see supplement Sec. I D). Typical spectra in the case of $k=0$ and $k=4$ are presented in Fig. 1(b), as the energy detuning between 2-level emitter and cavity photonic mode is varied. The white curves show the spectral form at resonance $\omega_{a}=\omega_{X}$. The asymmetry in the emission lineshape is suppressed for the Jaynes-Cummings coupling ($k=0$) but becomes pronounced in the emitter-optomechanical interaction ($k=4$). Despite the model being rather simple, it captures the essential physics underpinning our experimental observations. As presented in Fig. 1(a), we do not observe any asymmetry in any of our control experiments where the hBN was not irradiated with N⁺. This is the central result of this work, showing that the phonons involved in the photon-phonon coupling are not thermally excited, but rather arise during the light-matter coupling of $V_{B}^{-}$ centers. As such, they give rise to a novel emitter-induced optomechanical coupling.

We note that the asymmetric cavity lineshape is only observed for high-Q irradiated cavities. We use bi-peak fitting to quantify the asymmetry via the ratio between the intensity of two peaks (for details see supplement Sec. I C) and present the results in Fig. 1(c). A threshold Q-factor of $\sim 10^{4}$ is clearly observed, meaning that the $V_{B}^{-}$-induced photon-phonon coupling rate needs to exceed the system decay rate to observe the asymmetric lineshape. This threshold behavior is well reproduced in the theoretical calculation, as presented by the solid line in Fig. 1(c) for the case $k=4$.

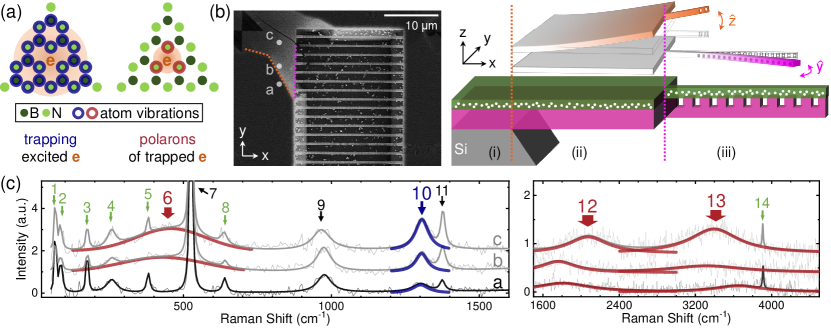
Generally, as schematically depicted in Fig. 2(a), two different phonon processes are involved in the $V_{B}^{-}$ emission process: Firstly, the negatively charged electronic state $V_{B}^{-}$ is generated by trapping an excited electron that relaxes via phonon-assisted processes [31, 32]. Secondly, the excited electron decays again as the polaron with localized phonons to produce a broad phonon sideband in the PL spectrum. The electron-phonon spatial overlap [33, 34] depicted schematically in Fig. 2(a) indicates that, extended phonons involving the vibration of multiple atoms around $V_{B}^{-}$ (blue rings) govern the trapping photo-physics, whilst more localized phonons primarily involving neighboring atoms (red rings) dominate the polarons. J. Li et al. [29] recently reported Raman studies of $V_{B}^{-}$ and unveiled these extended and highly localized phonons via boron isotope characterization.

To confirm this picture for $V_{B}^{-}$ emission in Fig. 2(a) and the interaction with mechanical modes in nanocavities, we recorded spatially resolved PL and Raman spectroscopy from another sample (Sample-B) that is homogeneously irradiated by 30 keV N⁺ ions with a fluence (dose) of $10^{14}\ \mathrm{ions/cm^{2}}$ [25, 35, 36] as depicted in Fig. 2(b). Sample-B contains three different regions of interest: (i) the non-underetched region with hBN on a planar Si₃N₄/Si substrate corresponding to the dark surrounding region in the SEM image, (ii) the large suspended membrane with hBN/Si₃N₄ layers suspended on underetched Si corresponding to the large bright region at left top, and (iii) suspended nanobeam cavities. Typical Raman spectra recorded from three different positions labelled $a$-$c$ in Fig. 2(b) are presented in Fig. 2(c). The observed Raman features are labelled 1-14. Peaks 7 and 9 at 524 and 975 $\mathrm{cm^{-1}}$ are the bulk Si₃N₄ phonons [37]. Peak 11 at 1377 $\mathrm{cm^{-1}}$ is the bulk hBN phonon $E_{2g}$ [29]. The other peaks are not observed in Si₃N₄ nor non-irradiated hBN (see supplement Sec. II B). Hence, they are indentified as being related to the $V_{B}^{-}$ centers. Peak 6 around 450 $\mathrm{cm^{-1}}$ (red curve) is the highly localized phonon, and peak 10 at 1306 $\mathrm{cm^{-1}}$ (blue) is the extended phonon depicted in the context of Fig. 2(a), which have been previously identified [29]. We observe two other broad Raman features at higher energies: peak 12 around 1800 $\mathrm{cm^{-1}}$ (quadruple of peak 6) and peak 13 around 3600 $\mathrm{cm^{-1}}$ (double of peak 12). Broader Raman linewidth typically implies stronger spatial confinement of the phonon mode [38, 39, 40]. In addition, peaks 6, 12 and 13 are the only $V_{B}^{-}$ phonons exhibiting distinguishable energy shifts when moving the laser spot e.g., between the three positions in Fig. 2(c). These common features indicate that peaks 12 and 13 stem from multi-phonon states of peak 6, and are also highly localized at the $V_{B}^{-}$ center. Peaks 1-5, 8 and 14 are discussed in supplement Sec. III B, due to they exhibit little correlation to the $V_{B}^{-}$ emission.

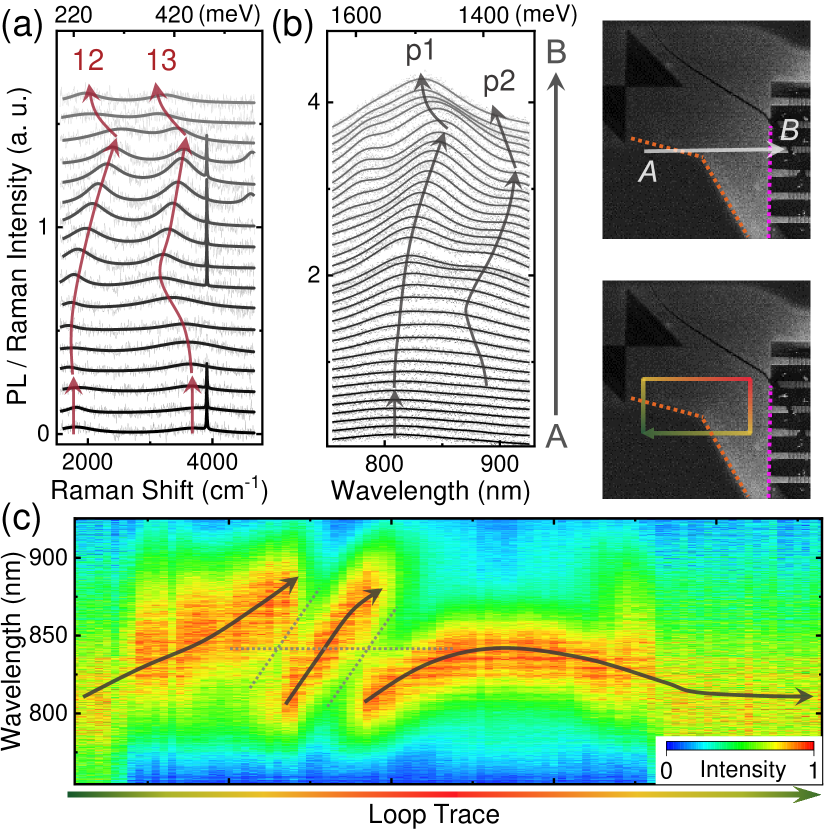
In Fig. 3(a)(b), we present Raman and PL spectra of $V_{B}^{-}$ recorded from positions along the line $A\rightarrow B$ illustrated in the inset. This line includes the three regions (i)-(iii) depicted in Fig. 2(b). Position-dependent energy shifts of the Raman and PL peaks in the three regions are marked with the arrows. Their generic shifts exhibit remarkable correlations i.e., the shifts of Raman peak 12 and 13 in Fig. 3(a) track the shifts of PL peak p1 and p2 in 3(b). This observation strongly suggests that PL peak p1 and p2 are phonon sidebands arising from the highly localized phonons Raman peak 12 and 13. Moreover, we observe that the position-dependent shifts of PL peaks and $V_{B}^{-}$ phonons exhibit pronounced anticrossings. Fig. 3(c) shows PL spectra recorded from various positions along a closed clockwise loop on the sample illustrated in the inset. As depicted by the dashed lines in Fig. 3(c), two anticrossings are observed at which one spectral feature disappears and is replaced by another. This combined with the identity of spectra at the beginning and end of loop provide strong evidence for the phonon polaritons induced by the position-dependent mechanical modes. Similar feature and anticrossings between highly localized phonons are also observed from the spatially resolved Raman spectra (see supplement Sec. II E), further supporting this conclusion.

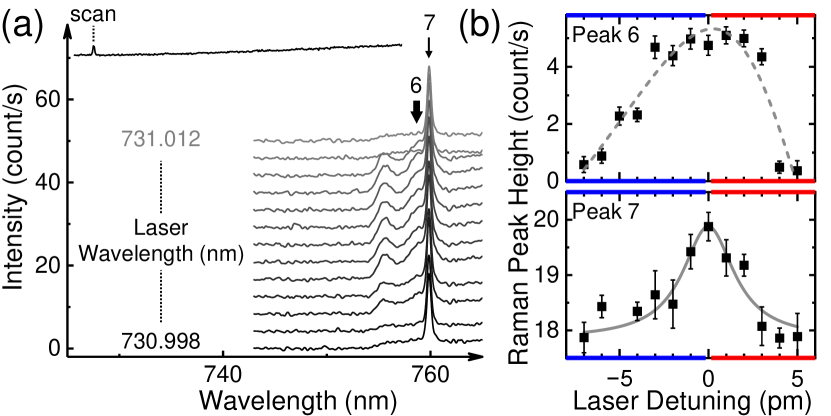
Finally, we explore the emitter-optomechanical interaction by controlling the optomechanical cavity modes via resonant excitation of the cavity itself. Hereby, the spectrum is detected as a narrowband ($\leq 1$MHz) cw-laser is tuned from 730.998 and 731.012 nm encompassing an ultra-high-Q cavity photonic mode at $\sim$ 731 nm. Typical results obtained from such resonant excitation are presented in Fig. 4(b) which shows the intensity of Raman peak 6 and 7 as a function of laser-cavity detuning. The population of photons in the cavity is enhanced for both red and blue detunings. The enhanced cavity photons couple to the phonons of Si₃N₄ and $V_{B}^{-}$ thus enhance the corresponding Raman signals [41]. In contrast, the population of cavity mechanical phonons is reduced at red detunings (cooling) but enhanced at blue detunings (heating) [7]. As presented in Fig. 4(b) upper panel, the enhancement of peak 6 arising from $V_{B}^{-}$ phonon is pronounced, varying by $>10\times$ as the laser is tuned through the cavity photonic mode. Moreover, this enhancement is asymmetric with respect to detuning, being weaker with the cooling of cavity vibrations (red detuning) but stronger with the heating (blue detuning). This observation reveals that the cavity mechanical modes induce the coupling between cavity photons and $V_{B}^{-}$ phonons [27]. In contrast, the enhancement of Si₃N₄ phonon peak 7 is much weaker ($10\%$) and nearly symmetric, indicating that the cavity photons couple to Si₃N₄ phonon directly without the participation of cavity vibrations.

In summary, we report on the interaction between $V_{B}^{-}$ centers and optomechanical modes in a hBN nanocavity. PL and Raman data demonstrate the $V_{B}^{-}$-induced cavity optomechanical coupling and the control of $V_{B}^{-}$ transitions and polarons through cavity optomechanics. This emitter-optomechanical interaction stems from the ultra-high Q-factor of our nanocavity and the phonon-induced light-matter coupling. These results reveal that the coupling between multiple degrees of freedom arise from the intrinsic phonon processes in the system. The phononic features are strong since hBN is an atomically thin layered material that is highly sensitive to local deformation [42, 43, 44, 45]. Our work extends cavity QED to the regime where electronic systems are simultaneously coupled to both phononic and photonic degrees of freedom. We believe that such hybrid interface in nanosystem will open up interesting perspectives for quantum sensing and meteorology, as well as quantum transduction.