Emergent Spinon Dispersion and Symmetry Breaking in Two-Channel Kondo Lattices

The screening of a magnetic impurity by the conduction electrons in a metal is governed by the Kondo effect. The multichannel version is when several channels compete for a single impurity, as a result of which the spin is frustrated and a new critical ground state formed with a fractional residual impurity entropy. In the two-channel case, this entropy $\frac{1}{2}\log 2$ corresponds to a Majorana fermion. If the channel symmetry is broken, the weaker channels decouple and the stronger-coupled channels win to screen the impurity at low temperature Andrei and Destri (1984); Affleck et al. (1992); Emery and Kivelson (1992); Affleck and Ludwig (1993).

While the case of a single impurity is well understood, much less is known about Kondo lattices where a lattice of spins is screened by conduction electrons Hewson (1993); Si et al. (2014); Coleman (2015), especially if multiple conduction channels are involved Cox and Jarrell (1996). The most established fact is the prediction of a large Fermi surface (FS) in the Kondo-dominated regime of the single-channel Kondo lattice Oshikawa (2000). In the multichannel case, the continuous channel symmetry naturally leads to new patterns of entanglement which are potentially responsible for the non-Fermi liquid physics Jarrell et al. (1996, 1997), symmetry breaking, and possibly fractionalized order parameter Komijani et al. (2018). This partly arises from the fact that the residual entropy seen in the impurity has to eventually disappear at zero temperature in the case of a lattice.

Beside fundamental interest, a pressing reason for studying this physics is that the multichannel Kondo lattice (MCKL), and in particular 2CKL, seems to be an appropriate model for several heavy-fermion compounds, e.g. the family of PrTr₂Zn₂₀ (Tr=Ir,Rh) Onimaru and Kusunose (2016); Patri and Kim (2020) as well as recent proposals that MCKLs may support nontrivial topology Hu et al. (2021); Kornjaca et al. (2021) and non-Abelian Kondo anyons Lopes et al. (2020); Komijani (2020).

The MCKL model is described by the Hamiltonian

where $H_{c}=-t_{c}\sum_{\left\langle ij\right\rangle}(c^{\dagger}_{i\alpha a}c^{\vphantom{\dagger}}_{j\alpha a}+\mathrm{H.c.})$ is the Hamiltonian of the conduction electrons and Einstein summation over spin $\alpha,\beta=1\dots N$ and channel $a,b=1\dots K$ indices is assumed. This model has SU($N$) spin and SU($K$) channel symmetries and we are interested in analyzing the effect of a channel symmetry breaking $H\to H+\sum_{j}\Delta\vec{J}_{j}\cdot\vec{\cal O}_{j}$, where $\vec{\cal O}_{j}\equiv(\vec{S}_{j}\cdot c^{\dagger}_{ja}\vec{\sigma}c^{\vphantom{\dagger}}_{jb})\vec{\tau}_{ab}$ and $\vec{\tau}$’s act as Pauli matrices in the channel space Hoshino et al. (2011). At first look, at least certain deformation of the MCKL can be thought of as a channel magnet. (A naïve strong coupling limit is not a spin-singlet, but the Nozières doublet. See supplementary materials SM for a deformation that changes this.) In the $J_{K}\to\infty$ limit SM , the spin is quenched due to formation of Kondo singlet with either (for $K=2$) of the channels, leading to a doublet over which $\vec{\cal O}$ acts like $\vec{\tau}$ Schauerte et al. (2005); SM . Interaction among adjacent doublets leads to a “channel magnet” $H_{\rm eff}\propto\frac{t^{2}}{J_{K}}\sum_{\left\langle ij\right\rangle}\vec{\cal O}_{i}\cdot\vec{\cal O}_{j}$. While channel Weiss-field favors a channel anti-ferromagnetic (channel AFM) super-exchange interaction, the mean-field theory predicts a variety of channel ferromagnetic (channel FM) and channel AFM solutions [Fig. 1(b)] depending on the conduction filling.

On the other hand, some differences to a channel magnet are expected since the winning channel has a larger FS Komijani et al. (2018); Wugalter et al. (2020) and the order parameter $\vec{\cal O}$ is strongly dissipated by coupling to fermionic degrees of freedom. Although a channel-symmetry broken ground state is predicted by both single-site dynamical mean-field theory (DMFT) Hoshino et al. (2011); Hoshino and Kuramoto (2015) and static mean-field theory Van Dyke et al. (2019); Zhang et al. (2018); Wugalter et al. (2020), it has not been observed in recent cluster DMFT studies Inui and Motome (2020). Furthermore, the effective theory of fluctuations in the large-$N$ limit Wugalter et al. (2020) predicts a disordered phase below the lower critical dimension but the nature of this quantum paramagnet is unclear. In 1D, Andrei and Orignac have used non-Abelian bosonization to show Andrei and Orignac (2000) that the ground state is gapless and fractionalized (dispersing Majoranas for $K\!=\!2$), a prediction that contradicts the analysis by Emery and Kivelson Emery and Kivelson (1993), and has not been confirmed by the density matrix renormalization group calculations Schauerte et al. (2005).

Resolving these issues requires a technique that is applicable to arbitrary dimensions and goes beyond static mean field and DMFT by capturing both quantum and spatial fluctuations. Here, we show that the dynamical large-$N$ approach, recently applied successfully to study Kondo lattices Rech et al. (2006); Komijani and Coleman (2018, 2019); Wang et al. (2020); Shen et al. (2020); Wang and Yang (2021); Drouin-Touchette et al. (2021); Han et al. (2021), is precisely such a technique.

We assume the spins transform as a spin-$S$ representation of SU($N$). In the impurity case We use 0D to refer to the impurity problem , the spin is fully screened for $K=2S$ whereas it is overscreened and underscreened for $K>2S$ and $K<2S$, respectively Zinn-Justin and Andrei (1998). The focus of this Letter is on the Kondo-dominated regime of the double-screened case $K/2S=2$ which is schematically shown in Fig. 1(a). We use Schwinger bosons $S_{j\alpha\beta}=b^{\dagger}_{j\alpha}b^{\vphantom{\dagger}}_{j\beta}$ to form a symmetric representation of spins with the size $2S=b^{\dagger}_{j\alpha}b^{\vphantom{\dagger}}_{j\alpha}$. We then rescale $J_{K}\to J_{K}/N$ and treat the model (1) in the large-$N$ limit, by sending $N,K,S\to\infty$, but keeping $s=S/N$ and $\gamma=K/N=4s$ constant. The constraint is imposed on average via a uniform Lagrange multiplier $\mu_{b}$.

In the present large-$N$ limit, the Ruderman-Kittel-Kasuya-Yosida (RKKY) interaction is $\mathrm{O}(1/N)$ [inset of Fig. 2(a)] and we need to include an explicit Heisenberg interaction $H\to H+J_{H}\sum_{\left\langle ij\right\rangle}\vec{S}_{i}\cdot\vec{S}_{j}$ between nearest neighbors $\left\langle ij\right\rangle$ to couple the impurities. Nevertheless, we will show that an infinitesimal $J_{H}$ is sufficient to produce significant magnetic correlations due to a novel variant of RKKY interaction. For simplicity we limit ourselves to ferromagnetic correlations $J_{H}<0$.

For a ${\cal V}$ site lattice, the Lagrangian becomes Parcollet and Georges (1997); Komijani and Coleman (2018)

Here, $b$’s are bosonic spinons and $\chi$’s are Grassmannian holons that mediate the local Kondo interaction. In momentum space, the electrons and bosons have dispersions $\epsilon_{k}=-2t_{c}\cos k-\mu_{c}$ and $\varepsilon_{k}=-2t_{b}\cos k-\mu_{b}$, respectively. $t_{b}$ is the (assumed to be homogeneous) nearest neighbor hopping of spinons due to large-$N$ decoupling of $J_{H}$ term Komijani and Coleman (2018). Here, we focus on a half-filled conduction band $\mu_{c}=0$, but similar results are obtained at other commensurate fillings SM . In the large-$N$ limit the dynamics is dominated by the non-crossing Feynman diagrams, resulting in boson and holon self-energies [$\vec{r}\equiv(j,\tau)$]

whereas $\Sigma_{c}$ is $\mathrm{O}(1/N)$ and thus the electrons propagator $G_{c}^{-1}(k,{\rm z})={\rm z}-\epsilon_{k}$ remains bare, with ${\rm z}$ complex frequency. Equations (3) together with the Dyson equations $G_{b}^{-1}(k,{\rm z})={\rm z}-\varepsilon_{k}-\Sigma_{b}(k,{\rm z})$ and $G_{\chi,a}^{-1}(k,{\rm z})=-J_{K,a}^{-1}-\Sigma_{\chi}(k,{\rm z})$ form a set of coupled integral equations that are solved iteratively and self-consistently, while $\mu_{b}$ is adjusted to satisfy the constraint. Thermodynamic variables are then computed from Green’s functions Rech et al. (2006); Komijani and Coleman (2018).

First, we study the case in which $J_{H}$ is absent, or $\varepsilon_{k}=-\mu_{b}$. In this limit, the self-energies remain local $\Sigma_{b,\chi}(n,\tau)\to\delta_{n0}\Sigma_{b,\chi}(\tau)$ and the problem reduces to the impurity problem Parcollet and Georges (1997). It has never been studied whether the large-$N$ overscreened impurities are susceptible to symmetry breaking Affleck et al. (1992). To do so, we assume that half of $K$ channels are coupled to the impurity with $J_{K}+\Delta J$ and the other half with $J_{K}-\Delta J$. This corresponds to a uniform symmetry breaking deformation $\Delta{\cal L}=(\Delta J/J_{K}^{2})\sum_{j}[\bar{\chi}_{j1}\chi_{j1}-\bar{\chi}_{j2}\chi_{j2}]$ of the Lagrangian.

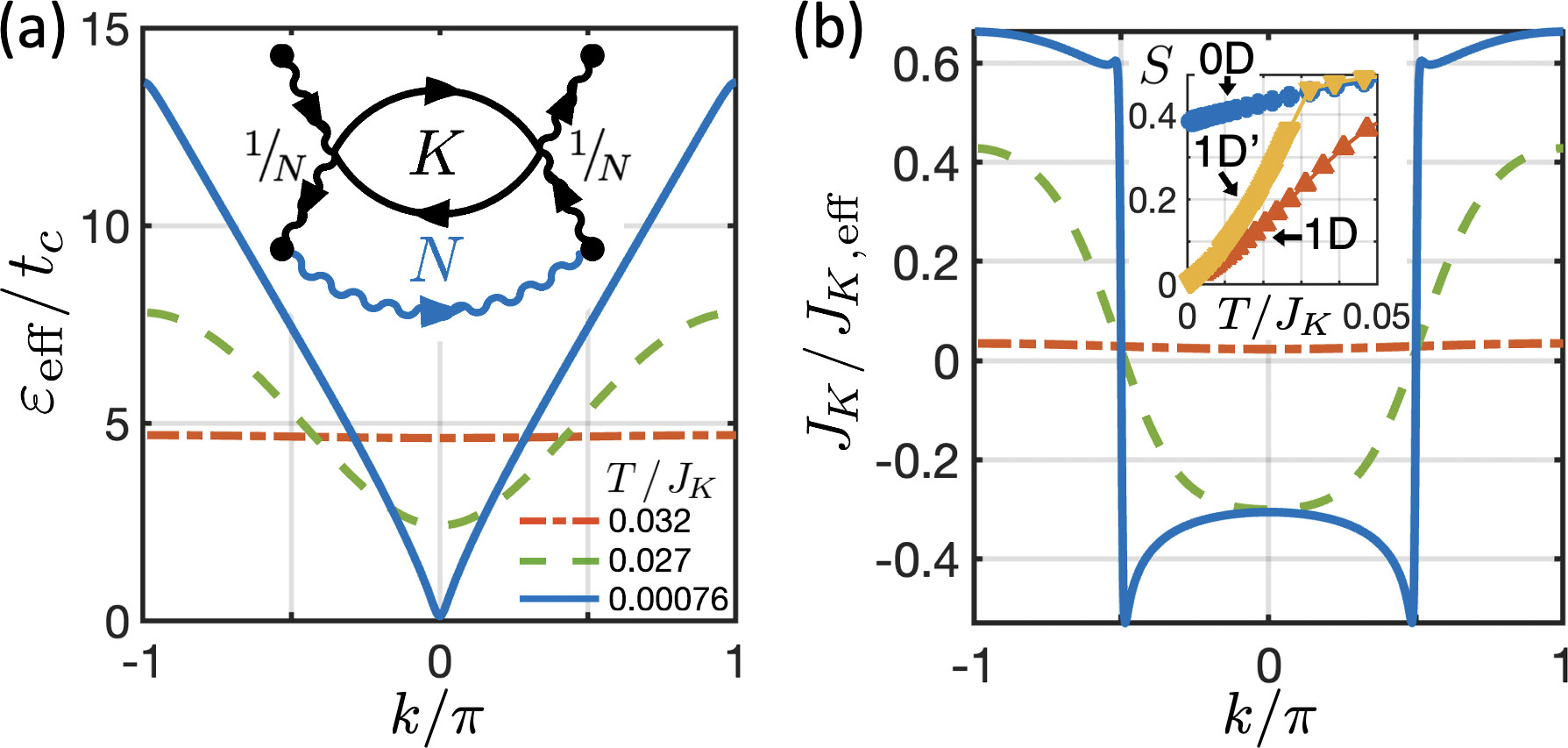
Figure 1(c) shows the entropy of the 2CK impurity model as a function of channel asymmetry, verifying that the impurity is indeed critical with respect to channel symmetry breaking. In symmetric 2CK, the ground state entropy at large-$N$ is fractional with a universal dependence on $(\gamma,s)$ Parcollet and Georges (1997); SM .

Next, we focus on finite $t_{b}$ case for two settings of 1D and $\infty\text{D}$, which correspond to a Bethe lattice with coordination numbers $z=2$ and $z=\infty$. In 1D, $G(k,{\rm z})$ and $\Sigma(k,{\rm z})$ depend on $k$ and ${\rm z}$, but in $\infty\text{D}$, self-energies have no spatial dependence and the Green’s functions of spinons/electrons obey $G_{b,c}^{-1}={\rm z}+\mu^{\vphantom{\dagger}}_{b,c}-\Sigma^{\vphantom{\dagger}}_{b,c}({\rm z})-t_{b,c}^{2}G^{\vphantom{\dagger}}_{b,c}$.

Importantly, the criticality of overscreened impurity solution ensures that an infinitesimal spinon hopping seed $t_{b}\sim 0$ can get an O(1) amplification [inset of Fig. 2(a)] and dispersions for spinons and holons are dynamically generated. Restricting ourselves to translationally invariant solutions with lattice periodicity ${\rm a}$, this effect can be succinctly represented by the zero-frequency spinon and holon effective dispersion $J_{K,{\rm eff}}^{-1}(k)\equiv-{\rm Re}[G_{\chi}^{-1}(k,\omega=0)]$ and $\varepsilon_{\rm eff}(k)\equiv-{\rm Re}[G_{b}^{-1}(k,\omega=0)]$, shown in Figs. 2(a) and 2(b) for various temperatures. This emergent spinon dispersion is independent of the choice of the seed and agrees qualitatively with the finite $t_{b}$ results SM . The consumption of the residual entropy in the lattice by the emerging dispersion is visible in the inset of Fig. 2(b). We stress that in 1D, this apparent transition most likely becomes a crossover when N is finite Read (1985). In the case of $\infty$D, the system is prone to spin or channel magnetization, as discussed later. Such symmetry breakings would consume the residual entropy SM .

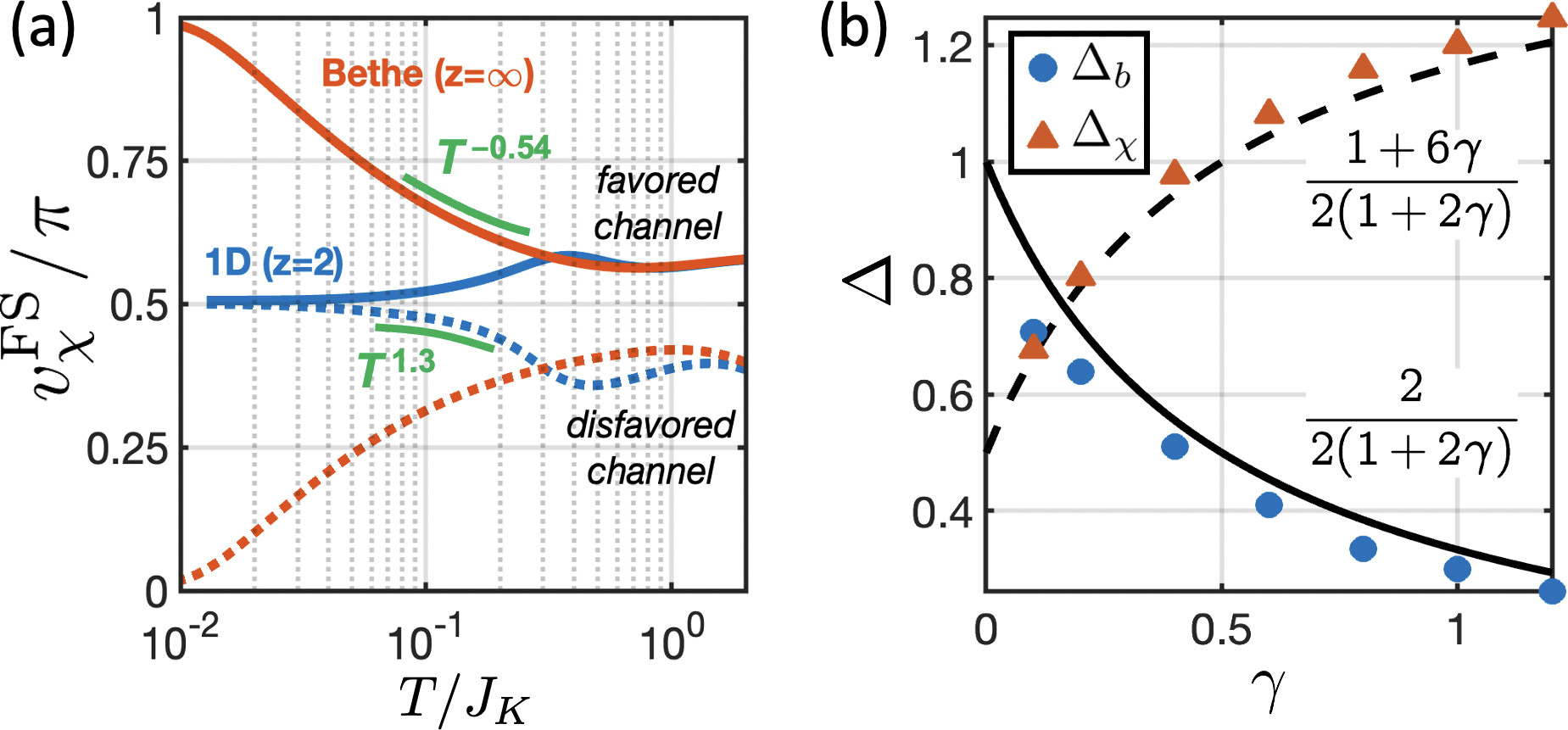
Figures 3(a) and 3(b) shows the finite frequency spectral function of spinons and holons, respectively. Both are dominated by a sharp mode with emergent Lorentz invariance. The spinons are gapless and linearly dispersing and the holons form a FS. The temperature collapse of Fig. 3(c) confirms that the spectra are critical with the local spectra obeying a $T^{1-2\Delta_{b,\chi}}G^{\prime\prime}_{b,\chi}(x=0,\omega)=f_{b,\chi}(\omega/T)$ behavior. Figure 3(d) shows similar collapse for the case of infinite-coordination Bethe lattice ($\infty$D). A marked difference between the two cases is that $\Delta_{\chi}>1/2$ for 1D, which leads to $-G^{\prime\prime}_{\chi}$ minima at $\omega\sim 0$, whereas $\Delta_{\chi}<1/2$ in $\infty$D, manifested as a peak at $\omega\sim 0$.

What is the effect of channel symmetry breaking on the volume of FS? According to Luttinger’s theorem, the FS volume is related to electron phase shift $v_{a}^{\mathrm{FS}}={\cal V}^{-1}\sum_{k}{\delta_{a}(k)}$ for a $d$ dimensional lattice. From $K=4S$ case of the Ward identity Coleman et al. (2005), the electron phase shift is related to that of holons $N\delta_{c,a}(k)=\delta_{\chi,a}(k)$, which itself is defined as

The locus of points at which $J^{-1}_{K,{\rm eff}}(k)$ changes sign defines a holon FS which generalizes to any dimension. In 1D, holons are occupied for $\left|k\right|<\pi/2$. So, we find that $v_{\chi,a}^{\mathrm{FS}}=2\pi S/K=\pi/2$ and the total change in electron FS is $N\Delta v_{c,a}^{\mathrm{FS}}=\pi/2$, corresponding to a large FS in the critical phase. We use Eq. (4) to study the effect of a uniform symmetry breaking field $\Delta{\cal L}$. Figure 4(a) shows how FSs of slightly favored and disfavored channels evolve as a function of $T$ in the two cases. In 1D, the FS asymmetry disappears, restoring a channel symmetric criticality at low $T$, consistent with the Mermin-Wagner theorem. On the other hand, in $\infty$D the asymmetry grows and one channel totally decouples from the spins, with gapped spinons and also gapped holons for both channels. The exponents are related to $\Delta_{\chi}$; varying $\Delta J$ in Eq. (4) we find

Assuming $\left|G_{\chi}(\vec{r})\right|\sim\left|\vec{r}\right|^{-2\Delta_{\chi}}$, the holon FS is unstable against symmetry breaking when $G^{\prime\prime}_{\chi}(k_{F},0+i\eta)\sim T^{2\Delta_{\chi}-d-1}$ diverges. This $2\Delta_{\chi}<d+1$ regime coincides with when the symmetry breaking term $\Delta J$ is relevant, in the renormalization group (RG) sense. On the other hand instability of the entire holon FS requires the divergence of $G^{\prime\prime}_{\chi}(x=0,0+i\eta)\sim T^{2\Delta_{\chi}-1}$, i.e. $2\Delta_{\chi}<1$ which is a more stringent condition and agrees with Fig. 4(a), confirming $\Delta_{\chi}=1/2$ as the marginal dimension.

Figure 4(a) shows that the symmetry breaking $\Delta{\cal L}$ is relevant in $\infty$D, but is irrelevant in 1D. To establish this from the microscopic model, one has to access the infrared (IR) fixed point. From the numerics we see that the system flows to a critical IR fixed point, in which spinons and holons are critical in addition to electrons. For an impurity $G_{b}\sim\left|\tau\right|^{-2\Delta_{b}}$ and $G_{\chi}(\tau)\sim\left|\tau\right|^{-2\Delta_{\chi}}$ are reasonable at $T=0$. The exponents are known Parcollet and Georges (1997); SM :

and coincide with those of the $\infty$D in the small $t_{b}$ regime we are interested here SM . In the presence of a dimensionless $\lambda_{0}=\Delta J/\rho J_{K}^{2}$, the RG analysis $d\lambda/d\ell=(1-2\Delta_{\chi})\lambda$ predicts a dynamical scale $w\sim T_{K}\lambda_{0}^{1+\gamma}$ [cf. Fig. 1(c)].

The 1D case is more subtle; as $T\to 0$, we see from Fig. 2 that $J^{-1}_{K,\mathrm{eff}}(\pm k_{F})\to 0$ and $\varepsilon_{\rm eff}(0)\to 0$ at the IR fixed point This is not the case for the spinon’s $\pi$-mode, $\varepsilon_{\rm eff}$≠0() (±π/a). This means that the Kondo coupling flows to strong coupling at $\left|k\right|<k_{F}$, to weak coupling at $\left|k\right|>k_{F}$, and gets critical at $k=\pm k_{F}$, while the spinons are gapless at $k\!=\!0$. At these momenta, the Dyson equation has the scale-invariant form $G_{b}\Delta\Sigma_{b}|_{k\sim 0}=G_{\chi}\Delta\Sigma_{\chi}|_{k\sim\pm k_{F}}=-1$.

We can obtain a low-energy description by expanding fields near zero energy, e.g. $\psi(x)\sim e^{ik_{F}x}\psi_{R}+e^{-ik_{F}x}\psi_{L}$ for electrons and holons. In 1+1 dimensions, the conformal invariance of the fixed point dictates the following form for the $T=0$ Green’s functions $G(x,\tau)=G(z,\bar{z})$:

where $z=v\tau+ix$ and $\bar{\rho}=2s/{\rm a}$. The $G_{cR/L}$ is obtained from $G_{\chi R/L}$ by $\Delta_{\chi}\to 1/2$. These Green’s functions can be conformally mapped to finite-$T$ via $z\to({\beta}/{\pi})\sin({\pi z}/{\beta})$ replacement. Furthermore, in terms of $q=k+i\omega/v$, they have the Fourier transforms:

where $\zeta_{n}(\Delta)\equiv 2^{1-2\Delta}\Gamma(1-\Delta+n/2)/\Gamma(n/2+\Delta)$. From matching the powers of frequency in Eqs. (3), (7) and (8), we conclude that $\Delta_{b}+\Delta_{\chi}=3/2$ in order to satisfy the self-consistency. Moreover, from the matching of the amplitudes of the Green’s functions we find SM

Note that $\Delta_{\chi}>1/2$, ensuring that channel symmetry breaking perturbations are irrelevant in 1D. These are in excellent agreement with the exponents extracted from $\omega/T$ scaling [Fig. 4(b)] and we have established a semianalytical framework to interpolate between 1D and $\infty\text{D}$.

The emergent dispersion in Fig. 2, the scaling dimensions in Eq. (9), and their relation to symmetry breaking in Fig. 4 are the central results of this Letter. In the following we discuss some of the implications of these results for physical observables that are independent of our fractionalized description, leaving the details to SM .

The fractionalization $S_{\alpha\beta}\sim b^{\dagger}_{\alpha}b^{\vphantom{\dagger}}_{\beta}$ or $b^{\dagger}_{\alpha}c^{\vphantom{\dagger}}_{a\alpha}\sim\chi_{a}$ contraction are related to order parameter fractionalization Komijani et al. (2018); Tsvelik and Coleman (2021). In the long time/distance limit, correlation functions of $b^{\dagger}_{\alpha}c^{\vphantom{\dagger}}_{a\alpha}$ and that of $\chi^{\vphantom{\dagger}}_{a}$ are given by $\Sigma_{\chi}$ and $G_{\chi}$, respectively and thus, have exponents that add up to zero. On the other hand, correlators of gauge-invariant operators ${\cal X}_{ab}\equiv\bar{\chi}_{a}\chi_{b}$ and ${\cal O}_{ab}\equiv b^{\dagger}_{\alpha}b^{\vphantom{\dagger}}_{\beta}c^{\dagger}_{b\beta}c^{\vphantom{\dagger}}_{a\alpha}$ are exactly equal since both can be constructed by taking derivatives of free energy with respect to $\Delta J^{ab}$, either before or after Hubbard-Stratonovitch transformation. A diagrammatic proof of this equivalence is provided in SM . Scaling analysis gives $\chi_{\mathrm{ch}}(x=0)\sim T^{4\Delta_{\chi}-1}$ and $\chi_{\mathrm{ch}}^{\rm 1D}(q=0)\sim T^{4\Delta_{\chi}-2}$ up to a constant shift coming from the regular part of free energy.

Another nontrivial feature of 2CK impurity fixed point is its magnetic instability Affleck et al. (1992) whose large-$N$ incarnation is $\Delta_{b}<1/2$ for the impurity (or $\infty\text{D}$) in Eq. (6). From Eq. (9), we see that this also holds for 1D 2CKL for $\gamma>1/2$. This is reflected in the divergence of the uniform $\chi_{m}(q=0)$ static magnetic susceptibilities as a function of $T$. Using scaling analysis $\chi_{m}^{\mathrm{1D}}(q=0)\sim T^{4\Delta_{b}-2}$ and $\chi_{m}(x=0)\sim T^{4\Delta_{b}-1}$ up to a constant shift, in good agreement with numerics SM . Note that this critical spin behavior is different from the gapped spin sector observed in Emery and Kivelson (1993); Schauerte et al. (2005), but is qualitatively consistent with Andrei and Orignac (2000).

Lastly, the fact that the fixed point discussed above is IR stable follows from the fact that the interaction is exactly marginal due to $\Delta_{b}+\Delta_{\chi}=3/2$ and that vertex corrections remain $\mathrm{O}(1/N)$. The 1+1D correlators (7) can be obtained from three sets of decoupled Luttinger liquids for each of the $c,b,\chi$ fields with fine-tuned Luttinger parameters that give the correct exponents. Such a spinon-holon theory will have a Virasoro central charge $c_{0}/N=1+\gamma$. On the other hand the coset theory of Andrei and Orignac (2000); Azaria et al. (1998); SM predicts $c_{AO}/N=\gamma/(1+\gamma)$. We have used $T\to 0$ heat-capacity and the excitation velocities $v$ to compute the central charge according to $C/T=(\pi k_{B}^{2}/6v)c$ as a function of $\gamma$ and found $c=c_{0}$ SM . Note that there is no contradiction with the $c$-theorem since the UV theory is not Lorentz invariant due to ferromagnetism. The discrepancy with $c_{AO}$ is likely rooted in inability of Schwinger bosons to capture gapless spin liquids Arovas and Auerbach (1988).

In summary, we have shown that the dynamical large-$N$ approach can capture symmetry breaking in multichannel Kondo impurities and lattices in the presence of both emergent and induced ferromagnetic correlations within an RG framework with explicit examples on 0D, 1D, and $\infty$D. The scaling analysis enables an analytical solution to the critical exponents and susceptibilities which are in good quantitative agreement with numerics, and is applicable to higher dimensional CFTs. A determination of the upper and lower critical dimensions and the effect of antiferromagnetic correlations are left to a future work Ge and Komijani .

Acknowledgment—The authors acknowledge fruitful discussions with P. Coleman and N. Andrei. This work was performed in part at Aspen Center for Physics, which is supported by NSF Grant No. PHY-1607611. Computations for this research were performed on the Advanced Research Computing Cluster at the University of Cincinnati, and the Penn State University’s Institute for Computational and Data Sciences’ Roar supercomputer.