Emergent Recurrent Extension Phase Transition in a Quasiperiodic Chain
Abstract
We study -wave superconducting quasiperiodic chains with staggered potential. The result shows a counter-intuitive phase transition phenomenon, i.e., recurrent extension phase transition (REPT). By analyzing the participation ration and scaling behavior, we prove the existence of REPT phenomenon, which, in concrete terms, means that the system will repeatedly return from the intermediate phase to the extended phase as the quasiperiodic or staggered strength grows. Furthermore, our finding is also quite different from the traditional understanding of intermediate phase (composed only of the pure extended phase and pure localized phase) in that, the new intermediate phase described here, stemming from the competition between staggered potential and -wave pairing, actually falls into three types by bringing in the critical phase. To be specific, the new intermediate phases are composed of the critical + extended states, the critical + localized states, and the critical + extended + localized states, respectively.
I Introduction
In the late 1950s, G. Feher and E. A. Gere of Bell Laboratories first discovered the relaxation of electron spin GFeher1959a ; GFeher1959b . To explain this phenomenon, P. W. Anderson proposed the famous Anderson Localization theory that when metal doping exceeds the threshold value, conductivity of the system will change dramatically from the metallic phase to the insulating phase PWAnderson1958 . Later in the 1960s, N. F. Mott pointed out that the localized state and the extended state can coexist in some cases, giving rise to mobility edge in the system NFMott1967 . According to the scaling theory of disordered systems, when the system dimension , any strength of disorder will nudge the system into the localized phase, leaving the system’s metallic-insulating phase transition to be destroyed EAbrahams1979 ; PALee1985 ; FEvers2008 ; BHetenyi2021 . However, when , such phase transition is allowed by increasing the disorder strength and adjusting the Fermi energy before the critical disorder strength due to the presence of the mobility edge. Disorder-induced Anderson localization in low-dimensional systems is trivial, but its application to the study of topological phase transitions JLi2009 ; CWGroth2009 ; HMGuo2010 ; EJMeier2018 ; DWZhang2020b ; GGLiu2020 ; SStutzer2018 ; WZhang2021 ; ANava2023 , many-body localization APal2010 ; DAHuse2013 ; DJLuitz2015 ; RNandkishore2015 ; EAltman2015 ; FAlet2018 ; DAbanin2019 , and etc. reveals many novel phenomena.
Compared with random disordered systems, quasiperiodic systems that entail less numerical computation and relatively convenient analytical deduction have been widely used to study Anderson localization and mobility edges. Meanwhile, quasiperiodic systems have been implemented on many experimental platforms, including photonic crystal YLahini2009 ; YEKraus2012 ; MVerbin2013 ; MVerbin2015 ; PWang2020 , optical waveguide arrays SAGredeskul1989 ; DNChristodoulides2003 ; TPertsch2004 , cold atom experiments GRoati2008 ; GModugno2010 ; MLohse2016 ; SNakajima2016 ; HPLuschen2018 ; FAAnK2021 , and other related fields DTanese2014 ; PRoushan2017 ; FAAn2018 . As a typical low-dimensional quasiperiodic model, the Aubry-André-Harper (AAH) chain has been extensively studied over the past few decades PGHarper1955 ; SAubry1980 . This can be attributed to the self-duality property of the AAH model, which means the distribution of its eigenfunctions in both real space and momentum space is exactly the same for the critical point. Based on this, one can easily obtain the critical point of phase transition through analytical deduction SAubry1980 , so as to well grasp the characteristics of the extended and localized phase transition.
Previous theoretical studies have suggested that the mobility edge of AAH model can be achieved by introducing a long-range hopping JBiddle2010 ; XDeng2019 ; NRoy2021 , a dimer hopping SRoy2021 ; LZhou2022 , a spin-orbit coupling MKohmoto2008 ; LZhou2013 , or a controlled quasiperiodic potential SGaneshan2015 ; YWang2020a ; XLi2017 ; HYao2019 ; APadhan2022 . Then in recent experiments, the above mobility edge phenomenon has been realized in different platforms one after another HPLuschen2018 ; QLin2022 ; JGao2023 . Besides, duality transformation JBiddle2010 ; SGaneshan2015 ; MGoncalves2023 ; MGoncalves2022a ; MGoncalves2022b and the famous Avila global theory AAvila2015 ; XCZhou2022 ; YWang2020a ; YWang2021a ; YLiu2021a ; YLiu2021b ; YLiu2021c ; YCZhang2022a ; YCZhang2022b ; ZHWang2022 ; ZHXu2022 ; YWang2022c ; SLJiang2023 ; XWei2023 provide us with an analytical alternative to deal with mobility edges. In addition to the mobility edge caused by the coexistence of the traditional extended and localized state, quasiperiodic systems are capable of inducing novel mobility edges. As mentioned above, this is because the phase transition critical point in AAH model features self-duality, which causes the corresponding eigenstate to be a multifractal critical state, neither extended nor localized. Here, the system shows a multifractal critical phase, obviously different from the energy level statistics TGeisel1991 ; SYJitomirskaya1999 , wave function distribution TCHalsey1986 ; ADMirlin2006 , and dynamic behavior of the pure extended and localized phases HHiramoto1988 ; RKetzmerick1997 . Though the multifractal critical behaviors of the system at the critical point seem very attractive, its application in experiments is limited due to the highly demanding techniques in preparation. Recent years have witnessed lively discussions on how to stretch the critical point out to a critical region, with an aim to improve the robustness of the system in the multifractal critical phase. By introducing -wave superconducting pairing JWang2016 ; MYahyavi2019 ; TLiu2021a ; JFraxanet2022 , spin-orbit coupling YWang2022a ; YWang2022b , off-diagonal quasiperiodic hopping FLiu2015 ; JCCCCestari2016 ; LWang2017 ; TLiu2021b ; LZTang2021 ; TXiao2021 ; YCZhang2022a ; XCZhou2022 ; LZTang2022 and other means YCZhang2022b ; XLin2022 ; SZLi2022 , the multifractal critical region has been successfully wrought. The emergence of critical states has enriched the concept of mobility edges, and novel energy-dependent mobility edges for the coexistence of critical, extended and localized states have been predicted in many studies in recent years YWang2022a . In addition to localization phase transitions, the AAH model is also valuable for the study of topological phases in quasicrystals, for it can be mapped to the two-dimensional integer quantum Hall effect by means of a continuous U(1) metric transformation FMei2012 ; YEKraus2012a ; YEKraus2012b ; LJLang2012 ; XCai2013 ; SGaneshan2013 ; FLiu2015 ; MNChen2016 ; JCCCCestari2016 ; LWang2017 ; QBZeng2020 ; LZTang2021 ; TXiao2021 ; LZTang2022 ; PHe2022 ; DWZhang2020a ; HJiang2019 .
So far, fruitful results have been achieved in the study of quasiperiodic systems, and the most remarkable among them is multiple re-localization, i.e., by manipulating quasiperiodic parameters, repeated re-localization can emerge in the system VGoblot2020 ; SRoy2021 ; APadhan2022 ; WHan2022 ; LZhou2022 ; YWang2022b ; RQi2023 ; EGuan2023 ; ZLu2023 ; HWang2023 ; SGanguly2023 ; XPJiang2023 . However, no paper has yet proved or disproved whether an ever-growing quasiperiodic strength will bring the system back from the localized or intermediate phases (coexistence of different states) to the extended phase. So what is the real-world situation? To find out the answer, we study the phase transition of the -wave superconducting paired AAH model with staggered on-site potential. The results demonstrate the novel intermediate-extended phase transition, which proves the system will indeed revert from the intermediate phase to the extended phase as the quasiperiodic strength grows. Furthermore, the introduction of staggered potentials also enables the emergence of new-types mobility edges.
The paper is organized as follows. We introduced the model in Sec. II. We discuss observable quantities and the recurrent extension phenomenon in Sec. III. Then, we investigate the emergent intermediate phases through various observable quantities and the corresponding scaling analysis in Sec. IV. Main findings of this paper are concluded in Sec. V.
II Model
We start from the -wave superconducting paired AAH model with the staggered on-site potential and the corresponding Hamiltonian reads
| (1) |
where () is the annihilation (generation) operator at site , is the total number of lattices, corresponds to the strength of the nearest neighboring hopping, and denotes the intensity of -wave pairing. The on-site potential is composed of two parts. One is the quasiperiodic part , where stands for the quasiperiodic strength, and indicate the irrational number and phase shift DWZhang2018 , respectively. The other one is the staggered potential , where refers to the intensity of the staggered potential.
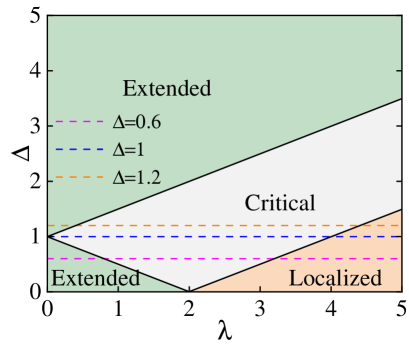
Under the condition of and , Eq. (1) can be reduced to the standard AAH model PGHarper1955 ; SAubry1980 , whose critical point of phase transition is . When and , the system becomes the -wave superconducting paired AAH model and the phase diagram is exhibited in Fig. 1, where the line of separates the localized from the critical phase, while the line of draws a distinction between the critical and the extended phases JWang2016 . When and , however, the system will exhibit re-entrant localized phase transition APadhan2022 .
In the particle-hole picture, one can diagonalize the Hamiltonian Eq. (1) by Bogoliubov-de Gennes (BDG) transformation AKitaev2001 , and then we obtian
| (2) |
where with the energy level index . and denote the two components of the wave function at site . The eigenspectra and the corresponding eigenstates are determined by Schrödinger equation , where Hamiltonian is a matrix of . The expression takes the form
| (3) |
where
| (4) |
| (5) |
For periodic boundary conditions (PBCs),
| (6) |
while for open boundary conditions (OBCs),
| (7) |
The dimension of the corresponding BDG Hamiltonian is . During numerical calculation, we set the system size , where stands for the -th Fibonacci number, which satisfies , and . Besides, the irrational number is set as . Without loss of generality, we take as the unit of energy and select periodic boundary conditions in the process of calculation. Since the value of has no qualitative impact on the system, we set in the following analysis.
III Recurrent Extension Phase Transition
III.1 Phase diagram for
Inverse participation ratio (IPR) and normalized participation ratio (NPR) are the core observables to determine the localization properties of the system SRoy2021 ; XLi2020 ; APadhan2022 ; XLi2017 , whose definitions take the form
| (8) |
where represents the eigenstate index, and denote the expansion coefficients of the -th eigenstate at site on the BDG basis. By calculating the average IPR and the average NPR , one can determine the extended, localized and intermediate phases, respectively. In concrete terms, the extended (localized) phase corresponds to () and (). For the intermediate phases, however, both and are of finite values due to the coexistence of different states in the system XLi2017 . Based on this, one can define
| (9) |
to distinguish the pure phase (pure extended or pure localized phase) from the intermediate phase SRoy2021 ; XLi2020 ; APadhan2022 . In the following analysis, we set , where the dimension of the BDG Hamiltonian matrix corresponding to the system is greater than . So the intermediate phase (pure phase) corresponds to ().
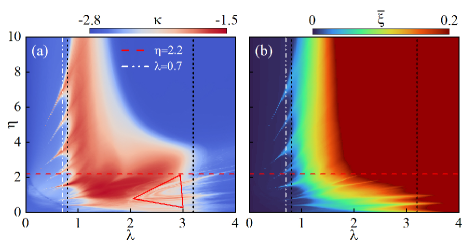
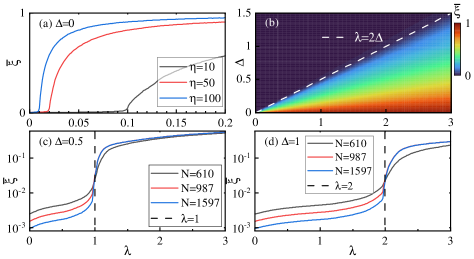
The phase diagram for is plotted in Fig. 2. As is shown, corresponds to the case with no staggered potential, i.e., the system will gradually move from the extended, critical, and eventually into the localized phase, with the critical points of phase transition being and (black dashed lines), respectively, which corresponds to purple dashed line in Fig. 1.
The introduction of staggered potential will bring about richer phases. Firstly, different from the pure extended phase that emerges in the standard -wave superconducting AAH model, the introduction of staggered potential will give rise to mobility edges and the intermediate phase for . Specifically, within a certain parameter range (around ), the emergent recurrent extension occurs, i.e., the system transforms from the extended phase to intermediate phase and then back to the extended phase with an increasing quasiperiodic strength (red dashed line in Fig. 2). This REPT phenomenon can be clearly seen from the and average IPR phase diagrams on the plane, as shown in Fig. 2. In the figure, one can also find that with the increase of , there are still several other regions in the system where REPT occurs, however, the value of should not be taken too large. We show in the following part of the paper that when tends to infinity, REPT phenomenon will disappear and the system will display a clear transition boundary between extended and localized phase.
Secondly, in the region of (between two black dashed lines, when is of critical phase), when the staggered potential intensity is relatively large (), the system is easier to enter the localized phase with the increasing . However, when is relatively small, there exists a region with a large fluctuation of , which is marked by red triangular in Fig. 2(a). Due to the unusual features of fluctuation, one can naturally expect new intermediate phases and the corresponding mobility edges in this region. We will discuss such regions in the next section.
Thirdly, for , the quasiperiodic potential will prevail. Now that the staggered on-site potential does not have much leverage on it, the system always stays in the localized phase.
Besides, the fractal dimension serves as a valid indicator to identify the mobility edge and distinguish different phases. The corresponding fractal dimension of -th eigenstate reads
| (10) |
The extended, localized and critical phases correspond to , and , respectively YWang2020a ; YWang2022a .
Moreover, the scaling index for multifractal analysis has a similar effect HHiramoto1989 ; HGrussbach1995 ; SSchiffer2021 ; JWang2016 . The probability of the nth eigenstate on the site is represented by the wave function , which satisfies the normalization condition . The scaling index of multifractal analysis for the th eigenstate is defined by the probability measure as
| (11) |
Since the occupation probability on all sites is for a completely extended wave function, the corresponding scaling index . For a localized wave function, the occupation probability is non-zero at just a few sites, therefore for such occupied sites and for the other sites. For a multifractal wave function, the scaling index is distributed in a finite interval . Thus, by considering the thermodynamic limit , one can characterize the localization properties of a wave function by . To be specific, for , indicates the extended (localized) states, whereas corresponds to the multifractal state.
In the next subsection, we will prove the REPT phenomenon through the results of , , , , and . To better reveal the REPT, we consider two most representative cases in the above phase diagram: (1) Fix the staggered intensity at (red dashed line) to study the effect of quasiperiodic potential on the system phase transition. (2) Fix the quasiperiodic potential at (white dashed line) to observe how the staggered potential will affect the phase transition.
III.2 -induced REPT
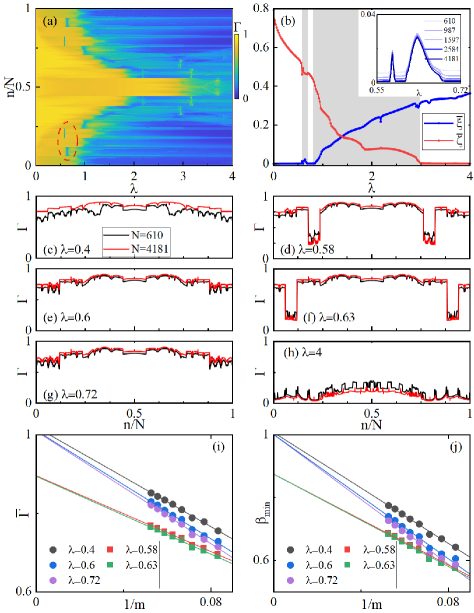
Now let’s focus on the first case . We first calculate fractal dimension corresponding to different energy levels of the system, which is a good indicator in distinguishing different phases. One can notice that the situation of appears sporadically in the system near [shown by red circle in Fig. 3(a)], which means the system is not in the pure extended state and the intermediate phase is about to emerge [see Fig. 3(a)]. When further increases, however, the system will resume its extension property. This is consistent with the phase diagram we have scanned through , i.e., emergent REPT will occur in the system. To better identify the emergent REPT, we plot the average IPR and average NPR in Fig. 3(b). The rises and falls multiple times around , which consistently demonstrates that the extended phase (white region) and the intermediate phase (gray region) will alternate in the region of quasiperiodic strength around . We show in the inset the variation of the with increasing system size near . It can be seen that the of the extended phase is constantly decaying towards 0, while the intermediate phase will gradually converge to form two distinct peaks. This is a sufficient explanation for the occurrence of REPT near .
Besides, we show the scaling behavior of the fractal dimension of all eigenstates under different quasiperiodic intensities . As shown in the figure, as the size of the system increases, corresponding to eigenstates of the extended phase (), the intermediate phase () and the localized phase () tend to 1; partly to 1 and partly to 0; and to 0, respectively.
Behavior at finite sizes can initially determine the phase of the system. Further, we fit the case up to the thermodynamic limit by scaling analysis. We define the average fractal dimension and average sacling index for all eigenstates. Scaling properties of different are shown in Fig. 3(i)(j), where the result of the thermodynamic limit () is obtained by the linear fit and extrapolation method. For the extended phase (dots), both and can reach 1 in the thermodynamic limit, while for the intermediate phase (squares), the corresponding and can never reach 1 in the thermodynamic limit due to the coexistence of the localized phase and the extended phase.
The above results show that as increases, the system will switch back to the extended state with the ever-increasing quasiperiodic strength, i.e., REPT occurs. This phenomenon of reentry into the extended state with the increase of quasiperiodic strength in weak quasiperiodic region is what we dub as the Type-I REPT phenomenon. From the phase diagram Fig. 2, one can see that the Type-I REPT phenomenon is relatively weak and the region where it first enters the intermediate phase is small.
III.3 -induced REPT
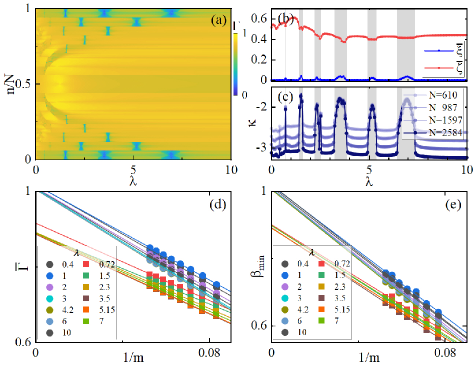
Then we discuss the second case of REPT. By fixing the quasiperiodic strength , one can see clearly how the REPT can be manipulated by tuning the staggered potential. Fig. 4(a) shows of all eigenstates versus staggered potential. The result reveals that the system repeatedly exhibits the coexistence of localization and extension properties with the increasing staggered potential, which confirms the multiple REPT. Further, we compute the average IPR and NPR , which both have similar periodic variations [see Fig. 4(b)]. In addition, we show the for different system sizes as a function of in Fig. 4(c). For the extended phase, for large sizes, hence decreases with increasing system size. For the intermediate phase, , which remains constant as the system size increases. The occurrence of REPT is well illustrated in Fig. 4(b)(c). These indicator quantities consistently prove that the system can repeatedly switch between the extended phase and the intermediate phase. Finally, For the extended phase (dots), both and can reach 1 in the thermodynamic limit, whereas for the intermediate phase (squares), it is between 0 and 1. We dub this multiple REPT phenomenon occurring with the changing staggered potential in the weak quasiperiodic region as Type-II REPT phenomenon.
III.4 The limits of the large
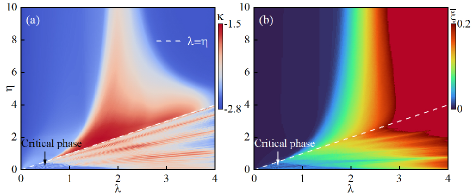
Another interesting phenomenon occurs when is very large. From Fig. 2 we can see that as increases, the region of the extended and localized phases gradually expands and encroaches upon the region of the intermediate phase, a phenomenon that we also observe in other parameters [see Fig. 6(a) and 8(a)]. It is as if to show that the system at has an exact extended-localized phase transition point.
First, we considered the case of , and Eq. 1 returns to the AAH model with the staggered potential. In this case, the system will exhibit multiple reentrant localization phenomenon. Besides, one can find that staggered potential will enhance AAH model’s localization properties in the extended region (), making it easier for the system to enter the localized phase. Especially when is large, even very small quasiperiodic potential can make the system localized APadhan2022 . As shown in Fig. 5(a), we demonstrate the average IPR as a function of for at different . In the case of a large , the localization phase transition point exhibits . By analogy, when , an arbitrarily small can induce a localization phase transition.
However, with the introduction of -wave superconductivity, as shown in Fig. 5(b), the localization phase transition point at exhibits the same behavior as when (where is is small enough to be ignored). We further depict as a function of for various system sizes. Notably, it becomes evident that the localization phase transition points for both and conform to the relational equation: . Remarkably, these phase transition critical points remain invariant with the increasing system size. This large situation reminds us of the self-dual relationship of the AAH model. The difference in localization properties between and leads to the production of a new re-entrant phase transition.
IV The intermediate phase and mobility edge
In addition to the REPT phenomenon, one can also notice dramatic fluctuation of in the red triangle region of Fig. 2, which is neither characteristic of pure phase nor traditional intermediate phase, but of brand new phases and new mobility edges in this region. The core difference between the new mobility edge and the traditional one lies in the critical phase. To discuss this type of region more comprehensively, next we will examine the and cases, which emerge with all types of new mobility edges. To distinguish from the traditional intermediate state (where the extended and the localized states coexist), we categorized all the possible intermediate states in the system formed by the critical state and other states into several types and named each one of them. Their composition and terminology are summarized in Table 1.
| Int. Phases | Components |
|---|---|
| Int. I | Extended + Localized |
| Int. II | Extended + Critical |
| Int. III | Localized + Critical |
| Int. IV | Extended + Localized + Critical |
IV.1 The case of
is the critical case for the superconducting paired AAH model, which has only one transition point between the critical and localized phases ( corresponds to the blue dashed line in Fig. 1). We show the and average IPR in the plane in Fig. 6(a)(b), respectively. One can see a boundary in the figure, i.e., the white dashed line of . This boundary divides the region where has obvious fluctuations and another region where is relatively stable, which means that there will be different intermediate phases (with or without participation of the critical phase) on both sides of this critical boundary. Detailed evidence will be provided in the following part. Note that, in addition to the rich intermediate phases in the system, the results of and jointly reveal that when the staggered potential strength and the quasiperiodic strength are relatively weak (The area labelled in the lower left of the figure), there still exists a pure critical phase.
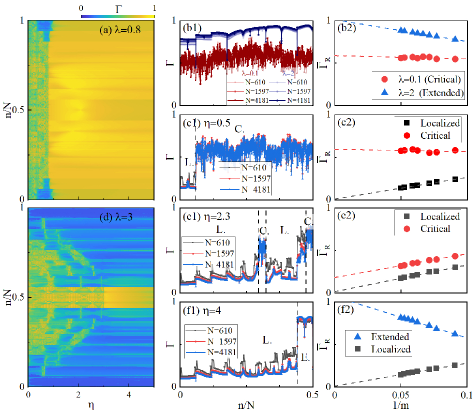
To prove the above conclusion, we further discuss the fractal dimensions for different . Firstly, in Fig. 7(a), we show how corresponding to all eigenstates in the system changes with when is fixed. It is not difficult to notice that in the region with small , behaves neither as an extended state () nor as a localized state (), but somewhere in between, which is evidence for the existence of a critical phase. As increases, some of the eigenstates are localized. Interestingly, as , the critical state is instantaneously extended and thus enters the conventional intermediate phase. Specifically, the system undergoes the following phase transitions: critical phase Int. III Int. I extended phase. Further, we selected , and in Fig. 7(b1)(c1) to discuss the fractal dimension at different system sizes. Since regions of and are symmetric, we exhibit only the results of region . For (), the of all eigenstates increases (invariably) with the system size, which is a good proof of the extended property (critical property) of the system. While for , the well characterizes the localized states (decreasing with the increasing system size) and the critical state as the system size increases, indicating that the system is in the Int. III phase.
Since the number of eigenstates will increase with the growing system size, to grasp the more accurate scaling behavior of the system, we define the average fractal dimension in region as
| (12) |
where is the eigenstates’ number of region , and correspond to the extended, localized, and critical regions, respectively. For extended (localized) states, the average fractal dimension () tends to be () as the system size increases, while corresponding to the critical state falls between and under the scaling limit. As shown in Fig. 7(b2)(c2), in the thermodynamic limit, with is able to reach 1, while lies between 0 and 1, indicating that it is in the extended and critical phases, respectively. For , the of the critical and localized regions in the thermodynamic limit are around 0.6 and 0, respectively, indicating that the system is in the Int. III phase.
Secondly, we show the case of in Fig. 7(d)-(f). The results show that in the region () the system is in Int. III phase (Int. I phase). As increases, the system undergoes a phase transition from Int. III phase to Int I phase at the critical point . Due to the multifractal property of the wavefunction, the different critical states have large numerical fluctuations. Therefore, one can see that the of new type intermediate phases will be quite different from that of the conventional intermediate phase. But exactly which type of intermediate phase it is going to be indeed needs further discussion.
IV.2 The case of
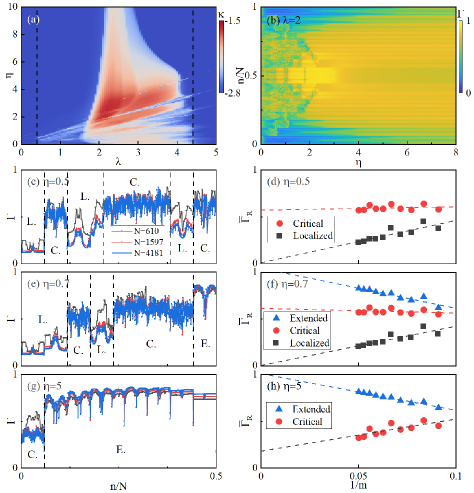
Then we consider the more general case of with the relevant phase diagram shown in Fig. 8(a). When (the case of red dashed line in Fig. 1), the system can be reduced to the standard -wave superconducting paired AAH model. In this condition, the extended-critical phase transition and the critical-localized phase transition of the system occur at and , respectively. The introduction of staggered potential will result in the emergent intermediate phases in the region of . Fig. 8(a) shows that fluctuates in the region with weak staggered potential, and the fluctuation will become more significant as increases, which suggests the occurrence of intermediate phases where different states coexist. To ascertain what exactly these intermediate phases are, we calculate the corresponding fractal dimensions with respect to different staggered potential. As shown in Fig. 8(b) for , with the increase of , special phase transitions occur. To be more specific, the phase transitions occur gradually as follows: Int. III phase Int. IV phase Int. III phase Int. IV phase Int. II phase extended phase.
Fig. 8(c)-(h) show the results of the eigenstate scaling analysis. Here, scaling behaviors of fractal dimensions are discussed for (c)(d), (e)(f) and (g)(h), respectively. Specifically, when , the fractal dimension will be alternately of the localized phase and the critical phase as increases, which is the evidence of Int. III phase. When , the fractal dimension indicates the coexistence of the localized, critical and extended states in the system, which proves the existence of Int. IV phase. Finally, when , the fractal dimension shows that the critical phase and the extended phase coexist in the system, which is the evidence of Int. II phase.
Further, the scaling analysis of the fractal dimension for different regions is shown in Fig. 8(d), (f) and (h), and the average fractal dimension in different regions again confirms the existence of three intermediate phases, i.e, Int. III, Int. IV and Int. II phases.
V Conclusion
In summary, we investigate the -wave paired quasiperiodic model with staggered on-site potential. On the one hand, we report for the first time the reentry to the extended phase with increasing quasiperiodic intensity, i.e., the REPT phenomenon. Furthermore, we prove that multiple REPT phenomena can emerge in the system with varying staggered potential strength. On the other hand, different from the traditional intermediate phase (composed only of the extended and localized states), we find that there are novel intermediate phases in the system, which contain the critical states. Through the fractal dimension and scaling behavior analysis, we prove that there are three types of intermediate phases, namely, the extended state + the critical state; the localized state + the critical state; and the extended state + the localized state + the critical state, respectively. Since quasiperiodic models have already been successfully implemented in various tabletop experiments YLahini2009 ; YEKraus2012 ; MVerbin2013 ; MVerbin2015 ; PWang2020 ; SAGredeskul1989 ; DNChristodoulides2003 ; TPertsch2004 ; GRoati2008 ; GModugno2010 ; MLohse2016 ; SNakajima2016 ; HPLuschen2018 ; FAAnK2021 ; DTanese2014 ; PRoushan2017 ; FAAn2018 , the REPT phenomena and intermediate phase predicted in this paper are expected to be observed in the near future.
Acknowledgements.
This work was supported by the National Key Research and Development Program of China (Grant No.2022YFA1405300), the National Natural Science Foundation of China (Grant No.12074180), and the Guangdong Basic and Applied Basic Research Foundation (Grants No.2021A1515012350).References
- (1) G. Feher, Electron spin resonance experiments on donors in silicon. I. Electronic structure of donors by the electron nuclear double resonance technique, Phys. Rev. 114. 1219 (1959).
- (2) G. Feher and E. A. Gere, Electron Spin Resonance Experiments on Donors in Silicon. II. Electron Spin Relaxation Effects, Phys. Rev. 114, 1245 (1959).
- (3) P. W. Anderson, Absence of diffusion in certain random lattices, Phys. Rev. 109, 1492 (1958).
- (4) N. F. Mott, Electrons in disordered structures, Adv. Phys. 50, 865 (1967).
- (5) E. Abrahams , P. W. Anderson, D. C. Licciardello and T. V. Ramakrishnan, Scaling Theory of Localization: Absence of Quantum Diffusion in Two Dimensions, Phys. Rev. Lett. 42, 673 (1979).
- (6) P. A. Lee and T. V. Ramakrishnan, Disordered electronic systems, Rev. Mod. Phys. 57, 287 (1985).
- (7) F. Evers and A. D. Mirlin, Anderson transitions, Rev. Mod. Phys. 80, 1355 (2008).
- (8) B. Hetényi, S. Parlak, and M. Yahyavi, Scaling and renormalization in the modern theory of polarization: Application to disordered systems, Phys. Rev. B 104, 214207 (2021).
- (9) J. Li, R. L. Chu, J. K. Jain, and S. Q. Shen, Topological Anderson Insulator, Phys. Rev. Lett. 102, 136806 (2009).
- (10) C. W. Groth, M. Wimmer, A. R. Akhmerov, J. Tworzydło, and C. W. J. Beenakker, Theory of the Topological Anderson Insulator, Phys. Rev. Lett. 103, 196805 (2009).
- (11) H. M. Guo, G. Rosenberg, G. Refael, and M. Franz, Topological Anderson Insulator in Three Dimensions, Phys. Rev. Lett. 105, 216601 (2010).
- (12) E. J. Meier, F. A. An, A. Dauphin, M. Maffei, P. Massignan, T. L. Hughes, and B. Gadway, Observation of the topological Anderson insulator in disordered atomic wires, Science 362, 929 (2018).
- (13) S. Stützer, Y. Plotnik, Y. Lumer, P. Titum, N. H. Lindner, M. Segev, M. C. Rechtsman, and A. Szameit, Photonic topological Anderson insulators, Nature 560, 461 (2018).
- (14) G. G. Liu, Y. Yang, X. Ren, H. Xue, X. Lin, Y. H. Hu, H. X. Sun, B. Peng, P. Zhou, Y. Chong, and B. Zhang, Topological Anderson Insulator in Disordered Photonic Crystals, Phys. Rev. Lett. 125, 133603 (2020)
- (15) D.-W. Zhang, L.-Z. Tang, L.-J. Lang, H. Yan, and S.-L. Zhu, Non-hermitian topological Anderson insulators, Sci. China Phys. Mech. Astron. 63, 267062 (2020).
- (16) W. Zhang, D. Zou, Q. Pei, W. He, J. Bao, H. Sun, and X. Zhang, Experimental Observation of Higher-Order Topological Anderson Insulators, Phys. Rev. Lett. 126, 146802 (2021).
- (17) A. Nava, G. Campagnano, P. Sodano, and D. Giuliano, Lindblad master equation approach to the topological phase transition in the disordered Su-Schrieffer-Heeger model, Phys. Rev. B 107, 035113 (2023).
- (18) A. Pal and D. A. Huse, Many-body localization phase transition, Phys. Rev. B 82, 174411 (2010).
- (19) D. A. Huse, R. Nandkishore, V. Oganesyan, A. Pal, and S. L. Sondhi, Localization-protected quantum order, Phys. Rev. B 88, 014206 (2013).
- (20) D. J. Luitz, N. Laflorencie, and F. Alet, Many-body localization edge in the random-field heisenberg chain, Phys. Rev. B 91, 081103(R) (2015).
- (21) R. Nandkishore and D. A. Huse, Many-body localization and thermalization in quantum statistical mechanics, Annu. Rev. Condens. Matter Phys. 6, 15 (2015).
- (22) E. Altman and R. Vosk, Universal dynamics and renormalization in many-body-localized systems, Annu. Rev. Condens. Matter Phys. 6, 383 (2015).
- (23) F. Alet and N. Laflorencie, Many-body localization: An introduction and selected topics, C. R. Phys. 19, 498 (2018).
- (24) D. A. Abanin, E. Altman, I. Bloch, and M. Serbyn, Colloquium: Many-body localization, thermalization, and entanglement, Rev. Mod. Phys. 91, 021001 (2019).
- (25) Y. Lahini, R. Pugatch, F. Pozzi, M. Sorel, R. Morandotti, N. Davidson, and Y. Silberberg, Observation of a Localization Transition in Quasiperiodic Photonic Lattices, Phys. Rev. Lett. 103, 013901 (2009).
- (26) Y. E. Kraus, Y. Lahini, Z. Ringel, M. Verbin, and O. Zilberberg, Topological States and Adiabatic Pumping in Quasicrystals, Phys. Rev. Lett. 109, 106402 (2012).
- (27) M. Verbin, O. Zilberberg, Y. E. Kraus, Y. Lahini, and Y. Silberberg, Observation of Topological Phase Transitions in Photonic Quasicrystals, Phys. Rev. Lett. 110, 076403 (2013).
- (28) M. Verbin, O. Zilberberg, Y. Lahini, Y. E. Kraus, and Y. Silberberg, Topological pumping over a photonic Fibonacci quasicrystal, Phys. Rev. B 91, 064201 (2015).
- (29) P. Wang, Y. Zheng, X. Chen, C. Huang, Y. V. Kartashov, L. Torner, V. V. Konotop, and F. Ye, Localization and delocalization of light in photonic moiré lattices, Nature 577, 42 (2020).
- (30) S. A. Gredeskul and Y. S. Kivshar, Generation of Dark Solitons in Optical Fibers, Phys. Rev. Lett. 62, 977 (1989).
- (31) D. N. Christodoulides and Y. Silberberg, Discretizing light behaviour in linear and nonlinear waveguide lattices, Nature (London) 424, 817 (2003).
- (32) T. Pertsch, U. Peschel, J. Kobelke, K. Schuster, H. Bartelt, S. Nolte, A. Tünnermann, and F. Lederer, Nonlinearity and Disorder in Fiber Arrays, Phys. Rev. Lett. 93, 053901 (2004).
- (33) G. Roati, C. D’Errico, L. Fallani, M. Fattori, C. Fort, M. Zaccanti, G. Modugno, M. Modugno, and M. Inguscio, Anderson localization of a non-interacting Bose-Einstein condensate Nature 453, 895 (2008).
- (34) G. Modugno, Anderson localization in Bose-Einstein condensates, Rep. Prog. Phys. 73, 102401 (2010).
- (35) M. Lohse, C. Schweizer, O. Zilberberg, M. Aidelsburger, and I. Bloch, A Thouless quantum pump with ultracold bosonic atoms in an optical superlattice, Nat. Phys. 12, 350 (2016).
- (36) S. Nakajima, T. Tomita, S. Taie, T. Ichinose, H. Ozawa, L. Wang, M. Troyer, and Y. Takahashi, Topological Thouless pumping of ultracold fermions, Nat. Phys. 12, 296 (2016).
- (37) H. P. Lüschen, S. Scherg, T. Kohlert, M. Schreiber, P. Bordia, X. Li, S. Das Sarma, and I. Bloch, Single-Particle Mobility Edge in a One-Dimensional Quasiperiodic Optical Lattice, Phys. Rev. Lett. 120, 160404 (2018).
- (38) F. A. An, K. Padavić, E. J. Meier, S. Hegde, S. Ganeshan, J. H. Pixley, S. Vishveshwara, and B. Gadway, Interactions and Mobility Edges: Observing the Generalized Aubry-André Model, Phys. Rev. Lett. 126, 040603 (2021).
- (39) D. Tanese, E. Gurevich, F. Baboux, T. Jacqmin, A. Lemaître, E. Galopin, I. Sagnes, A. Amo, J. Bloch, and E. Akkermans, Fractal Energy Spectrum of a Polariton Gas in a Fibonacci Quasiperiodic Potential, Phys. Rev. Lett. 112, 146404 (2014).
- (40) P. Roushan, C. Neill, J. Tangpanitanon, V.M. Bastidas, A. Megrant, R. Barends, Y. Chen, Z. Chen, B. Chiaro, A. Dunsworth, A. Fowler, B. Foxen, M. Giustina, E. Jeffrey, J. Kelly, E. Lucero, J. Mutus, M. Neeley, C. Quintana, D. Sank, A. Vainsencher, J. Wenner, T. White, H. Neven, D. G. Angelakis, J. Martinis, Spectroscopic signatures of localization with interacting photons in superconducting qubits, Science 358, 6367 (2017).
- (41) F. A. An, E. J. Meier, and B. Gadway, Engineering a flux-dependent mobility edge in disordered zigzag chains, Phys. Rev. X 8, 031045 (2018).
- (42) P. G. Harper, Single Band Motion of Conduction Electrons in a Uniform Magnetic Field, Proc. Phys. Soc. A 68, 874 (1955).
- (43) S. Aubry and G. André, Analyticity breaking and Anderson localization in incommensurate lattices, Ann. Israel Phys. Soc 3, 18 (1980).
- (44) J. Biddle and S. Das Sarma, Predicted Mobility Edges in One-Dimensional Incommensurate Optical Lattices: An Exactly Solvable Model of Anderson Localization, Phys. Rev. Lett. 104, 070601 (2010).
- (45) X. Deng, S. Ray, S. Sinha, G. V. Shlyapnikov, and L. Santos, One-Dimensional Quasicrystals with Power-Law Hopping, Phys. Rev. Lett. 123, 025301 (2019).
- (46) N. Roy and A. Sharma, Fraction of delocalized eigenstates in the long-range Aubry-André-Harper model, Phys. Rev. B 103, 075124 (2021).
- (47) S. Roy, T. Mishra, B. Tanatar, and S. Basu, Reentrant Localization Transition in a Quasiperiodic Chain, Phys. Rev. Lett. 126, 106803 (2021).
- (48) L. Zhou and W. Han, Driving-induced multiple -symmetry breaking transitions and reentrant localization transitions in non-Hermitian Floquet quasicrystals, Phys. Rev. B 106, 054307 (2022).
- (49) M. Kohmoto and D. Tobe, Localization problem in a quasiperiodic system with spin-orbit interaction, Phys. Rev. B 77, 134204 (2008).
- (50) L. Zhou, H. Pu, and W. Zhang, Anderson localization of cold atomic gases with effective spin-orbit interaction in a quasiperiodic optical lattice, Phys. Rev. A 87, 023625 (2013).
- (51) S. Ganeshan, J. H. Pixley, and S. Das Sarma, Nearest Neighbor Tight Binding Models with an Exact Mobility Edge in One Dimension, Phys. Rev. Lett. 114, 146601 (2015).
- (52) X. Li, X. Li, and S. Das Sarma, Mobility edges in one-dimensional bichromatic incommensurate potentials, Phys. Rev. B 96, 085119 (2017).
- (53) H. Yao, H. Khouldi, L. Bresque, and L. Sanchez-Palencia, Critical behavior and fractality in shallow one-dimensional quasi-periodic potentials, Phys. Rev. Lett. 123, 070405 (2019).
- (54) Y. Wang, X. Xia, L. Zhang, H. Yao, S. Chen, J. You, Q. Zhou, and X.-J. Liu, One-Dimensional Quasiperiodic Mosaic Lattice with Exact Mobility Edges, Phys. Rev. Lett. 125, 196604 (2020).
- (55) A. Padhan, M. K. Giri, S. Mondal, and T. Mishra, Emergence of multiple localization transitions in a one-dimensional quasiperiodic lattice, Phys. Rev. B 105 L220201 (2022).
- (56) Q. Lin, T. Li, L. Xiao, K. Wang, W. Yi, and P. Xue, Topological Phase Transitions and Mobility Edges in Non-Hermitian Quasicrystals, Phys. Rev. Lett. 129, 113601 (2022).
- (57) J. Gao, I. M. Khaymovich, X.-W. Wang, Z.-S. Xu, A. Iovan, G. Krishna, A. V. Balatsky, V. Zwiller and A. W. Elshaari, Experimental probe of multi-mobility edges in quasiperiodic mosaic lattices, arXiv:2306.10829.
- (58) M. Gonçalves, B. Amorim, E. V. Castro, and P. Ribeiro, Hidden dualities in 1d quasiperiodic lattice models, SciPost Phys. 13, 046 (2022).
- (59) M. Gonçalves, B. Amorim, E. V. Castro, and P. Ribeiro, Critical phase dualities in 1D exactly-solvable quasiperiodic models, arXiv:2208.07886.
- (60) M. Gonçalves, B. Amorim, E. V. Castro, and P. Ribeiro, Renormalization group theory of one-dimensional quasiperiodic lattice models with commensurate approximants, Phys. Rev. B 108, L100201 (2023).
- (61) Y.-C. Zhang, R. Yuan, and Y. Wang, Anderson localization of a one-dimensional lattice model with mosaic quasi-periodic off-diagonal disorders, arXiv:2212.10715.
- (62) Y.-C. Zhang and Y.-Y. Zhang, Lyapunov exponent, mobility edges, and critical region in the generalized Aubry-André model with an unbounded quasiperiodic potential, Phys. Rev. B 105, 174206 (2022).
- (63) X.-C. Zhou, Y. Wang, T.-F. Jeffrey Poon, Q. Zhou, and X.-J. Liu, Exact new mobility edges between critical and localized states, arXiv:2212.14285 (2022).
- (64) Y. Wang, X. Xia, Y. Wang, Z. Zheng, and X.-J. Liu, Duality between two generalized Aubry-André models with exact mobility edges, Phys. Rev. B 103 174205 (2021).
- (65) Y. Liu, Y. Wang, Z. Zheng, and S. Chen, Exact non-Hermitian mobility edges in one-dimensional quasicrystal lattice with exponentially decaying hopping and its dual lattice, Phys. Rev. B 103 134208 (2021).
- (66) Y. Liu, Y. Wang, X.-J. Liu, Q. Zhou, and S. Chen, Exact mobility edges, -symmetry breaking, and skin effect in one-dimensional non-Hermitian quasicrystals, Phys. Rev. B 103 014203 (2021).
- (67) Y. Liu, Q. Zhou, and S. Chen, Localization transition, spectrum structure, and winding numbers for one-dimensional non-Hermitian quasicrystals, Phys. Rev. B 104 024201 (2021).
- (68) Z.-H. Wang, F. Xu, L. Li, D.-H. Xu, and B. Wang, Topological superconductors and exact mobility edges in non-Hermitian quasicrystals, Phys. Rev. B 105 024514 (2022).
- (69) Z.-H. Xu, X. Xia, and S. Chen, Exact mobility edges and topological phase transition in two-dimensional non-Hermitian quasicrystals, Sci. China Phys. Mech. Astron. 65 227211 (2022).
- (70) Y. Wang, L. Zhang, Y. Wan, Y. He, and Y. Wang, Two-dimensional vertex-decorated Lieb lattice with exact mobility edges and robust flat bands, Phys. Rev. B 107, L140201 (2023).
- (71) S.-L. Jiang, Y. Liu, and L.-J. Lang, General mapping of one-dimensional non-Hermitian mosaic models to non-mosaic counterparts: Mobility edges and Lyapunov exponents, Chin. Phys. B 32, 097204 (2023).
- (72) X. Wei, L. Wu, K. Feng, T. Liu, and Y. Zhang, Exact mobility edges in finite-height Wannier-Stark ladders, arXiv:2308.15516.
- (73) A. Avila, Global theory of one-frequency Schrödinger operators, Acta. Math. 1, 215 (2015).
- (74) T. Geisel, R. Ketzmerick, and G. Petschel, New Class of Level Statistics in Quantum Systems with Unbounded Diffusion, Phys. Rev. Lett. 66, 1651 (1991).
- (75) S. Y. Jitomirskaya, Metal-insulator transition for the almost Mathieu operator, Ann. Math. 150, 1159 (1999).
- (76) T. C. Halsey, M. H. Jensen, L. P. Kadanoff, I. Procaccia, and B. I. Shraiman, Fractal measures and their singularities: The characterization of strange sets, Phys. Rev. A 33, 1141 (1986).
- (77) A. D. Mirlin, Y. V. Fyodorov, A. Mildenberger, and F. Evers, Exact Relations between Multifractal Exponents at the Anderson Transition, Phys. Rev. Lett. 97, 046803 (2006).
- (78) H. Hiramoto and S. Abe, Dynamics of an electron in quasiperiodic systems. II. Harper’s model, J. Phys. Soc. Jpn. 57, 1365 (1988).
- (79) R. Ketzmerick, K. Kruse, S. Kraut, and T. Geisel, What Determines the Spreading of a Wave Packet? Phys. Rev. Lett. 79, 1959 (1997).
- (80) J. Wang, X.-J. Liu, G. Xianlong, and H. Hu, Phase diagram of a non-Abelian Aubry-André-Harper model with -wave superfluidity, Phys. Rev. B 93, 104504 (2016).
- (81) M. Yahyavi, B. Hetényi, and B. Tanatar, Generalized Aubry-André-Harper model with modulated hopping and -wave pairing, Phys. Rev. B 100, 064202 (2019).
- (82) T. Liu, S. Cheng, H. Guo, and G. Xianlong, Fate of Majorana zero modes, exact location of critical states, and unconventional real-complex transition in non-Hermitian quasiperiodic lattices, Phys. Rev. B 103, 104203 (2021).
- (83) J. Fraxanet, U. Bhattacharya, T. Grass, M. Lewenstein, and A. Dauphin, Localization and multifractal properties of the long-range Kitaev chain in the presence of an Aubry-André-Harper modulation, Phys. Rev. B 106, 024204 (2022).
- (84) Y. Wang, L. Zhang, W. Sun, T.-F. J. Poon, and X.-J. Liu, Quantum phase with coexisting localized, extended, and critical zones, Phys. Rev. B 106, L140203 (2022).
- (85) Y. Wang, Mobility edges and critical regions in a periodically kicked incommensurate optical Raman lattice, Phys. Rev. A 106, 053312 (2022).
- (86) T. Liu and X. Xia, Dual mapping and quantum criticality in quasiperiodic Su-Schrieffer-Heeger chains, Phys. Rev. B 104, 134202 (2021).
- (87) F. Liu, S. Ghosh, and Y. D. Chong, Localization and adiabatic pumping in a generalized Aubry-André-Harper model, Phys. Rev. B 91, 014108 (2015).
- (88) J. C. C. Cestari, A. Foerster, and M. A. Gusmão, Fate of topological states in incommensurate generalized Aubry-André models, Phys. Rev. B 93, 205441 (2016).
- (89) L. Wang, N. Liu, S. Chen, and Y. Zhang, Quantum walks in the commensurate off-diagonal Aubry-André-Harper model, Phys. Rev. A 95, 013619 (2017).
- (90) T. Xiao, D. Xie, Z. Dong, T. Chen, W. Yi, and B. Yan, Observation of topological phase with critical localization in a quasi-periodic lattice, Sci. Bull. 66, 2175 (2021).
- (91) L.-Z. Tang, G.-Q. Zhang, L.-F. Zhang, and D.-W. Zhang, Localization and topological transitions in non-Hermitian quasiperiodic lattices, Phys. Rev. A 103, 033325 (2021).
- (92) L.-Z. Tang, S.-N. Liu, G.-Q. Zhang, and D.-W. Zhang, Topological Anderson insulators with different bulk states in quasiperiodic chains, Phys. Rev. A 105 063327 (2022).
- (93) S.-Z. Li, X.-J. Yu, S.-L. Zhu, Z. Li, Anderson localization and swing mobility edge in curved spacetime, Phys. Rev. B 108, 094209 (2023).
- (94) X. Lin, X. Chen, G.-C. Guo, M. Gong, The general approach to the critical phase with coupled quasiperiodic chains, arXiv:2209.03060 (2022).
- (95) X. Cai, L.-J. Lang, S. Chen, and Y. Wang, Topological Superconductor to Anderson Localization Transition in One-Dimensional Incommensurate Lattices, Phys. Rev. Lett. 110, 176403 (2013).
- (96) F. Mei, S.-L. Zhu, Z.-M. Zhang, C. H. Oh, and N. Goldman, Simulating topological insulators with cold atoms in a one-dimensional optical lattice, Phys. Rev. A 85, 013638 (2012).
- (97) Y. E. Kraus and O. Zilberberg, Topological Equivalence between the Fibonacci Quasicrystal and the Harper Model, Phys. Rev. Lett. 109, 116404 (2012).
- (98) Y. E. Kraus, Y. Lahini, Z. Ringel, M. Verbin, and O. Zilberberg, Topological States and Adiabatic Pumping in Quasicrystals, Phys. Rev. Lett. 109, 106402 (2012).
- (99) L.-J. Lang, X. Cai, and S. Chen, Edge States and Topological Phases in One-Dimensional Optical Superlattices, Phys. Rev. Lett. 108, 220401 (2012).
- (100) S. Ganeshan, K. Sun, and S. D. Sarma, Topological ZeroEnergy Modes in Gapless Commensurate Aubry-André-Harper Models, Phys. Rev. Lett. 110, 180403 (2013).
- (101) M. N. Chen, F. Mei, W. Shu, H.-Q. Wang, S.-L. Zhu, L. Sheng, and D. Y. Xing, Topological phases of the kicked Harper-Kitaev model with ultracold atoms, J. Phys.: Condens. Matter 29, 035601 (2016).
- (102) Q.-B. Zeng, Y.-B. Yang, and Y. Xu, Topological phases in non-Hermitian Aubry-André-Harper models, Phys. Rev. B 101, 020201(R) (2020).
- (103) P. He, Y.-G. Liu, J.-T Wang, and S.-L. Zhu, Damping transition in an open generalized Aubry-André-Harper model, Phys. Rev. A 105, 023311 (2022).
- (104) D.-W. Zhang, Y.-L. Chen, G.-Q. Zhang, L.-J. Lang, Z. Li, and S.-L. Zhu, Skin superfluid, topological Mott insulators, and asymmetric dynamics in an interacting non-Hermitian Aubry-André-Harper model, Phys. Rev. B 101, 235150 (2020).
- (105) H. Jiang, L.-J. Lang, C. Yang, S.-L. Zhu, and S. Chen, Interplay of non-Hermitian skin effects and Anderson localization in nonreciprocal quasiperiodic lattices, Phys. Rev. B 100, 054301 (2019).
- (106) V. Goblot, A. Štrkalj, N. Pernet, J. L. Lado, C. Dorow, A. Lemaître, L. Le Gratiet, A. Harouri, I. Sagnes, S. Ravets, A. Amo, J. Bloch, and O. Zilberberg, Emergence of criticality through a cascade of delocalization transitions in quasiperiodic chains, Nat. Phys. 16, 832 (2020).
- (107) W. Han and L. Zhou, Dimerization-induced mobility edges and multiple reentrant localization transitions in non-Hermitian quasicrystals, Phys. Rev. B 105 054204 (2022).
- (108) R. Qi, J. Cao, and X.-P. Jiang, Multiple localization transitions and novel quantum phases induced by a staggered on-site potential, Phys. Rev. B 107, 224201 (2023).
- (109) E. Guan, G. Wang, X.-W. Guan, and X. Cai, Reentrant localization and mobility edges in a spinful Aubry-André-Harper model with a non-Abelian potential, Phys. Rev. A 108, 033305 (2023).
- (110) Z. Lu, Y. Zhang, Z. Xu, Robust Topological Anderson Insulator Induced Reentrant Localization Transition, arXiv:2306.06818.
- (111) H. Wang, X. Zheng, J. Chen, L. Xiao, S. Jia, and L. Zhang, Fate of the reentrant localization phenomenon in the one-dimensional dimerized quasiperiodic chain with long-range hopping, Phys. Rev. B 107, 075128 (2023).
- (112) S. Ganguly, S. Sarkar, K. Mondal, S. K. Maiti, Phenomenon of multiple reentrant localization in a double-stranded helix with transverse electric field, arXiv:2306.14452.
- (113) X.-P. Jiang, Y. Qiao, and J.-P. Cao, Mobility edges and reentrant localization in one-dimensional dimerized nonHermitian quasiperiodic lattice, Chin. Phys. B 30, 097202 (2021).
- (114) D.-W. Zhang, Y.-Q. Zhu, Y. X. Zhao, H. Yan, and S.-L. Zhu, Topological quantum matter with cold atoms, Advances in Physics 67, 253 (2018).
- (115) A. Kitaev, Unpaired Majorana fermions in quantum wires Upsekhi Fizicheskikh Nauk 171, 131 (2001).
- (116) X. Li and S. Das Sarma, Mobility edge and intermediate phase in one-dimensional incommensurate lattice potentials, Phys. Rev. B 101, 064203 (2020).
- (117) H. Hiramoto and M. Kohmoto, Scaling analysis of quasiperiodic systems: Generalized Harper model, Phys. Rev. B 40, 8225 (1989).
- (118) H. Grussbach and M. Schreiber, Determination of the mobility edge in the Anderson model of localization in three dimensions by multifractal analysis, Phys. Rev. B 51, 663(R) (1995).
- (119) S. Schiffer, X.-J. Liu, H. Hu, and J. Wang, Anderson localization transition in a robust -symmetric phase of a generalized Aubry-André model, Phys. Rev. A 103, L011302 (2021).