Embedding a differentiable mel-cepstral synthesis filter
to a neural speech synthesis system
Abstract
This paper integrates a classic mel-cepstral synthesis filter into a modern neural speech synthesis system towards end-to-end controllable speech synthesis. Since the mel-cepstral synthesis filter is explicitly embedded in neural waveform models in the proposed system, both voice characteristics and the pitch of synthesized speech are highly controlled via a frequency warping parameter and fundamental frequency, respectively. We implement the mel-cepstral synthesis filter as a differentiable and GPU-friendly module to enable the acoustic and waveform models in the proposed system to be simultaneously optimized in an end-to-end manner. Experiments show that the proposed system improves speech quality from a baseline system maintaining controllability. The core PyTorch modules used in the experiments will be publicly available on GitHub111https://github.com/sp-nitech/diffsptk.
Index Terms— Speech synthesis, neural networks, mel-cepstrum, MLSA filter, end-to-end training
1 Introduction
In statistical parametric speech synthesis [1], linear time-variant synthesis filters such as line spectral pairs (LSP) synthesis filter [2], mel-cepstral synthesis filter [3], and WORLD vocoder [4] are traditionally used as a waveform model to bridge the gap between acoustic features and the audio waveform. An important advantage of linear synthesis filters is that they can easily control voice characteristics and the pitch of synthesized speech by modifying input acoustic features. However, the speech quality is often limited due to the linearity of the filters. In 2016, the first successful neural waveform modeling, WaveNet [5], was proposed, enabling various nonlinear synthesis filters [6, 7, 8, 9] to have been intensively developed by researchers. Nonlinear neural synthesis filters outperform linear synthesis filters and can synthesize high-quality speech comparable to human speech. However, their generation of the waveform which is quite different from training data does not work well, resulting in less controllability of speech synthesis systems. The main reason is that the nonlinear synthesis filters ignore the clear relationship between acoustic features and the audio waveform, which is simply described by conventional linear synthesis filters. There have been a number of attempts to solve the problem, especially in terms of pitch [10, 11, 12]. Although they introduced special network structures against neural black-box modeling, the problem has yet to be fully solved.
In this paper, to take the advantage of both linear and nonlinear synthesis filters, we embed a mel-cepstral synthesis filter in a neural speech synthesis system. The main advantages of the proposed system are as follows: 1) Voice characteristics and the pitch of synthesized speech can be easily modified in the same manner as using the conventional mel-cepstral synthesis filter. 2) Since the embedded filter is essentially differentiable, speech waveform can be accurately modeled by the simultaneous optimization of the neural waveform model and the neural acoustic model that predicts acoustic features from text. 3) The neural waveform model is enough to have less trainable parameters because the mel-cepstral synthesis filter captures the rough relationship between acoustic features and the audio waveform. The proposed system may not require a complex training strategy such as using generative adversarial networks (GANs) [7] because the rough relationship is already constructed by the embedded filter without training.
The main concern about the proposed system is how to implement the mel-cepstral synthesis filter as a differentiable parallel processing module for efficient model training. Usually, the mel-cepstral synthesis filter is widely implemented as an infinite impulse response (IIR) filter [3]. This recursive property is not suitable for parallel processing. We solve the problem by formulating the mel-cepstral synthesis filter as cascaded finite impulse response (FIR) filters, i.e., stacked time-variant convolutional layers.
2 Related work
Tokuda and Zen [13, 14] combined a neural acoustic model and a cepstral synthesis filter [15]. The acoustic model was trained by directly maximizing the likelihood of waveform rather than minimizing cepstral distance. The speech quality was still limited due to the linearity of the cepstral synthesis filter. LPCNet [6] combined an all-pole filter with recurrent neural networks for fast waveform generation. ExcitNet [16] also used an all-pole filter as the backend of waveform generation. They did not introduce a specific signal-processing structure into their excitation generation modules.
In 2020, differentiable digital signal processing (DDSP) has been proposed [17]. The main idea is similar to our work: a differentiable linear filter is embedded in a neural waveform model. One of the main differences is that DDSP assumes a sinusoidal model as a linear synthesis filter. In the DDSP framework, an acoustic model for speech synthesis is not unified currently [18]. Nercessian [19] proposed a differentiable WORLD synthesizer for audio style transfer. The synthesizer uses log mel-spectrogram as a compact representation of spectrum and aperiodicity ratio while our work uses a mel-cepstral representation.

3 Linear synthesis system
Linear synthesis systems assume the following relation between an excitation signal and a speech signal :
| (1) |
where and are -transforms of and , respectively. The time-variant linear synthesis filter is parameterized with a compact spectral representation for speech application, e.g., text-to-speech synthesis and speech coding. In the mel-cepstral analysis [20], the spectral envelope is modeled using -th order mel-cepstral coefficients :
| (2) |
where
| (3) |
is a first-order all-pass function. Since the scalar parameter controls the intensity of frequency warping, the voice characteristics of can be easily modified by changing the value of . The paper uses Eq. (2) as a linear synthesis filter to have the benefits from the property.
Usually, a mixed excitation signal is assumed as the excitation . Namely,
| (4) |
where and are -transforms of white Gaussian noise and pulse train computed from fundamental frequency , respectively. The and are zero-phase linear filters represented as
| (5) | |||||
| (6) | |||||
| (7) |
where
| (10) |
and is a mel-cepstral representation of aperiodicity ratio [4]. The aperiodicity ratio represents the intensity of the aperiodic components of for each frequency bin and its values are in . Equation (4) describes a simple relationship between and , but there is a limit to accurate modeling of the speech signal .
4 Proposed method
To generate speech waveform with high controllability, our approach models speech waveform by extending the conventional linear synthesis filter as
| (11) | |||||
where and are nonlinear filters represented by trainable neural networks called prenets. To capture speech components that cannot be well captured by acoustic features including mel-cepstral coefficients and , the prenets are conditioned on the two -dimensional latent variable vectors, and . The latent variable vectors and as well as acoustic features are jointly estimated by the acoustic model from text.

An overview of the proposed speech synthesis system is shown in Fig. 1. Since all linear filters are inherently differentiable, the acoustic model and prenets can be simultaneously optimized by minimizing the objective
| (12) |
where is the loss between the predicted and ground-truth acoustic features, is the loss between predicted and ground-truth speech samples, and is a hyperparameter to balance the two losses. In this paper, the multi-resolution short-time Fourier transform (STFT) loss [7] is used as :
| (13) |
where
| (14) | |||||
| (15) |
and is the predicted speech waveform, is an amplitude spectrum obtained by STFT under -th analysis condition, is a normalization term, is the Frobenius norm, and is the norm. Note that during training, ground-truth fundamental frequencies are used to generate the pulse train fed to .
4.1 Differentiable mel-cepstral synthesis filter
Directly implementing Eq. (2) as a digital filter is difficult because it includes the exponential function. To solve the problem, the mel-log spectrum approximation (MLSA) filter [3] has been proposed and is widely used in various applications [1, 15]. The MLSA filter replaces the exponential function with a lower-order rational function using the modified Páde approximation. However, the MLSA filter is based on a recursive computation; previously computed values as well as the input signal are used for computing the current value . This makes training the proposed system with GPU machines very inefficient because they are suitable for parallel computing rather than deep recursive computations.
To solve this, we first convert the mel-cepstral coefficients to cepstral coefficients using a linear transformation [21]:
| (16) |
where is the -th order cepstral coefficients computed from . Then, by applying the Maclaurin expansion of the exponential function to Eq. (16), we obtain
| (17) |
The infinite series is truncated at the -th term. Equation (17) shows that the mel-cepstral synthesis filter can be implemented as -stage FIR filters, i.e., time-variant convolutional layers whose weights are dynamically computed from estimated mel-cepstral coefficients.
Another approach to implement the mel-cepstral synthesis filter is to design a single FIR filter whose filter coefficients correspond to an impulse response converted from the cepstral coefficients [22]. Note that this approach requires a large GPU memory to handle a filter with many thousands of taps. Due to GPU machine resources, the paper did not use the latter approach in experiments though it is computationally faster than the former approach described in Eq. (17).
5 Experiment
5.1 Experimental setup
The task to evaluate the proposed system was singing speech synthesis in which pitch controllability is quite important. We used an internal Japanese corpus containing 70 songs by a female singer: 60 songs were used for training and the remaining were used for testing. The speech signals were sampled at a rate of 48 kHz. The acoustic features consisted of 49-th order mel-cepstral coefficients of spectral envelope, log fundamental frequency, 24-th order mel-cepstral coefficients of aperiodicity ratio, and vibrato parameters. The mel-cepstral coefficients were extracted from the smoothed spectrum analyzed by WORLD [4] using the mel-cepstral analysis [20] with . The aperiodicity ratio was computed by the TANDEM-STRAIGHT algorithm [23] and was also compressed by the mel-cepstral analysis with the same . The acoustic features were normalized to have zero mean and unit variance. For the duration predictor in Fig. 1, five-state, left-to-right, no-skip hidden semi-Markov models [24] were built to obtain the time alignment between the acoustic and score features extracted from the input score. The input feature for the acoustic model was an 844-dimensional feature vector including the score and duration features. The acoustic model was the stack of three fully connected layers, three convolutional layers, two bidirectional LSTM layers, and a linear projection layer [25]. For the prenets and , the same network architecture of the Parallel WaveGAN generator [7] was used except that the number of channels was reduced by half. The parameters were optimized through the Adam optimizer [26] with a learning rate of and mini-batch size of 8. The models were trained for 260K steps using a single GPU machine with random initialization. The learning rate was reduced by half to 130K steps.
The dimension of and was 30. The order of cepstral coefficients in Eq. (16) was 199 for and 24 for . The order of the Maclaurin expansion in Eq. (17) was set to 20. For the multi-resolution STFT loss, and the window sizes were set to where the hop sizes were % overlap. Since it is computationally expensive to compute for the entire audio waveform, we randomly cropped the predicted acoustic feature sequence to 70 frame segments and fed them to the linear filters in the same manner as VITS [27] during training. The loss in the acoustic feature domain in Eq. (12) was
| (18) |
where and are ground-truth and predicted acoustic features, respectively, denotes their -th order dynamic components, and was set to 2 [28]. In Eq. (18),
| (19) |
where is the dimension of the acoustic features, is the length of the acoustic features, and is a trainable -dimensional time-invariant diagonal covariance matrix. The parameter was not used for inference. The hyperparameter in Eq. (12) was chosen to be .
The methods to compare were as follows:
-
•
MS-sg A baseline system in which sg means stop gradient. The acoustic model was trained using only the objective . The prenets and were not used. The waveform was synthesized by feeding the predicted acoustic features to the mel-cepstral synthesis filter described in Eq. (17).
-
•
MS Same as MS-sg except that the acoustic model was trained using the two objectives and .
-
•
PMS-sg The acoustic model and prenets were simultaneously trained using Eq. (12). However, the loss propagated through only and to the acoustic model, i.e., mel-cepstral coefficients were not explicitly affected by .
-
•
PMS The acoustic model and the prenets were simultaneously trained using Eq. (12).
-
•
PN-sg The acoustic model was trained using only the objective . The waveform was synthesized by feeding the predicted acoustic features to the PeriodNet [12], which is a neural vocoder suitable for singing speech synthesis. The PeriodNet model was separately trained on the same training data. Note that the joint training of the acoustic and PeriodNet models is fairly difficult due to computational resources.
5.2 Experimental result
Two subjective listening tests were conducted. Both tests evaluated the naturalness of synthesized speech by the mean opinion score (MOS) test method., but the second test shifted the pitch up 12 semitones to assess the robustness against fundamental frequencies. Each of the 12 participants rated 10 phrases randomly selected from the 10 test songs.
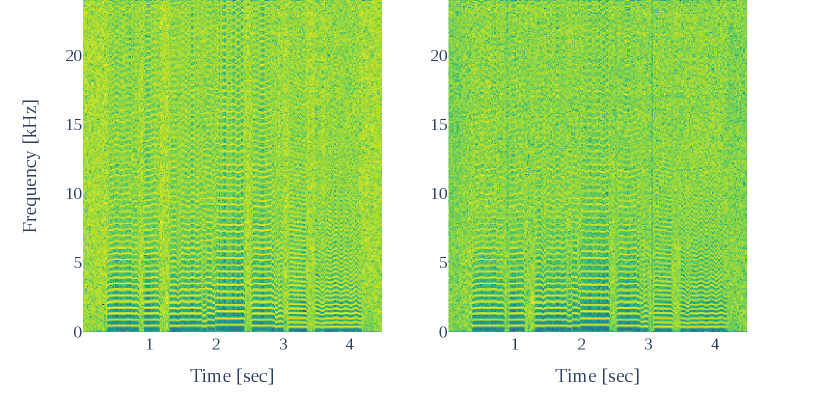
Figure 4 shows the result of the first test. MS obtained a higher score than MS-sg. This means that considering the loss in the waveform domain is effective to improve speech quality. PMS further improved from MS. This indicates that the prenets can compensate for the modeling ability of the simple linear filter. Although PMS did not use any GAN-based training and the network size was smaller than the PeriodNet model, the score was close to PN-sg. PMS-sg obtained a much lower score than PMS, indicating the importance of the simultaneous optimization. Figure 4 shows the result of the second test. Even though PMS includes the prenets, PMS achieved a similar score to that of MS. This robustness cannot be seen in PN-sg, a pure neural waveform model. We observed that the proposed system could also control voice characteristics via the frequency warping parameter without degradation. Audio samples are available on our demo page222https://www.sp.nitech.ac.jp/~takenori/sample_icassp2023.html. To see the effect of the prenets, the spectrograms of excitation signals with and without the prenets are plotted in Fig. 5. The prenets mainly work on the higher frequency domain, which cannot be well captured by mel-cepstral coefficients.


6 Conclusion
This paper proposed a neural speech synthesis system with an embedded mel-cepstral synthesis filter. Experimental results showed that the proposed system can synthesize speech with reasonable quality and has very high robustness against fundamental frequencies. Future work includes to investigate the optimal network architecture of the prenets and to introduce GAN training to boost the performance of the proposed system.
References
- [1] Alan W. Black, Heiga Zen, and Keiichi Tokuda, “Statistical parametric speech synthesis,” in IEEE International Conference on Acoustics, Speech and Signal Processing, 2007, vol. 4, pp. 1229–1232.
- [2] Noboru Sugamura and Fumitada Itakura, “Speech analysis and synthesis methods developed at ECL in NTT –from LPC to LSP–,” Speech Communication, vol. 5, no. 2, pp. 199–215, 1986.
- [3] Satoshi Imai, Kazuo Sumita, and Chieko Furuichi, “Mel log spectrum approximation (MLSA) filter for speech synthesis,” Electronics and Communications in Japan, vol. 66, no. 2, pp. 11–18, 1983.
- [4] Masanari Morise, Fumiya Yokomori, and Kenji Ozawa, “WORLD: A vocoder-based high-quality speech synthesis system for real-time applications,” IEICE Transactions on Information and Systems, vol. E99-D, no. 7, pp. 1877–1884, 2016.
- [5] Aäron van den Oord, Sander Dieleman, Heiga Zen, Karen Simonyan, Oriol Vinyals, Alex Graves, Nal Kalchbrenner, Andrew W Senior, and Koray Kavukcuoglu, “WaveNet: A generative model for raw audio,” arXiv:1609.03499, 2016.
- [6] Jean-Marc Valin and Jan Skoglund, “LPCNet: Improving neural speech synthesis through linear prediction,” in IEEE International Conference on Acoustics, Speech and Signal Processing, 2019, pp. 5891–5895.
- [7] Ryuichi Yamamoto, Eunwoo Song, and Jae-Min Kim, “Parallel WaveGAN: A fast waveform generation model based on generative adversarial networks with multi-resolution spectrogram,” in IEEE International Conference on Acoustics, Speech and Signal Processing, 2020, pp. 6199–6203.
- [8] Jungil Kong, Jaehyeon Kim, and Jaekyoung Bae, “HiFi-GAN: Generative adversarial networks for efficient and high fidelity speech synthesis,” in Advances in Neural Information Processing Systems, 2020, vol. 33, pp. 17022–17033.
- [9] Nanxin Chen, Yu Zhang, Heiga Zen, Ron J. Weiss, Mohammad Norouzi, and William Chan, “WaveGrad: Estimating gradients for waveform generation,” 2009.00713, 2020.
- [10] Xin Wang, Shinji Takaki, and Junichi Yamagishi, “Neural source-filter waveform models for statistical parametric speech synthesis,” IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol. 28, pp. 402–415, 2020.
- [11] Yi-Chiao Wu, Tomoki Hayashi, Patrick Lumban Tobing, Kazuhiro Kobayashi, and Tomoki Toda, “Quasi-periodic WaveNet: An autoregressive raw waveform generative model with pitch-dependent dilated convolution neural network,” IEEE/ACM Transactions on Audio, Speech and Language Processing, vol. 29, pp. 1134–1148, 2021.
- [12] Yukiya Hono, Shinji Takaki, Kei Hashimoto, Keiichiro Oura, Yoshihiko Nankaku, and Keiichi Tokuda, “PeriodNet: A non-autoregressive raw waveform generative model with a structure separating periodic and aperiodic components,” IEEE Access, vol. 9, pp. 137599–137612, 2021.
- [13] Keiichi Tokuda and Heiga Zen, “Directly modeling speech waveforms by neural networks for statistical parametric speech synthesis,” in IEEE International Conference on Acoustics, Speech and Signal Processing, 2015, pp. 4215–4219.
- [14] Keiichi Tokuda and Heiga Zen, “Directly modeling voiced and unvoiced components in speech waveforms by neural networks,” in IEEE International Conference on Acoustics, Speech and Signal Processing, 2016, pp. 5640–5644.
- [15] Keiichi Tokuda, Takao Kobayashi, and Satoshi Imai, “Adaptive cepstral analysis of speech,” IEEE Transactions on Speech and Audio Processing, vol. 3, no. 6, pp. 481–489, 1995.
- [16] Eunwoo Song, Kyungguen Byun, and Hong-Goo Kang, “ExcitNet vocoder: A neural excitation model for parametric speech synthesis systems,” in 27th European Signal Processing Conference, 2019, pp. 1–5.
- [17] Jesse Engel, Lamtharn (Hanoi) Hantrakul, Chenjie Gu, and Adam Roberts, “DDSP: Differentiable digital signal processing,” in International Conference on Learning Representations, 2020.
- [18] Giorgio Fabbro, Vladimir Golkov, Thomas Kemp, and Daniel Cremers, “Speech synthesis and control using differentiable DSP,” arXiv:2010.15084, 2020.
- [19] Shahan Nercessian, “Differentiable WORLD synthesizer-based neural vocoder with application to end-to-end audio style transfer,” arXiv:2208.07282, 2022.
- [20] Keiichi Tokuda, Takao Kobayashi, Takeshi Chiba, and Satoshi Imai, “Spectral estimation of speech by mel-generalized cepstral analysis,” Electronics and Communications in Japan (Part 3), vol. 76, no. 2, pp. 30–43, 1993.
- [21] Alan V. Oppenheim and Don H. Johnson, “Discrete representation of signals,” Proceedings of the IEEE, vol. 60, no. 6, pp. 681–691, 1972.
- [22] Alan V. Oppenheim and Ronald W. Schafer, Discrete-time signal processing, Prentice-Hall Signal Processing Series. Pearson, third edition, 2009.
- [23] Hideki Kawahara, Masanori Morise, Toru Takahashi, Hideki Banno, Ryuichi Nisimura, and Toshio Irino, “Simplification and extension of non-periodic excitation source representations for high-quality speech manipulation systems,” in Interspeech, 2010, pp. 38–41.
- [24] Heiga Zen, Keiichi Tokuda, Takashi Masuko, Takao Kobayashi, and Tadashi Kitamura, “A hidden semi-Markov model-based speech synthesis system,” IEICE Transactions on Information and Systems, vol. E90–D, no. 5, pp. 825–834, 2007.
- [25] Yukiya Hono, Kei Hashimoto, Keiichiro Oura, Yoshihiko Nankaku, and Keiichi Tokuda, “Sinsy: A deep neural network-based singing voice synthesis system,” IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol. 29, pp. 2803–2815, 2021.
- [26] Diederik Kingma and Jimmy Ba, “Adam: A method for stochastic optimization,” arXiv:1412.6980, 2014.
- [27] Jaehyeon Kim, Jungil Kong, and Juhee Son, “Conditional variational autoencoder with adversarial learning for end-to-end text-to-speech,” arXiv:2106.06103, 2021.
- [28] Kazuhiro Nakamura, Shinji Takaki, Kei Hashimoto, Keiichiro Oura, Yoshihiko Nankaku, and Keiichi Tokuda, “Fast and high-quality singing voice synthesis system based on convolutional neural networks,” in IEEE International Conference on Acoustics, Speech and Signal Processing, 2020, pp. 7239–7243.