Electronic Correlation Effects on Stabilizing a Perfect Kagome Lattice and Ferromagnetic Fluctuation in LaRu₃Si₂

A perfect Kagome lattice features flat bands due to the destructive interference of electron hoppings within the geometrically frustrated structure Syôzi (1951); Mielke (1991); Tasaki (1992); Sachdev (1992); Tang et al. (2011). When flat bands are near the Fermi level, it usually induces strong electronic correlation effects such as unconventional superconductivity Cao et al. (2018); Balents et al. (2020); Aoki (2020); Heikkilä and Volovik (2016); Jiang et al. (2022); Nie et al. (2022), magnetism Mielke (1991); Tasaki (1992), topological phases Tang et al. (2011) and exotic charge density waves Jiang et al. (2021); Teng et al. (2022). In recent years, these flat-bands-induced correlation effects have been widely studied in Kagome metals, for example, FeSn Kang et al. (2020a); Lin et al. (2020), FeGe Huang and Lu (2020); Teng et al. (2022), Fe₃Sn₂ Ye et al. (2018); Lin et al. (2018); Yin et al. (2018), CoSn Kang et al. (2020b); Liu et al. (2020); Yin et al. (2020a); Meier et al. (2020); Huang et al. (2022), RT₆Ge₆ (R=rare-earth elements, T=Mn, Cr) Yin et al. (2020b); Yang et al. (2022). But how electronic correlation, in turn, stabilizes a perfect Kagome lattice has rarely been explored. Here, we study such effect in a Kagome metal LaRu₃Si₂ Vandenberg and Barz (1980); Li et al. (2016, 2011); Mielke et al. (2021); Gong et al. (2022), using density functional theory (DFT) plus $U$ Anisimov et al. (1991) and plus dynamical mean-field theory (DMFT) Georges et al. (1996); Lichtenstein et al. (2001); Kotliar et al. (2006).

LaRu₃Si₂ is a superconductor with a highest $T_{c}\sim 7.8$ K Vandenberg and Barz (1980) among the known Kagome superconductors at ambient conditions. It is a paramagnetic metal at high-temperate. Non-Fermi-liquid (NFL) behavior was inferred from transport experiments, indicating substantial electronic correlations from Ru-$4d$ orbitals Li et al. (2011). A recent DFT calculation based on the electron-phonon coupling mechanism yields a $T_{c}\sim 1.2$ K, much smaller than the experimental value Mielke et al. (2021), also indicating other factors such as electronic correlations and magnetic fluctuations must be considered to understand its superconductivity.

The perfect Kagome structure of LaRu₃Si₂ with space group P6/mmm is shown in Fig. 1(a) and 1(c). The Kagome layer consists of pure Ru atoms, different from most other Kagome materials in which an anion usually resides in the center of the hexagon of the Kagome structure. Adjacent to the Kagome layer is a layer consisting of a triangular lattice of La and a honeycomb lattice of Si. However, a previous X-Ray diffraction study shows that LaRu₃Si₂, in reality, crystallizes into a slightly distorted Kagome structure with a doubling of the $c$-axis and the space group P6₃/m Vandenberg and Barz (1980) (see Fig. 1(b) and 1(e)). Given only one kind of ion (Ru) present in the Kagome layer of LaRu₃Si₂, it provides an ideal platform for studying its electronic correlation effects on stabilizing a perfect Ru Kagome lattice, since it rules out possible crystalline field effects of anion on the stability of the Kagome lattice.

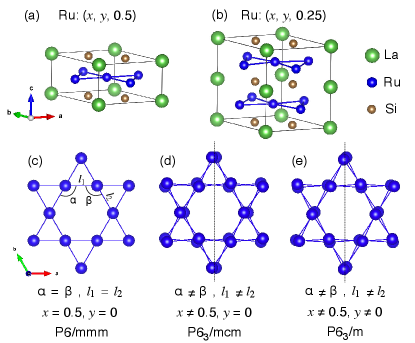
Our calculations find that increasing electronic correlation can stabilize a perfect Kagome lattice and induce substantial ferromagnetic fluctuations in LaRu₃Si₂. By comparing the calculated magnetic susceptibilities to experimental data, LaRu₃Si₂ is found to be on the verge of the transition from a distorted to a perfect Kagome lattice. It thus shows moderate but non-negligible electronic correlations and ferromagnetic fluctuations, consistent with the experimentally observed NFL behavior Li et al. (2011). Furthermore, our calculations show that the distorted Kagome structure of LaRu₃Si₂ may hold higher symmetry (space group P6₃/mcm, see Fig. 1(d)) than that reported by previous experiment (P6₃/m) Vandenberg and Barz (1980), which should be further examined by high-resolution crystal structure refinement with high-quality samples.

We perform DFT+U calculations using the VASP package Kresse and Furthmüller (1996); Blöchl (1994), with exchange-correlation functional of both local density approximation (LDA) and generalized gradient approximation (GGA) Perdew et al. (1996). The energy cutoff of the plane-wave basis is set to be 500 eV, and a $\Gamma$-centered $21\times 21\times 21$ K-point grid is used. The internal atomic positions are relaxed in the non-magnetic states, until the force of each atom is smaller than 1 meV/Å. The rotationally invariant DFT+U method introduced by Liechtenstein et al. Liechtenstein et al. (1995) is used, which is parameterized by Hubbard $U$ and Hund’s coupling $J_{H}$ (LDAUTYPE=1 or 4). It turns out that the spin-orbital coupling (SOC) of Ru would not change the main conclusions, so we only present the non-SOC results in the main text, and a SOC result is presented in the Supporting Information (Fig. S1) sup . The energies of two magnetic orders, ferromagnetic (FM) and A-type anti-ferromagnetic (AFM) (Fig. S2) sup , are also calculated by GGA+U.

We also perform fully charge self-consistent LDA+DMFT calculations in the paramagnetic states of LaRu₃Si₂, using the code EDMFTF developed by Haule et al. Haule et al. (2010); Haule and Birol (2015) based on the WIEN2K package Blaha et al. (2020). We choose a wide hybridization energy window from -10 to 10 eV with respect to the Fermi level. All five Ru-$4d$ orbitals are considered as correlated ones and a local Coulomb interaction Hamiltonian with rotationally invariant form is applied. The local Anderson impurity model is solved by the continuous time quantum Monte Carlo (CTQMC) solver Gull et al. (2011). We use an “exact” double counting scheme invented by Haule Haule (2015). The self-energy on real frequency $\Sigma(\omega)$ is obtained by the analytical continuation method of maximum entropy. We follow the method introduced by Haule et al. Haule and Pascut (2016) to perform structure relaxation in the framework of LDA+DMFT. All the calculations are preformed at $T=290$ K. Following Ref. Haule and Birol (2015), we use the Yukawa representation of the screened Coulomb interaction, in which there is an unique relationship between $U$ and $J_{H}$. If $U$ is specified, $J_{H}$ is uniquely determined by a code in EDMFTF tut . Their values are tabulated in the Supporting Information (Table S1) sup and are also used for the DFT+U calculations.

To reveal the role of electronic correlation effects on stabilizing a perfect Kagome lattice in LaRu₃Si₂, (1) we vary the Hubbard $U$ from 0 to 6 eV in our calculation; (2) we perform a comparative study on a hypothetical crystal structure LaFe₃Si₂ with the same lattice parameters and initial atomic positions as LaRu₃Si₂, since Fe-$3d$ orbitals are expected to show stronger electronic correlations than Ru-$4d$ orbitals. To uncover how the adjacent LaSi₂ layers affect the stability of the Ru₃ Kagome layer, we also perform comparative calculations by varying the lattice parameter ratio $c/a$ with the fixed crystal volume from experiment. The experimental lattice parameters are $a=5.676$ Å, $c=7.12$ Å, which gives a volume of 198.65 ų Vandenberg and Barz (1980). Crystal structure with space group P6₃/m and Ru sites at ($x=0.52$, $y=0.01$, $z=0.25$) is constructed as the starting point for relaxation (see Fig. 1(b) and 1(e)). However, all the relaxations converge to the higher symmetry structure with space group P6₃/mcm ($x\neq 0.5$, $y=0$, $z=0.25$), where an additional $C_{2}$ and mirror symmetry is present (see Fig. 1(d)). Therefore, we will only discuss the results of space group P6₃/mcm below.

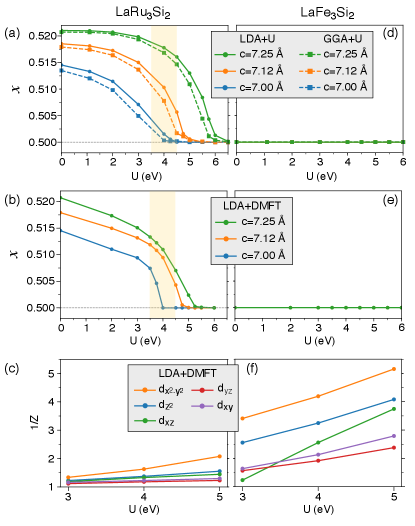
Fig. 2(a)-(b) and (d)-(e) show the fractional coordinate $x$ of Ru (Fe) relaxed by LDA+U, GGA+U and LDA+DMFT methods, for different $c/a$ ratio. For LaRu₃Si₂, as increasing $U$, all the methods yield a tendency that $x$ is decreasing and approaching to the value of a perfect Kagome lattice ($=0.5$). We note that LaFe₃Si₂ converges to the perfect Kagome structure even at $U=0$. Comparing to LDA+U, the GGA+U method that is expected to better describe the correlation effects, gives smaller $x$ (dashed curves in Fig. 2(a)). Fig. 2(c) and (f) show the LDA+DMFT calculated orbital-resolved quasi-particle mass-enhancement, $m^{\star}/m^{DFT}=1/Z$, due to the electronic correlation effects, where $Z$ is quasi-particle weight. The system is more correlated as $1/Z$ deviates more from 1. The electronic correlation become stronger as increasing $U$, and LaFe₃Si₂ shows much stronger correlation than LaRu₃Si₂ as expected. The most correlated orbital is $d_{x^{2}-y^{2}}$ which contributes to the flat bands near the Fermi level (see below). Therefore, these results indicate that strong electronic correlation would stabilize a perfect Kagome lattice consisting of transition metal ions in the system of LaX₃Si₂ (X=Ru, Fe).

Fig. 2(a)-(b) also show that increasing the lattice parameter ratio $c/a$, i.e., longer distance between the Ru₃ Kagome layer and LaSi₂ layer, tends to increase $x$ and distort the Kagome plane. Thus, larger Hubbard $U$ is required to stabilize a perfect Kagome lattice at larger ratio of $c/a$.

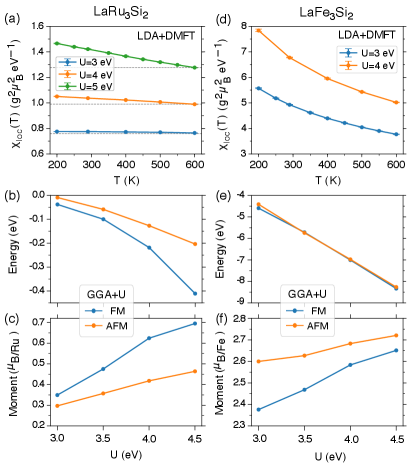
Fig. 3(a) and (d) show the local magnetic susceptibilities $\chi_{\text{loc}}(T)$ calculated by LDA+DMFT for different $U$. For LaRu₃Si₂ , $\chi_{\text{loc}}(T)$ shows Pauli paramagnetism behavior at $U=3$ eV, while it shows a Curie-Weiss-like behavior at $U=5$ eV. In between, $\chi_{\text{loc}}(T)$ slightly increases as decreasing temperate, which is consistent with that measured by experiment (see Fig.7 in Ref. Li et al. (2011)). Based on this, we infer that the actual Hubbard $U$ for LaRu₃Si₂ is about 4 eV. At this $U$ value, LaRu₃Si₂ is thus found to be on the verge of crystallizing into a perfect Kagome structure, according to the relaxation results at the experimental lattice parameters shown as the orange curves in Fig. 2(a),(b). At $U=4$ eV, the mass-enhancement of the most correlated orbital $d_{x^{2}-y^{2}}$ is about 1.63 (Fig. 2(c)). This indicates a moderate electronic correlation in LaRu₃Si₂, consistent with a slightly large Wilson ratio $R=2.88$ ($R=1$ for non-interacting electron gas) and a NFL contribution to the electronic specific heat, found by the transport experiment Li et al. (2011). In contrast, $\chi_{\text{loc}}(T)$ shows a well-defined Curie-Weiss behavior for LaFe₃Si₂, indicating much stronger electronic correlation and magnetism.

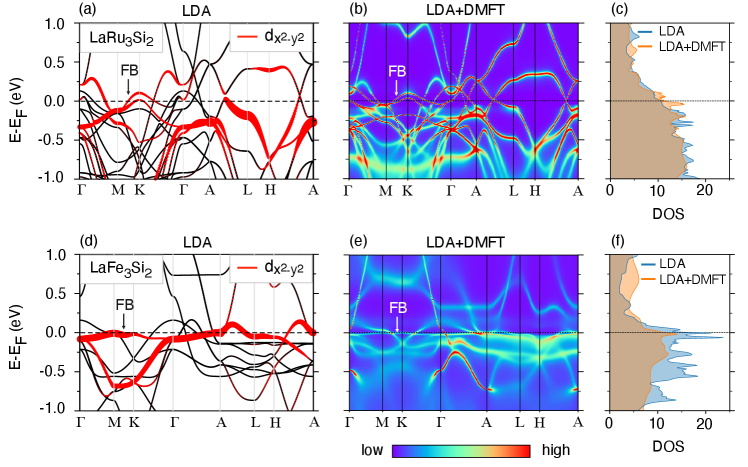
Fig. 3(b) and (e) show the energies of the FM and AFM orders with respect to the non-magnetic phase calculated by GGA+U, and Fig. 3(c) and (f) show the corresponding ordered magnetic moments. LaFe₃Si₂ has very low energies in magnetic states compared to its non-magnetic state and large ordered magnetic moments, suggesting that it tends to order as decreasing temperature. Its FM and AFM states are very close in energies, indicating comparable inter-layer FM and AFM couplings. LaRu₃Si₂ shows much weaker magnetism compared to LaFe₃Si₂, but the FM and AFM states are still found to be energetically stable at the static mean-field level. Its FM state has significantly lower energy than the AFM state. Although no magnetic orders have been observed experimentally in LaRu₃Si₂, the stable FM state found by GGA+U calculation suggests that substantial FM fluctuations may exist in LaRu₃Si₂. Such FM fluctuations should be attributed to the flat bands near the Fermi level, derived from the Kagome lattice.

Fig. 4 shows the LDA and LDA+DMFT calculated band structures and density of states (DOS) at $U=4$ eV and $J_{H}=0.782$ eV in the paramagnetic states. Extremely flat bands with $d_{x^{2}-y^{2}}$ characters clearly exist near the Fermi level in LaFe₃Si₂. However, such bands in LaRu₃Si₂ are not as flat as that in LaFe₃Si₂. By comparing the band structures between the distorted and perfect Kagome lattice of LaRu₃Si₂, we found that the magnitude of distortion of the Kagome lattice have small effects on the flat bands in LaRu₃Si₂. Actually, it is mainly caused by the more extended $4d$ orbitals that will induce non-vanishing hoppings among distant Kagome lattice sites and result in imperfect destructive interference of hoppings. In LaRu₃Si₂, the flat bands would induce substantial FM fluctuations, as shown in Fig. 3(b).

To summarize, by taking the Kagome system LaX₃Si₂ (X=Ru, Fe) as an example, we have demonstrated that strong electronic correlations could play important roles in stabilizing a perfect Kagome plane. We show that LaRu₃Si₂ is on the verge of becoming a perfect Kagome lattice and it thus exhibits moderate electronic correlation and substantial ferromagnetic fluctuations. Previous study has shown that the electron-phonon couplings alone are not nearly enough to account for a superconducting $T_{c}$ of 7.8 K in LaRu₃Si₂ Mielke et al. (2021). The electronic correlations and ferromagnetic fluctuations found in our study may play significant roles in enhancing $T_{c}$ of LaRu₃Si₂, which is worthy of further study.

As shown in the Fig. S3 in the Supporting Information sup , the only obvious difference in the simulated powder diffraction pattern of LaRu₃Si₂ between the space group P6₃/mcm and P6₃/m is an additional reflection at (1 0 1) for P6₃/m. However, its intensity is very weak compared to the main peak such that it is very difficult to be resolved experimentally. Further high-resolution crystal structure refinement with high-quality sample is required to determine whether LaRu₃Si₂ crystallizes into the space group P6₃/mcm or not. Our result thus provides a reference for the crystal structure refinement of LaRu₃Si₂.

This work was supported by USTC Research Funds of the Double First-Class Initiative (No. YD2340002005). All the calculations presented in this work were preformed on TianHe-1A, the National Supercomputer Center in Tianjin, China.