Electromagnetic evanescent field associated with surface acoustic wave:
Response of metallic thin films

First we consider the vacuum half-space ($z>d$). We demonstrate that the evanescent field is a universal feature of vacuum electromagnetic waves forced to propagate slower than the speed of light $c$. Noting $\mu_{0}\varepsilon_{0}=1/c^{2}$, Eq. (LABEL:eq:TM_TE) yields

$\displaystyle\frac{q^{2}v^{2}}{c^{2}}\begin{pmatrix}E_{x}\\ E_{y}\\ E_{z}\\ \end{pmatrix}$

$\displaystyle=$

$\displaystyle\begin{pmatrix}-\partial_{z}^{2}E_{x}+iq\partial_{z}E_{z}\\ \left(q^{2}-\partial_{z}^{2}\right)E_{y}\\ iq\partial_{z}E_{x}+q^{2}E_{z}\\ \end{pmatrix}.$

(11)

Imposing the vanishing boundary condition at $z\rightarrow\infty$, one obtains from Eq. (11),

	$\displaystyle\begin{pmatrix}E_{x}\\ E_{z}\\ \end{pmatrix}$	$\displaystyle=$	$\displaystyle C^{\rm TM}\begin{pmatrix}1\\ i\gamma\\ \end{pmatrix}e^{-q\left(z-d\right)/\gamma},$		(12)
	$\displaystyle E_{y}$	$\displaystyle=$	$\displaystyle C^{\rm TE}e^{-q\left(z-d\right)/\gamma},$		(13)

where $\gamma=1/\sqrt{1-v^{2}/c^{2}}$ is the Lorentz factor, and we assume $q>0$ in the following. The integration constants, $C^{\rm TE}$ and $C^{\rm TM}$, will be determined by the boundary conditions at $z=d$. Equations (12) and (13) represent the transverse magnetic (TM) and the transverse electric (TE) modes, respectively.

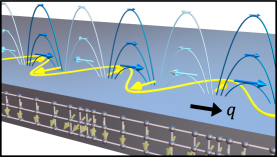
The above solution has been derived independently of the boundary conditions at $z=d$. This shows that any electromagnetic waves in vacuum that decay at infinity $(z\rightarrow\infty)$ automatically take the form of the evanescent wave Bliokh et al. (2014), as pointed out for the special case of the Bleustein-Glyaev type SAW Bleustein (1968); Gulyaev (1969) in highly symmetric piezoelectric materials Li (1996). As an example, the TM mode Eq. (12) is schematically illustrated in Fig. 2. The electric and magnetic field lines display the presence of an electromagnetic field associated with the SAW. Note that going beyond the electrostatic approximation predicts a nonzero magnetic field, hence the transverse component of the electric field, associated with the SAW. Although the magnetic field component is significantly smaller compared to the free electromagnetic field, this result can potentially be relevant because it directly couples to electron spin and magnetization Jiang et al. (2023); Kline et al. (2024).

Next we consider the solution inside a conducting slab. We assume that the conductor is isotropic, and introduce the reduced speed of light $c_{m}=(\mu_{0}\varepsilon_{0}\varepsilon_{r})^{-1/2}$, the skin depth $\delta_{m}=\sqrt{2/qv\mu_{0}\sigma_{c}}$, and the Thomas-Fermi length $\lambda_{\mathrm{TF}}=\sqrt{D_{e}\varepsilon_{0}\varepsilon_{r}/\sigma_{c}}$. One then obtains

$$\left(\frac{q^{2}v^{2}}{c_{m}^{2}}+\frac{2i}{\delta_{m}^{2}}\right)\begin{pmatrix}E_{x}\\ E_{y}\\ E_{z}\\ \end{pmatrix}\\ =\begin{pmatrix}-\partial_{z}^{2}E_{x}+iq\partial_{z}E_{z}\\ \left(q^{2}-\partial_{z}^{2}\right)E_{y}\\ iq\partial_{z}E_{x}+q^{2}E_{z}\\ \end{pmatrix}+\frac{2i\lambda_{\mathrm{TF}}^{2}}{\varepsilon_{0}\varepsilon_{r}\delta_{m}^{2}}\begin{pmatrix}iq\rho\\ 0\\ \partial_{z}\rho\\ \end{pmatrix},$$

(14)

with

$$\rho=\varepsilon_{0}\varepsilon_{r}\left(iqE_{x}+\partial_{z}E_{z}\right).$$

(15)

The general solutions are written in the form,

$$\bm{E}=\bm{E}^{\rm TM}+\bm{E}^{\rm TE}+\bm{E}^{\rm L},$$

(16)

where $\nabla\cdot\bm{E}^{\rm TM}=\nabla\cdot\bm{E}^{\rm TE}=0$, $\nabla\times\bm{E}^{\rm L}=0$, and

	$\displaystyle\begin{pmatrix}E_{x}^{\rm TM}\\ E_{z}^{\rm TM}\\ \end{pmatrix}=$	$\displaystyle\ C_{+}^{\rm TM}\begin{pmatrix}1\\ -iq/\alpha\\ \end{pmatrix}e^{\alpha\left(z-d\right)}+C_{-}^{\rm TM}\begin{pmatrix}1\\ iq/\alpha\\ \end{pmatrix}e^{-\alpha z},$		(17)
	$\displaystyle E_{y}^{\rm TE}=$	$\displaystyle\ C^{\rm TE}_{+}e^{\alpha\left(z-d\right)}+C^{\rm TE}_{-}e^{-\alpha z},$
	$\displaystyle\begin{pmatrix}E_{x}^{\rm L}\\ E_{z}^{\rm L}\\ \end{pmatrix}=$	$\displaystyle\ C_{+}^{\rm L}\begin{pmatrix}iq/Q\\ 1\\ \end{pmatrix}e^{Q\left(z-d\right)}+C_{-}^{\rm L}\begin{pmatrix}-iq/Q\\ 1\\ \end{pmatrix}e^{-Qz},$

with

	$\displaystyle\alpha$	$\displaystyle=$	$\displaystyle q\sqrt{1-\frac{v^{2}}{c_{m}^{2}}-\frac{2i}{\left(q\delta_{m}\right)^{2}}},$		(18)
	$\displaystyle Q$	$\displaystyle=$	$\displaystyle\frac{1}{\lambda_{\rm TF}}\sqrt{1+\left(q\lambda_{\rm TF}\right)^{2}-i\eta},$		(19)
	$\displaystyle\eta$	$\displaystyle=$	$\displaystyle\frac{qv\varepsilon_{0}\varepsilon_{r}}{\sigma_{c}}=\frac{v^{2}}{2c_{m}^{2}}\left(q\delta_{m}\right)^{2},$		(20)

whereas the other components vanish, $E^{\rm TM}_{y}=E^{\rm L}_{y}=E^{\rm TE}_{x}=E^{\rm TE}_{z}=0$. Thus, the electric field consists of TM, TE, and longitudinal components with two integration constants each. Note that $\eta$ represents the ratio of displacement current ($\varepsilon_{r}\varepsilon_{0}\partial_{t}E$) to drift current ($\sigma_{c}E$), which is several orders of magnitude smaller than unity in metals for microwave frequency field. For later use, we give electric current density and charge density,

$$\begin{pmatrix}J_{x}\\ J_{z}\\ \end{pmatrix}=\sigma_{c}\begin{pmatrix}E^{\rm TM}_{x}\\ E^{\rm TM}_{z}\\ \end{pmatrix}+i\eta\sigma_{c}\begin{pmatrix}E^{\rm L}_{x}\\ E^{\rm L}_{z}\\ \end{pmatrix},\\ \ J_{y}=\sigma_{c}E_{y}^{\rm TE}$$

(21)

$$\rho=-i\varepsilon_{0}\varepsilon_{r}\frac{Q^{2}}{q}\left(1-\frac{q^{2}}{Q^{2}}\right)E_{x}^{\mathrm{L}}.$$

(22)

Without relying on the electrostatic approximation, we have obtained the precise decay length of the transverse components, Eq. (18), which explicitly takes the skin effect into account. Equation (18) reproduces the previous result $\alpha=q$ Ingebrigtsen (1970) if we neglect the skin effect ($\delta_{m}\to\infty$) and take the limit $v/c\rightarrow 0$, whereas it reduces to the ordinary skin effect if we set $v=c_{m}$. Since the SAW velocity $v$ is about five orders of magnitude smaller than the speed of light, $v/c_{m}\ll 1$ is always satisfied. Thus the difference between the updated $\alpha$ [Eq. (18)] and the conventional one Ingebrigtsen (1970) comes from the imaginary term under the square root. The derived expression suggests that the contribution of the skin effect cannot be neglected when $\delta_{m}$ is comparable to $q^{-1}$ and in such a case it predicts a shorter decay length than the conventional model. Such a situation occurs in materials with sufficiently large conductivity and thus the result obtained here can be important especially for metallic films.

Let us proceed to discuss the boundary conditions that can be imposed independently of the other regions. Equation (17) has six integration constants corresponding to three dynamical degrees of freedom; two for photons and another for conduction electrons. Two of the constants can be eliminated by imposing $J_{z}=0$ at the boundaries, enabling one to express $C_{\pm}^{\rm L}$ in terms of $C_{\pm}^{\rm TM}$;

$\displaystyle\begin{pmatrix}C_{+}^{\rm L}\\ C_{-}^{\rm L}\\ \end{pmatrix}=$

$\displaystyle\ \frac{qe^{Qd}}{2\alpha\eta\sinh Qd}\begin{pmatrix}1-e^{-\left(Q+\alpha\right)d}&-e^{-\alpha d}+e^{-Qd}\\ e^{-\alpha d}-e^{-Qd}&-1+e^{-\left(Q+\alpha\right)d}\\ \end{pmatrix}\begin{pmatrix}C_{+}^{\rm TM}\\ C_{-}^{\rm TM}\\ \end{pmatrix}.$

(23)

Thus the general solutions in the conducting slab have four constants to be determined by the electromagnetic boundary conditions. At this stage, one already sees that the ratio $C^{\rm L}_{\pm}/C_{\pm}^{\rm TM}$ is roughly equal to $q/\alpha\eta$. This is a robust consequence of the current conservation at the boundaries and holds irrespective of the materials outside as long as they are insulating. Then, from Eq. (21), the ratio of the in-plane current induced by the longitudinal field to that by the transverse field is $\sim(q/\alpha)\cdot(q/Q)$. As explicitly shown in Sec. VI, there typically exists a hierarchy $\eta\ll q/Q\ll\alpha/q\sim 1$, so that the in-plane current is induced mostly by the transverse field. As for the electric field [Eq. (17)], the longitudinal component dominates near the interface whereas the transverse one decays slower and becomes prominent in relative terms into the depth of the metal, which is a different behavior from the electric current. This is because the electric current contains the diffusive component induced by the charge accumulation in addition to the drift current proportional to the electric field. Note that these estimates can be easily confirmed for films of infinite thickness, where $C_{+}^{\rm L/TM/TE}=0$, and

$\displaystyle\begin{pmatrix}E_{x}\\ E_{z}\\ \end{pmatrix}$

$\displaystyle\propto i\eta\begin{pmatrix}i\alpha/q\\ -1\\ \end{pmatrix}e^{-\alpha z}-\begin{pmatrix}iq/Q\\ -1\\ \end{pmatrix}e^{-Qz},\quad E_{y}\propto e^{-\alpha z},$

(24)

$\displaystyle\begin{pmatrix}J_{x}\\ J_{z}\\ \end{pmatrix}$

$\displaystyle\propto i\eta\sigma_{c}\Bigg{[}\begin{pmatrix}i\alpha/q\\ -1\\ \end{pmatrix}e^{-\alpha z}-\begin{pmatrix}iq/Q\\ -1\\ \end{pmatrix}e^{-Qz}\Bigg{]},\quad J_{y}\propto\sigma_{c}e^{-\alpha z}.$

(25)

In general, the analytical solutions for this case ($z<0$) are either unavailable or intractable mainly because the system intrinsically lacks rotational symmetry. Since our model ignores mechanical degrees of freedom in the conductor, the electromagnetic field inside the piezoelectric substrate affects the conducting slabs only via the boundary conditions, i.e., the amplitudes of the electric and magnetic fields at $z=-0$. Taking advantage of this, we merely outline the framework of the numerical calculation here, avoiding the actual evaluation of the electromagnetic field and treating their interface values as input parameters in the later analysis.

The solutions can be computed by simultaneously solving Eqs. (8) and (LABEL:eq:TM_TE) under the constraints Eqs. (4) and (7) and given boundary conditions Tiersten (1963); Tseng and White (1967); Campbell and Jones (1968); Ingebrigtsen (1969). Eliminating $\bm{D}$ by Eq. (7), there exist six unknown functions, $\bm{u}$ and $\bm{E}$, governed by the six time-evolution equations (8) and (LABEL:eq:TM_TE) with one constraint Eq. (4), implying five dynamical degrees of freedom. The equations are explicitly shown in Eq. (41) in Appendix IX.1, which do not contain the second order derivative of $E_{z}$ with respect to $z$. This makes it harder to determine the order of the equations in $\partial_{z}$, or the number of the integration constants. One may thus algebraically eliminate $E_{z}$ and $\partial_{z}E_{z}$ from the seven equations (Eqs. (8), (LABEL:eq:TM_TE), and Eq. (4)) and obtain five equations of second order in $\partial_{z}$ for five dependent variables ($u_{x},u_{y},u_{z},E_{x}$, and $E_{y}$), which yields ten integration constants. The number is reduced by half by demanding either exponential decay towards $z=-\infty$ Ingebrigtsen and Tonning (1969). The stress-free boundary condition, i.e., the vanishment of the stress normal to the substrate surface, should be able to eliminate three of the five remaining constants, leaving two to be determined through the electromagnetic boundary conditions, which in fact encode the information of the adjoining medium, i.e., the conductor facing vacuum in our case.

Let us discuss the relation between the results described above and those obtained from the electrostatic approximation. First, we comment on the definition of the electrostatic approximation. It is often the case that one neglects the time derivative of $\bm{B}$. Setting $\partial_{t}\bm{B}=\bm{0}$ in Eq. (1) leads to $\nabla\times\bm{E}=\bm{0}$, which allows one to use $\bm{E}=-\nabla\phi$. However, Eq. (3) does not exactly hold when $\partial_{t}\bm{B}=\bm{0}$: substituting $\partial_{t}\bm{B}=\bm{0}$ into the time derivative of Eq. (3) multiplied by $\mu_{0}$ reads

$\displaystyle\mu_{0}\partial_{t}^{2}\bm{D}+\mu_{0}\partial_{t}\bm{J}=0.$

(35)

This is the requirement to justify the electrostatic approximation. When $\bm{E}^{\rm TM}$, $\bm{E}^{\rm TE}$ and $\bm{E}^{\rm L}$ in Eq. (17) are plugged into Eq. (35), one obtains

$\displaystyle-q^{2}\quantity[\quantity(\frac{v}{c_{m}})^{2}+\frac{2i}{\quantity(q\delta_{m})^{2}}]\quantity(\bm{E}^{\rm TM}+\bm{E}^{\rm TE})=0.$

(36)

Equation (36) shows that we must assume $1/(q\delta_{m})\ll 1$ together with $v/c_{m}\ll 1$ to uphold Eq. (3) under $\partial_{t}\bm{B}=\bm{0}$. We therefore define the electrostatic approximation as $\partial_{t}\bm{B}=\bm{0}$ and $\nabla\times\bm{E}=\bm{0}$, where the latter emerges from substituting the former into Eq. (1). Indeed, this is the approach taken by Ingebrigtsen Ingebrigtsen (1970). The sufficient conditions to uphold all the Maxwell equations under the electrostatic approximation are $1/(q\delta_{m})\ll 1$ and $v/c_{m}\ll 1$. Note that $1/(q\delta_{m})$ is independent of $v/c_{m}$. For the case under interest here, the former is of the order unity while the latter is small, providing an example where $v/c_{m}\ll 1$ is not a sufficient condition to justify the electrostatic approximation.

Here we remark on how our results fit into the electrostatic approximation. The electric field is then purely longitudinal, which should be screened by free charges and cannot penetrate into the conductor beyond the electrostatic screening length ($\sim\lambda_{\rm TF}$). This apparently contradicts our results [Eq. (17)] in which the transverse component remains nonzero and unscreened up to a much larger distance $\sim q^{-1}$ even in the electrostatic limit. To resolve this puzzle, one should carefully distinguish two possible definitions of the longitudinal and transverse components. Namely, one may call $\bm{E}^{\mathrm{L}}$ ($\bm{E}^{\mathrm{T}}$) longitudinal (transverse) if
(i) $\nabla\times\bm{E}^{\mathrm{L}}=\bm{0}$ ($\nabla\cdot\bm{E}^{\mathrm{T}}=0$),
or if
(ii) $\nabla\cdot\bm{E}^{\mathrm{L}}\neq 0$ ($\nabla\times\bm{E}^{\mathrm{T}}\neq\bm{0}$).
So far, we have used (i) to classify longitudinal and transverse fields, which conforms with the terminology often used. However, (ii) is better adapted in the screening argument as it is the condition for generating the screening charges and currents through the Gauss’ and Ampère-Maxwell law, respectively. The difference between the two definitions is usually immaterial, but it does matter when $\bm{E}=-\nabla\phi$ and $\nabla^{2}\phi=0$, i.e., when $\phi$ is a harmonic function. Such a harmonic $\bm{E}$ qualifies to be longitudinal as well as transverse under (i), whereas it is neither of them according to (ii). It turns out that $\bm{E}^{\mathrm{TM}}$ in Eq. (17) is exactly the harmonic $\bm{E}$ under the electrostatic approximation. That is, $\bm{E}^{\mathrm{TM}}$ satisfies both $\nabla\cdot\bm{E}^{\mathrm{TM}}=0$ and $\left(\nabla\times\bm{E}^{\mathrm{TM}}\right)_{y}\propto iq\left(\alpha^{2}/q^{2}-1\right)E_{z}^{\mathrm{TM}}\rightarrow 0$ as $\alpha\to q$. Thus $\bm{E}^{\mathrm{TM}}$ is longitudinal by (i) but is not by (ii). If we were to use (ii), it is reasonable to have $\bm{E}^{\mathrm{TM}}$ that penetrates deep into the conductor with a decay length of $\sim q^{-1}$. Note that abandoning the electrostatic approximation removes such ambiguity: the longitudinal and transverse components are clearly distinguished (there is no equivalent harmonic component) and they are respectively screened by induced charges and currents.

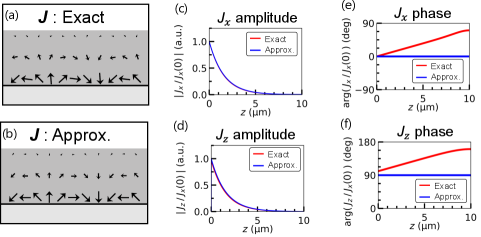
As shown in Section III.2, calculations with and without the electrostatic approximation provide quantitatively different results unless $1/\quantity(q\delta_{m})\ll 1$.

To see this, we estimate the distribution of the electric current in films with large electrical conductivity: $\sigma_{c}=5\times 10^{7}~{}(\mathrm{\Omega\cdot m})^{-1}$m. With these parameters, $q/Q\sim 10^{-5}$, $\eta\sim 10^{-10}$ and $\delta_{m}=3.6\ \upmu$m. Consequently, we have $q\delta_{m}=2.3$ that violates the condition for the electrostatic approximation.

Figure 3 shows the profiles of the electric current density profiles $J_{x},J_{z}$ with and without the electrostatic approximation. The solutions under the approximation are obtained by substituting $v/c_{m}=0$ and $1/(q\delta_{m})=0$ into those without it. We set the film thickness $d=10\ \upmu$m to display the changes along the $z$-axis. Without the approximation, the electric current changes its phase monotonically along the $z$-axis whereas the phase remains constant under the approximation This is caused by the imaginary part of $\alpha$ [Eq. (18)], which is not negligible for films with large conductivity. As is evident from the plots shown in Fig. 3(a,b), the phase change manifests itself in the current flow distribution along the $z$-axis. At a given position in the $x$-$y$ plane, the current changes its direction as one moves along the $z$-axis when the electrostatic approximation is abandoned, whereas the direction remains the same throughout the entire film when the approximation is maintained.

Next, we model an experimental setup in which SAW-induced spin current was foundKawada et al. (2021). In accordance with the experiments, the film conductivity and thickness are set to $\sigma_{c}=10^{6}~{}(\mathrm{\Omega\cdot m})^{-1}$ and $d=1$ nm, respectively; however, qualitatively similar results are obtained as long as $d\lesssim 1/\alpha\sim 100$ nm. These parameters return $q/Q\sim 10^{-5}$, $\eta\sim 10^{-8}$ and $\delta_{m}=25\ \upmu$m. Thus $1/(q\delta_{m})\sim 0.06$, allowing one to use the electrostatic approximation. However, here we do not apply the approximation and follow the discussion described above.

From the parameters defined above, $\left|\alpha d\right|\sim qd\sim 10^{-3}$ and $Qd\sim 20$ hold so that $\sinh\alpha d\sim 10^{-3}$, $\cosh\alpha d\sim 1$, $\sinh Qd\sim\cosh Qd\gg 1$. Therefore, Eq. (34) is well approximated by

$$C_{0}^{\rm TM}\sim\frac{2e^{-Qd}}{\varepsilon_{r}qd}\frac{E_{x0}}{\eta/qd+iq/Q},\quad C_{0}^{\rm TE}\sim E_{y0}.$$

(37)

Note that $\eta$ cannot be set to zero even at this leading order. Using the same approximations, one obtains

	$\displaystyle\begin{pmatrix}E_{x}^{\rm TM}\\ E_{z}^{\rm TM}\\ \end{pmatrix}$	$\displaystyle\sim$	$\displaystyle\frac{\eta}{2qd}\frac{E_{x0}}{\eta/qd+iq/Q}\begin{pmatrix}e^{q(z-d)}+e^{-qz}\\ -i(e^{q(z-d)}-e^{-qz})\\ \end{pmatrix}$		(38)
		$\displaystyle\sim$	$\displaystyle\frac{\eta}{qd}\frac{E_{x0}}{\eta/qd+iq/Q}\begin{pmatrix}1\\ i(qd/2-qz)\\ \end{pmatrix},$
	$\displaystyle\begin{pmatrix}E_{x}^{\rm L}\\ E_{z}^{\rm L}\\ \end{pmatrix}$	$\displaystyle\sim$	$\displaystyle\frac{E_{x0}e^{-Qz}}{\eta/qd+iq/Q}\begin{pmatrix}iq/Q\\ -1\\ \end{pmatrix}.$		(39)

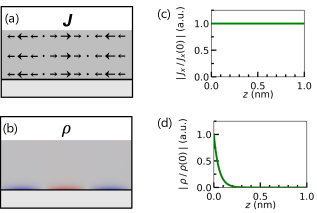
As shown in Eqs. (21) and (22), $\bm{E}^{\rm L}$ is effectively screened by the small factor $\eta$ while $\bm{E}^{\rm TM}$ remains sizable in the film. Therefore, the charge current inside metal is completely dominated by the transverse contribution whereas the charge density is mostly induced by $E_{z}^{\rm L}$. We note that $\left|E_{x}^{\rm TM}\right|\gg\left|E_{z}^{\rm TM}\right|$ is consistent with $\nabla\cdot\bm{E}^{\rm TM}=0$ as the smallness of $E_{z}^{\rm TM}$ is a result of cancellation between the $C_{+}^{\rm TM}$ and $C_{-}^{\rm TM}$ terms; such cancellation is absent in the $z$ derivative $\partial_{z}E^{\rm TM}_{z}$ because of the sign change of the latter term.

The uniformity of the electric current and the localization of the charge density within the metallic thin film are directly demonstrated by evaluating Eqs. (21) and (22) using Eq. (17). The results are schematically illustrated in Fig. 4 (a) and (b). Due to the small factor of $\eta$ originating from the electrostatic screening, the longitudinal components of $\bm{J}$ that originates from $\bm{E}^{\rm L}$ localized at the film surfaces become negligibly small. In addition, cancellation between $C_{+}^{\rm TM}$ and $C_{-}^{\rm TM}$ results in a significant decrease of $J_{z}$ overall. The charge density $\rho$ is confined at the interface between the substrate and film to screen out $E^{\rm L}_{z}$ coming from the substrate. To illustrate the distribution along $z$ more quantitatively, the absolute values of $J_{x}$ and $\rho$ are plotted against $z$ in Fig. 4 (c) and (d). We see that $J_{x}$ is almost uniform along $z$ in the whole film and $\rho$ is concentrated within the range of the Thomas-Fermi length from the substrate surface.

Recent experimental work has demonstrated that SAWs induce an ac spin current in metallic thin films with significant spin-orbit interaction, an effect referred to as the acoustic spin Hall effect Kawada et al. (2021). The observed spin current flows parallel to the surface normal with its polarization orthogonal to both the flow and SAW propagation directions, and is distributed uniformly across the film thickness direction. Under the assumption that electric fields are efficiently screened by conduction electrons and decay rapidly in metals, the latter feature suggests that the spin current should have a mechanical origin rather than electromagentic one. From this work, however, we conclude that the SAW-induced electric field generates an electric current uniformly in the thickness direction in metallic thin films. This allows the uniform spin current to flow in strong spin orbit metals via the spin Hall effect, which can reasonably explain the microscopic origin of the acoustic spin Hall effect.

Here we explicitly describe equations for SAWs in a piezoelectric substrate. To emphasise the algebraic structure, let us introduce three-by-three matrices

$$\begin{gathered}G_{ij}=c_{i1j1},\quad S_{ij}=c_{i3j3},\quad T_{ij}=c_{i3j1},\\ X_{ij}=e_{ij1},\quad Y_{ij}=e_{ij3}.\end{gathered}$$

(40)

Equations (8) and (LABEL:eq:TM_TE) under the constraints Eqs. (4) and (7) can be written as

	$\displaystyle\begin{pmatrix}\partial_{z}^{2}\hat{S}+iq\partial_{z}\left(\hat{T}+\hat{T}^{T}\right)-q^{2}\hat{G}-\rho_{p}q^{2}v^{2}\hat{I}&-iq\hat{X}^{T}-\partial_{z}\hat{Y}^{T}\\ \frac{iq\hat{X}+\partial_{z}\hat{Y}}{\varepsilon_{0}}&\partial_{z}^{2}\hat{I}_{3}-iq\partial_{z}\hat{I}_{2}+q^{2}\left(\frac{\hat{\varepsilon}}{\varepsilon_{0}}\frac{v^{2}}{c^{2}}-\hat{I}_{1}\right)\\ \end{pmatrix}\begin{pmatrix}\bm{u}\\ \bm{E}\\ \end{pmatrix}$	$\displaystyle=0,$		(41)
	$\displaystyle\left\{\partial_{z}^{2}Y_{3j}+iq\partial_{z}\left(X_{3j}+Y_{1j}\right)-q^{2}X_{1j}\right\}u_{j}+\left(\partial_{z}\varepsilon_{3j}+iq\varepsilon_{1j}\right)E_{j}$	$\displaystyle=0,$		(42)

where $\hat{I}$ is the three-by-three unit matrix and

$$\hat{I}_{1}=\begin{pmatrix}0&0&0\\ 0&1&0\\ 0&0&1\\ \end{pmatrix},\quad\hat{I}_{2}=\begin{pmatrix}1&0&0\\ 0&0&0\\ 0&0&1\\ \end{pmatrix},\quad\hat{I}_{3}=\begin{pmatrix}1&0&0\\ 0&1&0\\ 0&0&0\\ \end{pmatrix}.$$

(43)

Since Eq. (41) does not contain second order derivative on $E_{z}$, the mathematical structure of the problem is harder to see than the other cases. One formal approach is to eliminate $E_{z}$ and $\partial_{z}E_{z}$ by using the last of Eq. (41) and Eq. (42), which should leave an equation for $\bm{u},E_{x},E_{y}$ of second order in $\partial_{z}$. Although this procedure cannot be used to eliminate $E_{z}$ when $\varepsilon_{33}=\varepsilon_{13}=0$, it is applicable for the Rayleigh-type SAW, the system of our interest. Then, one expects to obtain five independent solutions of the form $\propto e^{kz},(k>0)$, and the stress-free boundary condition

$$\left(\partial_{z}\hat{S}+iq\hat{T}\right)\bm{u}-\hat{Y}^{T}\bm{E}=0$$

(44)

should be able to eliminate three of the five arbitrary constants, leaving two to be determined through the electromagnetic boundary conditions.

In the main text, we expressed the electric field inside the conducting slab in terms of the electric field at the substrate/film interface. As we mentioned in the last paragraph of Sec. IV, obtaining $v$ and the relative amplitude between $E_{x0}$ and $E_{y0}$ requires the continuity of $H_{x}$ and $D_{z}$ at $z=0$. The conditions are equivalent to equating the surface impedance of both sides, as described by Refs. Ingebrigtsen (1969, 1970). The surface impedance is defined in each region independently. We first derive the analytical formula of the surface impedances in the conducting slab, which read

	$\displaystyle Z^{\rm TE}=$	$\displaystyle-i\sqrt{\frac{\mu_{0}}{\epsilon_{0}}}\frac{v}{c}\frac{q}{\alpha}\frac{C_{+}^{\rm TE}e^{-\alpha d}+C_{-}^{\rm TE}}{C_{+}^{\rm TE}e^{-\alpha d}-C_{-}^{\rm TE}},$		(45)
	$\displaystyle Z^{\rm TM}=$	$\displaystyle-i\sqrt{\frac{\mu_{0}}{\epsilon_{0}}}\frac{c}{\varepsilon_{r}v}\frac{\alpha\left(C_{+}^{\rm TM}e^{-\alpha d}-C_{-}^{\rm TM}\right)-iq\left(C_{+}^{\rm L}e^{-Qd}+C_{-}^{\rm L}\right)}{q\left(C_{+}^{\rm TM}e^{-\alpha d}+C_{-}^{\rm TM}\right)-iQ\left(C_{+}^{\rm L}e^{-Qd}-C_{-}^{\rm L}\right)}.$

From Eqs. (31) and (32), one obtains the surface impedance for the conducting slab as

$$Z^{\rm TE}=i\sqrt{\frac{\mu_{0}}{\epsilon_{0}}}\frac{v}{c}\frac{q}{\alpha}\frac{q\tanh\alpha d+\alpha\gamma}{q+\alpha\gamma\tanh\alpha d},$$

(46)

	$\displaystyle Z^{\rm TM}=$	$\displaystyle i\sqrt{\frac{\mu_{0}}{\varepsilon_{0}}}\frac{c}{v}\frac{1}{\varepsilon_{r}\left(1-i\eta\right)}\frac{\alpha}{q}\Bigg{[}\left(\frac{q}{Q}\cosh Qd\sinh\alpha d-\frac{i\alpha\eta}{q}\sinh Qd\cosh\alpha d\right)\frac{\varepsilon_{r}\left(1-i\eta\right)}{\gamma}$
		$\displaystyle+\left(\frac{q^{2}}{Q^{2}}-\frac{\alpha^{2}\eta^{2}}{q^{2}}\right)\sinh Qd\sinh\alpha d+\frac{2i\alpha\eta}{Q}\left(1-\cosh Qd\cosh\alpha d\right)\Bigg{]}$
		$\displaystyle\Bigg{/}\left[\left\{\frac{\varepsilon_{r}\left(1-i\eta\right)}{\gamma}\sinh Qd+\frac{q}{Q}\cosh Qd\right\}\sinh\alpha d-\frac{i\alpha\eta}{q}\sinh Qd\cosh\alpha d\right].$		(47)

$Z^{\rm TM}$ agrees with the expression given in Ref. Ingebrigtsen (1970) when setting $\alpha=q$ and $\gamma=1$. The expression of $Z^{\rm TE}$ can be derived only when the electrostatic approximation $v/c\rightarrow 0$ is not employed. Assuming $q\delta_{m}$ is neither very small nor large, $Z^{\rm TM}$ involves two small parameters; $q/Q$ and $\eta$. In any case, the dominant contributions arise from the terms proportional to $\varepsilon_{r}$ in both the numerator and denominator. We also remark that the limit $\sigma_{c}\rightarrow\infty$ implies $Q\rightarrow\infty,\eta\rightarrow 0$, which yields a well-defined limit and $Z^{\rm TM}=0$ consistent with the so-called shorted boundary condition Campbell and Jones (1968).

Next we outline how the surface impedance of the adjoining piezoelectric medium can be obtained. The general structure of the bulk solution of the electromagnetic fields can be inferred as discussed in Sec. III.3. This solution should contain two arbitrary constants that characterize it (for instance, $E_{x0}$ and $E_{y0}$), allowing for the numerical computation of the surface impedance $Z^{\rm TE}$, $Z^{\rm TM}$ on the side $z<0$ if the value of $v$ is determined.