Electrically driven resonant magnetization, spin-pumping and charge-to-spin conversion from chiral-spin modes at THz frequencies
Abstract
Chiral-spin modes are collective excitations of a spin-orbit (SO) coupled system that lead to resonances in many observables. Here we identify resonances in “cross-response”, i.e., electric-field induced magnetization and magnetic-field induced electric currents, known also as the Edelstein effect and its inverse, respectively. We show that the chiral-spin modes resonantly enhance the electrically induced magnetization. As specific examples, we consider a single-valley two-dimensional electron gas with Rashba or Dresselhaus SO coupling and a two-valley Dirac system with proximity-induced Rashba and valley-Zeeman SO couplings. We suggest an architecture for a spin-pumping experiment based on THz excitation of chiral-spin modes, which would demonstrate a resonant enhancement of charge-to-spin conversion.
Introduction:
A plethora of fundamentally important and potentially useful phenomena arise from spin-orbit (SO) interaction which couples the charge and spin degrees of freedom in electron systems. These include the spin Hall effect [1, 2] (observed in GaAs-based heterostructures [3, 4]), inverse spin Hall effect [5] (observed via optical induction of spin polarization [6, 7]), dynamical spin accumulation [8], Edelstein effect [9, 10] (observed in GaAs heterojunctions [11] and possibly also in strained InGaAs [12]), inverse-Edelstein/spin-galvanic effect (observed in GaAs heterojunctions [13] and at Bi/Ag interface [14] and explained subsequently in Ref. [15]), etc. There are also resonances due to spin splitting in materials that can be seen via the electric-dipole spin resonance (EDSR) [16, 17, 18] (found in bulk semiconductors [19, 20], quantum wells [21], quantum dots [22, 23] and nanowire-based qubits [24]). In this effect, spin excitations between spin split states can happen by absorbing energy from an external oscillatory -field, a phenomenon that is absent in electrons without SO interaction. The spin splitting in early works was extrinsically induced by a static -field. However, it was shown that the intrinsic spin splitting due to SO interaction of Bloch states itself leads to resonances from the so called chiral-spin modes (CSMs) [25, 26, 27, 28], which can be probed by both oscillatory - and -fields. Hitherto not detected via EDSR, CSMs lead to resonances which have been observed by Raman spectroscopy at zero fields in topological surface states of Bi2Se3 [29] and at finite fields in CdTe quantum wells [30, 31, 32, 33, 34, 35]. These modes have also been predicted to exist in proximity-induced SO coupled multi-valley systems like monolayer graphene [36, 37].
In this letter we point out that there are other direct consequences of the CSMs, in the form of resonant magnetization and current density induced by oscillatory electric and magnetic fields, that are relevant for spintronics in the ultrafast regime 111The -field is assumed to act only on electron spins.. Consider the linear response of matter to and fields, which can be written in terms of the induced magnetization and current () as 222These are momentum and frequency dependent and the arguments are suppressed for brevity.
| (1a) | |||||
| (1b) | |||||
where and are the cross response tensors that arise solely due to SO interaction, as opposed to the direct-response tensors, spin susceptibility() and conductivity (), which exist already without SO coupling but are modified by the latter. Here we show that near a CSM resonance frequency due to Rashba type SO interaction in both single and multi-valley systems, the induced magnetization and electric current are given by
| (2a) | |||||
| (2b) | |||||
where and are the Pauli paramagnetic susceptibility and dc conductivity of the electron gas without SO coupling ( being the momentum relaxation rate), respectively, is the Compton wavevector (we set ) with and being the bare electron mass and speed of light in vacuum, respectively, where with being the SO splitting at the Fermi momentum which sets the CSM frequency and is the Fermi velocity, , and is the effective Landé g-factor. The resonances occur in the ballistic regime where , with being the effective spin-relaxation time. The first term in Eq. (2a) describes a chiral-spin resonance (CSR), i.e., an electron spin resonance in the absence of a static magnetic field [25, 40]. The second term is the resonant magnetization induced by the electric field, which is one of the main results of this Letter. It is phase-shifted by with respect to the electric field and, for an electromagnetic wave with , is larger than the first term by a factor of , which is for a typical semiconductor structure. The Edelstein effect is, in fact, the static limit of the cross-response . Next, the first term in Eq. (2b) is the Drude tail of the Ohmic current, while the second term is the EDSR, i.e, SO-enabled resonant coupling between the -field and electron spins. The EDSR amplitude is proportional to , which is typically small (), and therefore the EDSR signal needs to have a high quality factor to be visible against the Drude tail [27]. Finally, the third term in Eq. (2b) is another cross-response: a resonant electric current induced by an oscillatory magnetic field.
In this Letter, we derive the high-frequency, microscopic forms of the cross-response phenomenological coefficients in Eqs. (1a) and (1b) for a single valley [specifically a 2D electron gas (2DEG)] system with Rashba or Dresselhaus SO coupling and a multivalley [specifically monolayer graphene] system with substrate-induced Rashba and/or valley-Zeeman (Ising) SO coupling. We also discuss potential applications of cross-responses in these systems, such as spin-pumping and charge-to-spin conversion. In what follows, we focus on the non-interacting case; the role of electron-electron interactions is detailed in the companion paper [41].
Kinetic equation.
To find the tensor of response function, we employ a kinetic equation for the non-equilibrium density matrix [42, 43]
where denotes the commutator of operators and , and and are SO-free and SO parts of the Hamiltonian, respectively. The two cases on the right-hand side correspond to driving with - and -fields with frequency , respectively. Here, where is the equilibrium distribution function, is the Bohr magneton, and is the vector of spin matrices. The collision-integral term is modeled as with a single relaxation time , as the distinction between the momentum and spin relaxation times is not essential in the ballistic limit. The magnetization and electric current are then determined as
| (3) |
where denotes the anticommutator of operators and , and . Here and thereafter, all bold-faced vectors are in the plane of a 2D system, while the -component, if needed, will be labeled explicitly. We focus on doped/gated semiconductors or semi-metals subject to the following condition , where is the characteristic SO energy scale and is the bandwidth. The first inequality justifies the kinetic-equation approach, while the second one allows one to neglect lattice effects.
EDSR and resonant Edelstein effects due to Rashba SO coupling.
First, we study linear response to an oscillatory -field in the presence of Rashba SO coupling. For a 2DEG, the corresponding SO part of the Hamiltonian is given by [44], while for graphene one obtains after projecting out the fully occupied band [37], where is a identity matrix in the valley subspace and is the unit vector of . Solving for (see Ref. [41]) we find that the conductivity is given by , where
| (4) |
is the dc conductivity of a normal metal, is the total density of states at the Fermi level (as appropriate for 2DEG and graphene), and . The subscripts in denote a response in which is induced by . Similarly, for the cross-responses in Eq. (1a) we find that
| (5) |
and is the dc “Edelstein conductivity” [9]. The poles of the resonance factors are at the CSR frequency which, in the non-interacting limit, coincides with . Equations. (EDSR and resonant Edelstein effects due to Rashba SO coupling.) and (5) can be re-written as
| (6) |
which makes it clear that the induced magnetization is in-plane and perpendicular to . The resonance in is the EDSR effect due to an intrinsic spin splitting [25, 40, 37], while that in can be termed as the “resonant Edelstein effect”.
EDSR and resonant Edelstein effect due to Dresselhaus SO coupling.
A 2DEG formed in a non-centrosymmetric semiconductor harbors a Dresselhaus SO coupling, which is a projection of bulk Dresselhaus coupling onto the 2D plane. For (001) crystal plane of a semiconductor with symmetry, the Dresselhaus Hamiltonian is given by [45]. The resonance in the electric conductivity remains the same modulo a replacement [28]. However, there is an important change to the tensor structure of the Edelstein conductivity, namely
| (7) |
where is given by the first line of Eq. (5). As opposed to the Rashba case, is now along the vector obtained by reflecting about the -axis. This orientational property of allows one to distinguish between Rashba and Dresselhaus types of SO coupling. This is not possible with the direct response. We note that the anisotropic aspect of the tensor has been explored in the context of both the Edelstein effect and its inverse in the static and diffusive regime [46, 47, 48, 49, 50, 51, 52]; in the present work, we explore its dynamical version in the ballistic regime.
Valley-Zeeman SO coupling.
A multivalley (honeycomb) system mounted on a heavy-atom substrate, e.g., graphene on a transition-metal dichalcogenide (TMD), harbors not only Rashba but also valley-Zeeman (VZ, also called Ising) SO coupling, which acts as an out-of-plane Zeeman field of the sign which alternates between the valleys [53]. The corresponding term in the Hamiltonian reads [54, 55]. If both Rashba and VZ couplings are present, we find
| (8) | |||||
| (9) |
where sets the resonance frequency and is defined after Eq. (5). Although the spin splitting depends on both and , the amplitude of the cross-response resonance is still proportional only to because only the Rashba SO interaction allows for a coupling between electron spins and -field.
CSR and resonant inverse Edelstein effect.
We now turn to a resonant response to the oscillatory -field. Solving the kinetic equation for the case of Rashba SO coupling, we obtain
| (10) |
where is the paramagnetic susceptibility of a normal metal. Equation (CSR and resonant inverse Edelstein effect.) applies both to 2DEG and graphene. The proportionality of to reflects Onsager reciprocity [15].
Discussion.
Using Eqs (EDSR and resonant Edelstein effects due to Rashba SO coupling.),(5) and (CSR and resonant inverse Edelstein effect.), and expressing in terms of , we can combine the results into the universal form presented in Eqs (1). In the companion paper [41], we show that electron correlations renormalize the resonance frequencies and, for the case of a multivalley system, also split both direct and cross-response resonances into two [37]. Finally, we avoid the subtle effect of disorder in the diffusive limit () by focusing on the region near the resonance, where .
In Fig. 1a,b we show -driven (i.e. ) and -driven (i.e. ) current and magnetization, denoted by and , respectively, for a multivalley system. The results for a single-valley system are similar [41]. Several features need to be pointed out. i) Electrically driven responses (both direct and cross) are orders of magnitude stronger than magnetically driven ones even away from the resonance. In fact, with pulsed electric fields of MVcm-1 [56, 57, 58], the peak magnetic moment density near CSRs from Eq. (5) is found to be per square nm of the sample (for graphene on TMDs we have [59]). ii) Although the total current induced by the -field is much larger than that induced by the -field, most of the former is due to a featureless Drude background while the EDSR peak is barely discernible, even for a large quality factor, e.g., . On the other hand, the resonance in a much smaller -induced current is well resolved. Note that for normal incidence, with both - and -fields being in the 2DEG plane, the -induced part of the current would be masked by the Ohmic response. However, if the electromagnetic wave is incident at a grazing angle with the electric field pointing out of the plane, the Ohmic response would be absent allowing full access to the resonance in the inverse Edelstein effect. iii) For magnetization, the resonances are well resolved in both direct (-induced) and cross (-induced) cases, but the signal is stronger in the cross-response. This remains true as long as , or . This is easily satisfied near resonance and below it, but not at higher frequencies.
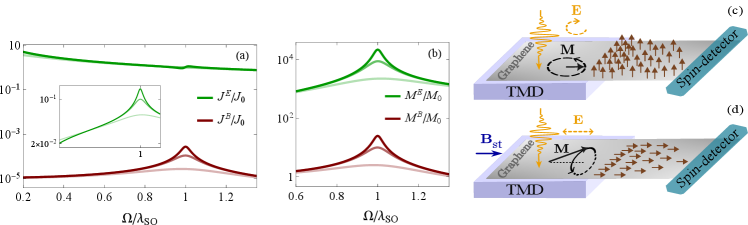
Spin-pumping.
Precessing magnetization of a magnet pumps spin to an adjacent non-magnetic layer (without pumping charge) [60, 61], producing a flow of spins , polarized along the precession axis 333There can be an additional channel if such contacts can be designed [60].. Here, is the spin-mixing conductance which is controlled by the properties of an interface between the magnetic and non-magnetic layers. Conventionally, spin-pumping is achieved by exciting a ferromagnetic resonance (FMR), which lies typically in the GHz range. Recently, ultrafast spin-pumping using antiferromagnetic resonance (aFMR) in the sub-THz regime has also been demonstrated [63, 64]. Given that the SO-induced spin-splitting in graphene on TMD is in the THz range [59, 65], we propose a different architecture for ultrafast spin-pumping, based on the resonant Edelstein effect. The proposed setup is shown in Figs. 1, panels c) and d). Panel c) depicts an all-electric platform, in which a circularly polarized THz pulse is incident on a region of graphene in direct contact with a TMD layer, which induces both Rashba and VZ types of SO coupling in graphene. Via the resonant Edelstein effect, the -field of the pulse induces precessing magnetization which leads to flow of spins, polarized out-of-plane, through a region of pristine graphene towards a detector, based, e.g., on inverse spin-Hall effect. Alternatively, one can also inject spins polarized in-plane using a linearly polarized pulse and, in addition, applying a static -field in the plane of the graphene layer, as depicted in Fig. 1d). While the induced magnetization is linearly polarized in the absence of a static -field (), the latter introduces elliptic polarization with its axis along . The ellipticity is proportional to [40, 28]. The choice of graphene was made due to its long spin relaxation length [66, 67] (without TMD substrate) and also the fact that ferromagnet-based on-chip spin injection to graphene has been demonstrated [68]. According to Ref. [59], in graphene on TMDs, which makes the resonance reasonably sharp.
Resonantly enhanced charge-to-spin conversion.
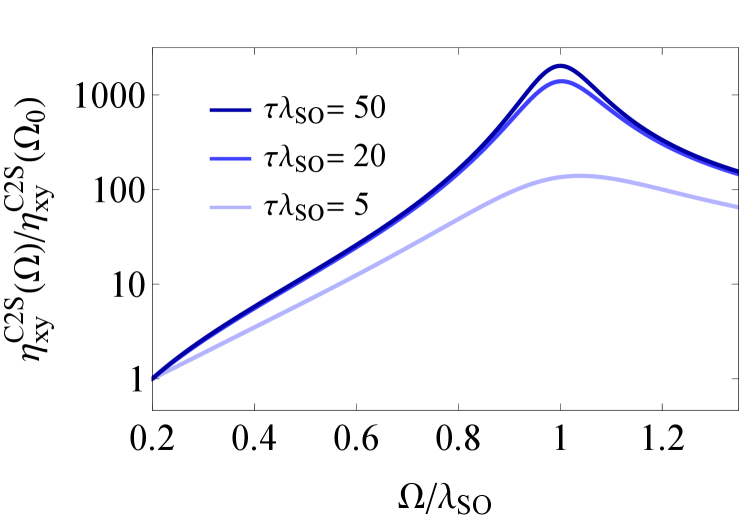
In spintronics, to quantify the charge-to-spin (C2S) conversion in the diffusive limit, researchers have introduced an intrinsic figure-of-merit (which we shall denote by ) such that with dimensions of 1/velocity [69]. The reported value of is [70, 71, 72], which is only achieved when is tuned to the bottom of the Rashba-split bands. For the practical case of larger , is known to drop quickly [69]. In the ballistic limit, we may extend this notion to “dynamical” figure-of-merit tensor for the C2S conversion: . In Fig. 2 we show that operating near a CSR provides a large enhancement in C2S conversion merit tensor (), and that too in the large limit where the conversion is known to be suppressed in the diffusive regime.
Conclusion:
We have shown that intrinsic spin splitting in SO coupled systems leads to resonances in cross-responses, namely, resonant Edelstein and inverse Edelstein effects. We have also shown that the resonant Edelstein effect provides the largest induced magnetization of all responses and proposed schemes to use this enhancement for spin pumping in the THz regime for ultrafast spintronics. Finally, we have also shown that an intrinsic figure-of-merit for charge-to-spin conversion is also enhanced near the resonances.
Acknowledgments:
We thank P. Armitage, F.S. Bergeret, and X.-X. Zhang for stimulating discussions. MS and SM were funded by the Natural Sciences and Engineering Research Council of Canada (NSERC) Grant No. RGPIN-2019-05486. A.K. was supported by the FSU Quantum Postdoctoral Fellowship from Florida State University. A.K. also acknowledges support from Canada First Research Excellence Fund and by the Natural Sciences and Engineering Research Council of Canada (NSERC) under Grant No. RGPIN-2019-05312 during his time at Sherbrooke. DLM was supported by the US National Science Foundation via grant DMR-2224000.
References
- D’yakonov and Perel’ [1971] M. I. D’yakonov and V. I. Perel’, Sov. Phys.–JETP Letters 13, 657 (1971).
- Hirsch [1999] J. E. Hirsch, Phys. Rev. Lett. 83, 1834 (1999).
- Kato et al. [2004a] Y. K. Kato, R. C. Myers, A. C. Gossard, and D. D. Awschalom, Science 306, 1910 (2004a), https://www.science.org/doi/pdf/10.1126/science.1105514 .
- Wunderlich et al. [2005] J. Wunderlich, B. Kaestner, J. Sinova, and T. Jungwirth, Phys. Rev. Lett. 94, 047204 (2005).
- Averkiev and Dyakonov [1983] N. Averkiev and M. I. Dyakonov, Sov. Phys. Semicond. 17, 393 (1983).
- Bakun et al. [1984] A. Bakun, B. Zakharchenya, A. Rogachev, M. Tkachuk, and V. Fleisher, Sov. Phys. JETP Lett. 40, 1293 (1984).
- Tkachuk et al. [1986] M. Tkachuk, B. Zakharchenya, and V. Fleisher, Sov. Phys. JETP Lett. 44, 59 (1986).
- Duckheim et al. [2009] M. Duckheim, D. L. Maslov, and D. Loss, Phys. Rev. B 80, 235327 (2009).
- Edelstein [1990] V. Edelstein, Solid State Communications 73, 233 (1990).
- Aronov et al. [1991] A. Aronov, Y. B. Lyanda-Geller, and G. Pikus, Journal of Experimental and Theoretical Physics Letters 73, 537 (1991).
- Silov et al. [2004] A. Y. Silov, P. A. Blajnov, J. H. Wolter, R. Hey, K. H. Ploog, and N. S. Averkiev, Applied Physics Letters 85, 5929 (2004).
- Kato et al. [2004b] Y. K. Kato, R. C. Myers, A. C. Gossard, and D. D. Awschalom, Phys. Rev. Lett. 93, 176601 (2004b).
- Ganichev et al. [2002] S. Ganichev, E. Ivchenko, V. Belkov, S. Tarasenko, M. Sollinger, D. Weiss, W. Wegscheider, and W. Prettl, Nature 417 (2002).
- Sánchez et al. [2013] J. C. R. Sánchez, L. Vila, G. Desfonds, S. Gambarelli, J. P. Attané, J. M. De Teresa, C. Magén, and A. Fert, Nature Communications 4, 2944 (2013).
- Shen et al. [2014a] K. Shen, G. Vignale, and R. Raimondi, Phys. Rev. Lett. 112, 096601 (2014a).
- Rashba and Efros [2003] E. I. Rashba and A. L. Efros, Appl. Phys. Lett. 83, 5295 (2003).
- Efros and Rashba [2006] A. L. Efros and E. I. Rashba, Phys. Rev. B 73, 165325 (2006).
- Duckheim and Loss [2006] M. Duckheim and D. Loss, Nature Physics 2, 195 (2006).
- Bell [1962] R. L. Bell, Phys. Rev. Lett. 9, 52 (1962).
- McCombe et al. [1967] B. D. McCombe, S. G. Bishop, and R. Kaplan, Phys. Rev. Lett. 18, 748 (1967).
- Schulte et al. [2005] M. Schulte, J. G. S. Lok, G. Denninger, and W. Dietsche, Phys. Rev. Lett. 94, 137601 (2005).
- Nowack et al. [2007] K. C. Nowack, F. H. L. Koppens, Y. V. Nazarov, and L. M. K. Vandersypen, Science 318, 1430 (2007), https://www.science.org/doi/pdf/10.1126/science.1148092 .
- Pioro-Ladrière et al. [2008] M. Pioro-Ladrière, T. Obata, Y. Tokura, Y.-S. Shin, T. Kubo, K. Yoshida, T. Taniyama, and S. Tarucha, Nature Physics 4, 776 (2008).
- Nadj-Perge et al. [2010] S. Nadj-Perge, S. M. Frolov, E. P. A. M. Bakkers, and L. P. Kouwenhoven, Nature 468, 1084 (2010).
- Shekhter et al. [2005] A. Shekhter, M. Khodas, and A. M. Finkel’stein, Phys. Rev. B 71, 165329 (2005).
- Ashrafi and Maslov [2012] A. Ashrafi and D. L. Maslov, Phys. Rev. Lett. 109, 227201 (2012).
- Maiti et al. [2015] S. Maiti, V. Zyuzin, and D. L. Maslov, Phys. Rev. B 91, 035106 (2015).
- Kumar and Maslov [2017] A. Kumar and D. L. Maslov, Phys. Rev. B 95, 165140 (2017).
- Kung et al. [2017] H.-H. Kung, S. Maiti, X. Wang, S.-W. Cheong, D. L. Maslov, and G. Blumberg, Phys. Rev. Lett. 119, 136802 (2017).
- Perez et al. [2007] F. Perez, C. Aku-leh, D. Richards, B. Jusserand, L. C. Smith, D. Wolverson, and G. Karczewski, Phys. Rev. Lett. 99, 026403 (2007).
- Baboux et al. [2013] F. Baboux, F. Perez, C. A. Ullrich, I. D’Amico, G. Karczewski, and T. Wojtowicz, Phys. Rev. B 87, 121303 (2013).
- Baboux et al. [2015] F. Baboux, F. Perez, C. A. Ullrich, G. Karczewski, and T. Wojtowicz, Phys. Rev. B 92, 125307 (2015).
- Perez et al. [2016] F. Perez, F. Baboux, C. A. Ullrich, I. D’Amico, G. Vignale, G. Karczewski, and T. Wojtowicz, Phys. Rev. Lett. 117, 137204 (2016).
- Maiti and Maslov [2017] S. Maiti and D. L. Maslov, Phys. Rev. B 95, 134425 (2017).
- Karimi et al. [2017] S. Karimi, F. Baboux, F. Perez, C. A. Ullrich, G. Karczewski, and T. Wojtowicz, Phys. Rev. B 96, 045301 (2017).
- Raines et al. [2021] Z. M. Raines, V. I. Fal’ko, and L. I. Glazman, Phys. Rev. B 103, 075422 (2021).
- Kumar et al. [2021] A. Kumar, S. Maiti, and D. L. Maslov, Phys. Rev. B 104, 155138 (2021).
- Note [1] The -field is assumed to act only on electron spins.
- Note [2] These are momentum and frequency dependent and the arguments are suppressed for brevity.
- Maiti et al. [2016] S. Maiti, M. Imran, and D. L. Maslov, Phys. Rev. B 93, 045134 (2016).
- Saleh et al. [2025] M. Saleh, A. Kumar, D. Maslov, and S. Maiti, arXiv:2501.14059 (2025).
- Lifshitz and Pitaevskii [1980] E. Lifshitz and L. Pitaevskii, Statistical Physics, Part 2, Course of Theoretical Physics, v. IX (Butterworth and Heinmann, 1980).
- Maslov et al. [2022] D. L. Maslov, A. Kumar, and S. Maiti, JETP 135, 549 (2022).
- Bychkov and Rashba [1984] Y. A. Bychkov and E. I. Rashba, Sov. Phys.–JETP Letters 39, 66 (1984).
- Dyakonov [2017] M. Dyakonov, in Spin Physics in Semiconductors, edited by M. Dyakonov (Springer, 2017) pp. 1–28.
- Raichev [2007] O. E. Raichev, Phys. Rev. B 75, 205340 (2007).
- Shen et al. [2014b] K. Shen, R. Raimondi, and G. Vignale, Phys. Rev. B 90, 245302 (2014b).
- Gorini et al. [2017] C. Gorini, A. Maleki Sheikhabadi, K. Shen, I. V. Tokatly, G. Vignale, and R. Raimondi, Phys. Rev. B 95, 205424 (2017).
- Maleki Sheikhabadi et al. [2018] A. Maleki Sheikhabadi, I. Miatka, E. Y. Sherman, and R. Raimondi, Phys. Rev. B 97, 235412 (2018).
- Tao and Tsymbal [2021] L. L. Tao and E. Y. Tsymbal, Phys. Rev. B 104, 085438 (2021).
- Suzuki and Kato [2023] Y. Suzuki and Y. Kato, Phys. Rev. B 107, 115305 (2023).
- Dey et al. [2024] A. Dey, A. Nandy, and S. K., arXiv arXiv:2408.05188 (2024).
- Kormányos et al. [2014] A. Kormányos, V. Zólyomi, N. D. Drummond, and G. Burkard, Phys. Rev. X 4, 011034 (2014).
- Wang et al. [2015] Z. Wang, D.-K. Ki, H. Chen, H. Berger, A. H. MacDonald, and A. F. Morpurgo, Nature Communications 6, 8339 (2015).
- Cummings et al. [2017] A. W. Cummings, J. H. Garcia, J. Fabian, and S. Roche, Phys. Rev. Lett. 119, 206601 (2017).
- Oh et al. [2014] T. I. Oh, Y. J. Yoo, Y. S. You, and K. Y. Kim, Applied Physics Letters 105, 041103 (2014).
- Schlauderer et al. [2019] S. Schlauderer, C. Lange, S. Baierl, T. Ebnet, C. P. Schmid, D. C. Valovcin, A. K. Zvezdin, A. V. Kimel, R. V. Mikhaylovskiy, and R. Huber, Nature 569, 383 (2019).
- Ouyang et al. [2021] C. Ouyang, S. Li, J. Ma, B. Zhang, X. Wu, W. Ren, X. Wang, D. Wang, Z. Ma, T. Wang, T. Hong, P. Yang, Z. Cheng, Y. Zhang, K. Jin, and Y. Li, Communications Physics 4, 5 (2021).
- Wang et al. [2016] Z. Wang, D.-K. Ki, J. Y. Khoo, D. Mauro, H. Berger, L. S. Levitov, and A. F. Morpurgo, Phys. Rev. X 6, 041020 (2016).
- Tserkovnyak et al. [2002] Y. Tserkovnyak, A. Brataas, and G. E. W. Bauer, Phys. Rev. Lett. 88, 117601 (2002).
- Costache et al. [2006] M. V. Costache, M. Sladkov, S. M. Watts, C. H. van der Wal, and B. J. van Wees, Phys. Rev. Lett. 97, 216603 (2006).
- Note [3] There can be an additional channel if such contacts can be designed [60].
- Vaidya et al. [2020] P. Vaidya, S. A. Morley, J. van Tol, Y. Liu, R. Cheng, A. Brataas, D. Lederman, and E. del Barco, Science 368, 160 (2020), https://www.science.org/doi/pdf/10.1126/science.aaz4247 .
- Li et al. [2020a] J. Li, C. B. Wilson, R. Cheng, M. Lohmann, M. Kavand, W. Yuan, M. Aldosary, N. Agladze, P. Wei, M. S. Sherwin, and J. Shi, Nature 578, 70 (2020a).
- Wang et al. [2019] D. Wang, S. Che, G. Cao, R. Lyu, K. Watanabe, T. Taniguchi, C. N. Lau, and M. Bockrath, Nano Lett. 19, 7028 (2019).
- Ingla-Aynés et al. [2015] J. Ingla-Aynés, M. H. D. Guimarães, R. J. Meijerink, P. J. Zomer, and B. J. van Wees, Phys. Rev. B 92, 201410 (2015).
- Drögeler et al. [2016] M. Drögeler, C. Franzen, F. Volmer, T. Pohlmann, L. Banszerus, M. Wolter, K. Watanabe, T. Taniguchi, C. Stampfer, and B. Beschoten, Nano Letters 16, 3533 (2016).
- Indolese et al. [2018] D. Indolese, S. Zihlmann, P. Makk, C. Jünger, K. Thodkar, and C. Schönenberger, Phys. Rev. Appl. 10, 044053 (2018).
- Offidani et al. [2017] M. Offidani, M. Milletarì, R. Raimondi, and A. Ferreira, Phys. Rev. Lett. 119, 196801 (2017).
- Ghiasi et al. [2019] T. S. Ghiasi, A. A. Kaverzin, P. J. Blah, and B. J. van Wees, Nano Letters 19, 5959 (2019), pMID: 31408607.
- Li et al. [2020b] L. Li, J. Zhang, G. Myeong, W. Shin, H. Lim, B. Kim, S. Kim, T. Jin, S. Cavill, B. S. Kim, C. Kim, J. Lischner, A. Ferreira, and S. Cho, ACS Nano 14, 5251 (2020b).
- Monaco et al. [2021] C. Monaco, A. Ferreira, and R. Raimondi, Phys. Rev. Res. 3, 033137 (2021).