Electric quadrupole form factors of singly heavy baryons with spin 3/2
Abstract
We study the electromagnetic form factors of the lowest-lying singly heavy baryons in a pion mean-field approach, which is also known as the SU(3) chiral quark-soliton model. In the limit of the heavy-quark mass, the dynamics inside a singly heavy baryon is governed by the valence quarks, while the heavy quark remains as a mere static color source. In this framework, a singly heavy baryon is described by combining the colored soliton with the singly heavy quark. In the infinitely heavy-quark mass limit, we can compute the electric quadrupole form factors of the baryon sextet with spin 3/2 with the rotational and linear corrections of the explicit flavor SU(3) symmetry breaking taken into account. We find that the sea-quark contributions or the Dirac-sea level contributions dominate over the valence-quark contributions in lower region. We examined the effects of explicit flavor SU(3) symmetry breaking in detail. The numerical results are also compared with the recent data from the lattice calculation with the unphysical value of the pion mass considered, which was used in the lattice calculation.
I Introduction
Conventional lowest-lying singly heavy baryons consist of a heavy quark and two light valence quarks. In the limit of the infinitely heavy-quark mass (), the physics of singly heavy baryons becomes simple: The spin of the heavy quark is conserved in this limit and hence it leads also to the conservation of the spin of the light-quark degrees of freedom, i.e. . This is known as the heavy-quark spin symmetry Isgur:1989vq ; Georgi:1990um . In the limit, we do not distinguish a charm quark from a bottom quark, which gives up heavy-quark flavor symmetry. On the other hand, chiral symmetry and its spontaneous breakdown still play an important part in describing the singly heavy baryons because of the presence of the light quarks inside a singly heavy baryon Yan:1992gz . Then the singly heavy baryons consisting of two light valence quarks can be represented in terms of irreducible representations of flavor SU(3) symmetry: , thus we have the two representations for the lowest-lying singly heavy baryons, i.e. the baryon antitriplet and sextet. The baryon antitriplet has the total spin that comes from and , whereas the baryon sextet can have either or with and .
In a pion mean-field approach, which is also known as the SU(3) chiral quark-soliton model (QSM), a singly heavy baryon can be viewed as the valence quarks bound by the pion mean fields that are created from the presence of the valence quarks Diakonov:2010tf ; Yang:2016qdz . In fact, this idea is taken from Witten’s seminal paper on baryons in the large limit Witten:1979kh . This pion mean-field approach has successfully reproduced the mass spectra of the lowest-lying singly heavy baryons Yang:2016qdz and even explained the nontrivial isospin mass splittings of them Yang:2020klp . Interestingly, the corrections from the heavy quark mass are indeed negligible in the description of the isospin mass splittings of the singly heavy baryons as shown in Ref. Yang:2020klp , although they provide hyperfine interactions to remove the spin degeneracy of the baryon sextet.
Recently, the electromagnetic (EM) form factors of singly heavy baryons have been studied for the first time within lattice QCD Can:2013tna ; Can:2015exa . While there are no experimental data on the EM form factors of the singly heavy baryons to date, the results from the lattice calculation provide a clue to the internal structure of singly heavy baryons. Thus, it is also of great importance to investigate the EM form factors of the singly heavy baryons. In Ref. Kim:2018nqf ; Kim:2019wbg , we have studied the electric monopole and magnetic dipole form factors of the singly heavy baryons in detail, based on the QSM. Since we consider the limit of the infinitely heavy-quark mass, there is no physical difference between the heavy baryons with spin 1/2 and those with 3/2 except for the value of the spin. On the other hand, the baryon sextet with spin 3/2 has yet another structure that arises from its higher spin, which is revealed by the electric quadrupole () form factor. The form factor of a baryon exhibits how the baryon is deformed. It is also known that the pion clouds play a significant role in understanding this deformation Pascalutsa:2006up . This will be also discussed in the present work. We will also examine the effects of flavor SU(3) symmetry breaking on the form factors of the baryon sextet with spin 3/2. The numerical results for will be compared with that from the lattice calculation.
The present work is organized as follows: In Section II, we briefly recapitulate the general formalism for the electric quadrupole form factors within the framework of the chiral quark-soliton model. In Section III, we present the numerical results and discuss them in detail. The final Section is devoted to the summary and conclusion.
II Electric quadrupole form factors in the QSM
We start with the EM current for a singly heavy baryon, which is defined by
| (1) |
where stands for the light-quark field in SU(3) flavor space and denotes the heavy-quark field for the charmed or bottom quark. The charge operator is expressed as
| (2) |
The in the second term in Eq. (1) denotes the charge corresponding to a heavy quark, which has the value for the charm quark and for the bottom quark. The matrix element of between baryons with spin 3/2 can be parametrized in terms of four different real form factors as follows:
| (3) | ||||
| (4) |
where denotes the mass of a singly heavy baryon in the baryon sextet with spin 3/2. The metric tensor of Minkowski space is defined as . represents the momentum transfer and its square is written as with . means the Rarita-Schwinger spinor for a singly heavy baryon with spin 3/2, carrying the momentum and the spin component projected along the direction of the momentum. designates the antisymmetric tensor . Note that when one takes the limit of the infinitely heavy quark mass (), the heavy-quark current given in the second part of Eq. (1) can be safely neglected for the EM form factors. It gives only a constant contribution to the electric form factors as already shown in Ref. Kim:2018nqf .
It is more convenient to introduce the Sachs-type form factors or the multipole EM form factors, in particular, when the EM structure of a baryon with spin 3/2 is examined. The electric quadrupole form factor reveals how the shape of a baryon with spin 3/2 is deviated from the rotationally symmetric one. The Sachs-type form factors can be expressed in terms of given in Eq. (4)
| (5) | ||||
| (6) | ||||
| (7) | ||||
| (8) |
where . Since , have been already investigated in Ref. Kim:2018nqf , we will focus on the electric quadrupole form factors of the baryon sextet with spin 3/2, i.e., in the present work. At , yields the electric quadrupole moment
| (9) |
which reveals how much the charge distribution of a baryon is deformed from a spherical shape. If has a negative value (), then the baryon takes a cushion shape, whereas if is positive (), then it looks like a rugby-ball shape.
We want to mention that the form factors vanish in the present work. In fact, any chiral solitonic approaches yield the null results of the form factors because of the hedgehog structure Kim:2019gka . However, the experimental data on is absent to date and its value should be very tiny even if it is measured. In fact, one could compute the form factors if one takes into account the next-to-next-to-leading order in the expansion. This means that the form factors should be strongly suppressed in the large limit. Thus, we will focus in the present work on the form factors of the baryon sextet with spin 3/2.
The SU(3) QSM is constructed based on the following low-energy effective partition function in Euclidean space, defined by
| (10) |
where and denote respectively the quark and pseudo-Nambu-Goldstone boson fields. Having integrated over quark fields, we can express the partition function in terms of the effective chiral action , which is defined by
| (11) |
where represents the functional trace running over spacetime and all relevant internal spaces. The denotes the number of colors. is the dynamical quark mass that arises from spontaneous symmetry breaking of chiral symmetry. represents the chiral field that consists of the pseudo-Nambu-Goldstone (pNG) fields , , which is expressed as
| (12) |
with
| (13) |
We assume isospin symmetry, i.e., . The average mass of the up and down quarks is defined by . Then, the matrix of the current quark masses is written as . is written as
| (14) |
where and denote the singlet and octet components of the current quark masses, defined by and , respectively. The single-quark Hamiltonian is defined by
| (15) |
Since the pion field has flavor indices, one has to combine a minimal symmetric ansatz will be the hedgehog ansatz with which the flavor indices can be coupled to three-dimensional spatial axes. The pion fields are then expressed in terms of a single function , which is called the profile function, as follows
| (16) |
with . Then the SU(2) chiral field is written as
| (17) |
with . The SU(3) chiral field can be constructed by Witten’s trivial embedding Witten:1983tx
| (20) |
which preserves the hedgehog ansatz.
Integration over in Eq. (10) quantizes the pNG fields. In the large limit, the meson mean-field approximation is justified Witten:1979kh ; Witten:1983tx . Thus, we can carry out the integration over in Eq. (10) around the saddle point, where is satisfied. This saddle-point approximation yields the equation of motion that can be solved self-consistently. The solution provides the self-consistent profile function of the chiral soliton. A detailed method of the self-consistent procedure can be found in Ref. Christov:1995vm .
While the quantum fluctuations of the self-consistent pion fields can be ignored by the large argument, the fluctuations along the direction of both the rotational and translational zero modes cannot be ignored, since they are not at all small. Note that rotational and translational zero modes are related to rotational and translational symmetries. Thus, the zero modes can be taken into account by the following rotational and translational transformations
| (21) |
where is an SU(3) unitary matrix. So, the functional integral over can be approximated by those over zero modes
| (22) |
The integration over translational zero modes will naturally give the Fourier transform of the EM densities. We refer to Ref. Kim:1995mr for a detailed description of the zero-mode quantization in the present scheme.
Having carried out the zero-mode quantization, we obtain the collective Hamiltonian as
| (23) |
where
| (24) |
and denote the moments of inertia for the soliton, of which the explicit expressions can be found in Appendix A. The parameters , , and for heavy baryons arise from the breaking of flavor SU(3) symmetry, which are defined by
| (25) |
where are the anomalous moments of inertia, of which the expressions are found in Appendix A. Note that the number of light valence quarks for a singly heavy baryon is . This means that the expression for the valence part of contains also in place of . It can be related to the sigma term as follows: . The detailed expressions for the moments of inertia and are given in Ref. Kim:2018xlc .
The presence of the symmetry-breaking part in the collective Hamiltonian, , have the baryon wavefunctions mixed with those in higher SU(3) representations. In the present case, the collective wavefunctions for the baryon antitriplet () and the sextet () are obtained respectively as Kim:2018xlc
| (26) |
with the mixing coefficients
| (35) |
in the basis for the antitriplet and for the sextets with both spin 1/2 and 3/2. The parameters , , and are explicitly written as
| (36) |
The collective wavefunction for the soliton with valence quarks is then obtained in terms of the SU(3) Wigner functions
| (37) |
where represents the dimension of the representation and a charge corresponding to the soliton state , i.e., . and stand for the flavor and spin quantum numbers corresponding to the soliton for the singly heavy baryon. Finally, the complete wavefunction for a singly heavy baryon can be derived by coupling the soliton wavefunction to the heavy quark spinor
| (38) |
where denote the Pauli spinors for the heavy quark and the Clebsch-Gordan coefficients.
The matrix elements of the EM current (4) can be computed within the QSM by representing them in terms of the functional integral in Euclidean space,
| (39) | ||||
| (40) |
where the baryon states and are, respectively, defined by
| (41) | ||||
| (42) |
The heavy baryon current can be constructed from the valence quarks
| (43) |
where represent spin-flavor indices and color indices. The matrices are taken to consider the quantum numbers of the soliton. The creation operator can be constructed in a similar way. The calculation of the baryonic correlation function given in Eq. (40) is a tedious one, so we will present here only the final expressions for the form factor, As for the detailed formalism, we refer to Refs. Christov:1995vm ; Kim:1995mr .
The final expressions for the electric quadrupole form factors of the baryon sextet with spin 3/2 can be written as
| (44) |
where stands for the spherical Bessel function with order 2 and the corresponding density of the form factors is given as
| (45) | ||||
| (46) |
The densities of form factors and can be found in Appendix A. In the limit of , the charge distribution of the heavy quark becomes a point-like static charge given as . This leads to . This implies that the form factors of the singly heavy baryons are solely governed by the light quarks in the limit.
Having calculated the matrix elements of the collective operators in Eq. (46), we arrive at the final expressions for the form factors of the baryon sextet with spin 3/2
| (47) |
where , , and denote respectively the symmetric terms, the flavor SU(3) symmetry-breaking ones from the effective chiral action, and those from the mixed collective wavefunctions, expressed explicitly as
| (48) | ||||
| (52) | ||||
| (59) |
where stands for the charge of the light-quark components of the corresponding baryons. We can derive similar sum rules for the electric quadrupole moments of singly heavy baryons with spin 3/2 as follows Kim:2019gka
| (60) | |||
| (61) |
Even though the flavor SU(3) symmetry is broken, we still can find the following sum rules
| (62) | ||||
| (63) | ||||
| (64) |
III Results and discussion
In the QSM, there are several parameters to fix. Since the sea-quark or Dirac-sea contributions contain divergent integrals, one has to introduce a regularization to tame the divergences. In the present work, we introduce the proper-time regularizations with the cutoff mass. This can be fixed by using the pion decay constant MeV. The average mass of the up and down current quarks is determined by the physical pion mass MeV (see Appendix B for details). While the mass of the strange current quark can be also fixed by reproducing the kaon mass, which gives MeV, we preferably use MeV, since this value of yields the best results for the hyperon mass splittings Blotz:1992pw ; Christov:1995vm . The remaining parameter is the dynamical quark mass , which is the only free parameter of the model. However, MeV is known to be the best value in reproducing various observables in the light baryon sector Christov:1995vm . Thus, we will use this value also in the present calculation.






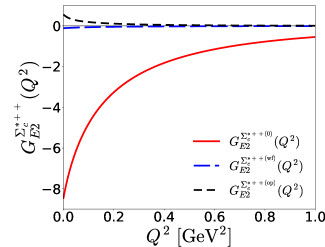
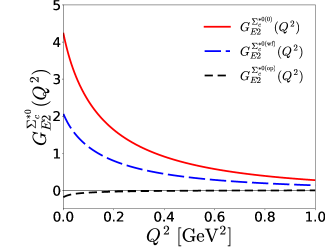
It was shown that in the calculation of the form factors of the baryon decuplet the sea-quark contributions turn out to be rather important, we will first examine the valence- and sea-quark contributions separately. In Fig. 1, we draw the numerical results for the form factors of the baryon sextet with spin 3/2. As expected, the general behaviors of the valence- and sea-quark contributions to the form factors of the heavy singly baryons are rather similar to those of the baryon decuplet. As shown in Fig. 1, the valence-quark contributions decrease off mildly as increases, whereas the sea-quark or Dirac-sea contributions fall off drastically in the smaller region, so that they govern the dependence of the form factors. In particular, the magnitudes of the sea-quark contributions are quite larger than in the region of smaller . Thus, they are the main contributions to the electric quadrupole moments of the baryon sextet with spin 3/2. Considering the fact that the electric quadrupole moment exhibits how the corresponding baryon is deformed, the present results provide certain physical implications. Recent investigations on the gravitational form factors of baryons within the QSM indicate that the valence quarks are mainly located in the inner part of a baryon, while the sea quarks lie in its outer part Goeke:2007fp ; Kim:2020nug . Thus, the sea-quark contributions, which can be also interpreted as pion clouds, mainly describe how a singly heavy baryon with spin 3/2 is deformed. The present results are in line with what was discussed in Ref. Pascalutsa:2006up , where the significance of the pion clouds in the electric quadrupole moment of the isobar was discussed .






In Fig. 2, we show how much the effects of flavor SU(3) symmetry breaking contribute to the form factors of the baryon sextet with spin 3/2. As expressed in Eqs. (52) and (59), there are two different corrections to the form factors. The first one arises from the current-quark mass term in the effective chiral action given in Eq. (11), whereas the second one comes from the wavefunction corrections (26). each correction affects form factors in a different way, as shown in Fig. 3. The wavefunction corrections to the form factor of are negligibly tiny and the corrections from the current-quark mass term is also small. As a result, the corrections turn out to be negligible, as shown in the upper left panel of Fig. 2. On the other hand, the wavefunction corrections contribute noticeably to the form factors of , while those from the current-quark mass term are of the same order as in the case of . In the case of and , the wavefunction corrections to are even larger than those from the mass term. This can be understood by examining Eqs. (52) and (59).






In the left panel of Fig. 4, we compare the results for the form factors of the baryon with that from the lattice calculation. We employ for this comparison the unphysical pion mass MeV that is used in the lattice calculation. Note that there is only one lattice data with large uncertainty.
We anticipate more accurate lattice data in the near future, so that one can draw a clear conclusion. In the right panel of Fig. 4, we depict the results of as a function of the pion mass with fixed. As expected, the present results fall off slowly as increases.
| [ fm2] | ||||||
|---|---|---|---|---|---|---|
| MeV | ||||||
| MeV |
For completeness, we present the results for the electric quadrupole moments of the baryon sextet with spin 3/2. Table 1 lists those of the in the second and third rows, which correspond to the SU(3) symmetric and breaking cases, respectively. As already shown in Fig. 2, those of the charged baryon sextet have negative values of , which indicates that the positively charged singly heavy baryons with spin 3/2 take oblate shapes. On the other hand, those of the neutral ones get positive values, so they are distorted in prolate forms. It is interesting to see that the of the doubly positive-charged is approximately 8 times larger than that of the singly positive-charged one. This can be understood by examining Eqs. (47).
IV Summary and conclusion
In the present work, we have investigated the electric quadrupole form factors of the lowest-lying singly heavy baryons with spin 3/2 in a pion mean-field approach, also knwon as the SU(3) chiral quark-soliton model. In the limit of an infinitely heavy quark, a heavy quark inside a singly heavy baryon can be regarded as a mere static color source. This means that the light valence quarks govern the quark dynamics inside a heavy baryon. The presence of the light valence quarks make the vacuum polarized, which produces the pion mean fields. The valence quarks are bound by the attraction provided by the pion mean fields self-consistently, from which a colored soliton consisting of the valence quarks arises. We call this soliton as a soliton. Then the singly heavy baryon can be constructed by coupling the soliton with a heavy quark. This is called the pion mean-field approach for the singly heavy baryons. Based on this pion mean-field approach, we computed the electric qudrupole form factors of the baryon sextet with spin 3/2, taking into account the rotational and linear corrections.
We first examined the valence- and sea-quark contributions separately. As in the case of the baryon decuplet, the contributions from the sea quarks or the Dirac-sea level quarks govern the electric quadrupole form factors, in particular, in the smaller region. Considering the fact that the electric quadrupole moment of a baryon provides information on how the baryon is deformed, we can draw the following physical implications: the deformation of a singly heavy baryon is also mainly governed by the sea-quark contributions or the pion cloud effects. We found a similar feature in the case of the baryon decuplet. The effects of the explicit flavor SU(3) symmetry breaking are also sizable except for the case of the and . Since there are two different linear corrections, we have scrutinized each effect in detail. To compare the present results with those from the lattice calculation, we have computed the electric quadrupole form factor with the unphysical value MeV adopted, which was used by the lattice work. We also showed how the value of the form factor at a fixed is changed as the increases. As expected from previous works, the value of the form factor falls off as increases. We also presented the results for the electric quadrupole moment. The charged singly-heavy baryons have consistently negative values of the electric quadrupole moments. This indicates that the charged baryons take oblate shapes. On the other hand, the neutral baryons take prolate shapes, having the positive values of the electric quadrupole moments.
Acknowledgements.
The authors are grateful to Gh.-S. Yang for valuable discussions. They want to express the gratitude to M. Oka and K. U. Can for providing us with the lattice data. The present work was supported by Basic Science Research Program through the National Research Foundation of Korea funded by the Ministry of Education, Science and Technology (2018R1A2B2001752 and 2018R1A5A1025563). J.-Y. Kim acknowledges partial support by the DAAD doctoral scholarship.Appendix A Densities for the form factor and moments of inertia
In this Appendix, we provide the explicit expressions for the and densities of the electric quadrupole form factors in Eq. (46)
| (65) | ||||
| (66) | ||||
| (67) | ||||
| (68) |
where the regularization functions are defined by
| (69) | |||
| (70) |
with the proper-time regulator Christov:1995vm . Here, and denotes the state of the valence and sea quarks with the corresponding eigenenergies and of the single-quark Hamiltonian , respectively.
The moments of inertia () and anomalous moments of inertia () are expressed respectively as
| (71) | ||||
| (72) | ||||
| (73) | ||||
| (74) |
Appendix B Fixing the model parameters
The chiral condensate and the pion decay constant can be derive from the effective chiral action given in Eq. (11). The chiral condensate are written as
| (75) |
and the pion decay constant are given by
| (76) |
with proper-time regulator . The pion mass is determined by the pole position of the pion propagator that is obtained by a low-energy effective chiral theory given by Eq. (11)
| (77) |
The above-given expressions satisfy the Gell-Mann–Oakes–Renner (GMOR) relation. With Eqs. (75), (76) and (77), one can determine the cutoff mass. The average value of the up and down current quark masses is obtained as . The strange current quark mass is fixed by the hyperon mass splittings by treating perturbatively up to the second-order corrections Blotz:1992pw ; Christov:1995vm ; Kim:2018xlc . The preferable value of is found to be .
References
- (1) N. Isgur and M. B. Wise, Phys. Lett. B 232, 113 (1989).
- (2) H. Georgi, Phys. Lett. B 240, 447 (1990).
- (3) T. M. Yan, H. Y. Cheng, C. Y. Cheung, G. L. Lin, Y. C. Lin and H. L. Yu, Phys. Rev. D 46, 1148-1164 (1992) doi:10.1103/PhysRevD.46.1148
- (4) D. Diakonov, [arXiv:1003.2157 [hep-ph]].
- (5) G. S. Yang, H.-Ch. Kim, M. V. Polyakov and M. Praszałowicz, Phys. Rev. D 94, 071502 (2016).
- (6) E. Witten, Nucl. Phys. B 160, 57 (1979).
- (7) G. S. Yang and H.-Ch. Kim, Phys. Lett. B 808, 135619 (2020).
- (8) K. U. Can, G. Erkol, B. Isildak, M. Oka and T. T. Takahashi, JHEP 1405, 125 (2014).
- (9) K. U. Can, G. Erkol, M. Oka and T. T. Takahashi, Phys. Rev. D 92, 114515 (2015).
- (10) M. D. Scadron, Phys. Rev. 165, 1640-1647 (1968).
- (11) E. Witten, Nucl. Phys. B223, 433 (1983).
- (12) J. Y. Kim and H.-Ch. Kim, Phys. Rev. D 97, 114009 (2018).
- (13) J. Y. Kim and H.-Ch. Kim, [arXiv:1912.01437 [hep-ph]].
- (14) V. Pascalutsa, M. Vanderhaeghen and S. N. Yang, Phys. Rept. 437, 125-232 (2007).
- (15) D. Diakonov, V. Y. Petrov and P. V. Pobylitsa, Nucl. Phys. B 306, 809 (1988).
- (16) M. Wakamatsu and H. Yoshiki, Nucl. Phys. A 524, 561 (1991).
- (17) C. V. Christov, A. Blotz, H.-Ch. Kim, P. Pobylitsa, T. Watabe, T. Meissner, E. Ruiz Arriola and K. Goeke, Prog. Part. Nucl. Phys. 37, 91 (1996).
- (18) H.-Ch. Kim, A. Blotz, M. V. Polyakov, and K. Goeke, Phys. Rev. D 53, 4013 (1996).
- (19) D. Diakonov, [hep-ph/9802298].
- (20) J. Y. Kim, H.-Ch. Kim and G. S. Yang, Phys. Rev. D 98, 054004 (2018).
- (21) J. Y. Kim and H.-Ch. Kim, arXiv:1909.00123 [hep-ph].
- (22) G. S. Yang and H.-Ch. Kim, Phys. Lett. B 781, 601 (2018).
- (23) G. S. Yang and H.-Ch. Kim, Phys. Lett. B 801, 135142 (2020). [arXiv:1909.03156 [hep-ph]].
- (24) J. Y. Kim and H.-Ch. Kim, Eur. Phys. J. C 79, 570 (2019).
- (25) A. Blotz, D. Diakonov, K. Goeke, N. W. Park, V. Petrov and P. V. Pobylitsa, Nucl. Phys. A 555, 765 (1993).
- (26) C. Alexandrou, T. Korzec, T. Leontiou, J. W. Negele and A. Tsapalis, PoS LATTICE 2007, 149 (2007).
- (27) K. Goeke, J. Grabis, J. Ossmann, M. Polyakov, P. Schweitzer, A. Silva and D. Urbano, Phys. Rev. D 75, 094021 (2007).
- (28) J. Y. Kim, H.-Ch. Kim, M. V. Polyakov and H. D. Son, arXiv:2008.06652 [hep-ph].
- (29) A private communication with U. Can (2019).