Electric Dipole Polarizability of 40Ca
Abstract
The electric dipole strength distribution in 40Ca between 5 and 25 MeV has been determined at RCNP, Osaka, from proton inelastic scattering experiments at very forward angles. Combined with total photoabsorption data at higher excitation energy, this enables an extraction of the electric dipole polarizability fm3. Together with the measured in 48Ca, it provides a stringent test of modern theoretical approaches, including coupled cluster calculations with chiral effective field theory interactions and state-of-the art energy density functionals. The emerging picture is that for this medium-mass region dipole polarizabilities are well described theoretically, with important constraints for the neutron skin in 48Ca and related equation of state quantities.
Introduction.– The nuclear equation of state (EOS) determines not only basic properties of nuclei [1] but also plays a key role for the properties of neutron stars and the dynamics of core-collapse supernovae and neutron star mergers [2]. New observations from neutron stars and mergers provides constraints for the EOS of neutron-rich matter that can be compared with those derived from nuclear physics (see, e.g., Refs. [3, 4, 5]). However, while the EOS of symmetric nuclear matter is well determined around saturation density, the properties of neutron-rich matter are less explored experimentally. The latter depends on the symmetry energy, whose properties are typically encoded in an expansion around saturation density , with the symmetry energy at saturation density and its density dependence .
Theoretically, a model-dependent correlation between and the neutron-skin thickness in nuclei with neutron excess has been established [6, 7, 8, 9]. This correlation was also recently confirmed in ab initio computations of the neutron skin in 208Pb [10]. Experimental attempts to determine the neutron skin thickness have been performed with a variety of probes (see, e.g., Ref. [11] and references therein), but many of them suffer from systematic uncertainties entering in the description of the reaction processes. Parity-violating elastic electron scattering (a weak process mediated by the boson) can be used for a nearly model-independent extraction of the neutron distribution in nuclei and, by comparison with accurately measured charge radii, the neutron skin thickness. Recently, results with this technique have been reported by the CREX and PREX collaborations for 48Ca [12] and 208Pb [13], respectively. The values inferred with selected nuclear models favor a comparatively small neutron skin in the former and a large skin in the latter case.
Alternatively, the electric dipole polarizability has been established as a possible measure of the neutron skin, based on the strong correlation with [8, 14]. Data for extracted from proton inelastic scattering experiments at extreme forward angles have been presented for both 48Ca [15] and 208Pb [16]. In these papers, two theoretical approaches have been used to describe : ab initio coupled-cluster (CC) calculations [17, 18] starting from chiral two- and three-nucleon interactions [19, 20] and energy density functional (EDF) theory [21].
Attempts to simultaneously describe (208Pb) and the parity-violating asymmetry from PREX and CREX with EDF models have shown limited success [22, 23, 24, 25]. The values derived for [13] and [26] from PREX are in tension with EDFs capable of describing [27] the presently available results on in 48Ca [15], 68Ni [28], 120Sn [29, 30], and 208Pb [16]. While the CREX results is in excellent agreement with ab initio predictions [18], the PREX result is in mild tension with the recent ab initio computations of 208Pb [10].
Correlations between experimental observables and symmetry energy properties are well explored in EDF theory [6, 7, 8, 14], but predictions for isovector observables like are less well constrained. On the other hand, ab initio calculations provide a direct link to the EOS, as nuclear matter properties can be calculated based on the same chiral interactions [19, 18, 31, 10, 32]. Results presented here are based on the set of two- and three-nucleon interactions from Refs. [19, 20] applied to study in 48Ca [18, 15]. The calculations of the response are based on merging the Lorentz Integral Transform approach with CC theory, as described in Refs. [33, 34]. Recent work has extended the original two-particle–two-hole (2p-2h) CC truncation to include correlations up to three-particle–three-hole (3p-3h), so-called triples corrections, in the computation of [35]. Their inclusion leads to a reduction of the predictions for (48Ca) of the order of 10%, allowing an improved simultaneous description of the charge radius [35]. A similar improvement was achieved for 68Ni [36].
In this Letter, we present the measurement of the dipole polarizability for 40Ca and confront it with CC and EDF calculations. This tests the emerging picture that nuclear theory can describe very well the neutron skin in medium-mass nuclei and related observables.
Experiment.– Cross sections for the 40Ca reaction have been measured at RCNP, Osaka, at an incident proton energy of 295 MeV. Data were taken with the Grand Raiden spectrometer [37] in a laboratory scattering angle range and for excitation energies in the range MeV. Dispersion matching techniques were applied to achieve an energy resolution of about 30 keV (full width at half maximum). The experimental techniques and the raw data analysis are described in Ref. [38].
In the top panel of Fig. 1 we show representative energy spectra measured at laboratory scattering angles , , , and . The predominant cross sections lie in the energy region above 10 MeV. strength in 40Ca is known to be concentrated in a single prominent transition at 10.32 MeV [39]. The cross sections above 10 MeV show a broad resonance structure peaking at about 19 MeV increasing towards . The angular dependence is consistent with relativistic Coulomb excitation of transitions. We identify this resonance structure as the isovector giant dipole resonance.
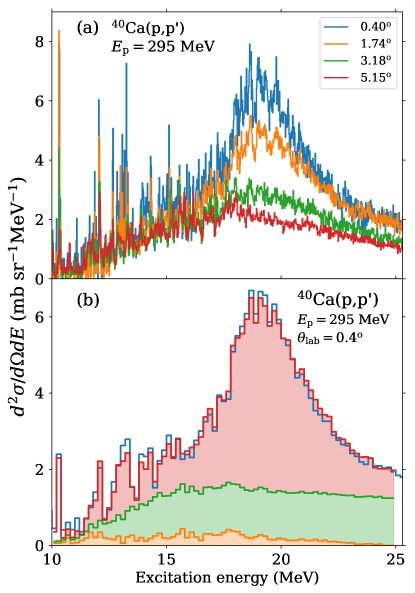
The various contributions to the spectra were separated using a multipole decomposition analysis (MDA) as described in Ref. [40]. Results for the most forward angle measured are presented in the bottom part of Fig. 1 as example, where the spectra was rebinned to 200 keV. Theoretical angular distributions for the relevant multipoles were obtained from Distorted Wave Born Approximation calculations with transition amplitudes from quasiparticle-phonon-model calculations similar to the analysis of 48Ca [15]. Additionally, a background due to pre-equilibrium multistep scattering was considered. Its angular dependence was taken from experimental systematics [41, 42] while the amplitude was derived by two means. Initially, an unconstrained fit was done at each energy bin of the set of spectra. The resulting cross sections could be well approximated by a simple Fermi function but showed strong fluctuations for certain excitation energy bins due to the similarity to some of the theoretical angular distributions. Thus, in the final analysis, the continuum contribution was determined by fitting a Fermi function to the unconstrained excitation energy dependence.
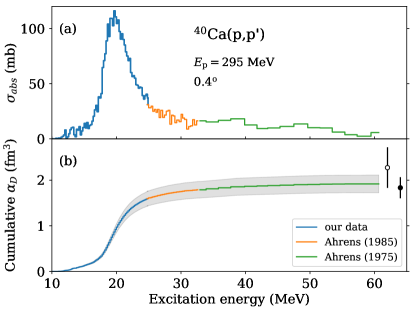
Photoabsorption cross sections and dipole polarizability.– The cross sections resulting from the MDA were converted into equivalent photoabsorption cross sections using the virtual photon method [45]. The virtual photon spectrum was calculated in an eikonal approach [46] to Coulomb excitation, integrated over the distribution of scattering angles covered in the solid angle of each angular bin. The photoabsorption spectra derived from scattering data at and were essentially identical, and that at deviated only slightly, consistent with an estimate of the grazing angle () at which Coulomb-nuclear interference becomes relevant. The resulting photoabsorption cross section is displayed as blue histogram in Fig. 2 (a).
The electric dipole polarizability was obtained from the photoabsorption cross section over the energy range MeV leading to a contribution 1.60(14) fm3. The integration was extended to 60 MeV, where the cumulative sum plotted in Fig. 2 (b) shows saturation. The data at higher excitation energies were taken for MeV from Ref. [44] and for MeV from Ref. [43] to obtain the total fm3. The uncertainty considers systematic errors of (i) the absolute cross sections, (ii) the MDA (determined as described, e.g., in Ref. [47]), and (iii) the parameterization of the continuum background (evaluated by varying the amplitude of the Fermi function), added in quadrature. The latter, dominating the total uncertainty budget, was estimated by the variation needed to change the value of the MDA fit by one. Statistical errors turned out to be negligible. A detailed breakdown of the error contributions is given in Table 1.
| Source | Value (%) |
|---|---|
| Trigger efficiency | 0.1 |
| Drift chamber efficiency | 0.8 |
| Charge collection | 0.3 |
| Target thickness | 1.0 |
| Determination of solid angle | 3.0 |
| MDA | 1.2 |
| Background parameterization | 8.3 |
| Total | 9.0 |
Comparison with coupled-cluster calculations.– The extracted value of serves as a benchmark for CC theory [33, 18, 35, 34]. Coupled-cluster calculations were recently performed for the dipole polarizability of 48Ca [15] and 68Ni [36], which led to an improved understanding of the neutron and proton distributions in nuclei, as well as their difference encoded in the neutron skin. We have performed CC computations of in 40Ca starting from a Hartree-Fock reference state considering a basis of 15 major harmonic oscillator shells. To gauge the convergence of our results we varied the oscillator frequency in the range MeV. Three-nucleon contributions had an additional energy cut of .
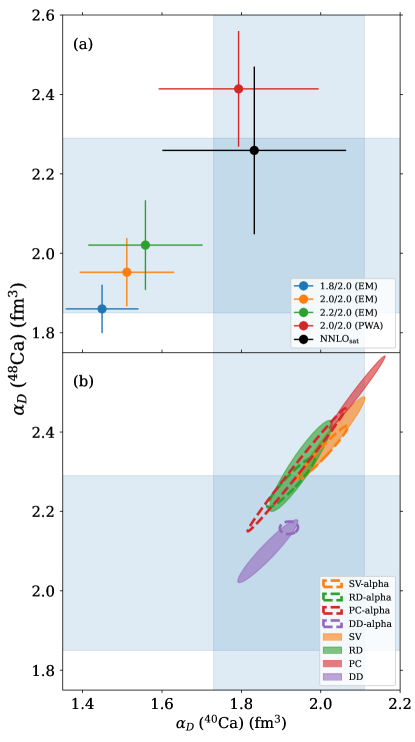
Figure 3 explores the correlation between for 40Ca and 48Ca as predicted by theory. Panel (a) shows the CC results including triples contributions, not available for 40Ca so far. The theoretical uncertainties for the different Hamiltonians stem from the truncation of the CC expansion and the residual dependence on CC convergence parameters, calculated as described in Ref. [34]. Similarly to 48Ca, we find that the inclusion of 3p-3h correlations reduces the value of (40Ca) by an amount varying between 10% – 20% for different interactions. While the EM and PWA interactions [19] are not simultaneously compatible with both 40Ca and 48Ca experimental data, the set of employed interactions shows an approximately linear trend between the two quantities overlapping with both experimental results. A particular improvement in the reproduction of both (48Ca) and (40Ca) is seen for the NNLOsat interaction [20], which is capable of accurately describing binding energies and radii of nuclei up to 40Ca as well the saturation point of symmetric nuclear matter. The different interactions predict a range of symmetry energy parameters MeV, MeV [18], with the NNLOsat values at the lower end ( MeV, MeV).
Comparison with EDF approaches.– Recently, it was investigated whether the dipole polarizability and the parity-violating asymmetry for 208Pb and 48Ca can be simultaneously accounted for with modern EDFs [24]. We use the four representative forms of functionals from that study: non-relativistic Skyrme functionals SV [48] and RD [49], the latter with different forms of density dependence, and relativistic functionals DD [50] with finite-range meson-exchange coupling and PC [51] with point coupling. All four have been calibrated to the same set of ground-state data to determine the model parameters. With these sets, it was shown that PREX and CREX results for (and ) cannot be consistently explained within the model uncertainties while the were reproduced. Hence, the present result in 40Ca provides an important test of the global predictive power of these EDFs.
Figure 3 (b) displays the EDF results for with error ellipses (for their definition see Refs. [22, 24]). The parametrizations as given from the ground-state fits are shown by filled ellipses. The DD functional performs rather well. The other predictions tend to slightly overestimate the experimental mean values of both 40Ca and 48Ca, while their error ellipses do overlap with the experimental bands, except for PC. In all cases, the two values are highly correlated. We note that the same holds for the description of (208Pb) [16] after correction for the quasi-deuteron contribution [27]. Thus, all the models are capable to account for the mass dependence of the polarizability.
The dashed ellipses show results from a refit where additionally the experimental value of 208Pb [16] corrected for the quasideuteron part [27] was included yielding the functionals SV-alpha; RD-alpha, PC-alpha, and DD-alpha [22, 24]. This improves the agreement with experiment, particularly for the PC model, and shrinks most error ellipsoids. The uncertainty reduction is especially large for the DD model because this functional has the least isovector freedom. The linear trend shown by the different theoretical approaches in Fig. 3 is similar although the CC calculations tend to underestimate the in 40Ca and perform nicely for 48Ca. The bulk symmetry energies range from MeV for DD to 35 MeV for PC and accordingly from 32 MeV to 82 MeV for . The fits which include also in 208Pb narrow the prediction to MeV and MeV which correlates nicely to the narrower range of predictions for in 40,48Ca.
Conclusions.– We have extracted the dipole polarizability of 40Ca from a combination of relativistic Coulomb excitation measurement in inelastic proton scattering under very forward angles with total photoabsorption data at high excitation energies. Together with a similar analysis on 48Ca the new data serve as a benchmark test of state-of-the art theoretical approaches. A representative set of EDFs can describe these data. An improvement is obtained when the EDFs are optimized by adding the dipole polarizability of 208Pb to the calibration dataset. Coupled-cluster computations for the NNLOsat interaction simultaneously describe well the dipole polarizability of 40Ca and 48Ca, as well as the corresponding charge radii and the neutron skin thickness [34]. A nearly linear systematic trend is obtained for other interactions, as in the case of EDF theory. This analysis supports the robustness of current theoretical approaches in the description of and their constraints of symmetry energy parameters discussed, e.g., in Refs. [22, 24, 52].
Acknowledgements.
This work was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project-ID 279384907 –- SFB 1245, through the Cluster of Excellence “Precision Physics, Fundamental Interactions, and Structure of Matter” (PRISMA+ EXC 2118/1, Project ID 39083149), by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics under award numbers DE-SC0013365 and DE-SC0023175 (NUCLEI SciDAC-5 collaboration), under the contract DE-AC05-00OR22725 with UT-Battelle, LLC (Oak Ridge National Laboratory), and by the University of Cape Town. Computer time was provided by the Innovative and Novel Computational Impact on Theory and Experiment (INCITE) programme. This research used resources of the Oak Ridge Leadership Computing Facility at the Oak Ridge National Laboratory, which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC05-00OR22725.References
- Roca-Maza and Paar [2018] X. Roca-Maza and N. Paar, Nuclear equation of state from ground and collective excited state properties of nuclei, Prog. Part. Nucl. Phys. 101, 96 (2018).
- Lattimer [2021] J. M. Lattimer, Neutron Stars and the Nuclear Matter Equation of State, Annu. Rev. Nucl. Part. Sci. 71, 433 (2021).
- Raaijmakers et al. [2021] G. Raaijmakers, S. K. Greif, K. Hebeler, T. Hinderer, S. Nissanke, A. Schwenk, T. E. Riley, A. L. Watts, J. M. Lattimer, and W. C. G. Ho, Constraints on the Dense Matter Equation of State and Neutron Star Properties from NICER’s Mass-Radius Estimate of PSR J0740+6620 and Multimessenger Observations, Astrophys. J. Lett. 918, L29 (2021).
- Essick et al. [2021] R. Essick, I. Tews, P. Landry, and A. Schwenk, Astrophysical constraints on the symmetry energy and the neutron skin of with minimal modeling assumptions, Phys. Rev. Lett. 127, 192701 (2021).
- Huth et al. [2022] S. Huth, P. T. H. Pang, I. Tews, T. Dietrich, A. Le Fèvre, A. Schwenk, W. Trautmann, K. Agarwal, M. Bulla, M. W. Coughlin, and C. Van Den Broeck, Constraining neutron-star matter with microscopic and macroscopic collisions, Nature 606, 276 (2022).
- Brown [2000] B. A. Brown, Neutron radii in nuclei and the neutron equation of state, Phys. Rev. Lett. 85, 5296 (2000).
- Centelles et al. [2009] M. Centelles, X. Roca-Maza, X. Viñas, and M. Warda, Nuclear symmetry energy probed by neutron skin thickness of nuclei, Phys. Rev. Lett. 102, 122502 (2009).
- Reinhard and Nazarewicz [2010] P.-G. Reinhard and W. Nazarewicz, Information content of a new observable: The case of the nuclear neutron skin, Phys. Rev. C 81, 051303(R) (2010).
- Roca-Maza et al. [2011] X. Roca-Maza, M. Centelles, X. Viñas, and M. Warda, Neutron skin of , nuclear symmetry energy, and the parity radius experiment, Phys. Rev. Lett. 106, 252501 (2011).
- Hu et al. [2022] B. Hu, W. Jiang, T. Miyagi, Z. Sun, A. Ekström, C. Forssén, G. Hagen, J. D. Holt, T. Papenbrock, S. R. Stroberg, and I. Vernon, Ab initio predictions link the neutron skin of 208Pb to nuclear forces, Nat. Phys. 18, 1196 (2022).
- Thiel et al. [2019] M. Thiel, C. Sfienti, J. Piekarewicz, C. J. Horowitz, and M. Vanderhaeghen, Neutron skins of atomic nuclei: per aspera ad astra, J. Phys. G: Nucl. Part. Phys. 46, 093003 (2019).
- Adhikari et al. [2022] D. Adhikari et al. (CREX Collaboration), Precision determination of the neutral weak form factor of , Phys. Rev. Lett. 129, 042501 (2022).
- Adhikari et al. [2021] D. Adhikari et al. (PREX Collaboration), Accurate determination of the neutron skin thickness of through parity-violation in electron scattering, Phys. Rev. Lett. 126, 172502 (2021).
- Roca-Maza et al. [2013] X. Roca-Maza, M. Brenna, G. Colò, M. Centelles, X. Viñas, B. K. Agrawal, N. Paar, D. Vretenar, and J. Piekarewicz, Electric dipole polarizability in 208Pb: Insights from the droplet model, Phys. Rev. C 88, 024316 (2013).
- Birkhan et al. [2017] J. Birkhan, M. Miorelli, S. Bacca, S. Bassauer, C. A. Bertulani, G. Hagen, H. Matsubara, P. von Neumann-Cosel, T. Papenbrock, N. Pietralla, V. Y. Ponomarev, A. Richter, A. Schwenk, and A. Tamii, Electric dipole polarizability of and implications for the neutron skin, Phys. Rev. Lett. 118, 252501 (2017).
- Tamii et al. [2011] A. Tamii et al., Complete electric dipole response and the neutron skin in , Phys. Rev. Lett. 107, 062502 (2011).
- Hagen et al. [2014] G. Hagen, T. Papenbrock, M. Hjorth-Jensen, and D. Dean, Coupled-cluster computations of atomic nuclei, Rep. Prog. Phys. 77, 096302 (2014).
- Hagen et al. [2016] G. Hagen, A. Ekström, C. Forssén, G. R. Jansen, W. Nazarewicz, T. Papenbrock, K. A. Wendt, S. Bacca, N. Barnea, B. Carlsson, C. Drischler, K. Hebeler, M. Hjorth-Jensen, M. Miorelli, G. Orlandini, A. Schwenk, and J. Simonis, Neutron and weak-charge distributions of the 48Ca nucleus, Nat. Phys. 12, 186 (2016).
- Hebeler et al. [2011] K. Hebeler, S. K. Bogner, R. J. Furnstahl, A. Nogga, and A. Schwenk, Improved nuclear matter calculations from chiral low-momentum interactions, Phys. Rev. C 83, 031301(R) (2011).
- Ekström et al. [2015] A. Ekström, G. R. Jansen, K. A. Wendt, G. Hagen, T. Papenbrock, B. D. Carlsson, C. Forssén, M. Hjorth-Jensen, P. Navrátil, and W. Nazarewicz, Accurate nuclear radii and binding energies from a chiral interaction, Phys. Rev. C 91, 051301(R) (2015).
- Bender et al. [2003] M. Bender, P.-H. Heenen, and P.-G. Reinhard, Self-consistent mean-field models for nuclear structure, Rev. Mod. Phys. 75, 121 (2003).
- Reinhard et al. [2021] P.-G. Reinhard, X. Roca-Maza, and W. Nazarewicz, Information content of the parity-violating asymmetry in , Phys. Rev. Lett. 127, 232501 (2021).
- Piekarewicz [2021] J. Piekarewicz, Implications of PREX-2 on the electric dipole polarizability of neutron-rich nuclei, Phys. Rev. C 104, 024329 (2021).
- Reinhard et al. [2022] P.-G. Reinhard, X. Roca-Maza, and W. Nazarewicz, Combined theoretical analysis of the parity-violating asymmetry for and , Phys. Rev. Lett. 129, 232501 (2022).
- Yüksel and Paar [2023] E. Yüksel and N. Paar, Implications of parity-violating electron scattering experiments on (CREX) and (PREX-II) for nuclear energy density functionals, Phys. Lett. B 836, 137622 (2023).
- Reed et al. [2021] B. T. Reed, F. J. Fattoyev, C. J. Horowitz, and J. Piekarewicz, Implications of PREX-2 on the equation of state of neutron-rich matter, Phys. Rev. Lett. 126, 172503 (2021).
- Roca-Maza et al. [2015] X. Roca-Maza, X. Viñas, M. Centelles, B. K. Agrawal, G. Colò, N. Paar, J. Piekarewicz, and D. Vretenar, Neutron skin thickness from the measured electric dipole polarizability in , , and , Phys. Rev. C 92, 064304 (2015).
- Rossi et al. [2013] D. M. Rossi et al., Measurement of the dipole polarizability of the unstable neutron-rich nucleus , Phys. Rev. Lett. 111, 242503 (2013).
- Hashimoto et al. [2015] T. Hashimoto et al., Dipole polarizability of and nuclear energy density functionals, Phys. Rev. C 92, 031305(R) (2015).
- Bassauer et al. [2020a] S. Bassauer et al., Evolution of the dipole polarizability in the stable tin isotope chain, Phys. Lett. B 810, 135804 (2020a).
- Drischler et al. [2019] C. Drischler, K. Hebeler, and A. Schwenk, Chiral interactions up to next-to-next-to-next-to-leading order and nuclear saturation, Phys. Rev. Lett. 122, 042501 (2019).
- Keller et al. [2023] J. Keller, K. Hebeler, and A. Schwenk, Nuclear equation of state for arbitrary proton fraction and temperature based on chiral effective field theory and a Gaussian process emulator, Phys. Rev. Lett. 130, 072701 (2023).
- Bacca et al. [2013] S. Bacca, N. Barnea, G. Hagen, G. Orlandini, and T. Papenbrock, Phys. Rev. Lett. 111, 122502 (2013).
- Simonis et al. [2019] J. Simonis, S. Bacca, and G. Hagen, First principles electromagnetic responses in medium-mass nuclei, Eur. Phys. J. A 55, 241 (2019).
- Miorelli et al. [2018] M. Miorelli, S. Bacca, G. Hagen, and T. Papenbrock, Computing the dipole polarizability of with increased precision, Phys. Rev. C 98, 014324 (2018).
- Kaufmann et al. [2020] S. Kaufmann et al., Charge radius of the short-lived and correlation with the dipole polarizability, Phys. Rev. Lett. 124, 132502 (2020).
- Fujiwara et al. [1999] M. Fujiwara et al., Magnetic spectrometer Grand Raiden, Nucl. Instrum. Methods Phys. Res., Sect. A 422, 484 (1999).
- Tamii et al. [2009] A. Tamii et al., Measurement of high energy resolution inelastic proton scattering at and close to zero degrees, Nucl. Instrum. Methods Phys. Res., Sect. A 605, 326 (2009).
- Gross et al. [1979] W. Gross, D. Meuer, A. Richter, E. Spamer, O. Titze, and W. Knüpfer, A strong magnetic dipole excitation in 40Ca observed in high-resolution inelastic electron scattering and coherent spin-flip transitions due to ground-state correlations, Phys. Lett. B 84, 296 (1979).
- von Neumann-Cosel and Tamii [2019] P. von Neumann-Cosel and A. Tamii, Electric and magnetic dipole modes in high-resolution inelastic proton scattering at , Eur. Phys. J. A 55, 110 (2019).
- Kalbach and Mann [1981] C. Kalbach and F. M. Mann, Phenomenology of continuum angular distributions. I. Systematics and parametrization, Phys. Rev. C 23, 112 (1981).
- Chadwick and Obložinský [1994] M. B. Chadwick and P. Obložinský, Continuum angular distributions in preequilibrium nuclear reactions: Physical basis for Kalbach systematics, Phys. Rev. C 50, 2490 (1994).
- Ahrens et al. [1975] J. Ahrens, H. Borchert, K. Czock, H. Eppler, H. Gimm, H. Gundrum, M. Kröning, P. Riehn, G. S. Ram, A. Zieger, and B. Ziegler, Total nuclear photon absorption cross sections for some light elements, Nucl. Phys. A 251, 479 (1975).
- Ahrens [1985] J. Ahrens, The total absorption of photons by nuclei, Nucl. Phys. A 446, 229 (1985).
- Bertulani and Baur [1988] C. A. Bertulani and G. Baur, Electromagnetic processes in relativistic heavy ion collisions, Phys. Rep. 163, 299 (1988).
- Bertulani and Nathan [1993] C. Bertulani and A. Nathan, Excitation and photon decay of giant resonances from high-energy collisions of heavy ions, Nucl. Phys. A 554, 158 (1993).
- Bassauer et al. [2020b] S. Bassauer et al., Electric and magnetic dipole strength in , Phys. Rev. C 102, 034327 (2020b).
- Klüpfel et al. [2009] P. Klüpfel, P.-G. Reinhard, T. J. Bürvenich, and J. A. Maruhn, Variations on a theme by Skyrme: A systematic study of adjustments of model parameters, Phys. Rev. C 79, 034310 (2009).
- Erler et al. [2010] J. Erler, P. Klüpfel, and P.-G. Reinhard, Exploration of a modified density dependence in the Skyrme functional, Phys. Rev. C 82, 044307 (2010).
- Nikšić et al. [2002] T. Nikšić, D. Vretenar, P. Finelli, and P. Ring, Relativistic Hartree-Bogoliubov model with density-dependent meson-nucleon couplings, Phys. Rev. C 66, 024306 (2002).
- Nikšić et al. [2008] T. Nikšić, D. Vretenar, and P. Ring, Relativistic nuclear energy density functionals: Adjusting parameters to binding energies, Phys. Rev. C 78, 034318 (2008).
- Lattimer [2023] J. M. Lattimer, Constraints on nuclear symmetry energy parameters, Particles 6, 30 (2023).