Eigenvalue analysis of stress-strain curve of two-dimensional amorphous solids of dispersed frictional grains with finite shear strain
Abstract
The stress-strain curve of two-dimensional frictional dispersed grains interacting with a harmonic potential without considering the dynamical slip under a finite strain is determined by using eigenvalue analysis of the Hessian matrix. After the configuration of grains is obtained, the stress-strain curve based on the eigenvalue analysis is in almost perfect agreement with that obtained by the simulation, even if there are plastic deformations caused by stress avalanches. Unlike the naive expectation, the eigenvalues in our model do not indicate any precursors to the stress-drop events.
I Introduction
Amorphous materials consisting of dispersed repulsive grains, such as powders, colloids, bubbles, and emulsions, behave as fragile solids above jamming density Jaeger96 ; Durian95 ; Wyart05 ; Baule18 ; Liu98 . When we consider a response of such materials to an applied strain , the rigidity is independent of the strain in the linear response regime, whereas it exhibits softening in the nonlinear regime Nagamanasa14 ; Knowlton14 ; Kawasaki16 ; Leishangthem17 ; Bohy17 ; Ozawa18 ; Clark18 ; Boschan19 ; Singh20 ; Otsuki21 . Above the yielding points, there are some plastic events, such as stress avalanches in the collection of grains.
The Hessian matrix determined by the configuration of grains is commonly used for amorphous solids consisting of frictionless grains Wyart05 ; WyarLettt05 ; Ellenbroek06 ; Lerner16 ; Gartner16 ; Bonfanti19 ; Baule18 ; Morse20 . To determine the rigidity, eigenvalue analysis of the Hessian matrix DeGiuli14 ; Mizuno16 ; Maloney04 ; Maloney06 ; Lemaitre06 ; Zaccone11 ; Palyulin18 , is commonly used, but we have only obtained semi-quantitative agreements between the theory and simulation so far Zaccone11 ; Palyulin18 . Recently, some researchers examined the applicability of the instantaneous normal mode analysis to systems that are not fully equilibrated and found qualitative agreement between the analysis and simulation Oyama21 ; Kriuchevskyi22 , although they could not get quantitatively accurate results. Some studies have suggested that the decrement of the non-zero smallest eigenvalue of the Hessian matrix with the strain is a precursor of an avalanche or stress drop near a critical strain Maloney04 ; Maloney06 ; Manning11 ; Dasgupta12 ; Ebrahem20 . Correspondingly, some studies indicated that the rigidity and the stress should behave as and near , where and are the regular parts of the rigidity and stress conversing to constants at , respectively Maloney04 ; Maloney06 ; Karmakar10PRL ; Richard20 .
In general, the frictional force between the grains cannot be ignored in physical situations. Because the frictional force generally depends on the contact history, Hessian analysis is not applicable to such systems. Thus, Chattoraj et al. adopted the Jacobian matrix instead of the Hessian matrix to discuss the stability of the configuration of frictional grains under strain Chattoraj19 . They performed eigenvalue analysis under athermal quasi-static shear processes and determined the existence of oscillatory instability originating from interparticle friction at a certain strain Chattoraj19 ; Chattoraj19E ; Charan20 . Moreover, some studies have performed an analysis of the Hessian matrix with the aid of an effective potential for frictional grains Somfai07 ; Henkes10 . Recently, Liu et al. suggested that Hessian matrix analysis with another effective potential can be used, even if slip processes exist Liu21 . Previous studies Somfai07 ; Henkes10 have reported that the friction between grains causes a continuous change in the functional form of the density of states (DOS), which differs from that of frictionless systems. So far, there have been few theoretical studies to determine the rigidity of the frictional grains.
In our previous study Ishima2022 , we developed an analysis of the Jacobian matrix to determine the rigidity of two-dimensional amorphous solids consisting of frictional grains interacting with the Hertzian force in the linear response to an infinitesimal strain. In the study, we ignore the dynamic friction caused by the slip processes of contact points. We found that there are two modes in the DOS for a sufficiently small tangential-to-normal stiffness ratio. Rotational modes exist in the region of low-frequency or small eigenvalues, whereas translational modes exist in the region of high-frequency or large eigenvalues. The rigidity determined by the translational modes is in good agreement with that obtained by the molecular dynamics simulations, whereas the contribution of the rotational modes is almost zero. Nevertheless, there are several shortcomings in the previous analysis. (i) The analysis can be used only in the linear response regime, where the base state is not influenced by the applied strain. (ii) As a result, we cannot discuss the behavior of plastic deformations or avalanches of grains. (iii) Even if we restrict our interest to the linear response regime, we cannot include the effect of tangential contact for the preparation of the initial configuration. (iv) We also ignored the effect of Coulomb’s slip between the contacted grains Ishima2022 .
The purpose of this study is to overcome the shortcomings of our previous study except for point (iv) Ishima2022 . Thus, we analyze a collection of two-dimensional grains interacting with repulsive harmonic potentials within the contact radius, without considering Coulomb’s slip between the grains. Owing to the special properties of the harmonic potential, the eigenvalue analysis of the Jacobian matrix becomes equivalent to that of the Hessian matrix. Subsequently, using the eigenvalue analysis of the Hessian matrix, we demonstrate that the theoretical rigidity under a large strain agrees with that obtained by the simulation.
The remainder of this paper is organized as follows. In Sec. II, we introduce the model to be analyzed in this study. In Sec. III, we summarize the theoretical framework for determining the rigidity of an amorphous solid consisting of frictional grains without considering Coulomb’s slip process. In Sec. IV, we present the results of the stress-strain relation obtained using the theory formulated in Sec. III. We also compare the theoretical results with the simulation results to demonstrate the relevancy of our theoretical analysis. In Sec. V, we summarize the obtained results and address future tasks to be solved. In Appendix A, we numerically demonstrate the absence of history-dependent tangential deformations in our system. In Appendix B, we explain the detailed behavior of the eigenvalue near the stress-drop points. In Appendix C, we present some detailed properties of the Hessian matrix in a harmonic system. In Appendix D, we present some properties of the Jacobian matrix in a harmonic system and demonstrate its equivalency to the Hessian matrix. Appendix E presents the detailed properties of rigidity.
II Model
Our system contains frictional circular disks embedded in a two-dimensional space. To prevent the system from crystallization, it contains an equal number of grains with diameters and Luding01 . We assume that the mass of grain is proportional to , where is the diameter of -th grain. For later convenience, we introduce as the mass of grain having a diameter . In this study, , and denote and components of the position of -th grain, and the rotational angle of the -th grain, respectively. We introduce the generalized coordinates of the -th grain as follow:
| (1) |
where , , and the superscript T denotes the transposition.
Let the force, and -component of the torque acting on the -th grain be and , respectively. Then, the equations of motion of -th grain are expressed as
| (2) | ||||
| (3) |
with mass and momentum of inertia of -th grain. In a system without volume forces, such as gravity, we can write
| (4) | ||||
| (5) |
where we have adopted the notation for arbitrary variable such as and . Here, and are the force and -component of the torque acting on the -th grain from the -th grain, respectively. As a simplified description of the drag terms from the background fluid, is a damping constant uniformly acting on grains, and is given by
| (6) |
where we have introduced the normal unit vector between -th and -th grains as . The force can be divided into the normal part and tangential part as
| (7) |
where and is Heaviside’s step function, taking for and otherwise. We assume that the contact force is expressed as
| (8) | ||||
| (9) |
where and are the stiffness parameters of normal and tangential contacts, respectively. The contact force can be derived from the harmonic potential. In Eqs. (8) and (9) we have introduced and
| (10) |
where we have used
| (11) |
with , , , and the integration over the duration time of contact between -th and -th grains with the trajectory of the contact point between -th and -th grains at . As shown in Appendix A, we have confirmed that the second term on the right-hand side (RHS) of Eq. (10) is zero for harmonic systems, although we do not have any mathematical proof for this statement thus far. For simplicity, we consider neither the effects of Coulomb’s slip in the tangential equation of motion nor the dissipative contact force, where the tangential forces including the effect of Coulomb’s slip process, satisfy
| (12) |
where is the friction constant.
We impose the Lees-Edwards boundary conditions Lees72 ; Evans08 , where the direction parallel to the shear strain is the -direction. After generating a stable grain configuration via isotropic compression starting from a random configuration by using Eqs. (2)-(10) without strain (see detail in Ref. Ishima2022 ), we apply a step strain to all grains, where -coordinate of the position of the -th grain is shifted by an affine displacement . Here, the superscript FB denotes the force-balance (FB) state at which and for arbitrary . As shown in Sec. III.1, the FB state is equivalent to the potential minimum for harmonic grains. Subsequently, the system is relaxed to an FB state. We further apply the step strain associated with the subsequent relaxation process again to obtain the state at . By repeating this process, we can reach a deformed state with the strain .
The plastic deformations for a large depend on the choice of Morse20 . Moreover, the theoretical formulation assumes . Therefore, we adopt the backtracking method Lerner09 ; Karmakar10PRE . If a plastic event is encountered under a fixed , the system is restored to its original state without a plastic event. Subsequently, we apply a new strain, , to the system. Even if we encounter a plastic event with , we further examine the smaller step strain of . We repeat this procedure until we reach (see Appendix B).
We introduce the rate of nonaffine displacements for with or and as:
| (13) | ||||
| (14) |
Our system is characterized by the generalized coordinate . The configuration in the FB state at strain is denoted by . The shear stress at for one sample is given by:
| (15) |
The rigidity for one sample is defined as
| (16) |
where the differentiation on the RHS of Eq. (16) is defined as follows:
| (17) |
In the numerical calculation, we use a non-zero but sufficiently small for the evaluation of . Then, the averaged rigidity is defined as
| (18) |
where is the ensemble average.
III Theoretical Analysis
In this section, we introduce Hessian matrix in Sec. III.1 and theoretical expressions of rigidity in Sec. III.2.
III.1 Hessian matrix for frictional grains
Because the Hessian matrix is equivalent to the Jacobian matrix for harmonic grains, as shown in Appendices C.1 and D.3, in this study, we adopt the Hessian matrix (), where the element is given by Saitoh19 :
| (19) |
where and are any of and , while and express the grain indices. Here, we have introduced the effective potential energy between the contacted -th and -th grains as:
| (20) |
where is defined as
| (21) |
with
| (22) | ||||
| (23) |
under the virtual displacements and from the FB state at and , respectively.
The Hessian matrix introduced in Eq. (19) can be written as
| (24) |
where is a submatrix of the Hessian for a pair of grains and satisfying:
| (25) |
See Appendix C.1 for an explicit expression of each component of the Hessian matrix. Note that if the -th and -th grains are not in contact with each other.
Because is a real symmetric matrix, its eigenvalues and eigenvectors are also real. Using the decomposition of the potential, the Hessian matrix can be divided into
| (26) |
where
| (27) | ||||
| (28) |
for and
| (29) | ||||
| (30) |
for . Here, we have introduced
| (31) | ||||
| (32) |
To determine the explicit expression of each component of the Hessian matrix, refer to Appendix C.1.
The eigenequation of the Hessian matrix is given by
| (33) |
where is the right eigenvector corresponding to the -th eigenvalue of . Because the Hessian matrix is a real symmetric matrix, its left eigenequation is equivalent to its right eigenequation. Such properties remain unchanged even under the Lees-Edwards boundary conditions (see Appendix C.2). If all eigenstates are non-degenerate, satisfies the orthonormal relation with normalization , where .
III.2 Expressions of the rigidity via eigenmodes
In this subsection, we consider the rigidity introduced in Eq. (18). See Appendix E for the detailed properties of .
Let us introduce and as
| (34) |
Because the FB state is the minimum state of the potential energy, as shown in Appendix C.1, satisfies
| (35) |
where is the ket vector containing for all components.
Introducing
| (36) |
one can write
| (37) |
where we have used Eqs. (13) and (14). The first and second terms on the RHS of Eq. (37) represent the strain derivatives of the forces for the contributions from the affine and nonaffine displacements, respectively. In Eq. (37) we have introduced , which is defined as:
| (38) |
We have used in Eq. (37), which is defined as
| (39) |
and
| (40) |
for . Note that or does not affect , because the affine displacements are instantaneously applied to the system as a step strain. Thus, the integral interval of the tangential displacement during the affine deformation is zero.
Expanding the nonaffine displacements by the eigenvectors of and using the fact that the left-hand side of Eq. (37) is zero, we obtain
| (41) |
where and are the -th eigenvalues of , and the eigenvector corresponding to , respectively. Here, on the RHS of Eq. (41) excludes low-frequency modes for to maintain the numerical accuracy. Note that satisfies the orthonormal relation , if all eigenstates are non-degenerate. The expression for in Eq. (41) leads to a discontinuous change in at a critical strain for a plastic event because the eigenvectors and eigenvalues are discontinuously changed at this point.
The rigidity is decomposed into two parts:
| (42) |
where and are the rigidities corresponding to the affine and nonaffine displacements, respectively, for one sample. With the aid of Eqs. (15), (18), and (40), the expressions for and can be obtained as:
| (43) | ||||
| (44) |
where we have introduced
| (45) | ||||
| (46) |
Substituting Eq. (41) into Eq. (44), can be rewritten as
| (47) |
where we have introduced
| (48) |
The affine rigidity can be also expressed as
| (49) |
where
| (50) |
To verify the validity of the theoretical treatment, we introduce the theoretical stress with the aid of Eq.(42) as
| (51) |
IV Results and discussion
We verify the validity of the shear modulus obtained by the eigenvalue analysis by comparing it with that obtained by the simulation. First, we have confirmed the quantitative accuracy of our analysis to obtain the rigidity in the linear response regime of our system (see Appendix E.2), as in Ref. Ishima2022 .
For the numerical FB condition, we use the condition for arbitrary , where we adopt for the numerical calculation. In our simulation, we also adopt . In this study, we present the results for , the area fraction , and with the ensemble averages of samples, except for Appendix E.2. Note that the we analyze only the systems with which is sufficiently larger than the jamming density for a two-dimensional system. We ignore the effect of dissipation in the eigenequation because the velocity of each grain is sufficiently small to incur infinitesimal agitation from the FB state. The time step used for the simulation, , is set to with , and numerical integration is performed using the velocity Verlet method.
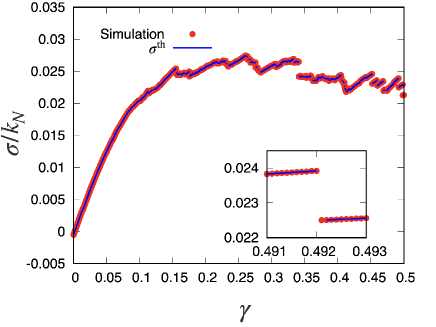
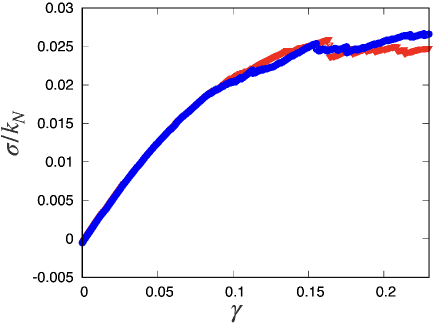
Now, let us consider a nonlinear regime in which there are many plastic events caused by stress avalanches. Here, we regard an event as plastic if the condition (i) or (ii) is satisfied.
Figure 1 shows a typical example of the stress-strain curve obtained by one sample of the collection of grains based on both the simulation and eigenvalue analysis developed in the previous section under the condition . It should be noted that the difference between the theoretical and simulation results is almost invisible, even in the presence of avalanches. However, the eigenvalue analysis cannot be used immediately after plastic events, that is, for (see the inset of Fig. 1), because the stress is not determined by Eq. (51) immediately after a plastic event.
Figure 2 shows a comparison of the stress-strain curve for (blue circles) with those for (red triangles). From the figure, we cannot find any dependence for , but some differences for larger can be observed as a result of stress avalanches.
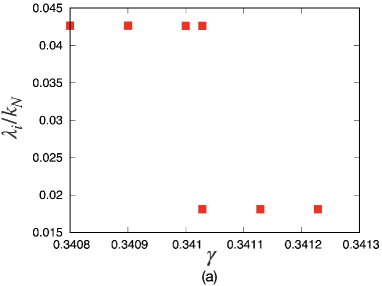
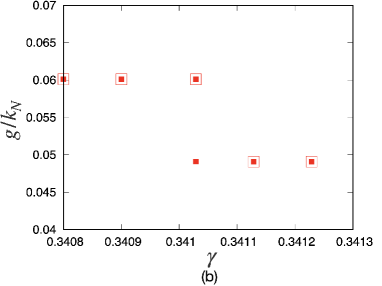
We might expect that some precursors of a stress-drop event can be detected from the behavior of the smallest non-zero eigenvalue. To verify this expectation, we plot the smallest non-zero eigenvalues in Fig. 3(a) near a critical strain with . It can be observed that the eigenvalues changes discontinuously at the critical strain ( for ), where the critical strain converges if (see Appendix B for details). Notably, there is no precursor for the smallest eigenvalue below the critical strain, in contrast to Refs. Maloney04 ; Maloney06 ; Manning11 ; Dasgupta12 , where non-harmonic potentials are used. Correspondingly, we cannot find any singularity of the rigidity as as in Fig. 3(b) for predicted in Refs. Maloney04 ; Maloney06 ; Karmakar10PRL ; Richard20 . The absence of the precursors and singularities in our model can be understood in the form of the Hessian matrix presented in Appendix D.3. In non-harmonic systems, some elements of the Hessian matrix become zero as when the contact between the -th and -th grains disappears. This leads to the precursors and singularities Maloney04 ; Maloney06 . However, in the harmonic systems, the corresponding element approaches a non-zero constant in the limit (see Appendix D.3), which results in the absence of the precursors.
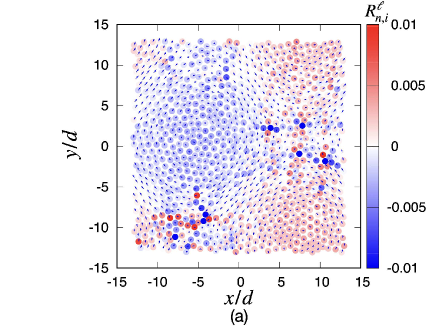
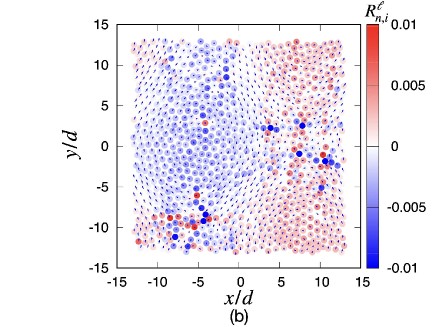
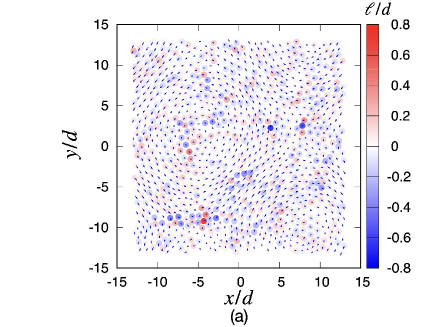
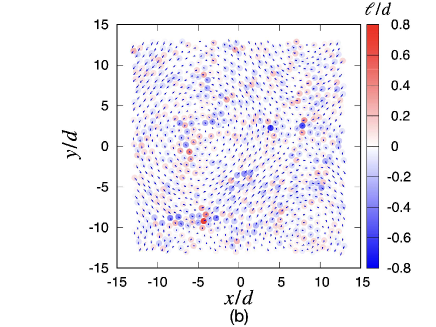
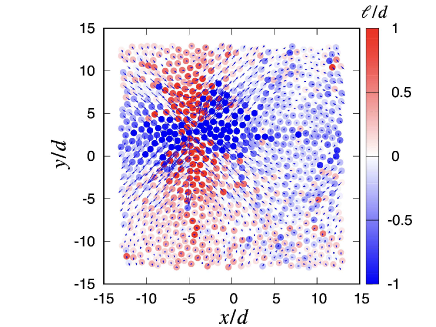
Figure 4 shows a set of plots of the eigenvectors corresponding to the smallest eigenvalue at (a) and at (b), where is the strain immediately after the plastic event, and is the strain just before the event. As shown in Fig. 4, changes in eigenvectors owing to the stress drop event can be observed. Here, we find the existence of domains of grains of clockwise rotation and counter-clockwise rotation, and the collective motion of grains between two domains. We may observe the excitation of the quadrupole-like mode, although its structure is not sufficiently clear.
Figure 5 is the comparison of obtained by the eigenvalue analysis (a) with that by the simulation (b) at , where in the simulation is evaluated by with . It is obvious that the difference between the two figures is invisible, though the quadrupole-like structure cannot be clearly seen as in Fig. 4. Nevertheless, we can find the collective motion of grains in both figures.
Because we cannot use the eigenvalue analysis at the critical strain for a plastic event, let us analyze the nonaffine displacement between and caused by an avalanche using the simulation:
| (52) |
where
| (53) |
Figure 6 shows a plot of the nonaffine displacement around a yielding point based on the simulation for at . This figure indicates that (i) grains move with rotations, which is one of the effects of mutual frictions between grains, and (ii) the existence of a quadrupole consisting of four domains of collective rotating grains exists. In particular, the rotations of the grains are sharply changed on the boundary between the domains. Unfortunately, cannot be described by the eigenvalue analysis, because expresses the configuration change, which is unstable for a small change in .
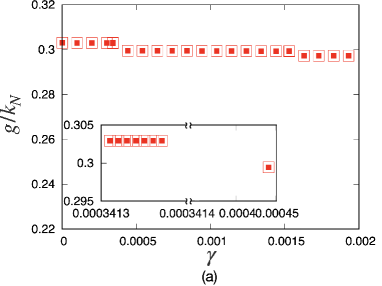
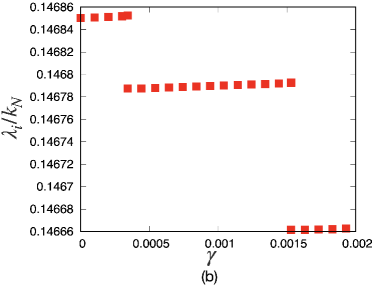
Figures 7 (a) and (b) show plots of the rigidity and smallest eigenvalue from to , which includes two plastic events based on the one-sample calculation of the collection of grains with . One can find an almost perfect agreement of the rigidity between the eigenvalue analysis and simulation, except for the yielding points (see Fig. 7 (a)). We find discontinuous changes in the smallest eigenvalue at the yielding point, where the rigidity changes discontinuously (see Fig. 7 (b). As expected, the magnitude of the discontinuous change in rigidity at the yielding point in Fig. 7 (a) for is smaller than that for a point of a stress drop for , as shown in Fig. 3.
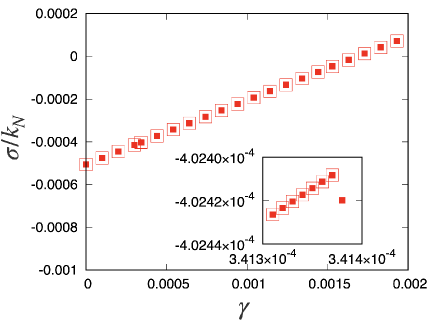
Figure 8 shows the stress-strain curve corresponding to Fig. 7. It is difficult to find the plastic events in the main figure of Fig. 8, but we can find a small stress drop at this point if we use a close-up figure in the inset. We verify the creation and annihilation of contacting pairs at the stress drop points. The stress expression in Eq. (51) cannot be used at the yielding point; thus a disagreement exists between the eigenvalue analysis and simulation at the point in the inset of Fig. 8.
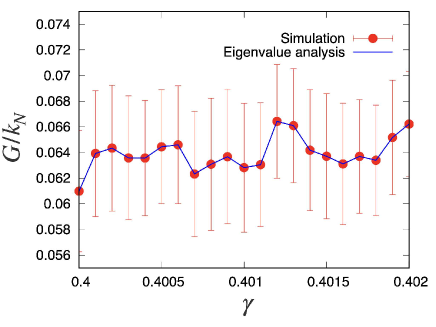
Figure 9 plots the rigidity of over 30 samples for , where we have omitted the data if stress drop events take place. We verify that rigidity based on the eigenvalue analysis reproduces the results of the simulation. Note that non-monotonic changes in originate from changes in the contact points and configuration of grains.
V Conclusion
In this paper, we have demonstrated that eigenvalue analysis of the Hessian matrix provides precise descriptions of the rigidity and stress of dispersed frictional grains in which the contact force is described by the harmonic potential, in spite of stress-drop events, such as stress avalanches. However, our model does not contain any slip processes between contacting grains. This success is a natural extension of the previous studies on frictionless grains Maloney04 ; Maloney06 to frictional grains and of our previous study on the linear response regime Ishima2022 to the nonlinear response regime. Two remarkable features of the contacting model are described by the harmonic potential. First, the tangential contact force in this model is no longer a history-dependent one. This leads to the significant simplification of the theoretical analysis. Second, unlike the naive expectation, the eigenvalues in our model do not indicate any precursors for the stress-drop events. In essence, stress-drop events take place suddenly by releasing contact points.
Some future tasks that need to be addressed are as follows. First, we need to consider the effect of slips, which causes a significant difference from our model because history-dependent contacts play important roles in the presence of slip events. Second, we must extend our analysis to nonlinear interacting models, such as the Hertzian contact model in a three-dimensional space. We plan on working on these points in the future.
VI ACKNOWLEDGMENTS
The authors thank N. Oyama for the fruitful discussions and useful comments. This work was partially supported by a Grant-in-Aid from the MEXT for Scientific Research (Grant No. JP22K03459, JP21H01006, and JP19K03670) and a Grant-in-Aid from the Japan Society for Promotion of Science JSPS Research Fellow (Grant No. JP20J20292).
Appendix A Absence of the second term on RHS of Eq. (10)
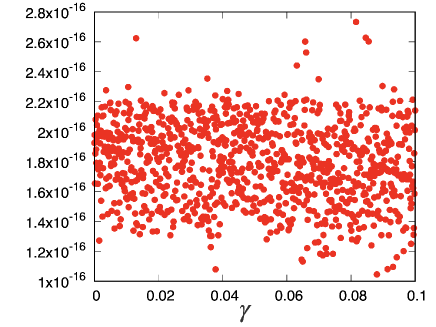
Thus far, we could not prove that the second term on RHS of Eq. (10) can be regarded as zero with numerical accuracy, but we verify that this term is zero, at least, in the numerical simulation of harmonic systems as follows: Let us calculate the ratio of the second term in Eq. (10) to the first term using
| (54) |
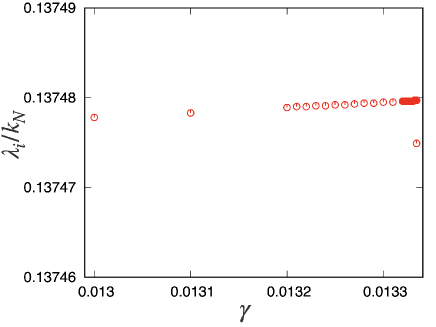
Figure 10 shows the plots of the largest Err in contacting pairs against , which indicates . As our calculation is based on double precision, which has only 16 significant digits, Err can be regarded as zero.
Appendix B The behavior of the smallest eigenvalue near stress-drop points
In this appendix, we provide an in-depth explain the behavior of the smallest eigenvalue in the vicinity of the stress-drop points in detail. We adopt the following protocol to reduce the step strain small in the vicinity of the stress-drop point. We adopt in the appendix. We use if there is no plastic event during the strain increment . If we find a stress drop during the strain from to , we restore the system to the state , and examine . If we do not find any stress drop, we further add the strain with ; if we still have a stress drop, we repeat the procedure of restoring and adding strain . This protocol is repeated to detect stress drop events until we reach . In this appendix, we illustrate how the results depend on the choice of , where the smallest value of is .
Figure 11 presents the stress-strain curves obtained using this protocol. The upper branch in Fig. 11 represents the shear stress below the stress drop, and the lower branch represents the shear stress above the stress drop. The smallest in the lower branch and the largest in the upper branch strongly depend on . As shown in Fig. 12, the stress drop takes place at for , whereas the critical strain for the stress drop approaches 0.013334 as decreases, where is 0.013334 for .
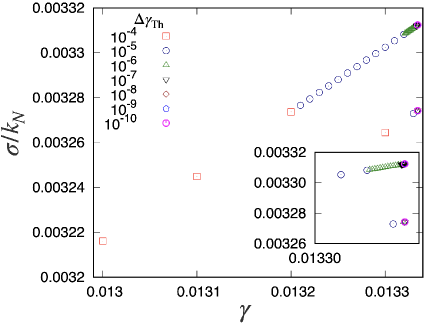
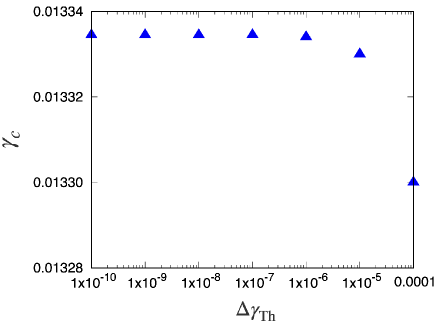
Figure 13 plots the behavior of the smallest eigenvalue against corresponding to Fig. 11 for immediately below the stress drop point, where the symbols correspond to the analysis for the corresponding as in Fig. 11. We have confirmed that there is no precursor of the eigenvalues below as observed in Hertzian and Lennard-Jones systems Maloney04 ; Maloney06 ; Manning11 . Thus, the harmonic system does not have any precursors in the behavior of the smallest eigenvalue.
Appendix C Some properties of the Hessian matrix in a harmonic system
In this appendix, we briefly summarize the properties of the Hessian matrix of the harmonic contact model. In Sec. C.1, we explicitly express the elements of the Hessian matrix in this model. In Sec. C.2, we demonstrate that the symmetry of the Hessian matrix still holds even under the Lees-Edwards boundary condition.
C.1 The explicit expression for the Hessian matrix
In this appendix, we present an explicit expression for the Hessian matrix. To this end, we return to the effective potential in Eq. (20). It is straightforward to obtain
| (55) | ||||
| (56) | ||||
| (57) | ||||
| (58) | ||||
| (59) | ||||
| (60) | ||||
| (61) | ||||
| (62) | ||||
| (63) |
Thus, we obtain
| (64) | ||||
| (65) | ||||
| (66) | ||||
| (67) | ||||
| (68) | ||||
| (69) |
for and
| (70) | ||||
| (71) | ||||
| (72) | ||||
| (73) | ||||
| (74) | ||||
| (75) |
C.2 Effect of the boundary condition to the Hessian matrix
In this appendix, we explain the influence of strain and the boundary condition on the Hessian matrix in detail to determine whether the symmetry of the Hessian matrix is still maintained, even if we consider a system with non-zero strain.
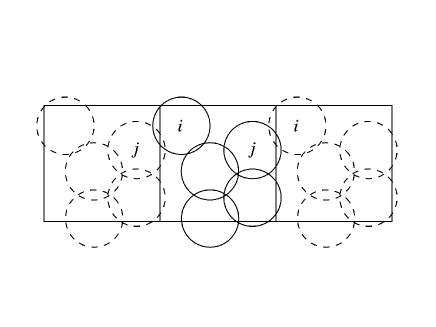
First, let us consider the case in which particle interacts with the particle through a mirror image in -direction, as shown in Fig. 14. In this case, is given by
| (76) |
where . Similarly, is given by
| (77) |
Thus, satisfies
| (78) |
Then, we obtain
| (79) |
Thus, the result is independent of the strain, and the symmetry of the Hessian is still valid in this case.
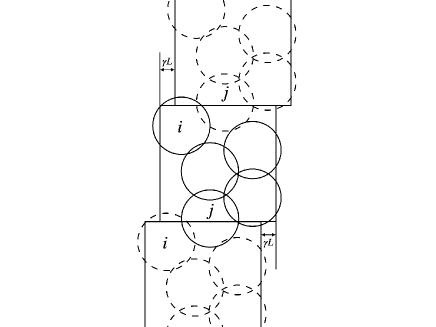
Next, let us consider the case in which the particle interacts with the particle through a mirror image in the -direction (see Fig. 15). In this case, is given by
| (80) |
where . Similarly, is given by
| (81) |
Since the relation
| (82) |
we obtain
| (83) |
Thus, and depend on in the same way. With the aid of Eqs. (80),(81) and (83), the Hessian matrix depends on if the particle interacts with another particle through the mirror image in -direction, although the symmetry of the Hessian is still maintained.
Appendix D Some properties of the Jacobian matrix in a harmonic system and its equivalency to the Hessian matrix
In this appendix, we briefly summarize the properties of the Jacobian matrix for the harmonic contact model that was previously used in the description of frictional grains Chattoraj19 ; Chattoraj19E ; Charan20 ; Ishima2022 . In Sec.D.1, we present explicit forms of the diagonal and non-diagonal blocks of the Jacobian matrix. In Sec.D.2, we present the derivation of the Jacobian for the harmonic contact model. In Sec. D.3, we explicitly write the elements of the Jacobian matrix in the model.
D.1 Jacobian block elements
Let us write a sub-matrix , which is the block element of the Jacobian obtained from Eq. (19):
| (84) |
where the superscripts and correspond to -components, and and are the particle numbers. Here, are -component of and scaled torque that the -th particle receives from the -th particle, respectively. The sub-matrix for is given by
| (85) |
where we have used , and . Here, the superscripts and correspond to components.
D.2 Derivation of Jacobian matrix in the harmonic system
Let us consider only the normal and tangential elastic contact forces
| (86) | ||||
| (87) |
where the integration of
| (88) |
is performed during the contact between the -th and -th grains. Since Eq. (88) does not contain the second term on RHS of Eq. (10), may not be perpendicular to . Nevertheless, we adopt Eq. (88) for simplicity. Here, is defined as
| (89) |
where is defined as
| (90) |
Each component of Eq. (89) is written as
| (91) | ||||
| (92) |
The derivative of the normal force is given by
| (93) | ||||
| (94) |
where Kronecker’s delta satisfies for and otherwise. We have used
| (95) | ||||
| (96) |
to obtain Eq. (93).
The derivative of the tangential force is written as
| (97) | ||||
| (98) |
where and are defined, respectively, as
| (99) | ||||
| (100) |
Here, and in Eqs. (97) and (98) satisfy the following:
| (101) | ||||
| (102) |
The derivation of Eqs. (101) and (102) are as follows Chattoraj19 . From Eq. (89), can be written as
| (103) |
Then, satisfies
| (104) |
Similarly, also satisfies
| (105) |
Here, is the function of and . We obtain the differential form of :
| (106) |
Next, we obtain Eqs. (101), (102), by comparing Eqs. (104) and (105) using Eq. (106).
Because the scaled torque satisfies
| (107) |
we obtain
| (108) | ||||
| (109) |
where we have used and .
D.3 Explicit form of Jacobian for particles interacting with harmonic force
From Sec. D.2, the off-diagonal elements of the Jacobian matrix with are given by
| (110) | ||||
| (111) | ||||
| (112) | ||||
| (113) | ||||
| (114) | ||||
| (115) | ||||
| (116) | ||||
| (117) | ||||
| (118) |
Notably, the elements of the Jacobian matrix are independent of .
With the aid of Eq. (84), the elements in the diagonal block are given by
| (119) | ||||
| (120) | ||||
| (121) | ||||
| (122) | ||||
| (123) | ||||
| (124) | ||||
| (125) | ||||
| (126) | ||||
| (127) |
The expressions in Eqs. (110)-(127) are equivalent to Eqs. (64)-(75) for a Hessian matrix. Thus, we conclude that the Jacobian matrix is equivalent to the Hessian matrix for the harmonic system without considering Coulomb’s slip.
Appendix E The detailed properties of rigidity
This appendix consists of two sections. In Appendix E.1, we present the detailed expressions of rigidity . In Appendix E.2, we demonstrate the quantitative accuracy of the Hessian analysis in the linear response regime by comparing the theoretical evaluation of the rigidity with that obtained by the numerical simulation as in Ref. Ishima2022 .
E.1 The expression of
The symmetrized shear stress in Eq. (15) is expressed as
| (128) |
where
| (129) |
Substituting Eq. (128) into Eq. (17), we obtain
| (130) |
Substituting Eq. (130) into Eq. (128), the rigidity is expressed as
| (131) |
By expanding in Eq. (131) by from the finite strain , we obtain
| (132) |
Similarly, by expanding in Eq. (131) from the zero strain state, we obtain
| (133) |
Moreover, using and , and can be written as
| (134) |
E.2 The rigidity of the harmonic model in the linear response regime
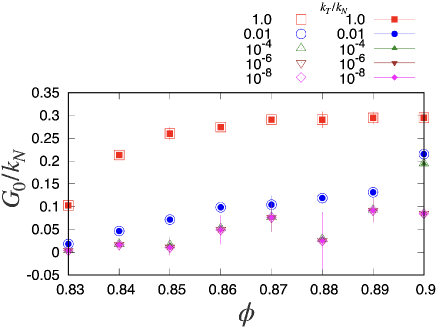
In this appendix, we verify the validity of our method to evaluate the rigidity for frictional harmonic grains in the linear response regime for various and as in Ref. Ishima2022 . Figure 16 presents the results of the rigidity, in which obtained by the eigenvalue analysis (filled symbols) is in perfect agreement with that obtained by the simulation (open symbols). Here we take the average over 5 ensembles for each and . This figure confirms the validity of the theoretical method in the linear response regime.
References
- (1) H. M. Jaeger, S. R. Nagel, and R. P. Behringer, Granular solids, liquids, and gases, Rev. Mod. Phys. 68, 1259 (1996).
- (2) D. J. Durian, Foam Mechanics at the Bubble Scale, Phys. Rev. Lett. 75, 4780 (1995).
- (3) M. Wyart, On the rigidity of amorphous solids, Ann. Phys. Fr. 30, 1 (2005).
- (4) A. Baule, F. Morone, H. J. Herrmann, and H. A. Makse, Edwards statistical mechanics for jammed granular matter, Rev. Mod. Phys. 90, 015006 (2018).
- (5) A. Liu and S. Nagel, Jamming is not just cool any more, Nature (London) 396, 21 (1998).
- (6) K. Hima Nagamanasa, S. Gokhale, A. K. Sood, and R. Ganapathy, Experimental signatures of a nonequilibrium phase transition governing the yielding of a soft glass, Phys. Rev. E 89, 062308 (2014).
- (7) E. D. Knowlton, D. J. Pine, and L. Cipelletti, A microscopic view of the yielding transition in concentrated emulsions, Soft Matter 10, 6931 (2014).
- (8) T. Kawasaki and L. Berthier, Macroscopic yielding in jammed solids is accompanied by a nonequilibrium first-order transition in particle trajectories, Phys. Rev. E 94, 022615 (2016).
- (9) P. Leishangthem, A. D.S. Parmar, and S. Sastry, The yielding transition in amorphous solids under oscillatory shear deformation, Nat. Commun. 8, 14653 (2017).
- (10) S. Dagois-Bohy, E. Somfai, B. P. Tighe, and M. van Hecke, Softening and yielding of soft glassy materials, Soft Matter 13, 9036 (2017).
- (11) M. Ozawa, L. Berthier, G. Biroli, A. Rosso, and G. Tarjus, Random critical point separates brittle and ductile yielding transitions in amorphous materials, Proc. Natl.Acad. Sci. U.S.A. 115, 6656 (2018).
- (12) A. H. Clark, J. D. Thompson, M. D. Shattuck, N. T. Ouellette, and C. S. O’Hern, Critical scaling near the yielding transition in granular media, Phys. Rev. E 97, 062901 (2018).
- (13) J. Boschan, S. Luding, and B. P. Tighe, Jamming and irreversibility, Granul. Matter 21, 58 (2019).
- (14) M. Singh, M. Ozawa, and L. Berthier, Brittle yielding of amorphous solids at finite shear rates, Phys. Rev. Materials 4, 025603 (2020).
- (15) M. Otsuki and H. Hayakawa, Softening and residual loss modulus of jammed grains under oscillatory shear in absorbing state, Phys. Rev. Lett. 128, 208002 (2022).
- (16) M. Wyart, S. R. Nagel, and T. A. Witten, Geometric origin of excess low-frequency vibrational modes in weakly connected amorphous solids, Eur. Phys. Lett. 72, 486 (2005).
- (17) W. G. Ellenbroek, E. Somfai, M. van Hecke, and W. van Saarloos, Critical Scaling in Linear Response of Frictionless Granular Packings near Jamming, Phys. Rev. Lett. 97, 258001 (2006).
- (18) E. Lerner, G. Düring, and E. Bouchbinder, Statistics and Properties of Low-Frequency Vibrational Modes in Structural Glasses, Phys. Rev. Lett. 117, 035501 (2016).
- (19) L. Gartner and E. Lerner, Nonlinear plastic modes in disordered solids, Phys. Rev. E 93, 011001(R) (2016).
- (20) S. Bonfanti, R. Guerra, C. Mondal, I. Procaccia, and S. Zapperi, Elementary plastic events in amorphous silica, Phys. Rev. E 100 060602(R) (2019).
- (21) P. Morse, S. Wijtmans, M. van Deen, M. van Hecke, and M. L. Manning, Differences in plasticity between hard and soft spheres, Phys. Rev. Res. 2, 023179 (2020).
- (22) E. DeGiuli, E. Lerner, C. Brito, and M. Wyart, Force distribution affects vibrational properties in hard-sphere glasses, Proc. Natl. Acad. Sci. U.S.A. 111, 17054 (2014).
- (23) H. Mizuno, K. Saitoh, and L. Silbert, Elastic moduli and vibrational modes in jammed particulate packings, Phys. Rev. E 93, 062905 (2016).
- (24) C. Maloney and A. Lemaître, Universal Breakdown of Elasticity at the Onset of Material Failure, Phys. Rev. Lett. 93, 195501 (2004).
- (25) C. Maloney and A. Lemaître, Amorphous systems in athermal, quasistatic shear, Phys. Rev. E 74, 016118 (2006).
- (26) A. Lemaître and C. Maloney, Sum Rules for the Quasi-Static and Visco-Elastic Response of Disordered Solids at Zero Temperature, J. Stat. Phys. 123, 415 (2006).
- (27) A. Zaccone and E. Scossa-Romano, Approximate analytical description of the nonaffine response of amorphous solids, Phys. Rev. B 83, 184205 (2011).
- (28) V. V. Palyulin, C. Ness, R. Milkus, R. M. Elder, T. W. Sirk, and A. Zaccone, Parameter-free predictions of the viscoelastic response of glassy polymers from non-affine lattice dynamics, Soft Matter 14, 8475 (2018).
- (29) N. Oyama, H. Mizuno and A. Ikeda, Instantaneous Normal Modes Reveal Structural Signatures for the Herschel-Bulkley Rheology in Sheared Glasses, Phys. Rev. Lett. 127, 108003 (2021).
- (30) I. Kriuchevskyi, T. W. Sirk, and A. Zaccone, Predicting plasticity of amorphous solids from instantaneous normal modes, Phys. Rev. E 105, 055004 (2022).
- (31) M. L. Manning and A. J. Liu, Vibrational Modes Identify Soft Spots in a Sheared Disordered Packing, Phys. Rev. Lett. 107, 108302 (2011).
- (32) R. Dasgupta, S. Karmakar, and I. Procaccia, Universality of the Plastic Instability in Strained Amorphous Solids, Phys. Rev. Lett. 108, 075701 (2012).
- (33) F. Ebrahem, F. Bamer, and B. Markert, Origin of reversible and irreversible atomic-scale rearrangements in a model two-dimensional network glass, Phys. Rev. E 102, 033006 (2020).
- (34) S. Karmakar, A. Lemaître, E. Lerner,1 and I. Procaccia, Predicting Plastic Flow Events in Athermal Shear-Strained Amorphous Solids, Phys. Rev. Lett., 104, 215502 (2010).
- (35) D. Richard, M. Ozawa, S. Patinet, E. Stanifer, B. Shang, S. A. Ridout, B. Xu, G. Zhang, P. K. Morse, J.-L. Barrat, L. Berthier, M. L. Falk, P. Guan, A. J. Liu, K. Martens, S. Sastry, D. Vandembroucq, E. Lerner, and M. L. Manning, Predicting plasticity in disordered solids from structural indicators, Phys. Rev. Materials 4, 113609 (2020).
- (36) J. Chattoraj, O. Gendelman, M. Pica Ciamarra, and I. Procaccia, Oscillatory Instabilities in Frictional Granular Matter, Phys. Rev. Lett. 123, 098003 (2019).
- (37) J. Chattoraj, O. Gendelman, M. P. Ciamarra, and I. Procaccia, Noise amplification in frictional systems: Oscillatory instabilities, Phys. Rev. E 100, 042901 (2019).
- (38) H. Charan, O. Gendelman, I. Procaccia, and Y. Sheffer, Giant amplification of small perturbations in frictional amorphous solids, Phys. Rev. E 101, 062902 (2020).
- (39) E. Somfai, M. van Hecke, W. G. Ellenbroek, K. Shundyak, and W. van Saarloos, Critical and noncritical jamming of frictional grains, Phys. Rev. E 75, 020301(R) (2007).
- (40) S. Henkes, M. van Hecke, and W. van Saarloos, Critical jamming of frictional grains in the generalized isostaticity picture, Eur. Phys. Lett. 90, 14003 (2010).
- (41) K. Liu, J. E. Kollmer, K. E. Daniels, J. M. Schwarz, and S. Henkes, Spongelike Rigid Structures in Frictional Granular Packings, Phys. Rev. Lett. 126, 088002 (2021).
- (42) D. Ishima, K. Saitoh, M. Otsuki and H. Hayakawa, Theory of rigidity and density of states of two-dimensional amorphous solids of dispersed frictional grains in the linear response regime, arXiv:2207/06632.
- (43) S. Luding, Global equation of state of two-dimensional hard sphere systems, Phys. Rev. E 63, 042201 (2001).
- (44) A. Lees and S. Edwards, The computer study of transport processes under extreme conditions, J. Phys. C: Solid State Phys. 5, 1921 (1972).
- (45) D. J. Evans and G. P. Morriss, Statistical Mechanics of Nonequilibrium Liquids, 2nd ed. (Cambridge University Press, Cambridge, UK, 2008).
- (46) E. Lerner and I. Procassia, Locality and nonlocality in elastoplastic responses of amorphous solids, Phys. Rev. E 79, 066109 (2009).
- (47) S. Karmakar, E. Lerner, I. Procaccia, and J. Zylberg, Statistical physics of elastoplastic steady states in amorphous solids: Finite temperatures and strain rates, Phys. Rev. E 82, 031301 (2010).
- (48) K. Saitoh, R. Shrivastava, and S. Luding, Rotational sound in disordered granular materials, Phys. Rev. E 99, 012906 (2019).