Efficient reanalysis of events from GWTC-3 with RIFT and asimov
Abstract
Different waveform models can yield notably different conclusions about the properties of individual gravitational wave events. For instance, previous analyses using the SEOBNRv4PHM, IMRPhenomXPHM models, and NRSur7dq4 have led to varying results regarding event properties. This variability complicates the interpretation of the data and understanding of the astrophysical phenomena involved. There is an ongoing need to reassess candidate events with the best available interpretations and models. Current approaches lack efficiency or consistency, making it challenging to perform large-scale reanalyses with updated models or improved techniques. It is imperative that investigations into waveform systematics be reproducible. Frameworks like asimov can facilitate large-scale reanalyses with consistent settings and high-quality results, and can reliably show how different waveform models affect the interpretation of gravitational wave events. This, in combination with other provided tools, allow for reanalysis of several events from the GWTC-3 catalog. We include access to full analysis settings that facilitate public use of GWOSC data on the Open Science Grid, particularly those conducted with the IMRPhenomPv2, SEOBNRv4PHM, SEOBNRv5PHM, and NRSur7dq4 waveform models. Our parameter inference results find similar conclusions to previously published work: for several events, all models largely agree, but for a few exceptional events these models disagree substantially on the nature of the merging binary.
I Introduction
Since the discovery of GW150914_095045 by the Advanced LIGO [1] and Virgo [2, 3] detectors, now joined by KAGRA [4], the first four observing runs (referred to as O1, O2, O3, and O4) of the LIGO/Virgo/KAGRA network by the LVK Collaboration have identified the characteristic gravitational wave signature of coalescing compact binaries [5]. Independent analyses of the public data have also contributed to the candidate event census; see, e.g., [6, 7, 8] and references therein. For each candidate event, the GW strain data can be compared to approximate models for the emitted gravitational radiation from a coalescing (quasicircular) compact binary, to deduce the distribution of plausible source binary parameters consistent with the data; see, e.g., [5, 9] and references therein.
Lacking an efficient global solution for the two-body problem in general relativity, inferences about compact binary parameters are performed with one or more of several approximate models for the outgoing radiation. As a concrete example, analysis of new events in the GWTC-3 catalog paper employed two waveform models, known as SEOBNRv4PHM [10, 11] and IMRPhenomXPHM [12], as did a subsequent reanalysis with a different inference strategy [13]. A recent study [14] reanalyzed many of these same events with yet another waveform model, NRSur7dq4 [15]. As in previous analyses real events such as the GWTC-2 catalog [16], these waveform models can and do draw somewhat different conclusions about individual events’ properties. Both the GWTC-3 catalog and its reanalysis identified several events with notably different properties [16, 14]. More broadly, many investigations repeatedly identify differences between even the best presently-available waveform models, such that the properties of some astrophysically currently accessible events will be notably different when interpreted with different models [17, 18, 19, 20, 21, 22, 14].
Given the substantial and ongoing need to reassess candidate events with the best available interpretations, frameworks that enable efficient large-scale reanalysis of events have become vital tools for gravitational wave astronomy. In this work, we apply and refine one framework to manage analyses of many events with consistent settings: asimov [23], managing the RIFT parameter inference engine [24, 9]. Our full analysis settings and software are publicly available, including worked exmaples on how to use public GWOSC data and the Open Science Grid to analyze some of these events [25]. In an associated technical data releases and appendicies, we demonstrate how to use previous asimov settings, generate asimov-compatible settings from existing public analyses [14], and operate the end-to-end production of our inference results.
As an application of our framework, we revisit several of the analyses presented in GWTC-3 with SEOBNRv4PHM: specifically, the high-mass events reanalyzed with NRSur7dq4 [14]. Though performed with RIFT, the previously published GWTC-3 analyses provided extremely few posterior samples, due to their use of calibration marginalization implemented via rejection sampling. In this work, given the negligible impact of calibration marginalization on astrophysical source properties, we perform comparable reanalyses to produce large, high-quality sets of posterior samples without calibration marginalization. To demonstrate the utility of our framework for reproducible investigation of waveform systematics, we also perform these analyses with several other contemporary waveform models, including IMRPhenomPv2 [26], NRSur7dq4, SEOBNRv4PHM [10, 11], and SEOBNRv5PHM [22, 27].
This paper is organized as follows. In Section II we describe our parameter inference approach, the asimov infrastructure, and the selected O3 events reanalyzed in this work. In Section III we demonstrate our reanalyses of these events. We first describe selected anecdotal examples to highlight waveform systematics. Then, following previous studies, we present large-scale summary figures and tables, characterizing all the events used.
II Methods
II.1 Parameter inference with RIFT
In a coalescing quasicircular orbit, a compact binary can be fully defined by 15 parameters. Among these, eight are the intrinsic parameters - signified by - which encompass any factors describing the physical properties of the individual objects within the system - the binary’s masses, spin magnitudes, spin angles, and azimuthl spin angles. Extrinsic parameters - signified by - consist of the other seven values necessary to describe its spacetime position and orientation relative to the detectors.
RIFT interprets gravitational wave observations by comparing them with predicted gravitational wave signals in a two-step iterative process. In the first stage, RIFT has numerous workers concurrently calculate a marginal likelihood
| (1) |
for many different values of , where is the likelihood of the gravitational wave signal in the multi-detector network; see [28, 24] for further details. In the second stage, RIFT will use accumulated marginal likelihood evaluations to construct an approximation to which is then used to infer the detector-frame posterior distribution
| (2) |
where the prior represents the prior distribution on intrinsic parameters.
RIFT inference is performed using the spin-weighted spherical harmonic waveforms or [28, 29, 24, 30], usually computed from binary parameters through the lalsimulation or gwsignal library. In this work, we will present RIFT inferences performed using several families of models. For the SEOB family of models, we employ SEOBNRv4PHM [10, 11] and SEOBNRv5PHM [22, 27]. Among surrogate models calibrated to numerical relativity, we employ the NRSur7dq4 model [15]. While we will not use RIFT to analyze these events with IMRPhenomXPHM [12], we will compare our results to analyses performed by others, including analyses using this waveform.
II.2 Asimov automation and standardization
The asimov infrastructure provides a framework for managing suites of parameter inference calculations. This framework in particular provides not only a mechanism for storing event-specific and algorithm-specific settings, but also a mechanism to implement these settings, launching and overseeing production analyses with a variety of parameter inference tools. Starting with the GWTC-3 and GWTC-2.1 papers, the LVK began performing its analyses using asimov; in particular, the asimov configurations needed to perform these analyses are available [23]. In this work, we minimally adapt these settings with pipeline- and approximant-specific adjustments.
The default analysis settings define a specific frequency range for each event, usually covering from up to some maximum frequency where is the largest frequency used in the original LVK PSD.
Other groups, however, have performed their own large-scale reanalyses using their own framework and metadata storage. To facilitate comparison with specific sets of previous reanalyses [12] and [14], we implemented and provide tools to convert from their metadata format to a standard asimov configuration file. Since not all of the metadata used for previous analyses is compatible with asimov, some differences are expected between the original analyses and our attempt at reproducing a comparable analysis. For our analyses, we use asimov to get the PSDs by running Bayeswave for all events. However, we also provide tools to retrieve PSDs from previous publications and provide a demonstration on how this method also be used.
II.3 Selected O3 events and settings
The GWTC-3 paper, covering the second half of O3 (henceforth denoted as O3b), presented several analyses performed by the LVK, including many events analyzed with SEOBNRv4PHM via RIFT. The default design choices underlying these analyses prioritized matching the configuration of corresponding analyses with another code, notably including the effects of calibration marginalization. Thus, after first using RIFT to analyze events with SEOBNRv4PHM, these analyses were postprocessed with rejection sampling, to account for the impact of calibration marginalization. Previous studies have demonstrated that calibration marginalization has little impact on intrinsic or extrinsic parameters, modulo a modest effect in some cases on the source sky location. By contrast, the decimation performed by the O3b rejection sampling provides surprisingly few samples to downstream users. For this reason, the reanalyses presented below will omit calibration marginalization entirely.
Table 1 lists the events we have selected for reanalysis. In our demonstration, we chose to reanalyze the same set of O3b events recently reanalyzed with NRSur7dq4 [14]. The table also provides metadata needed to initiate a RIFT analysis: the specific event time and approximate mass range to investigate. By default, RIFT accesses this information from a single file, nominally produced by real search codes (a “coincidence” file commonly denoted coinc.xml), but alternatively generated from median search results. For complete reproducibility of pre-existing LVK analyses, we list meta-information enumerated by the event’s internal gracedb characteristic event identifier along with a secondary identifier identifying the characteristic event geocenter time and mass. These identifiers sometimes differ from the preferred released event, because of small but important differences between full inference and the event time or other parameters targeted by searches. For public reanalyses, we have also generated our own alternative characteristic information, disseminated along with our configuration files.
| Event | Superevent | GID | GPS Time |
|---|---|---|---|
| GW191109_010717 | S191109d | G354219 | 1257296855.216458 |
| GW191222_033537 | S191222n | G358088 | 1261020955.123615 |
| GW191230_180458 | S191230an | G358883 | 1261764316.406738 |
| GW200112_155838 | S200112r | G359994 | 1262879936.090936 |
| GW200128_022011 | S200128d | G361407 | 1264213229.901367 |
| GW200129_065458 | S200129m | G361581 | 1264316116.433214 |
| GW200208_130117 | S200208q | G363349 | 1265202095.949707 |
| GW200209_085452 | S200209ab | G363458 | 1265273710.17476 |
| GW200216_220804 | S200216br | G364262 | 1265926102.879405 |
| GW200219_094415 | S200219ac | G364600 | 1266140673.196691 |
| GW200220_061928 | S200220ad | G364748 | 1266214786.632 |
| GW200220_124850 | S200220aw | G364783 | 1266238148.15 |
| GW200224_222234 | S200224ca | G365380 | 1266618172.401773 |
| GW200302_015811 | S200302c | G366190 | 1267149509.516065 |
| GW200311_115853 | S200311bg | G367788 | 1267963151.398 |
In this work, we will perform inference on either the publicly-released GWTC-3 data from GWOSC [31], or (to facilitate use of settings adopted in prior work) bit-equivalent internal data. Following the analyses used for LVK publications, we use GWOSC-released deglitched data when appropriate. Unless otherwise noted, we generate independent PSD estimates using Bayeswave [32, 33, 34]. However, while as a second alternative and for comparison, when alternatively gathered PSDs from existing analyses of the GWTC-3 catalog [5]; examples of this configuration are also disseminated in our configuraiton repository [25].
III Results
III.1 Summary statistics
Following [14], Figures 1 and 2 illustrate a simple summary statistic – the Jensen-Shannon (JS) divergence – quantifying differences between marginal one-dimensional posterior distributions inferred for each event. The vertical dashed red line corresponds to a JS divergence of , above which differences between one-dimensional marginal distributions are easily identified by eye. The top panels of Figures 1 and 2 show comparisons between inferences with three state-of-the-art waveform models compared to inferences derived with an older model (IMRPhenomPv2) known to omit important physics and higher-order modes. Except for a handful of notable exceptions (GW191109, GW200302, GW200129), most analyses with IMRPhenomPv2 are broadly consistent with analyses done with more sophisticated waveforms. We demonstrate how this counterintuitive result arises using concrete examples in the next section. By contrast, the bottom panels of Figures 1 and 2 show familiar differences when comparing results between different state-of-the-art waveform models. These comparisons suggest that almost every event has some parameter in which notable waveform differences occur. Likewise, these comparisons suggest that every pair of waveforms (including SEOBNRv4PHM and SEOBNRv5PHM) has at one or more event where conclusions derived using those two waveforms differ by more than our ad hoc JS threshold. These two bottom panels present qualitatively similar results as previous work [14] – see their Figures 3 and 4 – albeit now performed exclusively with RIFT and using a different set of waveform models for comparison (i.e., including SEOBNRv5PHM and IMRPhenomPv2, but omitting IMRPhenomXPHM).




III.2 Detailed posterior comparisons: Best available models
Using the summary statistics provided above and in previous work [14], we have identified five events that merit further discussion: GW200129, GW191109, GW200216, and both events on the date GW200220. In an appendix and associated data release, we present posterior inferences for all events in our sample. In both the appendix and our own figures, for comparison and to normalize the scale of differences presented in this work, we also present the IMRPhenomXPHM results produced for GWTC-3 [5]. We also present NRSur7dq4 results provided by a previous study, for validation [14].
GW200129 has inspired considerable followup investigation, including claims of precession [35], eccentricity [36], and validation studies to assess stability of results under different data cleaning methods [37, 38]. As illustrated in Figure 3, in our benchmark analyses, using public cleaned frames and with a (common) independently generated PSD, we find our three waveform models draw dramatically different conclusions about this event, most notably the spin magnitudes of the two masses. For this event, even the two similar models SEOBNRv4PHM and SEOBNRv5PHM lead to notably different conclusions. Our analysis with NRSur7dq4 favors even more extreme mass ratios, primary spins, and than our two SEOBNR results. However, as discussed below (“comparison to previous results”), our analyses with NRSur7dq4 do not produce as extreme conclusions about the mass ratio and spin as found in another independent reanalysis [14], which employs slightly different settings (e.g., an independently-generated PSD).




By contrast, for GW200216 (Figure 4), GW200220_061928 (Figure 5), and GW200220_124850 (Figure 6), our inferences using the two SEOBNR models are very consistent with each other, and differ from NRSur7dq4 primarily in the mass ratio and spin magnitude distributions. In all three cases, the NRSur7qd4 analysis favors a wider mass ratio distribution and slightly prefers larger spins, while our two SEOBNR analyses favor comparable mass ratios and lower spins.
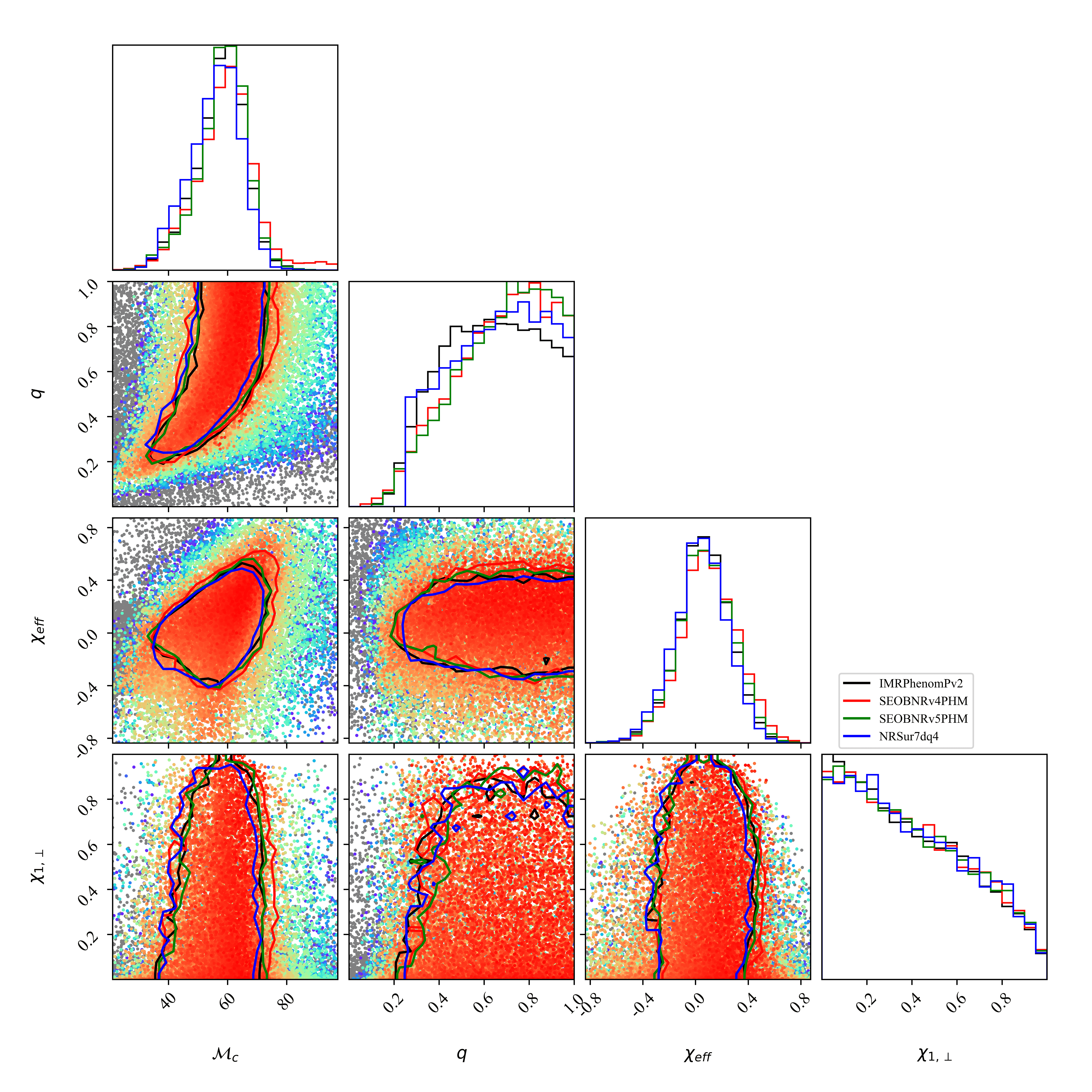


For GW191109, our inferences once again depend more sentitively on the assumed waveform, as illustrated in Figures 7 and 8. As might be expected given the high mass of the event and the model’s simplified physics, interpretations drawn using IMRPhenomPv2 in particular produce strikingly different conclusions about the mass ratio, primary spin, and even than analyses performed with any other waveform. By contrast, though waveform systematics change the posterior distributions modestly, when , comparing analyses performed in this work with state-of-the-art waveforms (SEOBNRv4PHM, SEOBNRv5PHM, and NRSur7dq4), we find coarsely good overall agreement.




III.3 Detailed posterior comparisons: IMRPhenomPv2
Despite the substantial and frequent differences seen between different calculations that both use state-of-the-art waveforms, analyses using IMRPhenomPv2 seem to be surprisingly comparable to the results derived using all other waveforms in this study; see the top panels of Figures 1 and 2. To investigate this numerical incongruity, in Figures 8 and 9 we illustrate the posteriors derived using all models, including IMRPhenomPv2. For many events and parameters, all one-dimensional posteriors are in good agreement, modulo truncation effects associated with the finite mass ratio range required for NRSur7dq4. However, more frequently than for other waveforms, the posteriors for IMRPhenomPv2 may differ substantially from the consensus conclusions derived with state-of-the-art waveforms.
III.4 Other Comparisons with previous work
Figures 8 and 9 show that for most of the events studied here, our estimates with NRSur7dq4, SEOBNRv4PHM, and SEOBNRv5PHM largely agree with results derived using previous analyses with NRSur7dq4 and IMRPhenomXPHM. This agreement is reassuring, given our analysis settings (e.g., the PSD) do not necessarily perfectly match the assumptions adopted in these previous works. However, for two events, these figures reveal striking differences between our analyses and these previous works.
For GW200129, the differences between previous studies and this work are frequent and significant. Interpreted using the assumptions of the previous study, both IMRPhenomXPHM and NRSurd7q4 would suggest a posterior extending to mass ratio down to and peaking near , and primary spins that are preferentially very large. By contrast, our analyses generally prefer nearly comparable mass ratios and show no preference towards large primary spin; indeed, all our analyses point against primary spin. To validate the robustness of our conclusions, Figure 3 shows the underlying marginal likelhood data used to build our posterior distributions. In all cases, we don’t find points with high marginal likelihood at very asymmetric mass ratio , nor (to a lesser extent) with near-extremal transverse spin.
For GW191109, the differences between previous studies and this work are less extreme but still noteworthy, with both external posterior results (IMRPhenomXPHM and NRSur7dq4) exhibiting unexpected structure relative to the consensus conclusions presented in this work. For example, the external NRSur7dq4 posterior favors a different total mass and strongly disfavors equal mass. The external IMRPhenomXPHM posterior favors a wide mass distribution and unexpected complexity in its conclusions about and mass ratio. By contrast, using the assumptions employed in this work, our different approximations produce qualitatively similar results, though differing in details (e.g., as noted for this event SEOBNRv4PHM and SEOBNRv5PHM ddraw slightly different conclusions).
For two more events (GW200220_124850 and GW200216) we see more modest differences between the results in this work and our reference analysis using NRSur7dq4. For other events (e.g., GW200224 and GW200220_061928), the external analysis performed with IMRPhenomXPHM seems to be an outlier relative to the consensus provided by other analyses, including the external NRSur7dq4 result. We point out these differences to help target future investigations such as head-to-head replication studies with different inference codes, which is outside the scope of this work.
IV Conclusions
In this work, we demonstrate reanalysis of several O3 binary black hole mergers, using multiple state-of-the-art waveform models with consistent analysis settings. Combining the asimov production-quality inference automation and the RIFT distributed parameter inference code, our proof-of-concept calculations show concretely how to perform these and related analyses at scale, without requiring access to special-purpose or closely-held computing or data resources. Our analysis is impactful because of the systematic differences this specific study illuminates: in astrophysically tantalizing real events, binary black hole parameter inferences can draw very different conclusions about source parameters. This framework and related studies like it remain a critical ingredient to better understand how precisely and accurately we can infer source (and thus population) parameters of gravitational wave sources, given our still-imperfect understanding of how to approximate the gravitational waves emitted from compact binary mergers.
In this work, we have emphasized real high-mass sources primarily due to their high detection rate: more sources provides more opportunity to identify significant systematic differences between different models. That said, we anticipate that the primary utility of the specific approach outlined in this work will be highest for longer sources, whose many cycles tightly constrain binary parameters and which could better illuminate systematic differences, as in GW190412. Too, we anticipate that for the next few years at least, ongoing waveform development will only increase the number and kind of waveform comparison studies needed for each event. For example, even in this study, we have neglected both physical degrees of freedom (e.g., eccentricity) and alternative waveform families (e.g., TEOBResumS).
V Acknowledgments
This material is based upon work supported by NSF’s LIGO Laboratory which is a major facility fully funded by the National Science Foundation.
Appendix A Posteriors for all events
Figure 8 shows one-dimensional marginal posteriors for the first eight events presented in this study, and Figure 9 shows the other seven. In these figures, the IMRPhemonPv2, SEOBNRv4PHM, SEOBNRv5PHM and NRSur7dq4 results were generated as a part of our investigation. By contrast, the NRSur7dq4-previous results are provided for comparison and were previously reported in [14], and IMRPhenomXPHM were previously reported in [12].

.

.
References
- LIGO Scientific Collaboration et al. [2015] LIGO Scientific Collaboration, J. Aasi, B. P. Abbott, R. Abbott, T. Abbott, M. R. Abernathy, K. Ackley, C. Adams, T. Adams, P. Addesso, and et al., Advanced LIGO, Classical and Quantum Gravity 32, 074001 (2015), arXiv:1411.4547 [gr-qc] .
- Accadia and et al [2012] T. Accadia and et al, Virgo: a laser interferometer to detect gravitational waves, Journal of Instrumentation 7 (03), P03012.
- Acernese et al. [2015] F. Acernese, M. Agathos, K. Agatsuma, D. Aisa, N. Allemandou, A. Allocca, J. Amarni, P. Astone, G. Balestri, G. Ballardin, and et al., Advanced Virgo: a second-generation interferometric gravitational wave detector, Classical and Quantum Gravity 32, 024001 (2015), arXiv:1408.3978 [gr-qc] .
- Akutsu et al. [2021] T. Akutsu, M. Ando, K. Arai, Y. Arai, S. Araki, A. Araya, N. Aritomi, Y. Aso, S. Bae, Y. Bae, L. Baiotti, R. Bajpai, M. A. Barton, K. Cannon, E. Capocasa, M. Chan, C. Chen, K. Chen, Y. Chen, H. Chu, Y. K. Chu, S. Eguchi, Y. Enomoto, R. Flaminio, Y. Fujii, M. Fukunaga, M. Fukushima, G. Ge, A. Hagiwara, S. Haino, K. Hasegawa, H. Hayakawa, K. Hayama, Y. Himemoto, Y. Hiranuma, N. Hirata, E. Hirose, Z. Hong, B. H. Hsieh, C. Z. Huang, P. Huang, Y. Huang, B. Ikenoue, S. Imam, K. Inayoshi, Y. Inoue, K. Ioka, Y. Itoh, K. Izumi, K. Jung, P. Jung, T. Kajita, M. Kamiizumi, N. Kanda, G. Kang, K. Kawaguchi, N. Kawai, T. Kawasaki, C. Kim, J. C. Kim, W. S. Kim, Y. M. Kim, N. Kimura, N. Kita, H. Kitazawa, Y. Kojima, K. Kokeyama, K. Komori, A. K. H. Kong, K. Kotake, C. Kozakai, R. Kozu, R. Kumar, J. Kume, C. Kuo, H. S. Kuo, S. Kuroyanagi, K. Kusayanagi, K. Kwak, H. K. Lee, H. W. Lee, R. Lee, M. Leonardi, L. C. C. Lin, C. Y. Lin, F. L. Lin, G. C. Liu, L. W. Luo, M. Marchio, Y. Michimura, N. Mio, O. Miyakawa, A. Miyamoto, Y. Miyazaki, K. Miyo, S. Miyoki, S. Morisaki, Y. Moriwaki, K. Nagano, S. Nagano, K. Nakamura, H. Nakano, M. Nakano, R. Nakashima, T. Narikawa, R. Negishi, W. T. Ni, A. Nishizawa, Y. Obuchi, W. Ogaki, J. J. Oh, S. H. Oh, M. Ohashi, N. Ohishi, M. Ohkawa, K. Okutomi, K. Oohara, C. P. Ooi, S. Oshino, K. Pan, H. Pang, J. Park, F. E. P. Arellano, I. Pinto, N. Sago, S. Saito, Y. Saito, K. Sakai, Y. Sakai, Y. Sakuno, S. Sato, T. Sato, T. Sawada, T. Sekiguchi, Y. Sekiguchi, S. Shibagaki, R. Shimizu, T. Shimoda, K. Shimode, H. Shinkai, T. Shishido, A. Shoda, K. Somiya, E. J. Son, H. Sotani, R. Sugimoto, T. Suzuki, T. Suzuki, H. Tagoshi, H. Takahashi, R. Takahashi, A. Takamori, S. Takano, H. Takeda, M. Takeda, H. Tanaka, K. Tanaka, K. Tanaka, T. Tanaka, T. Tanaka, S. Tanioka, E. N. Tapia San Martin, S. Telada, T. Tomaru, Y. Tomigami, T. Tomura, F. Travasso, L. Trozzo, T. Tsang, K. Tsubono, S. Tsuchida, T. Tsuzuki, D. Tuyenbayev, N. Uchikata, T. Uchiyama, A. Ueda, T. Uehara, K. Ueno, G. Ueshima, F. Uraguchi, T. Ushiba, M. H. P. M. van Putten, H. Vocca, J. Wang, C. Wu, H. Wu, S. Wu, W. R. Xu, T. Yamada, K. Yamamoto, K. Yamamoto, T. Yamamoto, K. Yokogawa, J. Yokoyama, T. Yokozawa, T. Yoshioka, H. Yuzurihara, S. Zeidler, Y. Zhao, and Z. H. Zhu, Overview of KAGRA: Detector design and construction history, Progress of Theoretical and Experimental Physics 2021, 05A101 (2021), arXiv:2005.05574 [physics.ins-det] .
- Abbott et al. [2023a] R. Abbott, T. D. Abbott, F. Acernese, K. Ackley, C. Adams, N. Adhikari, R. X. Adhikari, V. B. Adya, C. Affeldt, D. Agarwal, and et al., GWTC-3: Compact Binary Coalescences Observed by LIGO and Virgo during the Second Part of the Third Observing Run, Physical Review X 13, 041039 (2023a), arXiv:2111.03606 [gr-qc] .
- Nitz et al. [2023] A. H. Nitz, S. Kumar, Y.-F. Wang, S. Kastha, S. Wu, M. Schäfer, R. Dhurkunde, and C. D. Capano, 4-OGC: Catalog of Gravitational Waves from Compact Binary Mergers, Astrophys. J. 946, 59 (2023), arXiv:2112.06878 [astro-ph.HE] .
- Venumadhav et al. [2020] T. Venumadhav, B. Zackay, J. Roulet, L. Dai, and M. Zaldarriaga, New binary black hole mergers in the second observing run of Advanced LIGO and Advanced Virgo, Phys. Rev. D 101, 083030 (2020), arXiv:1904.07214 [astro-ph.HE] .
- Wadekar et al. [2023] D. Wadekar, J. Roulet, T. Venumadhav, A. K. Mehta, B. Zackay, J. Mushkin, S. Olsen, and M. Zaldarriaga, New black hole mergers in the LIGO-Virgo O3 data from a gravitational wave search including higher-order harmonics, arXiv e-prints , arXiv:2312.06631 (2023), arXiv:2312.06631 [gr-qc] .
- Wofford et al. [2023] J. Wofford, A. B. Yelikar, H. Gallagher, E. Champion, D. Wysocki, V. Delfavero, J. Lange, C. Rose, V. Valsan, S. Morisaki, J. Read, C. Henshaw, and R. O’Shaughnessy, Improving performance for gravitational-wave parameter inference with an efficient and highly-parallelized algorithm, Phys. Rev. D 107, 024040 (2023).
- Cotesta et al. [2018] R. Cotesta, A. Buonanno, A. Bohé, A. Taracchini, I. Hinder, and S. Ossokine, Enriching the symphony of gravitational waves from binary black holes by tuning higher harmonics, Phys. Rev. D 98, 084028 (2018), arXiv:1803.10701 [gr-qc] .
- Ossokine et al. [2020] S. Ossokine, A. Buonanno, S. Marsat, R. Cotesta, S. Babak, T. Dietrich, R. Haas, I. Hinder, H. P. Pfeiffer, M. Pürrer, C. J. Woodford, M. Boyle, L. E. Kidder, M. A. Scheel, and B. Szilágyi, Multipolar effective-one-body waveforms for precessing binary black holes: Construction and validation, Phys. Rev. D 102, 044055 (2020), arXiv:2004.09442 [gr-qc] .
- Pratten et al. [2021] G. Pratten, C. García-Quirós, M. Colleoni, A. Ramos-Buades, H. Estellés, M. Mateu-Lucena, R. Jaume, M. Haney, D. Keitel, J. E. Thompson, and S. Husa, Computationally efficient models for the dominant and subdominant harmonic modes of precessing binary black holes, Phys. Rev. D 103, 104056 (2021), arXiv:2004.06503 [gr-qc] .
- Dax et al. [2023] M. Dax, S. R. Green, J. Gair, M. Pürrer, J. Wildberger, J. H. Macke, A. Buonanno, and B. Schölkopf, Neural Importance Sampling for Rapid and Reliable Gravitational-Wave Inference, Phys. Rev. Lett. 130, 171403 (2023), arXiv:2210.05686 [gr-qc] .
- Islam et al. [2023] T. Islam, A. Vajpeyi, F. H. Shaik, C.-J. Haster, V. Varma, S. E. Field, J. Lange, R. O’Shaughnessy, and R. Smith, Analysis of GWTC-3 with fully precessing numerical relativity surrogate models, arXiv e-prints , arXiv:2309.14473 (2023), arXiv:2309.14473 [gr-qc] .
- Varma et al. [2019] V. Varma, S. E. Field, M. A. Scheel, J. Blackman, D. Gerosa, L. C. Stein, L. E. Kidder, and H. P. Pfeiffer, Surrogate models for precessing binary black hole simulations with unequal masses, Physical Review Research 1, 033015 (2019), arXiv:1905.09300 [gr-qc] .
- The LIGO Scientific Collaboration et al. [2021] The LIGO Scientific Collaboration, the Virgo Collaboration, R. Abbott, T. D. Abbott, S. Abraham, F. Acernese, K. Ackley, A. Adams, C. Adams, R. X. Adhikari, V. B. Adya, C. Affeldt, and et al., GWTC-2: Compact Binary Coalescences Observed by LIGO and Virgo during the First Half of the Third Observing Run, Physical Review X 11, 021053 (2021), arXiv:2010.14527 [gr-qc] .
- Williamson et al. [2017] A. Williamson, J. Lange, R. O’Shaughnessy, J. Clark, P. Kumar, J. Bustillo, and J. Veitch, Inferring parameters of potentially rapidly precessing binary black holes: Systematic challenges for future graviational wave measurements, Phys. Rev. D 96, 124041 (2017).
- Shaik et al. [2020] F. Shaik, J. Lange, S. Field, R. O’Shaughnessy, V. Varma, and et al, Impact of subdominant modes on the interpretation of gravitational-wave signals from heavy binary black hole systems, Phys. Rev. D 101, 124054 (2020).
- Abbott et al. [2023b] R. Abbott, T. D. Abbott, F. Acernese, K. Ackley, C. Adams, N. Adhikari, R. X. Adhikari, V. B. Adya, C. Affeldt, D. Agarwal, and et al., GWTC-3: Compact Binary Coalescences Observed by LIGO and Virgo during the Second Part of the Third Observing Run, Physical Review X 13, 041039 (2023b), arXiv:2111.03606 [gr-qc] .
- The LIGO Scientific Collaboration et al. [2020a] The LIGO Scientific Collaboration, the Virgo Collaboration, B. P. Abbott, R. Abbott, T. D. Abbott, S. Abraham, F. Acernese, K. Ackley, C. Adams, V. B. Adya, and et al., GW190412: Observation of a Binary-Black-Hole Coalescence with Asymmetric Masses, Phys. Rev. D 102, 043015 (2020a).
- The LIGO Scientific Collaboration et al. [2020b] The LIGO Scientific Collaboration, the Virgo Collaboration, B. P. Abbott, R. Abbott, T. D. Abbott, S. Abraham, F. Acernese, K. Ackley, C. Adams, V. B. Adya, and et al., Properties and Astrophysical Implications of the 150 M⊙ Binary Black Hole Merger GW190521, Astrophys. J. Lett. 900, L13 (2020b), arXiv:2009.01190 [astro-ph.HE] .
- Ramos-Buades et al. [2023] A. Ramos-Buades, A. Buonanno, H. Estellés, M. Khalil, D. P. Mihaylov, S. Ossokine, L. Pompili, and M. Shiferaw, SEOBNRv5PHM: Next generation of accurate and efficient multipolar precessing-spin effective-one-body waveforms for binary black holes, arXiv e-prints , arXiv:2303.18046 (2023), arXiv:2303.18046 [gr-qc] .
- Williams et al. [2023] D. Williams, J. Veitch, M. Chiofalo, P. Schmidt, R. Udall, A. Vajpeyi, and C. Hoy, Asimov: A framework for coordinating parameter estimation workflows, The Journal of Open Source Software 8, 4170 (2023), arXiv:2207.01468 [gr-qc] .
- Lange et al. [2018] J. Lange, R. O’Shaughnessy, and M. Rizzo, Rapid and accurate parameter inference for coalescing, precessing compact binaries, Submitted to PRD; available at arxiv:1805.10457 (2018).
- Fernando [2024] D. Fernando, Repository for settings is available at https://git.ligo.org/deanna.fernando/settings.git, (2024).
- Hannam et al. [2014] M. Hannam, P. Schmidt, A. Bohé, L. Haegel, S. Husa, F. Ohme, G. Pratten, and M. Pürrer, Simple Model of Complete Precessing Black-Hole-Binary Gravitational Waveforms, Phys. Rev. Lett. 113, 151101 (2014), arXiv:1308.3271 [gr-qc] .
- Mihaylov et al. [2023] D. P. Mihaylov, S. Ossokine, A. Buonanno, H. Estelles, L. Pompili, M. Pürrer, and A. Ramos-Buades, pySEOBNR: a software package for the next generation of effective-one-body multipolar waveform models, arXiv e-prints , arXiv:2303.18203 (2023), arXiv:2303.18203 [gr-qc] .
- Pankow et al. [2015] C. Pankow, P. Brady, E. Ochsner, and R. O’Shaughnessy, Novel scheme for rapid parallel parameter estimation of gravitational waves from compact binary coalescences, Phys. Rev. D 92, 023002 (2015), arXiv:1502.04370 [gr-qc] .
- O’Shaughnessy et al. [2017] R. O’Shaughnessy, J. Blackman, and S. Field, An architecture for efficient multimodal parameter estimation with linear surrogate models, Class. Quantum Grav. 10.1088/1361-6382/aa7649 (2017).
- Wysocki et al. [2019] D. Wysocki, R. O’Shaughnessy, J. Lange, and Y.-L. L. Fang, Accelerating parameter inference with graphics processing units, Phys. Rev. D 99, 084026 (2019), arXiv:1902.04934 [astro-ph.IM] .
- Abbott et al. [2021] R. Abbott, T. D. Abbott, S. Abraham, F. Acernese, K. Ackley, C. Adams, R. X. Adhikari, V. B. Adya, C. Affeldt, M. Agathos, and et al., Open data from the first and second observing runs of Advanced LIGO and Advanced Virgo, SoftwareX 13, 100658 (2021), arXiv:1912.11716 [gr-qc] .
- Cornish and Littenberg [2015] N. J. Cornish and T. B. Littenberg, Bayeswave: Bayesian inference for gravitational wave bursts and instrument glitches, Classical and Quantum Gravity 32, 135012 (2015), arXiv:1410.3835 [gr-qc] .
- Littenberg and Cornish [2015] T. B. Littenberg and N. J. Cornish, Bayesian inference for spectral estimation of gravitational wave detector noise, Phys. Rev. D 91, 084034 (2015), arXiv:1410.3852 [gr-qc] .
- Chatziioannou et al. [2019] K. Chatziioannou, C.-J. Haster, T. B. Littenberg, W. M. Farr, S. Ghonge, M. Millhouse, J. A. Clark, and N. Cornish, Noise spectral estimation methods and their impact on gravitational wave measurement of compact binary mergers, Phys. Rev. D 100, 104004 (2019), arXiv:1907.06540 [gr-qc] .
- Hannam et al. [2022] M. Hannam, C. Hoy, J. E. Thompson, S. Fairhurst, V. Raymond, M. Colleoni, D. Davis, H. Estellés, C.-J. Haster, A. Helmling-Cornell, S. Husa, D. Keitel, T. J. Massinger, A. Menéndez-Vázquez, K. Mogushi, S. Ossokine, E. Payne, G. Pratten, I. Romero-Shaw, J. Sadiq, P. Schmidt, R. Tenorio, R. Udall, J. Veitch, D. Williams, A. B. Yelikar, and A. Zimmerman, General-relativistic precession in a black-hole binary, Nature (London) 610, 652 (2022), arXiv:2112.11300 [gr-qc] .
- Gupte et al. [2024] N. Gupte, A. Ramos-Buades, A. Buonanno, J. Gair, M. C. Miller, M. Dax, S. R. Green, M. Pürrer, J. Wildberger, J. Macke, and B. Schölkopf, Evidence for eccentricity in the population of binary black holes observed by LIGO-Virgo-KAGRA, arXiv e-prints , arXiv:2404.14286 (2024), arXiv:2404.14286 [gr-qc] .
- Payne et al. [2022] E. Payne, S. Hourihane, J. Golomb, R. Udall, D. Davis, and K. Chatziioannou, Curious case of GW200129: Interplay between spin-precession inference and data-quality issues, Phys. Rev. D 106, 104017 (2022), arXiv:2206.11932 [gr-qc] .
- Macas et al. [2024] R. Macas, A. Lundgren, and G. Ashton, Revisiting the evidence for precession in GW200129 with machine learning noise mitigation, Phys. Rev. D 109, 062006 (2024), arXiv:2311.09921 [gr-qc] .