Efficient Quantum Digital Signatures without Symmetrization Step

Cryptography is essential for uncounted amount of applications that rely on non-repudiation, integrity and confidentiality of data. The two pillars of modern cryptography are encryption and digital signatures Diffie and Hellman (1976), where encryption guarantees confidentiality and digital signatures provide integrity and non-repudiation. Traditionally, public-key cryptography algorithms, such as the Rivest-Shamir-Adleman algorithm Rivest et al. (1978), are designed to simultaneously provide encryption and digital signature service. However, relying on the computational difficulty of certain mathematical problems, public-key cryptosystems are usually vulnerable to quantum computing attacks Shor (1994). Quantum key distribution (QKD) allows two remote users to share a secret key string with information-theoretic security Bennett and Brassard (1984); Ekert (1991). By combining one-time pad encryption Shannon (1949) and QKD, one can implement information communication with perfect confidentiality Chen et al. (2009). In addition, the direct transmission of private information is made possible in principle by quantum encryption Qi et al. (2019).

Digital signatures are widely applied in e-mails, electronic commerce and software distribution to ensure data integrity and non-repudiation Pirandola et al. (2020). Similar to QKD used for encryption service, quantum digital signatures (QDS) are expected to provide information-theoretic security to sign documents. The first QDS protocol was proposed in 2001 Gottesman and Chuang (2001), but it is unfeasible because of challenging experimental requirements. In the next decade or so, great efforts have been made in developing QDS protocols and an important achievement was the removal of the requirement of quantum memory Clarke et al. (2012); Dunjko et al. (2014); Collins et al. (2014); Wallden et al. (2015); Croal et al. (2016). Nevertheless, the security analysis of the early QDS protocols are based on secure quantum channels, i.e., there is no eavesdropping, which is a conflicting assumption. In 2016, two independent QDS protocols were proposed and proved to be secure against the general attacks without the assumption of secure quantum channels Yin et al. (2016a); Amiri et al. (2016). Importantly, their experimental devices and techniques have already been widely employed in QKD. These two protocols are important steps towards practical QDS Pirandola et al. (2020). The one in Yin et al. (2016a) is based on non-orthogonal encoding. The other Amiri et al. (2016) utilizes orthogonal encoding, which results in the need of an additional symmetrization step in the protocol. In addition, great achievements have been made in the experimental and theoretical research of information-theoretically secure QDS  Puthoor et al. (2016); Yin et al. (2017a); Collins et al. (2017); Yin et al. (2017b); Roberts et al. (2017); Zhang et al. (2018); Thornton et al. (2019); An et al. (2019); Ding et al. (2020); Zhang et al. (2020); Wang et al. (2015, 2017), including the field test of measurement-device-independent (MDI) QDS Yin et al. (2017b).

For the orthogonal encoding based protocol Amiri et al. (2016) (see also Puthoor et al. (2016); Zhang et al. (2020)), the need of the symmetrization step, which requires an additional secure classical channel, is the main issue. Currently, secure classical channels can only be realized by combining QKD and one-time pad encryption. The symmetrization step will consume $6L$ bits of secret key generated by QKD if one uses $L$ bits as the signature Yin et al. (2017b). Specially, in the worst case where the signer is located in the middle of two receivers, the low secret key rate of QKD between the two receivers severely limits the real-time signature rate of QDS. Besides, considering a quantum network with $J$ users, there will be a need of $J(J-1)/2$ secure classical channels Roberts et al. (2017), which is an unrealistically high amount in a real quantum network. For the non-orthogonal encoding based protocol Yin et al. (2016a), it does not require the symmetrization step. However, the signer has to send the same quantum states to two receivers. Only coincidence detection events, i.e., the two receivers both have click, are valid events. Let $\eta$ be the probability that one receiver has click, if the signer sends $N$ quantum states to the two receivers, there will be only $\eta^{2}N$ valid events. Therefore, the signature rate quadratically scales with the probability of detection events.

Here, inspired by the original protocol in Yin et al. (2016a), we propose an efficient quantum digital signature protocol without symmetrization step. A novel classical post-processing operation called post-matching method is exploited in our protocol. With the help of the post-matching method, the requirement of coincidence detection is removed. Given that the signer sends $N$ quantum states to receivers, there will be $\eta N$ valid events. Therefore the signature rate decays linearly with the probability of detection events. Simulation results show that the signature rate of our scheme is $2$ or even $3$ orders of magnitude higher than that of Ref. Yin et al. (2016a) in large attenuation case, and is comparable to orthogonal encoding based protocol.

There are three participants in our protocol, namely the signer Alice and the receiver Bob and Charlie. As determined by Alice, either Bob or Charlie can be the authenticator of the signature, and the other becomes the verifier. There are noisy insecure quantum channels connecting Alice-Bob and Alice-Charlie, and authenticated classical channels between the three participants. There are three stages in our protocol: key generation, estimation and messaging. In our protocol, the three stages can be performed separately, which means they can generate raw keys and store them for a long time, and continue the estimation and messaging stage whenever Alice wants to sign the message. This makes our protocol more practical.

Our protocol exploits non-orthogonal encoding to generate logical bits Scarani et al. (2004). There are four quantum states: $\left|H\right\rangle$, $\left|V\right\rangle$, $\left|+\right\rangle$ and $\left|-\right\rangle$, where $\left|H\right\rangle$ and $\left|V\right\rangle$ are the eigenstates of the Pauli Z operator and $\left|+\right\rangle$ and $\left|-\right\rangle$ ( $\left|\pm\right\rangle=\frac{1}{\sqrt{2}}($$\left|H\right\rangle$$\pm$ $\left|V\right\rangle$$)$) are the eigenstates of the Pauli X operator. These four quantum states can be arranged into four sets: $\{\left|H\right\rangle,\left|+\right\rangle\}$, $\{\left|+\right\rangle,\left|V\right\rangle\}$, $\{\left|V\right\rangle,\left|-\right\rangle\}$, $\{\left|-\right\rangle,\left|H\right\rangle\}$, where the first state in each set is encoded with bit value 0 and the second is encoded with 1. Alice randomly sends quantum states to receivers and assigns each quantum state to a set. The receivers randomly choose Z or X basis to perform polarization measurement on each quantum state. If the measurement outcome is orthogonal to one of the states in the set, the receiver obtains a conclusive result with bit value 0 or 1, otherwise the receiver obtains an inconclusive result, denoted by $\bot$. Note that the set assigned by Alice should contain the quantum state she sent. For example, if Alice sends $\left|H\right\rangle$, she should assign it to set $\{\left|H\right\rangle,\left|+\right\rangle\}$ or $\{\left|-\right\rangle,\left|H\right\rangle\}$. When she assigns it to the set $\{\left|H\right\rangle,\left|+\right\rangle\}$ and Bob’s measurement outcome is $\left|-\right\rangle$ ($\left|V\right\rangle$), Bob obtains a conclusive result with bit value $0$ $(1)$.

The decoy-state method Wang (2005); Lo et al. (2005) with three intensities is exploited to deal with photon-number-splitting attack for coherent state source. Data from the decoy state and vacuum state will be used for parameter estimation, and only data from the signal state will be used as test bits and secret keys. The setup for our QDS protocol is presented in Fig. 1. In the following part of the paper, we use superscripts $c$, $u$, $t$, $*$, overline (underline), to denote conclusive results, untest bits, test bits, expected value and the upper bound (lower bound) of expected value, respectively. We also use subscripts $P$ ($P\in\{A,B,C\}$), $11$ and $\lambda$ ($\lambda\in\{\mu,\nu,0\}$) to denote Alice (Bob, Charlie), single-photon pair components and intensity respectively. Detailed descriptions of our protocol are given below.

(2) For each quantum state, Bob and Charlie randomly choose X or Z basis to perform polarization measurement. Bob announces all the click events in $A_{B,m}$ through authenticated classical channel. Alice and Bob discard all the data that has no click. They keep the left data of length $n$, denote as $S_{AB,m}$ (kept by Alice) and $S_{B,m}$ (kept by Bob). Alice and Charlie perform the same step. As a result, Alice has four data strings $S_{AB,0}$, $S_{AB,1}$, $S_{AC,0}$ and $S_{AC,1}$, Bob (Charlie) has two strings $S_{B,0}$($S_{C,0}$) and $S_{B,1}$($S_{C,1}$). Since Alice randomly and independently chooses quantum states, the quantum states that Bob and Charlie receive are uncorrelated.

(3) Alice announces the intensity information of all pulses. According to the intensity information, the three participants divide each of their data strings into three strings, namely $\mu$ string, $\nu$ string and $0$ string. For example, Bob divides $S_{B,m}$ into $S_{B,m}^{\mu}$, $S_{B,m}^{\nu}$ and $S_{B,m}^{0}$.

(4) For the data strings corresponding to each intensity $\lambda$ ($\lambda\in\{\mu,\nu,0\}$), Alice takes $S_{AB,m}^{\lambda}$ as the reference and changes the order of elements in $S_{AC,m}^{\lambda}$. Denote the changing result as $S^{\prime\lambda}_{AC,m}$, Alice should make $S^{\lambda}_{AB,m}$ and $S^{\prime\lambda}_{AC,m}$ identical. Without loss of generality, she requests Charlie to change the order of elements in $S_{C,m}^{\lambda}$ into the same order. We call this the post-matching method. After post-matching, the data obtained by Bob and Charlie can be correlated. Detailed description of post-matching method is given in Fig. 2.

(5) Using the rules for generating logical bits, Alice randomly assigns each element in $S_{AB,m}^{\lambda}$ a set. The three participants ‘translate’ their data strings into raw key strings denoted as $K_{A,m}^{\lambda}$, $K_{B,m}^{\lambda}$ and $K_{C,m}^{\lambda}$. Note that they do not announce which bits are conclusive results.

(2) Bob and Charlie announce $\{E_{B}^{ct}$, $P_{B}^{c}\}$ and $\{E_{C}^{ct}$, $P_{C}^{c}\}$. The three participants publicly negotiate to determine the values of authentication security threshold $T_{a}$ and verification security threshold $T_{v}$.

(2) After receiving $\{m,K_{A,m}^{u}\}$ forwarded by Bob, Charlie calculates the mismatch rate of conclusive results $E_{C}^{cu}$ between $K_{A,m}^{u}$ and $K_{C,m}^{u}$. Charlie accepts the message if $E_{C}^{cu}<T_{v}$. When both Bob and Charlie accept the message, Alice successfully signs the message.

In our protocol, Alice randomly chooses unrelated quantum states to send to Bob and Charlie. After post-matching, it is equivalent to Alice simultaneously sending the same quantum states to Bob and Charlie. To perform post-matching, Alice exposes information of order, but does not leak information of quantum states. In this case, eavesdroppers can not obtain more information of quantum states compared with the case where Alice actually sends two copies of quantum states. Thus the security analysis of our protocol can directly follow the lines in Ref. Yin et al. (2016a). In the three-participant scenario, transferability and nonrepudiation are equivalent. Accordingly, there are three security criteria: robustness, security against forging and security against repudiation. For simplicity, we just briefly present our results. For more detail, refer to Ref. Yin et al. (2016a).

We assume only single-photon pairs that Alice sends to Bob and Charlie are secure. In this case, Bob and Charlie both receive a single-photon. Using Chernoff bound Chernoff (1952), the probability of a successful forgery attack $\varepsilon_{for}$ can be given by

where $E_{BF11}^{*}$ is the expected value of minimum mismatch rate of conclusive results of the single-photon pair components between $K_{A,m}^{u}$ and $K_{BF,m}^{u}$, $T_{v11}=T_{v}n^{cu}/n^{cu}_{11}$ is the error rate threshold of single-photon pair, $n^{cu}=(1-t)n_{\mu}^{c}$ is the number of conclusive results in $K_{C,m}^{u}$, $n^{cu}_{11}=(1-t)s_{C11}^{c\mu}$ is the number of single-photon pair components in $K_{C,m}^{u}$ and $s_{C11}^{c\mu}$ is the number of events in which Bob and Charlie both receive a single-photon in $\mu$ string and Charlie has a conclusive result.

To obtain the value of $E_{BF11}^{*}$, one should exploit decoy state method to estimate $s_{C11}^{c\mu}$ and $t_{C11}^{c\mu}$, where $t_{C11}^{c\mu}$ is the number of events that Bob and Charlie both receive a single-photon in $\mu$ string, Charlie has a conclusive result, and his classical bit is mismatching with Alice’s. We use $n_{P\lambda}$ to denote the number of detection events of the participant $P$ of intensity $\lambda$ and $m_{P\alpha}$ to denote the number of mismatching bits. The expected value of parameter $x$ can be acquired by the variant of Chernoff bound Yin et al. (2020): $\overline{x}^{*}=x+\beta+\sqrt{2\beta x+\beta^{2}}$ and $\underline{x}^{*}=x-\frac{\beta}{2}-\sqrt{2\beta x+\frac{\beta^{2}}{4}}$ with $\beta=\ln\frac{1}{\varepsilon_{1}}$, where $\epsilon_{1}$ is the failure probability of the Chernoff bound.

The overall secrecy is:

where $\epsilon_{2}$ is the failure probability of random sampling without replacement.

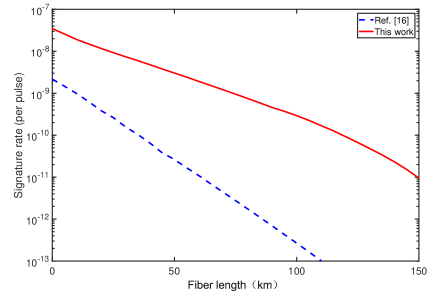
In order to show the performance of our protocol, we simulate a fiber-based QDS system. Define signature rate $R:=\frac{1}{2N}$, where $2N$ is the minimum number of pulses required to securely sign a one-bit message. Fig. 3 shows the signature rate $R$ as a function of transmission distance. We consider the case where channels between Alice-Bob and Alice-Charlie are symmetric.

The security bounds are set to $\varepsilon_{for}\leq 10^{-10}$, $\varepsilon_{rob}\leq 10^{-10}$, $\varepsilon_{rep}\leq 10^{-10}$ and $\varepsilon_{1}=\varepsilon_{2}\leq(10^{-9}-3\times 10^{-10})/12$. We numerically optimize the minimum number of pulses required to securely sign a one-bit message with the free parameters $\{\mu,\nu,p_{\mu},p_{\nu},t\}$ by global search algorithm. For a fair comparison, we simulate the performance of the original protocol in Ref. Yin et al. (2016a) with the same experimental parameters. As shown in Fig. 3, the solid red line represents the signature rate of this work and the blue dashed line represents the original QDS protocol. Obviously, our protocol requires far less number of pulses to sign a one-bit message. Specifically, at $50$ km and $100$ km, our protocol requires $3.3\times 10^{8}$ and $3.4\times 10^{9}$ pulses to sign a one-bit message, but the protocol in Ref. Yin et al. (2016a) requires $3.8\times 10^{10}$ and $3.7\times 10^{12}$ pulses. The signature rate of our protocol is 2 or even 3 orders of magnitude higher than the original protocol at long distance.

We also simulate the performance of orthogonal encoding based protocol Amiri et al. (2016) with the cost of symmetrization taken into consideration. Assume Bob and Charlie utilize three-intensity decoy-state BB84 QKD protocol to perform symmetrization. Define the effective signature rate $R_{{\rm{eff}}}:=\min\{\frac{1}{2N},\frac{R_{QKD}}{6L}\}$, where $L$ is the length of key generated by key generation protocol in [17] and $R_{QKD}$ is the secret key rate of QKD. Note that $\frac{6L}{R_{QKD}}$ is the number of pulses required for QKD to perform symmetrization Yin et al. (2017b). $R_{QKD}$ is simulated by the key rate formula in Lim et al. (2014), where we choose error-correction efficiency $f=1.22$, data post-processing block size $N=10^{10}$, secrecy $\varepsilon_{sec}=10^{-10}$ and the same experimental parameters as Fig. 3.

Denote the angle between Alice-Bob and Alice-Charlie as $\theta$, the distance between Alice and Bob (Charlie) as $D_{AB}$ ($D_{AC}$), and the distance between Bob and Charlie as $D_{BC}$. In symmetric case, $D_{AB}=D_{AC}$, and $D_{BC}=2\sin(\frac{\theta}{2})D_{AB}$. At short distance where $R_{QKD}$ is very high, $R_{{\rm{eff}}}$ is mainly determined by $\frac{1}{2N}$. When $\theta$ is close to $\pi$, the transmission distance of QKD ($D_{BC}$) increases much faster than $D_{AB}$. In this case, $R_{{\rm{eff}}}$ is determined by $\frac{R_{QKD}}{6L}$ at long distance. We simulate the case of $\theta=\frac{2}{3}\pi$ and $\theta=\pi$. As shown in Fig. 4, the signature rate of Amiri et al. (2016) is higher than that of our protocol at short distance, but when distance between the two receivers is large, the signature rate will be severely limited by the low secret key rate of QKD in the symmetrization step. By contrast, our protocol decays much slower and has a significantly longer transmission distance.

In addition, the typical experimental parameters and corresponding signature rate of some recent QDS experiments are listed in Table. 1. This work shows a comparable performance with orthogonal encoding based protocol An et al. (2019) even though the latter does not execute the symmetrization step. We remark that the symmetrization step is essential to the complete protocol, as demonstrated in experiments Roberts et al. (2017); Yin et al. (2017b).

In this paper, we have proposed a non-orthogonal encoding based efficient quantum digital signature protocol. A novel method called post-matching is applied, which can increase the signature rate from decaying with $\eta^{2}$ to $\eta$. Our protocol has a high signature rate and does not require the symmetrization operation thereby overcomes the major obstacles of existing QDS protocols. This protocol can be directly implemented with current commercially available QKD devices. Therefore, it should be the preferred solution to the application of QDS. This work is a great step for the development of quantum network with QDS. Moreover, we believe the key idea of post-matching method has the potential to be applied in various cryptographic tasks that require to establish multiparty correlations, such as multiparty quantum communication  Fu et al. (2015).

National Natural Science Foundation of China (61801420); Key Research and Development Program of Guangdong Province (2020B0303040001); Fundamental Research Funds for the Central Universities.