Efficient Quantization Strategies for Latent Diffusion Models
Abstract
Latent Diffusion Models (LDMs) capture the dynamic evolution of latent variables over time, blending patterns and multimodality in a generative system. Despite the proficiency of LDM in various applications, such as text-to-image generation, facilitated by robust text encoders and a variational autoencoder, the critical need to deploy large generative models on edge devices compels a search for more compact yet effective alternatives. Post Training Quantization (PTQ), a method to compress the operational size of deep learning models, encounters challenges when applied to LDM due to temporal and structural complexities. This study proposes a quantization strategy that efficiently quantize LDMs, leveraging Signal-to-Quantization-Noise Ratio (SQNR) as a pivotal metric for evaluation. By treating the quantization discrepancy as relative noise and identifying sensitive part(s) of a model, we propose an efficient quantization approach encompassing both global and local strategies. The global quantization process mitigates relative quantization noise by initiating higher-precision quantization on sensitive blocks, while local treatments address specific challenges in quantization-sensitive and time-sensitive modules. The outcomes of our experiments reveal that the implementation of both global and local treatments yields a highly efficient and effective Post Training Quantization (PTQ) of LDMs.
1 Introduction

Diffusion models (DMs) have a compelling ability to generate complex patterns via emulating dynamic temporal evolution in a data representation space. Latent diffusion models (LDMs) captures the temporal dynamics in a latent data representation space. With a combination of text encoder(s) and an image variational autoencoder[34, 33], the LDMs outperform other visual generative models in various computer vision applications [15, 51, 19, 42, 24]. Within a UNet denoising model [35], downsampling blocks reduce the spatial dimensions of the input data to capture high-level features and minimize computational complexity, and upsampling blocks increase the spatial dimensions of the data to recover finer details for more accurate approximation. These blocks in LDMs capture finner and sparse details and generate high-quality outputs. Nonetheless, the generalization of LDMs is hindered by their extensive parameter count, posing challenges for deploying these large generative models on edge devices[49]. The pressing demand for practical usage on such devices necessitates a more efficient deployment for LDMs.
Among various technique to enable an efficient deployment of large generative models, quantization reduces numerical precision to enhance efficiency, while post-training quantization (PTQ) fine-tunes this process after training for a balanced model size and computational efficiency. PTQ distinguishes itself from other efficiency methods like pruning and distillation [9, 41, 36, 27] by avoiding structural modifications to UNet [9, 20, 3, 28], bypassing the need for original training data [36, 27], and eliminating the requirement for model retraining [30, 40, 26]. While quantization on Large Language Models (LLMs) exhibits promising compression results [48, 1], its success in language generative models does not seamlessly extend to LDMs due to two main challenges. First, local down-and-up spatial compression are prone to magnify quantization error. Second, global temporally dynamic activation outliers are disposed to impede quantization performance. Prior works [21, 11, 43] address global dynamic activation by selecting uniformly distributed calibration data across inference timesteps, dealing dynamic activation ranges with optimized quantization methods. A more in-depth analysis is needed for an efficient LDM quantization at local and global levels.
In this work, we analyze LDM quantization under the lens of relative quantization noise. We propose an efficient quantization strategy that adeptly identifies blocks or modules sensitive to quantization, enabling the adaptation of tailored solutions for swift and efficient quantization. See Figure 1 for an overview. The contributions of this work are as following:
-
•
This is the first work to propose an efficient quantization strategy that determines effective quantization solutions for LDMs at both global (block) and local (module) levels via analyzing relative quantization noise.
-
•
We adapt an efficient metric to account for both accumulated global quantization noise and relative local quantization noise.
-
•
Globally, we suggest a hybrid quantization approach that adeptly selects a specific LDM block for the initiation of higher-precision quantization, mitigating elevated relative quantization noise.
-
•
Locally, our proposal involves the implementation of a smoothing mechanism to alleviate activation quantization noise, achieved through qualitative identification of the most sensitive modules.
-
•
We suggest a single-sampling-step calibration, capitalizing on the robustness of local modules to quantization when diffusion noise peaks in the final step of the forward diffusion process. A single-sampling-step calibration remarkably improves the efficiency and performance of quantization.
2 Preliminaries
In this section, we expound upon the foundational understanding of LDMs and the concept of Quantization.
2.1 Latent Diffusion Models
DMs [39, 13] involve two processes: forward diffusion and reverse diffusion. Forward diffusion process adds noise to input image, to iteratively and reverse diffusion process denoises the corrupted data, to iteratively. LDMs involve the same two processes but in the latent space instead of original data space. We reiterate the diffusion processes in the latent space.
The forward process adds a Gaussian noise, , to the example at the previous time step, . The noise-adding process is controlled by a noise scheduler, .
The reverse process aims to learn a model to align the data distributions between denoised examples and uncorrupted examples at time step with the knowledge of corrupted examples at time step .
To simplify the optimization, [13] proposes only approximate the mean noise, , to be denoised at time step by assuming that the variance is fixed. So the reverse process or the inference process is modeled as:
| (1) | ||||


2.2 Quantization
Post-training quantization (PTQ) reduces numerical representations by rounding elements to a discrete set of values, where the quantization and de-quantization can be formulated as:
| (2) |
where denotes the quantization scale parameters. round(·) represents a rounding function [4, 47]. and are the lower and upper bounds for the clipping function . Calibrating parameters in the PTQ process using weight and activation distribution estimation is crucial. A calibration relying on min-max values is the most simple and efficient method but it leads to significant quantization loss (see examples in Figure 2), especially when outlier values constitute a minimal portion of the range [46]. More complicated optimized quantization is applied to eliminate the outliers for better calibration. For example, PTQ4DM [37] and Q-Diffusion [21] apply reconstruction-based PTQ methods [23] to diffusion models. PTQD [11] further decomposes quantization noise and fuses it with diffusion noise. Nevertheless, all these methods demand a significant increase in computational complexity. In this study, our exclusive experimentation revolves around min-max quantization due to its simplicity and efficiency. Additionally, we aim to demonstrate how our proposed strategy proficiently mitigates the quantization noise inherent in min-max quantization.
3 Method
3.1 Quantization Strategy


In general, a homogeneous quantization strategy is applied to all parts in a network for its simplicity. In other words, the same precision quantization is applied to all modules. Though different quantization schemes coincide in mixed-precision quantization [6, 8, 44] and non-uniform quantization [22, 50, 14], additional training or optimization is required to configure more challenging quantization parameters. LDMs consist of many downsampling and upsampling blocks (Figure 3(b)). The concatenated blocks in LDMs pose challenges for end-to-end quantization, given dynamic activation ranges and recursive processing across steps and blocks. In contrast to prior attempts to uniformly quantize all blocks, our approach suggests an efficient quantization strategy by initiating a hybrid quantization at a specific block and subsequent blocks.
We attentively discover that quantizing up to a specific block in LDM imposes minimum loss in image generating quality. In Figure 3(a), as we measure FID for a progressive homogeneous quantization on LDM 1.5, blocks nearer to the output exhibit higher sensitivity to quantization. Identifying these sensitive blocks beforehand at a low cost facilitates the implementation of a decisive strategy. However, computing FID is computationally expensive and time-consuming. An efficient metric is required to pinpoint sensitive blocks (and modules) for the development of an improved quantization strategy.
3.2 Relative Quantization Noise
We denote and are the full-precision model and quantized model respectively. If we simplify the iterative denoising process as (3), where the timestep embedding and text embedding are omitted for simplicity, intuitively each parameterized module contributes quantization noise and the recursive process will only accumulate these noise. This behaviour is modeled as (4) where is an accumulative function. This is akin to conducting sensitivity analysis to scrutinize how the accumulation of quantization impact on each block or module and influence the quality of the generated images.
| (3) |
| (4) |
We need a computationally efficient function to identify sensitive blocks in if the accumulated is too high, and identify sensitive modules if the relative is too high. In other words, the necessitates three key properties:
-
•
Accumulation of iterative quantization noise needs to be ensured as the global evaluation of the quantization noise at the output directly reflect image quality.
-
•
Relative values across different modules provide qualitative comparisons to identify local sensitivity.
-
•
Convenient computation allows an efficient evaluation and analysis which expedites quantization process.
Hence metrics like MSE is not sufficient to make realtive and fair local comparisons, and FID is not efficient to facilitate the quantization process.
We adapt a relative distance metric, [17], as the :
| (5) |
where represents the whole model for global sensitivity evaluation and a module for local sensitivity evaluation. Other works have associated with the quantization loss. [38] evaluates for quantization loss on a convolutional neural network (CNN). [18] optimizes as the metric to efficiently learn the quantization parameters of the CNN. [31] computes at the end of inference steps to quantify the accumulated quantization loss on softmax operations in diffusion models. [32] assesses to fairly compare the bit options for the quantized weight in a deep neural network. Therefore is an optimal candidate for and also it offers three major advantages:
-
•
At global levels, instead of modeling an accumulative function , we evaluate the time-averaged at the output of the , i.e. . Averaging the relative noise at the output comprises an end-to-end accumulation nature. A low indicates a high quantization noise, which leads to poorly generated images. We justify this correlation as qualitative measure and FID and show the correlation in Figure 4.
-
•
At local levels, is a relative metric that measures the noise ratio between the full-precision and quantized values. This aids a fair comparison between local modules to identify the sensitive modules.
-
•
A small number of examples is sufficient to compute the instantaneously with high confidence (Supplementary C). This swift computation enables an efficient assessment of quantization noise and the quality of the generated image, in comparison to FID and IS.

3.3 Block Sensitivity Identification and Global Hybrid Quantization

| (6) |
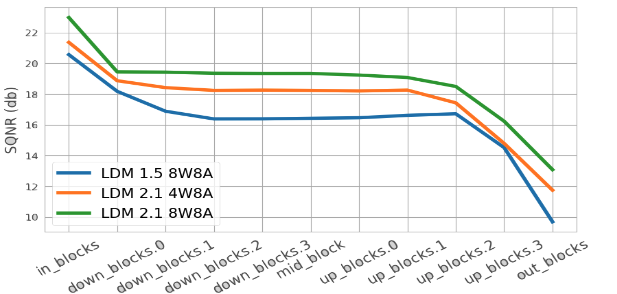
Conventionally, the quantization is applied with a consistent precision on the whole model. But the quantization fails with low-bit precision constantly [21, 11] and there is no substantiate evidence to identify the root cause for these failures. We measure the time-averaged at the output of which is denoted as shown in Eq (6). Progressively quantizing each block in examines the sensitivity of each block based on . Once blocks with high sensitivity are identified, a higher-precision quantization can be applied to alleviate quantization noise from these blocks. The proposed global hybrid quantization is illustrated in Figure 5(b). We first explore the sensitivity of each block in the UNet by quantizing first blocks, and leave the rest blocks unquantized. In Figure 5(a), the block sensitivity of different LDMs at different quantization bits consistently indicates that latter blocks in up blocks are severely sensitive to quantization. Using the time-averaged , sensitive blocks can be identified efficiently and a higher precision quantization can be applied on these blocks collectively.
3.4 Module Sensitivity Identification and Local Noise Correction

Similarly to block sensitivity analysis, we evaluate at each module and visualize the sensitivity at different inference steps. We intend to formulate a local sensitivity first and identify local sensitive modules as illustrated in Figure 6. We visualize the for each module at two inference steps, , and the average over all 50 sampling steps when quantizing LDM 1.5 with 8A8W in Figure 6 (Illustration for other LDMs in Supplementary A). A low local only suggests that one module is sensitive to quantization noise, and vice versa. From the module sensitivity across inference time and across the whole model, two types of root causes for the local sensitivity can be identified and will be addressed respectively.
3.4.1 Quantization Corrections to Sensitive Modules
The first root cause for the high quantization sensitivity can be identified by listing modules with the lowest . In fact, three types of operations are consistently sensitive to quantization: a).Spatial sampling operations; b). Projection layers after the attention transformer block; c).Shortcut connection in up blocks. (See Supplementary A for details). Though c). is addressed in [21] via splitting connections, we analyse all sensitive modules with relative noise and provide a uniform solution. After identifying these modules, the activation ranges can be collected across inference steps. In Figure 7 we visualize the average activation ranges over output channels operations a) and b). It is obvious that there are outliers in some channels in the activation. As discussed in Section 1, these outliers pose difficult challenges to quantization as they stretch the activation range. An apparent solution is to use per-channel activation quantization on these sensitive operations, but per-channel activation cannot be realized with any hardware [48, 16, 2]. We adapt SmoothQuant [48] to resolve the outlier quantization challenges for selected sensitive modules:
| (7) |
where is the input activation to a parameterized module with weight . is the scale to mitigate the outliers in channel and migrate the quantization burden to weight with a migration factor . Though can be fused to the parameterized module weights for efficient computation, cannot be fused to previous layers as proposed in [48], which means there is a trade-off between the efficiency and performance. We examine this trade-off in section 5 via computing the number of total operations and the proportion of sensitive modules to apply SmoothQuant.



3.4.2 Quantization Sensitivity to Diffusion Noise
The second root cause for the high quantization sensitivity can be identified as the difference between the first inference step and the last inference step (dash lines in Figure 6). For all modules, this discrepancy suggests that the quantization parameters are most robust when the diffusion noise is scheduled at maximum. In general, the quantization parameters are calibrated via inferencing a number of steps with any noise schedulers. As demonstrated in section 2, the noise scheduler induces gradually changing noise at each forward diffusion step. Hence the activation range is more dynamic when calibrating across multiple steps. This coincides with the problems identified in [21, 11, 37]. This variation causes high quantization noise. Unlike the proposed solutions in prior works, we proposed to only calibrate with a single step, as the variation in maximized diffusion noise will be constrained so that a tighter can be calibrated for better and faster quantization. See Figure 8 for examples.


4 Experiment Setup and Evaluation
Dataset and Quantization Setting We evaluation our proposed quantization procedures in conditional text-to-image generation. Unconditional calibration over 1k images is performed (conditional calibration aggravates the quantization loss as difference between conditional and unconditional features induces further quantization noise). The evaluation dataset is random 10k generations from MS-COCO validation [25] as conducted in [21, 10, 5]. The classifier-free guidance scale is set to 7.5. We only quantize parameterized modules (convolutional layers and fully connected layers). For all quantization, we apply only min-max symmetric quantization scheme to highlight the raw improvement of proposed procedures. Two quantization settings will be explored 8W8A, 4W8A for low-bit and lower-bit quantization demonstrations. In the global hybrid quantization, fp16 quantization will be applied to sensitive blocks. The default configurations for LDMs are listed in Supplementary
Evaluation Metrics For each experiment, we report the FID [12] and to evaluate the performance on generating images of size 512 by 512 for LDM 1.5, LDM 2.1, 1024 by 1024 for LDM XL. All results on baselines and proposed procedures are controlled by a fixed random seed to ensure reproducibility of results. To evaluate the computational efficiency, we calculate Bit Operations (BOPs) for a conditional inference step through the diffusion model using the equation , where denotes Multiply-And-Accumulate operations, and and represent the bit width of weights and activations, respectively, as stated in [11, 45].
Statistics Preparation It is optional to collect relative quantization noise after quantizng a LDM model as the analysis is consistent across different models and quantization settings as suggested in section 3. However, for a general LDM it is advised to quantize the model with a specific quantization setting to perform the analysis. For the local outlier correction, the maximum of the absolute activation range needs to be recorded first to calculate in (7).
4.1 Results and Discussions
4.1.1 Global Hybrid Quantization
To validate the generalization of proposed quantization strategy, we evaluate the global hybrid quantization procedures on three different LDM models: LDM 1.5, 2.1 base, XL 1.0 base. Note that we only employ single-sampling-step calibration for the hybrid quantization and the smoothing mechanism is not included for better efficiency.
| Method | Bits(W/A) | Size(Mb) | TBops | FID | (db) |
|---|---|---|---|---|---|
| 32fp/32fp | 3278.81 | 693.76 | 18.27 | - | |
| LDM 1.5 | 8/8+16fp/16fp | 906.30 | 99.34 | 16.58 | 20.45 |
| 4/8+16fp/16fp | 539.55 | 86.96 | 21.76 | 18.17 | |
| 32fp/32fp | 3303.19 | 694.77 | 19.03 | - | |
| LDM 2.1 | 8/8+16fp/16fp | 913.80 | 99.45 | 18.52 | 19.26 |
| 4/8+16fp/16fp | 544.70 | 87.04 | 21.94 | 18.48 | |
| 32fp/32fp | 9794.10 | 6123.35 | 19.68 | - | |
| LDM XL | 8/8+16fp/16fp | 2562.26 | 604.06 | 16.48 | 20.66 |
| 4/8+16fp/16fp | 1394.30 | 449.28 | 21.55 | 18.50 |



We report the best configuration on hybrid quantization. Besides shrinking the operational size of the LDM models, the hybrid quantization significantly improves computational efficiency. For all LDMs, the upsampling blocks that are closer to the output are most sensitive to the quantization. Even though the process is recursive, these blocks contribute most quantization noise at the end of each sampling step. By replacing these blocks with higher-precision quantized blocks, these hybrid blocks filter out most quantization noise which is illustrated as an increase in shown in the ablation. Interestingly, the FID suggests that the hybrid quantized LDMs is on-par or even better than the full-precision models. The unreliability of FID to quantify quality of image perception is mentioned in other works [7, 29]. But aligns with the intuition that lower bit quantization accumulates higher quantization noise and hence generates more lossy images.
4.1.2 Local Noise Correction
We evaluate the sole power of the proposed local noise corrections on two different LDM models: LDM 1.5, XL 1.0 base.
| Method | Bits(W/A) | Size(Mb) | TBops | FID | (db) |
|---|---|---|---|---|---|
| 32fp/32fp | 3278.82 | 693.76 | 18.27 | - | |
| 8/8 | 820.28 | 43.63 | 213.72 | 11.04 | |
| LDM 1.5 | + corrections | 820.28 | 43.63 | 24.51 | 17.78 |
| 4/8 | 410.53 | 21.96 | 296.45 | 9.73 | |
| + corrections | 410.53 | 21.96 | 57.71 | 15.71 | |
| 32fp/32fp | 9794.10 | 6123.35 | 19.68 | - | |
| 8/8 | 2450.21 | 385.13 | 76.90 | 16.57 | |
| LDM XL | + corrections | 2450.21 | 385.13 | 22.33 | 18.21 |
| 4/8 | 1226.23 | 193.85 | 237.40 | 12.29 | |
| + corrections | 1226.23 | 193.85 | 44.41 | 13.71 |
To demonstrate the benefit of local quantization strategy, we conduct experiments using the local noise correction on the identified sensitive modules and the single-sampling-step calibration without hybrid global quantization. We adapt SmoothQuant to the most sensitive modules to balance the increased computation and reduced quantization noise. Since we only calibrate quantization parameters with min-max values, the end-to-end quantized baselines generate very noisy images as high FID and low listed in Table 2. However, with both local quantization strategy implemented, the generated images restore its quality to a large extend. Though we notice there is a gap to the full-precision generated images, the qualitative examples demonstrate much coherent and clear images after the local noise corrections. Note that optimized quantization calibration methods like entropy-based, percentile-based, and BRECQ can further improve the quality. (See Supplementary B.)




4.2 Qualitative Examples
We present qualitative examples for both global hybrid strategy Figure 9 and local noise correction strategy Figure 10. Qualitatively, LDM XL is more robust to min-max quantization but LDM 1.5 generates extensively corrupted images with naive min-max quantization. Nonetheless, the local noise corrections can significantly improve the quality of the images by just identifying 10% of most sensitive modules.
5 Ablations
We perform all ablations on LDM 1.5 8W8A quantization setting for consistency.
| in_blocks | down_blocks | mid_block | up_blocks | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 0 | 1 | 2 | 3 | out_blocks | |||
| TBOPs | 173.63 | 161.00 | 148.98 | 136.91 | 135.46 | 133.14 | 128.19 | 99.34 | 68.97 | 43.64 | 43.63 |
| FID | 18.54 | 18.15 | 17.98 | 17.54 | 17.56 | 17.69 | 16.98 | 16.94 | 16.58 | 21.31 | 27.97 |
5.1 Hybrid Quantization Configurations
As mentioned in Section 3.3, we examine the different hybrid quantization configurations to verify the block sensitivity shown in Figure 5(a). We explore all hybrid quantization configurations on LDM 1.5 and evaluate FID and computational efficiency in Table 3. Though FID suggests that higher-precision quantization generates less presentable images, which contrasts to the expectation. We argue that FID is not an optimal metric to quantize the quantization loss when the quantization noise is low. Only when significant quantization noise corrupts the image, a high FID indicates the generated images are too noisy.
5.2 Local Quantization Corrections
As we obtain the local sensitivity for the LDM, we can identify the sensitive local modules from most sensitive to least sensitive based on . We explore the portion of the modules to adapt SmoothQuant and evaluate . Note that both statistic preparation and computation on proportionally increase with the number of identified modules. As the 10% most sensitive modules identified, SmoothQuant can effectively address the activation quantization challenge as increases and saturate till 90%. And smoothing least sensitive modules results in deterioration due to unnecessary quantization mitigation. With different mitigation factor, , the behaviour remains consistent, only higher reduces quantization errors by alleviating activation quantization challenge.

We also adapt SmoothQuant to the hybrid quantization to evaluate the benefit of such activation quantization noise correction. 10% most sensitive modules are identified and applied with SmoothQuant (). FID and are reported. 1-step calibration significantly reduces the quantization noise for the hybrid quantization. However, SmoothQuant does not make visible difference. This is because identified sensitive modules reside mostly in the upsampling blocks, which are replaced with higher-precision quantization and therefore the quantization noise is already reduced by the hybrid strategy.
| FID | ||
|---|---|---|
| hybrid | 27.31 | 17.16 |
| + 1-step calibration | 16.58 | 20.45 |
| ++ SmoothQuant | 16.75 | 20.41 |
5.3 Number of Calibration Steps
As we discuss in 3.4.2, we notice that calibrate on multiple sampling steps is problematic for quantization due to gradually changing activation ranges. And quantization parameters are most robust to the added diffusion noise at first sampling step (last forward diffusion step). Hence calibrating on fewer sampling steps leads to less vibrant activation ranges, which results in better quantization calibration. We evaluate the effect on the number of calibration steps on the relative quantization error, , and FID. It is obvious that the proposed 1-step calibration significantly improves the calibration efficiency () compared to calibration methods proposed in [21, 11, 37], where calibration data are sampled from all 50 sampling steps.
| Steps |
|
FID | |||
|---|---|---|---|---|---|
| 50 | 213.72 | 11.04 | |||
| 2 | 47.892 | 13.55 | |||
| 1 | 27.971 | 14.05 |
5.4 Efficient metric Computation
We develop an efficient computation of by forward passing two same inputs to all input modules. And we rearrange the output of all modules so that first half of the output is full-precision output, and the second half of the output is quantized output. In this way, can be computed at all modules with a single forward pass and with a small number of examples. Other complicated optimization like Q-Diffusion or PTQ4DM collects thousands of calibration data over all 50 sampling steps. Detailed description is included in Supplementary C.
6 Conclusions
In summary, this work introduces an innovative quantization strategy, the first of its kind, providing effective quantization solutions for Latent Diffusion Models (LDMs) at both global and local levels by analyzing relative quantization noise, namely , as the pivoting metric for sensitivity identification. The proposed hybrid quantization solution at global levels identifies a specific LDM block for higher-precision quantization, so that it mitigates relative quantization noise. At local levels, a smoothing mechanism targets the most sensitive modules to alleviate activation quantization noise. Additionally, a single-sampling-step calibration is proposed, leveraging the robustness of local modules to quantization when diffusion noise is strongest in the last step of the forward diffusion process. The collected quantization strategy significantly improves quantization efficiency, marking a notable contribution to LDM optimization strategies.
References
- Bai et al. [2022] Haoli Bai, Lu Hou, Lifeng Shang, Xin Jiang, Irwin King, and Michael R Lyu. Towards efficient post-training quantization of pre-trained language models. Advances in Neural Information Processing Systems, 35:1405–1418, 2022.
- Banner et al. [2019] Ron Banner, Yury Nahshan, and Daniel Soudry. Post training 4-bit quantization of convolutional networks for rapid-deployment. Advances in Neural Information Processing Systems, 32, 2019.
- Bolya and Hoffman [2023] Daniel Bolya and Judy Hoffman. Token merging for fast stable diffusion. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 4598–4602, 2023.
- Cai et al. [2020] Yaohui Cai, Zhewei Yao, Zhen Dong, Amir Gholami, Michael W Mahoney, and Kurt Keutzer. Zeroq: A novel zero shot quantization framework. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 13169–13178, 2020.
- Cao et al. [2018] Yue Cao, Bin Liu, Mingsheng Long, and Jianmin Wang. Hashgan: Deep learning to hash with pair conditional wasserstein gan. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 1287–1296, 2018.
- Chen et al. [2021] Weihan Chen, Peisong Wang, and Jian Cheng. Towards mixed-precision quantization of neural networks via constrained optimization. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 5350–5359, 2021.
- Chong and Forsyth [2020] Min Jin Chong and David Forsyth. Effectively unbiased fid and inception score and where to find them. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pages 6070–6079, 2020.
- Dong et al. [2019] Zhen Dong, Zhewei Yao, Amir Gholami, Michael W Mahoney, and Kurt Keutzer. Hawq: Hessian aware quantization of neural networks with mixed-precision. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 293–302, 2019.
- Fang et al. [2023] Gongfan Fang, Xinyin Ma, and Xinchao Wang. Structural pruning for diffusion models. arXiv preprint arXiv:2305.10924, 2023.
- Gu et al. [2022] Shuyang Gu, Dong Chen, Jianmin Bao, Fang Wen, Bo Zhang, Dongdong Chen, Lu Yuan, and Baining Guo. Vector quantized diffusion model for text-to-image synthesis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 10696–10706, 2022.
- He et al. [2023] Yefei He, Luping Liu, Jing Liu, Weijia Wu, Hong Zhou, and Bohan Zhuang. Ptqd: Accurate post-training quantization for diffusion models. arXiv preprint arXiv:2305.10657, 2023.
- Heusel et al. [2017] Martin Heusel, Hubert Ramsauer, Thomas Unterthiner, Bernhard Nessler, and Sepp Hochreiter. Gans trained by a two time-scale update rule converge to a local nash equilibrium. Advances in neural information processing systems, 30, 2017.
- Ho et al. [2020] Jonathan Ho, Ajay Jain, and Pieter Abbeel. Denoising diffusion probabilistic models. Advances in neural information processing systems, 33:6840–6851, 2020.
- Jeon et al. [2022] Yongkweon Jeon, Chungman Lee, Eulrang Cho, and Yeonju Ro. Mr. biq: Post-training non-uniform quantization based on minimizing the reconstruction error. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 12329–12338, 2022.
- Kim et al. [2022] Gwanghyun Kim, Taesung Kwon, and Jong Chul Ye. Diffusionclip: Text-guided diffusion models for robust image manipulation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 2426–2435, 2022.
- Krishnamoorthi [2018] Raghuraman Krishnamoorthi. Quantizing deep convolutional networks for efficient inference: A whitepaper. arXiv preprint arXiv:1806.08342, 2018.
- Lathi [1990] Bhagwandas P Lathi. Modern digital and analog communication systems. Oxford University Press, Inc., 1990.
- Lee et al. [2018] Jun Haeng Lee, Sangwon Ha, Saerom Choi, Won-Jo Lee, and Seungwon Lee. Quantization for rapid deployment of deep neural networks. arXiv preprint arXiv:1810.05488, 2018.
- Li et al. [2023a] Bo Li, Kaitao Xue, Bin Liu, and Yu-Kun Lai. Bbdm: Image-to-image translation with brownian bridge diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 1952–1961, 2023a.
- Li et al. [2023b] Muyang Li, Ji Lin, Chenlin Meng, Stefano Ermon, Song Han, and Jun-Yan Zhu. Efficient spatially sparse inference for conditional gans and diffusion models. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2023b.
- Li et al. [2023c] Xiuyu Li, Yijiang Liu, Long Lian, Huanrui Yang, Zhen Dong, Daniel Kang, Shanghang Zhang, and Kurt Keutzer. Q-diffusion: Quantizing diffusion models. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 17535–17545, 2023c.
- Li et al. [2019] Yuhang Li, Xin Dong, and Wei Wang. Additive powers-of-two quantization: An efficient non-uniform discretization for neural networks. arXiv preprint arXiv:1909.13144, 2019.
- Li et al. [2021] Yuhang Li, Ruihao Gong, Xu Tan, Yang Yang, Peng Hu, Qi Zhang, Fengwei Yu, Wei Wang, and Shi Gu. Brecq: Pushing the limit of post-training quantization by block reconstruction. arXiv preprint arXiv:2102.05426, 2021.
- Lim and Kim [2023] Sangbeom Lim and Seungryong Kim. Image guided inpainting with parameter efficient learning. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 1103–1111, 2023.
- Lin et al. [2014] Tsung-Yi Lin, Michael Maire, Serge Belongie, James Hays, Pietro Perona, Deva Ramanan, Piotr Dollár, and C Lawrence Zitnick. Microsoft coco: Common objects in context. In Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, September 6-12, 2014, Proceedings, Part V 13, pages 740–755. Springer, 2014.
- Lu et al. [2022] Cheng Lu, Yuhao Zhou, Fan Bao, Jianfei Chen, Chongxuan Li, and Jun Zhu. Dpm-solver: A fast ode solver for diffusion probabilistic model sampling in around 10 steps. Advances in Neural Information Processing Systems, 35:5775–5787, 2022.
- Meng et al. [2023] Chenlin Meng, Robin Rombach, Ruiqi Gao, Diederik Kingma, Stefano Ermon, Jonathan Ho, and Tim Salimans. On distillation of guided diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 14297–14306, 2023.
- Moon et al. [2023] Taehong Moon, Moonseok Choi, EungGu Yun, Jongmin Yoon, Gayoung Lee, and Juho Lee. Early exiting for accelerated inference in diffusion models. In ICML 2023 Workshop on Structured Probabilistic Inference & Generative Modeling, 2023.
- Naeem et al. [2020] Muhammad Ferjad Naeem, Seong Joon Oh, Youngjung Uh, Yunjey Choi, and Jaejun Yoo. Reliable fidelity and diversity metrics for generative models. In International Conference on Machine Learning, pages 7176–7185. PMLR, 2020.
- Nichol and Dhariwal [2021] Alexander Quinn Nichol and Prafulla Dhariwal. Improved denoising diffusion probabilistic models. In International Conference on Machine Learning, pages 8162–8171. PMLR, 2021.
- Pandey et al. [2023a] Nilesh Prasad Pandey, Marios Fournarakis, Chirag Patel, and Markus Nagel. Softmax bias correction for quantized generative models. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 1453–1458, 2023a.
- Pandey et al. [2023b] Nilesh Prasad Pandey, Markus Nagel, Mart van Baalen, Yin Huang, Chirag Patel, and Tijmen Blankevoort. A practical mixed precision algorithm for post-training quantization. arXiv preprint arXiv:2302.05397, 2023b.
- Podell et al. [2023] Dustin Podell, Zion English, Kyle Lacey, Andreas Blattmann, Tim Dockhorn, Jonas Müller, Joe Penna, and Robin Rombach. Sdxl: Improving latent diffusion models for high-resolution image synthesis. arXiv preprint arXiv:2307.01952, 2023.
- Rombach et al. [2022] Robin Rombach, Andreas Blattmann, Dominik Lorenz, Patrick Esser, and Björn Ommer. High-resolution image synthesis with latent diffusion models. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pages 10684–10695, 2022.
- Ronneberger et al. [2015] Olaf Ronneberger, Philipp Fischer, and Thomas Brox. U-net: Convolutional networks for biomedical image segmentation. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, October 5-9, 2015, Proceedings, Part III 18, pages 234–241. Springer, 2015.
- Salimans and Ho [2022] Tim Salimans and Jonathan Ho. Progressive distillation for fast sampling of diffusion models. arXiv preprint arXiv:2202.00512, 2022.
- Shang et al. [2023] Yuzhang Shang, Zhihang Yuan, Bin Xie, Bingzhe Wu, and Yan Yan. Post-training quantization on diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 1972–1981, 2023.
- Sheng et al. [2018] Tao Sheng, Chen Feng, Shaojie Zhuo, Xiaopeng Zhang, Liang Shen, and Mickey Aleksic. A quantization-friendly separable convolution for mobilenets. In 2018 1st Workshop on Energy Efficient Machine Learning and Cognitive Computing for Embedded Applications (EMC2), pages 14–18. IEEE, 2018.
- Sohl-Dickstein et al. [2015] Jascha Sohl-Dickstein, Eric Weiss, Niru Maheswaranathan, and Surya Ganguli. Deep unsupervised learning using nonequilibrium thermodynamics. In International conference on machine learning, pages 2256–2265. PMLR, 2015.
- Song et al. [2020] Jiaming Song, Chenlin Meng, and Stefano Ermon. Denoising diffusion implicit models. arXiv preprint arXiv:2010.02502, 2020.
- Song et al. [2023] Yang Song, Prafulla Dhariwal, Mark Chen, and Ilya Sutskever. Consistency models. 2023.
- Tumanyan et al. [2023] Narek Tumanyan, Michal Geyer, Shai Bagon, and Tali Dekel. Plug-and-play diffusion features for text-driven image-to-image translation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 1921–1930, 2023.
- Wang et al. [2023] Changyuan Wang, Ziwei Wang, Xiuwei Xu, Yansong Tang, Jie Zhou, and Jiwen Lu. Towards accurate data-free quantization for diffusion models. arXiv preprint arXiv:2305.18723, 2023.
- Wang et al. [2019] Kuan Wang, Zhijian Liu, Yujun Lin, Ji Lin, and Song Han. Haq: Hardware-aware automated quantization with mixed precision. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pages 8612–8620, 2019.
- Wang et al. [2020] Ying Wang, Yadong Lu, and Tijmen Blankevoort. Differentiable joint pruning and quantization for hardware efficiency. In European Conference on Computer Vision, pages 259–277. Springer, 2020.
- Wei et al. [2022] Xiuying Wei, Yunchen Zhang, Xiangguo Zhang, Ruihao Gong, Shanghang Zhang, Qi Zhang, Fengwei Yu, and Xianglong Liu. Outlier suppression: Pushing the limit of low-bit transformer language models. Advances in Neural Information Processing Systems, 35:17402–17414, 2022.
- Wu et al. [2020] Di Wu, Qi Tang, Yongle Zhao, Ming Zhang, Ying Fu, and Debing Zhang. Easyquant: Post-training quantization via scale optimization. arXiv preprint arXiv:2006.16669, 2020.
- Xiao et al. [2023] Guangxuan Xiao, Ji Lin, Mickael Seznec, Hao Wu, Julien Demouth, and Song Han. Smoothquant: Accurate and efficient post-training quantization for large language models. In International Conference on Machine Learning, pages 38087–38099. PMLR, 2023.
- Zhang et al. [2022] Angela Zhang, Lei Xing, James Zou, and Joseph C Wu. Shifting machine learning for healthcare from development to deployment and from models to data. Nature Biomedical Engineering, 6(12):1330–1345, 2022.
- Zhang et al. [2018] Dongqing Zhang, Jiaolong Yang, Dongqiangzi Ye, and Gang Hua. Lq-nets: Learned quantization for highly accurate and compact deep neural networks. In Proceedings of the European conference on computer vision (ECCV), pages 365–382, 2018.
- Zhang et al. [2023] Lvmin Zhang, Anyi Rao, and Maneesh Agrawala. Adding conditional control to text-to-image diffusion models. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 3836–3847, 2023.
Appendix A Module Sensitivity
We show module sensitivity for LDM 2.1 and LDM XL here. The quantization setting is 8W8A for both models.

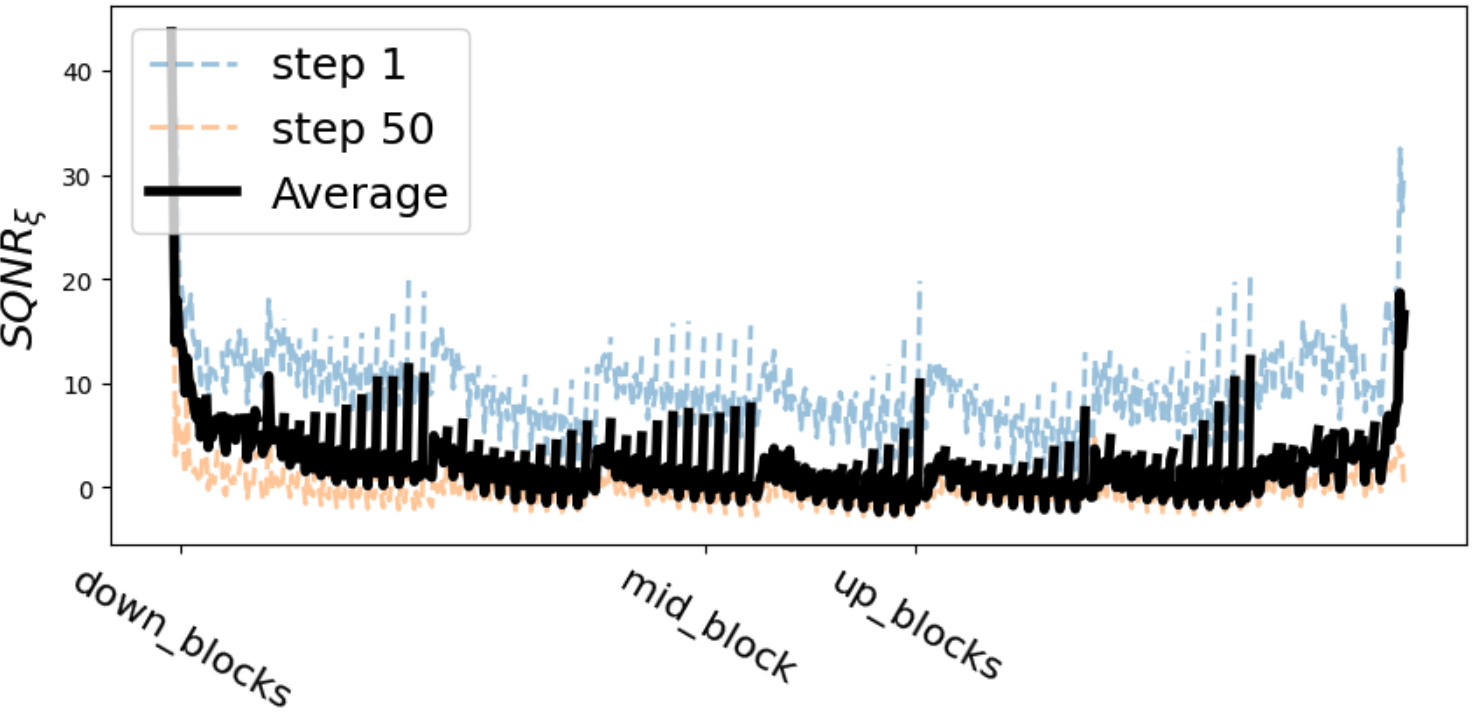
We notice that LDM XL has more robust modules compared to LDM 1.5 and LDM 2.1. We deduce that cross-attention modules are switched to middle section of the model instead of the head-and-tail sections. The cross-attention modules fluactuate the quantization sensitivity because different quantization tolerances between the text-input modules and image-input modules. But the general trend remains similar in all three models that sensitive modules can be identified as they are associated with low . And the quantization parameters are more robust in the first step of inference.
We also list the 5% most sensitive modules in all three models.
For LDM 1.5 and 2.1, three kinds of operations are identified as most sensitive: a). Sampling operations; b). Transformer output projection; c). Shortcut connection. But for LDM XL, the transformer projection consistently deteriorates the quantization noise. There can be a specific solution to LDM XL for this consistent deterioration. But the smoothing mechanism can address the problem to a extend.
Appendix B Quantization Optimization
We list the number of samples, number of inference steps required for different optimized quantization and compare with our proposed method. While other optimized methods require 50 calibration steps, we only require 1 step for activation range register, and 1 step for calibration. Though other complicated quantizations benefit the quality as indicated by higher , our proposed method is highly efficient and the quality is on-par compared with others.
| No. Samples | No. Steps | Efficiency | ||
|---|---|---|---|---|
| Entorpy | 512 | 50 | 18.02 | |
| Percentile | 256 | 50 | 17.13 | |
| BREQ | 1024 | 50 | 18.86 | |
| Our | 256 | 1+1 | 17.78 |
Appendix C Efficient Computation of SQNR
To efficiently compute the relative metric , we aim to compute the score on the fly without storing any computational expensive feature maps. This means we compute the score with a single forward pass. To realize this efficient computation, the model should have a switch that controls the quantized and unquantized states. Two identical inputs are passed to every input node and each will only flow through quantized state or unquantized state afterwards. For every module, it is therefore possible to compute the relative quantization noise at the output instantaneously. A pseudo code is shown as following:
Though the duplicated input halves the maximum number of executable samples per batch, we argue the efficiency is more beneficial for our proposed strategy and we justify that we only need a small number of examples to compute a compelling .We measure the time-averaged relative difference between computed with 1024 samples and that computed with 64 samples for all modules. The result is shown in Figre 13. The small relative difference ( 0.07% at maximum) suggests that computing with just 64 samples is comparable with 1024 samples.

Appendix D LDM Configurations
| Image Size | Inference Steps | Sampler | |
|---|---|---|---|
| LDM 1.5 | 512, 512 | 50 | PNDMScheduler |
| LDM 2.1 | 512, 512 | 50 | PNDMScheduler |
| LDM XL | 1024, 1024 | 50 | EulerDiscreteScheduler |
Appendix E Activation Outliers
We visualize activation ranges in 3d for 4 examples at three operations we mentioned. The red region suggests high activation range and blue region suggests low activation range. As mentioned, the outlier in certain channels make the min-max quantization difficult.


