Efficient Perception, Planning, and Control Algorithm for Vision-Based Automated Vehicles
Abstract
Autonomous vehicles have limited computational resources and thus require efficient control systems. The cost and size of sensors have limited the development of self-driving cars. To overcome these restrictions, this study proposes an efficient framework for the operation of vision-based automatic vehicles; the framework requires only a monocular camera and a few inexpensive radars. The proposed algorithm comprises a multi-task UNet (MTUNet) network for extracting image features and constrained iterative linear quadratic regulator (CILQR) and vision predictive control (VPC) modules for rapid motion planning and control. MTUNet is designed to simultaneously solve lane line segmentation, the ego vehicle’s heading angle regression, road type classification, and traffic object detection tasks at approximately 40 FPS for 228 228 pixel RGB input images. The CILQR controllers then use the MTUNet outputs and radar data as inputs to produce driving commands for lateral and longitudinal vehicle guidance within only 1 ms. In particular, the VPC algorithm is included to reduce steering command latency to below actuator latency, preventing performance degradation during tight turns. The VPC algorithm uses road curvature data from MTUNet to estimate the appropriate correction for the current steering angle at a look-ahead point to adjust the turning amount. The inclusion of the VPC algorithm in a VPC-CILQR controller leads to higher performance on curvy roads than the use of CILQR alone. Our experiments demonstrate that the proposed autonomous driving system, which does not require high-definition maps, can be applied in current autonomous vehicles.
Index Terms:
Automated vehicles, autonomous driving, deep neural network, constrained iterative linear quadratic regulator, model predictive control, motion planning.I Introduction
The use of deep neural network (DNN) techniques in intelligent vehicles has expedited the development of self-driving vehicles in research and industry. Self-driving cars can operate automatically because equipped perception, planning, and control modules operate cooperatively [1, 2, 3]. The most common perception components used in autonomous vehicles include cameras and radar/lidar devices; cameras are combined with DNN to recognize relevant objects, and radars/lidars are mainly used for distance measurement [2, 4]. Because of limitations related to sensor cost and size, current Active Driving Assistance Systems (ADASs) primarily rely on camera-based perception modules with supplementary radars [5].
To understand complex driving scenes, multi-task DNN (MTDNN) models that output multiple predictions simultaneously are often applied in autonomous vehicles to reduce inference time and device power consumption. In [6], street classification, vehicle detection, and road segmentation problems were solved using a single MultiNet model. In [7], the researchers trained an MTDNN to detect drivable areas and road classes for vehicle navigation. DLT-Net, presented in [8], is a unified neural network for the simultaneous detection of drivable areas, lane lines, and traffic objects. The network localizes the vehicle when a high-definition (HD) map is unavailable. The context tensors between subtask decoders in DLT-Net share mutual features learned from different tasks. A lightweight multi-task semantic attention network was proposed in [9] to achieve simultaneous object detection and semantic segmentation; this network boosts detection performance and reduces computational costs through the use of a semantic attention module. YOLOP [10] is a panoptic driving perception network that simultaneously performs traffic object detection, drivable area segmentation, and lane detection on an NVIDIA TITAN XP GPU at a speed of 41 FPS (frames per second). In the commercially available TESLA Autopilot system [11], images from cameras with different viewpoints are entered into separate MTDNNs that perform driving scene semantic segmentation, monocular depth estimation, and object detection tasks. The outputs of these MTDNNs are further fused in bird’s-eye-view (BEV) networks to directly output a reconstructed aerial-view map of traffic objects, static infrastructure, and the road itself.
In a modular self-driving system, the environmental perception results can be sent to an optimization-based model predictive control (MPC) planner to generate spatiotemporal curves over a time horizon. The system then reactively selects optimal solutions over a short interval as control inputs to minimize the gap between target and current states [12]. These MPC models can be realized with various methods [e.g., active set, augmented Lagrangian, interior point, or sequential quadratic programming (SQP)] [13, 14] and are promising for vehicle optimal control problems. In [15], a linear MPC control model was proposed that addresses vehicle lane-keeping and obstacle avoidance problems by using lateral automation. In [16], an MPC control scheme combining longitudinal and lateral dynamics was designed for following velocity trajectories. Ref. [17] proposed a scale reduction method for reducing the online computational efforts of MPC controllers, and they applied it to longitudinal vehicle automation, achieving an average computational time of approximately 4 ms. In [14], a linear time-varying MPC scheme was proposed for lateral automobile trajectory optimization. The cycle time for the optimized trajectory to be communicated to the feedback controller was 10 ms. In addition, [18] investigated automatic weight determination for car-following control, and the corresponding linear MPC algorithm was implemented using CVXGEN [19], which solves the relevant problem within 1 ms.
The constrained iterative linear quadratic regulator (CILQR) method was proposed to solve online trajectory optimization problems with nonlinear system dynamics and general constraints [20, 21]. The CILQR algorithm constructed on the basis of differential dynamic programming (DDP) [22] is also an MPC method. The computational load of the well-established SQP solver is higher than that of DDP [23]. Thus, the CILQR solver outperforms the standard SQP approach in terms of computational efficiency; compared with the CILQR solver, the SQP approach requires a computation time that is 40.4 times longer per iteration [21]. However, previous CILQR-relates studies [20, 21, 23, 24] have focused on nonlinear Cartesian-frame motion planning. Alternatively, planning within the Frenét-frame can reduce problem dimensions because it enables vehicle dynamics to be solved in tangential and normal directions separately with the aid of road reference line [25]; furthermore, the corresponding linear dynamic equations [18, 26] do not have adverse effects when high-order Taylor expansion coefficients are truncated in the CILQR framework [cf. Section II]. These considerations motivated us to use linear CILQR planners to control automated vehicles.

We proposed an MTDNN in [27] to directly perceive ego vehicle’s heading angle () and distance from the lane centerline () for autonomous driving. The vision-based MTDNN model in [27] essentially provides the information necessary for ego car navigation within Frenét coordinates without the need for HD maps. Nevertheless, this end-to-end autonomous driving approach performs poorly in environments that are not shown during the training phase [2]. In [28], we proposed an improved control algorithm based on a multi-task UNet architecture (MTUNet) that comprises lane line segmentation and pose estimation subnets. A Stanley controller [30] was then designed to control the lateral automation of an automobile. The Stanley controller takes and yielding from the network as it’s input for lane-centering [29]. The improved algorithm outperforms the model in [27] and has comparable performance to a multi-task-learning reinforcement-learning (MTL-RL) model [31], which integrates RL and deep-learning algorithms for autonomous driving. However, our algorithms presented in [28] have a variety of problems as follows. 1) Vehicle dynamic models are not considered in the Stanley controller, and the model has poor performance for lanes with rapid curvature changes [32]. 2) The proposed self-driving system does not consider road curvature, resulting in poor vehicle control on curvy roads [33]. 3) The corresponding DNN perception network lacks object detection capability, which is a core task in automated driving. 4) The DNN input has high dimensional resolution of 400 400, which results in long training and inference times.

To address these shortcomings, this paper proposes a new system for real-time automated driving based on the developments described in [28, 29]. First, a YOLOv4 detector [34] is added to the MTUNet for object detection. Second, the inference speed of MTUNet was increased by reducing the input size without sacrificing network performance. Third, a vision predictive control (VPC) algorithm is proposed for reducing the steering command delay by enabling steer correction at a look-ahead point by applying road curvature information. The VPC algorithm can also be combined with the lateral CILQR algorithm (denoted VPC-CILQR) to rapidly perform motion planning and automobile control. As shown in Fig. 1, the vehicle actuation latency () was shorter than the steering command latency () in our simulation. This delay may also be present in automated vehicles [35] or autonomous racing systems [36] and may induce instability in the system being controlled. Equipping the vehicle with low-level computers could further increase this steering command lag. Therefore, compensating algorithms such as VPC are key to cost-efficient automated vehicle systems.
In general, the research method of this paper is similar to those in [51, 52], which have also presented self-driving systems based on lane detection results. In [51]. an optimal LQR scheme with the sliding-mode approach was proposed to implement preview path tracking control for intelligent electric vehicles with optimal torque distribution between their motors. In [52], a safeguard-protected preview path tracking control algorithm was presented. The proposed preview control strategy comprises feedback and feedforward controllers for stabilizing tracking errors and preview control, respectively. The proposed controller was implemented and validated on open roads and Mcity, an automated vehicle platform. The tested vehicle was equipped with a commercial Mobileye module to detect lane markings.
The main goal of this work was to design a computationally efficient automated driving system for real-time lane-keeping and car-following. The contributions of this paper are as follows:
-
1.
The proposed MTDNN scheme can execute simultaneous driving perception tasks at a speed of 40 FPS. The main difference between this scheme and previous MTDNN schemes is that the post-processing methods provide crucial parameters (lateral offset, road curvature, and heading angle) that improve local vehicular navigation.
-
2.
The VPC-CILQR controller comprising the VPC algorithm and lateral CILQR solver is proposed to improve driverless vehicle path tracking. The method has a low online computational burden and can respond to steering commands in accordance with the concept of look-ahead distance.
-
3.
We propose a vision-based framework comprising the aforementioned MTDNN scheme and CILQR-based controllers for operating an autonomous vehicle; the effectiveness of the proposed framework was demonstrated in challenging simulation environments without maps.
The remainder of this paper is organized as follows: the research methodology is presented in Section II, the experimental setup is described in Section III, and the results are presented and discussed in Section IV. Section V concludes this paper.
II Methodology
The following section introduces each part of the proposed self-driving system. As depicted in Fig. 1, our system comprises several modules. The DNN is an MTUNet that can solve multiple perception problems simultaneously. The CILQR controllers receive data from the DNN and radars to compute driving commands for lateral and longitudinal motion planning. In the lateral direction, the lane line detection results from the DNN are input to the VPC module to compute steering angle corrections at a certain distance in front of the ego car. These corrections are then sent to the CILQR solver to predict a steering angle for the lane-keeping task. This two-step algorithm is denoted VPC-CILQR throughout the article. The other CILQR controller handles the car-following task in the longitudinal direction.
II-A MTUNet network
As indicated in Fig. 2, the proposed MTDNN is a neural network with an MTUNet architecture featuring a common backbone encoder and three subnets for completing multiple tasks at the same time. The following sections describe each part.
II-A1 Backbone and segmentation subnet
The shared backbone and segmentation (seg) subnet employ encoder-decoder UNet-based networks for pixel-level lane line classification task. Two classical UNets (UNet2 [28] and UNet1 [37]) and one enhanced version (MultiResUNet [37], denoted as MResUNet throughout the paper) were used to investigate the effects of model size and complexity on task performance. For UNet2 and UNet1, each repeated block includes two convolutional (Conv) layers, and the first UNet has twice as many filters as the second. For MResUNet, each modified block consists of three 3 3 Conv layers and one 1 1 Conv layer. Table I summarizes the filter number and related kernel size of the Conv layers used in these models. The resulting total number of parameters of UNet2/UNet1/MResUNet is 31.04/7.77/7.26 M, and the corresponding total number of multiply accumulate operations (MACs) is 38.91/9.76/12.67 G. All 3 3 Conv layers are padded with one pixel to preserve the spatial resolution after the convolution operations are applied [38]. This setting reduces the network input size from 400 400 to 228 228 but preserves model performance and increases inference speed compared with the models in our previous work (the experimental results are presented in Section IV) [28]. That network used unpadded 3 3 Conv layers [39], and zero padding was therefore applied to the input to equalize the input–output resolutions [40]. In the training phase, the weighted cross-entropy loss is adopted to deal with the lane detection sample imbalance problem [41, 42] and is represented as
| (1) |
where and are the numbers of foreground and background samples in a batch of images, respectively; is a predicted score; is the corresponding label; and is the sigmoid function.
II-A2 Pose subnet
This subnet is mainly responsible for whole-image angle regression and road type classification problems, where the road involves three categories (left turn, straight, and right turn) designed to prevent the angle estimation from mode collapsing [28, 43]. The network architecture of the pose subnet is presented in Fig. 2; the pose subnet takes the fourth Conv-block output feature maps of the backbone as its input. Subsequently, the input maps are fed into shared parts including two consecutive Conv layers and one global average pooling (GAP) layer to extract general features. Lastly, the resulting vectors are passed separately through two fully connected (FC) layers before being mapped into a sigmoid/softmax activation layer for the regression/classification task. Table II summarizes the number of filters and output units of the corresponding Conv and FC layers, respectively. The expression MTUNet2/MTUNet1/MTMResUNet in Table II represents a multi-task UNet scheme in which subnets are built on the UNet2/UNet1/MResUNet model throughout the article. The pose task loss function, including L2 regression loss () and cross-entropy loss (), is employed for network training; this function is represented as follows:
| (2a) | |||
| (2b) |
where and are the ground truth and estimated value, respectively; is the input batch size; and and are true and softmax estimation values, respectively.
II-A3 Detection subnet
The detection (det) subnet takes advantage of a simplified YOLOv4 detector [34] for real-time traffic object (leading car) detection. This fully-convolutional subnet that has three branches for multi-scale detection takes the output feature maps of the backbone as its input, as illustrated in Fig. 2. The initial part of each branch is composed of single or consecutive 3 3 filters for extracting contextual information at different scales [37], and a shortcut connection with one 1 1 filter from the input layer for residual mapping. The top of the addition layer contains sequential 1 1 filters for reducing the number of channels. The resulting feature maps of each branch have six channels (five for bounding box offset and confidence score predictions, and one for class probability estimation) with a size of = 15 15 to divide the input image into grids. In this article, we select = 3 anchor boxes, which are then shared between three branches according to the context size. Ultimately, spatial features from three detecting scales are concatenated together and sent to the output layer. Table III presents the design of detection subnet of MTUNets. The overall loss function for training comprises objectness (), classification (), and complete intersection over union (CIoU) losses () [44, 45]; these losses are constructed as follows:
| (3a) | ||||
| (3b) | ||||
| (3c) | ||||
where = 1/0 or 0/1 indicates that the -th predicted bounding box does or does not contain an object, respectively; / and / are the true/estimated objectness and class scores corresponding to each box, respectively; and is a hyperparameter intended for balancing positive and negative samples. With regard to CIoU loss, and are the central points of the prediction () and ground truth () boxes, respectively; is the related Euclidean distance; is the diagonal distance of the smallest enclosing box covering and ; is a tradeoff hyperparameter; and is used to measure aspect ratio consistency [44].
| Conv-block | UNet2 [28] | UNet1 [37] | MResUNet [37] |
|---|---|---|---|
| Block/9 | 64 (3 3)b | 32 (3 3) | 8 (3 3), 17 (3 3), |
| 64 (3 3) | 32 (3 3) | 26 (3 3), 51 (1 1) | |
| Block2/8 | 128 (3 3) | 64 (3 3) | 17 (3 3), 35 (3 3), |
| 128 (3 3) | 64 (3 3) | 53 (3 3), 105 (1 1) | |
| Block3/7 | 256 (3 3) | 128 (3 3) | 35 (3 3), 71 (3 3), |
| 256 (3 3) | 128 (3 3) | 106 (3 3), 212 (1 1) | |
| Block4/6 | 512 (3 3) | 256 (3 3) | 71 (3 3), 142 (3 3), |
| 512 (3 3) | 256 (3 3) | 213 (3 3), 426 (1 1) | |
| Block5 | 1024 (3 3) | 512 (3 3) | 142 (3 3), 284 (3 3), |
| 1024 (3 3) | 512 (3 3) | 427 (3 3), 853 (1 1) | |
| aBlock1 of UNet2/UNet1 only contains one 3 3 Conv layer | |||
| bThe notation ( ) represents a Conv layer with filters of kernel size | |||
| Layer | MTUNet2 | MTUNet1 |
|---|---|---|
| MTMResUNet | ||
| Conv1 | 1024 (3 3) | 512 (3 3) |
| Conv2 | 1024 (3 3) | 512 (3 3) |
| FC1-2 | 256, 256 | 256, 256 |
| FC3-4 | 1, 3 | 1, 3 |
| Layer | MTUNet2 | MTUNet1 |
|---|---|---|
| MTMResUNet | ||
| Conv1-6 | 512 (3 3) | 384 (3 3) |
| Conv7-9 | 512 (1 1) | 384 (1 1) |
| Conv10-12 | 256 (1 1) | 256 (1 1) |
| Conv13-15 | 256 (1 1) | 256 (1 1) |
| Conv16-18 | 6 (1 1) | 6 (1 1) |
II-B The CILQR algorithm
This section first briefly describes the concept behind CILQR and related approaches based on [20, 21, 46, 47]; it then presents the lateral/longitudinal CILQR control algorithm that takes the MTUNet inference and radar data as its inputs to yield driving decisions using linear dynamics.
II-B1 Problem formulation
Provided a sequence of states and the corresponding control sequence are within the preview horizon , the system’s discrete-time dynamics are satisfied, with
| (4) |
from time to . The total cost denoted by , including running costs and the final cost , is presented as follows:
| (5) |
The optimal control sequence is then written as
| (6) |
with an optimal trajectory . The partial sum of from any time step to is represented as
| (7) |
and the optimal value function at time starting at takes the form
| (8) |
with the final time step value function .
In practice, the final step value function is obtained by executing a forward pass using the current control sequence. Subsequently, local control signal minimizations are performed in the proceeding backward pass using the following Bellman equation:
| (9) |
To compute the optimal trajectory, the perturbed function around the -th state-control pair in Eq. (9) is used; this function is written as follows:
| (10) | ||||
This equation can be approximated to a quadratic function by employing a second-order Taylor expansion with the following coefficients:
| (11a) | |||
| (11b) | |||
| (11c) | |||
| (11d) | |||
| (11e) |
The second-order coefficients of the system dynamics (, , and ) are omitted to reduce computational effort [23, 46]. The values of these coefficients are zero for linear systems [e.g., Eq. (19) and Eq. (25)], leading to fast convergence in trajectory optimization.
The optimal control signal modification can be obtained by minimizing the quadratic :
| (12) |
where
| (13a) | |||
| (13b) |
are optimal control gains. If the optimal control indicated in Eq. (12) is plugged into the approximated to recover the quadratic value function, the corresponding coefficients can be obtained [48]:
| (14a) | |||
| (14b) |
Control gains at each state (, ) can then be estimated by recursively computing Eqs. (11), (13), and (14) in a backward process. Finally, the modified control and state sequences can be evaluated through a renewed forward pass:
| (15a) | |||
| (15b) |
where . Here is the backtracking parameter for line search; it is set to 1 in the beginning and designed to be reduced gradually in the forward-backward propagation loops until convergence is reached.
If the system has the constraint
| (16) |
which can be shaped using an exponential barrier function [20, 24]
| (17) |
or a logarithmic barrier function [21], then
| (18) |
where , , and are parameters. The barrier function can be added to the cost function as a penalty. Eq. (18) converges toward the ideal indicator function as increases iteratively.
II-B2 Lateral CILQR controller
The lateral vehicle dynamic model [26] is employed for steering control. The state variable and control input are defined as and , respectively, where is the lateral offset, is the angle between the ego vehicle’s heading and the tangent of the road, and is the steering angle. As described in our previous work [28, 29], and can be obtained from MTUNets and related post-processing methods, and it is assumed that . The corresponding discrete-time dynamic model is written as follows:
| (19) |
where
with coefficients
Here, is the ego vehicle’s current speed along the heading direction and is the sampling time. The model parameters for the experiments are as follows: vehicle mass = 1150 kg, cornering stiffness = 80 000 N/rad, = 80 000 N/rad, center of gravity point = 1.27 m, = 1.37 m, and moment of inertia = 2000 kgm2.
The objective function () containing the iterative linear quadratic regulator (), barrier (), and end state cost () terms can be represented as
| (20a) | |||
| (20b) | |||
| (20c) | |||
| (20d) |
Here, the reference state = , / is the weighting matrix, and and are the corresponding barrier functions:
| (21a) | |||
| (21b) |
where () is used to limit control inputs and the high (low) steer bound is rad. The objective of is to control the ego vehicle moving toward the lane center.
The first element of the optimal steering sequence is then selected to define the normalized steering command at a given time as follows:
| (22) |
II-B3 Longitudinal CILQR controller
In the longitudinal direction, a proportional-integral (PI) controller [49]
| (23) |
is first applied to the ego car for tracking reference speed under cruise conditions, where and / are the tracking error and the proportional/integral gain, respectively. The normalized acceleration command is then given as follows:
| (24) |
When a slower preceding vehicle is encountered, the AccelCmd must be updated to maintain a safe distance from that vehicle to avoid a collision; for this purpose, we use the following longitudinal CILQR algorithm.
The state variable and control input for longitudinal inter-vehicle dynamics are defined as and , respectively, where , , and are the ego vehicle’s acceleration, jerk, and distance to the preceding car, respectively. The corresponding discrete-time system model is written as
| (25) |
where
Here, / is the preceding car’s speed/acceleration, and is the measurable disturbance input [50]. The values of and are measured by the radar; is known; and is assumed. Here, MTUNets are used to recognize traffic objects, and the radar is responsible for providing precise distance measurements.
The objective function () for the longitudinal CILQR controller can be written as,
| (26a) | |||
| (26b) | |||
| (26c) | |||
| (26d) |
Here, the reference state , and is the reference distance for safety. / is the weighting matrix, and , and are related barrier functions:
| (27a) | |||
| (27b) | |||
| (27c) |
where is used for maintaining a safe distance, and () and () are used to limit the ego vehicle’s jerk and acceleration to [1, 1] m/s3 and [5, 5] m/s2, respectively.
The first element of the optimal jerk sequence is then chosen to update AccelCmd in the car-following scenario as
| (28) |
The brake command (BrakeCmd) gradually increases in value from 0 to 1 when is smaller than a certain critical value during emergencies.
II-C The VPC algorithm
The problematic scenario for the VPC algorithm is depicted in Fig. 3, which presents a top-down view of fitted lane lines produced using our previous method [29]. First, the detected line segments [Fig. 3(a)] were clustered using the density-based spatial clustering of applications with noise (DBSCAN) algorithm. Second, the resulting semantic lanes were transformed into BEV space by using a perspective transformation. Third, the least-squares quadratic polynomial fitting method was employed to produce parallel ego-lane lines [Fig. 3(b)]; either of the two polynomials can be represented as . Fourth, the road curvature was computed using the formula
| (29) |
Because the curvature estimate from a single map is noisy, an average map obtained from eight consecutive frames was used for curve fitting. The resulting curvature estimates were then used to determine the correction value for the steering command in this study.

As shown in Fig. 3(b), at is the current steering angle. The desired steering angles at and can be computed using the local lane curvature [21]:
| (30a) | |||
| (30b) |
where is an adjustable parameter. Hence, the predicted steering angle at a look-ahead point can be represented as
| (31) |
Compared with those in existing LQR-based preview control methods [51, 52], fewer tuning parameters are required when the VPC algorithm is included in the steering geometry model; moreover, the algorithm can be combined with other path-tracking models. For example, a VPC-CILQR controller can update the CILQR steering command [Eq. (22)] as follows:
| (32) |

In summary, the proposed VPC algorithm uses the future road curvature at a look-ahead point 10 m in front of the ego car (Fig. 3) as input to generate the updated steering inputs. This algorithm is applied before the ego car enters a curvy road to improve tracking performance. Accurate and complete future road shape prediction is crucial for developing preview path-tracking control algorithms [52]. However, whether the necessary information can be obtained is greatly dependent on the maximum perception range of lane detection modules. As demonstrated in Fig. 5, LLAMAS [57] data are more useful than TORCS [28] or CULane [56] datasets for developing algorithms with such path-tracking functionality. A nonlinear MPC approach using high-quality predicted lane curvature data can achieve better control performance over the proposed method; however, if computational cost is a concern, such a nonlinear approach may not necessarily be preferred. The following sections describe validation experiments where the proposed algorithm was compared against other control algorithms.
| Dataset | Scenarios | No. of images | Labels | No. of traffic objects | Sources |
|---|---|---|---|---|---|
| CULane | urban, | 28368 | 80437 | [56], | |
| highway | ego-lane lines, | this work | |||
| LLAMAS | highway | 22714 | bounding boxes | 29442 | [57], |
| this work | |||||
| TORCS | 42747 | ego-lane lines, | 30189 | [28] | |
| bounding boxes, | |||||
| ego’s heading, | |||||
| road type |

III Experimental setup
The proposed MTUNets extract local and global contexts from input images to simultaneously perform segmentation, detection, and pose tasks. Because the these tasks have different learning rates [40, 53, 54], the proposed MTUNets were trained in a stepwise instead of end-to-end manner to help the backbone network learn common features. The training strategy, image data, and validation are described as follows.
III-A Network training strategy
The MTUNets were trained in three stages. The pose subnet was first trained through stochastic gradient descent (SGD) with a batch size (bs) of 20, momentum (mo) of 0.9, and learning rate (lr) starting from and decreasing by a factor of 0.9 every 5 epochs for a total of 100 epochs. The detection and pose subnets were then trained jointly with the parameters obtained in the first training stage and using the SGD optimizer with bs = 4, mo = 0.9, and lr = , , and for the first 60 epochs, the 61st to 80th epochs, and the last 20 epochs, respectively. All subnets (detection, pose, and segmentation) were trained together in the last stage with the pretrained model obtained in the previous stage and using the Adam optimizer. Bs and mo were set to 1 and 0.9, respectively, and lr was set to for the first 75 epochs and for the last 25 epochs. The total loss in each stage was a weighted sum of the corresponding losses [55].
III-B Image datasets
We conducted experiments on the artificial TORCS [28] and real-world CULane [56] and LLAMAS [57] datasets. The summary statistics of the datasets are presented in Table IV. The customized TORCS dataset has joint labels for all tasks, whereas the original CULane/LLAMAS dataset only contained lane line labels. Thus, we annotated each CULane and LLAMAS image with traffic object bounding boxes to mimic the TORCS dataset. Correspondingly, the TORCS, CULane, and LLAMAS datasets had approximately 30 K, 80 K, and 29 K labeled traffic objects, respectively. To determine anchor boxes for the detection task, the -means algorithm [58] was applied to partition the ground truth boxes. The CULane and LLAMAS datasets lack ego vehicle angle labels; therefore, these datasets could only be used for evaluations in segmentation and detection tasks. The ratio of the number of images used in the training phase to that used in the test phase was approximately 10 for all datasets, as in our previous works [28, 29]. Recall/average precision (AP; IoU was set to 0.5), recall/F1 score, and accuracy/mean absolute error (MAE) were used to evaluate model performance in detection, segmentation, and pose tasks, respectively.
| Network | Dataset | Task config. | Det | Seg | Pose | |||
|---|---|---|---|---|---|---|---|---|
| Recall | AP (%) | Recall | F1 score | Heading | Road type | |||
| MAE (rad) | accuracy (%) | |||||||
| MTUNet2 | CULane | Det + Seg | 0.858 | 65.32 | 0.694 | 0.688 | - | - |
| MTUNet1 | 0.831 | 58.67 | 0.658 | 0.595 | - | - | ||
| MTMResUNet | 0.852 | 54.28 | 0.559 | 0.568 | - | - | ||
| MTUNet2 | LLAMAS | Det + Seg | 0.942 | 64.42 | 0.935 | 0.827 | - | - |
| MTUNet1 | 0.946 | 59.96 | 0.936 | 0.831 | - | - | ||
| MTMResUNet | 0.950 | 57.40 | 0.736 | 0.748 | - | - | ||
| MTUNet2 | TORCS | Pose | - | - | - | - | 0.004 | 90.42 |
| MTUNet1 | - | - | - | - | 0.005 | 90.48 | ||
| MTMResUNet | - | - | - | - | 0.006 | 83.77 | ||
| MTUNet2 | Det + Seg | 0.976 | 71.51 | 0.905 | 0.889 | - | - | |
| MTUNet1 | 0.974 | 66.14 | 0.904 | 0.894 | - | - | ||
| MTMResUNet | 0.968 | 66.12 | 0.833 | 0.869 | - | - | ||
| MTUNet2 | Det + Seg + Pose | 0.952 | 65.83 | 0.922 | 0.883 | 0.005 | 87.08 | |
| MTUNet1 | 0.956 | 59.25 | 0.901 | 0.882 | 0.004 | 94.30 | ||
| MTMResUNet | 0.959 | 51.88 | 0.830 | 0.855 | 0.007 | 80.46 | ||
III-C Autonomous driving simulation
The open-source driving environment TORCS provides sophisticated physics and graphics engines; it is therefore ideal for not only visual processing but also vehicle dynamics research [59]. The ego vehicle controlled by our self-driving framework was driven autonomously on unseen TORCS roads [e.g., Tracks A and B in Fig. 4] to validate the effectiveness of our approach. All experiments, including both MTUNet training and testing and driving simulations, were conducted on a PC equipped with an INTEL i9-9900K CPU, 64 GB of RAM, and an NVIDIA RTX 2080 Ti GPU with 4352 CUDA cores and 11 GB of GDDR memory. The control frequency for the ego vehicle in TORCS was approximately 150 Hz on this computer.
| Network | Task config. | Params | MACs | FPS |
|---|---|---|---|---|
| MTUNet | Pose | 19.37 M | 13.93 G | 74.02 |
| MTUNet | 4.98 M | 3.51 G | 122.72 | |
| MTMResUNet | 5.37 M | 2.70 G | 99.08 | |
| MTUNet | Det + Seg | 68.62 M | 47.36 G | 24.44 |
| MTUNet | 21.70 M | 12.89 G | 43.58 | |
| MTMResUNet | 21.97 M | 15.98 G | 27.79 | |
| MTUNet | Det + Seg + Pose | 83.31 M | 50.55 G | 23.28 |
| MTUNet | 25.50 M | 13.69 G | 40.77 | |
| MTMResUNet | 26.56 M | 16.95 G | 27.30 |
| Lateral | Longitudinal | |
| CILQR-/SQP-based | CILQR/SQP | |
| Dynamic model | Eq. (19) | Eq. (25) |
| Sampling time () | 0.05 s | 0.1 s |
| Pred. horizon () | 30 | 30 |
| Ref. dist. () | - | 11 m |
| Weighting matrixes | = | = |
| Maneuver | Track | Speed (km/h) | VPC-CILQR | CILQR | VPC-SQP | SQP | ||||
| Lane-keeping | (rad) | (m) | (rad) | (m) | (rad) | (m) | (rad) | (m) | ||
| A | 76 | 0.0086 | 0.0980 | 0.0083 | 0.1058 | 0.0122 | 0.1071 | 0.0118 | 0.1187 | |
| A | 80 | 0.0099 | 0.1091 | 0.0098 | 0.1097 | - | - | - | - | |
| B | 50 | 0.0079 | 0.0748 | 0.0074 | 0.0775 | 0.0099 | 0.1286 | 0.0121 | 0.1470 | |
| B | 60 | 0.0078 | 0.0779 | 0.0079 | 0.0783 | 0.0099 | 0.1083 | 0.0112 | 0.1147 | |
| Car-following | (m/s) | (m) | (m/s) | (m) | (m/s) | (m) | (m/s) | (m) | ||
| Ba | - | - | - | 0.1971 | 0.4201 | - | - | 0.2629 | 0.4930 | |
| Related trajectories | Figs. 6, 10 | Figs. 7, 11, 14 | Figs. 8, 12 | Figs. 9, 13, 14 | ||||||
| aComputation from 1150 to 1550 m | ||||||||||
| Task | VPC | CILQR | SQP |
|---|---|---|---|
| Lane-keeping | 15.56 ms | 0.58 ms | 9.70 ms |
| Car-following | - | 0.65 ms | 14.01 ms |
IV Results and discussions
Table V presents the performance results of the MTUNet models on the testing data for various tasks. Table VI lists the number of parameters, computational complexity, and inference speed of each scheme as a comparison of computational efficiency. As described in Section II, although the input size of the MTUNet models was reduced by the use of padded 3 3 Conv layers, model performance was not affected; MTUNet2/MTUNet1 achieved similar results to our previous model in the segmentation and pose tasks on the TORCS and LLAMAS datasets [28]. For complex CULane data, the MTUNet model performance performed worse than the SCNN [56], the original state-of-the-art method for this dataset; however, the SCNN had lower inference speed because of its higher computational complexity [10]. The MTUNet models are designed for real-time control of self-driving vehicles; the SCNN model is not. Of the three considered MTUNet variants, MTUNet2 and MTUNet1 outperformed MTMResUNet on all datasets if each model jointly performed the detection and segmentation tasks (first, second, and fourth row of Table V). This result differs from that of a previous study on a single-segmentation task for biomedical images [37]. Task gradient interference can reduce the performance of an MTDNN [62, 63]; in this case, the MTUNet2 and MTUNet1 models outperformed the complex MTMResUNet network because of their elegant architecture. When the pose task was included (last row of Table V), MTUNet2 and MTUNet1 also outperformed MTMResUNet on all evaluation metrics; the decreasing AP scores for the detection task are attributable to an increase in false positive (FP) detections. However, for all models, the inclusion of the pose task only decreased the recall scores for the detection task by approximately 0.02 (last two rows of Table V); nearly 95 of the ground truth boxes were still detected during when the models simultaneously performed all tasks. Following the method for efficiency analysis used in [64] (Sec. V. B. in [64]), this study computed the densities of the detection AP and road type accuracy scores using the data in the last row of Table V/VI. MTUNet1 had higher efficiency in terms of parameter utilization than did MTUNet2. MTUNet1 was 3.26 times smaller than MTUNet2 and achieved a 1.75 times faster inference speed (40.77 FPS); this speed is comparable to that of the YOLOP model [10]. These results indicate that MTUNet1 is the most efficient model for collaborating with controllers to achieve automated driving. The MTUNet1 model can also be run on a low-performance computer with only a few gigabytes of GDDR memory. For a computer with a GTX 1050 Max-Q GPU with 640 CUDA cores and 4 GB of GDDR memory, the MTUNet1 model achieved an inference speed of 14.69 FPS for multi-task prediction. Fig. 5 presents example MTUNet1 network outputs for both traffic objects and lane detection on all datasets.





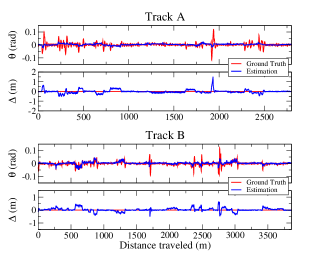


To objectively evaluate the dynamic performance of the autonomous driving algorithms, lane-keeping and car-following maneuvers were performed on the challenging tracks, Tracks A and B, as shown in Fig. 4. The SQP-based controllers were implemented using the ACADO toolkit [65] for comparison with the CILQR-based controllers. All settings for these algorithms were the same as summarized in Table VII. For the lateral control experiments, autonomous vehicles were designed to drive at various cruise speeds on Tracks A and B. The and results for the VPC-CILQR, CILQR, VPC-SQP, and SQP algorithms are presented in Figs. 6–13. The results of the CILQR and SQP controllers for the longitudinal control experiments are presented in Fig. 14. The MAEs for , , , and in Figs. 6–14 are listed in Table VIII. Table IX presents the average time to arrive at a solution for the VPC, CILQR, and SQP algorithms. The inference time was shorter for VPC than MTUNet1 (24.52 ms). Moreover, the CILQR had a computation speed that was faster than the ego vehicle control period (6.66 ms); the SQP solvers were slower. Specifically, the computation time per cycle for the lane-keeping and car-following tasks, respectively, for the SQP solvers were 16.7 and 21.5 times longer than those of the CILQR solvers. A discussion of the results for all the tested controllers are presented as follows.

In Figs. 6–9, all methods, including the MTUNet1 model, could effectively guide the ego car to drive along the lane center to complete one lap at cruise speeds of 76 and 50 km/h on Tracks A and B, respectively. The discrepancy in the between the MTUNet1 estimation and the ground truth trajectory was attributable to curvy or shadowy road segments, which may induce vehicle jittering [31]. Nevertheless, the values estimated from lane line segmentation were more robust in difficult scenarios than those obtained with the end-to-end method [61]. Therefore, these values can be used by controllers to effectively correct errors and return the ego car to the road’s center. The maximum deviations from the ideal zero values on Track A (g-track-3 in [31]) were smaller when the ego car was controlled by the VPC-CILQR controller (shown in Fig. 6) than when it was controlled by the CILQR [21] (Fig. 7) or MTL-RL [31] algorithms. Note that the vehicle speed in the MTL-RL control framework on Track A for that study was 75 km/h, which is slower than that in this study. This finding indicates that for curvy roads, the VPC-CILQR algorithm better minimized than did the other investigated algorithms. Due to the lower computation efficiency of the standard SQP solver [21], the SQP-based controllers were less effective for maintaining the ego vehicle’s stability than the CILQR-based controllers on the curviest sections of Tracks A and B (Figs. 8 and 9). Moreover, the VPC-SQP algorithm outperformed the SQP algorithm alone, further demonstrating the effectiveness of the VPC algorithm. In terms of MAE, the VPC-CILQR controller outperformed the other methods in terms of -MAE on both tracks (data for 76 and 50 km/h in Table VIII). However, -MAE was 0.0003 and 0.0005 rad higher on Tracks A and B, respectively, for the VPC-CILQR controller than the CILQR controller. This may have been because the optimality of CILQR solution is losing if the external VPC algorithm is applied to it. This problem could be solved by applying standard MPC methods with more general lane-keeping dynamics, such as the lateral control model presented in [52], which uses road curvature to describe vehicle states. This nonlinear MPC design is computationally expensive and may not meet the requirements for real-time autonomous driving.
In Figs. 10–13, the ego car was guided to drive along the central lane by the MTUNet1 model at higher cruise speeds (80 and 60 km/h on Tracks A and B, respectively) than those in Figs. 6–9. For ego vehicles with the VPC-CILQR and CILQR controllers (Figs. 10 and 11), the maximum deviations were approximately half of the lane width (2 m). In particular, the ego cars controlled by the SQP-based algorithms unintentionally left the ego-lane at the curviest section of Track A (Figs. 12 and 13). This was attributed to the slower reaction times of SQP-based algorithms (9.70 ms) than of CILQR-based algorithms (0.58 ms). Therefore, higher controller latency may not only result in ego car instability but also unsafe driving, particularly when the vehicle enters a curvy road at high speed.
The car-following maneuver in Fig. 14 was performed on a section of Track B. The ego vehicle was initially cruising at 76 km/h and approached a slower preceding car with speed in the range of 63 to 64 km/h. For all ego vehicles with the CILQR or SQP controllers, the vehicle speed was regulated, the preceding vehicle was tracked, and the controller maintained a safe distance between the vehicles. However, the uncertainty in the optimal solution led to differences between the reference and response trajectories [18]. For the longitudinal CILQR and SQP controllers, respectively, -MAE was 0.1971 and 0.2629 m/s, and -MAE was 0.4201 and 0.4930 m (second row of Table VIII). Hence, CILQR again outperformed SQP in this experiment. A supplementary video featuring the lane-keeping and car-following simulations can be found at https://youtu.be/Un-IJtCw83Q.
V Conclusion
In this study, a vision-based self-driving system that uses a monocular camera and radars to collect sensing data is proposed; the system comprises an MTUNet network for environment perception and VPC and CILQR modules for motion planning. The proposed MTUNet model is an improvement on our previous model [28]; we have added a YOLOv4 detector and increased the network’s efficiency by reducing the network input size for use with TORCS [28], CULane [56], and LLAMAS [57] data. The most efficient MTUNet model, namely MTUNet1, achieved an inference speed of 40.77 FPS for simultaneous lane line segmentation, ego vehicle pose estimation, and traffic object detection tasks. For vehicular automation, a lateral VPC-CILQR controller was designed that can plan vehicle motion based on the ego vehicle’s heading, lateral offset, and road curvature as determined by MTUNet1 and postprocessing methods. The longitudinal CILQR controller is activated when a slower preceding car is detected. The optimal jerk is then applied to regulate the ego vehicle’s speed to prevent a collision. The MTUNet1 and VPC-CILQR controller can collaborate for ego vehicle operation on challenging tracks in TORCS; this algorithm outperforms methods based on the CILQR [21] or MTL-RL [31] algorithms for the same path-tracking task on the same large-curvature roads. Moreover, the self-driving vehicle with long-latency SQP-based controllers tended to leave the lane on some curvy routes. By contrast, the short-latency CILQR-based controllers could drive stably and safely in the same scenarios. In conclusion, the experiments demonstrated the applicability and feasibility of the proposed system, which comprises perception, planning, and control algorithms. It is suitable for real-time autonomous vehicle control and does not require HD maps. A future study can apply the proposed autonomous driving system to a real vehicle operating on actual roads.
References
- [1] S. Grigorescu, B. Trasnea, T. Cocias, and G. Macesanu, “A survey of deep learning techniques for autonomous driving,” J. Field Robot, vol. 37, pp. 362-386, 2020.
- [2] E. Yurtsever, J. Lambert, A. Carballo and K. Takeda, “A Survey of Autonomous Driving: Common Practices and Emerging Technologies,” IEEE Access, vol. 8, pp. 58443-58469, 2020.
- [3] A. Tampuu, T. Matiisen, M. Semikin, D. Fishman and N. Muhammad, “A Survey of End-to-End Driving: Architectures and Training Methods,” IEEE Trans. Neural Netw. Learn. Syst., vol. 33, no. 4, pp. 1364-1384, April 2022.
- [4] Y. Li and J. Ibanez-Guzman, “Lidar for Autonomous Driving: The Principles, Challenges, and Trends for Automotive Lidar and Perception Systems,” IEEE Signal Process. Mag., vol. 37, no. 4, pp. 50-61, July 2020.
- [5] “Active Driving Assistance Systems: Test Results and Design Recommendations,” Consumer Reports, Nov 2020.
- [6] M. Teichmann, M. Weber, M. Zöllner, R. Cipolla and R. Urtasun, “MultiNet: Real-time Joint Semantic Reasoning for Autonomous Driving,” in IEEE Intelligent Vehicles Symposium (IV), 2018, pp. 1013-1020.
- [7] F. Pizzati and F. García, “Enhanced free space detection in multiple lanes based on single CNN with scene identification,” in IEEE Intelligent Vehicles Symposium (IV), 2019, pp. 2536-2541.
- [8] Y. Qian, J. M. Dolan and M. Yang, “DLT-Net: Joint Detection of Drivable Areas, Lane Lines, and Traffic Objects,” IEEE Trans. Intell. Transp. Syst., vol. 21, no. 11, pp. 4670-4679, Nov. 2020.
- [9] C.-Y. Lai, B.-X. Wu, V. M. Shivanna and J.-I. Guo, “MTSAN: Multi-Task Semantic Attention Network for ADAS Applications,” IEEE Access, vol. 9, pp. 50700-50714, 2021.
- [10] D. Wu, M. Liao, W. Zhang, X. Wang, X. Bai, W. Cheng, W. Liu, “YOLOP: You Only Look Once for Panoptic Driving Perception,” Mach. Intell. Res., vol. 19, pp. 550–562, 2022.
- [11] “Artificial Intelligence & Autopilot,” www.tesla.com/AI. https://www.tesla.com/AI (accessed May. 21, 2023).
- [12] B. Paden, M. Čáp, S. Z. Yong, D. Yershov and E. Frazzoli, “A Survey of Motion Planning and Control Techniques for Self-Driving Urban Vehicles,” IEEE Trans. Intell. Veh., vol. 1, no. 1, pp. 33-55, March 2016.
- [13] W. Lim, S. Lee, M. Sunwoo and K. Jo, “Hybrid Trajectory Planning for Autonomous Driving in On-Road Dynamic Scenarios,” IEEE Trans. Intell. Transp. Syst., vol. 22, no. 1, pp. 341-355, Jan. 2021.
- [14] B. Gutjahr, L. Gröll and M. Werling, “Lateral Vehicle Trajectory Optimization Using Constrained Linear Time-Varying MPC,” IEEE Trans. Intell. Transp. Syst., vol. 18, no. 6, pp. 1586-1595, June 2017.
- [15] V. Turri, A. Carvalho, H. E. Tseng, K. H. Johansson and F. Borrelli, “Linear model predictive control for lane keeping and obstacle avoidance on low curvature roads,” in 16th International IEEE Conference on Intelligent Transportation Systems (ITSC 2013), 2013, pp. 378-383.
- [16] A. Katriniok, J. P. Maschuw, F. Christen, L. Eckstein and D. Abel, “Optimal vehicle dynamics control for combined longitudinal and lateral autonomous vehicle guidance,” in European Control Conference (ECC), 2013, pp. 974-979.
- [17] S. E. Li, Z. Jia, K. Li and B. Cheng, “Fast Online Computation of a Model Predictive Controller and Its Application to Fuel Economy–Oriented Adaptive Cruise Control,” IEEE Trans. Intell. Transp. Syst., vol. 16, no. 3, pp. 1199-1209, June 2015.
- [18] W. Lim, S. Lee, J. Yang, M. Sunwoo, Y. Na and K. Jo, “Automatic Weight Determination in Model Predictive Control for Personalized Car-Following Control,” IEEE Access, vol. 10, pp. 19812-19824, 2022.
- [19] J. Mattingley and S. Boyd, “CVXGEN: A code generator for embedded convex optimization,” Optim. Eng., vol. 13, no. 1, pp. 1-27, 2012.
- [20] J. Chen, W. Zhan and M. Tomizuka, “Constrained iterative LQR for on-road autonomous driving motion planning,” in IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), 2017, pp. 1-7.
- [21] J. Chen, W. Zhan and M. Tomizuka, “Autonomous Driving Motion Planning With Constrained Iterative LQR,” IEEE Trans. Intell. Veh., vol. 4, no. 2, pp. 244-254, June 2019.
- [22] D. H. Jacobson and D. Q. Mayne, Differential Dynamic Programming. New York, USA: Elsevier, 1970.
- [23] J. Ma, Z. Cheng, X. Zhang, Z. Lin, F. L. Lewis and T. H. Lee, “Local Learning Enabled Iterative Linear Quadratic Regulator for Constrained Trajectory Planning,” IEEE Trans. Neural Netw. Learn. Syst., vol. 34, no. 9, pp. 5354-5365, Sept. 2023.
- [24] Y. Pan, Q. Lin, H. Shah and J. M. Dolan, “Safe Planning for Self-Driving Via Adaptive Constrained ILQR,” in IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2020, pp. 2377-2383.
- [25] M. Werling, J. Ziegler, S. Kammel, and S. Thrun, Optimal trajectory generation for dynamic street scenarios in a Frenét frame, in: IEEE International Conference on Robotics and Automation (ICRA), 2010, pp. 987-993.
- [26] K. Lee, S. Jeon, H. Kim and D. Kum, “Optimal Path Tracking Control of Autonomous Vehicle: Adaptive Full-State Linear Quadratic Gaussian (LQG) Control,” IEEE Access, vol. 7, pp. 109120-109133, 2019.
- [27] D.-H. Lee, K.-L. Chen, K.-H. Liou, C.-L. Liu, and J.-L. Liu, “Deep learning and control algorithms of direct perception for autonomous driving,” Appl. Intell. vol. 51, pp. 237-247, 2021.
- [28] D.-H. Lee, C.-L. Liu, “Multi-task UNet architecture for end-to-end autonomous driving”, 2021, arXiv:2112.08967. [Online]. Available: https://arxiv.org/abs/2112.08967
- [29] D.-H. Lee, C.-L. Liu, “End-to-end deep learning of lane detection and path prediction for real-time autonomous driving,” Signal, Image and Video Processing, vol. 17, pp. 199–205, 2023.
- [30] S. Thrun et al., “Stanley: The robot that won the DARPA grand challenge,” J. Field Robot, vol. 23, pp. 661-692, 2006.
- [31] D. Li, D. Zhao, Q. Zhang, and Y. Chen, “Reinforcement learning and deep learning based lateral control for autonomous driving,” IEEE Comput. Intell. Mag. vol. 14, no. 2, pp. 83-98, May 2019.
- [32] J. Liu, Z. Yang, Z. Huang, W. Li, S. Dang and H. Li, “Simulation Performance Evaluation of Pure Pursuit, Stanley, LQR, MPC Controller for Autonomous Vehicles,” in IEEE International Conference on Real-time Computing and Robotics (RCAR), 2021, pp. 1444-1449.
- [33] P. Lu, C. Cui, S. Xu, H. Peng and F. Wang, “SUPER: A Novel Lane Detection System,” IEEE Trans. Intell. Veh., vol. 6, no. 3, pp. 583-593, Sept. 2021.
- [34] C. -Y. Wang, A. Bochkovskiy and H. -Y. M. Liao, “Scaled-YOLOv4: Scaling Cross Stage Partial Network,” in IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2021, pp. 13024-13033.
- [35] J. -M. Georg, J. Feiler, S. Hoffmann and F. Diermeyer, ”Sensor and Actuator Latency during Teleoperation of Automated Vehicles,” in IEEE Intelligent Vehicles Symposium (IV), 2020, pp. 760-766.
- [36] J. Betz et al., “TUM autonomous motorsport: An autonomous racing software for the Indy Autonomous Challenge,” J. Field Robot, vol. 40, pp. 783–809, 2023.
- [37] N. Ibtehaz, M. S. Rahman, “MultiResUNet: Rethinking the U-Net architecture for multimodal biomedical image segmentation,” Neural Networks, vol. 121, pp. 74-87, 2020.
- [38] K. Simonyan, A. Zisserman, “Very Deep Convolutional Networks for Large-Scale Image Recognition,” in International Conference on Learning Representations (ICLR), 2015, pp. 1-14.
- [39] O. Ronneberger, P. Fischer, and T. Brox, “U-Net: Convolutional networks for biomedical image segmentation,” in International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI), Springer, 2015, pp. 234-241.
- [40] T. Bruls, W. Maddern, A. A. Morye, and P. Newman, “Mark yourself: Road marking segmentation via weakly-supervised annotations from multimodal data,” in IEEE International Conference on Robotics and Automation (ICRA), 2018, pp. 1863-1870.
- [41] S. Xie and Z. Tu, “Holistically-nested edge detection,” in IEEE International Conference on Computer Vision (ICCV), 2015, pp. 1395-1403.
- [42] Q. Zou, H. Jiang, Q. Dai, Y. Yue, L. Chen and Q. Wang, “Robust lane detection from continuous driving scenes using deep neural networks,” IEEE Trans. Veh. Technol, vol. 69, no. 1, pp. 41-54, Jan. 2020.
- [43] H. Cui, V. Radosavljevic, F.-C. Chou, T.-H. Lin, T. Nguyen, T.-K. Huang, J. Schneider, and N. Djuric, “Multimodal trajectory predictions for autonomous driving using deep convolutional networks,” in International Conference on Robotics and Automation (ICRA), 2019, pp. 2090-2096.
- [44] Z. Zheng, P. Wang, W. Liu, J. Li, R. Ye, and D. Ren. “Distance-IoU Loss: Faster and better learning for bounding box regression,” in Proceedings of the AAAI Conference on Artificial Intelligence (AAAI), 2020, vol. 34, no. 7, pp. 12993-13000.
- [45] J. I. Choi and Q. Tian, “Adversarial Attack and Defense of YOLO Detectors in Autonomous Driving Scenarios,” in IEEE Intelligent Vehicles Symposium (IV), 2022, pp. 1011-1017.
- [46] Y. Tassa, T. Erez and E. Todorov, “Synthesis and stabilization of complex behaviors through online trajectory optimization,” in IEEE/RSJ International Conference on Intelligent Robots and Systems, 2012, pp. 4906-4913.
- [47] Y. Tassa, N. Mansard and E. Todorov, “Control-limited differential dynamic programming,” in IEEE International Conference on Robotics and Automation (ICRA), 2014, pp. 1168-1175.
- [48] B. Plancher, Z. Manchester and S. Kuindersma, “Constrained unscented dynamic programming,” in IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2017, pp. 5674-5680.
- [49] C. V. Samak, T. V. Samak, and S. Kandhasamy, “Control Strategies for Autonomous Vehicles,” 2021, arXiv:2011.08729. [Online]. Available: https://arxiv.org/abs/2011.08729
- [50] W. Qiu, Q. Ting, Y. Shuyou, G. Hongyan, and C. Hong, “Autonomous vehicle longitudinal following control based on model predictive control,” in 34th Chinese Control Conference (CCC), IEEE, 2015, pp. 8126-8131.
- [51] X. Zhang and X. Zhu, “Autonomous path tracking control of intelligent electric vehicles based on lane detection and optimal preview method,” Expert Syst. Appl., vol. 121, pp. 38-48, 2019.
- [52] S. Xu, H. Peng, P. Lu, M. Zhu and Y. Tang, “Design and Experiments of Safeguard Protected Preview Lane Keeping Control for Autonomous Vehicles,” IEEE Access, vol. 8, pp. 29944-29953, 2020.
- [53] W. Liu, D. Anguelov, D. Erhan, C. Szegedy, S. Reed, C. Fu, and A. Berg, “SSD: Single Shot MultiBox Detector,” in European Conference on Computer Vision (ECCV), 2016, pp. 21-37.
- [54] J. Redmon and A. Farhadi, “YOLO9000: Better, Faster, Stronger,” in IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2017, pp. 6517-6525.
- [55] S. Lee et al., “VPGNet: Vanishing Point Guided Network for Lane and Road Marking Detection and Recognition,” in IEEE International Conference on Computer Vision (ICCV), 2017, pp. 1965-1973.
- [56] X. Pan, J. Shi, P. Luo, X. Wang, and X. Tang. “Spatial as deep: spatial CNN for traffic scene understanding,” in The Thirty-Second AAAI Conference on Artificial Intelligence (AAAI-18), 2018, no. 891, pp. 7276–7283.
- [57] K. Behrendt, R. Soussan, “Unsupervised Labeled Lane Markers Using Maps,” in IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), 2019, pp. 832-839.
- [58] J. MacQueen et al., “Some methods for classification and analysis of multivariate observations,” in Proceedings of the fifth Berkeley symposium on mathematical statistics and probability, 1967, pp. 281–297.
- [59] W. Bernhard et al., “TORCS: The open racing car simulator,” 2014. [Online]. Available: http://www.torcs.org
- [60] K. Fitzpatrick, “Horizontal Curve Design: An Exercise in Comfort and Appearance,” Transp. Res. Rec., vol. 1445 pp. 47-53, 1994.
- [61] C. Chen, A. Seff, A. Kornhauser, and J. Xiao, “DeepDriving: Learning affordance for direct perception in autonomous driving,” in Proceedings of the IEEE International Conference on Computer Vision, 2015, pp. 2722-2730.
- [62] T. Standley, A. R. Zamir, D. Chen, L. Guibas, J. Malik, and S. Savarese, “Which tasks should be learned together in multi-task learning?” in Proc. 37th Int. Conf. Mach. Learn. (ICML), vol. 119, Jul. 2020, pp. 9120-9132.
- [63] I. Kokkinos, “UberNet: Training a Universal Convolutional Neural Network for Low-, Mid-, and High-Level Vision Using Diverse Datasets and Limited Memory,” in IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2017, pp. 5454-5463.
- [64] S. Bianco, R. Cadene, L. Celona and P. Napoletano, “Benchmark Analysis of Representative Deep Neural Network Architectures,” IEEE Access, vol. 6, pp. 64270-64277, 2018.
- [65] B. Houska, H. J. Ferreau, and M. Diehl, “ACADO toolkit-An open source framework for automatic control and dynamic optimization,” Optim. Control Appl. Methods. vol. 32, no. 3, pp. 298-312, 2011.