Efficient optical beam displacement measurements using high-order Hermite-Gaussian modes

Introduction.—The measurement of an optical beam displacement is essential for many technological applications, such as atomic force microscopy [1, 2], optical tweezers, satellite alignment, and even for biological purposes as for single molecule tracking [3, 4, 5]. In atomic force microscopy, the measured deflection of a laser beam reflected on a cantilever indirectly probes the roughness of a surface since it is related to the amount of optical tilt. In the field of optical tweezers, the displacement of the equilibrium position of a particle held by the tweezers can be precisely determined by measuring the displacement of a laser beam [6], allowing, for example, force measurements between the particle and another one that is interacting with it with piconewton resolution [7]. In satellite alignments, an optical sensor coupled to a satellite allows its positioning relative to a laser beam emitted by another satellite, ensuring better mutual alignment [8].

The standard way to measure a small optical displacement is using a lens followed by a split detector positioned in the focal plane of the lens [1]. This simple arrangement is capable of reaching around 64% of the maximum theoretical precision [9], however it is only applicable to a beam in the fundamental Gaussian mode. One way to overcome this limitation is by using spatial multimode light in which one of the modes is in a squeezed detection mode [10, 11, 12]. A more efficient way to measure small displacements in a Gaussian mode of a laser beam is to measure the first order Hermite-Gaussian mode ($HG_{1,0}$) of the displaced beam, which can be achieved through homodyne detection in that particular mode [13, 14, 15]. In order to beat the standard quantum noise limit (SQL), it is necessary to prepare the probe beam with a $HG_{1,0}$ squeezed mode, where improvements of 2 dB were obtained for displacements measurements [15, 14]. Other techniques involving weak-value amplification were also developed [16, 17, 18], where the amplification effect comes at a cost of reduced statistics of the post-selected events, which may limit the overall precision [19, 20], although it can asymptotically reach the ultimate precision limit with a judicious post-selection [21, 22, 23]. However, all these schemes consider the probe state in a Gaussian mode.

A more general situation can be considered when the probe laser beam is prepared in a high-order Hermite-Gaussian ($HG_{m,0}$) mode. In this case, the minimum measurable displacement in the horizontal direction is reduced by a factor of $\sqrt{2m+1}$ [24]. For that, a homodyne measurement is required in which the local oscillator is in a superposition of $HG_{m-1,0}$ and $HG_{m+1,0}$. An improvement factor of $\sim 2$ was obtained in the signal-to-noise (SNR) when the probe was in the $HG_{1,0}$ mode and the local oscillator in a suboptimal mode $HG_{2,0}$ [24]. Recently, it was possible to prepare the optimal local oscillator for the probe modes up to $HG_{4,0}$, yielding an enhancement by $9.2$ dB in the SNR [25]. Moreover, a weak-value-based measurement can also be conceived which provides the same $\sqrt{2m+1}$ improvement factor [26]. It is worth pointing out that squeezed $HG_{m-1,0}$ / $HG_{m+1,0}$ modes of the probe state also bring metrological advantages to the measurement, however it is a challenging task to produce such quantum states, which are still very fragile to losses. Nonetheless, an enhancement of 10 dB and 8.6 dB were obtained in the SNR for tilt and displacement measurements, respectively, with a squeezed fourth-order Hermite-Gaussian beam [27], yielding an improvement factor of 3.2 and 2.7, respectively, in the measurement.

In this Letter, we present a novel technique to achieve the enhancements coming from the Hermite-Gaussian modes for optical beam displacements measurements, namely, the lateral displacement and angular displacement (tilt). The technique relies on an interferometric approach which is metrologically efficient for small displacements. It does not demand homodyne detection, and, therefore, does not require a local oscillator with a much stronger intensity and a high mode-matching with the probe beam, making it experimentally more practical.

Theory.—Consider a coherent state of a laser beam in a collimated Hermite-Gaussian ($HG_{m,0}$) spatial mode of order $m$ propagating in the $z$ direction:

$$u_{m}(\vec{r})=\sqrt{\frac{2\times 2^{-m}}{\pi w^{2}m!}}\,H_{m}\left(\frac{\sqrt{2}x}{w}\right)e^{-\frac{(x^{2}+y^{2})}{w^{2}}}e^{ikz}\,,$$

(1)

where $H_{m}(x)$ is the Hermite polynomial of order $m$, $w$ is the beam width and $k$ is the wavenumber. An angular displacement in the laser beam $g$ can be seen as an unitary operator $\exp(-ig\hat{x})$, where $\hat{x}$ is the transverse position operator and $g$ is the transverse momentum acquired by the beam. Under a small tilt ($gw\ll 1$), the beam can be expanded in the original $HG$ basis as

$$e^{-ig\hat{x}}u_{m}\approx u_{m}+\frac{igw}{2}\left(\sqrt{m+1}\,u_{m+1}+\sqrt{m}\,u_{m-1}\right)\\ ,$$

(2)

for $m\geq 1$ and neglecting second-order terms in the series expansion.

The lower bound for the uncertainty on the estimation of the parameter $g$, $\delta g$, is provided by the Cramér-Rao bound which establishes that $\delta g\geq 1/\sqrt{F(g)}$, where $F(g)$ is the Fisher information associated to the set of probabilities $P_{i}(g)$ of a given measurement, such that $F(g)=\sum_{i}1/P_{i}(g)\left[dP_{i}(g)/dg\right]^{2}$. The maximization of the Fisher information over all possible quantum measurements leads to the quantum Fisher information, and for a unitary operation, its value is given by $\mathcal{F}=4(\langle\hat{H}^{2}\rangle-\langle\hat{H}\rangle^{2})$, where $\hat{H}$ is the generator of the unitary transformation and the average is taken with respect to the initial quantum state [28]. Therefore, the quantum Fisher information for a coherent state with a mean photon number $N$ in the spatial mode of Eq.(1) is given by

$$\mathcal{F}=N\langle u_{m}|\hat{x}^{2}|u_{m}\rangle=N(2m+1)w^{2}\,,$$

(3)

from which we can evidence the metrological enhancement provided by the higher order modes once the uncertainty $\delta g$ is reduced by a $\sqrt{2m+1}$ factor.

By measuring the probabilities of detecting the photon state in the original mode $u_{m}$ ($P_{m}$) or in the populated modes $u_{m+1}$ and $u_{m-1}$ ($P^{\prime}_{m}$), we get the following probabilities from Eq.(2): $P_{m}=1-(2m+1)g^{2}w^{2}/4$ and $P^{\prime}_{m}=(2m+1)g^{2}w^{2}/4$. The Fisher information arising from this (binary) measurement with $N$ uncorrelated photons from a coherent state is given by

$$F(g)=N(2m+1)w^{2}+\mathcal{O}(g^{2}w^{2})\,.$$

(4)

Hence, the proposed measurement is efficient under the small tilt approximation.

For the lateral displacement $d$, the unitary operator is given by $\exp{(-id\hat{p})}$, where

$$\hat{p}=-i\frac{\partial}{\partial x}\,.$$

(5)

Thus, the quantum Fisher information for this process is given by

$$\mathcal{F}=N\langle u_{m}|\hat{p}^{2}|u_{m}\rangle=\frac{4N(2m+1)}{w^{2}}\,.$$

(6)

Analogously, expanding the displaced mode in the original mode basis, we have that

$$e^{-id\hat{p}}u_{m}\approx u_{m}+\frac{d}{w}\left(\sqrt{m+1}\,u_{m+1}-\sqrt{m}\,u_{m-1}\right)\,,$$

(7)

and the probabilities associated with measuring the photon in the original state ($u_{m}$) and the populated ones ($u_{m+1}$ and $u_{m-1}$) are given by $P_{m}=1-(2m+1)d^{2}/w^{2}$ and $P^{\prime}_{m}=(2m+1)d^{2}/w^{2}$. The corresponding Fisher information with $N$ uncorrelated photons is then

$$F(g)=\frac{4N(2m+1)}{w^{2}}+\mathcal{O}(d^{2}/w^{2})\,,$$

(8)

showing once again the efficiency in the proposed measurement protocol.

In order to realize such measurements, we used a Mach-Zehnder interferometer with an additional mirror in one arm. When the longitudinal phase difference in the two arms are equivalent to zero ($\varphi=0$), the odd spatial modes acquires a $\pi$ phase difference with respect to the even spatial modes due to the extra reflection in one arm, such that the bright port for the odd modes corresponds to the dark port for the even modes [29]. Therefore, the modes are separated by their parity, and hence, the mode intensities regarding the second and third terms in the expansions (2) and (7), which are proportional to the probabilities $P_{m}$ and $P^{\prime}_{m}$, are obtained by monitoring the output ports of the interferometer in the situation where $\varphi=0$. In fact, due to the conservation of energy, knowing the total power of the input beam, it is sufficient to monitor only one port of the interferometer, to measure the increase (decrease) in optical power in the dark (bright) port.

It is straightforward to show that for a horizontally polarized beam, the field in one output port on the interferometer is given by $E=E_{e}\sin\varphi/2+E_{o}\cos\varphi/2$, where $E_{e(o)}$ is the even (odd) spatial mode of the input beam, and $\varphi$ is the longitudinal phase difference in the interferometer. Since the optical power $I$ is proportional $|E|^{2}$, we have for the output power

$$I=\frac{I_{tot}}{2}\left(1+\nu_{m}\cos\varphi\right)\,,$$

(9)

where $I_{tot}$ is the total input optical power, and $\nu_{m}=|(|E_{o}|^{2}-|E_{e}|^{2})|/(|E_{o}|^{2}+|E_{e}|^{2})=(|I_{o}-I_{e}|)/(I_{o}+I_{e})$ is the visibility of the interferometer for the mode $m$, which reveals the contrast between the different parity modes. For a well-defined input parity mode ($u_{m}$) the visibility is equal to 1. However, for displaced beams with respect to the optical axis of the interferometer, the visibility will be different from 1, once they can be seen as the expressions (2) and (7), which present a small component in the opposite parity. Since the optical power in a given mode is proportional to the probabilities of individual photons, we can write that $\nu_{m}=1-2P^{\prime}_{m}$, such that

	$\displaystyle\nu_{m}^{(g)}$	$\displaystyle=$	$\displaystyle 1-(2m+1)g^{2}w^{2}/2$		(10)
	$\displaystyle\nu_{m}^{(d)}$	$\displaystyle=$	$\displaystyle 1-2(2m+1)d^{2}/w^{2}\,,$		(11)

for the angular and lateral displacement, respectively.

Applying an external modulation $\Omega$ in the displacement parameters such that $g\to g_{0}+g\sin(\Omega t)$ and $d\to d_{0}+d\sin(\Omega t)$, where $g_{0}$ and $d_{0}$ account for an unavoidable experimental offset, and substituting Eqs.(10) and (11) into (9) with their respective modulations, we end up with

	$\displaystyle I^{(d)}=\frac{I_{tot}}{2}\Big{[}\Gamma_{0}-4(2m+1)\frac{d_{0}d}{w^{2}}\cos\varphi\sin(\Omega t)$
	$\displaystyle+(2m+1)\frac{d^{2}}{w^{2}}\cos\varphi\cos(2\Omega t)\Big{]}\,,$		(12)
	$\displaystyle I^{(g)}=\frac{I_{tot}}{2}\Big{[}\Gamma^{\prime}_{0}-(2m+1)g_{0}gw^{2}\cos\varphi\sin(\Omega t)$
	$\displaystyle+(2m+1)\frac{g^{2}w^{2}}{4}\cos\varphi\cos(2\Omega t)\Big{]}.$		(13)

Therefore, we see that there are two spectral components ($\Omega$ and $2\Omega$) that carry information about the displacement, which will be maximized at $\varphi=\{0,\pi\}$, precisely when the interferometer acts as a parity selector. The frequency $2\Omega$ will be most relevant, since its magnitude depends only on the amplitude of the modulation, unlike the frequency component $\Omega$. Moreover, they exhibit the magnification factor of $(2m+1)$ that characterizes the metrological enhancement present in Eqs.(3) and (6).

Experiment.—The experimental setup is depicted in Fig.(1). A spatial light modulator (Hamamatsu LCOS-SLM X10468) is used to generate the spatial modes $u_{m}$ ¹¹1We utilized the repository [31] to generate the necessary holograms for producing the transverse modes from a $633$ nm He-Ne laser beam. The generated beam is collimated by the lenses $L_{1}$ and $L_{2}$ to a width of $w=590\,\mu m$. Two piezoelectric actuators are attached to the mirror mount just before the interferometer: the $PZT_{L}$ is attached to the back of the mirror to ensure a pure lateral displacement of the beam; the $PZT_{A}$ is screw actuator (Thorlabs Polaris-P20A) installed on a mirror mounting barrel to ensure an angular displacement. On one of the interferometer mirrors, we coupled a third piezoelectric actuator ($PZT$) which allows us to fine-tune the relative phase $\varphi$ of the interferometer. The output ports of the interferometer are monitored by a CCD camera, to visually check the interference quality, and a photo-detector (Thorlabs PDA100A2).

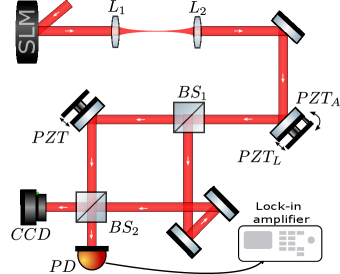
Initially, we align the interferometer with the incoming laser beam in order to ensure the highest possible visibility, and we consider this as our starting point. The visibility we obtained for the Gaussian ($u_{0}$) mode is $97\%$. Since high-order modes are more sensitive to misalignment, we eventually have to fine-tune the alignment in one of the interferometer mirrors when dealing with these modes. After the initial alignment procedures, we apply the displacement (lateral or angular) modulation with peak-to-peak drive voltage of $0.8$ V at a frequency $\Omega=650$ Hz, well bellow the mechanical resonance of the piezos. The measured signal is demodulated in a lock-in amplifier at frequency $2\Omega$ in order to measure the amplitude of the applied modulation. As seen from Eqs.(12) and (13) the demodulated signal is proportional to $\cos\varphi$, which implies that it is maximized at the constructive (destructive) output port, when $\varphi=0$ ($\varphi=\pi$). Therefore, we experimentally drive the interferometer piezoactuator (PZT) in order to maximize the demodulated signal for each incoming transverse mode $u_{m}$. Ideally, the interferometer would be phase-locked at this position, but we have verified that the phase is quite stable during the measurements for each transverse mode.

The experimental results for the angular displacement is depicted in Fig.(2). It shows the amplitude of the demodulated signal at frequency $2\Omega$ as a function of the input spatial mode for a given modulation amplitude $g$. The gain in the lock-in amplifier was set to $80$ dB. In order to capture the dependency solely with the mode order $m$, we fixed the optical power to $P=2\,\mu W$, except for modes $m=\{16,17,18,19,20\}$, which were taken at $P=1.5\,\mu W$, in order to avoid $1\,V$ saturation signal at the lock-in amplifier. However, we carefully rescaled their values owing to its proportionality to the input optical power.

We note from Eq.(13), that the amplitude at frequency $2\Omega$ is linearly proportional to the mode order $m$, as $V_{2\Omega}=V_{0}(2m+1)$, where $V_{0}$ is the signal value for the Gaussian mode. Thus, to check the dataset trend, we performed a linear fit with $V_{0}$ as the free parameter. The obtained value $32.35$ mV agrees with the experimental value $(33\pm 2)$ mV , where the error was taken from the random fluctuations over repeated measurements.

This result shows the magnification coming from the Hermite-Gauss mode order $m$, which amplifies the signal but not the noise. The overall effect is the increase in the signal-to-noise (SNR), which allows for detection of smaller tilt values. Regarding Eq.(13), we see the estimated value of $g$ is inversely proportional to $\sqrt{2m+1}$, which attest the metrological gain deriving from the quantum Fisher information (3). In fact, our setup was able to achieve a magnification factor of $41$ ($m=20$) in the SNR, which accounts for a improvement factor of $6.4$ in the estimability of the tilt. This result would correspond to a $16$ dB squeezed light approach in the $HG_{1,0}$ mode, a value not reached so far, to the best of our knowledge.

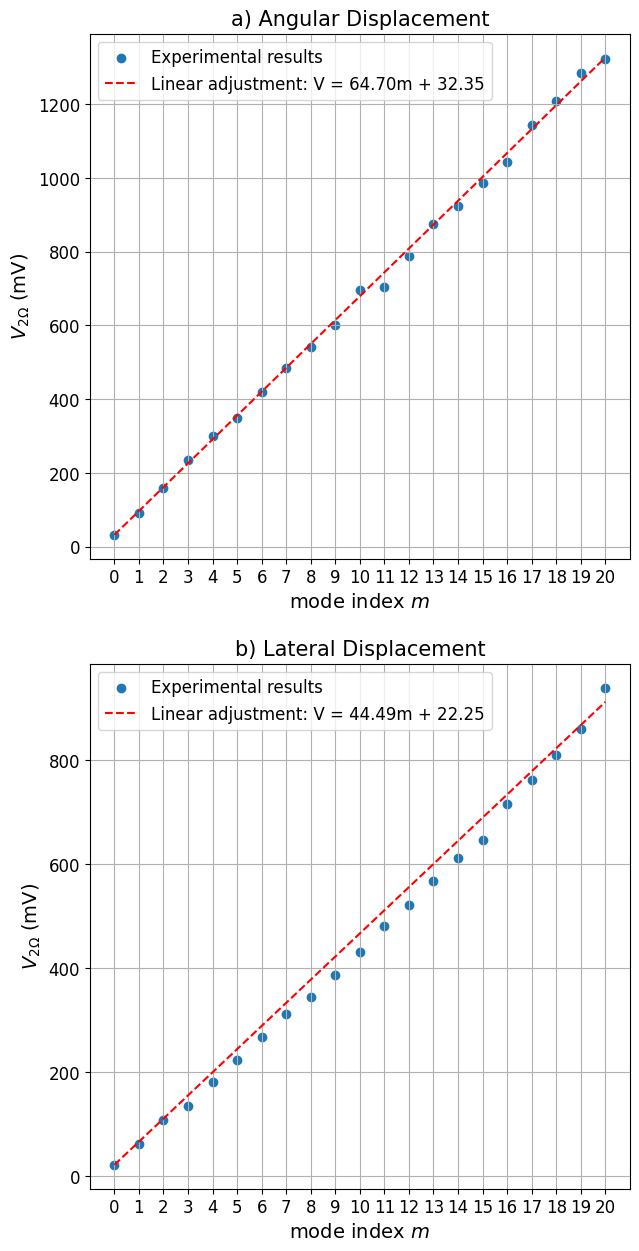
The results concerning the lateral displacement are shown in Fig.(2). The same analysis was realized for the data set as in the angular displacement. The input power was slightly lower for modes $m=\{15,16,17,18,19,20\}$, due to the low SLM efficiency for such high-order modes, but proper rescale was taken, as in the previous case. The fitting result for the $V_{0}$ parameter was $22.25$ mV, which matches with the experimental value $(23\pm 2)$ mV, showing good agreement with the theory.

Conclusion.—We have described an interferometric technique to measure lateral and angular displacements of an optical beam, which has relevant technological applications, as atomic force microscopy, for instance. The technique relies on the enhanced metrological performance provided by the Hermite-Gaussian modes. We were able to improve the SNR by a factor of $41$ compared to the Gaussian mode in both displacements. One major limitation is the production of such high-order modes, which tends to lose efficiency as $m$ increases; moreover, since the mode width increases with the order, bigger optics are required, which imposes limitations on our small setup. On the other hand, there is no need for a mode-matched local oscillator with a higher intensity or a multimode squeezed state of light, which, to our point of view, makes the technique more practical.

Acknowledgements.—The authors would like to acknowledge the financial support from the Brazilian agencies: Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES), Fundação Carlos Chagas Filho de Amparo à Pesquisa do Estado do Rio de Janeiro (FAPERJ) and Instituto Nacional de Ciência e Tecnologia de Informação Quântica (INCT-IQ 465469/2014-0). A. L. S. S. J. acknowledges financial support from Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP).