Efficient generation of multiqubit entanglement states using rapid adiabatic passage

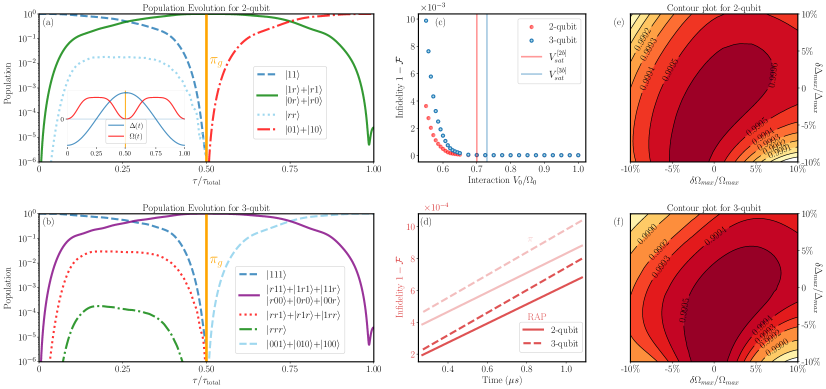
To generate a two-qubit Bell state, we start with the two atoms in state $|11\rangle$ with strong Rydberg-Rydberg interaction strength $V_{0}$ within the blockade regime. We adopt the profiles in Eq. (II) for the RAP pulse, with optimized parameters $\Omega_{\text{max}}=0.17\Omega_{0}$ and $\Delta_{\text{max}}=0.24\Omega_{0}$ to achieve the optimal population transfer. The first RAP results in a transfer from the $|11\rangle$ state to the $\frac{1}{\sqrt{2}}(|1r\rangle+|r1\rangle)$ state due to the Rydberg blockade. Subsequently, there are two approaches to achieve a two-qubit Bell state encoded in ground states $|0\rangle$ and $|1\rangle$: (i) Apply a fast $\pi_{g}$ pulse between $|0\rangle$ and $|1\rangle$, and then followed by another RAP sweep, to generate the Bell state $\frac{1}{\sqrt{2}}(|10\rangle+|01\rangle)$ [31]. The overall population evolution of the states can be observed in Fig. 2(a). It is evident that the state transfer is almost perfect, indicating that the desired state is fully transferred during the RAP process. (ii) Alternatively, adjust the laser to couple states $|0\rangle$ with $|r\rangle$, while decoupling $|1\rangle$ and $|r\rangle$, and then perform an RAP sweep to achieve the transition $\frac{1}{\sqrt{2}}(|1r\rangle+|r1\rangle)$ $\to$ $\frac{1}{\sqrt{2}}(|10\rangle+|01\rangle)$ [29]. If the two ground states are taken from hyperfine levels with small energy splitting, specific configurations of laser polarization are needed, or one can encode the qubit in fine-structure levels [63, 64]. Both approaches can achieve the Bell state $\frac{1}{\sqrt{2}}(|10\rangle+|01\rangle)$ using double RAP pulses. Assuming the time required for the $\pi_{g}$ pulse and laser frequency changes are negligible, the achieved Bell state fidelity of both approaches remains almost the same.

Now we extend to three qubits. To achieve optimal single Rydberg excitation symmetry within the blockade regime, three atoms are placed at the vertices of an equilateral triangle [65, 62]. The pulse sequence for three qubits is the same as in the two-qubit case, using identical parameters and involving two RAP pulses with a $\pi_{g}$ pulse sandwiched in between. The state evolves starting from $|111\rangle$ as follows: A single RAP sweep realizes a state transition to $\frac{1}{\sqrt{3}}(|11r\rangle+|1r1\rangle+|r11\rangle)$. This is followed by a fast $\pi_{g}$ pulse between the ground states $|0\rangle$ and $|1\rangle$. Another RAP pulse is then performed, eventually preparing the $W$ state $\frac{1}{\sqrt{3}}(|001\rangle+|010\rangle+|100\rangle)$. The state evolution process of three qubits is shown in Fig. 2(b). It can be observed that the single-excitation property is well maintained, and the double-excitation component remains small due to the Rydberg blockade. The proposed scheme is adaptable to more qubits. Intuitively, a three-dimensional atomic arrangement might be essential to ensure single excitation across multiple atoms. For instance, with four qubits, a three-dimensional equilateral pyramid would yield optimal single-excitation performance. However, arranging atoms in three dimensions is more challenging than in two dimensions in practical experiments [21, 66, 67].

To incorporate dissipative effects, we assess fidelity in a system of neutral Cs atoms utilizing $|r\rangle=|107P_{3/2};m_{J}=3/2\rangle$ as the Rydberg state [25], with dissipation channels $\hat{L}_{1}=\sqrt{\gamma_{r}/16}|0\rangle\langle r|$, $\hat{L}_{2}=\sqrt{\gamma_{r}/16}|1\rangle\langle r|$, and $\hat{L}_{3}=\sqrt{7\gamma_{r}/8}|r\rangle\langle r|$ in Eq. (4). The total dissipation rate is $\gamma_{r}=1/(540\,\mu s)$  [25]. In Fig. 2(c), we find that increasing the interaction strength does not notably improve fidelity, signifying the onset of saturation interaction, henceforth referred to as $V_{\rm sat}$, as demonstrated by vertical solid lines. We then optimize the parameters under realistic $\Omega_{0}$, including the maximal Rabi frequency $\Omega_{\text{max}}$, maximal detuning $\Delta_{\text{max}}$, and also the saturation interaction strength $V_{\rm sat}$. In Fig. 2(c), we determined that to achieve optimal fidelity, interaction strengths of $V_{0}\geq V^{\rm[2b]}_{\rm sat}\simeq 0.70\Omega_{0}$ for the 2-qubit system, and $V_{0}\geq V^{\rm[3b]}_{\rm sat}\simeq 0.73\Omega_{0}$ for the 3-qubit setup are adequate, without considering dissipative effects.

One can use also resonant $\pi$-pulse between the $|1\rangle$ and $|r\rangle$ states to achieve coherent population inversion, similar to the aforementioned RAP pulses. However, the Rabi frequency will differ for different numbers of qubits [30, 62], and population in the Rydberg states will adversely affect the fidelity due to dissipative effects. We have compared the fidelity of our RAP scheme (light solid red line) with that of the $\pi$-pulse scheme (deep red solid line) over different total times, as shown in Fig. 2(d). It is evident that the fidelity of the RAP scheme consistently outperforms the $\pi$-pulse scheme for transitions between $|1\rangle$ and $|r\rangle$ scheme. With increasing total evolution time $\tau_{\rm tot}$, the fidelity decreases due to spontaneous emission and dephasing of the Rydberg state, but still maintains over 0.9993 within 1 $\mu$s.

We analyze the robustness of our present scheme using $\Omega_{0}/(2\pi)=100$ MHz for Cs atoms, considering Rabi pulse strength and laser detuning fluctuations within $\pm 10\%$. As depicted in Fig. 2(e) for 2-qubit case and Fig. 2(f) for 3-qubit case, despite such significant fluctuations, the W-state fidelity remains above 0.999 for both cases. This demonstrates that our proposed scheme is highly robust against parameter variations, which is one of the advantages of RAP. Regarding the impact of Doppler frequency shifts, we categorize them as fluctuations in detuning frequency [25, 27]. For Cs atoms at a temperature of 10 $\mu$K, the detuning fluctuation is only about $\pm 0.3\%$ [25], indicating that the impact of Doppler shifts on our scheme is minute.

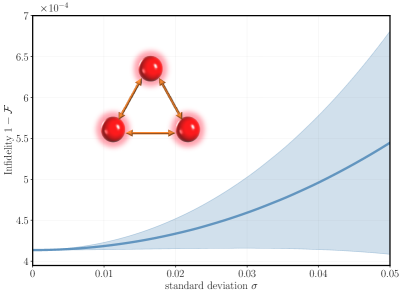
Furthermore, we evaluate the robustness of our scheme against atomic position fluctuations for the 3-qubit case. We start with an initial configuration where atoms occupy the vertices of an equilateral triangle [cf. inset of Fig. 3] with a unit side length, and an initial interaction of $(2\pi)\,200$ MHz between adjacent atoms at a distance of 8.14 $\mu$m [25]. These atoms are then subjected to position fluctuations, modeled as a two-dimensional uncorrelated Gaussian distribution, $\mathbf{X}_{i}\equiv(x_{i},y_{i})\sim N(0,0,\sigma^{2},\sigma^{2})$, where $i=1,2,3$. For each value of $\sigma$, we randomly sample the positions of the three vertices according to the Gaussian distribution and recalculate the interaction between adjacent atoms. To assess the impact of these position fluctuations, we calculated the average fidelity over 30 random sampled configurations for every $\sigma$. As depicted in Fig. 3, the light blue shading represents one standard deviation, and the solid line indicates the average fidelity. For the maximum considered $\sigma=0.05$, these fluctuations translate into an interatomic distance variation of $[-400,400]$ nm along two orthogonal coordinates within one standard deviation. Even with such significant atomic position fluctuations, the fidelity remains above 0.9993, underscoring the robustness and potential applicability of our scheme in realistic scenarios.

For the three-qubit case, we consider a two-dimensional triangular arrangement with symmetric blockade between any two atoms. However, for four qubits, three-dimensional configurations are experimentally challenging [66], so we focus on two-dimensional asymmetric distributions. Using the same RAP parameters and setting $\Omega_{0}/(2\pi)=100$ MHz, we obtain similar fidelity for four qubits whether the atoms are arranged in a three-dimensional equilateral pyramid or a two-dimensional square, assuming sufficiently large interaction strength. This results in a fidelity of 0.9997, demonstrating the scheme’s tolerance to asymmetry and its potential for generating single-excitation entangled $W$-states in large-scale atomic arrays.

The entangling operation we discussed earlier rely on strong Rydberg interaction. Here, we propose generating Bell states between two atoms with weak interaction using an ancillary qubit. This involves placing three atoms in a straight line with equal spacing [68, 69], as shown in Fig. 4(c) (inset). The scheme requires strong interaction between adjacent atoms although nearly zero interaction between the end atoms, making it well-suited to the van der Waals interaction, which scales as the inverse sixth power of the atomic distance [70, 71]. This configuration allows us to achieve entanglement generation between distant atoms by strategically moving a single relay atom into position [72].

For realistic parameter analysis, we consider the Rydberg state $|r\rangle=|70S_{1/2};m_{J}=-1/2\rangle$ of ⁸⁷Rb atoms [30, 73, 32, 74]. Initially, three atoms are prepared in the state $|010\rangle$, with the middle atom initialized in the $|1\rangle$ state. The interaction between adjacent atoms is set to $V_{0}=0.96\Omega_{0}$, resulting in a weaker interaction of $V_{1}=V_{0}/2^{6}=0.015\Omega_{0}$ between atoms separated by a larger distance. We apply three global RAP pulses, as shown in Fig. 4(a), with a $\pi_{g}$ pulse inserted between each pair of RAP pulses and continuously changing frequency detuning. This setup ensures optimal conditions for entanglement generation, with a total scaled time of $\Omega\tau_{\rm tot}/(2\pi)=81$.

The state transformation proceeds as follows: First, $|010\rangle\xrightarrow[]{\text{RAP}}|0r0\rangle\stackrel{{\scriptstyle\pi_{g}}}{{\longrightarrow}}|1r1\rangle$. Then, the second RAP pulse symmetrically generates the state $\frac{1}{\sqrt{2}}(|11r\rangle+|r11\rangle)$, which transforms to $\frac{1}{\sqrt{2}}(|00r\rangle+|r00\rangle)$ after the second $\pi_{g}$ pulse. Finally, with the third RAP pulse, we obtain $\frac{1}{\sqrt{2}}(|001\rangle+|100\rangle)$. The middle atom can then be traced out, yielding the Bell state $\frac{1}{\sqrt{2}}(|01\rangle+|10\rangle)$ between the two initially weakly interacting qubits. The atomic population during the evolution is shown in Fig. 4(b). As depicted, the transition to the target state is nearly complete by the end of the process.

We first consider $\Omega_{0}=(2\pi)100$ MHz (corresponding to a total time of 0.81 $\mu$s) and a Rydberg state decay rate of $\gamma_{r}=1/(147\mu s)$ [75, 76]. Additionally, we introduce a dump level $|d\rangle$, which is designed to capture all decays from the Rydberg state. Under these conditions, the scheme achieves a fidelity of 0.993. To assess its robustness against atomic positional fluctuations, we examined their impact on fidelity. Starting with atoms separated by a unit distance and interacting with $V_{0}=(2\pi)\,96$ MHz, each atom underwent one-dimensional Gaussian fluctuations along the line with amplitude $\sigma$. For $\sigma=0.04$, this results in a positional variation of $[-230,230]$ nm within one standard deviation. We calculated the average fidelity and standard deviation over 30 random samples for each $\sigma$, shown in Fig. 4(c), where the light blue shadow represents one standard deviation and the solid line denotes the mean. We calculated the average fidelity and standard deviation over 30 random samples for each $\sigma$, as shown in Fig. 4(c). In these tests, the fidelity remains above 0.97, demonstrating the robustness of the scheme against positional fluctuations. We also assessed the robustness of this scheme to optimized parameter fluctuations, as illustrated in the contour plot in Fig. 4(d). Fluctuations of $\pm$5% in $\Delta_{\text{max}}$ and $\pm$2% in $\Omega_{\text{max}}$ were considered. The fidelity remains above 0.980 across most of the parameter space, with slight reductions observed at the edges of the plot. Note that in Ref. [32], the atom temperature of approximately $10\,\mu$K leads to fluctuating Doppler shifts in the addressing lasers of order $(2\pi)\,43$ kHz, as well as fluctuations in atomic position that result in variations in Rydberg interaction strengths, which is well below the 0.5% parameter variation considered here. Consequently, fidelity remains above 0.990 from Fig. 4(d). This analysis highlights the scheme’s greater resilience against variations in laser detuning compared to fluctuations in Rabi frequency. Despite these challenges, this scheme provides valuable insights into achieving entanglement among weakly coupled atoms.

Furthermore, we demonstrate generating four-qubit GHZ states by positioning four atoms at the vertices of a square [cf. inset of Fig. 5(c)] and utilizing van der Waals interactions to induce specific atomic excitations. The interaction between adjacent atoms is $V_{0}$, and for diagonal atoms, it is $V_{1}=V_{0}/\sqrt{2}^{6}$. Parameters are set to $V_{0}/\Delta_{\text{max}}=4.05$ and $V_{0}/\Omega_{\text{max}}=4.85$, which may need adjustment for varying interaction strengths. This ensures the adiabatic condition $V_{1}\ll\Delta_{\text{max}},\Omega_{\text{max}}\ll V_{0}$ holds across different interaction strengths [77]. It is worth noting that our linear relationship between parameters $\{\Omega_{\rm max},\Delta_{\rm max}\}$ and $V_{0}$ is a simple empirical rule and may not maximize fidelity. As a consequence, the Rydberg blockade leads to singly excited adjacent atoms, while weaker interactions result in doubly excited diagonal atoms, establishing symmetry conducive to GHZ state construction. For optimal fidelity, further optimization of $\Delta_{\text{max}}$ and $\Omega_{\text{max}}$ is necessary across different $V_{0}$ values. The global RAP pulse in Fig. 5(a) remains consistent with previous setups, with a $\pi_{g}$ pulse sanwithed by two RAP pulses. We choose $V_{0}=1.13\Omega_{0}$ as an example, the parameter chosen is depicted in Fig. 5(a). Initially, atoms are prepared in state $|1111\rangle$. The state transformation proceeds as follows:

where the specific double Rydberg excitation can be revealed in Fig. 5(b) during the full evolution process. The fidelity plot in Fig. 5(c) shows saturation interaction at $V_{0}=1.13\Omega_{0}$. Considering dissipation and taking $\Omega_{0}=(2\pi)\,100$ MHz, the fidelity achieved for $V_{0}=(2\pi)113$ MHz is approximately 0.9956. Figure 5(d) demonstrates the robustness against parameter fluctuations, further indicating suboptimal parameter choices for specific $V_{0}$. Additionally, a local qubit $\pi_{g}$ pulse can flip the state of every other site to prepare the canonical form of the GHZ state, $(|0000\rangle+|1111\rangle)/\sqrt{2}$, from $(|0101\rangle+|1010\rangle)/\sqrt{2}$ [32].

Expanding on our approach, which utilizes the relationship between atomic positions and interactions to achieve specific atomic excitations for entangled states, we foresee extending this method to larger atomic arrays. In larger setups, the spatial arrangement facilitates tailored atom excitations [72], thereby enabling the generation of high-fidelity and robust GHZ states. This approach aligns with methodologies described in Refs. [32, 71], indicating potential scalability of our scheme.