Efficient Diversity-Driven Ensemble for Deep Neural Networks
Abstract
The ensemble of deep neural networks has been shown, both theoretically and empirically, to improve generalization accuracy on the unseen test set. However, the high training cost hinders its efficiency since we need a sufficient number of base models and each one in the ensemble has to be separately trained. Lots of methods are proposed to tackle this problem, and most of them are based on the feature that a pre-trained network can transfer its knowledge to the next base model and then accelerate the training process. However, these methods suffer a severe problem that all of them transfer knowledge without selection and thus lead to low diversity. As the effect of ensemble learning is more pronounced if ensemble members are accurate and diverse, we propose a method named Efficient Diversity-Driven Ensemble (EDDE) to address both the diversity and the efficiency of an ensemble. To accelerate the training process, we propose a novel knowledge transfer method which can selectively transfer the previous generic knowledge. To enhance diversity, we first propose a new diversity measure, then use it to define a diversity-driven loss function for optimization. At last, we adopt a Boosting-based framework to combine the above operations, such a method can also further improve diversity. We evaluate EDDE on Computer Vision (CV) and Natural Language Processing (NLP) tasks. Compared with other well-known ensemble methods, EDDE can get highest ensemble accuracy with the lowest training cost, which means it is efficient in the ensemble of neural networks.
Index Terms:
deep neural networks, ensemble learning, knowledge transfer, diversity, efficientI Introduction
Deep Neural Network has aroused people’s concern and it has been widely used in many real applications [1, 2]. Unfortunately, a neural network may converge to different local minimums during the training process, and its generalization ability may be unstable accordingly [3]. Lots of methods have been proposed to tackle this problem, one famous approach is ensemble learning.
The ensemble of deep neural networks trained on the same dataset is proved theoretically and experimentally to improve the generalization accuracy in many practical applications[4, 5]. For example, motivated by the idea of Knowledge Distillation [6], the base models in Born-Again Networks(BANs) are trained from the supervision of the earlier fitted model [7]. By training with the objective of matching the full softmax distribution of the pre-trained model, BANs can get a rich source of training signal. As a result, additional gains can be achieved with an ensemble of multiple base models.
Like BANs, ensemble learning is usually designed to randomly initialize each base model. Accordingly, the neural network can converge to different local minimums and tend to make different predictions on the same sample, then the weak samples can benefit from the ensemble of these neural networks [8]. However, the training cost of the ensemble grows linearly with the number of the base models since each neural network added to the ensemble needs to be trained. Even on high-performance hardware, training a single deep neural network can take several days to complete. If each base model is trained from scratch, a large ensemble of neural networks will require significant training time and computational resources.
To reduce the training cost, many useful methods have been proposed in recent years[9, 11, 10]. A commonly used idea is to transfer the knowledge of the pre-trained model to next base model, and the most typical one is Snapshot Ensemble [12]. By periodically resetting the learning rate and decaying it with a cosine annealing [13], a neural network in Snapshot Ensemble can converge to different local minimums along its optimization path. Unlike Bagging [14], which trains each individual network independently, Snapshot Ensemble saves the model parameter before resetting the learning rate and treats each model replica as a base model. Therefore, it has the ability to get multiple base models with less training cost.
However, the neural network has many local minimums, and the base models in an ensemble may be trapped in the same or nearby local minimums. We call this phenomenon low diversity, which causes less accurate ensemble model. Specifically, this phenomenon is more likely to happen in Snapshot Ensemble. Initialized with the weights of the former base model, the current neural network in Snapshot Ensemble is unable to learn more specific knowledge if given limited training budget, thus it would make similar predictions to the former one and the diversity is reduced accordingly. The ensemble accuracy can be significantly improved if the base models have both high diversity and accuracy [15]. As a result, Snapshot Ensemble is not efficient to get high generalization accuracy due to its low diversity.
To enhance diversity, the goal is to get multiple base models whose predictions are negatively correlated. Negative Correlation Learning (NCL) [16] is proposed to achieve this goal, it negatively correlates the errors made by each base model explicitly so that the diversity can be enhanced. Based on this idea, AdaBoost.NC [17] uses an ambiguity term derived theoretically for classification ensemble to introduce diversity. Experiments show it can get both high diversity and generalization accuracy than the original AdaBoost.M2 [18] algorithm. However, AdaBoost.NC studies the ambiguity decomposition with the 0-1 error function, such diversity definition is flawed as it loses massive raw information of the softmax outputs. Besides, AdaBoost.NC trains each base model without using the prior knowledge. So, the base model in AdaBoost.NC cannot converge well in a limited time and thus this will lead to an ensemble with high bias.
To sum up, all the methods above have non-negligible drawbacks regarding the training cost or diversity, and there lacks an ensemble learning method which is able to train diverse and accurate neural networks with a limited training budget. Therefore, we study how to reduce the training cost and increase the diversity of an ensemble.
To accelerate convergence, we propose to adaptively transfer knowledge contained in one neural network to another neural network. It is well established that DNN generally learns generic features in its lower layers and task-specific features in its upper layers [19]. As shown in Snapshot Ensemble, it transfers both the generic and task-specific features, which results in low diversity. To avoid this situation, we propose a method to efficiently select the generic knowledge contained in the first several layers of a neural network. By transferring this previous generic knowledge, we can train each neural network significantly faster than approaches that train each model from scratch. More importantly, the total training time will grow much slower as we increase the ensemble size.
To guarantee diversity, we propose a diversity-driven loss function to optimize each base model. This loss function has a weighted average of two different objective functions. The first one is to learn the distribution from the training data, and the other is to negatively correlate the softmax outputs which also called soft target [6] of the former ensemble network. For the classification tasks using deep neural networks, our work is the first, to the best of our knowledge, to achieve the diversity explicitly by using a diversity-driven loss function.
Last, as Boosting is a diversity encouraging strategy, we use Boosting to construct the training pipeline for further improving the diversity. Our method is efficient in producing high diversity base models, thus we call it Efficient Diversity-Driven Ensemble(EDDE). To theoretically analyze the relationship between EDDE and other representative methods, we calculate their bias and variance within the same training budget. We run this experiment on the dataset CIFAR100 [20] using ResNet-32 [21], and the result is shown in Figure 1.

In theory, the ensemble accuracy can be significantly improved if the base models in the ensemble are accurate and diverse [22], which is equal to say the base models of a good ensemble should both have low bias and high variance. Seen from Figure 1, given the same and limited training budget, AdaBoost.NC can get the highest variance but also introduce the highest bias. On the contrary, Snapshot Ensemble is able to train a set of base models with low bias but it also faces a problem of low variance. As for BANs, it cannot get a high variance and low bias at the same time. Therefore, all these baselines face the bias-variance dilemma [23]. Our method EDDE outperforms them since it can rapidly produce a set of base models which has low bias and high variance. Given a limited training budget, we test EDDE in the CV and NLP scenarios, and the experiments show that it can get the state-of-art ensemble accuracy than other well-known methods.
The main contributions of EDDE can be summarized as follows:
-
•
We propose a knowledge transfer strategy which can accelerate the training process without reducing the diversity and we also propose a method to efficiently select the generic knowledge which we should transfer.
-
•
We propose a novel diversity measure and use it to explicitly define a diversity-driven loss function. Besides, such a measure can numerically compare the diversity among each ensemble method.
-
•
We propose a Boosting-based framework to combine the knowledge transfer and optimization process, and such training pipeline can further improve the diversity.
The remainder of this paper is organized as follows. We describe the related work in Section II. Section III introduces some preliminaries and notations. The learning algorithm is introduced in Section IV and Section V presents the experimental results. Finally, we conclude this paper in Section VI.
II Related work
II-A Ensemble learning
Ensemble learning is an art of combining the predictions of different machine learning models, and it has achieved state-of-the-art performance in many challenges such as the Netflix Prize and various Kaggle competitions [24]. From the algorithmic level, Bagging, Boosting and Stacking are very representative algorithms.
Bagging is an ensemble strategy which uses the bootstrap aggregation to train multiple models while reducing variance. As a popular bagging method, Majority Voting [25] counts the votes from all base learners and makes the prediction using the most voted label. The other method is Averaging [26], which averages the softmax outputs of base learners. By averaging six residual networks, He et al [21] won the first place in ILSVRC 2015. Similarly, Snapshot Ensemble and BANs adopts an average strategy in its prediction process.
Another popular ensemble method is Boosting. It trains multiple base models sequentially and re-weights the training samples which are harder to train so that the latter models focus more on the difficult examples [27]. The idea of boosting neural networks has been around for many years [28]. BoostCNN incorporates boosting weights into the deep learning architecture [29], and it can select the best network structure in each iteration. Besides, deep incremental boosting [11] uses transfer learning to accelerate the initial warm-up phase of training each Boosting round. To enhance diversity, AdaBoost.NC propose an ambiguity decomposition strategy to negatively correlate the error made by other models.
Unlike Bagging and Boosting, Stacking [14] combines the outputs of each base model via a meta-learner. Based on the same idea, deep super learner [30] circularly appends the outputs of base models to the training data and uses the super learner to combine their outputs. Cheng Ju [31] adopts super Learner from the convolution neural network perspective, in which a CNN network is used to combine each output of the base model.
Besides, according to the usage of the training data, current methods of training ensemble of the deep neural networks can be classified into two categories. The first one is to train each network architecture with the entire dataset [12, 32], and the other one is to train it with a different subset of replacements from the original dataset [29]. Usually, a deep neural network has a large parameter space and it can get low bias if trained with the entire dataset [32]. However, this may bring higher training cost. As a sub-sampling method, Bagging and Boosting can enhance diversity but result in higher bias of base models since we train them with less unique samples in each iteration.
As we know, base models in an ensemble contribute more if they are diverse, otherwise there may be no gain in the combining process. However, all these methods individually train each base model without correlation and thus they cannot introduce diversity in an explicit way. Since there is no feedback from the combination stage to the individual design stage, it is possible that some of the independently designed networks may not make any contribution to the whole ensemble model. Furthermore, some of them train each network from scratch, requiring a lot of time and training resource.
II-B Negative correlated learning
Current methods for designing neural network ensemble usually train individual neural networks independently. However, the base models are likely to be trapped in the same nearby local minimums and result in low diversity, especially if we transfer the knowledge of the pre-trained base model [12]. Both theoretical and experimental studies show that the ensemble generalization ability can be largely enhanced if the base models in the ensemble are negatively correlated [33].
Negative correlation learning(NCL) is proposed to achieve this goal, all the individual networks in the NCL are trained simultaneously through the correlation penalty terms in their loss functions, thus the diversity can be introduced in an explicit way.
Based on the NCL, cooperative ensemble learning system (CELS) [34] encourages the individual networks to learn different aspects of a given dataset cooperatively and simultaneously. Besides, learning via Correlation-Corrected Data(NCCD) [35] embeds penalty values to every training sample instead of the error function.
However, all of their penalty terms are unfit to implement in classification ensembles. The AdaBoost.NC is proposed to solve this problem, it defines the penalty term with the correct/incorrect decision and introduces the error correlation information into the weights of the training data.
Although this definition can be used for classification ensembles with NCL, such coarse-grained definition may lose lots of useful information the model has learned before. Besides, AdaBoost.NC only provides a diversity-aware heuristic to adjust the weight of training data but fails to formalize an objective function that takes diversity into consideration. Therefore, the diversity of base models in AdaBoost.NC can be inferior, which limits the ensemble performance.
Our method EDDE differs AdaBoost.NC in two aspects. First, we propose a new diversity-driven loss function to explicitly increase diversity, while AdaBoost.NC introduce diversity by adjusting the sample weights. Compared with our diversity-driven loss function, using the sample weights to enhance diversity is not direct and robust. Besides, EDDE captures more information as we negatively correlate the soft target of former ensemble model.
| Symbols | Definitions |
|---|---|
| Training set | |
| The feature of the -th training sample | |
| The label of the -th training sample | |
| The one hot encoding of the -th training label | |
| The class of the training sample | |
| The weights of training sample | |
| The size of the training set | |
| The number of training iterations | |
| Controls the strength of the diversity-driven loss | |
| Controls the proportion of knowledge transfer | |
| The -th base neural network | |
| The ensemble of base models | |
| The weight of the -th base model | |
| The -th value of ’s soft target on sample | |
| The -th base model’s label prediction on sample | |
| The -th base model’s soft target on sample | |
| The -th ensemble model’s soft target on sample | |
| The similarity between model and on sample | |
| The bias of model on sample |
III PRELIMINARIES
In this section, we begin by introducing some notations related to EDDE. Table I lists the symbols used in this paper.
The -th sample in training set consists of the feature denoted by and the label denoted by , the bold entity denotes the one-hot encoding of the -th training label and the number of classes is denoted by . Given with sample weights and sample size , we can train a base model .
We use a diversity-driven optimization to enhance diversity, and controls the strength of the diversity-driven loss. Given a sample , both the base model and the ensemble can make a prediction, thus we can accordingly get their softmax outputs as the soft-target and . Note that is the prediction label and the bold is a vector of probabilities representing the conditional distribution over object categories on sample . We set the -th value of as , and this means the probability that sample belongs to the class . Besides, we define as the similarity between model and on sample , and we also set as the the bias of model on sample .
To accelerate the convergence, we propose a knowledge transfer strategy, and controls the proportion of knowledge we should transfer from the former pre-trained neural network. After iterations, we can get base models. For the base model , we can get its weight , and then add it to the ensemble model .
IV Efficient diversity-driven Ensemble
In this section, we introduce our framework EDDE in detail. The overall framework is shown in Figure 2. First, we describe the full pipeline and make an overview of EDDE. Next, we introduce the adaptive knowledge transfer strategy for fast training. Last, we explain our new diversity measure, diversity-driven loss and the Boosting-based framework.
IV-A Overview
To enhance diversity, we explicitly propose a diversity measure and use a diversity-driven optimization method to train each base neural network. Besides, to accelerate the convergence, we propose a knowledge transfer strategy which can accelerate the training process without decreasing the diversity. At last, we combine all the operations above in a Boosting-based framework. Figure 2 shows the full pipeline of EDDE.
Seen from Figure 2, during the training process of base model , we transfer the generic knowledge of the earlier fitted model to accelerate the convergence. Besides, we adopt a diversity-driven optimization to negatively correlate the soft-target of the former ensemble model . After each iteration, we add the to the ensemble and get a new ensemble model . Note that the weights of training samples are updated in each iteration and we use a Boosting-based strategy to construct the full pipeline.
IV-B Adaptive knowledge transfer for fast training
As the size of the ensemble grows, the training time grows linearly with the size of the ensemble. Therefore, it’s desirable to find a method to accelerate the convergence of each base model.
A simple way to achieve this goal is to use Transfer Learning. Transferred with the previous knowledge, an additional network can be hatched from the former pre-trained neural network and trained significantly faster than trained from scratch. Practically, this allows us to train very large ensembles of deep neural networks in the time taken to train just a couple from scratch [38].

Transfer learning [39] is a strategy where a machine learning model developed for a task is reused as the starting point for another model on a second task. In transfer Learning, we first train a base network on a base dataset, and then we repurpose the learned features, or transfer them, to a second target network to be trained on a target dataset. We can naturally transfer the knowledge of previously trained neural network to train another neural network , and may converge more quickly as it lies in a region near a good local minimum [40].
Take the Snapshot Ensemble for an example, all the weights of the pre-trained neural network are transferred to the current base neural network . Indeed, we can rapidly get a converged model . However, the model may make similar predictions as because starts training at the local minimum proposed by . That’s why the diversity in Snapshot Ensemble is limited. Classically, transfer learning aims to transfer the information from one domain to another domain and it hasn’t taken the diversity between each base models into consideration.
To guarantee the diversity in an ensemble, it is unsuitable to transfer all the pre-trained knowledge without selection. Fortunately, DNN generally learns generic features (e.g., edge detectors or color blob detectors) in its lower layers and task-specific features (e.g., parts of specific objects) in its upper layers [7]. The features in the upper layers are (weighted) combinations of the features in the lower layers and they are directly responsible for making predictions. Besides, the generic features contained in the earlier several layers of a neural network should be suitable for both base and target tasks, instead of specific to the base task. Inspired by this discovery, we naturally come up with the idea of using these generic features to accelerate the training process of the next base model.

The full procedure of our knowledge transfer is shown in Figure 3. We transfer the parameters of the earlier several layers of the teacher model to student model . Besides, in order not to decrease the diversity, we randomly initialize ’s remaining high-level layers since they contain the specific knowledge of the given dataset.
Note that we fine-tune both the transferred wights of the low layers and the randomly initialized weights of the high layers in each iteration, which means the transferred knowledge will not be fixed during the retraining processes. That’s because the fixed transferred knowledge adds too strong constraints (i.e., most of the parameters are not allowed to be updated) to the optimization task, and a better local minimum is not likely to be obtained given such constraints. By fine-tuning all the weights, each individual base model has the ability to converge to some good and different local minimums in a short time.
Like Snapshot Ensemble, we accelerate the convergence of each base model by transferring the knowledge of the former pre-trained neural network. The main difference is that we just transfer the generic knowledge. The core problem we face is how to find such generic features, which is also equal to say how many layers of weights we should transfer from one pre-trained neural network to the other untrained one.
We propose an efficient and adaptive method to tackle this problem. In our proposed method EDDE, we denote the parameter to determine the proportion of parameters we should transfer. If it gets too much, the diversity may be reduced; if it is too small, we cannot maximize the training speed. Therefore, we aim to find a that leverages a trade-off between model diversity and training speed.

As shown in Figure 4, to better analyze this problem, we assume the training set is split into folds, and we leave the last fold as the test set. We train a neural network using the first -1 folds, and initialize the next network according to . Then, we train with the first -2 folds. Finally, we predict ’s accuracy on the (-1)-th fold and the -th fold. In the above case, the pre-trained network has seen the (-1)-th fold while the next base model hasn’t. Besides, generally gets a higher accuracy on the (-1)-th fold than the -th fold due to overfitting. Different choices of can lead to different accuracy results:
-
•
If is large, we transfer a large portion of weights of , yielding a similar to . Since has specific knowledge on the (-1)-th fold, the accuracy of on the (-1)-th fold is higher than that on the -th fold.
-
•
If is small, we transfer a small portion of weights of , and therefore can be more different. Accordingly, has more possibility to forget the specific knowledge learned by from the (-1)-th fold. Since has never seen both the (-1)-th fold and the -th fold, the accuracy on these two folds are similar.
Motivated by the above analysis, we find that we can choose a according to ’s performance on the dataset, which saw but did not. In practice, we can start from and gradually reduce it, until performs similarly on two datasets — an exclusive dataset owned by and a shared test dataset. With this strategy, we can achieve a good trade-off between model diversity and training speed.
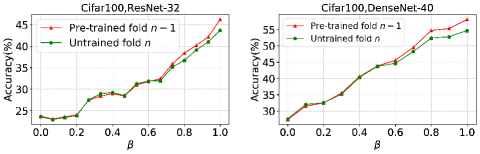
We also run an experiment to validate the above analysis. With different , we split the training set CIFAR-100 into six folds (). We firstly pre-train the model using the first 5 folds, then transfer the weights of to initialize our next base model . During the training process of , we calculate ’s mean accuracy of the first 5 epochs on the sixth fold and the fifth fold, the experimental result is shown in Figure 5. Seen from the experiments on ResNet-32 and DenseNet-40, as we gradually reduce to a suitable value, ’s accuracy on the fold may be similar to that on the untrained fold .
Remarkably, the pre-trained model can still be used in the ensemble process. Besides, the parameter only needs to be tuned with the first base model and we just fix this tuned value for the latter base models. In this way, we only need a few epochs to find how many parameters we need to transfer, which will not incur a large extra cost.
IV-C Diversity measure
Various diversity measures have been proposed [36] for the classifiers, and AdaBoost.NC is the first one to explore the ambiguity decomposition for classification ensembles. It names the penalty term as and defines it with the correct/incorrect decision. Suppose the practical output is 1 if is labeled correctly, and -1 otherwise. Given an ensemble model and the weight , we get the definition
| (1) |
It’s true that such a definition can be applied to a classification task, and can also be used in the negative correlated learning. However, it has severe drawbacks in two aspects. On the one hand, they ignore the original softmax outputs of each base model and use the concrete classification label, such coarse-grained definitions may lose lots of useful information the model has learned before. On the other hand, as the ensemble output is the hard target, we cannot get useful gradient information with such a definition. As a result, it is impossible to directly optimize a diversity-driven loss function using this definition. That’s also the reason why AdaBoost.NC enhance diversity just by changing the sample weights.
To sum up, it is desirable to propose a new diversity measure which can make full use of the softmax outputs of each network and can also be used in a diversity-driven optimization.
Therefore, we define a new diversity measure for two networks and . The diversity between these two base models is denoted as
| (2) |
Compared with the Eq. 1, our proposed diversity measure adopts the soft target, which contains more knowledge of the trained neural network. Besides, for each node in the softmax layer, we can get its gradient information with this definition. Such a feature is indispensable for our diversity-driven loss function.
Besides, we define the similarity between and as
| (3) |
The larger means model is more similar to model , thus their diversity becomes smaller accordingly. This definition will be used in our diversity-driven optimization latter.
As both the and are model’s softmax outputs, we have:
| (4) |

Last, to calculate the diversity of the ensemble network , we define
| (7) |
For numerically comparing the diversity of two ensemble model, we can use Eq. 7 to calculate their respectively.
IV-D Explicit diversity-driven loss for optimization
According to Knowledge Distillation, a simple student model can be trained with the objective of matching the full softmax distribution of the complex teacher model. As the soft targets can provide much more information per training case and get much less variance in the gradient between training cases, a student network can achieve better accuracy by virtue of knowledge transferred from the teacher model than it would if trained directly [7].
Motivated by the idea of Knowledge Distillation, EDDE also adopts the soft target in our loss function. However, the usage of the soft target is totally different in two aspects. First, we optimize the loss function with our self-defined diversity measure. More importantly, the student network in Knowledge Distillation matches the soft target of the teacher model, but EDDE aims to negatively correlate this soft-target since our goal is not to enhance accuracy but to increase the difference between each base model and the ensemble model. Note that the student model in EDDE has the same architecture as the teacher model, so the accuracy of base models can be guaranteed in EDDE.
Specially, we define the ensemble teacher model by a function where is the training sample, and is the learned weights of . Both the and are the vector of probabilities representing the conditional distribution over object categories given sample . One of our objectives is to find a new set of parameters for a student neural network such that
| (8) |
According to Eq. 8, the base model in each iteration is more likely to make different prediction to the former ensemble model .
Based on our diversity measure and the above objective, we define the penalty term as
| (9) |
Suppose we use the categorical cross-entropy as the loss function. We have two objectives when designing the objective function. The first objective is to minimize the error (Bias in Figure 6) of the base models, which is the cross entropy with the correct labels. The other is to maximize their difference (Variance in Figure 6). Based on this intuition, we define a weighted diversity-driven loss function on sample as
|
|
(10) |
The hyperparameter is used to adjust the strength of the second objective. Larger may introduce higher diversity, but the bias of the neural network may also be increased accordingly. As a result, this parameter needs to be carefully tuned in our experiments.
It is easy to get the gradient information with our diversity-driven loss function. For ’s output node , the partial derivative of with respect to the output is
|
|
(11) |
We use the standard back propagation (BP) algorithm [37] to optimize each network and its weights are updated with Eq. 11. To explain the optimization process in detail, we take the ensemble of three base models for an example. As shown in Figure 6, if we pre-train two base models and , we can combine them and get the ensemble model . Given the training data with sample weights , the pre-trained knowledge by , and two parameters and , we train the third model to negatively correlate the softmax outputs of , such procedure is correspond to the in line 7 of algorithm 1.
IV-E Boosting-based framework
To further enhance diversity, we use a Boosting-based framework to combine the diversity-driven optimization and the knowledge transfer strategy. As an art of combining the predictions of different machine learning models, Boosting is a very popular ensemble method and it has been widely used in many deep learning scenes [29]. It increases the weight of the misclassified samples for the next training process, as the weight of each sample can be changed in each cycle and the loss function is closely related to the sample weights, the optimization path is changed correspondingly and each base model may make different predictions as they can converge to different local minimums.
For each sample , we set as the similarity between model and on sample (line 8 of Algorithm 1). Besides, we set as the bias of model on sample (line 9 of Algorithm 1)
| (12) |
| (13) |
For a misclassified sample , we update its weights by (line 10 of Algorithm 1)
| (14) |
Larger means the individual base model has the same opinion with the ensemble model on sample . If sample is mis-classified by , the ensemble model probably cannot classify this sample either, thus we must give more attention on sample and the weight will be increased more. On the contrary, if is small, which means may has better ability to classify the sample , as it’s prediction is less similar to . In this way, it’s better to increase the less aggressively.
Note that the base models of traditional Boosting algorithm only needs to be weak and it is true that we can get a strong ensemble model if we have a large number of weak base learners. However, it’s hard to meet such condition in deep learning as each base model needs a high training cost. So for EDDE, we hope the base models have both high diversity and accuracy. As the sample weights we used for these base models are only to enhance diversity, we just update the weights based on . Due to this operation, the weight of each sample can be greatly changed. Since the loss function is closely related to the sample weights, the optimization path is changed correspondingly and the diversity can be further increased.
At last, we define the weight of each base model as (line 12 of Algorithm 1)
| (15) |
After we get the weight and the similarity of each sample , we can accordingly calculate the weight of each base model. A large means is very similar to , which indicates the model has the same opinion with the ensemble model . Usually, the prediction of the ensemble model is relatively more accurate, thus ’s prediction becomes more important accordingly. In this way, we can increase or decrease more if the is large.
For the prediction process, we average the softmax outputs of each base model with the model weight , and the ensemble model is defined as (line 16 of Algorithm 1)
| (16) |
Previous works have shown that training neural network ensemble through sub-sampled dataset may lead to low generalization accuracy as it reduces the number of unique data items seen by an individual neural network. A neural network has a large number of parameters and it is affected relatively more from this reduction in unique data items than the ensemble of other classifiers such as decision trees or SVMs [32]. Therefore, we use all the training set in each iteration.
To sum up, our method differs from traditional Boosting algorithms in three aspects.
-
•
we use all the training data instead of using the sub-sampling technique in each iteration as the less unique training samples may lead to low bias.
-
•
We train each base models based on the knowledge of the pre-trained one while the traditional Boosting methods train every network from scratch and introduce a high training cost.
-
•
we use a diversity-driven loss function to get each base model, and the weights update we use is totally different from the traditional Boosting methods.
V Experiments
To prove the validity and efficiency of EDDE, we conduct extensive experiments on the task of CV and NLP. We firstly introduce our experimental settings in section V-A and then study the effectiveness of our method EDDE in Section V-B. To clearly show the high efficiency of EDDE, we make an end-to-end comparison with other ensemble methods in Section V-C. In Section V-D, we show how diversity influences the generalization ability of an ensemble model. Besides, we simply analyze the influence of the parameter in Section V-E. At last, to prove the effectiveness of our diversity-driven loss and the knowledge transfer strategy, we make an ablation study in Section V-F. All the programs were implemented in Python using the Keras library111https://github.com/keras-team/keras.
V-A Experimental settings
Datasets
We use the The CIFAR-10 (C10) and CIFAR-100 (C100) datasets [20] for the CV task. Besides, we we also test EDDE in the NLP tasks with the IMDB [41] and MR [42] datasets.
The CIFAR-10 (C10) and CIFAR-100 (C100) datasets consist of 60000 32x32 pixels color images, and consist of 10 and 100 classes respectively. 50,000 images were used for training and another 10,000 ones were used for testing on each dataset. A widely used data augmentation scheme [21] is used before the training process.
Both the IMDB and MR dataset are reviews with one sentence per review, and they have been labeled as positive or negative. For the preprocessing of IMDB, we set the max length of each sentence to 120 and the max features to 5000. Note that the max length means we cut texts after this number of words and max features mean we just use the top max features most common words. As for the MR dataset, we use the same settings in [43].
Base networks
Baselines
To show the improvement of the ensemble learning, we firstly compare our method with a Single Model. Besides, we compared EDDE with BANs [7] as we are both motivated by the idea of Knowledge Distillation and we both use the soft target. To validate the importance of diversity, we compare with Snapshot Ensemble [12] as it introduces low diversity even it can accelerate the training process. Besides, as our method EDDE is a diversity-driven framework for neural networks, we also compare with the diversity-driven ensemble method AdaBoost.NC [17]. Last, we also run the experiments with Bagging [14] and AdaBoost.M1 [45] to validate the limitations of traditional ensemble methods in the field of deep learning.
Protocol
We train these networks with the stochastic gradient descent and set the initial learning rate to 0.1 for ResNet and Text-CNN, and 0.2 for DenseNet. Besides, All methods except Snapshot Ensemble use a standard learning rate schedule that we divide the learning rate by 10 when the training is at 50% and 75% of the total training epochs. For EDDE using ResNet, we set the parameters to 0.1 and to 0.7. As for the DenseNet, and are 0.2 and 0.5. For EDDE in NLP task, we transfer the knowledge of all the convolution layers of Text-CNN to initialize the next base model. For Snapshot Ensemble, we use the same settings as the original paper. The mini-batch we use for the MR, CIFAR and IMDB datasets are 50, 64 and 128 respectively.


Training budget.
For Bagging, AdaBoost.M1, AdaBoost.NC, and BANs, each base model is trained with a budget of 50 epochs for CIFAR dataset and 20 epochs for IMDB dataset. For Snapshot Ensemble on CIFAR dataset, we use the same settings in [12], in which snapshot variants are trained with 4 cycles (50 epochs per cycle) for DenseNets and 10 cycles (40 epochs per cycle) for ResNets. As for the IMDB and MR datasets, snapshot variants are trained with 5 cycles (20 epochs per cycle). For EDDE, we train the first base model with the same settings in Snapshot Ensemble, and each cycle after that is trained with 30 epochs for ResNet, 25 epochs for DenseNet and 10 epochs for Text-CNN.
V-B Effectiveness study
| Model | Method | C10 | C100 |
|---|---|---|---|
| ResNet-32 | Single Model | 92.73% | 69.11% |
| BANs | 92.81% | 71.36% | |
| Bagging | 92.58% | 71.41% | |
| AdaBoost.M1 | 92.22% | 71.17% | |
| AdaBoost.NC | 92.64% | 71.07% | |
| Snapshot | 93.27% | 72.17% | |
| EDDE | 94.11% | 74.38% | |
| DenseNet-40 | Single Model | 92.61% | 71.47% |
| BANs | 93.11% | 72.86% | |
| Bagging | 93.24% | 73.17% | |
| AdaBoost.M1 | 92.87% | 73.42% | |
| AdaBoost.NC | 93.17% | 73.61% | |
| Snapshot | 92.91% | 72.91% | |
| EDDE | 94.39% | 75.02% |
| Model | Method | IMDB | MR |
|---|---|---|---|
| Text-CNN | Single Model | 86.61% | 76.14% |
| BANs | 86.98% | 76.23% | |
| Bagging | 87.14% | 76.51% | |
| AdaBoost.M1 | 86.72% | 76.17% | |
| AdaBoost.NC | 86.87% | 76.26% | |
| Snapshot | 86.91% | 76.43% | |
| EDDE | 87.69% | 76.98% |
To validate the effectiveness of EDDE, we train different ensemble methods on different tasks, and the main results are summarized in Table II and Table III. For CIFAR dataset, the methods in the same group are trained for 200 epochs. EDDE is trained for 50 epochs for the IMDB and MR dataset, and the other methods in the same group are trained for 100 epochs. Note that the results of our method are colored in blue, and the best result for each network/dataset pair is bolded.
For the CV task, the experiments on CIFAR data show that EDDE can always get the highest ensemble accuracy in all cases. Take the result on CIFAR-100 using ResNet-32 for an example, EDDE achieves the accuracy rate of 74.38%, far outperforming the next-best model’s 72.17% under the same training cost. For the NLP task, EDDE only need half time to achieve 87.69% test accuracy in IMDB dataset and 76.98% test accuracy in the MR dataset, which means EDDE is superior the other ensemble methods both in the speed and accuracy. Through the experiments on the CV and NLP tasks, we observe that EDDE is capable of getting a high ensemble accuracy with a limited training budget.
V-C End-to-end comparison
As the most concern of EDDE is to efficiently get a high ensemble accuracy with a limited training budget, it’s necessary to make an end-to-end comparison to other ensemble methods. For EDDE and other baselines, we train each base model with the same network structures and dataset. Therefore, the training time per epoch for each ensemble method is same. Besides, the extra time cost brought by different ensemble method is trivial compared to the training time of deep neural networks. As a result, the training epochs can be treated as the training expense. We compare the ensemble accuracy of each method trained with different epochs in the CV tasks, and the result is shown in Figure 7.
We firstly see that the AdaBoost.M1, AdaBoost.NC and Bagging all have relatively low test accuracy during each period. The main reason is that they train each base model individually on a sub-sampled dataset, thus it’s hard to get enough base models with high accuracy in a short time. For BANs, it also gets a low ensemble accuracy in many cases. That is because it randomly initialized each base model without the prior knowledge and it cannot get high diversity and accuracy at the same time.
As we can see in Figure 7, EDDE gets a higher test accuracy than other methods in all cases. More concretely, from the left picture, we see EDDE achieves the accuracy of 73.67% within only 130 epochs, while the next-best model Snapshot Ensemble needs 400 epochs to achieves 72.98% ensemble accuracy, which means EDDE is more than 3 times faster than the next-best model in this scenario.
Similarly, as shown in the right picture in Figure 7, EDDE always gets higher ensemble accuracy than other methods using DenseNet-40. Because our knowledge transfer method is capable of accelerating the training process and the diversity-driven method can explicitly enhance diversity, EDDE can get the highest efficiency.
| Method | Training epochs | Average accuracy | Ensemble accuracy | Increased accuracy | Diversity |
|---|---|---|---|---|---|
| Snapshot Ensemble | 400 | 68.53% | 72.98% | 4.45% | 0.1322 |
| EDDE | 250 | 68.04% | 75.30% | 7.26% | 0.1702 |
| AdaBoost.NC | 400 | 66.81% | 72.76% | 5.95% | 0.1787 |
V-D Diversity analysis
We run an experiment on CIFAR100 using ResNet-32 and analyze the diversity between their first 8 base models. According to Eq. 3, we compute the pairwise similarity among each base model of Snapshot Ensemble, EDDE, and AdaBoost.NC. The result is shown in Figure 8.
For Snapshot Ensemble, the similarity between two nearby base models is high and it becomes higher when the model is trained longer. That’s because the next model is initialized with the former one, it’s more prone to converge to nearby local minimums during the two nearby training cycle. Besides, if trained longer, the base models becomes more accurate and they have more chance to make similar predictions.
On the contrary, it’s clear to see that the pairwise similarity of EDDE and AdaBoost.NC is smaller than Snapshot Ensemble. To further explore the significance of the diversity, we compute the increased accuracy of each ensemble methods. Besides, we also compute their concrete diversity according to Eq. 7. The experimental results are summarized in Table IV.
As shown in Table IV, the AdaBoost.NC can get the highest diversity of 0.1787. That’s because it trains the base models on different sub-sampled datasets. Besides, it randomly initializes the weights of each base model and then negatively correlates the former neural network by adjusting the sample weights. However, even given 400 training epochs, it gets the lowest average accuracy of 66.81%, which means all the base model cannot converge to a good local minimum given limited time.
As for the Snapshot Ensemble, it gets the highest average accuracy of 68.53% among these three methods since it transfers the knowledge of the pre-trained neural network to accelerate the training process of the current model. Unfortunately, as it transfers all the knowledge without selection, it gets the lowest diversity.
Seen from Table IV, the base models in EDDE can get both high diversity and average accuracy. Accordingly, EDDE gets the highest increased accuracy of 7.26% . Besides, EDDE achieves the 75.30% accuracy only using 250 epochs, while Snapshot Ensemble and AdaBoost.NC cannot get such accuracy even if trained with 400 epochs. Therefore, EDDE is efficient in the ensemble of deep neural networks.
V-E Exploration of hyperparameters
In order to investigate the influences of hyperparameters on EDDE, we vary their values and compare the ensemble accuracy accordingly. EDDE has two hyperparameters, controls the strength of the diversity-driven loss and determines the proportion of knowledge we should transfer from the pre-trained network. As we introduced in Section IV-B, we have proposed an effective method to find the optimal , so the only parameter we should tune in EDDE is . Therefore, we vary the parameter and run the experiment on ResNet-32 using CIFAR 100 dataset. The result is summarized in Table V.
| Method | Parameter | Ensemble accuracy |
|---|---|---|
| EDDE | = 0 | 73.86% |
| = 0.1 | 74.38% | |
| = 0.3 | 74.13% | |
| = 0.5 | 73.72% | |
| = 1 | 72.47% |
For analyzing the influence of , we set to 0, 0.1,0.3,0.5 and 1. We can observe from Table V that EDDE with the setting of 0.1 get the highest accuracy of 74.38% since EDDE can get the most balanced tradeoff between diversity and accuracy in this setting. However, when setting to 0, the ensemble accuracy is decreased to 73.86%. In this situation, our diversity-driven loss function is equal to the normal loss function, and the diversity of EDDE is reduced accordingly. On the contrary, if we set to 1, the ensemble accuracy has a sharp decline. A higher means we negatively correlate the previous soft target more, and it also means we give less attention to the true target. Accordingly, the network cannot converge well with a very high . However, according to Table II, even set to 1, EDDE trained with 200 epochs still outperforms Snapshot Ensemble trained with 400 epochs. Therefore, our method EDDE is robust to the hyperparameters.
V-F Ablation study
In order to show the effectiveness of our diversity-driven loss function and the knowledge transfer strategy, we add the ablation studies to measure their effect respectively.
We firstly train an ensemble model using EDDE without diversity-driven loss function, this strategy is denoted as EDDE (normal loss). Besides, like Snapshot Ensemble, we transfer all the pre-trained knowledge in EDDE, and we name this method EDDE (transfer all). Next, we individually train each base model without knowledge transfer, and this method is denoted as EDDE (transfer None). At last, we also compare EDDE with AdaBoost.NC using transfer learning (initialize each model using the weights of the pre-trained one), we name this method AdaBoost.NC (transfer). All these methods are tested in the CIFAR100 dataset using ResNet-32 and the training budget is 200 epochs for EDDE and 400 epochs for Adaboost.NC . The experimental results are summarized in Table VI.
| Method | Ensemble accuracy | Diversity | Average accuracy |
|---|---|---|---|
| EDDE | 74.38% | 0.1743 | 67.91% |
| EDDE (normal loss) | 73.86% | 0.1682 | 67.97% |
| EDDE (transfer all) | 73.37% | 0.1631 | 68.16% |
| EDDE (transfer none) | 70.78% | 0.1854 | 66.72% |
| AdaBoost.NC (transfer) | 72.64% | 0.1573 | 67.33% |
As shown in Tabel VI, the ensemble accuracy may decrease if we use a normal loss function. Besides, we can get a higher average accuracy of 68.16% if we transfer all the pre-trained knowledge, but the diversity may decrease accordingly. On the contrary, from the result of EDDE (Transfer none), we can get the highest diversity of 0.1854. However, given limited training budget, each base model cannot converge well without the knowledge transfer. As a result, EDDE (Transfer none) gets the lowest average accuracy and ensemble accuracy.
As for the AdaBoost.NC with transfer learning, it can get higher average accuracy compared with the original AdaBoost.NC, but its ensemble accuracy is not as high as EDDE due to its lower diversity and average accuracy. That’s because it trains base models on the sub-sampled datasets and transfers all the previous knowledge without selection.
Among all these methods, EDDE can get the most balanced tradeoff between average accuracy and diversity and it can get the highest ensemble accuracy of 74.38%, thus both the diversity-driven loss and the knowledge transfer are effective in EDDE.
VI Conclusion
Ensemble learning is useful in improving the generalization ability of deep neural networks. However, given limited training budget, current ensemble methods are not efficient as they cannot balance the tradeoff between diversity and accuracy. We proposed EDDE to tackle this problem. To improve diversity, we proposed a new diversity measure and optimize each base model with a diversity-driven loss function. To enhance the training speed and improve the accuracy, we proposed a knowledge transfer method which can efficiently transfer the generic knowledge from the pre-trained model. Last, we adopt a Boosting-based framework to further improve diversity and combine the operations above. Experimental results on the CV and NLP tasks have shown that our method EDDE is efficient in generating multiple neural networks with high diversity and accuracy. Given the same training budget, EDDE can get a more accurate ensemble model compared with the baselines.
VII Acknowledgement
This work is supported by the National Key Research and Development Program of China (No. 2018YFB1004403), NSFC (No. 61832001, 61702015, 61702016, 61572039), and PKU-Tencent joint research Lab.
References
- [1] Ciresan D C, Meier U, Masci J, et al. Flexible, high performance convolutional neural networks for image classification[C]//Twenty-Second International Joint Conference on Artificial Intelligence. 2011.
- [2] Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition[J]. arXiv preprint arXiv:1409.1556, 2014.
- [3] Zhang C, Bengio S, Hardt M, et al. Understanding deep learning requires rethinking generalization[J]. arXiv preprint arXiv:1611.03530, 2016.
- [4] Kieu T, Yang B, Guo C, et al. Outlier detection for time series with recurrent autoencoder ensembles[C]//28th international joint conference on artificial intelligence. 2019.
- [5] Wang S, Zhang N, Wu L, et al. Wind speed forecasting based on the hybrid ensemble empirical mode decomposition and GA-BP neural network method[J]. Renewable Energy, 2016, 94: 629-636.
- [6] Hinton G, Vinyals O, Dean J. Distilling the knowledge in a neural network[J]. arXiv preprint arXiv:1503.02531, 2015.
- [7] Furlanello, T., Lipton, Z. C., Tschannen, M., Itti, L., and Anandkumar, A. Born again neural networks. In Proc.Int.Conf. on Machine Learning (ICML), 2018.
- [8] Dietterich T G. Ensemble methods in machine learning[C]//International workshop on multiple classifier systems. Springer, Berlin, Heidelberg, 2000: 1-15.
- [9] Li Z, Hoiem D. Learning without forgetting[J]. IEEE transactions on pattern analysis and machine intelligence, 2018, 40(12): 2935-2947.
- [10] Zhang W, Jiang J, Shao Y, et al. Snapshot boosting: a fast ensemble framework for deep neural networks[J]. Science China Information Sciences, 2020, 63(1): 1-12.
- [11] Mosca A, Magoulas G D. Deep incremental boosting[J]. arXiv preprint arXiv:1708.03704, 2017.
- [12] G. Huang, Y. Li, G. Pleiss, Z. Liu, J. E. Hopcroft, and K. Q. Weinberger. Snapshot Ensembles: Train 1, get M for free. ICLR submission, 2017.
- [13] I. Loshchilov and F. Hutter, “Sgdr: Stochastic gradient descent with warm restarts,” in ICLR, 2017.
- [14] Breiman L. Stacked regressions[J]. Machine learning, 1996, 24(1): 49-64.
- [15] Polikar R. Ensemble based systems in decision making[J]. IEEE Circuits and systems magazine, 2006, 6(3): 21-45.
- [16] Liu Y, Yao X. Simultaneous training of negatively correlated neural networks in an ensemble[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 1999, 29(6): 716-725.
- [17] Wang S, Chen H, Yao X. Negative correlation learning for classification ensembles[C]//The 2010 International Joint Conference on Neural Networks (IJCNN). IEEE, 2010: 1-8.
- [18] Rokach L. Ensemble-based classifiers[J]. Artificial Intelligence Review, 2010, 33(1-2): 1-39.
- [19] Yosinski J, Clune J, Bengio Y, et al. How transferable are features in deep neural networks?[C]//Advances in neural information processing systems. 2014: 3320-3328.
- [20] Krizhevsky A, Hinton G. Learning multiple layers of features from tiny images[R]. Technical report, University of Toronto, 2009.
- [21] He K, Zhang X, Ren S, et al. Deep residual learning for image recognition[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2016: 770-778.
- [22] Granitto P M, Verdes P F, Ceccatto H A. Neural network ensembles: evaluation of aggregation algorithms[J]. Artificial Intelligence, 2005, 163(2): 139-162.
- [23] Geman S, Bienenstock E, Doursat R. Neural networks and the bias/variance dilemma[J]. Neural computation, 1992, 4(1): 1-58.
- [24] Hoch T. An Ensemble Learning Approach for the Kaggle Taxi Travel Time Prediction Challenge[C]//DC@ PKDD/ECML. 2015.
- [25] Dietterich T G. Ensemble methods in machine learning[C]//International workshop on multiple classifier systems. Springer, Berlin, Heidelberg, 2000: 1-15.
- [26] Naftaly U, Intrator N, Horn D. Optimal ensemble averaging of neural networks[J]. Network: Computation in Neural Systems, 1997, 8(3): 283-296.
- [27] Friedman J, Hastie T, Tibshirani R. The elements of statistical learning[M]. New York: Springer series in statistics, 2001.
- [28] Drucker H, Schapire R, Simard P. Improving performance in neural networks using a boosting algorithm[C]//Advances in neural information processing systems. 1993: 42-49.
- [29] Moghimi M, Belongie S J, Saberian M J, et al. Boosted Convolutional Neural Networks[C]//BMVC. 2016: 24.1-24.13.
- [30] Young S, Abdou T, Bener A. Deep Super Learner: A Deep Ensemble for Classification Problems[C]//Advances in Artificial Intelligence: 31st Canadian Conference on Artificial Intelligence, Canadian AI 2018, Toronto, ON, Canada, May 8–11, 2018, Proceedings 31. Springer International Publishing, 2018: 84-95.
- [31] Ju C, Bibaut A, van der Laan M. The relative performance of ensemble methods with deep convolutional neural networks for image classification[J]. Journal of Applied Statistics, 2018, 45(15): 2800-2818.
- [32] Lee S, Purushwalkam S, Cogswell M, et al. Why M heads are better than one: Training a diverse ensemble of deep networks[J]. arXiv preprint arXiv:1511.06314, 2015.
- [33] Tumer K, Ghosh J. Error correlation and error reduction in ensemble classifiers[J]. Connection science, 1996, 8(3-4): 385-404.
- [34] Liu Y, Yao X. A cooperative ensemble learning system[C]//1998 IEEE International Joint Conference on Neural Networks Proceedings. IEEE World Congress on Computational Intelligence (Cat. No. 98CH36227). IEEE, 1998, 3: 2202-2207.
- [35] Chan Z S H, Kasabov N. A preliminary study on negative correlation learning via correlation-corrected data (nccd)[J]. Neural Processing Letters, 2005, 21(3): 207-214.
- [36] Tang E K, Suganthan P N, Yao X. An analysis of diversity measures[J]. Machine learning, 2006, 65(1): 247-271.
- [37] Rumelhart D E, Hinton G E, Williams R J. Learning internal representations by error propagation[R]. California Univ San Diego La Jolla Inst for Cognitive Science, 1985.
- [38] Wasay A, Liao Y, Idreos S. Rapid Training of Very Large Ensembles of Diverse Neural Networks[J]. arXiv preprint arXiv:1809.04270, 2018.
- [39] Pan S J, Yang Q. A survey on transfer learning[J]. IEEE Transactions on knowledge and data engineering, 2009, 22(10): 1345-1359.
- [40] Seyyedsalehi S Z, Seyyedsalehi S A. A fast and efficient pre-training method based on layer-by-layer maximum discrimination for deep neural networks[J]. Neurocomputing, 2015, 168: 669-680.
- [41] Maas A L, Daly R E, Pham P T, et al. Learning word vectors for sentiment analysis[C]//Proceedings of the 49th annual meeting of the association for computational linguistics: Human language technologies-volume 1. Association for Computational Linguistics, 2011: 142-150.
- [42] Pang B, Lee L. A sentimental education: Sentiment analysis using subjectivity summarization based on minimum cuts[C]//Proceedings of the 42nd annual meeting on Association for Computational Linguistics. Association for Computational Linguistics, 2004: 271.
- [43] Y. Kim. Convolutional neural networks for sentence classification. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), pages 1746–1751, Doha, Qatar, October 2014. Association for Computational Linguistics.
- [44] Huang G, Liu Z, Van Der Maaten L, et al. Densely connected convolutional networks[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2017: 4700-4708.
- [45] Freund Y, Schapire R E. A decision-theoretic generalization of on-line learning and an application to boosting[J]. Journal of computer and system sciences, 1997, 55(1): 119-139.